Increased interstitial loading reduces the effect of microstructural variations in cardiac tissue

Abstract

Electrical propagation in diseased and aging hearts is strongly influenced by structural changes that occur in both the intracellular and interstitial spaces of cardiac tissue; however, very few studies have investigated how interactions between the two spaces affect propagation at the microscale. In this study, we used one-dimensional microstructural computer models of interconnected ventricular myocytes to systematically investigate how increasing the effective interstitial resistivity (ρ_oeff) influences action potential propagation in fibers with variations in intracellular properties such as cell coupling and cell length. Changes in ρ_oeff were incorporated into a monodomain model using a correction to the intracellular properties that was based on bidomain simulations. The results showed that increasing ρ_oeff in poorly coupled one-dimensional fibers alters the distribution of electrical load at the microscale and causes propagation to become more continuous. In the poorly coupled fiber, this continuous state is characterized by decreased gap junction delay, sustained conduction velocity, increased sodium current, reduced maximum upstroke velocity, and increased safety factor. Long, poorly coupled cells experience greater loading effects than short cells and show the greatest initial response to changes in ρ_oeff. In inhomogeneous fibers with adjacent well-coupled and poorly coupled regions, increasing ρ_oeff in the poorly coupled region also reduces source-load mismatch, which delays the onset of conduction block and reduces the dispersion of repolarization at the transition between the two regions. Increasing the ρ_oeff minimizes the effect of cell-to-cell variations and may influence the pattern of activation in critical regimes characterized by low intercellular coupling, microstructural heterogeneity, and reduced or abnormal membrane excitability.

pathological changes in myocardial architecture often create a heterogeneous substrate that supports abnormal electrical rhythms in the heart. In most cases, these architectural changes can be subdivided into two major categories: changes that occur in the intracellular space of the heart and changes that occur in the interstitial (extracellular) space. One of the most widely studied structural changes in the intracellular space involves the gap junction coupling between cells. A number of modeling and experimental studies have shown that changes in gap junction coupling can influence propagation speed, action potential waveshape, and the dynamics of sodium and calcium currents in the heart (16, 29, 33). In particular, lateral decoupling between cells has repeatedly been linked to slow conduction and conduction block, two properties that increase the likelihood of arrhythmia (7, 32).

Variation in myocyte size and shape is another source of heterogeneity in the intracellular space. In normal, healthy hearts, cell length and width can vary widely even among cells that are taken from a single source (5). Using one-dimensional (1-D) discontinuous models, Henriquez and Plonsey (16) have shown that changes in cell length alter features of action potential morphology such as the distribution of maximum upstroke velocity (V_max) along the cell and the time constant of the action potential foot. Experimental and modeling studies by Spach et al. (33) that compared conduction properties in small neonatal myocytes and larger adult myocytes have also shown that propagation speed and action potential waveshape are significantly affected not only by gap junction distribution but also by cell size. Myocyte hypertrophy caused by cardiac diseases such as heart failure and hypertension also increases conduction velocity (CV) and may offset the effects of decreases in intercellular coupling (37). The relative increases in cell length and width and the heterogeneity in cell size vary with the type of cardiomyopathy; however, very few modeling studies have systematically investigated the effect of cell size in conjunction with other microstructural changes that occur in cardiac disease (6, 11, 24).

In recent years, there have been several studies to explore another important but often-overlooked determinant of electrical propagation in the heart: the structure of the interstitial space (4, 9, 26, 33). Cardiac myocytes are surrounded by a heterogeneous interstitial space that contains a wide variety of components including ground substance, blood vessels, connective tissue, and collagen (2, 10). Even in healthy tissue, the electrical properties of the interstitial space vary nonlinearly depending on the size and the composition of the interstitial region. Wide regions of interstitial space that contain porous collagen may have low resistances to current flow, whereas narrow regions of interstitial space that primarily contain basement membrane and dense extracellular matrix proteins may have a very high resistance to current flow (21). Similarly to the intracellular space, changes in interstitial properties such as the resistivity of the space can also influence CV, action potential waveshape, and the dynamics of ionic currents (9, 14, 17).

As the relationship between structural remodeling and abnormal propagation observed in cardiac diseases such as atrial fibrillation has become more evident, several groups have turned their attention toward developing new therapies that reverse or limit the extent of structural remodeling (1, 12, 13). The successful application of these therapies may strongly depend on our fundamental understanding of how combined microscale heterogeneities in both the interstitial and intracellular spaces influence macroscale propagation in the heart (3, 4, 26, 38). In this study, we build upon previous modeling studies that have independently investigated the effects of interstitial and intracellular microstructure to gain a better understanding of the combined effect of these intracellular and interstitial heterogeneities on electrical propagation. Our findings suggest that increasing the effective interstitial resistivity (ρ_oeff) of poorly coupled tissue may actually help to improve conduction in heterogeneous regions of tissue and may promote the spread of abnormal rhythms in the heart.

METHODS

One of the most commonly used structural models of cardiac tissue is the bidomain model, which represents the intracellular and interstitial regions as two overlapping continuous domains. In the classical bidomain, the heterogeneities of the intracellular and interstitial spaces are averaged together and used to assign the bidomain conductivities (14). To study the combined effect of increased interstitial resistivity and microscale heterogeneities such as gap junction coupling and cell size on propagation, we revisited a discrete form of the bidomain model that has been used to look at the effect of discrete gap junctions on extracellular potential distributions (19, 35).

The governing equations for the 1-D discrete bidomain model can be expressed as follows:

$$\frac{\partial }{\partial x}\left(\frac{1}{{\rho }_{\mathrm{ieff}}(x)}\frac{\partial }{\partial x}{\varphi }_{\mathrm{i}}\right)={\beta }^{\prime }{I}_{\mathrm{m}}$$ (1)

$$\frac{\partial }{\partial x}\left(\frac{1}{{\rho }_{\mathrm{oeff}}(x)}\frac{\partial }{\partial x}{\varphi }_{\mathrm{e}}\right)=-{\beta }^{\prime }{I}_{\mathrm{m}}$$ (2)

$$I_{\mathrm{m}}=I_{\mathrm{ion}}+C_{\mathrm{m}}\frac{\partial V_{\mathrm{m}}}{\partial t}-I_{\mathrm{stim}}$$ (3)

where Φ_i is the intracellular potential, Φ_e is the extracellular potential, V_m = Φ_i − Φ_e is the transmembrane potential, I_m is the transmembrane current, ρ_ieff and ρ_oeff are the effective intracellular and interstitial resistivities, β′ is the modified surface-to-volume ratio, I_ion is the ionic current as calculated using the Luo-Rudy dynamic membrane model of guinea pig ventricular myocytes, C_m is the membrane capacitance equal to 1 μF/cm², and I_stim is the intracellular stimulus current (8, 23). ρ_ieff and ρ_oeff are functions of space and are equal to the resistivity of the subcellular region divided by the fraction occupied by the intracellular or interstitial domain: ρ_ieff = ρ_i/f_i and ρ_oeff = ρ_e/f_e, where f_i = 1 − f_e, where f_i and f_e are fractions of cross-sectional area occupied by the intracellular and interstitial space, respectively.

Although this form of the bidomain model is more structurally accurate, the fine discretization needed to create this model is computationally expensive, which makes it difficult to run large numbers of simulations efficiently particularly in multidimensions (20, 22). Previous studies of the classical continuous bidomain have applied the condition of equal anisotropy to reduce the continuous bidomain to an equivalent monodomain model that is less computationally expensive (15). In one dimension, when the ratio of the intracellular to interstitial resistivity along the fiber is equal to a constant, ρ_ieff(x) = kρoeff(x), the governing equation for the equivalent discrete monodomain can be expressed as follows:

$$\left(\frac{k}{1+k}\right)\frac{\partial }{\partial x}\left(\frac{1}{{\rho }_{\mathrm{ieff}}(x)}\frac{\partial }{\partial x}{V}_{\mathrm{m}}\right)={\beta }^{\prime }{I}_{\mathrm{m}}$$ (4)

As ρ_oeff approaches zero, Eq. 4 becomes equivalent to the traditional discrete monodomain equation (29).

In the case of the continuous bidomain, which has no spatial variation in ρ_ieff, the governing equation for the equivalent continuous monodomain (CMD) can be expressed as follows:

$$\frac{1}{{\rho }_{\mathrm{ieff}}+{\rho }_{\mathrm{oeff}}}\frac{{\partial }^2{V}_{\mathrm{m}}}{\partial x^2}={\beta }^{\prime }{I}_{\mathrm{m}}$$ (5)

The approach we used in this study was to approximate a more general form of the equivalent discrete monodomain, which incorporates spatial variations in ρ_ieff and unequal ratios of ρ_ieff and ρ_oeff, with a discrete version of Eq. 5. The governing equation for the approximate discrete monodomain (ADMD) model can be expressed as follows:

$$\frac{\partial }{\partial x}\left(\frac{1}{{\rho }_{\mathrm{ieff}}(x)+{\rho }_{\mathrm{oeff}}(x)}\frac{\partial V_{\mathrm{m}}}{\partial x}\right)={\beta }^{\prime }{I}_{\mathrm{m}}$$ (6)

All of the variables in the monodomain models are defined as in the case of the discrete bidomain.

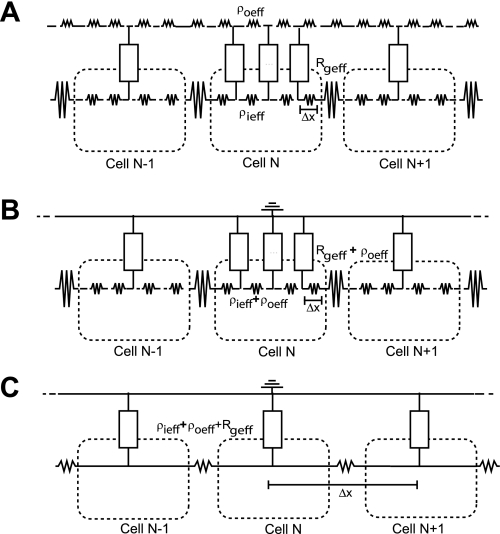
The first goal of this study was to quantitatively compare the 1-D ADMD model with the 1-D discrete bidomain model. Propagation was studied in a discrete 0.5-cm fiber composed of 50 cardiac cells, with no-flux boundary conditions applied to the beginning and the end of the fiber. Each cell had a cell length (L) of 100 μm and a radius (a) of 11 μm and was discretized into 10 elements with a Δx of 10 μm. Within the cell, ρ_i was set to 150 Ω-cm. The elements connecting adjacent cells were modified to incorporate the gap junction resistivity (R_g) that was set uniformly throughout the fiber to a value of 1.5 Ω-cm² (representing a well-coupled fiber) or 100 Ω-cm² (representing a poorly coupled fiber). Effective R_g (R_geff) was calculated as R_g/(f_iΔx). For this portion of the study, only three values of ρ_oeff were tested: 0.5 (nominal value), 2.5, and 10 kΩ-cm. The cable diagrams for the discrete bidomain and ADMD models are shown in Fig. 1, A and B.

Fig. 1.

Cable diagrams for the discrete bidomain model (A), the approximate discrete monodomain (ADMD) model (B), and the approximate continuous monodomain (CMD) model (C) with Δx equal to the length of single cell. ρ_ieff, effective intracellular resistivity; ρ_oeff, effective interstitial resistivity; R_geff, effective gap junction resistivity.

The second goal of the study was to use the ADMD model to systematically investigate the impact of interstitial resistivity as a function of cell coupling and cell length. Propagation was studied in the following discrete fibers: 1) fiber with normal cells (0.5-cm fiber composed of 50 cells with L = 100 μm), 2) fiber with short cells (0.5-cm fiber composed of 100 cells with L = 50 μm), 3) fiber with long cells (0.6-cm fiber composed of 40 cells with each L = 150 μm), and 4) fiber with cells of various lengths (0.5-cm fiber composed of 47 cells with a uniform distribution in length ranging from 50 to 100 μm, with an average length of 100 μm). Each cell had a radius of 11 μm and was discretized into elements of a length of 2 μm (Δx). The R_g for each cell in a given fiber was set to a value between 1.5 and 100 Ω-cm². The composition and size of the extracellular space may vary widely, particularly in the case of cardiac disease. With this in mind, ρ_oeff values between 0 and 25 kΩ-cm were tested to capture the response of the fiber under both normal conditions as well as extreme conditions that may only occur sporadically throughout the heart.

Previous studies have shown that setting the discretization element (Δx) of the continuous fiber equal to the length of a single cell gives a good approximation to the discontinuous propagation observed in real cardiac tissue (29). To test the accuracy of continuous models when both the intracellular and interstitial resistivities are increasing, the CV measured using the ADMD model was also compared with the value measured using the highly discretized and coarsely discretized equivalent continuous models. The cellular resistivity used in the continuous models was calculated by lumping together the ρ_ieff, R_g, and ρ_ieff from the ADMD model. An example of the equivalent CMD model is shown in Fig. 1C.

The third goal of the study was to investigate action potential propagation in inhomogeneous 1-D fibers that included abrupt changes in both intracellular and interstitial structure at a size scale larger than a single cell. As shown in Fig. 2, heterogeneity was introduced into the intracellular space by uniformly increasing the R_g of the poorly coupled region of the inhomogeneous fiber [R_g(PC)] in the first half of the fiber. Heterogeneity was also introduced into the interstitial space by increasing the ρ_oeff of the first half of the fiber to a value between 0.5 and 25 kΩ-cm. In the second half of the fiber, all properties were set to normal values (ρ_i = 150 Ω-cm, R_g = 1.5 Ω-cm², and ρ_oeff = 0.5 Ω-cm). The cell length (L = 100 μm) and cell diameter (a = 11 μm) were kept constant throughout the fiber. Measurements were taken for different combinations of ρ_oeff and R_g.

Fig. 2.

Representation of the inhomogeneous fiber. The first half of the fiber (cells 1–30; gray) is poorly coupled (R_g = 60–70 Ω-cm) and the second half of the fiber (white) is well coupled [gap junction resistivity (R_g) = 1.5 Ω-cm]. ρ_oeff is varied between 0.5 and 2.5 kΩ-cm in the first half of the fiber and kept constant at 0.5 kΩ-cm in the second half of the fiber. R_g(PC), R_g of the poorly coupled region of the inhomogeneous fiber; R_g(WC), R_g of the well-coupled region of the inhomogeneous fiber.

A single cell (Luo-Rudy dynamic model) was paced to a steady state at a basic cycle length of 1 s. The steady-state value of each state variable was then applied to each cell along the cable and served as the initial conditions. In all of the simulations, action potentials were initiated by stimulating the fiber at the two leftmost nodes using a single stimulus that was approximately two times threshold. CVs were computed based on measurements taken at x = 0.20 cm and x = 0.40 cm. Intracellular delays were computed by measuring the difference between the time the first node in the 41st cell reached −60 mV and the time the last node in the 41st cell reached −60 mV. Gap junction delay was measured as the difference between the time that the last node in 41th cell reached −60 mV and the first node in the 42st cell reached −60 mV. Maximum upstroke velocities were measured at the center of cell 21. The stimulus and boundary effects in the discontinuous fiber during depolarization were negligible at distances > 0.10 cm from the edges of the fiber. Consistent with the approach used by Shaw and Rudy (29), the amount of sodium charge generated during excitation was computed by summing the sodium current during the time interval defined by the maximum upstrokes of two neighboring cells. Safety factor (SF) was also measured using the method of Shaw and Rudy (29). A semi-implicit scheme with a conjugate gradient solver was used to solve the system of equations. The time step was kept constant at 2 μs, and output data were recorded every 10 μs. All simulations used the CardioWave software platform (25).

RESULTS

Comparison of the discrete bidomain model and the ADMD model.

The CVs and maximum upstroke velocities measured in well-coupled (R_g = 1.5 Ω-cm²) and poorly coupled (R_g = 100 Ω-cm²) ADMD fibers with ρ_oeff equal to 0.5, 2.5, and 10 kΩ-cm were compared with values obtained using the discrete bidomain model. In the well-coupled fiber, the CVs and maximum upstroke velocities measured using the ADMD model were within 1% of the values obtained using the discrete bidomain model. In the poorly coupled fiber, the percent difference between the maximum upstroke values remained below 1%; however, the percent difference between the CVs measured in the ADMD model and discrete bidomain models increased to 5%. As shown in Tables 1 and 2, the percent difference between the ADMD model and the discrete bidomain models for a fiber with a given level of coupling remained essentially the same as ρ_oeff increased. Because of the relatively small difference between the ADMD model and the discrete bidomain, the consistency in the percent error for a given level of coupling, and the speed of computation, the ADMD model was used throughout this study to investigate the effect of increased ρ_oeff on action potential propagation in both well-coupled and poorly coupled fibers.

Table 1.

Comparison of CVs measured in the ADMD and the discrete BD model

Rg,, Ω-cm2	1.5 (Well Coupled)			100 (Poorly Coupled)
ρoeff, kΩ-cm	0.5	2.5	10	0.5	2.5	10
BD:CV, cm/s	36.01	18.83	9.68	5.44	5.13	5.07
ADMD:CV, cm/s	35.71	18.66	9.60	5.18	4.86	4.82
%Difference	0.83	0.90	0.83	4.8	5.3	4.9

CV, conduction velocities; ADMD, approximate discrete monodomain model; BD, bidomain model; R_g, gap junction resistivity; ρ_oeff, effective interstitial resistivity.

Table 2.

Comparison of V_max values measured in the ADMD model and the discrete BD model

Rg, Ω-cm2	1.5 (Well Coupled)			100 (Poorly Coupled)
ρoeff, kΩ-cm	0.5	2.5	10	0.5	2.5	10
BD:Vmax, V/s	221	214	216	347	308	238
ADMD:Vmax, V/s	219	212	214	344	309	238
%Difference	0.90	0.93	0.93	0.86	0.30	0

V_max, maximum upstroke velocity.

Intracellular delay and gap junction delay.

To determine the effect of increased ρ_oeff on electrical loading at the microscale, we measured both the intracellular delay (within the cell) and the gap junction delay (between cells) in well-coupled and poorly coupled fibers with ρ_oeff ranging from 0 to 25 kΩ-cm.

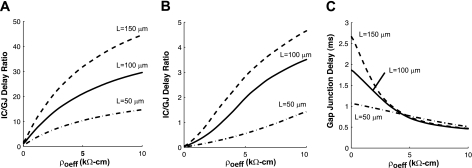
As shown in Fig. 3, A and B, increasing ρ_oeff caused the ratio of intracellular delay to gap junction delay (IC/GJ delay) to increase. In the well-coupled fiber, increasing ρ_oeff from 0 to 2.5 to 10 kΩ-cm caused the ratio to increase 30-fold. The largest IC/GJ delay was observed in long cells. In the poorly coupled fiber, the increase in the IC/GJ delay was much more dependent on the length of the cells. Long cells showed the steepest initial increase in the IC/GJ delay as ρ_oeff was increased from 0 to 2.5 to 10 kΩ-cm, but the overall increase in the IC/GJ delay in long cells was only 100-fold compared with 120-fold in shorter cells.

Fig. 3.

The ratio of intracellular to gap junction (IC/GJ) delay as a function of ρ_oeff in well-coupled fibers (A) and poorly coupled fibers (B) composed of cells of different lengths (L). C: gap junction delay as a function of ρ_oeff in poorly coupled fibers composed of cells of different lengths.

Increases in ρ_oeff were associated with not only an increase in intracellular delay but also a decrease in the gap junction delay, which also contributed to the increase in the IC/GJ delay as shown in Fig. 3, B and C, for the poorly coupled fiber. In the poorly coupled fibers with ρ_oeff = 0 kΩ-cm, the gap junction delay measured in the fibers with long cells was 150% larger than the gap junction delay measured in the fiber with short cells. As ρ_oeff increased, the gap junction delay decreased most rapidly in poorly coupled fibers composed of long cells. Increasing ρ_oeff from 0 to 2.5 kΩ-cm caused a 6% decrease in gap junction delay in fibers with short cells (L = 50 μm) but a 52% decrease in gap junction delay in fibers with long cells (L = 150 μm). At ρ_oeff = 10 kΩ-cm, the gap junction delays measured in fibers of all cell sizes were within 10% of each other.

Conduction velocity.

The changes in the intracellular and gap junction delays with changes in ρ_oeff manifest themselves macroscopically as changes in the CV. Uniformly increasing ρ_oeff in the well-coupled fiber (R_g = 1.5 Ω-cm², and L = 100 μm) from 0 to 2.5 to 10 kΩ-cm caused CV to decrease from 55.6 to 18.3 to 9.5 cm/s, an overall decrease of 83%. This decrease in CV followed the well-known relationship observed in highly discretized continuous fibers (18), $\theta =\sqrt{K/R}$, where K is a constant and R is the axial resistivity. In contrast, increasing ρ_oeff in the poorly coupled fiber caused the macroscopic CV to decrease more gradually and deviate from the square root relationship. When R_g was set equal to 100 Ω-cm², increasing ρ_oeff from 0 to 2.5 to 10 kΩ-cm caused CV to decrease slightly from 5.2 to 4.8 to 4.7 cm/s, a decrease of only 10%.

In this study, additional simulations performed in fibers composed of long cells or short cells showed that fibers composed of long, poorly coupled cells (R_g = 100 Ω-cm²) had higher CVs and slower decreases in CV as ρ_oeff increased. Increasing ρ_oeff from 0 to 10 kΩ-cm caused a 14% decrease in CV in fibers with short cells (L = 50 μm) but a 6% increase in CV in fibers with long cells (L = 150 μm). In the long, poorly coupled fiber, CV reached a plateau and increased slightly between ρ_oeff = 5 kΩ-cm and ρ_oeff = 10 kΩ-cm.

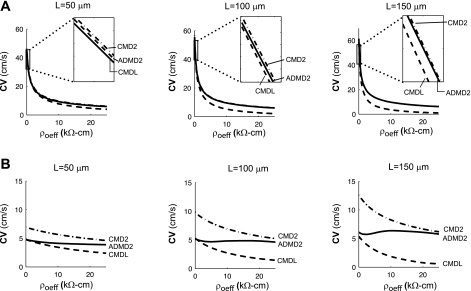
The CVs measured in the ADMD fibers were compared with the CVs measured in a highly discretized (ACMD2) continuous fiber and a coarsely discretized continuous fiber (ACMDL). As shown in Fig. 4A, the well-coupled fiber can be accurately represented using a continuous fiber. This is consistent with previous studies which have shown that the differences measured between the well-coupled discontinuous and highly discretized continuous fibers are minor (29). In the poorly coupled fiber, however, large differences in the resistivity of adjacent elements cause pronounced loading effects that are large enough to reduce the macroscopic CV to a much smaller value than predicted using an equivalent highly discretized continuous fiber (16, 31). When R_g = 100 Ω-cm and ρ_oeff = 0.5 kΩ-cm, the CV measured in the discrete fiber was almost 50% smaller than the CV obtained using the highly discretized continuous fiber. This issue is often addressed in computational studies by modeling poorly coupled tissue with a fiber that has a discretization length equal to the length of a single cell (∼100 μm) (29); however, as shown in Fig. 4B, this approximation becomes less accurate as cell length increases and as ρ_oeff increases. A detailed comparison of CV, intracellular delay, and gap junction delay in ADMD fibers composed of cells of different lengths is given in Table 3.

Fig. 4.

Plots of conduction velocity (CV) as a function of ρ_oeff for well-coupled (A) and poorly coupled (B) fibers composed of cells of length L. In each graph, 3 different equivalent models are shown: CMD2, CMD with Δx = 2 μm; ADMD2, ADMD with Δx = 2 μm; and CMDL, CMD with Δx = L.

Table 3.

IC delay, GJ delay, and CV in ADMD fibers of composed of cells of different lengths

Rg (1.5 Ω-cm)				Rg (100 Ω-cm)
ρoeff, kΩ-cm	IC delay, ms	GJ delay, ms	CV, cm/s	ρoeff, kΩ-cm	IC delay, ms	GJ delay, ms	CV, cm/s
L = 50 μm
0	0.0373	0.0734	45.14	0	0.0127	1.0676	4.63
0.5	0.1036	0.0542	31.69	0.5	0.0510	1.0427	4.57
2.5	0.2471	0.0374	17.57	2.5	0.1147	0.9995	4.37
10	0.5051	0.0344	9.27	10	0.7357	0.5164	3.99
L = 100 μm
0	0.0912	0.0885	55.64	0	0.0540	1.8672	5.20
0.5	0.2257	0.0586	35.18	0.5	0.2159	1.7498	5.08
2.5	0.5067	0.0377	18.36	2.5	0.8898	1.2027	4.78
10	1.0168	0.0344	9.51	10	1.6136	0.4602	4.73
L = 150 μm
0	0.1503	0.0954	61.05	0	0.1252	2.6723	5.35
0.5	0.3496	0.0602	33.72	0.5	0.4973	2.3903	5.19
2.5	0.7666	0.0375	18.65	2.5	1.7178	1.2845	4.99
10	1.5284	0.0343	9.60	10	2.1848	0.4695	5.65

IC delay, intracellular delay; GJ delay, gap junction delay; L, length.

Maximum upstroke velocity.

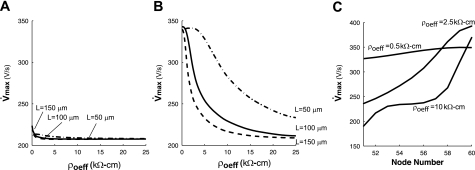
In classical discrete fibers, changes in the gap resistance alter the rate of rise of the action potential upstroke (29). Increases in ρ_oeff were also expected to modulate the action potential shape in both well- and poorly coupled fibers. Figure 5, A and B, shows that increases in ρ_oeff led to an overall decrease in the V_max measured at the center of each cell in the ADMD model. The V_max in both the well-coupled and poorly coupled ADMD fiber approached 207 V/s, the value measured in the highly discretized CMD2 fiber.

Fig. 5.

Maximum upstroke velocity at cell center as a function of ρ_oeff in well-coupled (A) and poorly coupled (B) fibers composed of cells of different lengths (L). C: profile of maximum upstroke velocity within a single poorly coupled cell with L = 100 μm as a function of ρ_oeff.

The intracellular variation of the V_max in the poorly coupled cell also changed as ρ_oeff increased (Fig. 5C). At normal values of ρ_oeff, the variation of V_max across the cell was ∼30 V/s. As ρ_oeff increased, V_max measured at the center of the cell decreased as noted above; however, V_max at the beginning of the cell decreased, whereas V_max at the end of the cell increased, which increased the variation in V_max across the cell to a maximum of 188 V/s. As ρ_oeff increased further, V_max across the entire cell eventually approached 207 V/s.

The change in upstroke velocity with increasing ρ_oeff depended on the length of the cell. Increasing ρ_oeff from 0 to 2.5 kΩ-cm caused a 1% increase in V_max in fibers with short cells (L = 50 μm) but a 25% decrease in V_max in fibers with long cells (L = 150 μm). In fibers composed of cells with varying lengths ranging from 50 to 100 μm, increasing ρ_oeff from 0.5 to 2.5 kΩ-cm decreased the mean V_max across the fiber from 339 ± 12 to 297 ± 50 V/s, a 12% decrease in the mean and a fourfold increase in the standard deviation. As ρ_oeff was increased further to 25 kΩ-cm, the mean V_max and standard deviation decreased to 224 ± 35 V/s.

Maximum sodium current.

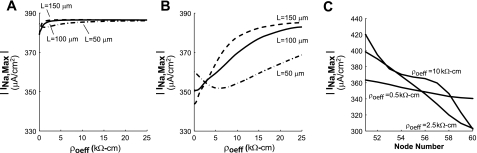
Simulations were also performed to investigate the effect of increased ρ_oeff on maximum sodium current (I_Na,max) in well-coupled and poorly coupled fibers. As shown in Fig. 6A, increasing ρ_oeff from 0 to 10 kΩ-cm in the well-coupled fiber caused I_Na,max to increase slightly from 380 to 386 μA/cm². Increasing ρ_oeff from 0 to 10 kΩ-cm in the poorly coupled fiber caused I_Na,max to increase from 351 to 386 μA/cm², an increase of 10%.

Fig. 6.

Maximum sodium current (I_Na,max) as a function of ρ_oeff in well-coupled (A) and poorly coupled (B) fibers composed of cells of different lengths (L). C: profile of I_Na,max within a single poorly coupled cell with L = 100 μm as a function of ρ_oeff.

The intracellular variation of I_Na,max in the poorly coupled cell also changed as ρ_oeff increased (Fig. 6C). At normal values of ρ_oeff, the variation in I_Na,max across the cell was ∼33 μA/cm². As ρ_oeff increased, I_Na,max measured at the center of the cell increased as noted above; however, I_Na,max at the beginning of the cell decreased, whereas I_Na,max at the end of the cell increased, which increased the variation in I_Na,max across the cell to a maximum of 120 μA /cm². As ρ_oeff increased further, the variation in I_Na,max across the cell gradually decreased to 0 μA/cm².

Note that as shown in Fig. 6B, the poorly coupled fiber with long cells had the lowest initial I_Na,max but showed the steepest increase in I_Na,max as ρ_oeff increased. In poorly coupled fibers composed of cells with varying lengths ranging from 50 to 150 μm, increasing ρ_oeff from 0.5 to 2.5 kΩ-cm did not significantly change the mean I_Na,max across the fiber (350 μA/cm² vs. 354 μA/cm² respectively) but increased the standard deviation in I_Na,max from 9 to 30 μA/cm², a threefold increase. As ρ_oeff was increased further, the mean I_Na,max increased by as much as 6%, and the standard deviation in I_Na,max gradually began to decrease. Short cells showed a delayed response to changes in ρ_oeff which led to a slight reduction in the average I_Na,max measured at ρ_oeff = 25 kΩ-cm in fibers with average cell length of 100 μm (I_Na,max = 378.0 μA/cm²) compared with fibers in which each cell was exactly 100 μm long (I_Na,max = 386.0 μA/cm²).

Safety factor.

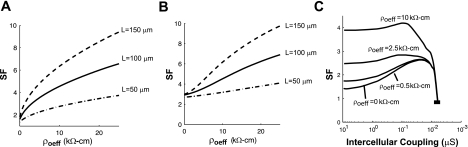
The SF for conduction is determined by a number of factors including the membrane excitability and gap junction coupling (29). Simulations were performed to determine how other structural parameters such as ρ_oeff and cell length influence SF. In the well-coupled fiber, SF increased twofold from 1.61 to 4.55 as ρ_oeff increased from 0 to 10 kΩ-cm. In the poorly coupled fiber, SF increased from 2.92 to 4.52 as the ρ_oeff increased from 0.50 to 10 kΩ-cm. Figure 7, A and B, shows SF as a function of ρ_oeff for well-coupled and poorly coupled fibers.

Fig. 7.

Safety factor (SF) as a function of ρ_oeff measured in well-coupled fibers (A) and poorly coupled fibers (B). C: SF measured as a function of both gap junction coupling and ρ_oeff.

Figure 7C is an alternate view of SF as a function of gap junction conductivity (g_j) for ρ_oeff = 0, 0.5, 2.5, and 10 kΩ-cm in fibers composed of cells with L = 100 μm. Similar to studies by Shaw and Rudy (29) which investigated SF in the ρ_oeff = 0 case, we found that that SF displayed biphasic behavior as g_j decreased. Increasing ρ_oeff caused an upward shift and a flattening of the SF versus the g_j curve for all levels of coupling > 0.0013 μC (300 Ω-cm²). The effect of ρ_oeff on SF was greatest in well-coupled cells; increasing ρ_oeff did not influence SF in fibers with g_j values < 0.0013 μS (R_g > 300 Ω-cm²) and did not prevent conduction block at g_j = 0.0061 μS (R_g = 621 Ω-cm²).

Corresponding simulations performed in fibers composed of long cells and short cells showed that fibers with long cells had a much a higher SF than fibers with short cells. As shown in Fig. 7, A and B, the difference in SF between long cells and short cells increased as ρ_oeff increased.

One-dimensional heterogeneous fiber.

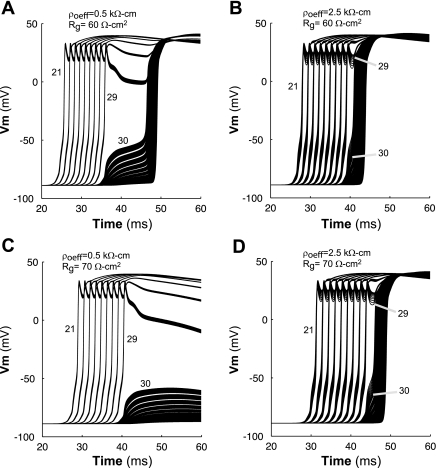
Several studies have shown that conduction can slow and eventually fail because of loading mismatches when a wavefront conducts from a poorly coupled region to a well-coupled region (36). Simulations were performed to investigate whether increasing ρ_oeff could also influence the conditions for conduction block in a fiber with macroscopic heterogeneities in coupling. When ρ_oeff was set to a normal value of 0.5 kΩ-cm throughout the fiber, a long conduction delay and eventually conduction block occurred at the transition from the poorly coupled region to the well-coupled region. As shown in Fig. 8, A and C, a transition delay occurred when R_g of the first half of the fiber [R_g(PC)] was increased from 1.5 to 60 Ω-cm, and conduction block occurred when R_g(PC) was further increased to 70 Ω-cm. Wang and Rudy (36) obtained a similar result in an earlier modeling study in which they used a traditional monodomain model to look at the effect of inhomogeneous coupling on action potential propagation.

Fig. 8.

Conduction along inhomogeneous fibers with different combinations of R_g and ρ_oeff. A: conduction delay when R_g(PC) in the first half of the fiber was increased from to 1.5 to 60 Ω-cm. B: reduced conduction delay when ρ_oeff was also increased from 0.50 to 2.5 kΩ-cm. C: conduction block when R_g(PC) was increased from to 1.5 to 70 Ω-cm. D: restored conduction when ρ_oeff was also increased from 0.50 to 2.5 kΩ-cm. The numbers shown (21, 29, and 30) indicate the cell number. V_m, membrane voltage.

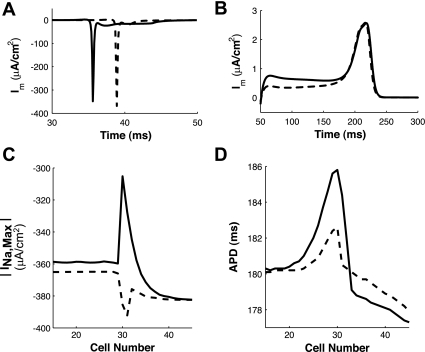
When ρ_oeff of the fiber with R_g(PC) = 60 Ω-cm was increased from 0.50 to 2.5 kΩ-cm as shown in Fig. 8, A and B, the conduction delay at the transition decreased from 1.4 to 0.10 ms. When ρ_oeff of the poorly coupled fiber with R_g(PC) = 70 Ω-cm was increased from 0.50 to 2.5 kΩ-cm as shown in Fig. 8, C and D, conduction was restored along the fiber. The improvement in conduction is due in large part to the increase in the sodium current as ρ_oeff was increased within the poorly coupled region (Fig. 9, A and C).

Fig. 9.

Membrane current (I_m) was measured at cell 29 in the inhomogeneous fiber with R_g(PC) = 60 Ωcm during depolarization (A) and repolarization (B). I_Na,max (C) and action potential duration (APD; D) was measured along the inhomogeneous fiber. Solid lines, ρ_oeff = 0.5 kΩ-cm; dashed lines, ρ_oeff = 2.5 kΩ-cm.

While it has been shown that increases in load caused by heterogeneous coupling can lead to an increased dispersion of repolarization at the boundary between the poorly coupled and well-coupled regions (30, 34), increasing ρ_oeff reduces the loading current during repolarization, thus reducing the dispersion of repolarization at the boundary between the poorly coupled and well-coupled region (Fig. 9, B and D).

DISCUSSION

Previous studies on the effect of cardiac structure on propagation have focused primarily on either the effect of poor coupling or on the effect of a restricted extracellular space (27, 29). This study suggests that the combination of poor coupling and increased ρ_oeff (caused by changes in interstitial volume or inherent material properties) may lead to paradoxical loading effects that enable slower, more continuous propagation at both the microscale and macroscale levels.

In the poorly coupled fiber, the large value of the gap junction resistance combined with source-load mismatch between the intracellular and the gap junction regions leads to large conduction delays between cells; to a certain extent, however, the large value of the gap junction resistance also helps to isolate the cells and protect them from the loading effects of neighboring cells. Increases in ρ_oeff increase the ratio of intracellular to gap junction resistivity, which initially increases loading effects but also reduces the additional charging delay caused by the mismatch between the gap junction resistance and the intracellular resistance. Long, poorly coupled cells experience greater loading effects at the cell boundaries than short cells because the gap junction has a lower relative contribution to the overall resistance of the cell and does not compensate for the source-load mismatch at the boundaries of the cell (16, 33).

These microscale changes in source-load mismatch caused by an increased ρ_oeff also affect macroscale measurements of CV, V_max, I_Na,max, and SF in poorly coupled tissue.

Conduction velocity.

As expected based on previous studies (16, 28, 33) of the effect of a restricted extracellular space, this study showed that increasing the ρ_oeff in well-coupled tissue slows the CV of the fiber. In the poorly coupled case, the interplay between the two factors influencing CV (overall increase in axial resistivity and reduced variations in spatial loading) led to paradoxical effects at the macroscale such as sustained or increased CV. This flattening of CV in response to increased extracellular resistivity is consistent with the findings of Cabo and Boyden (4). Because longer cells experience increased loading effects compared with shorter cells, they also have the most pronounced response to decreases in source-load mismatch as ρ_oeff increases. This suggests that increased ρ_oeff in anisotropic, multidimensional models may preferentially affect longitudinal rather than transverse conduction because the length of cells is much larger than the width. It is also important to note that as ρ_oeff in the poorly coupled fiber increases, neither continuous models with very small discretization lengths nor a continuous model with a discretization length equal to the length of a single cell accurately captures the behavior of the fiber.

V_max and I_Na,max.

As ρ_oeff increased, the V_max measured at the center of the cell decreased, whereas the available sodium current increased. This is in contrast to previous studies by Shaw and Rudy (29) that have shown a biphasic increase in V_max and a decrease in available sodium current as the axial resistivity of fiber increases.

In the study by Shaw and Rudy (29), the axial resistivity is increased by increasing the R_g and the fiber is modeled by lumping the intracellular and the gap junction resistivity into a single element with a Δx = 100 μm (the length of a single cell) (29). The increase in V_max was attributed to an increased intracellular confinement of sodium current-decreased load because of the large R_g between adjacent cells (IC/GJ delay < 1). This confinement of sodium current also reduces the variation of V_max across the cell. The decrease in sodium current observed in the Shaw and Rudy study as R_g increased was attributed to a dynamic inactivation of sodium channels during the long cell-to-cell delay.

In our study, the intracellular and gap junction resistivity are separated into discrete elements, and the axial resistivity is increased not only by increasing the R_g but also by increasing ρ_oeff in both the intracellular and gap junction regions of the cell. The increase in ρ_oeff increases the ratio of the intracellular resistivity to R_g, which increases the load from adjacent cells and the variation in V_max and I_Na,max at the boundaries of each cell. Because the center of the cell is more isolated from the changes in load at the boundaries of the cell, both the measured value and the variation of V_max measured in the center of the cells decreases as ρ_oeff increases.

In fibers with large ρ_oeff, where the interstitial space is the dominant source of resistance in both the intracellular region and the gap region, the variation in V_max and I_Na,max across the cell becomes very small and approaches that observed in a highly discretized continuous fiber. Uniform, highly discretized continuous fibers do not show any spatial changes in V_max or I_Na,max as the axial resistance changes (29). In an actual cardiac fiber, other factors that limit the amount of sodium channels in a given region may contribute to sodium channel inactivation as ρ_oeff increases.

Increased SF.

As ρ_oeff increased, SF also increased (for R_g < 120 Ω-cm²), whereas V_max decreased. This is in contrast to the case of the discrete fiber, where the increased axial resistivity is associated with the increased SF and the increased V_max (29). This increase in SF is primarily due to the increase in I_Na,max and the increase in current flowing into the cell from neighboring cells. For R_g values > 120 Ω-cm², increased ρ_oeff can no longer completely offset the sodium inactivation caused by slow cell-to-cell propagation, and, consequently, SF decreases.

Just as microscale variations in the intracellular and R_g increase the likelihood of slow conduction and conduction block, mismatches in loading between well-coupled and poorly coupled regions of tissue at the macroscale also contribute to slow conduction and conduction block in cardiac tissue. As shown in Figs. 8 and 9, increasing ρ_oeff in poorly coupled regions of tissue homogenizes variations caused by structural heterogeneity, reduces loading effects, and helps to delay the onset of conduction block. In diseased tissue characterized by reduced or abnormal membrane excitability, regional increases in ρ_oeff may also enable abnormal beats that are confined to a small, poorly coupled region of tissue to escape and activate the surrounding tissue.

Although the 1-D model used in this study is a very simple one and does not fully capture the complexity of propagation in the heart, it is nevertheless useful for understanding basic mechanisms of propagation and conduction failure. One of the main reasons for using the monodomain model in which the intracellular properties were modified to account for the interstitial space was to eventually extend to larger two-dimensional models of cardiac tissue where computation time will be more of an issue. The validity of the approach, however, will need to be tested, as was done here, over a range of coupling resistances (14, 15). In two dimensions, it will be possible to investigate the combined effect of interstitial and intracellular properties on the genesis of focal triggers and microreentrant activity.

GRANTS

This research was supported by National Heart, Lung, and Blood Institute Grant HL-093711-01A2 (to C. S. Henriquez).

DISCLOSURES

This research was partially supported by a United Negro College Fund/Merck Graduate Dissertation Fellowship (to M. L. Hubbard).