Improving solid to hollow core transmission for integrated ARROW waveguides

Abstract

Optical sensing platforms based on anti-resonant reflecting optical waveguides (ARROWs) with hollow cores have been used for bioanalysis and atomic spectroscopy. These integrated platforms require that hollow waveguides interface with standard solid waveguides on the substrate to couple light into and out of test media. Previous designs required light at these interfaces to pass through the anti-resonant layers. We present a new ARROW design which coats the top and sides of the hollow core with only SiO₂, allowing for high interface transmission between solid and hollow waveguides. The improvement in interface transmission with this design is demonstrated experimentally and increases from 35% to 79%. Given these parameters, higher optical throughputs are possible using single SiO₂ coatings when hollow waveguides are shorter than 5.8 mm.

1. Introduction

Hollow waveguides are interesting in the field of integrated optics because they allow for light guiding in low index media. Because light guiding does not rely on total internal reflection, hollow waveguides can be filled with water (n=1.33) or air (n=1.0), expanding the possibilities of studies in chemistry, biology, and physics. Some of the applications for which hollow waveguides are best suited include spectroscopy and labs-on-a-chip. Hollow waveguides have been created using Teflon AF [1, 2], nanoporous waveguides [3], photonic crystals [4, 5], and Bragg waveguides [6]. However, all of these approaches present difficulties to planar integration based on standard silicon processing, which is appealing because of lower fabrication costs.

Anti-resonant reflecting optical waveguides (ARROWs) were recently introduced as an attractive approach to realizing hollow waveguides [7, 8]. Solid-core ARROWs were first demonstrated by Duguay and are made by surrounding a guiding core with layers of different refractive indexes and thicknesses determined by the anti-resonance condition [9].

We fabricate hollow ARROW waveguides by surrounding a sacrificial core with ARROW layers of silicon nitride (SiN) and silicon dioxide (SiO₂), and all steps are based on standard silicon processing techniques [10]. We have previously demonstrated ARROW based sensing platforms, such as the one shown in Fig. 1, used for single particle and molecule detection, manipulation, and analysis in sub-picoliter volumes [11].

Fig. 1.

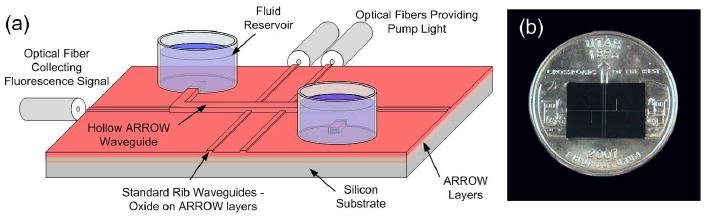
(a) ARROW based platform for sensing applications. (b) Actual device.

In order to make larger-scale integrated networks of hollow ARROW waveguides for labs-on-a-chip, the total optical throughput from one edge of the chip to the other must be improved. In this paper, we present a new ARROW design which simplifies design and fabrication, resulting in consistently high optical transmission. This paper will discuss the design, fabrication, and experimentally determined loss of this new design.

2. Transmission through ARROW based chips

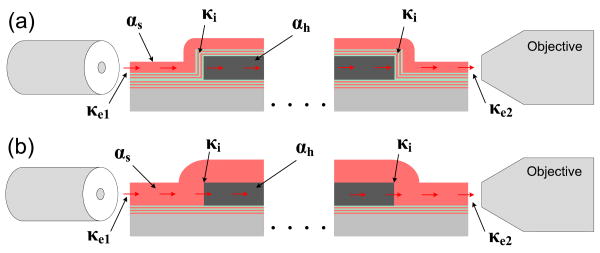
One metric to characterize ARROW based chips is edge to edge throughput, T. Transmission through an ARROW based chip is determined by several loss mechanisms, as shown in Fig. 2(a). First, light from an optical fiber must be coupled into a standard solid waveguide at the edge of the chip. The modes in the round core of the fiber do not perfectly match the modes supported by the solid waveguide, and the edge coupling efficiency, κ_e1, accounts for this.

Fig. 2.

Transmission through ARROW based chips with associated losses and efficiencies (a) for ARROWs and (b) for SOC ARROWs.

The second loss mechanism is the propagation loss in the solid-core waveguide, α_s. Additional loss occurs at the interface between solid and hollow waveguides, quantified by the interface coupling efficiency, κ_i. Finally, the hollow-core waveguide has its own propagation loss, α_h. For edge-to-edge throughput, the hollow-to-solid interface loss, the solid-core loss, and the coupling loss on the far side of the chip, κ_e2, must also be included. Since an objective is used to collect the output, κ_e2 ≈ 0.96 for a good-quality facet. The total throughput is given by Eq. (1) where l_s and l_h are the total lengths of the solid- and hollow-core waveguides, respectively.

$$T={\kappa }_{e1}{e}^{-{\alpha }_s{l}_s}{\kappa }_i{e}^{-{\alpha }_h{l}_h}{\kappa }_i{\kappa }_{e2}$$ (1)

We attribute α_s to material absorption and light scattering due to waveguide roughness, and κ_e1 depends primarily on cleaved facet quality and mode mismatch. In terms of waveguide design, the most promising areas for increasing throughput are reducing α_h and increasing κ_i. Design variations to reduce α_h have been discussed previously [12]. In theory, design optimization is also possible to create solid-to-hollow interfaces with κ_i ≈ 1 [13]. In practice, however, κ_i has been much lower for several reasons. First, it is difficult to achieve perfect mode coupling because of mode mismatch. Horizontal alignment of the solid and hollow cores is achieved through lithography and is limited by alignment tolerances of approximately 1 μm. For a regular ARROW transition, the mode centers in the solid and hollow cores are vertically aligned, but the modes are mismatched because of the additional ARROW layers below the solid core, as shown in Fig. 2(a). Second, the interface geometry contributes to the interface loss. Any roughness on the sacrificial core sidewall will increase the interface loss due to scattering, and any slant of the sidewall will increase the loss from the ideal, normal-interface case. Finally, the inherent roughness and non-idealities of the PECVD ARROW layers themselves contribute to the interface loss. As discussed previously, PECVD layers unevenly coat the vertical and horizontal surfaces of the rectangular sacrificial core, leading to thickness variations in the vertical ARROW layers at the interface [12], which make it very difficult to achieve the ideal of κ_i = 1.

3. Single over-coating (SOC) ARROW

In order to eliminate the dependence on layer thickness fluctuations introduced by the fabrication process, the top ARROW layers can be removed and replaced with a single over-coating. Such a structure, shown in Fig. 2(b), would allow for light to pass directly from the solid waveguide to the hollow core of the ARROW waveguide. Assuming ideal geometries, materials, and mode coupling at the interface, the transmission from solid to hollow waveguides for this structure can be as high as 99.8% for a SiO₂ top layer with a water-filled core, as predicted by the Fresnel transmission coefficient with the normal incidence approximation. This is close to ideal and much less dependent on fabrication variations than the regular ARROW design. This design also improves mode coupling efficiency at the interface because eliminating the top ARROW layers reduces the mode mismatch.

As shown in Fig. 2(b), the SOC design employs the usual bottom ARROW layers for confinement below the waveguide, but confinement above the waveguide is provided by total internal reflection off of the air-oxide interface. The thick top SiO₂ layer can also function as an ARROW layer for confinement if the thickness satisfies the ARROW condition [9].

One concern with this type of ARROW waveguide is how lossy the hollow waveguide will be because of the lack of multiple ARROW layers next to the core. Using an analytical method [14], the minimum loss is determined to be α_h = 0.49 cm⁻¹ for regular ARROWs and α_h = 2.47 cm⁻¹ for SOC ARROWs for horizontally polarized 532 nm light. On our integrated ARROW based sensor platforms, the typical hollow waveguide length is l_h = 4 mm. Based on these theoretical predictions and only considering α_h and κ_i on both ends of the waveguide, we are able to make predictions on how the SOC and regular ARROWs will compare for total throughput. As long as κ_i for a SOC ARROW is greater than 55%, the SOC ARROW will have greater overall throughput for this hollow-core length.

4. SOC ARROW fabrication

Fabrication of a SOC ARROW sensor platform, shown in Fig. 3, begins with etching into the silicon substrate to form a pedestal that the solid and hollow waveguides will later be formed upon. This silicon pedestal is necessary to surround the hollow core on three sides with a terminal layer of air, thereby improving optical confinement. KOH wet etching produces a pedestal with a very smooth surface, but it is also possible to form the pedestal through dry etching. After this, Plasma-Enhanced Chemical Vapor Deposition (PECVD) is used to deposit alternating layers of SiO₂ and SiN. Next, the sacrificial core material is deposited and patterned using standard contact lithography. While SU-8 (MicroChem) is used here, a variety of materials can be used to produce different core geometries [10]. After the core, the single over-coating of PECVD SiO₂ is deposited. Next, standard solid ridge waveguides are etched into the top layer using Reactive Ion Etching (RIE) to provide interfacing with the hollow waveguides. Finally, the sacrificial core is removed with an acid etch. An SEM cross section of a completed hollow SOC ARROW that was fabricated with this method is also shown in Fig. 3. Non-SOC ARROW sensor platforms are fabricated in a similar way, except they begin with a planar substrate and multiple top ARROW layers are used instead of the single over-coating.

Fig. 3.

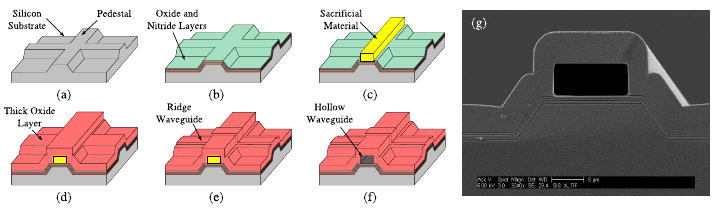
SOC ARROW Fabrication steps: (a) Pedestal etched into Si substrate. (b) ARROW layers deposited. (c) Sacrificial material deposited. (d) Top ARROW layer deposited. (e) Ridge waveguide etched into top layer. (f) Sacrificial core removed. (g) SEM image of fabricated device.

5. Optical characterization

Two different loss measurement techniques were used to characterize the losses of the two ARROW based sensor platforms shown in Fig. 2. Both devices had core dimensions of 5 × 12 μm and were tested with a frequency-doubled Nd:YAG laser at 532 nm. For the ARROW platform, the dielectric layers were (starting from the substrate - all values in nm): SiO₂/SiN/SiO₂/SiN/SiO₂/SiN-core-SiN/SiO₂/SiN/SiO₂/SiN/SiO₂ (268/100/268/100/268/100-5000-132/286/146/300/128/3016). For the SOC ARROW platform, the layers were: SiO₂/SiN/SiO₂/SiN/SiO₂/SiN-core-SiO₂ (268/100/268/100/268/100-5000-5000). Both designs used SiO₂ layers with a refractive index of 1.46, SiN layers with an index of 2.05, and water cores (n = 1.33).

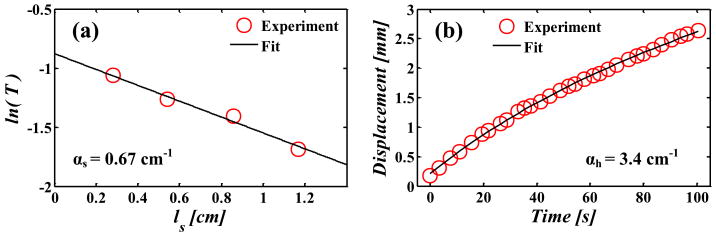
The solid waveguide loss for both platforms was determined using the standard cutback method. This method yielded α_s = 0.79 cm⁻¹ for regular ARROWs and α_s = 0.67 cm⁻¹ for SOC ARROWs. For the hollow waveguides, we used the method of optically induced particle transport [15], using 1 μm-diameter polystyrene spheres (n=1.59, Duke Scientific) in water. This method involved measuring the particle's displacement over time and extracting the waveguide loss from this data. The hollow-core loss was as low as α_h = 0.59 cm⁻¹ for regular ARROWs and α_h = 3.4 cm⁻¹ for SOC ARROWs. Figure 4(b) shows the data for the SOC ARROW loss measurements (note 31 out of 1795 points shown for clarity).

Fig. 4.

SOC ARROW loss measurements: (a) solid-core waveguide (b) liquid-core waveguide.

The discrepancy between these measured losses and those predicted can be attributed to several sources. First, although ARROWs have a broad transmission spectrum, these ARROW designs have higher loss at 532 nm than at the design wavelength of 633 nm. The 532 nm light was used for testing because the non-destructive characterization method of optically induced particle transport requires a high power laser. Second, the inherent roughness and voids in the PECVD films increase the losses due to scattering. Third, the films do not deposit uniformly, creating crevices at the corners, and the nonideal geometry has higher loss. Finally, for the SOC ARROW, since the pedestals are wider than the cores to allow for alignment, shoulders are created in the top SiO₂ (see Fig. 3) which cause light to be coupled into the cladding and increase the loss. Simulations show that these shoulders are the main contributors to SOC ARROW loss.

The solid-to-hollow waveguide interface coupling, κ_i, was determined after measuring the total edge-to-edge throughput, T, for the samples. By deducting the coupling loss and the solid and hollow waveguide loss contributions from the total throughput, we were able to ascertain the interface transmission efficiency using Eq. (1). For regular ARROWs, the interface transmission efficiency was 35 ± 9%, while for SOC ARROWs, it was 79 ± 19%. Therefore, the hollow waveguide insertion loss has been improved by a factor of about 2.26.

6. Conclusion and summary

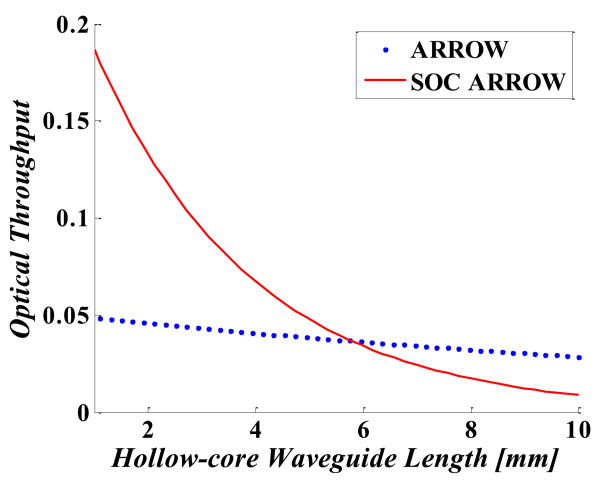
Based on the data reported, we see that SOC ARROWs have greater hollow waveguide losses but higher solid-hollow waveguide interface transmission efficiencies than the regular ARROWs. Figure 5 compares the throughput for ARROW platforms for the two designs, including hollow waveguide loss and interface transmission and assuming κ_e1 × κ_e2 = 0.55, α_s = 0.67 cm⁻¹, and l_s = 4 mm for both designs.

Fig. 5.

Chip throughput versus hollow waveguide length for ARROWs and SOC ARROWs.

Figure 5 shows that the total throughput for the SOC ARROW is higher for short hollow waveguide lengths for which interface coupling dominates over hollow-core waveguide loss. However, for hollow waveguides longer than about 5.8 mm, the throughput is higher for regular ARROWs. For otherwise identical samples, Eq. (1) can be used to define a crossover length, l_c, where the loss for SOC ARROWS becomes greater than for regular ARROWs: $l_c=\mathit{\text{ln}}({\kappa }_{i,\mathit{\text{soc}}}^2/{\kappa }_{i,\mathit{\text{arrow}}}^2)/({\alpha }_{h,\mathit{\text{soc}}}-{\alpha }_{h,\mathit{\text{aarrow}}})$ (here 5.8 mm). For the current integrated ARROW platforms using a hollow-core waveguide length of 4 mm, we have demonstrated a current system throughput improvement of 1.7 times with the use of a SOC ARROW.

One option to reduce the loss of the SOC ARROWs is to remove the shoulders to create a more ideal geometry. Another option to increase the overall throughput is to create a hybrid between the two designs. This can be accomplished by using the SOC structure at the solid-hollow interfaces while using the complete ARROW structure for most of the length of the hollow waveguide. This approach would take advantage of the high interface transmission efficiency of the SOC ARROW and the low hollow waveguide loss of the ARROW. While it is possible to fabricate such waveguides, the fabrication presents some challenges. Two options for making these hybrid waveguides are etching or using a lift-off technique to remove the top ARROW layers at the interfaces while leaving the layers intact over most of the length of the hollow waveguide. Then, a thick SiO₂ layer can be deposited that would function as the top ARROW layer for both structures.