Abstract
Neurodevelopmental changes regarding interference and magnitude processing were assessed in 3 age groups (children, n = 10; young adults, n = 11; elderly participants, n = 9) by using an functional magnetic resonance imaging version of the numerical Stroop task. Behaviorally, comparable distance and size congruity effects were found in all 3 age groups. Distance effects were most pronounced in the more difficult numerical task, whereas size congruity effects were comparable across tasks. In response to interference, an age-linear trend in the pattern of activation in left and right prefrontal and left middle temporal regions of the brain was observed. This implicates that with increasing age interference control requires increasing effort (possible explanations for children’s relatively lower interference effects are provided). In contrast, the distance effect produced a negative linear trend in right prefrontal, supplementary motor area, and intraparietal cortex. This suggests that relative to old adults, children and young adults had to recruit a larger network upon processing magnitude. The latter findings are even more remarkable considering that the behavioral effects were similar across groups. In summary, the developmental trajectories of interference control and magnitude processing differ, although these cognitive functions activate partially overlapping brain regions.
Keywords: congruity, developmental fMRI, interference, magnitude, Stroop task
Introduction
A major determinant of cognitive decline in old age is inhibition capacity (e.g., Hasher and Zacks 1988; Lustig et al. 2006; Martin et al. 2006). A classic test tapping inhibition and automaticity is the Stroop task (McLeod and MacDonald 2000) that requires participants to respond to relevant stimulus dimensions while suppressing the interference of task-irrelevant stimulus features. Interference load can be manipulated experimentally in Stroop tasks depending on the saliency of relevant and irrelevant stimulus features (Pansky and Algom 1999, 2002; McLeod and MacDonald, 2000).
Cognitive Interference, Its Neural Correlates and Development
In the so-called numerical Stroop task (or number–size interference task), participants are required to make magnitude classifications on Arabic numbers, paying attention to either the numerical or physical (font size) stimulus characteristics while ignoring the task-irrelevant stimulus feature (physical or numerical size, respectively; e.g., Tang et al. 2006). The so-called “congruity effect” depicts the fact that generally, both accuracy and response latency deteriorate when numerical and physical font size are incongruent (e.g., Besner and Coltheart 1979; Henik and Tzelgov 1982; Pansky and Algom 1999; Cohen Kadosh and Henik 2006). Importantly, in order to investigate cognitive interference between stimulus features, it is necessary to ascertain whether their mental numerical representations are readily available. In adult participants (e.g., Duncan and McFarland 1980; Dehaene and Akhavein 1995) as well as in children (Girelli et al. 2000; Rubinsten et al. 2002; but see Gebuis et al. 2008, for evidence on 5-year-old children), Arabic number magnitude is known to be activated automatically in a range of tasks and can be hardly ignored even if task irrelevant. Regarding the numerical Stroop task, it is thus crucial to investigate whether magnitude processing is established to a sufficient degree and to determine under which conditions the mental magnitudes are activated. This can best be achieved by observing the “distance effect” as it is thought to reflect intact magnitude knowledge (e.g., Moyer and Landauer 1967; Dehaene et al. 1990; Cohen Kadosh et al. 2005).
Likewise, interference control is mediated by a distributed frontoparietal network (Dosenbach et al. 2007; Fair et al. 2007, 2008) that matures between childhood and adulthood. Activations in this network are most pronounced in prefrontal areas including the anterior cingulate cortex (ACC; Bush et al. 1998, 2003) and the dorsolateral prefrontal cortex (DLPC; e.g., Banich et al. 2000; Adleman et al. 2002). Previous studies employing the numerical Stroop task corroborate the importance of prefrontal and—to a lesser extent—parietal regions in interference control (children: Kaufmann et al. 2006; adults: Kaufmann et al. 2005). Moreover, deficient interference control (reflected both in behavioral and imaging data) is a common characteristic of a variety of neurological and psychiatric conditions (children with attention-deficit hyperactivity-disorder [ADHD]: Smith et al. 2006; elderly patients with minimal cerebral impairments: Kaufmann, Ischebeck et al. 2008; patients with left parietal lesions: Ashkenazi et al. 2008) and might be associated with normal aging too (Paxton et al. 2007).
Age and Brain Correlates of Interference Processing
Recent studies have investigated the effects of age on the neural networks subserving interference control from childhood to adulthood (e.g., Rubia et al. 2006) and from adulthood to elderly age (e.g., Gazzaley et al. 2005; Townsend et al. 2006). Brain imaging studies covering the development up to adulthood as well as those covering adult development are suggestive about an increase of activation in prefrontal, cingulate, caudate, and posterior parietal regions associated with interference control (for an overview, see Adleman et al. 2002). According to Townsend et al. (2006), the stronger activations of the frontoparietal networks found in older relative to younger adults (reflected in both focused and shifting attention paradigms and irrespective of task relevancy) are most plausibly explained by age-related difficulties in processing selective information. One important limitation of previous studies is that they only have examined the impact of aging on interference as regards nonsymbolic information processing (Gazzaley et al. 2005; Townsend et al. 2006).
Magnitude Processing, Its Neural Correlates and Development
The development of numerical and arithmetic abilities has always been a key topic in psychological research on numerical cognition (e.g., Groen and Parkman 1972; Brigman and Cherry 2002; for recent reviews, see Butterworth 2005; Campbell 2005; Kaufmann and Nuerk 2005). Generally, children master core numerical skills such as magnitude discrimination and counting skills long before they enter primary school. Magnitude processing is a core skill in our society; and generally, children acquire magnitude-related knowledge very early in their development (e.g., Boucart and Humphreys 1994). For instance, preverbal infants of 5–6 months of age demonstrate numerical discrimination abilities as well as additive and subtractive expectation behavior for set sizes up to 3 or 4 (e.g., Wynn 1992, 1995) and might even discriminate larger set sizes provided the ratio is large enough (Xu and Spelke 2000; Xu 2003). The distance effect reflects a negative correlation between numerical distance and response latencies (i.e., longer response latencies upon processing adjacent numbers and vice versa) and is thought to reflect established magnitude knowledge or in other words: the integrity of the mental number line (Dehaene et al. 1993, see also Restle 1970; but see Cohen Kadosh, Brodsky, et al. 2008 and Cohen Kadosh, Lammertyn, and Izard 2008 for an alternative explanation). Magnitude knowledge is preserved in healthy elderly people and even in some individuals suffering from progressive dementia (Kaufmann et al. 2002; see also Kaufmann, Ischebeck, et al. 2008). Such as in other domains of cognitive activity, the development of numerical and arithmetical abilities reveals a diversity of developmental trajectories, with some abilities remaining unimpaired even in old age, whereas other ones decline with age (Duverne and Lemaire 2005). Unfortunately, there is a scarcity of studies investigating numerical cognition in the elderly, especially when the focus is on the cognitive representation of numbers as opposed to arithmetic skills. In a recent meta-analysis of 46 published studies, Wood, Nuerk, Willmes, et al. (2008) disclosed for the first time an effect of age on the size of the Spatial Numerical Association of Response Code (SNARC) effect, which is an index of the association between magnitude processing and space. Elderly participants were presented with a stronger SNARC effect size than younger participants. The authors discuss 2 aspects of their findings. On the one side, elderly people have had more time to strengthen the cognitive habit (Knoch et al. 2005) of associating number magnitude and space. On the other side, they are more vulnerable to interference from irrelevant automatic response code associations (Lustig et al. 2006).
Age and Brain Correlates of Number and Magnitude Processing
As regards the neural correlates of magnitude processing, there is converging evidence for a key role of intraparietal regions for number magnitude processing (for an overview, see Dehaene et al. 2003; Hubbard et al. 2005). Nonetheless, besides the parietal lobes, prefrontal areas have also been found to be implicated in number processing (animal studies: Nieder et al. 2002; Nieder and Miller 2004; children: Rivera et al. 2005; Kaufmann et al. 2006). Recent developmental functional magnetic resonance imaging (fMRI) studies reveal an increase of activation in the left intraparietal sulcus (IPS) in response to nonsymbolic magnitudes in young adults relative to 10-year-old children (Ansari and Dhital 2006). Moreover, Rivera et al. (2005) found stronger intraparietal response to mental arithmetic in young adults than in children. However, up-to-date, there is no study comparing the fMRI response to magnitude processing in adults and elderly participants.
Aims of the Present Study
The present study is the first one to examine the impact of aging 1) on the neural correlates of interference control and 2) on more abstract magnitude representation. The working hypothesis for the current study was partly based upon previous findings (similar, but not identical paradigm in adults: Kaufmann et al. 2005; identical paradigm as used here in children: Kaufmann et al. 2006). The most remarkable finding of the latter studies was that visual inspection of activation patterns in children and adults suggests the activation of only partially overlapping brain regions. Importantly, both groups exhibited comparable behavioral performance patterns characterized by distance and congruity (interference) effects. Thus, we expect that in all 3 age groups incorporated in the current study (i.e., children, young, and old adults), robust distance and congruity effects in behavioral test performance can be observed. With respect to imaging data, our assumption is that relative to children, young adults should recruit more distributed networks upon interference processing because number magnitude processing becomes more automatic with age and may increase the demand for interference control. The differences between children and elderly participants should be even more pronounced because of age-related difficulties in processing selective information (Gazzaley et al. 2005; Townsend et al. 2006). Regarding magnitude processing, our expectations are less straightforward. Although studies on nonsymbolic magnitude processing show an increase of activation in the IPS in children relative to adults (Ansari and Dhital 2006, Kaufmann, Vogel, et al. 2008), it can be that magnitude processing of Arabic numbers present with another development trajectory because their association with specific magnitudes is arbitrary and needs to be learned. Regarding the later development in adulthood, we expect that elderly participants and young adults should produce comparable fMRI activation because elderly participants’ ability to process magnitude should remain intact at this age. Overall, this study aims at elucidating the following questions: Which regions are responsible for interference control and magnitude processing across the life span? Which regions specifically associated with interference control and magnitude processing show differential activation depending on aging?
Materials and Methods
Participants
Originally 16 children, 11 young adults, and 13 elderly individuals were included in the study. Data from 6 children could not be assessed because of excessive movement artifacts (i.e., larger than 4 mm over the whole time series or larger than 1 mm between 2 scans) or technical problems with data recording. Additionally, data from 4 elderly individuals have been excluded from statistical analyses due to movement artifacts as well as subtle neuroradiological abnormalities detected post hoc by trained neuroradiologists (K.F. and G.T.). Thus, participants from 3 age groups were included in this study, children (n = 10, mean age = 9.4 years; standard deviation [SD] = 1.3; range: 8–12 years), young adults (n = 11, mean age = 29.5 years; SD = 6.1; range: 23–40 years), and elderly participants (n = 9, mean age = 68.1 years, SD = 7.1; range: 59–81 years). All participants were right-handed, had normal or corrected to normal vision, and had no reported history of major medical illness, neurological or psychiatric disorder, or substance abuse. Young and old adults had completed at least 12 years of education, participating children were attending grades 3–4 at time of testing (average IQ prorated from a short form of the WISC-III (German version of the Wechsler Intelligence Scale for Children, 3rd revision; Tewes et al. 1999) was 112 (SD = 6). The study was approved by the local ethical committee of the Medical University of Innsbruck and conducted according to the Convention of Helsinki. A written informed consent was obtained from all participants or, in the case of children, from their parents.
Tasks and Stimuli
The numerical Stroop task requires participants to make numerical and physical magnitude judgments on the relevant dimension of stimuli (physical/font size or numerical magnitude, respectively) while ignoring irrelevant stimulus characteristic (physical/font size or numerical magnitude, respectively). In our version of the Stroop task, 2 types of stimulus pairings were used: “incongruent” digit pairs (eliciting more or less cognitive interference, see below) and “neutral” digit pairs. Digit pairs were incongruent when physical and numerical magnitudes were incongruent (3 4 [the numerical larger digit being printed in a smaller font size]) and neutral when only physical or numerical magnitudes were varied at a time (numerical comparison: 3 4 [2 numerically distinct digits being printed in identical font sizes]; physical comparison 3 3 [the 2 numerically identical digits being printed in different font sizes]).
Two levels of incongruity were defined when forming incongruent digit pairs: maximally incongruent and minimally incongruent stimuli. Maximal incongruity was obtained when the relevant stimulus dimension presented a small distance, whereas the irrelevant dimension presented a large distance (e.g., 1 2, in the numerical comparison task). Minimal incongruity was obtained when the relevant stimulus dimension presented a large distance, whereas the irrelevant dimension presented a small distance (e.g., 1 2, in the physical comparison task). Importantly, stimuli being maximally incongruent in the numerical comparison task were minimally incongruent in the physical comparison task and vice versa. Therefore, exactly the same stimulus set was used in both numerical and physical tasks. The congruity effect was calculated upon subtracting the response latency and accuracy to weakly incongruent stimuli from the responses to strongly incongruent ones. Importantly, the distance effect was calculated upon comparing distances from neutral stimuli only.
The main reason for defining the size congruity effect as the difference between maximally and minimally incongruent trials is that one can obtain a reliable and robust measure of cognitive interference in the absence of confounds characteristic of other typical definitions (e.g., incongruent–congruent and incongruent–neutral). In the following, we describe shortly these confounds as well as some further advantages of our definition of the size congruity effect.
Comparison between incongruent versus congruent trials is confounded by the lack of guarantee that in congruent trials participants are following task instructions and trying to respond to the relevant dimension (while ignoring the irrelevant one). Therefore, the difference between these 2 conditions may be due not to different amounts of cognitive interference but to different degrees of the compliance to task instructions. Because in congruent trials both relevant and irrelevant dimensions are associated with the same response, there is no way to disclose what participants are really doing. In the Color–Word Stroop task, a similar problem has been identified and systematically discussed (see the inadvertent reading effect, McLeod and MacDonald 2000). As pointed out by these authors, the advantage in processing times of congruent trials in comparison to neutral ones does not correlate with the effect of interference (estimated from the difference between neutral and incongruent trials). Therefore, the cognitive processes involved in the facilitation of performance observed in congruent trials are probably not the same as those involved in interference processing, which are actually the main focus of the present manuscript.
Furthermore, comparison between incongruent versus neutral trials is also problematic because of perceptual and representational confounds. Although in incongruent trials, stimuli vary in 2 separated dimensions, in neutral trials, only 1 dimension varies. Therefore, visually neutral stimuli are “simpler” than incongruent ones, and some activation in extrastriate and parietal regions might be due to these trivial differences between stimuli. Moreover, neutral trials are task specific. Therefore, any difference between tasks in the size congruity effect can be attributed to the stimuli used in the neutral condition. Finally, by using neutral trials for computing the size congruity effect, the interpretability of the neural correlates specific to magnitude and size congruity as well as the impact of age on them are threatened because the same stimuli must be used for estimating the distance effect (neutral trials) and the size congruity effect (incongruent–neutral).
In sharp contrast, the difference between maximally and minimally incongruent stimuli is always due to different degrees of interference produced by these 2 conditions. Therefore, one can interpret the difference between these 2 conditions as a measure of the size congruity effect (see Kaufmann et al. 2005, 2006; Kaufmann, Ischebeck, et al. 2008). Moreover, when computing the size congruity effect as the difference between maximally and minimally incongruent trials, exactly the same stimuli can be used in numerical and physical tasks because those stimuli, which are maximally incongruent in the numerical task, are minimally incongruent in the physical task and vice versa. Therefore, 1 task serves as control for the other one.
In this design task, specific differences can be attributed with confidence to interference of the magnitude information conveyed by the irrelevant dimension and not to perceptual differences in stimulus set. We implemented 2 numerical distances (distances 1 and 4) and 2 physical distances. Stimuli were presented at the following visual angles: Arial font size 55: height 2.86°, width 1.91°; Arial font size 64: height 3.24°, width 2.10°; and Arial font size 73: height 3.81°, width 2.48°. Stimuli presentation and data recording were accomplished by using Presentation (Neurobehavioral Systems, Albany, CA, http://www.neurobs.com). Small numerical distances were always combined with a large physical difference and vice versa, thus yielding maximally and minimally incongruent stimuli. Identical parameters were used as in previous studies (Kaufmann et al. 2005, 2006; Kaufmann, Ischebeck, et al. 2008).
Design
Stimuli were presented blockwise (n = 6 trials per block), and experimental conditions (maximally incongruent, minimally incongruent, neutral far, and neutral close) were interspersed with rest blocks (fixation cross for 18 s). Thus, 16 blocks (n = 96 stimuli) were presented in a 2 (task) × 4 (condition) × 12 (stimuli per condition) design, stimulus duration 2000 ms, and interstimulus interval 1000 ms. Participants ought to indicate the side of the (numerically or physically) larger digit of the digit pair by pressing the corresponding button with the right or left index finger. The assignment of left and right responses was counterbalanced across participants. Instructions emphasized accuracy and speed, and the order of task presentation was counterbalanced across subjects.
MRI Image Acquisition and Preprocessing
fMRI data were acquired on a 1.5-T magnetic resonance scanner (Magnetom Vision, Siemens, Erlangen, Germany). Functional series were acquired by using an echo-planar image (EPI) sequence (time repetition/time echo = 2.7 s/66 ms/90°, matrix = 64 × 64, voxel size = 3.91 × 3.91 × 6.25 mm, 24 axial slices in 2 s). A T1-weighted anatomical data set was obtained from each participant (spatial resolution 0.98 × 0.98 × 1.4 mm). Data analysis was performed using SPM5 (Wellcome Department of Cognitive Neurology, London, UK). The functional images were motion corrected, normalized, and smoothed with a Gaussian kernel full width at half maximum = 8 mm.
Region of Interest Analyses
Regions of interest (ROIs) were defined using the toolbox marsbar (http://marsbar.sourceforge.net/). Masks for the extraction of brain activation from ROIs were defined as spheres with the center located at the maximum of activation clusters observed in second level contrasts. The spheres presented a diameter of 10 mm. Individual beta coefficients were estimated in every experimental condition and were compared statistically.
Results
Behavioral Data
Error rates and response latencies from 30 individuals (10 children, 11 young adults, and 9 elderly) are reported. Furthermore, due to technical problems, behavioral responses of 2 children could not be recorded in 2 experimental blocks. Behavioral data were replaced by the average mean reaction time (RT) and accuracy of their peers in these conditions. Only RTs of correct responses in the interval between ±3 SDs from the individual mean RT were considered for further analyses. Error rates were arcsine transformed before entering statistical analyses (Table 1).
Table 1.
Overview of the error rates (%Error) and SDs of error rates for the 3 age groups
| Children (n = 10) | Young adults (n = 11) | Elderly participants (n = 9) | ||||
|---|---|---|---|---|---|---|
| Close distance RT (SD) | Far distance RT (SD) | Close distance RT (SD) | Far distance RT (SD) | Close distance RT (SD) | Far distance RT (SD) | |
| % Error (SD) | % Error (SD) | %Error (SD) | %Error (SD) | %Error (SD) | %Error (SD) | |
| Physically neutral | 651 (57) | 641 (37) | 603 (100) | 528 (78) | 650 (68) | 578 (59) |
| 24 (21) | 10 (13) | 5 (8) | 0 (0) | 7 (8) | 5 (14) | |
| Numerically neutral | 765 (75) | 662 (75) | 653 (116) | 547 (69) | 722 (33) | 632 (57) |
| 30 (29) | 15 (19) | 3 (6) | 0 (0) | 10 (13) | 8 (13) | |
| Maximally incongruent RT (SD) |
Minimally incongruent RT (SD) |
Maximally incongruent RT (SD) |
Minimally incongruent RT (SD) |
Maximally incongruent RT (SD) |
Minimally incongruent RT (SD) |
|
| % Error (SD) | % Error (SD) | %Error (SD) | %Error (SD) | %Error (SD) | %Error (SD) | |
| Physically incongruent | 750 (77) | 667 (46) | 633 (99) | 532 (88) | 774 (113) | 635 (90) |
| 40 (24) | 15 (15) | 19 (17) | 3 (4) | 36 (39) | 9 (28) | |
| Numerically incongruent | 813 (64) | 729 (72) | 679 (95) | 577 (98) | 772 (97) | 688 (78) |
| 51 (24) | 32 (30) | 18 (6) | 2 (4) | 47 (42) | 20 (27) | |
Interference Control
RT analysis revealed that responses were in average 56 ms slower in the numerical magnitude judgment than in the physical magnitude judgment task (F1,27 = 11.68, P < 0.05). Responses also were significantly slower (100 ms) in the maximally incongruent condition than in the minimally incongruent one (F1,27 = 79.11, P < 0.05). Moreover, a significant effect of group (F2,27 = 14.75, P < 0.05) was observed. Scheffé’s post hoc comparisons revealed that young adult’s response latencies were faster than those of elderly participants (P = 0.001) and children (P < 0.001). Response latencies of elderly participants and children did not differ significantly. No interaction effect was observed in RT. Error rates in maximally incongruent trials were 22% higher than in minimally incongruent ones revealing thereby a strong size congruity effect (F1,27 = 42.80, P < 0.05). Furthermore, a significant effect of group (F2,27 = 9.14, P < 0.05) was observed. Scheffé’s post hoc comparisons revealed that young adults committed significantly fewer errors than elderly participants (P = 0.024) and children (P = 0.001). Error rates of elderly participants and children did not differ significantly. No interaction effects with participants’ group were observed in error rates.
Magnitude Processing
RT analysis revealed that responses were on average 55 ms slower in the numerical relative to the physical magnitude judgment task (F1,27 = 29.28, P < 0.05). Responses also were significantly slower (76 ms) for small distances than for large ones (F1,27 = 69.45, P < 0.05). Furthermore, the impact of distance on judgment speed was much more pronounced in the numerical judgment task (100 ms) than in the physical judgment task (52 ms) as revealed by the significant interaction between task and magnitude processing (F1,27 = 8.68, P < 0.05). Once more, a significant effect of group (F2,27 = 7.10, P < 0.05) was observed. Scheffé’s post hoc comparisons revealed that young adult’s response latencies were faster than those of children (P = 0.004). In contrast, response latencies differed only marginally between young adults and elderly participants (P = 0.084) and were comparable between elderly participants and children. No interaction effects with participants’ group were observed in RT. As regards response accuracy, error rates were 6.5% higher upon processing small relative to large distances (F1,27 = 12.17, P < 0.05). The significant interaction between distance and group (F2,27 = 3.67, P < 0.05) reflects the stronger distance effect in children (14%) relative to young adults (4%) and elderly participants (2%). Finally, a significant effect of group (F2,27 = 8.00, P < 0.05) was observed. Scheffé’s post hoc comparisons revealed that young adult’s error rates were significantly lower than those of children (P = 0.002) but only marginally significant between children and elderly participants (P = 0.057). Errors rates of young adults and elderly participants were comparable. No further interaction effects were observed in error rates.
fMRI Data
If not reported otherwise, activation patterns were described for the statistical threshold of P = 0.001, uncorrected, and a minimum cluster size k = 10 (Fig. 1).
Figure 1.
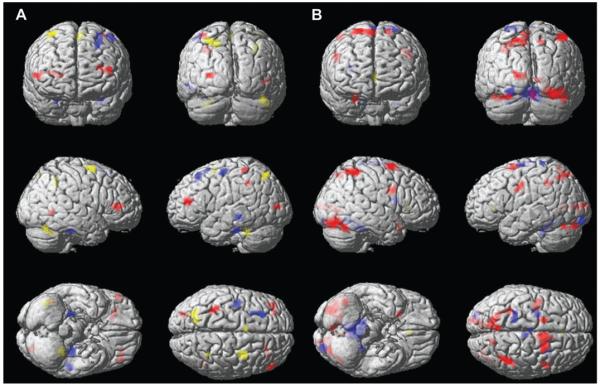
Brain activations in the 3 age groups (children = red, adults = yellow, and elderly participants = blue) elicited by interference control (A) and magnitude processing (B).
Error Monitoring
Children and elderly participants committed a large number of errors in both numerical and physical comparison tasks. For this reason, we decided to examine the impact of overall accuracy on brain activation before passing to the assessment of the impact of interference control and magnitude processing. Based on a conjunction analysis, we selected the ACC and the left IPS as 2 regions associated with error monitoring and examined whether individual average error rates correlated with interference control and magnitude processing in these ROIs. Results revealed that neither the fMRI signal observed in the ROI in the ACC (Talairach coordinates [TC]: 3, 25, 41) nor the one in the left parietal cortex (TC: −18, −56, 49) correlated with average error rates (the correlation was never stronger than ±r = 0.22; every P = not significant).
Interference Control
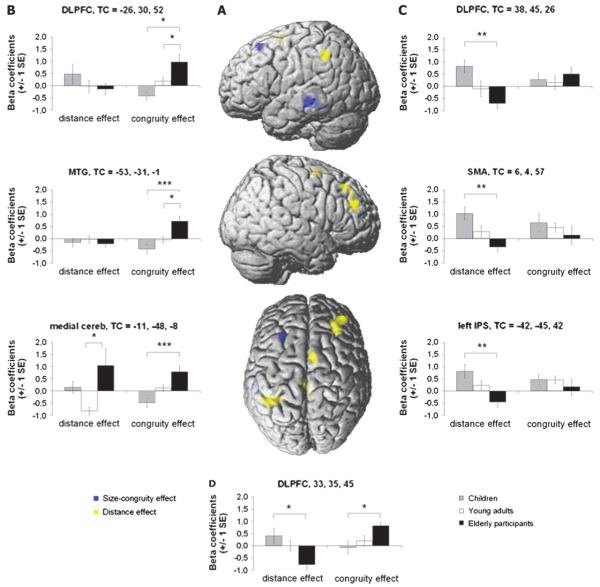
Activations obtained in response to interference control in each of the 3 age groups are depicted in Figure 1(A). Children (red clusters) activated the DLPC bilaterally as well as the anterior portions of the left IPS, left extrastriate cortex, and right temporo-occipital cortex. Adults (yellow clusters) activated significantly the left cingulate and right premotor cortex, portions of left posterior parietal cortex, and the cerebellum bilaterally. Elderly participants (blue clusters) activated the left premotor and DLPC, left middle temporal gyrus, and the hippocampal gyrus bilaterally. A conjunction analysis (cf., Friston et al. 2005) revealed 4 clusters of activation common to all age groups in response to interference. Activation clusters were located in the left premotor cortex (TC = −24, −4, 64; k = 12; Hotelling’s T(27) = 2.92; P < 0.001 and TC = −27, 0, 49; k =18; Hotelling’s T(27) = 2.32; P < 0.001), the left IPS (TC = −33, −45, 42; k = 11; Hotelling’s T(27) = 2.79; P < 0.001), and the right lateral cerebellum (TC = 48, −59, −21; k = 13; Hotelling’s T(27) = 2.33; P < 0.001; Fig. 2A–D).
Figure 2.
(A) Brain areas showing a significant positive association between congruity effect and age are shown in blue, whereas regions showing a negative association between the distance effect and age are shown in yellow. Graphics in (B–D) depict the statistical comparisons between age groups in the ROI analyses. (B) Regions showing a significant effect of age on the fMRI activation triggered by interference control. (C) Regions showing a significant effect of age on the fMRI activation triggered by magnitude processing. (D) Dorsolateral prefrontal region showing a significant effect of age on the fMRI activation triggered by both interference control and magnitude processing.
In order to examine the effect of age on fMRI signal strength observed in response to interference control, individual beta coefficients obtained in these regions were regressed on age. A positive association between interference control and age was observed in the DLPC, bilaterally, left middle temporal gyrus, and medial cerebellum (Fig. 2A, blue clusters). No cluster was found to show a negative association between interference control and age. (Beside the regression model, we also looked for nonlinear effects of age on size congruity and magnitude processing in a series of analysis of variance contrasts. No significant nonlinear effect of age on interference control and magnitude processing was observed.)
Magnitude Processing
Activation patterns obtained in the physical and numerical tasks were compared. No difference was observed between the activation patterns produced in the physical and numerical tasks. Moreover, activations obtained in each of the 3 age groups are depicted in Figure 1(A). Children activated the intraparietal, inferior temporal, extrastriate, and premotor cortex bilaterally. At the selected statistical threshold, adults only activated a small portion of the left orbitofrontal cortex. Elderly participants activated significantly the superior parietal cortex, bilaterally, left extrastriate cortex, and the medial cerebellum. A conjunction analysis did not reveal any activation clusters that became significant in all age groups at the rather liberal level of P = 0.005, uncorrected.
In order to examine the effect of age on activation extent observed in response to magnitude processing, the individual beta coefficients were regressed on age. No cluster showed a positive association between magnitude processing and age. However, significant negative associations between magnitude processing and age were observed in the right DLPC, the left inferior parietal cortex, and the right supplementary motor area (Fig. 2A, yellow clusters).
ROI Analyses
Individual beta coefficients were extracted for the 7 brain areas showing an association between age and interference control or between age and magnitude processing. Beta coefficients were statistically compared across the 3 age groups (Table 2). In response to interference control (i.e., size congruity effect), elderly participants showed increased activation in the left DLPC and the middle temporal gyrus in comparison to younger groups (Fig. 2B). Compared with children, elderly participants produced significantly stronger activations in the medial cerebellum and the right DLPC (Fig. 2B). Moreover, relative to children, elderly participants deactivated the DLPC and IPS as well as the supplementary motor area in response to magnitude comparison (i.e., distance effect; Fig. 2C, see also Fig. 2D). Finally, elderly participants activated the medial cerebellum significantly more than adults (Fig. 2C).
Table 2.
Linear and quadratic contrasts for the comparisons between groups
| TC | Linear contrast |
Quadratic contrast |
||||||
|---|---|---|---|---|---|---|---|---|
| F2,27 | MSE | P value | F2,27 | MSE | P value | |||
| Right DLPC | 38, 45, 26 | Distance effect | 14.36 | 11.06 | 0.001 | |||
| Supplementary motor area | 6, 4, 57 | Distance effect | 6.14 | 14.18 | 0.020 | |||
| Congruity effect | 20.23 | 7.70 | 0.000 | |||||
| Left intraparietal cortex | −42, −45, 42 | Distance effect | 14.74 | 7.61 | 0.001 | |||
| Right DLPC | 33, 35, 45 | Distance effect | 10.47 | 6.71 | 0.003 | |||
| Congruity effect | 8.19 | 3.81 | 0.008 | |||||
| Medial temporal gyrus | −53, −31, −1 | Congruity effect | 21.77 | 6.22 | 0.000 | |||
| Left DLPC | −26, 30, 52 | Congruity effect | 20.62 | 9.23 | 0.000 | |||
| Medial cerebellum | −11, −48, −8 | Distance effect | 6.14 | 3.34 | 0.020 | |||
| Congruity effect | 20.23 | 7.70 | 0.000 | |||||
MSE: mean squared error.
Finally, a region in the right DLPC showed an age-related increase in activation in response to interference control while showing an age-related decrease of activation in response to magnitude processing. In comparison to children, elderly participants also showed weaker blood oxygen level–dependent (BOLD) response to magnitude processing in this last area (Fig. 2D and Table 2).
Discussion
In the present study, the effect of age on brain activations obtained in response to interference control (i.e., size congruity effect) and magnitude processing (i.e., distance effect) was assessed. Brain areas recruited by interference control and magnitude processing were found to modulate the BOLD response in function of age. Moreover, specific developmental trajectories of interference control and magnitude processing were observed. An age-dependent increase of activation in response to interference control was observed in prefrontal, temporal, and cerebellar areas, implicating that interference control becomes more effortful with age. In contrast, a decrease of activation in response to magnitude processing was observed in prefrontal, intraparietal, and supplementary motor areas, revealing that relative to elderly and adults, children recruited a larger network upon processing magnitude. These findings will be discussed in more detail below.
Which Regions Are Responsible for Interference Control and Magnitude Processing from Childhood to Elderly?
Brain areas commonly activated by all age groups were found but were small. A small overlap of activations respective to interference control as well as to magnitude processing was found in the 3 age groups. A conjunction analysis showed consistent responses to interference processing in only 3 brain areas: the left premotor cortex, the left IPS, and the right lateral cerebellum. Interestingly, these specific regions do not figure among them whose activation was modulated by age. This suggests that the cognitive function these areas subserve when processing interference remains relatively constant across the life span. Importantly, the conjunction analysis did not reveal activation in the DLPC, an area commonly associated to conflict processing (Kaufmann et al. 2005; Kaufmann, Ischebeck, et al. 2008; van Veen and Carter 2005; Liu et al. 2006) and trial-by-trial interference control (Dosenbach et al. 2007). Lack of activation in the DLPC in the conjunction analysis suggests that the role of this brain area when processing interference changes with age. In response to interference control, children and adults also activated partially distinct frontoparietal networks: Children recruited the DLPC bilaterally as well as the anterior portions of the left parietal cortex, whereas adults activated significantly the left cingulate and right premotor cortex, and portions of left posterior parietal and right IPS. A possible reason for the differences between children and adults is the maturation of the cortical circuits (Fair et al. 2007). Dosenbach et al. (2007) and Fair et al. (2007) showed that relative to adults, the involvement of frontoparietal and cingulate structures is less specific in children in comparison to teenagers and adults. Furthermore, in children, interference control elicited activations in the left extrastriate cortex and right temporo-occipital cortex, whereas adults activated the cerebellum bilaterally. Elderly participants produced significant activations in the left DLPC and left middle inferior temporal gyrus as well as in the hippocampal gyrus bilaterally. The large diversity found in the activated areas in the different age groups suggests that the neural resources recruited upon solving the size congruity task depend on the actual level of brain maturation (Rubia et al. 2006) as well as on the integrity of different neural circuits supporting interference control (Gazzaley et al. 2005, Gazzaley and D’Esposito 2007).
In response to magnitude processing, children and elderly participants alike activated parietal areas associated with magnitude processing (Hubbard et al. 2005; Cohen Kadosh, Lammertyn, and Izard 2008), whereas adults failed to activate these cortical areas at the selected statistical threshold. Lack of significant intraparietal activation suggests that in young adults, the differential response to small distances was not much stronger than to large distances. However, upon considering the rather small sample sizes, the absence of a significant conjunction in intraparietal regions in response to magnitude processing does not necessarily mean that adults do not recruit these regions at all when processing magnitude. Furthermore, children also activated the inferior temporal, extrastriate, and premotor cortex, bilaterally, and elderly participants produced significant activations in the left extrastriate cortex and the medial cerebellum. Activations in these areas are compatible with the cognitive demands of the magnitude comparison task such as processing of visual stimuli and response selection (Cohen Kadosh et al. 2007; Donohue et al. 2008).
Because all age groups presented a reliable distance effect, it is plausible to assume that they processed stimuli up to the magnitude level (but for an alternative explanation, see Cohen Kadosh, Lammertyn, and Izard 2008). Figure 1(B) shows that the regions significantly activated by children and elderly participants in response to magnitude processing show only a partial overlap, although both of them are located in the parietal lobes. This suggests that the cognitive processes recruited by children and elderly participants may differ slightly. Although the more anterior parts of the IPS are associated to core magnitude processing (Dehaene et al. 2003; see also Wood, Nuerk, Sturm, and Willmes 2008), the more posterior parts of the parietal cortex are more involved in symbolic information processing (Wood et al. 2006, Wood, Nuerk, Moeller, et al. 2008) and the navigation on the mental number line (Dehaene et al. 2003). The strength of activation observed in 1 parietal area or another may change with age. These findings will be discussed in more detail below.
Developmental Trajectory of Interference Control
Behavioral responses were modulated by age and congruity. Interestingly, although children and elderly participants were significantly slower and less accurate than young adults, the behavioral effect of congruity was comparable across all groups. One could be tempted to conclude that in comparison to adults, children and elderly participants presented a deficit in similar mechanisms. Nonetheless, the present functional imaging findings as well as evidence from structural brain maturation processes defy this trivial explanation. Relative to children, brain activation was increased in the left and right DLPC, the left middle temporal gyrus, and the left medial cerebellum in elderly participants (Fig. 2B,D). These results are compatible with the literature on the development of neural correlates of interference control (Adleman et al. 2002). More specifically, an age-related increase in prefrontal activation has been reported in response to cognitive control (Rubia et al. 2006) and inhibition (Rubia et al. 2006). Accordingly, an age-related increase in activation in the left middle temporal gyrus has been attributed to increased cognitive demands when older participants process the visual information (Allison et al. 1994; McLeod and MacDonald 2000). Because children and elderly participants performed the interference task alike, increased activation in this area in elderly participants relative to children may suggest that the analysis of visual stimulus properties is more demanding for elderly in comparison to children. Finally, the increase of activation in the middle cerebellum is commonly reported as an index of response selection demands and task difficulty (Donohue et al. 2008).
Relative to children, elderly participants needed to activate the DLPC, bilaterally, as well as the left middle temporal gyrus and left middle cerebellum significantly more in order to reach the same efficiency in interference control (Fig. 2B,D). Although children’s poor performance in interference control was associated with weak DLPC activation, comparable performance in elderly participants was accompanied by very strong DLPC activations. In light of the differences observed in the functional findings in response to interference control, the interpretation of the comparable behavioral performance of children and elderly participants needs to be revisited. In adults, Rypma et al. (2006) have shown that performance proficiency is negatively correlated with the activation extents in prefrontal cortex. That is, at the same performance level, less proficient individuals produced stronger prefrontal activations. Consistent with the latter results, elderly participants were found to rely more on prefrontal regions upon interference processing when compared with adults in the present study. Also consistent with this evidence, Bub et al. (2006) suggest that greater Stroop interference in children is not due to lack of ability to inhibit irrelevant information but instead the result of a failure to maintain the task set. This is in line with the lower levels of DLPC activation children show in comparison to elderly participants. Moreover, it is well known that the prefrontal cortex in children is still not fully operational due to its late structural maturation (Diamond 2000; see also Dosenbach et al. 2007; Fair et al. 2007, 2008). Furthermore, these regions are known to be very susceptible to aging effects (Gazzaley et al. 2005; Townsend et al. 2006). Elderly participants are known to have difficulties selecting information and may then have to activate the DLPC more strongly in order to reach the same level of performance (similar congruity effect) of children. Hence, poor interference control in children is most likely attributable to weak prefrontal recruitment, whereas in elderly participants, poor interference control has previously been found to be associated with compensatory mechanisms necessary for keeping a certain level of cognitive functioning (e.g., Amieva et al. 2004; Yetkin et al. 2006; Kaufmann, Ischebeck, et al. 2008). Overall, a plausible though far rather speculative interpretation of the age-related activation differences observed here is that deficient interference processing of elderly participants may manifest at the response selection level, whereas suboptimal interference control of children occurs at a different information processing level (possibly at the input level of information processing such as task maintenance, etc.). In line with this account are the significant activation of the premotor cortex of young adults and elderly participants (Fig. 1A) as well as the activation in left parietal loci observed in children and young adults but not in elderly participants (see also Cohen Kadosh et al. 2007).
Developmental Trajectory of Magnitude Processing
Magnitude processing yielded a response pattern different from interference control. With respect to response latencies, young adults responded on average significantly faster than children but only marginally faster than elderly participants. Nonetheless, the distance effect observed in response latencies was comparable across the 3 age groups. Moreover, a more pronounced distance effect in the numerical relative to the physical task produced a significant interaction between task and magnitude processing. This result is in line with studies showing a larger distance effect in more demanding cognitive tasks (i.e., in the present study the numerical task; e.g., Henik and Tzelgov 1982; Kaufmann et al. 2005, 2006; Tang et al. 2006) because response latencies were longer in the numerical task. Moreover, it is widely accepted that relative to symbolic numerical stimulus features, physical ones are more salient and are processed faster (i.e., more automatically; see Henik and Tzelgov 1982; Szũcs et al. 2007) and therefore produce stronger interference on numerical processing. Importantly, moreover, no difference in brain activation due to task was observed. Finally, differences between numerical and physical comparison tasks seemed to be restricted to behavioral data because the similarities in the brain activations elicited in numerical and physical tasks upon distance processing were much more pronounced than the respective differential activations (see also Cohen Kadosh, Lammertyn, and Izard 2008). For these reasons, this difference between tasks will not be further interpreted.
As regards error rates, a larger distance effect was found in children relative to young adults and elderly, leading to a significant interaction between magnitude processing and group. In comparison to adults and elderly participants, children discriminated small distances much less accurately than large distances. As pointed out above, children and elderly participants activated distinct portions of the parietal cortex when solving the magnitude comparison task. On the one side, these results point out that both children and elderly participants are able to process number magnitude because a distance effect was always observed. On the other side, increased latencies reveal that magnitude comparison is more effortful for both children and elderly in comparison to adults. Nonetheless, although the high error rates committed by children most likely reflect a less accurate magnitude representation (Holloway and Ansari, 2009; Kaufmann and Nuerk 2008), the lower error rates exhibited by elderly participants are compatible with a more accurate magnitude representation. In elderly participants, longer response latencies may be attributed to a more general (domain unspecific) process of cognitive slowing, which has an impact on the general speed of information processing and response selection (Cohen Kadosh, Brodsky, et al. 2008 and Cohen Kadosh, Lammertyn, and Izard 2008).
Children also showed increased BOLD responses in comparison to elderly participants in the right supplementary motor area (SMA) and in the right DLPC. These activations may be attributed to a more effortful response selection in children (Garavan et al. 1999, 2002). Finally, in the left medial cerebellum, a significantly increased activation was found in elderly participants in comparison to adults. Activation in the medial cerebellum has been previously interpreted as an index for response selection demands and task difficulty (Donohue et al. 2008). The activation observed in these cerebellar regions may be necessary for elderly people to reach an accuracy comparable to that of adults but at the cost of slower responses in the magnitude comparison task.
Conclusions
Interference and magnitude processing are supported by a broad network of brain regions in children, young adults, and elderly individuals. Moreover, the developmental trajectories for these regions are clearly distinguishable. Specifically, interference control produced an age-linear increase of activation in prefrontal, middle temporal, and cerebellar cortex implicating that interference control becomes more effortful with age and triggers the use of compensatory mechanisms. In contrast, magnitude processing described a nonlinear decrease of activation in DLPC, intraparietal, and supplementary motor cortex. This reveals that with the consolidation of the magnitude representation, the network activation observed in response to magnitude processing decreases. Taken together, the present findings suggest that even under comparable behavioral conditions, the neural networks activated by children and elderly individuals are strongly modulated by brain maturation and by age-dependent differential recruitment of compensatory strategies alike.
Acknowledgments
Funding
Medical Research Foundation Tyrol, Austria (project number 121); Austrian Science Foundation (T286-B05) and Tyrolean Science Fund (UNI-0404/523) to L. Kaufmann.
Footnotes
Conflict of Interest: None declared.
References
- Adleman NE, Menon V, Blasey CM, White CD, Warsofsky IS, Glover GH, Reiss AL. A developmental fMRI study of the Stroop color-word task. Neuroimage. 2002;16:61–75. doi: 10.1006/nimg.2001.1046. [DOI] [PubMed] [Google Scholar]
- Allison T, McCarthy G, Nobre A, Puce A, Belger A. Human extrastriate visual cortex and the perception of faces, words, numbers, and colors. Cereb Cortex. 1994;5:544–554. doi: 10.1093/cercor/4.5.544. [DOI] [PubMed] [Google Scholar]
- Amieva H, Phillips LH, Della Sala S, Henry JD. Inhibitory functioning in Alzheimer’s disease. Brain. 2004;127:949–964. doi: 10.1093/brain/awh045. [DOI] [PubMed] [Google Scholar]
- Ansari D, Dhital B. Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. J Cogn Neurosci. 2006;18:1820–1828. doi: 10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ashkenazi S, Henik A, Ifergane G, Shelef I. Basic numerical processing in left intraparietal sulcus (IPS) acalculia. Cortex. 2008;44:439–448. doi: 10.1016/j.cortex.2007.08.008. [DOI] [PubMed] [Google Scholar]
- Banich MT, Milhalm MP, Atchley R, Cohen NJ, Webb A, Wszalek T, Kramer AF, Liang ZP, Wright A, Shenker J, et al. fMRI studies of Stroop tasks reveal unique roles of anterior and posterior brain systems in attentional selection. J Cogn Neurosci. 2000;12:988–1000. doi: 10.1162/08989290051137521. [DOI] [PubMed] [Google Scholar]
- Besner D, Coltheart M. Ideographic and alphabetic processing in skilled reading of English. Neuropsychologia. 1979;17:467–472. doi: 10.1016/0028-3932(79)90053-8. [DOI] [PubMed] [Google Scholar]
- Boucart M, Humphreys GW. Attention to orientation, size, luminance, and color: attentional failure within the form domain. J Exp Psychol Hum Percept Perform. 1994;20:61–80. doi: 10.1037//0096-1523.20.1.61. [DOI] [PubMed] [Google Scholar]
- Brigman S, Cherry KE. Age and skilled performance: contributions of working memory and processing speed. Brain Cogn. 2002;50:242–256. doi: 10.1016/s0278-2626(02)00510-9. [DOI] [PubMed] [Google Scholar]
- Bub DN, Masson ME, Lalonde CE. Cognitive control in children: stroop interference and suppression of word reading. Psychol Sci. 2006;17:351–357. doi: 10.1111/j.1467-9280.2006.01710.x. [DOI] [PubMed] [Google Scholar]
- Bush G, Shin LM, Holmes J, Rosen BR, Vogt BA. The Multi-Source Interference Task: validation study with fMRI in individual subjects. Mol Psychiatry. 2003;8:60–70. doi: 10.1038/sj.mp.4001217. [DOI] [PubMed] [Google Scholar]
- Bush G, Whalen PJ, Rosen BR, Jenike MA, McInerney SC, Rauch SL. The counting Stroop: an interference task specialized for functional neuroimaging—validation study with functional MRI. Hum Brain Mapp. 1998;6:270–282. doi: 10.1002/(SICI)1097-0193(1998)6:4<270::AID-HBM6>3.0.CO;2-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterworth B. The mathematical brain. McMillan; London: 2005. [Google Scholar]
- Campbell JID. The handbook of mathematical cognition. Psychology Press; Hove (UK): 2005. [Google Scholar]
- Cohen Kadosh R, Brodsky W, Levin M, Henik A. Mental representation: what can pitch tell us about the distance effect? Cortex. 2008;44:470–477. doi: 10.1016/j.cortex.2007.08.002. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh K, Linden DEJ, Gevers W, Berger A, Henik A. The brain locus of interference between number and size: a combined functional magnetic resonance imaging and event related potential study. J Cogn Neurosci. 2007;19:957–970. doi: 10.1162/jocn.2007.19.6.957. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Henik A. A common representation for semantic and physical properties: a cognitive-anatomical approach. Exp Psychol. 2006;53:87–94. doi: 10.1027/1618-3169.53.2.87. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Henik A, Rubinstein O, Mohr H, Dori H, van de Ven V, Zorzi M, Hendler T, Goebel R, Linden DE. Are numbers special? The comparison systems of the human brain investigated by fMRI. Neuropsychologia. 2005;43:1238–1248. doi: 10.1016/j.neuropsychologia.2004.12.017. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol. 2008;84:132–147. doi: 10.1016/j.pneurobio.2007.11.001. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Akhavein R. Attention, automaticity and levels of representation in number processing. J Exp Psychol Learn Mem Cogn. 1995;21:314–326. doi: 10.1037//0278-7393.21.2.314. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, Giraux P. The mental representation of parity and number magnitude. J Exp Psychol Gen. 1993;122:371–396. [Google Scholar]
- Dehaene S, Dupoux E, Mehler J. Is numerical comparison digital: analogical and symbolic effects in two-digit number comparison. J Exp Psychol Hum Percept Perform. 1990;16:626–641. doi: 10.1037//0096-1523.16.3.626. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cogn Neuropsychol. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Diamond A. Close interrelation of motor development and cognitive development and of the cerebellum and prefrontal cortex. Child Dev. 2000;71:44–56. doi: 10.1111/1467-8624.00117. [DOI] [PubMed] [Google Scholar]
- Donohue SE, Wendelken C, Bunge SA. Neural correlates of preparation for action selection as a function of specific task demands. J Cogn Neurosci. 2008;20:1–13. doi: 10.1162/jocn.2008.20042. [DOI] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA. Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci USA. 2007;104:11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan EM, McFarland CE. Isolating the effects of symbolic distance and semantic congruity in comparative judgments: an additive factors analysis. Mem Cognit. 1980;8:612–622. doi: 10.3758/bf03213781. [DOI] [PubMed] [Google Scholar]
- Duverne S, Lemaire P. Aging and arithmetic. In: Campbell JID, editor. The handbook of mathematical cognition. Psychology Press; London: 2005. pp. 397–412. [Google Scholar]
- Fair DA, Cohen AL, Dosenbach NU, Church JA, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. The maturing architecture of the brain’s default network. Proc Natl Acad Sci USA. 2008;105:4028–4032. doi: 10.1073/pnas.0800376105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Dosenbach NU, Church JA, Cohen AL, Brahmbhatt S, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. Development of distinct control networks through segregation and integration. Proc Natl Acad Sci USA. 2007;104:13507–13512. doi: 10.1073/pnas.0705843104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Penny WD, Glaser DE. Conjunction revisited. Neuroimage. 2005;15:653–660. doi: 10.1016/j.neuroimage.2005.01.013. [DOI] [PubMed] [Google Scholar]
- Garavan H, Ross TJ, Murphy K, Roche RA, Stein EA. Dissociable executive functions in the dynamic control of behavior: inhibition, error detection, and correction. Neuroimage. 2002;17:1820–1829. doi: 10.1006/nimg.2002.1326. [DOI] [PubMed] [Google Scholar]
- Garavan H, Ross TJ, Stein EA. Right hemispheric dominance of inhibitory control: an event-related functional MRI study. Proc Natl Acad Sci USA. 1999;96:8301–8306. doi: 10.1073/pnas.96.14.8301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazzaley A, Cooney JW, Rissman J, D’Esposito M. Top-down suppression deficit underlies working memory impairment in normal aging. Nat Neurosci. 2005;8:1298–1300. doi: 10.1038/nn1543. [DOI] [PubMed] [Google Scholar]
- Gazzaley A, D’Esposito M. Top-down modulation and normal aging. Ann N Y Acad Sci. 2007;1097:67–83. doi: 10.1196/annals.1379.010. [DOI] [PubMed] [Google Scholar]
- Gebuis T, Cohen Kadosh R, de Haan E, Henik A. Automatic quantity processing in 5-year olds and adults. Cogn Process. 2008 doi: 10.1007/s10339-008-0219-x. doi: 10.1007/s10339-008-0219-x. [DOI] [PubMed] [Google Scholar]
- Girelli L, Lucangeli D, Butterworth B. The development of automaticity in accessing number magnitude. J Exp Child Psychol. 2000;76:104–122. doi: 10.1006/jecp.2000.2564. [DOI] [PubMed] [Google Scholar]
- Groen GJ, Parkman JM. A chronometric analysis of simple addition. Psychol Rev. 1972;79:329–343. [Google Scholar]
- Hasher L, Zacks RT. Working memory, comprehension, and aging: a review and a new view. In: Bower GH, editor. The psychology of learning and motivation. Vol. 22. Academic Press; New York: 1988. pp. 193–225. [Google Scholar]
- Henik A, Tzelgov J. Is three greater than five: the relation between physical and semantic size in comparison tasks. Mem Cognit. 1982;10:389–395. doi: 10.3758/bf03202431. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J Exp Child Psychol. 2009 doi: 10.1016/j.jecp.2008.04.001. Forthcoming. [DOI] [PubMed] [Google Scholar]
- Hubbard EM, Piazza M, Pinel P, Dehaene S. Interactions between number and space in parietal cortex. Nat Rev Neurosci. 2005;6:435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Ischebeck A, Weiss E, Koppelstaetter F, Siedentopf C, Vogel SE, Gotwald T, Marksteiner J, Wood G. An fMRI study of the numerical Stroop task in individuals with and without minimal cognitive impairment. Cortex. 2008;44:1248–1255. doi: 10.1016/j.cortex.2007.11.009. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Koppelstaetter F, Delazer M, Siedentopf C, Rhomberg P, Golaszewski S, Felber S, Ischebeck A. Neural correlates of distance and congruity effects in a numerical Stroop task: an event-related fMRI study. Neuroimage. 2005;25:888–898. doi: 10.1016/j.neuroimage.2004.12.041. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Koppelstaetter F, Siedentopf C, Haala I, Haberlandt E, Zimmerhackl L-B, Felber S, Ischebeck A. Neural correlates of a number-size interference task in children. Neuroreport. 2006;17:587–591. doi: 10.1097/00001756-200604240-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L, Montanes P, Jacquier M, Matallana D, Eibl G, Delazer M. About the relationship between basic numerical processing and arithmetics in Alzheimer’s disease—a follow-up study. Brain Cogn. 2002;48:398–405. [PubMed] [Google Scholar]
- Kaufmann L, Nuerk H-C. Numerical development: current issues and future perspectives. Psychol Sci. 2005;47:142–170. [Google Scholar]
- Kaufmann L, Nuerk HC. Basic number processing deficits in ADHD: a broad examination of elementary and complex number processing skills in 9 to 12 year-old children with ADHD-C. Dev Sci. 2008;11:692–699. doi: 10.1111/j.1467-7687.2008.00718.x. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Vogel S, Wood G, Kremser C, Schocke M, Zimmerhackl L-B, Koten JW. A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex. 2008;44:376–385. doi: 10.1016/j.cortex.2007.08.003. [DOI] [PubMed] [Google Scholar]
- Knoch D, Brugger P, Regard M. Suppressing versus releasing a habit: frequency-dependent effects of prefrontal transcranial magnetic stimulation. Cereb Cortex. 2005;15:885–887. doi: 10.1093/cercor/bhh196. [DOI] [PubMed] [Google Scholar]
- Liu X, Banich MT, Jacobson BL, Tanabe JL. Functional dissociation of attentional selection within PFC: response and non-response related aspects of attentional selection as ascertained by fMRI. Cereb Cortex. 2006;16:827–834. doi: 10.1093/cercor/bhj026. [DOI] [PubMed] [Google Scholar]
- Lustig C, Hasher L, Tonev ST. Distraction as a determinant of processing speed. Psychon Bull Rev. 2006;13:619–625. doi: 10.3758/bf03193972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLeod CM, MacDonald PA. Interdimensional interference in the Stroop effect: uncovering the cognitive and neural anatomy of attention. Trends Cogn Sci. 2000;4:383–391. doi: 10.1016/s1364-6613(00)01530-8. [DOI] [PubMed] [Google Scholar]
- Martin S, Broillet D, Guerdoux E, Tarrago R. Inhibition and resource capacity during normal aging: a confrontation of the dorsal-ventral and frontal models in a modified version of negative priming. Encephale. 2006;32:253–262. doi: 10.1016/s0013-7006(06)76152-8. [DOI] [PubMed] [Google Scholar]
- Nieder A, Freedman DJ, Miller EK. Representation of the quantity of visual items in the primate prefrontal cortex. Science. 2002;297:1708–1711. doi: 10.1126/science.1072493. [DOI] [PubMed] [Google Scholar]
- Nieder A, Miller EK. A parieto-frontal network for visual numerical information in the monkey. Proc Natl Acad Sci USA. 2004;101:7457–7462. doi: 10.1073/pnas.0402239101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. The time required for judgments of numerical inequality. Nature. 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Pansky A, Algom D. Stroop and garner effects in comparative judgment of numerals: the role of attention. J Exp Psychol Hum Percept Perform. 1999;25:39–58. [Google Scholar]
- Pansky A, Algom D. Comparative judgment of numerosity and numerical magnitude: attention preempts automaticity. J Exp Psychol Learn Mem Cogn. 2002;28:259–274. doi: 10.1037//0278-7393.28.2.259. [DOI] [PubMed] [Google Scholar]
- Paxton JL, Barch DM, Racine CA, Braver TS. Cognitive control, goal maintenance, and prefrontal function in healthy aging. Cereb Cortex. 2007;18:1010–1028. doi: 10.1093/cercor/bhm135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Restle F. Speed of adding and comparing numbers. J Exp Psychol. 1970;83:274–278. [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb Cortex. 2005;24:50–60. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Rubia K, Smith AB, Woolley J, Nosarti C, Heyman I, Taylor E, Brammer M. Progressive interference of frontostriatal brain activation from childhood to adulthood during event-related tasks of cognitive control. Hum Brain Mapp. 2006;27:973–993. doi: 10.1002/hbm.20237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinsten O, Henik A, Berger A, Shahar-Shalev S. The development of internal representations of magnitude and their association with Arabic numerals. J Exp Child Psychol. 2002;81:74–92. doi: 10.1006/jecp.2001.2645. [DOI] [PubMed] [Google Scholar]
- Rypma B, Berger JS, Prabhakaran V, Bly BM, Kimberg DY, Biswal BB, D’Esposito M. Neural correlates of cognitive efficiency. Neuroimage. 2006;33:969–979. doi: 10.1016/j.neuroimage.2006.05.065. [DOI] [PubMed] [Google Scholar]
- Smith AB, Taylor E, Brammer M, Toone B, Rubia K. Task specific hypoactivation in prefrontal and temporal brain regions during motor inhibition and task switching in medication-naïve children and adolescents with attention-deficit hyperactivity disorder. Am J Psychiatry. 2006;163:957–960. doi: 10.1176/ajp.2006.163.6.1044. [DOI] [PubMed] [Google Scholar]
- Szũcs D, Soltész F, Jármi E, Csépe V. The speed of magnitude processing and executive functions in controlled and automatic number comparison in children: an electro-encephalography study. Behav Brain Funct. 2007;3:3–23. doi: 10.1186/1744-9081-3-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Critchley HD, Glaser DE, Donlan RJ, Butterworth B. Imaging informational conflict: a functional magnetic resonance imaging study of numerical stroop. J Cogn Neurosci. 2006;18:2049–2062. doi: 10.1162/jocn.2006.18.12.2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tewes U, Rossmann P, Schallberger U. Hamburg-Wechsler-Intelligenztest für Kinder III (HAWIK-III) Testzentrale; Göttingen (Bern): 1999. [Google Scholar]
- Townsend J, Adamo M, Haist F. Changing channels: an fMRI study of aging and cross-modal attention shifts. Neuroimage. 2006;31:1682–1692. doi: 10.1016/j.neuroimage.2006.01.045. [DOI] [PubMed] [Google Scholar]
- van Veen V, Carter CS. Separating semantic conflict and response conflict in the Stroop task: a functional MRI study. Neuroimage. 2005;27:497–504. doi: 10.1016/j.neuroimage.2005.04.042. [DOI] [PubMed] [Google Scholar]
- Wood G, Nuerk HC, Moeller K, Geppert B, Schnitker R, Weber J, Willmes K. All for one but not one for all: how multiple number representations are recruited in one numerical task. Brain Res. 2008;1187:154–166. doi: 10.1016/j.brainres.2007.09.094. [DOI] [PubMed] [Google Scholar]
- Wood G, Nuerk H-C, Sturm D, Willmes K. Using parametric regressors to disentangle properties of multi-feature processes. Behav Brain Funct. 2008;4:38. doi: 10.1186/1744-9081-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood G, Nuerk H-C, Willmes K. Neural representations of two-digit numbers: a parametric fMRI study. Neuroimage. 2006;46:358–367. doi: 10.1016/j.neuroimage.2005.07.056. [DOI] [PubMed] [Google Scholar]
- Wood G, Willmes K, Nuerk H-C, Fischer M. On the link between space and number: A meta-analysis of the SNARC effect. Psychol Sci Quart. 2008;50:489–525. [Google Scholar]
- Wynn K. Addition and subtraction by human infants. Nature. 1992;358:749–750. doi: 10.1038/358749a0. [DOI] [PubMed] [Google Scholar]
- Wynn K. Infants possess a system of numerical knowledge. Curr Dir Psychol Sci. 1995;4:172–177. [Google Scholar]
- Xu F. Numerosity discrimination in infants: evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E. Large number discrimination in 6-month old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Yetkin FZ, Rosenberg RN, Weiner MF, Purdy PD, Cullum CM. FMRI of working memory in patients with mild cognitive impairment and probable Alzheimer’s disease. Eur Radiol. 2006;16:193–206. doi: 10.1007/s00330-005-2794-x. [DOI] [PubMed] [Google Scholar]