Abstract
Lennard-Jones (LJ) parameters for a variety of model compounds have previously been optimized within the CHARMM Drude polarizable force field to reproduce accurately pure liquid phase thermodynamic properties as well as additional target data. While the polarizable force field resulting from this optimization procedure has been shown to satisfactorily reproduce a wide range of experimental reference data across numerous series of small molecules, a slight but systematic overestimate of the hydration free energies has also been noted. Here, the reproduction of experimental hydration free energies is greatly improved by the introduction of pair-specific LJ parameters between solute heavy atoms and water oxygen atoms that override the standard LJ parameters obtained from combining rules. The changes are small and a systematic protocol is developed for the optimization of pair-specific LJ parameters and applied to the development of pair-specific LJ parameters for alkanes, alcohols and ethers. The resulting parameters not only yield hydration free energies in good agreement with experimental values, but also provide a framework upon which other pair-specific LJ parameters can be added as new compounds are parametrized within the CHARMM Drude polarizable force field. Detailed analysis of the contributions to the hydration free energies reveals that the dispersion interaction is the main source of the systematic errors in the hydration free energies. This information suggests that the systematic error may result from problems with the LJ combining rules and is combined with analysis of the pair-specific LJ parameters obtained in this work to identify a preliminary improved combining rule.
1. Introduction
Computer simulations of atomic models are powerful tools that have improved the understanding of many biochemical phenomena, shedding new light on a range of systems from small molecule conformational preferences1,2 to the dynamics of a complete virus,3 protein-ligand binding,4 protein folding5 and nucleic acid dynamics.6 Underpinning such computer simulations is the concept of a force field: a parametrized set of simple differentiable mathematical functions that imitate the quantum mechanical Born-Oppenheimer energy surface and thus allow the calculation of the forces acting on atoms and molecules. Most of the force fields commonly used for the study of biomolecules are based around similar basic concepts,7 with a series of simplifying approximations introduced to render the simulation of large molecules computationally tractable. One such approximation is that the electrostatic properties of each atom are represented by a single effective point charge at the site of the nucleus, with energies of electrostatic interactions determined using a Coulomb potential. While this approximation has been both necessary and successful, it neglects the distortion of the electron density around an atom or molecule under the influence of an external field; such models based on fixed effective partial charges ignore the polarizability of the molecule. With increasing computational power available to researchers, the need to use simplified nonpolarizable potential functions in biomolecular simulations is lessened, and simulations based on force fields including an explicit representation of induced polarizability have become feasible.8,9,10 Moreover, it is known that there are certain situations in which the omission of polarizability may result in a force field unable to yield accurate results.7 For example, treatment of the cation-π interaction,11 which is potentially stronger than a conventional hydrogen bond12 and significant in many biological situations,13,14,15,16 has been shown to require polarizability.17
A number of different methods for the explicit inclusion of polarizability into molecular mechanics (MM) force fields are currently being considered.18 These include methods based on induced point-dipoles,19,20 classical Drude oscillators21 and the fluctuating charge model.22,23 The CHARMM Drude polarizable force field is an approach based on the classical Drude oscillator model24 in which polarizability is incorporated via the addition of a “Drude particle” associated with each heavy atom.21 This auxiliary Drude particle carries a point charge and is attached to its atomic nucleus by a harmonic spring; it is able to relax its position in response to an external field and the relative positions of the fixed charge at the nucleus and the displacement of the Drude particle then give rise to an induced dipole moment, accounting explicitly for the polarizability. To date, CHARMM Drude polarizable force field parameters have been developed for a variety of molecules, with a focus on small molecule analogues of the functional groups present within biological macromolecules. Specifically, force field parameters have been obtained for water;21,25 alkanes;26 alcohols;27 aromatics;28 ethers;29,30 N-containing aromatic heterocycles;31 amides,32 and sulfur-containing compounds.33 This parametrization has been achieved through extensive fitting to quantum mechanical and experimental reference data using methodologies that have become well-established.34,35 The resulting parameters have been shown to give satisfactory reproduction of many experimental properties, including liquid and crystal phase thermodynamic properties, liquid phase dielectric constants, dipole moments, interactions with rare gas molecules and vibrational spectra. However, the force field resulting from this well-established optimization protocol tends to slightly but systematically overestimate the hydration free energies relative to experimental values (ie. the calculated free energies are too favorable by about 1 kcal/mol).
Clearly, the ability to match experimental hydration free energies accurately, (ie. to within a fraction of a kcal/mol) is highly desirable for a force field that is targeted at the modeling of biomolecular systems. For example, as Xu et al. note, “hydration free energies of amino acids are important because they are directly related to protein folding, protein-protein and protein-membrane interactions.”36 Shirts and Pande further argue that one “cannot expect that calculations performed on more complicated systems, such as those used to compute ligand-protein binding free energies, will be any more accurate than the hydration free energies (or at least the relative hydration free energies) of the respective small constituents.”37 With many of the parameters developed for use in the CHARMM Drude polarizable force field targeted at small molecule analogues of amino acid side chains and drug-like functional groups, these statements alone indicate the importance that should be attached to the accurate reproduction of hydration free energies for all model compounds within the CHARMM Drude polarizable force field.
Accurate calculation of hydration free energies has long been a problem within MM force fields,37, 38, 39 and a variety of approaches have been used in attempts to overcome this problem. Mobley et al. examined the role of atomic partial charges by performing calculations using charge sets derived from increasingly advanced levels of ab initio calculation, ultimately concluding that modifying the atomic charges made little difference to the agreement between calculated and experimental hydration free energies.40 Xu et al. attempted to correct hydration free energies for aromatic groups using an approach in which π electron density was represented using a series of non-atom centered point charges,41,42,43 finding that a good reproduction of experimental values could be obtained but, ultimately, that the extra complexity of the model was not justified when comparable improvements could be obtained using a simple reparametrization of the atomic point charges.36 Having previously identified that additive force fields uniformly “underestimate the solubility of all the (amino acid) side chain analogs”44 Shirts and Pande37 came to a similar conclusion. They suggested that the inability of biomolecular force fields to reproduce hydration free energies arose because they were not generally included in the parametrization process. They also concluded that, through careful modification of parameters, it was possible to obtain accurate reproduction of hydration free energies without sacrificing the reproduction of other properties of interest. However, attempts to develop a complete set of parameters for the GROMOS force field based on the simultaneous reproduction of liquid phase thermodynamic properties, free energies of solvation in cyclohexane and hydration free energies were unsuccessful.39 The authors concluded that “for almost all functional groups (they) could not find a combination of a charge distribution and a set of van der Waals parameters that would reproduce the free enthalpy of hydration while simultaneously reproducing the density and heat of vaporization of the pure liquid.”39 Instead, they ultimately produced two sets of parameters: one for use in neat liquid simulations, and one for use in aqueous phase calculations. Unsurprisingly, the parameter set optimized to reproduce hydration free energies (termed 53A6) was subsequently shown45 to provide a better reproduction of the hydration free energies of a series of amino acid side chain analogs than did either the AMBER9946 or OPLS-AA47,48 models. Both of those models yielded hydration free energies that were systematically less favorable than the experimental results. The ability of the 53A6 parameter set to reproduce solvation free energies in a variety of non-aqueous solvents has also been tested, with the parameters yielding results that are generally “in satisfactory agreement with experiment.”49
One of the most persistently problematic areas for MM force fields has been the accurate representation of the “anomalous” hydration free energies of amines and amides, where the addition of hydrophobic methyl groups results in a more favorable hydration free energy.50,51 Early additive force fields failed to capture this effect,52 and attempts to remedy the problem via the inclusion of polarizability also proved unsuccessful.53,54 Ultimately, the work of Rizzo and Jorgensen55 and subsequently Chen et al.56 showed that the errors obtained were due to “nonoptimal parametrization” and that a good reproduction of experimental data could be obtained using a well parametrized additive model with “no need for models with more complex functional forms including explicit polarizability.”55
Within the CHARMM Drude polarizable force field, hydration free energies calculated using parameters obtained from optimizations primarily targeting the accurate reproduction of pure liquid properties are typically too favorable. Figure 1 shows the relationship between experimental hydration free energies and hydration free energies calculated using the CHARMM Drude polarizable force field taken from the literature, as well as a previously unpublished set of hydration free energies calculated for a series of S containing compounds.33 While the deviations are small, most are smaller than 1.5 kcal/mol, they are clearly indicative of a systematic problem. There are three points, representing ethane, cyclohexane and ethane thiol, that lie above the line of perfect correlation, indicating calculated values that are less favorable than the corresponding experimental values. The remaining 22 calculated values, which lie below the line, are more favorable than the corresponding experimental values. For the acyclic alkanes,26 errors range from 0.07 kcal/mol (4.0%) for ethane to −0.69 kcal/mol (−32.1%) for butane (Table 2). It is also notable that for the linear alkanes, experimental hydration free energies appear to increase with increasing chain length, while calculated hydration free energies decrease with increasing chain length; the hydration free energies are also too favorable with the alkane parameters57 for a CHARMM fluctuating charge58 polarizable force field and they do not show the decrease in solvation as a function of chain length. For the alcohols,27 the errors in the calculated values range from −0.09 kcal/mol (2%) for methanol to −1.54 kcal/mol (34%) for butan-2-ol, with the force field again failing to predict correctly the sign of the change in hydration free energy that occurs with increasing chain length (Table 2). Similar results were also obtained for the ethers30 (Table 2), where all hydration free energies are predicted by the Drude model to be too favorable, with errors ranging from −0.05 kcal/mol (2.6%) for dimethyl ether to −2.22 kcal/mol (71.2%) for tetrahydropyran.
Figure 1.
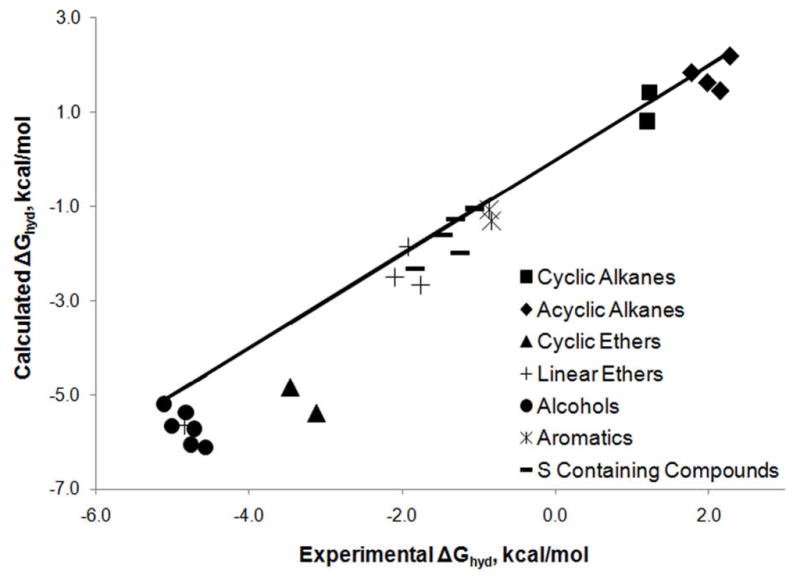
Comparison of experimental hydration free energies with published values calculated using the CHARMM Drude polarizable force field.
Table 2.
Hydration free energies of alkanes, alcohols and ethers, all values in kcal/mol.
| Molecule | Experimental ΔGhyd | Previously Reported Drude ΔGhyd | Error | Without pair-specific LJ parameters ΔGhyd | Error | With pair-specific LJ parameters ΔGhyd | Error |
|---|---|---|---|---|---|---|---|
| Alkanes | |||||||
| CPEN | 1.20a | 0.81 ± 0.39 | −0.39 | 0.10 ± 0.05 | −1.10 | 1.16 ± 0.08 | −0.04 |
| CHEX | 1.23a | 1.42 ±0.21 | 0.19 | 0.44 ± 0.05 | −0.79 | 1.22 ± 0.10 | −0.01 |
| ETHA | 1.77b | 1.84 | 0.07 | 1.64 ± 0.08 | −0.13 | 1.73 ± 0.10 | −0.04 |
| PROP | 1.98b | 1.63 | −0.35 | 1.32 ± 0.04 | −0.66 | 2.04 ± 0.08 | 0.06 |
| BUTA | 2.15b | 1.46 | −0.69 | 1.12 ± 0.12 | −1.04 | 2.08 ± 0.07 | −0.07 |
| IBUT | 2.28b | 2.19 | 0.09 | 1.47 ± 0.08 | −0.81 | 2.25 ± 0.02 | −0.03 |
| NEOP | 2.50c | N/A | N/A | 0.69 ± 0.10 | −1.81 | 2.25 ± 0.12 | −0.26 |
| Average | −0.91 | −0.06 | |||||
| Alcohols | |||||||
| MEOH | −5.11a | −5.20 ± 0.19 | −0.09 | −5.20 ± 0.08 | −0.09 | −5.20 ± 0.08 | −0.09 |
| ETOH | −5.01a | −5.66 ± 0.31 | −0.65 | −5.14 ± 0.07 | −0.13 | −4.85 ± 0.07 | 0.16 |
| PRO2 | −4.76a | −6.06 ± 0.23 | −1.30 | −5.50 ± 0.05 | −0.74 | −5.41 ± 0.05 | −0.65 |
| BUO2 | −4.57c | −6.11 ± 0.18 | −1.54 | −5.57 ± 0.08 | −1.00 | −4.21 ± 0.08 | 0.36 |
| PRO1 | −4.83a | −5.38 ± 0.16 | −0.55 | −5.21 ± 0.08 | −0.38 | −4.96 ± 0.08 | −0.13 |
| BUO1 | −4.72a | −5.72 ± 0.16 | −1.00 | −5.61 ± 0.09 | −0.89 | −4.74 ± 0.09 | −0.02 |
| Average | −0.54 | −0.06 | |||||
| Ethers | |||||||
| THF | −3.47c | −4.80 ± 0.08 | −1.33 | −4.83 ± 0.05 | −1.36 | −3.58 ± 0.05 | −0.11 |
| THP | −3.12c | −5.34 ± 0.27 | −2.22 | −5.40 ± 0.07 | −2.28 | −3.08 ± 0.10 | 0.04 |
| DEE | −1.76c | −2.77 ± 0.10 | −1.01 | −2.66 ± 0.15 | −1.76 | −1.83 ± 0.14 | −0.07 |
| DMOE | −4.84c | −5.61 ± 0.54 | −0.77 | −5.47 ± 0.11 | −0.63 | −5.05 ± 0.13 | −0.21 |
| DME | −1.92c | −1.97 ± 0.13 | −0.05 | −1.85 ± 0.07 | 0.07 | −1.85 ± 0.06 | 0.07 |
| MEE | −2.10d | −2.27 ± 0.25 | −0.17 | −2.51 ± 0.08 | −0.41 | −1.78 ± 0.08 | 0.32 |
| Average | −1.06 | 0.01 | |||||
| Overall Average | −0.84 | −0.03 | |||||
During optimization of Drude parameters for several series of molecules,27,31 attempts have been made to overcome this problem and provide an accurate reproduction of experimental hydration free energies. These attempts have focused on the use of specific atom-atom Lennard-Jones (LJ) parameters (ie. pair-specific LJ parameters), parameters that can be introduced using the NBFIX option in the CHARMM parameter file thereby overriding the standard LJ parameter combining rules. The use of pair-specific LJ parameters within the Drude model has focused on modifying the interaction between solute atoms and the O atom of the SWM4-NDP25 polarizable water model, and has generally been successful where applied. For example: in the alcohols, the inclusion of pair-specific parameters to modify the interaction between the hydroxyl O and the water O reduced the average error in calculated hydration free energies from 17% to −1%.27
Within the CHARMM Drude polarizable force field, the repulsion and dispersion components of the nonbond interaction energy, ELJ(r), are calculated using a standard LJ potential:
| (1) |
Where r is the separation between two interacting atoms and Rmin and ε are two empirical parameters, corresponding to the value of r at which ELJ(r) is a minimum, and the depth of the energy well, respectively. The values of Rmin and ε used to calculate the interaction between two atoms i and j are obtained from individual parameters assigned to each of the two interacting atoms via the following combining rules:
| (2) |
| (3) |
When pair-specific LJ parameters are used, however, these standard combining rules are overridden. Values of Rmin and ε for a given atom pair are not calculated from individual contributions arising from each atom, but instead are specified directly. This approach allows for the inclusion of pair-specific LJ parameters for any atom pairs of choice, while nonbond interactions involving all other atom pairs are calculated using Rmin and ε values obtained via the standard combining rules.
As mentioned above, the pair-specific LJ parameter approach to correcting calculated hydration free energies has been shown to work.27,31 An objective of the present work is, therefore, to extend this approach to allow for the development of new pair-specific LJ parameters in a more systematic fashion. As an example, consider the case of the alcohols, where alcohol hydration free energies were modified by introducing pair-specific LJ parameters.27 The alcohol parameters were built upon the alkane parameters with the nonbond parameter optimization focusing on the hydroxyls and adjacent aliphatic moieties; the remaining alkane parameters were directly transferred. However, when efforts were made to correct for the free energies of hydration, pair-specific LJ terms were introduced only for the hydroxyl O atoms. Changes were not made in the alkane LJ parameters, which were problematic, as stated above. This led to overcompensation in the case of the pair-specific LJ parameters for the interaction between the hydroxyl O atom and the water O atom. Accordingly, it is necessary to reconsider the implementation of pair-specific LJ parameters in the Drude polarizable force field.
If the pair-specific LJ approach is to be used to correct calculated hydration free energies within the CHARMM Drude polarizable force field, it is essential that these parameters be applied in a consistent way, which allows for the simultaneous representation of all classes of molecules. In addition, it would be useful for future force field developers if a general parametrization approach could be developed to allow for parameter optimization that is as systematic and straightforward as possible. With these goals in mind, the specific objectives of this work are:
The implementation of pair-specific LJ parameters in a hierarchical fashion, starting with the alkanes.
The development of a consistent set of pair-specific LJ parameters that give good reproduction of hydration free energies across all series of parametrized molecules.
The development of a reliable, systematic protocol for the determination of pair-specific LJ parameters.
2. Theory and Methods
The literature values of the hydration free energies calculated using the CHARMM Drude polarizable force field that are listed in Table 2 and illustrated in Figure 1 have been obtained from a series of distinct studies. To avoid any discrepancies introduced by small differences in free energy simulation methodologies and sampling, the first stage of this work was to re-calculate the free energy of hydration for every molecule considered in this study using an identical protocol. Specifically, free energies of aqueous solvation were calculated via the free energy perturbation (FEP) method59 using the staged protocol of Deng and Roux.38 In this method, the LJ potential is separated into purely repulsive and attractive parts using the scheme originally developed by Weeks, Chandler and Andersen (WCA).60
When a single solute molecule, u, is solvated in solvent v, with the coordinates of solute and solvent represented by X and Y respectively, the solute-solvent interaction potential, Euv(X,Y), comprises a short-range nonpolar contribution and a long-range electrostatic contribution:
| (4) |
The nonpolar contribution is given by the LJ equation (Equation 1) and, using the WCA scheme, is separated into contributions due to the repulsive and attractive (dispersion) interactions, so that
| (5) |
Where the repulsive and attractive contributions to the LJ potential are given by Equations 6 and 7.
| (6) |
| (7) |
With the WCA scheme applied, the total potential energy of the system can be written as
| (8) |
Where Eu is the internal potential energy of the solute molecule, Ev is the solvent potential energy and Euv represents the interaction between solvent and solute molecules, with the three terms corresponding to the Coulomb electrostatic, LJ-WCA core repulsion and LJ-WCA dispersive attraction, respectively. For the free energy perturbation calculation, coupling between the initial and final states (Ea and Eb) is achieved by means of a staging parameter. For both the electrostatic and dispersive interactions, a simple linear coupling of the initial and final states is used, with coupling parameters denoted λ and ξ (Equations 9 and 10).
| (9) |
| (10) |
For the solute-solvent core repulsion term, such linear scaling is not practical, and the repulsion term is instead transformed into a soft-core potential using the nonlinear staging parameter, s:
| (11) |
With the formulation in place, the reversible work corresponding to the insertion of the fully interacting solute into the solvent is calculated in three steps using three distinct staging parameters s, ξ and λ. Initially, the solute-solvent core repulsion is progressively introduced (Equation 12), followed by the dispersion interaction (Equation 13) and finally the electrostatic interaction (Equation 14). The total solvation free energy is then the sum of these three terms.
| (12) |
| (13) |
| (14) |
The computational details were identical to those described elsewhere,30 but with the simulation time extended to 50 ps of equilibration and 100 ps of production for a given value of the coupling and/or staging parameter (with coordinates saved every 0.1 ps), and all free energy values presented as the average of five (rather than three) separate calculations.
A long-range correction61 was also included to account for errors introduced by the truncation of LJ interactions. To calculate this long range correction, for every calculated value of the hydration free energy a single simulation of a single solute molecule in a box of 250 SWM4-NDP25 water molecules was run for 50 ps of molecular dynamics in the NVT ensemble, during which coordinates were saved every 1 ps. Following completion of the MD simulation, coordinates were extracted from the final 30 ps of the CHARMM trajectory file and energies were calculated for each set of coordinates using two different non-bonded interaction cutoff schemes. In the first scheme, nonbond pair lists were maintained to 14 Å with a cutoff of 12 Å used for both electrostatic and van der Waals (vdW) terms, with the latter truncated via an atom-based switch algorithm. In the second scheme, the only differences were that nonbond pair lists were maintained to 54 Å, and a cutoff of 50 Å was used. The difference in the vdW interaction energy calculated using the two non-bonded interaction cutoff schemes, averaged over all sets of coordinates, was taken as the long range correction. The longer cutoff used in these calculations (50 Å) was significantly larger than that used in previous work, where nonbond pair lists were maintained to 36 Å and a cutoff of 32 Å was used.30 The motivation for this change will be discussed in detail in the Results section. It should be noted that the box of 250 SWM4-NDP water molecules used in these calculations has a side length of approximately 20 Å. When a nonbond cutoff of 50 Å (or indeed 32 Å) is used, this means that periodic images of the solvent box must be used to calculate the total nonbond interactions. Each of these periodic images also includes one copy of the solute molecule, and so the total nonbond interaction energy includes a contribution due to solute-solute interactions. In practice, however, this contribution is small. The nearest solute image to the original solute molecule will be at a distance of 20 Å, and there will be six such images at this distance. Taking butane as an example, the solute-image solute interaction energy will be around −0.0005 kcal/mol per image, totaling −0.003 kcal/mol. Images at greater distances will have an even smaller impact. In addition, these solute molecules are occupying space that would otherwise be occupied by water molecules. A single butane molecule has a molecular volume of 160.5 Å,26 which is equivalent to the volume occupied by 5.3 water molecules.25 At a distance of 20 Å, 5.3 water molecules would contribute around −0.0003 kcal/mol to the total interaction energy. Overall, it can therefore be said that the overall error introduced by the presence of a single solute image at a distance of 20 Å is −0.0002 kcal/mol. Errors of this magnitude will have negligible impact on the final calculated results.
The computational method for calculation of the long-range correction described above has been applied in previous simulations involving the CHARMM Drude polarizable force field.27,30,31,33 To evaluate the quality of this long range correction calculation, the long range correction has also been evaluated analytically37,44,62 by solving Equation 15.
| (15) |
Where i runs over all solute atoms, r is the distance from solute atom i, ρ is the number density of solvent molecules, ε and Rmin are the LJ parameters between atom i and the O atom of the solvent water molecule (the H atoms of the SWM4-NDP water model have no LJ parameters), S(r) is the switching function used to reduce smoothly the interaction from its full value to 0, and ron is the distance at which the switching function is turned on. For this approach to be valid, it is required that the solvent radial distribution function g(r) = 1 at all points beyond ron. This is known to be true for the SWM4-NDP water model.25
The simulations described above were all performed using the program CHARMM63 without the inclusion of any pair-specific LJ parameters. The same procedure was also used to calculate an initial, uncorrected, hydration free energy for any molecule that had not had its hydration free energy evaluated as part of a previous study.
2.1 Pair-specific LJ Parameter Determination
Precise calculation of hydration free energies via the FEP method described above is a computationally intensive process, and it would be impractical to derive new pair-specific LJ parameters by scanning over ranges of Rmin and ε and using FEP to calculate the hydration free energy for every parameter combination. Instead, a method is implemented to provide an initial assessment of the approximate values of Rmin and ε that are likely to yield hydration free energies in good agreement with experimental results, so that the FEP calculation of actual hydration free energies can be reduced to only a small number of new parameter sets. To achieve this, initial molecular dynamics (MD) simulations were performed on each of the solute molecules in a box of 250 SWM4-NDP25 water molecules for 150 ps at a temperature of 298 K in the NPT ensemble, with periodic boundary conditions (PBC) and the SHAKE algorithm64 used to constrain covalent bonds to hydrogen. Electrostatic interactions were treated using particle-mesh Ewald (PME) summation65 with a coupling parameter of 0.34 and a sixth order spline for mesh interpolation. All simulations used the standard CHARMM Drude polarizable force field parameters, as described in the respective publications,26,27,30 and included no pair-specific LJ parameters. A timestep of 1 fs was employed, and coordinates were saved to a trajectory file every 100 steps.
Once these MD simulations were complete, the free energy changes associated with changing the LJ parameters could be calculated. The LJ parameters used in the original MD simulation were first used to evaluate the solute-solvent interaction energy for every set of coordinates saved to the trajectory file. The LJ parameters used in the original MD simulation were then modified, the trajectory file was reread and, for every set of coordinates, the solute-solvent interaction energy was re-evaluated using the new set of parameters. The difference in the solute-solvent interaction energies obtained using the original and modified LJ parameters was then used to estimate the free energy change associated with modifying the parameters. Once the free energy change for modifying the parameters in aqueous solution is obtained, it is straightforward to obtain the hydration free energy of the solute with the new LJ parameters by considering the thermodynamic cycle in Figure 2.
Figure 2.
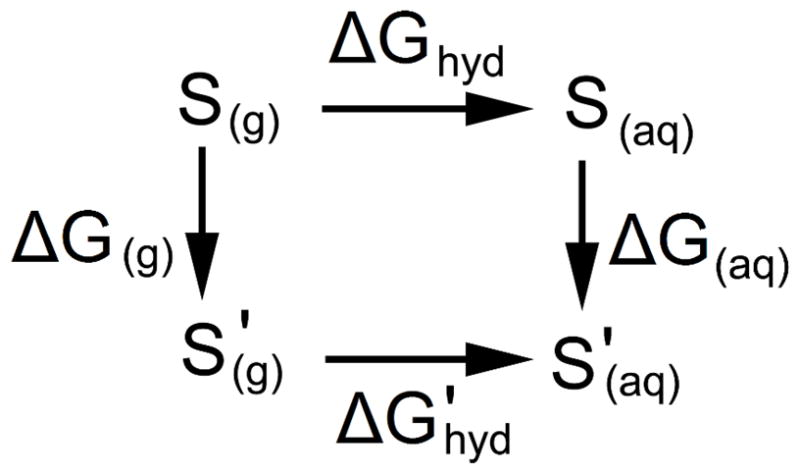
Thermodynamic cycle for calculating the free energy of hydration with a perturbed set of LJ parameters, ΔG′hyd, from the free energy of hydration with the original set of LJ parameters, ΔGhyd. S indicates the solute represented using the original set of LJ parameters; S′ indicates the solute represented using the perturbed set of LJ parameters.
The free energy of hydration associated with the new set of LJ parameters, ΔG′hyd, can be calculated from Equation 16.
| (16) |
Because, by design, only the parameters affecting interactions between the solute and the solvent are modified, ΔG(g) = 0 such that the free energy change associated with modifying the parameters in aqueous solution, ΔG(aq), is sufficient to provide for the difference between ΔGhyd and ΔG′hyd. The method described above for the calculation of ΔG(aq) is highly approximate because, in reality, the system will reorganize itself in response to any parameter change that changes the interaction energies and forces, whereas the approach outlined here assumes that the solvent structure around the solute is unaffected by the change in parameters. However, this technique is sufficient to provide a first approximation of parameter values that will yield a reasonable hydration free energy, and the impact of new parameter values can be assessed in a matter of seconds, rather than the approximately 2400 hours of CPU time required to evaluate a single hydration free energy using the full method outlined above.
Once this approximate method had been used to identify a set of pair-specific LJ parameters appropriate for calculation of the hydration free energy for a given solute, its free energy of hydration was evaluated using the full FEP method described above. Three independent FEP calculations were performed, and the resulting hydration free energy values were averaged to give a final result. This result was then compared to the relevant experimental value. If necessary, the pair-specific LJ parameters were adjusted again and the hydration free energy re-evaluated, with this process repeated until satisfactory agreement with experiment was obtained. During parametrization of the CHARMM Drude polarizable force field, the aim is generally that final calculated values should be within ~2% of the corresponding experimental values. In this work, where experimental target values can be extremely small, and uncertainties in calculated values relatively large, such an approach is less reasonable. Cyclopentane, for example, has an experimental hydration free energy of 1.20 kcal/mol: a 2% target would require a calculated value to be between 1.18 kcal/mol and 1.22 kcal.mol. Given that the uncertainty in the calculated value of ΔGhyd for cyclopentane with no pair-specific LJ parameters is 0.05 kcal/mol (Table 2) this level of accuracy is unrealistic. Rather, a goal where the final calculated hydration free energies should be within 0.1 kcal/mol of the corresponding experimental value is more reasonable. Once satisfactory agreement with experiment had been obtained, further FEP calculations were performed so that the final hydration free energy values presented in this work are the average of five individual calculations. The error in each calculation is given as the standard deviation of the mean calculated over 500 iterations of a bootstrap procedure using software by Wessa.66
To evaluate the effect that the introduction of pair-specific LJ parameters would have on other calculated properties, solute-water heterodimeric complexes were examined. The methods used and results obtained are described in the Supplementary Material that accompanies this paper.
2.2 Testing the Need for Pair-specific LJ Parameters
It has been shown in the past that the use of pair-specific LJ parameters allows for the correction of hydration free energies when LJ parameters derived to reproduce liquid phase thermodynamic properties are unable to, and this study aims to exploit this fact. There is, however, an important question that must also be addressed during this work: are pair-specific LJ parameters really essential or, as some have suggested, would it be possible, by including ΔGhyd values as target data in the initial parameter optimization, to find a set of LJ parameters that are able to reproduce accurately both the liquid phase thermodynamic data and solvation free energies simultaneously?
In an attempt to answer this question, the final pair-specific LJ parameters developed in this study were broken down into their constituent parts using the inverse of the standard LJ combining rules:
| (17) |
| (18)* |
Where Rmin and ε are the pair-specific LJ parameter values and the ODW atom LJ parameters are fixed, thereby transferring the whole of the effect of the pair-specific LJ parameters onto the solute heavy atoms. In this way, it was possible to generate a new set of atomic LJ parameters, Rmin/2 and εi, for every atom type considered in this study. Once this had been done, a series of calculations were performed to evaluate the molecular volume (Vm) and enthalpy of vaporization (ΔHvap) of each of four alkane and five ether molecules, to assess whether these new pair-specific LJ parameters would be appropriate for use in both the bulk liquid and aqueous solution, indicating that one set of parameters would be sufficient in both cases, and that specific heavy atom-ODW LJ parameters would be unnecessary. To calculate Vm and ΔHvap for each molecule ten liquid phase molecular dynamics simulations of 150 ps duration were performed. All ten liquid phase simulations were commenced from an identical pre-equilibrated box of 128 molecules, with a random number seed used to assign different initial velocities in each case. The first 50 ps were treated as equilibration, with the remaining 100 ps used for analysis. Volumes and energies were averaged over all ten simulations, and the gas phase contribution to the heat of vaporization was calculated from a single simulation of 2.5 ns, with 0.5 ns used for equilibration and 2.0 ns for analysis. All simulations were performed at the temperatures reported in Table 5.
Table 5.
Vm and ΔHvap calculated using LJ parameters obtained from the pair-specific LJ parameters calculated in this work, and compared to Vm and ΔHvap calculated using the standard CHARMM Drude polarizable force field LJ parameters.
| T/K | Experimental | Standard LJ | % err | Pair-specific LJ | %err | |
|---|---|---|---|---|---|---|
| Molecular Volumes | ||||||
| ETHA | 184.55 | 91.8 | 91.6 ± 0.3 | −0.2 | 95.6 ± 1.7 | 4.1 |
| PROP | 231.10 | 125.7 | 124.5 ± 0.4 | −1.0 | 136.7 ± 1.8 | 8.8 |
| BUTA | 272.65 | 160.5 | 160.9 ± 0.3 | 0.2 | 182.8 ± 1.8 | 13.9 |
| IBUT | 261.43 | 162.5 | 160.6 ± 0.3 | −1.2 | 187.4 ± 3.0 | 15.3 |
| THF | 298.15 | 135.6 | 134.8 ± 0.4 | −0.6 | 148.4 ± 1.6 | 9.5 |
| THP | 298.15 | 162.3 | 163.8 ± 0.8 | 0.9 | 188.7 ± 1.8 | 16.3 |
| DMOE | 298.15 | 173.6 | 178.1 ± 0.9 | 2.6 | 194.3 ± 1.3 | 11.9 |
| DME | 248.34 | 104.9 | 104.2 ± 0.8 | −0.7 | 108.3 ± 1.0 | 3.2 |
| MEET | 273.20 | 137.5 | 140.2 ± 0.8 | 2.0 | 152.8 ± 1.4 | 11.1 |
| Heats of Vaporization | ||||||
| ETHA | 184.55 | 3.53 | 3.42 ± 0.01 | −3.1 | 3.23 ± 0.03 | −8.5 |
| PROP | 231.10 | 4.51 | 4.48 ± 0.01 | −0.7 | 3.67 ± 0.02 | −18.6 |
| BUTA | 272.65 | 5.37 | 5.41 ± 0.03 | 0.7 | 3.66 ± 0.02 | −31.8 |
| IBUT | 261.42 | 5.12 | 5.03 ± 0.02 | −1.8 | 3.71 ± 0.04 | −27.5 |
| THF | 298.15 | 7.65 | 7.69 ± 0.03 | 0.9 | 5.66 ± 0.04 | −26.0 |
| THP | 298.15 | 8.26 | 8.41 ± 0.04 | 1.8 | 5.59 ± 0.04 | −32.3 |
| DMOE | 298.15 | 8.79 | 8.67 ± 0.07 | −1.4 | 6.82 ± 0.04 | −22.4 |
| DME | 248.34 | 5.14 | 5.18 ± 0.02 | 0.8 | 4.51 ± 0.02 | −12.3 |
| MEET | 280.60 | 5.90 | 5.85 ± 0.04 | −0.8 | 4.68 ± 0.04 | −20.7 |
3. Results
3.1 The Long Range Correction
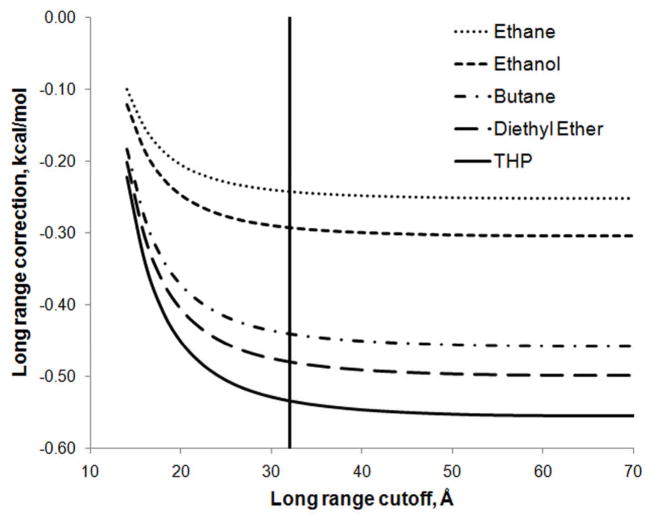
As noted above, in previous studies where the CHARMM Drude polarizable force field has been used to calculate hydration free energies, a cutoff of 32 Å has been used in the evaluation of the long-range correction associated with the truncation of the LJ interactions. In this study, the effect of the cutoff on the total long-range correction was examined and the results can be seen in Figure 4, where long-range corrections have been calculated for progressively larger molecules. While using a cutoff of 32 Å (denoted by the vertical line in Figure 4) captures the majority of the long-range correction, it is clear that at 32 Å the long range correction has not yet reached convergence. To achieve convergence (to two decimal places) for all of the molecules considered in this study, it was necessary to use a cutoff of at least 50 Å. The final long-range correction values obtained for all molecules in this study, both with and without pair-specific LJ parameters, are presented in Table 1 along with long-range correction values calculated analytically. The analytically calculated values can be considered the “correct” values, and it is encouraging to note that the numerically calculated values are very close to the analytically calculated values, with an average error of −0.011 kcal/mol and a maximum error of −0.018 kcal/mol. Such small errors will have minimal impact on the final hydration free energies and it can be concluded that the numerical method is valid for the evaluation of the long-range correction.
Figure 4.
Calculated hydration free energy of butane as a function of Rmin for the CD32A-ODW pair, with all other LJ parameters fixed. Rmin in Å, ΔGhyd in kcal/mol.
Table 1.
Calculated long range corrections, in kcal/mol, for molecules considered in this work.
| Molecule | Numerically Calculated Long Range Correctiona | Analytically Calculated Long Range Correction | ||
|---|---|---|---|---|
| Without pair-specific LJ parameters | With pair-specific LJ parameters | Without pair-specific LJ parameters | With pair-specific LJ parameters | |
| Alkanes | ||||
| CPEN | −0.505 ± 0.002 | −0.456 ± 0.002 | −0.519 | −0.468 |
| CHEX | −0.617 ± 0.002 | −0.575 ± 0.002 | −0.634 | −0.592 |
| ETHA | −0.250 ± 0.001 | −0.243 ± 0.001 | −0.255 | −0.248 |
| PROP | −0.353 ± 0.001 | −0.328 ± 0.002 | −0.361 | −0.334 |
| BUTA | −0.456 ± 0.002 | −0.409 ± 0.002 | −0.467 | −0.421 |
| IBUT | −0.441 ± 0.001 | −0.391 ± 0.002 | −0.455 | −0.405 |
| NEOP | −0.549 ± 0.001 | −0.487 ± 0.001 | −0.568 | −0.505 |
| Alcohols | ||||
| MEOH | −0.225 ± 0.001 | −0.225 ± 0.001 | −0.229 | −0.229 |
| ETOH | −0.303 ± 0.001 | −0.280 ± 0.002 | −0.311 | −0.288 |
| PRO2 | −0.392 ± 0.001 | −0.347 ± 0.001 | −0.404 | −0.357 |
| BUO2 | −0.494 ± 0.002 | −0.430 ± 0.001 | −0.511 | −0.444 |
| PRO1 | −0.402 ± 0.002 | −0.357 ± 0.001 | −0.414 | −0.368 |
| BUO1 | −0.504 ± 0.002 | −0.440 ± 0.001 | −0.521 | −0.454 |
| Ethers | ||||
| THF | −0.455 ± 0.002 | −0.408 ± 0.002 | −0.464 | −0.415 |
| THP | −0.553 ± 0.002 | −0.475 ± 0.001 | −0.564 | −0.484 |
| DEE | −0.495 ± 0.001 | −0.448 ± 0.003 | −0.506 | −0.458 |
| DMOE | −0.550 ± 0.001 | −0.499 ± 0.001 | −0.567 | −0.512 |
| DME | −0.309 ± 0.001 | −0.296 ± 0.002 | −0.317 | −0.303 |
| MEE | −0.401 ± 0.001 | −0.371 ± 0.002 | −0.411 | −0.381 |
Calculated values averaged over five independent simulations, with errors as ± 1 standard deviation.
3.2 Parametrization Strategy
One of the key objectives of this work was to obtain not only a set of useable parameters, but also a reliable method by which they should be obtained. The initial strategy employed was to vary Rmin until good agreement was obtained between the calculated and experimental hydration free energies. In particular, since all but one of the calculated hydration free energies were more favorable than their experimental equivalents, it was anticipated that increasing Rmin would be a good general strategy for making calculated free energies less favorable. For polar molecules this was based on the assumption that by increasing the radius at which the most favorable interaction occurs, atom pairs having favorable electrostatic interactions (specifically, hydrogen bonding interactions involving water molecules) would be pushed further apart, and these favorable electrostatic interactions would decrease. However, in the case of the nonpolar alkanes, such an approach is not appropriate because the LJ term dominates the free energy of aqueous solvation. For example, in the acyclic alkanes an increase in Rmin resulted in a more favorable free energy of hydration, as shown for butane in Figure 4.
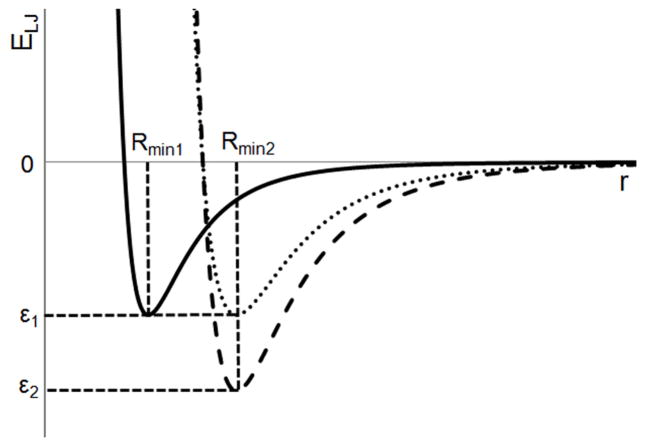
This effect can be explained by considering the functional form of the LJ term (Equation 1): Figure 5 shows two such LJ curves in which Rmin differs, but ε is unchanged. Comparison of these two curves shows that an atom-atom pair with a separation, r, greater than rint, the point at which the two curves intersect, will have a more favorable LJ interaction energy when Rmin = Rmin2 than when Rmin = Rmin1. An atom pair with a separation, r, less than rint, will have a less favorable interaction when Rmin = Rmin2 than when Rmin = Rmin1. Given the large number of atom-atom pairs with distances greater than rint, an increase in Rmin from Rmin1 to Rmin2 usually results in a more favorable total interaction. This in turn leads to the more favorable free energy of solvation of the alkanes with larger Rmin values on the C atoms, because the solvation free energy has a significant contribution from the LJ term as compared to more polar molecules. It is not until Rmin become so large that it causes significant short-range atom-atom repulsion that the LJ energy starts to become less favorable. Alternatively, increasing ε without changing Rmin (Figure 5) yields the more intuitive result where the overall LJ surface is more favorable at all atom-atom distances with the LJ interaction energy > 0. Importantly, varying ε also does not significantly impact the repulsive wall, which in the present study was that obtained from parameters based on the pure solvent or crystal simulations.
Figure 5.
Example LJ interaction energy curves. Comparing the two curves with ε = ε1: if the two curves intersect at a point rint, then all interactions with r > rint will become more favorable on moving from Rmin1 to Rmin2; all interactions with r < rint will become less favorable on moving from Rmin1 to Rmin2. Comparing the two curves with Rmin = Rmin2: moving from ε1 to ε2 results in interactions becoming more favorable at all values of r.
With these observations in mind a modified parametrization strategy was developed, having three distinct stages.
For polar molecules, attempt to correct the hydration free energy by varying only Rmin of heavy atom-ODW pairs, up to a maximum ΔRmin of 0.1 Å: if the calculated ΔGhyd in the absence of pair-specific LJ parameters is too favorable, only increasing Rmin is considered; if the calculated ΔGhyd in the absence of pair-specific LJ parameters is not favorable enough, only decreasing Rmin is considered.
In the case of nonpolar molecules, attempt to correct the free energy of hydration by varying only ε of heavy atom-ODW pairs.
If either 1 or 2 is unsuccessful, attempt to correct the hydration free energy by increasing both Rmin and ε of heavy atom-ODW atom pairs simultaneously.
To date, such an approach has been sufficient to give pair-specific LJ parameters that provide good agreement with experimental data in every case, with one exception. It is anticipated that, in the future, in the small number of cases where this scheme will not be successful, the molecules in question will need to be approached on a case-by-case basis: the only molecule for which pair-specific LJ parameters could not be obtained using this scheme in the present work will be discussed in detail below. All pair-specific LJ parameters obtained in this work are listed in Table 4.
Table 4.
Final pair-specific LJ parameters, and comparison to LJ parameters obtained using standard combining rules.a Atom names are as listed in Figure 6: atom types CD315A, CD315B and CD316A are from the test set molecules CPNM, TF2M and CHXM, respectively. No pair-specific LJ parameters were required for atoms Cg or Oa.
| Atom Name | Atom Type 1 | Atom Type 2 | Standard LJ parameters | Pair-specific LJ Parameters | Change in LJ parameters | |||
|---|---|---|---|---|---|---|---|---|
| ε | Rmin | ε | Rmin | Δε | ΔRmin | |||
| Ca | CD33A | ODW | −0.1283 | 3.8269 | −0.1233 | 3.8269 | 0.0050 | 0.0000 |
| Cb | CD32A | ODW | −0.1087 | 3.8869 | −0.0817 | 3.8869 | 0.0270 | 0.0000 |
| Cc | CD31A | ODW | −0.0681 | 3.9869 | −0.0211 | 3.9869 | 0.0470 | 0.0000 |
| Cd | CD30A | ODW | −0.0650 | 3.9869 | −0.0050 | 4.1869 | 0.0600 | 0.2000 |
| Ce | CD325A | ODW | −0.1125 | 3.8069 | −0.0965 | 3.8069 | 0.0160 | 0.0000 |
| Cf | CD326A | ODW | −0.1087 | 3.8869 | −0.0992 | 3.8869 | 0.0095 | 0.0000 |
| Ch | CD33E | ODW | −0.1481 | 3.7869 | −0.1431 | 3.7869 | 0.0050 | 0.0000 |
| Ci | CD32E | ODW | −0.1067 | 3.8069 | −0.0797 | 3.8069 | 0.0270 | 0.0000 |
| Cj | CD325B | ODW | −0.1125 | 3.8069 | −0.0925 | 3.8069 | 0.0200 | 0.0000 |
| Ck | CD326B | ODW | −0.1087 | 3.7969 | −0.0827 | 3.7969 | 0.0260 | 0.0000 |
| Ob | OD31B | ODW | −0.1779 | 3.5269 | −0.1779 | 3.4969 | 0.0000 | −0.0300 |
| Oc | OD30A | ODW | −0.1125 | 3.5269 | −0.0919 | 3.5469 | 0.0206 | 0.0200 |
| Od | OD305A | ODW | −0.1299 | 3.5069 | −0.1299 | 3.5269 | 0.0000 | 0.0200 |
| Oe | OD306A | ODW | −0.1299 | 3.5269 | −0.1299 | 3.5469 | 0.0000 | 0.0200 |
| N/A | CD315A | ODW | −0.0822 | 3.7869 | −0.0662 | 3.7869 | 0.0160 | 0.0000 |
| N/A | CD315B | ODW | −0.0822 | 3.7869 | −0.0622 | 3.7869 | 0.0200 | 0.0000 |
| N/A | CD316A | ODW | −0.0822 | 3.7869 | −0.0727 | 3.7869 | 0.0095 | 0.0000 |
ε in kcal/mol, Rmin in Å.
3.3 Hydration Free Energies
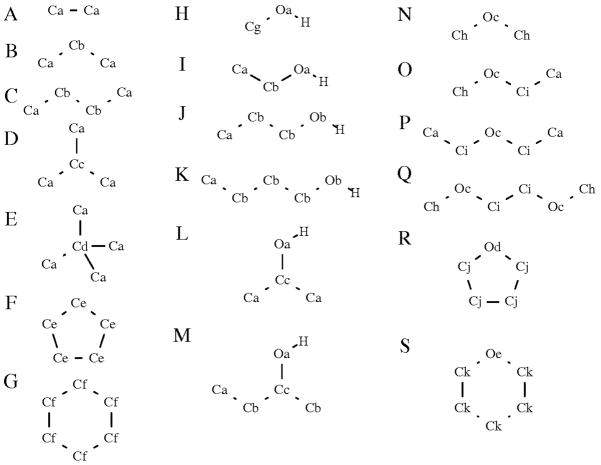
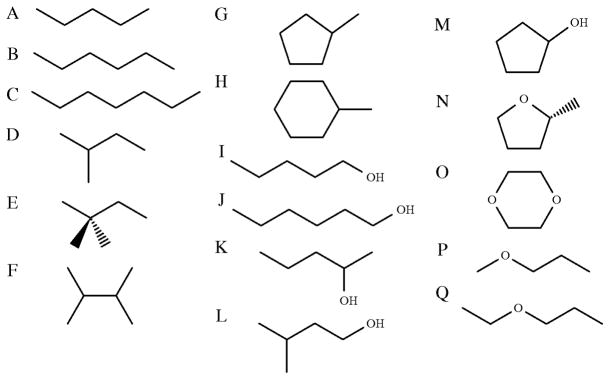
A total of nineteen molecules were chosen to comprise the “parametrization set” (Figure 6); the set of molecules that would be used to develop the pair-specific LJ parameters. With the aim of creating a consistent, systematic set of pair-specific LJ parameters for use across all molecules, it was necessary to take the alkanes as a starting point. For the alkanes, seven molecules were considered as part of the parametrization process: the acyclic alkanes ETHA; PROP; BUTA; IBUT, and NEOP, and the cyclic alkanes CPEN, and CHEX. The first step of the parametrization involved the development of pair-specific LJ parameters for the ethane methyl C atoms (Ca, Figure 6). Once these parameters had been developed, they were then used in the development of parameters for the Cb atoms, based on propane and butane; the Cc atom, based on isobutane, and the Cd atom, based on neopentane. While the C atom in CPEN was always treated as having a different atom type to the acyclic CH2 C atoms, CHEX C atoms were initially assigned the Ca atom type. However, it was not possible to obtain a set of pair-specific LJ parameters that gave good agreement across both the acyclic alkanes and CHEX and, ultimately, the C atoms of CHEX were assigned their own atom type. In this way it was possible to construct a consistent set of parameters that gave good agreement with experimental ΔGhyd values across the whole range of alkane molecules considered as part of the parametrization process (Table 2). Overall, the average error in the calculated hydration free energy has been reduced from −0.91 kcal/mol to −0.05 kcal/mol, with the root mean square deviation (RMSD) reduced from 1.02 kcal/mol to 0.10 kcal/mol, indicating that the systematically-too-favorable prediction of alkane hydration free energies has been corrected. In general, the agreement with experimental results obtained using the new pair-specific LJ parameters is excellent across all alkane molecules, with only NEOP (with a deviation of −0.25 kcal/mol from the experimental value) giving a deviation with magnitude greater than 0.07 kcal/mol from the corresponding experimental value. Moreover, the inclusion of pair-specific LJ parameters results in an accurate reproduction of the ordering of ΔGhyd values. The LJ parameters obtained using the standard combining rules incorrectly predicted that ΔGhyd values decrease with increasing chain-length. When pair-specific LJ parameters are included, hydration free energies become less favorable with increasing chain length, in agreement with experimental results.
Figure 6.
Compounds used in development of pair-specific LJ parameters: (a) ethane, ETHA; (b) propane, PROP; (c) butane, BUTA; (d) isobutane, IBUT; (e) neopentane, NEOP; (f) cyclopentane, CPEN; (g) cyclohexane, CHEX; (h) methanol, MEOH; (i) ethanol, ETOH; (j) propan-1-ol, PRO1; (k) butan-1-ol, BUO1; (l) propan-2-ol, PRO2; (m) butan-2-ol, BUO2; (n) dimethyl ether, DME; (o) methyl ethyl ether, MEET; (p) diethyl ether, DEET; (q) 1,2-dimethoxyethane, DMOE (r) tetrahydrofuran, THF; (s) tetrahydropyran, THP.
Examination of Table 4 reveals that the central C atom of NEOP (Cd in Figure 7; CHARMM atom type CD30A) is also the only alkane atom type for which it was necessary to break the “rules” for pair-specific LJ parameter development outlined above. The final pair-specific LJ parameters for Cd have Δε = 0.0600 and ΔRmin = 0.2000: for comparison, the largest change in any of the other alkane atom types is found in CD31A from IBUT (Cc, Figure 7), where Δε = 0.0470 and ΔRmin = 0.0000. Put simply, it appears that the CD30A atom of NEOP is being asked to do too much work. Before any pair-specific LJ parameters are added, NEOP gives the hydration free energy in worst agreement with experimental data (Table 2). In addition, the changes made to the methyl C atom (Ca) are extremely small, meaning that only the pair-specific LJ parameters for the CD30A atom type could be optimized to correct the calculated ΔGhyd. With this atom surrounded by methyl groups in NEOP, it is a significant distance from the nearest water molecules, thereby reducing the impact of any changes in the LJ parameters on ΔGhyd. While the magnitude of the difference upon moving from the combining-rule to pair-specific LJ parameters is not ideal, the CD30A atom type does not appear in biomolecular systems, which are the ultimate target of this small molecule work, and so was not a great cause for concern.
Figure 7.
Compounds used for testing pair-specific LJ parameters: (a) pentane, PENT; (b) hexane, HEXA; (c) heptane, HEPT; (d) 2-methylbutane, BU2M; (e) 2,2-dimethylbutane, BU22M; (f) 2,3-dimethylbutane, BU23M; (g) methylcyclopentane, CPNM; (h) methylcyclohexane, CHXM; (i) pentan-1-ol, PEO1; (j) hexan-1-ol, HXO1; (k) pentan-2-ol, PEO2; (l) 3-methylbutan-1-ol, B3MO1; (m) cyclopentanol, CPOH; (n) 2-(R)-methyl tetrahydrofuran, MTHF; (o) 1,4-dioxane, DIOX; (p) methyl propyl ether, MPET; (q) ethyl propyl ether, EPET.
It should be noted that two papers focused on the development of computational methods for estimating hydration free energies have reported experimental values of the hydration free energy for neopentane that are significantly different. Michielan et al. reported a value of 2.69 kcal/mol,67 while Ooi et al. reported a value of 2.50 kcal/mol.68 While Michielan et al. give no information on the source of the experimental value used in their work, Ooi et al. provide references to the original sources of their experimental data.69,70 For this reason, the experimental hydration free energy of neopentane used in this work is that obtained from the work of Ooi et al.
The alkane parameters were then applied to the alcohol and ether molecules, with the logic being that pair-specific LJ parameters for atom types not included in the alkanes should be built on top of the alkane pair-specific LJ parameters, so as to yield a set of parameters that is consistent across all molecules.
For the alcohols, inclusion of the alkane pair-specific LJ parameters has a dramatic effect on the calculated hydration free energies (Table 2). For MEOH, ETOH, PRO2 and BUO2, which share an atom type for the hydroxyl O, no further pair-specific LJ parameters were required to yield an acceptable improvement in the calculated ΔGhyd values. For the long chain primary alcohols PRO1 and BUO1, which possess a different O atom type to the other alcohols, the addition of the alkane pair-specific LJ parameters results in a slight overcorrection, making the ΔGhyd values, which were initially too favorable, not favorable enough. Pair-specific LJ parameters were applied to the O atom to rectify this overcorrection (Table 4). The resulting set of pair-specific LJ parameters gave an average error for the alcohols of −0.06 kcal/mol and an RMSD of 0.32 kcal/mol, compared to an average error of −0.54 kcal/mol and an RMSD of 0.65 kcal/mol for the values obtained using the LJ parameters obtained from the standard combining rules.
For the ethers, the situation was complicated by the presence of several C atom types that do not appear in the alkanes, corresponding to the C atoms adjacent to the ether O atoms in the linear ethers. For these atom types, the change in the LJ parameters needed to obtain pair-specific LJ parameters for the corresponding alkane atom was retained for use in the ether atom types, resulting in pair-specific LJ parameters that differ in magnitude, but show the same change relative to the combining rule LJ parameters. With these C atom pair-specific LJ parameters in place, it was a matter of adjusting only the Oc atom type pair-specific LJ parameters until optimal agreement with experiment was obtained. For the cyclic ethers THF and THP, a similar approach was attempted, in which the change in LJ parameters for the C atoms was transferred directly from the corresponding atom types in CPEN and CHEX. Using such an approach, however, very large changes were required to the Od/Oe-ODW LJ parameters to obtain acceptable hydration free energies. These changes not only violated the rules outlined above for the derivation of pair-specific LJ parameters, but also resulted in a significant worsening of the calculated gas phase heterodimer interactions with water molecules (Table S3 of the supporting information). Accordingly, for THF and THP this approach was abandoned and pair-specific LJ parameters for both the C and O atoms of both molecules were allowed to vary. The final set of pair-specific LJ parameters gave hydration free energies as shown in Table 2: the average error in the values calculated using the new pair-specific LJ parameters was 0.01 kcal/mol with an RMSD of 0.17 kcal/mol, compared to an average error of −0.95 kcal/mol and an RMSD of 1.21 kcal/mol in the values calculated without pair-specific LJ parameters.
Across all nineteen molecules considered in the parametrization process, the average error in the ΔGhyd values calculated using the pair-specific LJ parameters is −0.03 kcal/mol, with an RMSD of 0.21 kcal/mol. For ΔGhyd values calculated without the inclusion of any pair-specific LJ parameters, the average error is −0.84 kcal/mol and the RMSD is 0.99 kcal/mol. Performing a Student’s t-test71 results in the rejection of the null hypothesis that these two mean errors are the same (P-value = <0.0001): the difference between the average errors is statistically significant. Clearly, through the inclusion of pair-specific LJ parameters, the systematic error in the calculated ΔGhyd values has been eliminated, while at the same time the absolute error in the ΔGhyd values has also decreased.
To further ensure the utility of the pair-specific LJ parameters, the issue of sampling was considered: if free energy values are to be calculated accurately, it is important that all accessible conformations of a molecule and its aqueous environment be sampled to yield an adequate precision.37 While torsional modes tend to be most problematic when it comes to achieving adequate sampling, even non-torsional relaxation times are on the order of 2–10 ps. With, in this case, 100 ps of sampling per coupling value, this results in 10–100 independent samples. To assess whether the use of 100 ps/window in the free energy calculations represents a sufficient level of sampling, FEP calculations were performed for ETOH and THF using the method described above with 500 ps rather than 100 ps of production MD for every value of the coupling and/or staging parameter. These calculations were performed using the final values of the pair-specific LJ parameters obtained in this work. For ETOH the mean hydration free energy obtained over five independent calculations with the longer calculations was −4.73 ± 0.03 kcal/mol. The equivalent value obtained from the original, shorter, calculations was −4.81 ± 0.05 kcal/mol. Performing a Student’s t-test71 with a significance level of 0.05 leads to the acceptance of the null hypothesis that the two means are the same (P-value = 0.234). The same conclusion is also reached for THF (P-value = 0.555) where the shorter simulations gave ΔGhyd = −3.58 ± 0.07 kcal/mol and the longer simulations gave ΔGhyd = −3.62 ± 0.03 kcal/mol. Overall, it can be concluded that, for these molecules, performing longer MD simulations has no statistically significant effect on the calculated hydration free energies, and that the level of sampling used in the original calculations is adequate.
3.4 Test Compounds
To test the transferability of the parameters obtained above, simulations were performed on another seventeen compounds (Figure 7): six acyclic alkanes, three linear (PENT, HEXA, HEPT) and three branched (BU2M, BU22M, BU23M); two cyclic alkanes (CPNM, CHXM); four acyclic alcohols, three linear (PEO1, PEO2, HXO1) and one branched (B3MO1); one cyclic alcohol (CPOH); two acyclic ethers (MPET, EPET), and two cyclic ethers (MTHF, DIOX). This test set was designed to include at least one example of every atom type for which pair-specific LJ parameters had been developed above. In total, eighteen different atom types are represented within the test set. Fifteen of these were considered during the pair-specific LJ parameter optimization, with the remaining three having no pair-specific LJ parameters. For all seventeen molecules, simulations were performed both with and without the pair-specific LJ parameters developed above. For the fifteen atom types for which pair-specific LJ parameters had been explicitly parameterized, all of the pair-specific LJ parameters used in the simulation of these molecules were taken directly from Table 4. The three atom types for which pair-specific LJ parameters had not been explicitly calculated were the CHARMM atom types CD315B, CD315A and CD316A, corresponding to the ring C atoms bonded to the substituent methyl groups in MTHF, CPNM (and CPOH) and CHXM, respectively. These atom types have LJ parameters that differ from other C atoms in their respective rings, which have the same atom types as the THF, CPEN and CHEX ring C atoms.30 In such cases, where pair-specific LJ parameters have not been optimized, pair-specific LJ parameters were introduced based on the assumption that the change in the LJ parameters will be the same as the change needed to obtain pair-specific LJ parameters for the parent ring C atoms. Obtaining parameters by analogy in this manner is not a recommended procedure, and generally yields sub-optimal results. In this case, however, such an approach was deemed necessary to retain an objective test set. If the pair-specific LJ parameters for atom types present in the test set had been optimized, then the molecules containing these atoms types could no longer have been considered as part of the test set. It is anticipated that in future work where new pair-specific LJ parameters are required, such parameters would be obtained using the full optimization method outlined above. All parameters other than pair-specific LJ parameters had the standard CHARMM Drude polarizable force field values for alkanes, alcohols and ethers.26,27,30 A small number of dihedral and angle parameters that did not already exist within the CHARMM Drude polarizable force field were obtained by analogy to existing force field parameters. Again, such an approach is unlikely to yield high quality parameters, but was deemed sufficient for the current test.
With the parameters in place, for each molecule five independent calculations were performed to evaluate ΔGhyd using the FEP method described above. The final, average, value of ΔGhyd was then compared to the relevant experimental value, with a good reproduction of the experimental value taken to signify that the parameters are broadly transferable across a range of molecules.
The results of the calculations of hydration free energies on the test compounds are shown in Table 3. In all cases, the inclusion of the pair-specific LJ parameters results in a significant improvement in the calculated ΔGhyd, with the largest error being −0.65 kcal/mol for both MTHF and CPOH. In the calculations without any pair-specific LJ parameters, the error in the calculated value of ΔGhyd for MTHF is −1.74 kcal/mol, the error in the calculated value for CPOH is −1.38 kcal/mol and the largest error is −2.33 kcal/mol, obtained for DIOX. Overall, the average error across the whole set of test molecules is −0.14 kcal/mol (RMSD = 0.38 kcal/mol) when pair-specific LJ parameters are included, compared to −1.59 kcal/mol (RMSD = 1.63 kcal/mol) in their absence. Performing a Student’s t-test71 at a significance level of 0.05 results in rejection of the null hypothesis that the mean error in the ΔGhyd values calculated with pair-specific LJ parameters is the same as the mean error in the ΔGhyd values without pair-specific LJ parameters (P-value = <0.0001). From this it can be concluded that the inclusion of pair-specific LJ parameters results in a statistically significant improvement in the reproduction of hydration free energies. It should also be noted that the worst performing of the test set molecules, MTHF and CPOH, both include an atom type for which pair-specific LJ parameters have not been optimized, but rather selected by analogy to the corresponding THF atom types. This approach is not necessarily valid, and it is likely that by optimizing the pair-specific LJ parameters associated with this atom type, some improvement in the calculated value of the MTHF and CPOH hydration free energies could be obtained. It is also worth considering the issue of sampling. As noted above, adequate sampling of conformational space is essential if accurate ΔGhyd values are to be obtained for any molecule. It is also something that is increasingly difficult for molecules with increased flexibility, requiring multiple, long simulations. For a molecule such as HEPT, it is extremely unlikely that the entirety of conformational space has been well sampled using the approach outlined above, and the presented values of the hydration free energies should be treated with some caution. For the purpose of this study, however, where the calculations on these longer, more flexible molecules are not targeted at the production of highly accurate hydration free energies, but rather an assessment of whether the pair-specific LJ parameters have resulted in an improvement in the calculated ΔGhyd values, these calculations are considered adequate.
Table 3.
Free energies of hydration of test set molecules.
| Molecule | Experimental ΔGhyd | Without pair-specific LJ parameters ΔGhyd | Error | Without pair-specific LJ parameters ΔGhyd | Error |
|---|---|---|---|---|---|
| Alkanes | |||||
| PENT | 2.36a | 1.24 ± 0.09 | −1.12 | 2.61 ± 0.08 | 0.25 |
| HEXA | 2.48a | 0.85 ± 0.12 | −1.63 | 2.39 ± 0.12 | −0.09 |
| HEPT | 2.62a | 0.34 ± 0.10 | −2.28 | 2.81 ± 0.08 | 0.19 |
| BU2M | 2.38b | 0.55 ± 0.09 | −1.82 | 2.24 ± 0.05 | −0.14 |
| BU22M | 2.51b | 0.53 ± 0.15 | −1.98 | 1.95 ± 0.14 | −0.56 |
| BU23M | 2.34b | 0.87 ± 0.22 | −1.47 | 2.69 ± 0.12 | 0.36 |
| CPNM | 1.59b | 0.34 ± 0.07 | −1.25 | 1.64 ± 0.12 | 0.05 |
| CHXM | 1.70b | 0.31 ± 0.15 | −1.39 | 1.17 ± 0.08 | −0.53 |
| Alcohols | |||||
| PEO1 | −4.57b | −5.73 ± 0.07 | −1.16 | −4.66 ± 0.06 | −0.09 |
| HXO1 | −4.40b | −5.79 ± 0.25 | −1.39 | −4.81 ± 0.14 | −0.41 |
| PEO2 | −4.39b | −5.66 ± 0.11 | −1.27 | −4.02 ± 0.10 | 0.37 |
| B3MO1 | −4.42b | −5.74 ± 0.16 | −1.32 | −4.94 ± 0.08 | −0.52 |
| CPOH | −5.49b | −6.87 ± 0.06 | −1.38 | −6.14 ± 0.09 | −0.65 |
| Ethers | |||||
| MTHF | −3.34c | −5.09 ± 0.13 | −1.74 | −3.99 ± 0.10 | −0.65 |
| DIOX | −5.06b | −7.39 ± 0.13 | −2.33 | −5.30 ± 0.16 | −0.24 |
| MPET | −1.69c | −2.36 ± 0.11 | −1.69 | −1.60 ± 0.06 | 0.09 |
| EPET | −1.84c | −2.88 ± 0.08 | −1.84 | −1.59 ± 0.04 | 0.25 |
| Overall Average | −1.59 | −0.14 | |||
When developing optimized force field parameters such as this, it is important to be aware of the risk of overfitting: the situation that occurs when a statistical model describes the data within a training set extremely well, but fails in external test cases. The failure, which occurs when a model possess too many degrees of freedom in relation to the amount of data used for optimization, is often indicative of a model that is not correctly accounting for the underlying physics. In a case such as this study, where 14 pair-specific LJ parameters are fitted to 19 experimental data, the risk of overfitting is considerable. As a first test for overfitting, the performance of the pair-specific LJ parameters can be compared between the training set and the test set. To do this, a Student’s t-test71 was performed to assess whether the mean error observed in the training set was significantly different to the mean error observed in the test set; i.e., whether the fitted parameters are having a differential impact on the training versus the test set of molecules, which would indicate overfitting. From this analysis, a P-value of 0.3260 was obtained suggesting that the two means may be the same, and it is concluded that there is no significant difference between the mean error observed in the training set and the mean error observed in the test set. Thus, there is no evidence that the pair-specific LJ parameters perform any differently in the training set than they do in the test set. This supports the conclusion that the data is not overfitted. As a second test for overfitting, the modified Akaike Information Criterion (AICC)72 was considered. AICC is a method that can be used to assess the relative information content in competing models of the same data. It works by rewarding accurate reproduction of reference data, but penalizing the inclusion of additional parameters. AICC is evaluated via Equation 19
| (19) |
where k is the number of free parameters, n is the number of observations and RSS is the residual sum of squares. When comparing models, the model having the lowest AICC score is accepted as the best performing model. Here, there are two competing models: the model without pair-specific LJ parameters, which has no free parameters, and the model with pair-specific LJ parameters, which has 17 free parameters (14 from the original training set, with another 3 added for the test set molecules). Considering all molecules (training set + test set) together, the model without pair-specific LJ parameters has AICC = 21.70 and the model with pair-specific LJ parameters has AICC = −18.40. This result indicates that the inclusion of pair-specific LJ parameters results in a better model for the calculation of hydration free energies and further supports the conclusion that the model is not overfitted. In theory, it would also be possible to extend this AICC analysis to include the entire body of data used in the development of the CHARMM Drude polarizable force field, not just the solvation free energies. In practice, however, determining the number of free parameters and constructing a RSS with contributions from a variety of different properties would be difficult. What is clear is that the total number of parameters used in each model will be identical, apart from those introduced here, and that both models will give identical results in all areas that do not involve interactions with water. The total AICC values would depend on the magnitude of the contribution to the RSS arising from the additional data points: let us assume that the contribution to the RSS, per data point, would the same as the average contribution to the RSS, per data point, from the solvation free energy values obtained using the model including pair-specific LJ parameters. If this assumption were correct then, as long as the number of data points increases by more than about 1.3 times the number of parameters, the AICC value for the model including pair-specific parameters will be lower than that of the model without pair-specific LJ parameters.
3.5 Testing the Need for Pair-specific LJ Parameters
The question remains as to whether it is necessary to include pair-specific LJ parameters within the CHARMM Drude polarizable force field for the accurate calculation of hydration free energies. To address this, the pair-specific LJ parameters obtained here were inverted to back-generate a new set of type-specific LJ parameters, as described in the methods section. Using these new LJ parameters, simulations were performed on the bulk neat liquids to calculate thermodynamic properties for a number of alkane and ether molecules. For each of these molecules, the results of these calculations were compared to experimental results, and the results of calculations performed using the standard CHARMM Drude polarizable force field parameters (Table 5). In the initial development of CHARMM Drude polarizable models of small molecules, the reproduction of liquid (or crystal) phase thermodynamic data is considered to be of paramount importance, with parameter optimization performed to yield Vm and ΔHvap that are both within 2% of the experimental value. As Table 5 shows, this target is almost always achieved. When the corresponding values are calculated using the pair-specific LJ parameters, however, the agreement is considerably worse. Specifically, none of the calculated values are within the 2% target, with the majority of ΔHvap differing from the experimental target by more than 20%. Overall, using the LJ parameters obtained from the pair-specific LJ parameters, the average error in Vm is 11.2 % and the average error in ΔHvap is −25.0 %, compared to average errors of 0.4 % and −0.4 % in the calculated values of Vm and ΔHvap, respectively, obtained using the standard LJ parameters. Notably, there are systematic differences in the pure solvent properties obtained with the pair-specific parameters, where the Vm values are too large and the ΔHvap values are all too small. These results, combined with the systematic overestimation of the ΔGhyd values with the parameters based on the combining rules (Table 2), strongly indicate that the need for additional optimization of the LJ parameters is not associated with limitations in the optimization procedure but rather an inherent limitation in the energy function.
To better quantify the physical underpinnings of the need for the pair-specific LJ parameters the results of the FEP calculations were analyzed in greater detail. The free energy decomposition approach used to calculate ΔGhyd (Equation 8) allows for the separate contributions to ΔGhyd due to the WCA-repulsive, WCA-dispersive and electrostatic contributions to be quantified separately. By examining the change in these contributions upon going from LJ parameters obtained from the combining rules, to pair-specific LJ parameters, a more complete picture can be obtained. The results of this analysis are shown in Table 6 (complete details of the contributions are shown in Table S4 of the supplementary material). A fascinating trend is revealed: the contribution that is the most affected by the introduction of pair-specific LJ parameters is always associated with the dispersion interaction, with this term always becoming less favorable with the pair-specific LJ parameters. Even with the polar species, the ethers and alcohols, the dispersion term dominates; typically overriding a more favorable electrostatic contribution associated with the pair-specific LJ parameters. These trends allow for several observations. First, the repulsive term, which is dominated by the 1/r12 portion of the LJ potential, has the smallest contribution. This is re-assuring, as this aspect of the LJ treatment of vdW interactions is known to be a fairly poor approximation of a physically more accurate exponential repulsion.73 While criticism of the 1/r12 repulsion is still valid, this term does not adversely impact the free energies of aqueous solvation, suggesting that its use in the energy function is not having a significant adverse impact on force field calculations in general. Second, the observation that the electrostatics are not leading to systematic problems validates the inclusion of polarization in the model and suggests that its inclusion is satisfactorily modeling the change in the electronic response of the system in environments of different polarities. Finally, the analysis of the free energy decomposition points to some limitations in the treatment of the dispersive interactions. As the functional form of the dispersive interaction, ~1/r6, is physically correct,73 this indicates that the major limitations arise from the LJ combining rules.
Table 6.
Variation in the free energy contributions to ΔGhyd upon the introduction of pair-specific LJ parameters. All values in kcal/mol.
| Molecule | WCA-Repulsion | WCA-Dispersion | Electrostatic |
|---|---|---|---|
| Alkanes | |||
| CPEN | −0.16 | 1.18 | −0.01 |
| CHEX | −0.05 | 0.78 | 0.00 |
| ETHA | −0.09 | 0.19 | −0.01 |
| PROP | 0.05 | 0.67 | −0.06 |
| BUTA | −0.14 | 1.01 | −0.05 |
| IBUT | −0.01 | 1.01 | −0.28 |
| NEOP | 0.16 | 1.25 | 0.00 |
| Alcohols | |||
| MEOH | 0.00 | 0.00 | 0.00 |
| ETOH | −0.13 | 0.58 | −0.17 |
| PRO2 | −0.29 | 0.98 | −0.64 |
| BUO2 | 0.08 | 1.31 | −0.09 |
| PRO1 | −0.20 | 1.03 | −0.62 |
| BUO1 | −0.05 | 1.39 | −0.54 |
| Ethers | |||
| THF | −0.09 | 1.19 | 0.11 |
| THP | 0.26 | 1.84 | 0.15 |
| DEE | −0.11 | 1.17 | −0.29 |
| DMOE | −0.23 | 1.25 | −0.48 |
| DME | 0.05 | 0.34 | −0.40 |
| MEET | 0.00 | 0.76 | −0.06 |
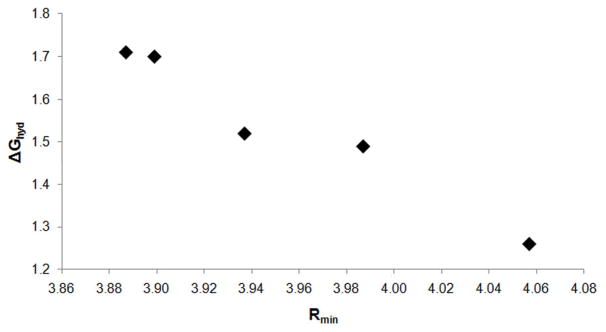
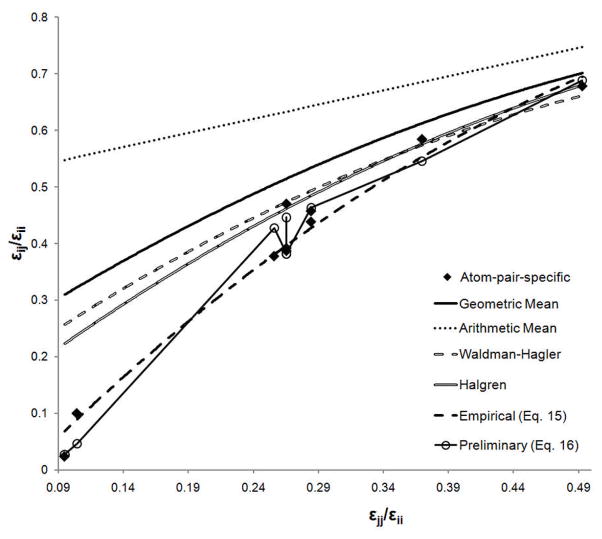
To investigate a possible limitation in the LJ combining rule, the graphical approach of Waldman and Hagler74 has been applied, focusing on the aliphatic carbon parameters in which the pair-specific parameters only included changes in ε. The plots, which are based on a reduced representation of change in εij as a function of εjj with the normalization based on εii, the well depth of the water oxygen, are shown in Figure 8. Included are the εij/εjj values for the aliphatic carbons based on the data in Table 4 along with curves associated with different types of combining rules. Comparing the pair-specific ε values obtained in this work to those that would be obtained using either an arithmetic combining rule or the geometric combining rule, Equation 3, which is used in CHARMM for the ε term, shows the limitation in these simple combining rules. The arithmetic mean is clearly inappropriate for ε, as previously discussed,74 and it is clear that the geometric mean combining rule overestimates the magnitudes of the ε values required to give an accurate reproduction of experimental data, consistent with the observation of Halgren that “the geometric-mean rule consistently overestimates the well depth for unlike-pair interactions.”75 This leads to the overestimation of the ΔGhyd values based on the combining rules (Table 2) and is consistent with the free energy decomposition (Table 6). Applying the combining rules of Waldman and Hagler or of Halgren (Figure 8) results in ε values that are of smaller magnitude compared to those from the geometric rule, but still too large to reproduce accurately the parameters obtained in this study.
Figure 8.
Waldman-Hagler graphical analysis of εij parameter values. Only εij values corresponding to interactions between C atoms and water O atoms are considered. i corresponds to the O water atom and j to the C atom.
Although none of the tested combining rules are able to reproduce the pair-specific ε values, the results of the graphical analysis are encouraging. The ε parameters obtained in this work behave in a very similar manner to those investigated by Waldman and Hagler for the noble gases. They lie on one single curve and, as Waldman and Hagler note, “if there is a valid combination rule g that correlates a, b, and c, then a plot of c/a vs b/a should lie on a single curve.”74 This suggests that there should be some combining rule that is able to generate the ε parameters obtained from the fitting performed in this work. Deriving that combining rule remains a non-trivial task, but an empirical fitting based on the geometric mean rule yields a combining rule (Equation 20) that gives an acceptable reproduction of the data shown in Figure 8.
| (20) |
While Equation 20 adequately models the data in Figure 8 it has no sound theoretical basis and does not fulfill the basic mathematical requirements of a combining rule.76 Accordingly, further analysis of the data was performed from which a preliminary combining rule with a more physical basis was empirically determined (Equation 21). Based around the ε combining rule proposed by Halgren,75 Equation 21 also incorporates a term based on the geometric mean rule for εRmin6 as proposed by Waldman and Hagler.74 The whole expression is then multiplied by an additional term that facilitates an accurate reproduction of the steeper gradient observed for the pair-specific ε parameters. While this equation is highly preliminary, being specific for only alkane carbons, and unlikely to be the ultimate solution to the problem, it does demonstrate that it is possible to find a combining rule that provides a good representation of the empirically fitted parameters obtained in this work. It also lends further support to the idea that improved combining rules would facilitate an improved force field. Considered in combination with previous studies that have shown that the combining rules used in CHARMM are sub-optimal,77,78 and that the use of alternative combining rules can give improved reproduction of experimental data,78,79 these results becomes even more persuasive.
| (21) |
The inability of available combining rules to treat the present results for the aliphatic carbons is suggested to be associated with the target data used in development of those rules. Combining rules to date have targeted experimental potential energy curves for rare gas homo- and heterodimers. Such data is limited in that it only includes binary interactions of nonpolar atoms whose interactions are dominated by dispersion interactions. The present data is based on complex mixtures of nonpolar and polar molecules, in which significant electrostatic contributions occur. The presence of these contributions is suggested to yield the trend shown in Figure 8; smaller ε values are required as the value of ε becomes smaller than that predicted by the standard combining rules. Such small ε values lead to a decrease in the dispersion contribution to ΔGhyd, which may be required due to favorable electrostatic contributions on the more polar systems being investigated. While speculative, these results clearly emphasize the importance of the target data in determining an appropriate combining rule for condensed phase studies of polar systems. In the present study this data has been generated based on extremely careful and systematic optimization of LJ parameters initially obtained based on a well-defined set of target data (ie. based on pure solvent or crystal properties and rare gas interactions) followed by additional optimization to obtain pair-specific LJ parameters to reproduce a second set of well-defined target data (experimental ΔGhyd data). The resulting sets of LJ parameters allowed for the development of the preliminary combining rules presented in Equations 20 and 21.
3.6 Implementing the New Parameters within the CHARMM Drude Polarizable Force Field
The analysis presented above indicates that the standard combining rule for ε is not adequate. This problem can be solved by either changing the form of the combining rule, or applying the derived pair-specific parameters in the context of the present energy function. Following the former course of action is daunting, and would require several steps. First, systematic optimization of the pair-specific LJ parameters would need to be performed in the context of the current combining rules for all the molecules in the force fields for which experimental ΔGhyd data is available. Once those values are obtained, a novel combining rule, similar to that in Equation 21, would need to be developed, taking into account the full range of molecules in the force field. Once this combining rule is decided upon, new LJ parameters for the entire force field would be required based on the new combining rule, starting with water, through the alkanes and onto the polar molecules and ions. Such a task, while possible, would take several years to complete; to indicate the timeline of such efforts, the first water model for the Drude polarizable force field was published in 2003.21 The alternative is to apply the pair-specific parameters presented in this study. While this represents a compromise, it is an improvement over the current combining rule based LJ parameters, leading to a better representation of the balance of energetics in bulk systems (eg. the interior of a protein or lipid bilayer) and in aqueous solution. Such an approach is not unprecedented as Shirts and Pande,37 for example, have demonstrated (for an additive force field) that it is possible to modify the standard TIP3P water model80 so as to eliminate the systematic error in hydration free energies without sacrificing the properties of liquid water. In practice, we plan to follow both paths. Over the long term we anticipate systematically optimizing pair-specific LJ parameters, leading to a new LJ combining rule for ε. In the short term we will extend the small molecule Drude force field to macromolecules using the current combining rule along with the pair-specific LJ parameters. Such an extension to macromolecules is not a trivial process and it is anticipated that additional limitations in the model will be identified. Corrections to those limitations will then be combined with an improved LJ combination rule to yield a second generation polarizable force field.
4. Conclusions
Pair-specific LJ parameters have been developed to describe the interactions between solute heavy atoms and water O atoms. These new parameters yield accurate calculated hydration free energies of alkanes, alcohols and ethers that provide a good reproduction of experimental reference values. The changes introduced are small in magnitude relative to the LJ parameters obtained using the standard CHARMM parameter combining rules, with the calculated results highly sensitive to these small magnitude changes. They have also been implemented in a hierarchical fashion beginning from the alkanes, and a parametrization protocol has been developed. This will allow for the addition of pair-specific LJ parameters to new functional groups as they are added to CHARMM Drude polarizable force field, in a fashion that is as straightforward and systematic as possible.
The LJ parameters developed in this work have also been used to calculate hydration free energies for a test set of alkane, alcohol and ether molecules not considered as part of the parametrization process. In these cases the new parameters yield an acceptable reproduction of experimental properties that is significantly improved compared to that obtained with the combining rule based LJ parameters. This suggests that the pair-specific LJ parameters are broadly transferable across the alkane, alcohol and ether molecules.
The pair-specific LJ parameters were also used to generate (via the inverse of the standard CHARMM combining rules) a new set of LJ parameters for use in liquid phase calculations of alkane and ether molecules. These parameters were found to give significant, systematic errors in the calculated values of Vm and ΔHvap. This result suggests that it will not be possible, within the existing framework of the CHARMM Drude polarizable force field, to find a single set of LJ parameters capable of producing both liquid phase thermodynamic data and hydration free energies in good agreement with experimental results.
The systematic optimization of pair-specific LJ parameters in the present study allowed for additional observations to be made. Decomposition of the calculated ΔGhyd results exploiting the WCA free energy methodology (Equation 8) allowed for the identification that the impact of the pair-specific LJ parameters was on the dispersion term. This result indicates the utility of the treatment of the repulsive aspect of the vdW interactions using the 1/r12 term and the suitability of the treatment of electronic polarizability using the classical Drude oscillator model. It also indicates limitations in the LJ combining rule leading to the overestimation of the free energies of solvation. This limitation was investigated in the context of the aliphatic carbons and a systematic difference between LJ parameters from the geometric combining rule used in CHARMM (Equation 3) as well as other published combining rules for ε. Based on this difference, new combining rules were proposed. These rules, while preliminary, indicate that improvements in the treatment of the vdW interactions in empirical force fields are possible, although significant additional work will be required to achieve such a goal.
Supplementary Material
Figure 3.
Dependence of the long-range LJ correction on the magnitude of the cutoff used. The vertical line indicates a cutoff of 32 Å, the previous “standard value” used in calculating the long-range correction with the CHARMM Drude polarizable force field.
Acknowledgments
The authors acknowledge financial support from the NIH (GM051501 and GM072558) and computational support from the DoD High Performance Computing, the Pittsburgh Supercomputing Center and the NSF/TeraGrid computational resources.
Footnotes
When applied for the calculation of energies or forces (eg. as in equation 1), ε has a positive value. However, within the CHARMM parameter file, by convention ε is always shown as negative, in both the NONBOND and NBFIX sections. For the sake of convenience, the CHARMM parameter file notation is used throughout this paper, and ε values are always shown to be negative.
Supporting Information Available. Methods and results for alkane, alcohol and ether gas phase heterodimer interactions with water molecules; full details of contributions to ΔGhyd obtained from WCA decomposition within FEP calculations. This information is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Macleod NA, Butz P, Simons JP, Grant GH, Baker CM, Tranter GE. Isr J Chem. 2004;44:27. [Google Scholar]
- 2.Macleod NA, Butz P, Simons JP, Grant GH, Baker CM, Tranter GE. Phys Chem Chem Phys. 2005;7:1432. doi: 10.1039/b501098e. [DOI] [PubMed] [Google Scholar]
- 3.Freddolino PL, Arkhipov AS, Larson SB, McPherson A, Schulten K. Structure. 2006;14:437. doi: 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
- 4.Wlodek ST, Clark TW, Scott LR, McCammon JA. J Am Chem Soc. 1997;119:9513. [Google Scholar]
- 5.Snow CD, Nguyen N, Pande VS, Grubele M. Nature. 2002;420:102. doi: 10.1038/nature01160. [DOI] [PubMed] [Google Scholar]
- 6.Banavali NK, Huang N, MacKerell AD., Jr J Phys Chem B. 2006;110:10997. doi: 10.1021/jp0561322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.MacKerell AD., Jr J Comput Chem. 2004;25:1584. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 8.Baucom J, Transue T, Fuentes-Cabrera M, Krahn JM, Darden TA, Sagui C. J Chem Phys. 2004;121:6998. doi: 10.1063/1.1788631. [DOI] [PubMed] [Google Scholar]
- 9.Babin V, Baucom J, Darden TA, Sagui C. J Phys Chem B. 2006;110:11571. doi: 10.1021/jp061421r. [DOI] [PubMed] [Google Scholar]
- 10.Harder E, Kim BC, Friesner RA, Berne BJ. J Chem Theory Comput. 2005;1:169. doi: 10.1021/ct049914s. [DOI] [PubMed] [Google Scholar]
- 11.Dougherty DA. Science. 1996;271:163. doi: 10.1126/science.271.5246.163. [DOI] [PubMed] [Google Scholar]
- 12.Reddy AS, Sastry GN. J Phys Chem A. 2005;109:8893. doi: 10.1021/jp0525179. [DOI] [PubMed] [Google Scholar]
- 13.Gallivan JP, Dougherty DA. Proc Natl Acad Sci USA. 1999;96:9459. doi: 10.1073/pnas.96.17.9459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wintjens R, Liévin J, Rooman M, Buisine E. J Mol Biol. 2000;302:395. doi: 10.1006/jmbi.2000.4040. [DOI] [PubMed] [Google Scholar]
- 15.Tsou LK, Tatko CD, Waters ML. J Am Chem Soc. 2002;124:14917. doi: 10.1021/ja026721a. [DOI] [PubMed] [Google Scholar]
- 16.Zacharias N, Dougherty DA. Trends Pharmacol Sci. 2002;23:281. doi: 10.1016/s0165-6147(02)02027-8. [DOI] [PubMed] [Google Scholar]
- 17.Aschi M, Mazza F, Di Nola A. J Mol Struct (Theochem) 2002;587:177. [Google Scholar]
- 18.Lopes PEM, Roux B, MacKerell AD., Jr Theor Chem Acc. 2009;124:11. doi: 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ma BY, Lii JH, Allinger NL. J Comput Chem. 2000;21:813. [Google Scholar]
- 20.Maple JR, Cao Y, Damm W, Halgren TA, Kaminski GA, Zhang LY, Friesner RA. J Chem Theory Comput. 2005;1:694. doi: 10.1021/ct049855i. [DOI] [PubMed] [Google Scholar]
- 21.Lamoureux G, MacKerell AD, Jr, Roux B. J Chem Phys. 2003;119:5185. doi: 10.1063/5.0019987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Patel S, Brooks CL., III J Comput Chem. 2004;25:1. doi: 10.1002/jcc.10355. [DOI] [PubMed] [Google Scholar]
- 23.Patel S, MacKerell AD, Jr, Brooks CL., III J Comput Chem. 2004;25:1504. doi: 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
- 24.Drude P. The Theory of Optics. Green; New York, NY: 1902. [Google Scholar]
- 25.Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD., Jr Chem Phys Lett. 2006;418:245. [Google Scholar]
- 26.Vorobyov IV, Anisimov VM, MacKerell AD., Jr J Phys Chem B. 2005;109:18988. doi: 10.1021/jp053182y. [DOI] [PubMed] [Google Scholar]
- 27.Anisimov VM, Vorobyov IV, Roux B, MacKerell AD., Jr J Chem Theory Comput. 2007;3:1927. doi: 10.1021/ct700100a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lopes PEM, Lamoureux G, Roux B, MacKerell AD., Jr J Phys Chem B. 2007;111:2873. doi: 10.1021/jp0663614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vorobyov I, Anisimov VM, Greene S, Venable RM, Moser A, Pastor RW, MacKerell AD., Jr J Chem Theory Comput. 2007;3:1120. doi: 10.1021/ct600350s. [DOI] [PubMed] [Google Scholar]
- 30.Baker CM, MacKerell AD., Jr J Mol Model. doi: 10.1007/s00894-009-0572-4. In Press. [DOI] [Google Scholar]
- 31.Lopes PEM, Lamoureux G, MacKerell AD., Jr J Comput Chem. 2009;30:1821. doi: 10.1002/jcc.21183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Harder E, Anisimov VM, Whitfield T, MacKerell AD, Jr, Roux B. J Phys Chem B. 2008;112:3509. doi: 10.1021/jp709729d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhu X, MacKerell AD., Jr J Comput Chem. In press. [Google Scholar]
- 34.Anisimov VM, Lamoureux G, Vorobyov IV, Huang N, Roux B, MacKerell AD., Jr J Chem Theory Comput. 2005;1:153. doi: 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]
- 35.Harder E, Anisimov VM, Vorobyov IV, Lopes PEM, Noskov SY, MacKerell AD, Jr, Roux B. J Chem Theory Comput. 2006;2:1587. doi: 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- 36.Xu Z, Luo HH, Tieleman P. J Comput Chem. 2006;28:689. doi: 10.1002/jcc.20560. [DOI] [PubMed] [Google Scholar]
- 37.Shirts MR, Pande VS. J Chem Phys. 2005;122:134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 38.Deng Y, Roux B. J Phys Chem B. 2004;108:16567. [Google Scholar]
- 39.Oostenbrink C, Villa A, Mark AE, van Gunsteren WF. J Comput Chem. 2004;25:1656. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 40.Mobley DL, Dumont É, Chodera JD, Dill KA. J Phys Chem. 2007;111:2242. doi: 10.1021/jp0667442. [DOI] [PubMed] [Google Scholar]
- 41.Hunter CA, Sanders JKM. J Am Chem Soc. 1990;112:5525. [Google Scholar]
- 42.Baker CM, Grant GH. J Chem Theory Comput. 2006;2:947. doi: 10.1021/ct060024h. [DOI] [PubMed] [Google Scholar]
- 43.Baker CM, Grant GH. J Chem Theory Comput. 2007;3:530. doi: 10.1021/ct600218f. [DOI] [PubMed] [Google Scholar]
- 44.Shirts MR, Pitera JW, Swope WC, Pande VS. J Chem Phys. 2003;119:5740. [Google Scholar]
- 45.Hess B, van der Vegt NFA. J Phys Chem B. 2006;110:17616. doi: 10.1021/jp0641029. [DOI] [PubMed] [Google Scholar]
- 46.Wang J, Cieplak P, Kollman PA. J Comput Chem. 2000;21:1049. [Google Scholar]
- 47.Kaminski G, Duffy EM, Matsui T, Jorgensen WL. J Phys Chem. 1994;98:13077. [Google Scholar]
- 48.Jorgensen WL, Maxwell DS, Tirado-Rives J. J Am Chem Soc. 1996;118:11225. [Google Scholar]
- 49.Geerke DP, van Gunsteren WF. Chem Phys Chem. 2006;7:671. doi: 10.1002/cphc.200500510. [DOI] [PubMed] [Google Scholar]
- 50.Ben-Naim A, Marcus Y. J Chem Phys. 1987;81:2016. [Google Scholar]
- 51.Wolfenden R. Biochem. 1978;17:201. doi: 10.1021/bi00594a030. [DOI] [PubMed] [Google Scholar]
- 52.Morgantini PY, Kollman PA. J Am Chem Soc. 1995;117:6057. [Google Scholar]
- 53.Meng EC, Caldwell JW, Kollman PA. J Phys Chem. 1996;100:2367. [Google Scholar]
- 54.Ding Y, Bernardo DN, Krogh-Jespersen K, Levy RM. J Phys Chem. 1995;99:11575. [Google Scholar]
- 55.Rizzo RC, Jorgensen WL. J Am Chem Soc. 1999;121:4827. [Google Scholar]
- 56.Chen IJ, Yin D, MacKerell AD., Jr J Comput Chem. 2002;23:199. doi: 10.1002/jcc.1166. [DOI] [PubMed] [Google Scholar]
- 57.Davis JE, Warren GL, Patel S. J Phys Chem B. 2008;112:8298. doi: 10.1021/jp8003129. [DOI] [PubMed] [Google Scholar]
- 58.Rick SW, Berne BJ. J Am Chem Soc. 1996;118:672. [Google Scholar]
- 59.Kollman P. Chem Rev. 1993;93:2395. [Google Scholar]
- 60.Weeks JD, Chandler D, Andersen HC. J Chem Phys. 1971;54:5237. [Google Scholar]
- 61.Lagüe P, Pastor RW, Brooks BR. J Phys Chem B. 2004;108:363. [Google Scholar]
- 62.Allen MP, Tildesley DJ. Computer Simulation of Liquids. 1. Oxford University Press; New York, NY: 1987. pp. 64–65. [Google Scholar]
- 63.Brooks BR, Brooks CL, III, MacKerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. J Comput Chem. 2009;30:1545. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ryckaert JP, Ciccotti G, Berendsen HJC. J Comput Phys. 1977;23:327. [Google Scholar]
- 65.Darden T, York D, Pedersen L. J Chem Phys. 1993;98:10089. [Google Scholar]
- 66.Wessa P. Free Statistics Software version 1.1.23-r5. Office for Research Development and Education; 2010. http://www.wessa.net. [Google Scholar]
- 67.Michieland L, Bacilieri M, Kaseda C, Moro S. Bioorg Med Chem. 2008;16:5733. doi: 10.1016/j.bmc.2008.03.064. [DOI] [PubMed] [Google Scholar]
- 68.Ooi T, Oobatake M, Némethy G, Scherage HA. Proc Natl Acad Sci USA. 1987;84:3086. doi: 10.1073/pnas.84.10.3086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cabani S, Gianni P, Mollica V, Lepori L. J Solution Chem. 1981;10:563. [Google Scholar]
- 70.Wolfenden R, Andersson L, Cullis PM, Southgate CCB. Biochem. 1981;20:849. doi: 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
- 71.Biometrika. 1908;6:1. Student. [Google Scholar]
- 72.Akaike H. J Econometrics. 1981;16:3. [Google Scholar]
- 73.Stone AJ. The Theory of Intermolecular Forces. 1. Oxford University Press; Oxford, United Kingdom: 1997. pp. 157–158. [Google Scholar]
- 74.Waldman M, Hagler AT. J Comput Chem. 1993;14:1077. [Google Scholar]
- 75.Halgren TA. J Am Chem Soc. 1992;114:7827. [Google Scholar]
- 76.Khalaf Al-Mata A, Rockstraw DA. J Comput Chem. 2003;25:660. doi: 10.1002/jcc.10418. [DOI] [PubMed] [Google Scholar]
- 77.Delhommelle J, Millie P. Mol Phys. 2001;99:619. [Google Scholar]
- 78.Song W, Rossky PJ, Maroncelli M. J Chem Phys. 2003;119:9145. [Google Scholar]
- 79.Ewig CS, Thatcher TS, Hagler AT. J Phys Chem B. 1999;103:6998. [Google Scholar]
- 80.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926. [Google Scholar]
- 81.Kelly CP, Cramer CJ, Truhlar DG. J Chem Theory Comput. 2005;1:1133. doi: 10.1021/ct050164b. [DOI] [PubMed] [Google Scholar]
- 82.Rizzo RC, Aynechi T, Case DA, Kuntz ID. J Chem Theory Comput. 2006;2:128. doi: 10.1021/ct050097l. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.