Abstract
Landscape features may serve as either barriers or gateways to the spread of certain infectious diseases, and understanding the way geographic structure impacts disease spread could lead to improved containment strategies. Here, we focus on modeling the space-time diffusion process of a raccoon rabies outbreak across several states in the Eastern United States. Specifically, we measure the impact that landscape features, such as mountains and rivers, have on the speed of infectious disease diffusion. This work combines statistical modeling with spatial operations in a geographic information system (GIS) to study disease diffusion. We use a GIS to create landscape feature variables and explore three analytic approaches. First, we use spatial prediction (kriging) to provide a descriptive pattern of the spread of the virus. Second, we use Bayesian areal wombling to detect barriers for infectious disease transmission and examine spatial coincidence with potential features. Finally, we input landscape variables into a hierarchical Bayesian model with spatially varying coefficients to obtain model-based estimates of their local impacts on transmission time in counties.
Keywords: GIS, wombling, hierarchical Bayesian models, infectious disease, spatial statistics, landscape ecology
1. Introduction
Rabies is a single-stranded RNA virus belonging to the genus Lyssavirus (Rhabdoviridae), maintained in populations of carnivorous (or omnivorous) mammals, such as dogs, bats, foxes, skunks, and raccoons. Due to its global distribution, severe consequences, and costly treatment, rabies remains a significant issue in public health worldwide. As an example of the economic impact of the spread of the virus, an estimated $300 million was spent on rabies control in the U.S. in 1997 alone (Krebs et al. 1998). Transmission typically occurs through bites or scratches from infected animals and transfer of the virus via the saliva of the infected animal to the injured person or animal. Different strains of rabies are associated with different host reservoirs (e.g., dog, coyote, skunk, fox, bat, and raccoon), but infected animals are capable of infecting different species of hosts. Most human fatalities in recent years are due to the particular strain associated with bats with the first documented human death due to the raccoon variant occurring in 2003 (Silverstein et al. 2003).
In this paper, we consider raccoon rabies transmission in the Eastern United States, a system reflecting an expanding wave of infection from a point source outbreak near the Virginia/West Virginia border, most likely due to the translocation of infected animals in the mid-to-late 1970s from endemic areas in South Georgia and Florida. Beginning around 1977, cases have steadily progressed away from this epicenter and spread throughout the Atlantic seaboard. To date, cases have been reported as far north as Maine and Ontario, as far east as the Atlantic Ocean, as far west as eastern Ohio, and as far south as Tennessee-North Carolina, approximately meeting up with the northern edge of an older and more slowly-moving wavefront from Florida/Georgia (Guerra et al. 2003).
The work presented here falls into the broad category of disease ecology and represents an intersection of population ecology, community ecology, epidemiology and environmental health focused on the study of (typically infectious) disease within a population of individuals, often incorporating the interactions between at-risk individuals with each other and with elements of their environment. Related concepts include “landscape ecology”, the study of the impact of local landscapes on animal and plant species presence and behavior (Turner 2005a and 2005b); Paulousky's “landscape epidemiology”, the study of the impact of the physical landscape on the spread of infectious disease (Paulousky 1966); and “landscape genetics” focusing on the role of landscape features on geographic and genetic differentiation of species into subpopulations (Manel et al. 2003). Spatial factors often play key roles in the spread of an infectious disease due to the heterogeneous geographic distributions of the at-risk individuals and their local environments. The growing availability of georeferenced data has led to an increased use of geographic information system (GIS) technology within disease ecology and related fields such as conservation medicine (Aguirre et al. 2002) and spatial epidemiology (Ostfeld et al. 2005). In work directly related to the topic under study here, Recuenco et al. (2007) found associations between elevated counts of raccoon rabies and environmental variables such as land use, land elevation, presence of major roads, and presence of major rivers. In addition, Smith et al. (2002) and Russell et al. (2004) used cellular automata models to measure associations between time to first raccoon rabies case and major rivers in Connecticut and New York. These works help motivate our investigation of the impacts of landscape features on the transmission of raccoon rabies. Our goal is to explore the spatial pattern in the time of first report of rabid raccoons for each county in the northeastern United States and investigate and quantify potential environmental factors that impact the rate of spread of this zoonotic disease.
2. Methods
2.1 Kriging
To begin, our data include the date of first report of a confirmed case of raccoon rabies for each county in the northeastern United States. County health departments are required to report suspected cases of rabies to the U.S. Centers for Disease Control and Prevention, and to submit tissue (brain) samples for confirmatory diagnosis. The raccoon rabies data consist of locations s = (s1, s2,…, sn) and associated times t = (t1, t2,…, tn) in months of observed first case in a county, where time begins at 0 months for the first reported raccoon rabies case in Pendleton County, West Virginia and 1,…,n represent the unique counties. We observe a set of environmental covariates for each observed location, denoted X(si). Figure 1 illustrates our study area with the geographic centroid of the index county (the county first reporting a case) in West Virginia illustrated by a star. Similar results appear in Biek et al. (2007) as background to their examination of genetic diversity among the stored virus samples.
Figure 1.
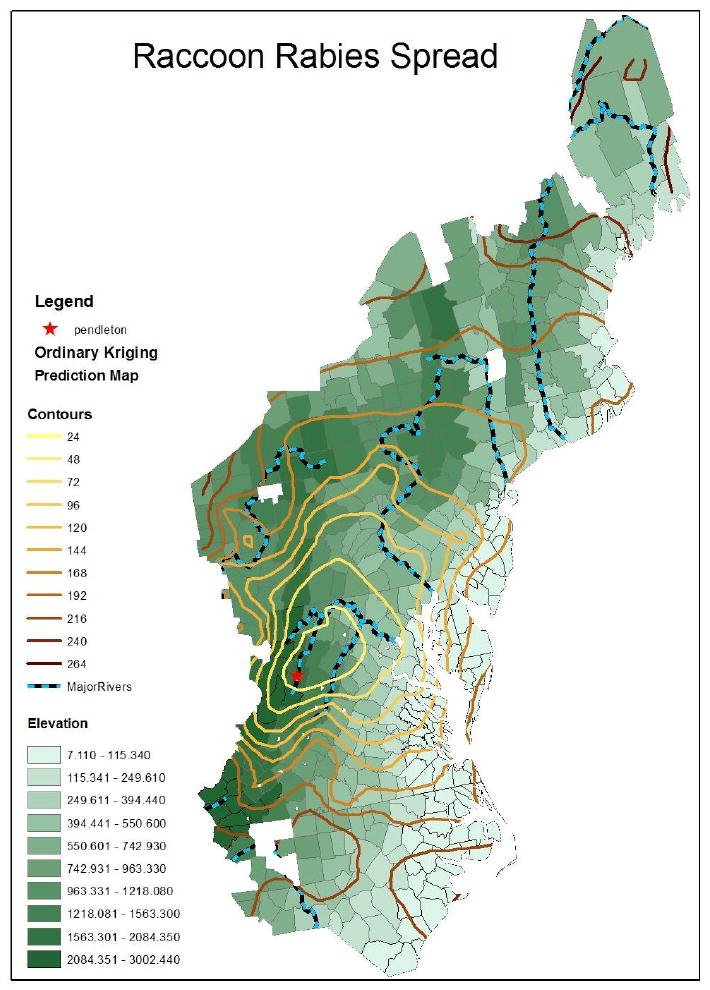
Ordinary kriging contours showing month intervals for week of first (reported and verified) appearance of raccoon rabies smoothed from county reports for the northeastern United States. The county reporting the first case is labeled by a star. Contours become darker progressively with time.
In order to clarify the spatial pattern, we use geostatistical spatial prediction to create a smooth contour surface representing the interpolated date of first appearance. Such prediction methods typically appear in the literature under the name ‘kriging’ in honor of a South African mining engineer who pioneered the predictive approach (Cressie 1993, Waller and Gotway 2004, Chapter 8). We use the analytic package Geostatistical Analyst (Johnston et al. 2001) within the geographic information system ArcGIS to implement ordinary kriging using our data. Kriging represents an optimal linear prediction by seeking weights which minimize the mean square prediction error (MSPE) associated with the predictions, subject to an unbiasedness constraint ensuring the expected value of the prediction at any location corresponds to the true, but unobserved, measurement at that location.
The shaded kriging contours in Figure 1 reveal a general spread of cases toward the northeast from the initial location. When we overlay the contours of the kriging predicted dates of first raccoon rabies appearance with land elevation and major rivers in Figure 1, we note several apparent impacts of physical geography on the disease spread. First, the compressed contours suggest spread into and eventually over the Appalachian Mountains at a slower rate than the spread we observe up the eastern seaboard. Associations with locations of major rivers (as suggested by previous work by Smith et al. 2002 and Russell et al. 2004) are also apparent with slight compression between contours as the wavefront crosses parallel to rivers (e.g., crossing the Potomac and Susquehanna Rivers), and somewhat faster spread when the wavefront is perpendicular to the river (e.g. up the Hudson River Valley and Connecticut River). It is important to note that Figure 1 provides a descriptive portrait of the outbreak to date, i.e., our use of kriging is simply as a data smoother and we make no adjustment for any local landscape covariates or potentially nonstationary or anisotropic covariance.
2.2 Bayesian Areal Wombling
We next move from pattern description to inference regarding potential barriers to spread, that is, identifying boundaries across which spread is slower than expected. Wombling is a general analytic method used in ecology for boundary analysis, i.e. determining boundaries, or barriers, on a spatial surface that separate areas of lower and higher values of a georeferenced variable (Fortin and Dale 2005). The method is named for the author of a seminal paper linking species differentiation with physical landscape barriers (Womble 1951). We follow work by Lu and Carlin (2005) and use a Bayesian hierarchical model-based framework for wombling, in contrast to previous algorithmic versions that typically use arbitrary critical values to identify boundaries. An advantage of the Bayesian approach is that it provides a direct estimate of the probability that a line segment between two adjacent areas is a barrier. The Bayesian model we use for modeling Yi, the time to first reported raccoon rabies case in each county i, is
| (2.1) |
where
| (2.2) |
is the expected value of time to first reported raccoon rabies case in each county, which includes a spatial random effect φi, and where τ is the precision. The spatial random effects follow an intrinsic conditionally autoregressive (CAR) prior, φ ∼ CAR(τC). This CAR distribution may be expressed via
| (2.3) |
where mi is the number of adjacent areas for area i and τC is the precision, where the superscript denotes the affiliation with the CAR prior and is not a power. We assign a flat prior to α and include a sum-to-zero constraint on the CAR random effects to allow identifiability of both α and the spatial random effects. See Besag et al. (1991) and Besag and Kooperberg (1995) for more details on the intrinsic CAR model. As in Lu and Carlin (2005), we use a smoothing model to limit detecting false boundaries that appear from extreme measures in lowly populated juxtaposed counties, similar to the practice of smoothing in disease mapping to avoid unstable rates from small population sizes. We assign prior distributions τ ∼ G(0.01, 0.01) and τC ∼G(0.01, 0.01) for the error precision and the CAR precision, respectively.
The boundary likelihood value (BLV) is used to determine whether a line separating two adjacent areas is a barrier and is defined as the absolute difference in times in first raccoon rabies case occurring in adjacent counties i and j,
| (2.4) |
Boundaries in wombling are either crisp or fuzzy. In crisp boundary wombling, lines are assigned a boundary membership value (BMV) of 1 if the BLV exceeds some prespecified threshold, 0 otherwise. The lines exceeding the threshold value are called boundary elements and the set of all boundary elements comprises the wombling boundary solution. In fuzzy boundary wombling, lines are assigned a partial membership value between 0 and 1 and thus give a better indication of the uncertainty in boundary membership than would be provided by crisp boundaries. In the Bayesian model approach, it is possible to calculate the probability that each separating line segment is a boundary using the posterior distribution of the BLVs. For any particular threshold value c, it is straightforward to calculate the posterior probability P(ΔiJ ≥ c | y) for each segment separating counties and consider this the associated BMV. Within the Bayesian framework, we use Markov chain Monte Carlo (MCMC) samples to calculate the probabilities for fuzzy boundaries. More specifically, the MCMC posterior estimate of the boundary probability is
| (2.5) |
where G is the number of MCMC samples (2,000 in this analysis). These probabilities may be mapped for all separating line segments to illustrate locations and strengths of potential boundaries. It is also possible to calculate the standard error of this binomial proportion.
2.3 Bayesian Spatially Varying Coefficient Model
While Bayesian areal wombling is beneficial for detecting and visualizing barriers that slow transmission of infectious diseases, the version of wombling described above does not provide direct inference on landscape variables in relation to the barriers. While landscape covariates may be included in the Bayesian CAR model to fit the response variable, doing so alone will not link local variation in landscape covariates to boundaries. To better make the connection between landscape variables and transmission time for raccoon rabies, we utilize a Bayesian spatially varying coefficient (SVC) model (Banerjee et al. 2004). The motivation for doing so is to model the underlying influences that lead to barriers in transmission. Suppose our inferential goal is to describe E[Yi | f(X (si))], the expected time of first report for raccoon rabies in county i given a function of the covariates associated with the county. The general Bayesian SVC model is
| (2.6) |
where
| (2.7) |
specifies the mean time to first reported raccoon rabies case at each county through covariate vector Xi and a vector of spatially varying regression coefficients βi. The prior on the regression coefficients in the SVC model takes into consideration the potential spatial dependence in the coefficients. The prior for our spatially varying coefficients is set to be an intrinsic multivariate CAR, or MCAR prior and is written as β ∼ MCAR(Ω). The MCAR prior for the vector of size p of spatially varying coefficients in each area i, βi = (βi1, βi2,…,βip)′, has a multivariate conditional distribution
| (2.8) |
where , κi is the set of neighboring areas for area i, and mi is the number of neighbors for area i. The diagonal elements of the variance-covariance matrix Ω are the conditional variances of the βk's and the off-diagonal elements are the conditional covariances between pairs of βk's. The prior for this within-area, between-coefficient p×p variance-covariance matrix is assigned to be a vague inverse Wishart distribution with hyperparameter scale matrix set to 0.02 · Ip×p, where I is the identity matrix, and degrees of freedom ν = p, Ω ∼ IW(ν, 0.02 · I). The prior for the error precision τ is set to be a conjugate gamma, τ ∼ G(0.01, 0.01).
The neighborhood adjacency list for the 428 counties in the study area used in the MCAR prior, and in the CAR prior in the Bayesian wombling model, is generated in GeoBUGS (Thomas et al. 2004). We use MCMC simulation in WinBUGS software (Spiegelhalter et al. 2003) to provide samples of model parameter values from their joint posterior distribution for inference in explaining raccoon rabies transmission time. We use a “burn-in” period of 200,000 iterations and the subsequent 100,000 samples from the joint posterior distribution to calculate posterior mean estimates for the model parameters.
We generated landscape variables for mean county elevation and presence of a major river in a county to use as inputs to the Bayesian SVC model as follows. We calculated mean elevation for each county from the United States Geological Survey (USGS) Geographic Names Information System (GNIS) using populated places data points with recorded elevation inside each county. We created the major river indicator variable by assigning a “1” to the variable for each county with a major river inside or along its borders using the GIS software ArcGIS 9.2 (ESRI 2005). We also use as a covariate year 2000 population density from the 2000 U.S. Census and ESRI. In addition, we calculated great circle distance between each county and the origin county using R software and the county centroid coordinates from ESRI. Maps of model parameter estimates were generated in R, GeoBUGS, and ArcGIS software packages.
As a baseline to assist in determining the covariates to use in the Bayesian SVC regression model, we first fitted a series of linear regression models with only one coefficient estimated for each covariate, in addition to an intercept, i.e. non-spatially varying coefficients. Based on the clear spatial trend in the response variable, we estimated a linear regression model with a second-order trend surface. The model is
| (2.9) |
where s1 and s2 are the spatial coordinates, x1 is mean elevation in feet, x2 is major river presence, and x3 is the natural log of population density. Population density is included as a surrogate for urbanicity and as a factor in raccoon rabies case reporting, as more populated areas are, in theory, more likely to report cases, although as areas become too populated, as in major cities, the quality of raccoon habitat decreases. In this model, all of the trend surface coefficients were statistically significant at the 0.05 significance level, as were the coefficients for elevation (positive in sign with p-value < 0.01) and log population density (positive in sign with p-value < 0.001). The p-value for the major river variable was 0.10. The coefficient of determination was 0.54.
Based on the results of the linear regression model, we elected to fit three Bayesian SVC models. The first model is
| (2.10) |
where the covariates are as previously defined. The second model is
| (2.11) |
where x4 is a binary indicator with a value of “1” if the mean county elevation ≥ 1,000 feet, and the other variables are as defined previously. The binary variable was included to better reflect the presence of mountain ranges. The value of 1,000 feet was selected to represent visually the higher elevation associated with the mountain ranges in the study area. Note that in this model the coefficient for log population density does not vary spatially. The prior for this parameter is assigned a vague normal distribution, β4 ∼ N(0, 1/0.00001). The third model is
| (2.12) |
where x5 is the distance between each county and the origin county and the coefficient for this covariate, β5, does not vary spatially. The prior for this parameter is assigned to be a vague normal, β5 ∼ N(0, 1/0.00001). Distance is included in this SVC model as it may be helpful, in addition to the MCAR prior, to capture the clear trend in the transmission time over space. In addition, elevation and population density are related to distance from the origin county, suggesting some effort to adjust for distance may be beneficial to model fit.
2.4 Bayesian Spatially Varying Coefficient Adjusted Areal Wombling
As an alternative to the Bayesian areal wombling model introduced above, one can calculate fuzzy wombling boundaries from a Bayesian SVC model, incorporating landscape variables to improve the fit of the response variable. This is achieved by calculating the BLVs from the posterior mean estimates of the response variable from the Bayesian SVC model. The Bayesian spatially varying coefficient adjusted areal wombling model is then a combination of the Bayesian SVC model in equations (2.6) – (2.8) and the BLV equation (2.4) and the BMV equation (2.5). The wombling BMVs can also be plotted on a map of spatially varying coefficients for certain landscape variables, such as major rivers, to better show the relationship between landscape effects and boundaries.
3. Results
In this section we present results from the Bayesian areal wombling model, the Bayesian SVC model, and the Bayesian SVC adjusted areal wombling model. Figure 2 is a series of fuzzy Bayesian areal wombling maps using categories of P(Δij ≥ c | y) for increasing two-year intervals of time to first raccoon rabies case as the threshold value c, with c = 24, 48, 72, and 96 months. Lines are shaded in increasingly darker gray corresponding to increasing posterior probability of being a barrier. The four categories of P(Δij ≥ c | y) and associated shading are (0.0, 0.4) - white, (0.4, 0.6) – light gray, (0.6, 0.8) - gray, (0.8, 1.0) – dark gray. Major rivers are also displayed in blue. As expected, there are fewer higher probability barrier lines as the time to first raccoon rabies case increases. There appears to be some alignment of boundaries, according to the highest category of probability of boundary membership, with the Potomac River, Susquehanna River, and the Ohio River. In addition, there are more boundaries in the Appalachian Mountains than in the eastern seaboard. This pattern echoes that of the kriging map in Figure 1, where a faster rate of spread was evident in the eastern seaboard than in the Appalachians. The majority of boundaries in the Appalachian Mountains are southwest of the origin county of Pendleton, West Virginia. This supports the idea that mountain ranges make poor habitats for raccoons, and as a result, the Appalachian Mountains helped limit the westward expansion of the raccoon rabies outbreak. Similarly, the Allegheny Mountains appear to have limited or slowed the northern expansion of the outbreak, as indicated by the number of high posterior probability wombling boundaries in this area. The alignment of barriers with mountain ranges is clearer in Figure 3, which shows the posterior probability of boundary lines for 36 months to first reported raccoon rabies case, along with major rivers (blue) and mean county elevation increasing with darker shaded green. The same probability line shading as in Figure 2 is used in Figure 3.
Figure 2.
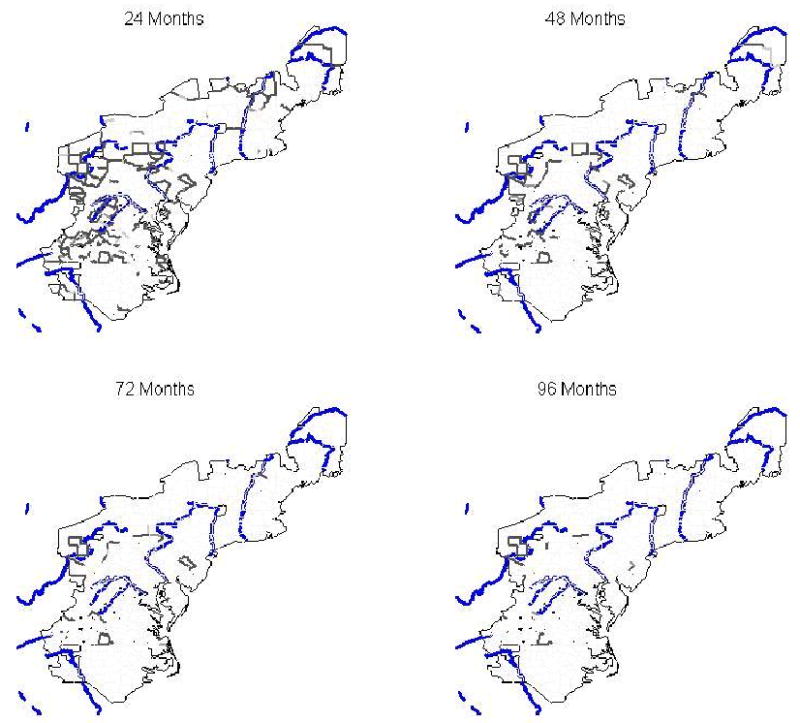
Posterior probabilities for Bayesian areal wombling barriers for four time points of first raccoon rabies case, along with major rivers (blue). Lines are shaded in increasingly darker gray corresponding to increasing probability of being a boundary. The four categories of P(Δij ≥ c | y) are (0.0, 0.4) - white, (0.4, 0.6) – light gray, (0.6, 0.8) - gray, (0.8, 1.0) – dark gray.
Figure 3.
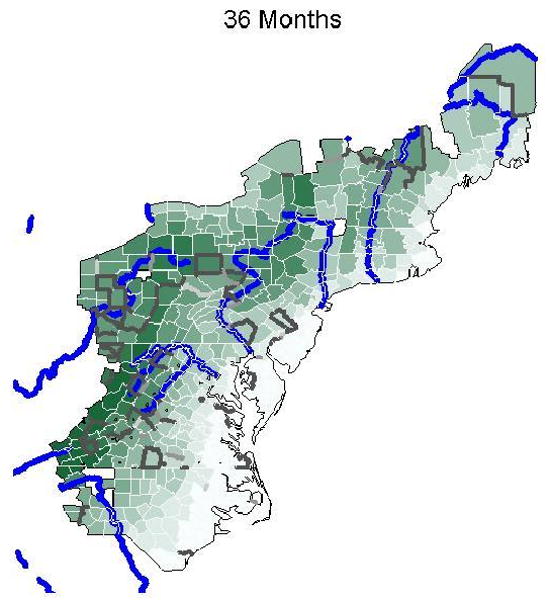
Posterior probabilities for Bayesian areal wombling barriers at 36 months to first raccoon rabies case, along with major rivers (blue) and mean elevation (increasing in green). Lines are shaded in increasingly darker gray corresponding to increasing probability of being a barrier. The four categories of P(Δij. ≥ c | y) are (0.0, 0.4) - white, (0.4, 0.6) – light gray, (0.6, 0.8) - gray, (0.8, 1.0) – dark gray.
While the Bayesian areal wombling results suggest some alignment of increased raccoon rabies transmission time with landscape barriers of major rivers and mountain ranges in some areas, the inferential basis for defining which landscape features impact the spread in a significant manner is limited. To enable more direct inference on the effect of landscape variables, we present the results from the Bayesian SVC model. We fitted three SVC models, as described in the Methods section. The fits of the models, adjusted for model complexity, are compared using the Deviance Information Criterion (DIC) (Spiegelhalter et al. 2002, Spiegelhalter et al. 2003). The DIC = D̄ + pD, where D̄ is the posterior mean of the deviance and pD is the effective number of parameters. The DIC values are 1281.8 for model M1, 1615.6 for M2, and 2030.9 for M3. Model M1 has a substantially lower DIC value than does the M2 model, which has a lower DIC than the M3 model. Neither restricting the elevation variable to higher values and population density to a global effect nor including distance as a global effect, with the global effect of population density, increase the accuracy of prediction of the response variable when considering model complexity. Due to space limitations, we only show the parameter estimates for model M1.
The parameter posterior mean estimates for the expected time to first raccoon rabies case and spatially varying regression coefficients from model M1 are mapped in Figure 4. The posterior mean times to first raccoon rabies case approximate the observed times shown in Figure 1, with a clear wavelike increase in time in a northeast direction from the origin county, as well as a less pronounced increase in the direction south. The same pattern, to a lesser degree, is evident in the spatially varying intercept, β1. The posterior mean coefficients for elevation are generally small in magnitude, with positive values in counties in New England and Pennsylvania and negative values elsewhere. The most negative values are to the east of and on the downward slope of the Appalachian Mountains, where the outbreak spread relatively quickly. The posterior mean estimates of the major river coefficients are positive, indicating increased time to arrival, in the Potomac and Susquehanna River Valleys and negative for other rivers. This tends to agree with the wombling boundary elements found near the Potomac River and Susquehanna River and with the kriging map that showed slightly compressed contours in these two areas compared with other river valley areas. The posterior mean estimates for the log population density coefficient are positive in New England, western Pennsylvania, and in the southern portion of the study area. The largest positive values are on the periphery of the study area, in more rural areas. There may be some difficulty in separating the effects of elevation and log population density, as the two exhibit negative correlation (r = −0.38). In addition, both variables are somewhat confounded with distance from the origin county.
Figure 4.
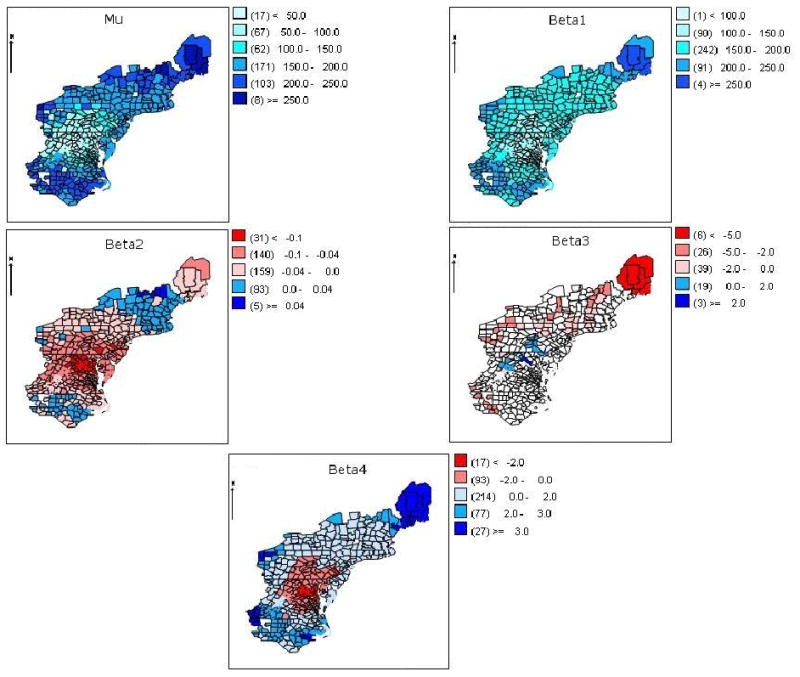
Posterior mean estimates of Bayesian SVC model M1 parameters μ, β1 (intercept), β2 (elevation), β3 (major river), β4 (log population density). A divergent color ramp indicates a transition from negative (red) to positive (blue) values.
The fuzzy boundaries for time to first raccoon rabies case from the Bayesian SVC adjusted areal wombling model with the response variable modeled through equation (2.10), M1, are quite similar in location to those from the Bayesian areal wombling model plotted in Figure 2, so for brevity we omit a map of them here. While the boundary locations are similar in the two models, the BMVs generally appear larger in the covariate adjusted version of wombling when mapped. The posterior probabilities of boundary membership for the Bayesian SVC wombling model are plotted against the posterior probabilities of boundary membership for the Bayesian wombling model in Figure 5 for threshold values of c = 24 and c = 96. The Bayesian SVC model results in less posterior variance around predicted values than observed for the Bayesian wombling model, which in turn results in tighter posterior classification of county borders as likely boundaries or not. More specifically, Figure 5 reveals how the adjustment for the local landscape effects refines the wombling results by emphasizing high probability barriers and diminishing the focus on low probability barriers through explaining more variation in the outcome by including the (spatially-varying) covariates. Additionally, the SVC model offers inference regarding the local impact of the GIS-defined landscape features without losing the wombling results. For the large time threshold of 96 months, the Bayesian SVC wombling posterior probabilities of boundary membership are predominantly valued near 1.0 or 0.0, indicating that the Bayesian SVC wombling fuzzy boundaries become closer to crisp boundaries as the threshold time becomes large.
Figure 5.
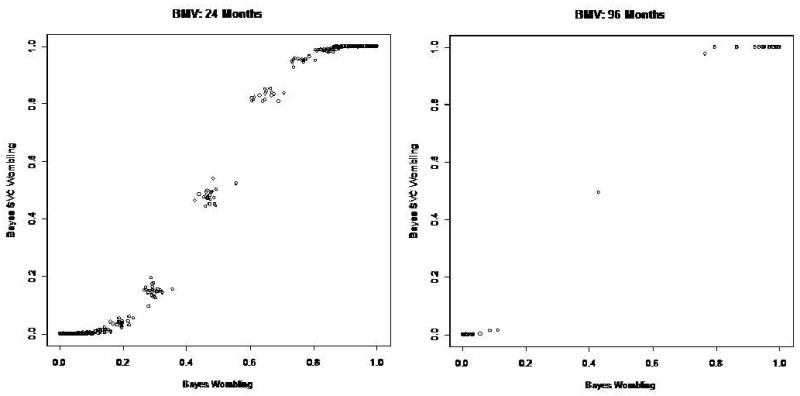
Posterior probabilities (BMVs) for Bayesian SVC adjusted areal wombling barriers versus posterior probabilities for Bayesian wombling for two time points of first raccoon rabies case.
4. Conclusions
In this work, we used kriging to provide descriptive visualization of the overall pattern of raccoon rabies transmission. We next used Bayesian areal wombling to first find likely landscape boundaries in the spread of a 1977 raccoon rabies outbreak and then utilized Bayesian SVC regression models to explain raccoon rabies spread with landscape variables that could represent potential transmission barriers or gateways. The results of the Bayesian wombling suggest several barriers to transmission in the Appalachian and Alleghany mountain ranges, as well as in the Susquehanna and Potomac River valleys. The results of the best fitting Bayesian SVC model further quantify the impact of the Potomac and Susquehanna Rivers in slowing the spread of raccoon rabies from the origin of Pendleton County, West Virginia. In addition, log population density and mean county elevation were found to be significantly positively related to raccoon rabies transmission time in a second-order trend surface linear regression model.
While the results from this work were illuminating, there are many potential future research opportunities with these raccoon rabies data. One research direction is to include variables to indicate similarity/difference in adjacent regions in a more complex Bayesian wombling model (see Lu et al. 2007). This may be especially helpful for including elevation change between counties and representing rivers that separate neighboring counties. Alternatively, one could choose to model the probability of raccoon rabies transmission along a semi-directed network, where directed links represent adjacent counties with a difference in time to first reported case. The objective would be to determine a probability of raccoon rabies flow along the network. Finally, the storage of virus specimens allows inclusion of genetic sequence information regarding evolution of the pathogen over the course of the outbreak and allows for additional detail in describing landscape influences on the spread of the disease by identifying samples that are close both temporally and phylogenetically. Moving from the spatial models above to a fully model-based approach linking spatio-temporal and phylogenetic dynamics with landscape influences presents considerable analytic challenges. However, rabies offers an attractive system for attempting such models, based on the close contact required for transmission, the terrestrial hosts for the virus, and the suggestive patterns observed above and in related work (Smith et al. 2002, Russell et al. 2003, Biek et al. 2007).
In summary, the analyses above illustrate hierarchical modeling approaches to identify and quantify local landscape influences on the spread of an epizoonotic outbreak of rabies. The approaches range from descriptive summaries to detailed quantification of spatially varying effects and reveal local details driving the observed pattern of spread. Coupled with mathematical models of diffusion, the analytic methods above can provide important information for the design and implementation of public health response to such outbreaks (e.g., distribution of vaccinated baits, veterinary surveillance, and public information campaigns).
Acknowledgments
The authors thank Leslie Real and the Center for Disease Ecology at Emory University for access to the date of first report data and for helpful discussions. This research is supported in part by National Institute of Environmental Health Sciences (NIEHS) grant 1T32ES012160. The views expressed herein are those of the authors and do not necessarily reflect those of NIEHS.
References
- Aguirre A, Ostfeld R, Tabor G, House C, Pearl M. Conservation Medicine: Ecological Health in Practice. Oxford: Oxford University Press; 2002. [Google Scholar]
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical Modeling and Analysis for Spatial Data. Chapman & Hall/CRC; Boca Raton: 2004. [Google Scholar]
- Besag J, Kooperberg C. On Conditional and Intrinsic Autoregressions. Biometrika. 1995;82:733–746. [Google Scholar]
- Besag J, York J, Mollie A. Bayesian Image Restoration, with Two Applications in Spatial Statistics. Annals of the Institute of Statistical Mathematics. 1991;43:1–59. with Discussion. [Google Scholar]
- Biek R, Henderson JC, Waller LA, Rupprecht CE, Real LA. A High-resolution Genetic Signature of Demographic and Spatial Expansion in Epizootic Rabies Virus. Proceedings of the National Academies of Sciences of the USA. 2007;104:7993–7998. doi: 10.1073/pnas.0700741104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressie N. Statistics for Spatial Data. Revised. New York: John Wiley and Sons; 1993. [Google Scholar]
- ESRI. ArcGIS 9.1 Users Guide. 2005. [Google Scholar]
- Fortin MJ, Dale M. Spatial Analysis: A Guide for Ecologists. Cambridge: Cambridge University Press; 2005. [Google Scholar]
- Guerra M, Curns A, Rupprecht C, Hanlon C, Krebs J, Childs J. Skunk and Raccoon Rabies in the Eastern United States: Temporal and Spatial Analysis. Emerging Infectious Diseases. 2003;9:1143–1150. doi: 10.3201/eid0909.020608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston K, Ver Hoef J, Krivoruchko K, Lucas N. Using ArcGIS Geostatistical Analyst. Redlands, CA: ESRI Press; 2001. [Google Scholar]
- Krebs J, Long-Marin S, Childs J. Causes, Costs and Estimates of Rabies Postexposure Prophylaxis Treatments in the United States. Journal of Public Health Management and Practice. 1998;4:56–62. doi: 10.1097/00124784-199809000-00009. [DOI] [PubMed] [Google Scholar]
- Lu H, Carlin BP. Bayesian Areal Wombling for Geographical Boundary Analysis. Geographical Analysis. 2005;3:7, 265–285. [Google Scholar]
- Lu H, Reilly CS, Banerjee S, Carlin BP. Bayesian Areal Wombling via Adjacency Modeling. Environmental and Ecological Statistics. 2007 to appear. [Google Scholar]
- Manel S, Schwartz M, Luikart G, Taberlet P. Landscape Genetics: Combining Landscape Ecology and Population Genetics. Trends in Ecology and Evolution. 2003;18:189–197. [Google Scholar]
- Ostfeld R, Glass G, Keesing F. Spatial Epidemiology: An Emerging (or Re-emerging) Discipline. Trends in Ecology and Evolution. 2005;20:328–336. doi: 10.1016/j.tree.2005.03.009. [DOI] [PubMed] [Google Scholar]
- Paulousky EN. Natural Nidality of Transmissible Diseases: With Special Reference to the Landscape Epidemiology of Zooanthroponoses. Urbana: University of Illinois Press; 1966. [Google Scholar]
- Recuenco S, Eidson M, Kulldorff M, Johnson G, Cherry B. Spatial and Temporal Patterns of Enzootic Raccoon Rabies Adjusted for Multiple Covariates. International Journal of Health Geographics. 2007;6:14. doi: 10.1186/1476-072X-6-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell C, Smith D, Waller LA, Childs J, Real LA. A Priori Prediction of Disease Invasion Dynamics in a Novel Environment. Proceedings of the Royal Society: Biological Sciences. 2004;271(1534):21–25. doi: 10.1098/rspb.2003.2559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverstein M, Salgado C, Bassin D, Bleck T, Lopes M, Farr B, Jenkins S, Sockwell D, Marr J, Miller G. First Human Death Associated with Raccoon Rabies, Virginia, 2003. Morbidity and Mortality Weekly Report. 2003;52:1102–1103. [PubMed] [Google Scholar]
- Smith D, Lucey B, Waller LA, Childs J, Real LA. Predicting the Spatial Dynamics of Rabies Epidemics on Heterogeneous Landscapes. Proceedings of the National Academy of Sciences, USA. 2002;99:3668–3672. doi: 10.1073/pnas.042400799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian Measures of Model Complexity and Fit. (B).Journal of the Royal Statistical Society. 2002;64:583–640. with Discussion. [Google Scholar]
- Spiegelhalter D, Thomas A, Best N, Lunn D. WinBUGS Users Manual, Version 1.4. 2003. [Google Scholar]
- Thomas A, Best N, Lunn D, Arnold R, Spiegelhalter D. GeoBUGS User Manual, Version 1.2. 2004. [Google Scholar]
- Turner MG. Landscape Ecology in North America: Past, Present, and Future. Ecology. 2005a;86:1967–1974. [Google Scholar]
- Turner MG. Landscape Ecology: What is the State of the Science? Annual Review of Ecology, Evolution, and Systematics. 2005b;36:319–344. [Google Scholar]
- Waller LA, Gotway C. Applied Spatial Statistics for Public Health Data. New York: John Wiley and Sons; 2004. [Google Scholar]
- Womble WH. Differential Systematics. Science. 1951;114:315–322. doi: 10.1126/science.114.2961.315. [DOI] [PubMed] [Google Scholar]


