Abstract
Trabecular architecture becomes more rod-like and anisotropic in osteoporotic and aging trabecular bone. In order to address the effects of trabecular type and orientation on trabecular bone damage mechanics, microstructural finite element modeling was used to identify the yielded tissue in ten bovine tibial trabecular bone samples compressed to 1.2% on-axis apparent strain. The yielded tissue was mapped onto individual trabeculae identified by an Individual Trabeculae Segmentation (ITS) technique, and the distribution of the predicted yielding among trabecular types and orientations was compared to the experimentally measured microdamage. Although most of the predicted yielded tissue was found in longitudinal plates (73 ± 11%), the measured microcrack density was positively correlated with the proportion of the yielded tissue in longitudinal rods (R2 = 0.52, p = 0.02), but not in rods of other directions or plates. The overall fraction of rods and the fractions of rods along the longitudinal and transverse axes were also correlated with the measured microcrack density. In contrast, diffuse damage area did not correlate with any of these quantities. These results agree with the findings that both in vitro and in vivo microcrack density is correlated with Structure Model Index (SMI), and are also consistent with decreased energy to failure in more rod-like trabecular bone. Together the results suggest that bending or buckling deformations of rod-like trabeculae may make trabecular structures more susceptible to microdamage formation. Moreover, while simple strain-based tissue yield criteria may account for macroscopic yielding, they may not be suitable for identifying damage.
Keywords: trabecular bone, microdamage, architecture, trabecular rod, osteoporosis
Introduction
Trabecular tissue loss and deterioration of trabecular architecture are two factors cited in the definition of osteoporosis [1]. Trabecular tissue loss is accompanied by topological changes, such as thinning of trabeculae [2] and the conversion of trabecular plates to rods [3], such that tissue loss and architectural changes are linked. As new diagnostic and treatment procedures are developed, there is a need for an improved mechanistic understanding of bone mechanics to better delineate the effects of density and architectural changes on fracture risk [4]. Microdamage is also believed to be an important factor that increases fracture risk in osteoporotic bone [5]. Microdamage occurs in vivo during activities of daily living, and can be repaired through remodeling [6, 7]. However, microdamage accumulation beyond the bone’s capacity to repair, especially in osteoporotic or aging bone, can adversely affect the mechanical properties of bone [8, 9].
Damage susceptibility in a material depends on interactions between local material properties, the presence of ultrastructural features that can enhance or inhibit crack formation and propagation, and the applied stress. In bone, matrix composition – such as mineralization and collagen chemistry [10–15] – is a major determinant of the material properties. Crack initiation and arrest sites include osteocyte lacunae and lamellar interfaces [16, 17]. Trabecular tissue stress depends on external loading, and is enhanced or attenuated at different tissue locations due to the porous trabecular architecture, and, as such, several architectural parameters are associated with increased microdamage [18, 19].
One architectural feature of trabecular bone that is associated with damage is the Structure Model Index (SMI). SMI is a morphometric measure of the degree to which a porous structure is composed of plate-like or rod-like elements. It takes on the value 0 for an ideal plate structure, and 3 for an ideal rod structure [20]. The density of microcracks initiated by overloading, as well as that of propagating microcracks, was positively correlated with the SMI of bovine samples [18]. In vivo microdamage in human vertebral trabecular bone is similarly correlated with SMI [19]. However, SMI is a single scalar metric, and does not provide details on the relative number or orientation of plates and rods. Individual Trabeculae Segmentation (ITS) is a technique that provides a detailed and objective characterization of the types and orientations of trabeculae [21]. Using this technique, plates have been shown to have a greater contribution to the elastic stiffness of trabecular bone than rods [21], and axially aligned trabeculae were found to provide the main resistance to axial loading [22].
Computational models provide a sample-specific means to study tissue level stress due to a given macroscopic loading for both elastic [23–25], and post-yield loading [23, 26]. Notably, locations of microdamage formation were associated with higher local von Mises stress calculated by linear finite element models [27]. However, there has been no direct correlation between calculated tissue yielding from nonlinear models and experimentally measured microdamage.
The application of nonlinear microstructural Finite Element Analysis (micro-FEA), ITS, and experimental measures of microdamage may provide improved insight into the roles of trabecular architecture and mechanical loading in microdamage susceptibility. As such, the objective of this study was to determine whether microdamage susceptibility is related to the presence of highly strained tissue in specific types and orientations of trabeculae. Specifically, 1) ITS was used to decompose trabecular bone samples into individual plate and rod elements; 2) micro-FEA was used to identify trabecular tissue loaded beyond the yield point; and 3) experimentally measured microdamage was correlated with the quantity and distribution of the predicted yielded tissue.
Materials and Methods
Ten cylindrical trabecular bone samples from the proximal tibia of young slaughter cattle (Martin’s Meats, Wakarusa, IN) were analyzed. The orientation of the samples was controlled using micro-CT imaging to ensure that the principal trabecular orientation was aligned with the axis of the samples. Briefly, a low-resolution scan was used to create finite element models that were subsequently used to determine the principal mechanical axes of cubic bone sections [28]. The calculated axes were used to orient the cubes, and a cylindrical core was cut using a diamond edge coring tool (Starlite Industries, Rosemont, PA) [28]. The cylinder axis was aligned with the principal axis within 4.70 ± 3.11° (mean ± S.D.), on average.
The cylindrical samples were scanned at 20 μm isotropic resolution in a micro-CT scanner (μCT-80, Scanco Medical AG, Brüttisellen, Switzerland) and the architecture was quantified using the standard software (μCT Evaluation program V4.3, Scanco Medical AG, Brüttisellen, Switzerland, Table 1).
Table 1.
Architectural parameters of the samples (n = 10)
| Parametersa | Mean | S.D. | Range |
|---|---|---|---|
| VFb | 0.243 | 0.044 | 0.190 – 0.320 |
| ρapp (g/cm3) | 0.462 | 0.085 | 0.363 – 0.610 |
| Tb.Th. (mm) | 0.184 | 0.034 | 0.133 – 0.235 |
| Tb.Sp. (mm) | 0.606 | 0.080 | 0.467 – 0.700 |
| SMI (−) | 0.568 | 0.391 | −0.131 – 1.078 |
| Conn.D. (1/mm3) | 5.410 | 2.674 | 2.611 – 11.449 |
| DA (−) | 1.828 | 0.195 | 1.603 – 2.265 |
VF = volume fraction; ρapp = apparent density; Tb.Th. = trabecular thickness; Tb.Sp. = trabecular spacing; SMI = structure model index; Conn.D. = connectivity density; and DA = degree of anisotropy.
Measured by Archimedes’ Principle.
A cuboid region, approximately 5 × 5 × 6 mm3 in size, was taken from the center of each cylindrical sample image, and the images were region-averaged to 40 μm isotropic resolution to reduce computational expenses while still maintaining sufficient fidelity for numerical convergence [29–32]. ITS was then used to identify individual plates and rods within each sample [22]. This method applies Digital Topological Analysis (DTA) to transform the thresholded micro-CT images into a collection of individual trabecular plates and rods. Individual trabeculae (plates and rods) were classified as longitudinal (0–30°), oblique (30–60°), and transverse (60–90°) with respect to the cylinder axis. The amount of bone tissue in each trabecular type, and within each of the three orientation categories was calculated.
Micro-FEA models were created from the 40 μm resolution images for each sample by directly converting the bone voxels into eight-node finite elements [33]. The trabecular tissue was modeled as a homogenous isotropic material with a specimen-specific back-calculated tissue modulus [34] and a Poisson’s ratio of 0.3. A bilinear elastic model with an asymmetric principal strain tissue yield criterion [23] was applied with compressive and tensile yield strains of 0.83% and 0.41%, respectively [35]. We verified that the yielded regions did not undergo unloading (although the surrounding elastically loaded tissue did), so that the bilinear constitutive model behaves similarly to a plasticity model [23]. However, the absence of tissue level softening does not allow the model to be used for apparent strains beyond the ultimate strain [25].
Each sample was analyzed with boundary conditions corresponding to 1.2% apparent compressive strain along the principal trabecular orientation. Geometric nonlinearity was not included, but the effects would be small for the dense bone samples and low apparent strain used here [31]. The nonlinear models were solved using a custom finite element code implementing an implicit incremental solution method.
The tissue level strains were analyzed to determine which trabeculae contained yielded tissue. Due to the porous architecture of trabecular bone, bone tissue can yield due to either compressive strain or tensile strain under apparent compressive loading. Tissue that had a principal strain exceeding either the compressive or tensile elastic strain limit (0.83% strain in compression and 0.41% strain in tension) was detected and segmented at 1.2% apparent strain. The locations of the yielded tissue were mapped onto individual trabeculae, and the distribution of the yielded tissue within each trabecular type and orientation combination was calculated. A predominance of compressive or tensile yielding suggested uniaxial compression or extension of trabeculae, while combined compressive and tensile yielding was taken as an indication of bending failure.
The amount and location of yielded tissue were compared to measurements of microdamage from a previous study in our laboratory on the same samples [36]. Briefly, in vivo microdamage was stained with alizarin. Subsequently, microdamage induced by a 2% apparent on-axis compressive overload was stained by xylenol orange, thereby allowing the two types of damage to be quantified separately [37]. The microcrack density (Cr.Dn.) and diffuse damage area (Dx.Ar.) were quantified by direct counting under 100X magnification on an epifluorescent microscope. The two-dimensional nature of the measurement did not allow damage in rods and plates to be differentiated.
The damage due to the overload was compared to the rod fraction – defined as the total number of rods divided by the total number of trabeculae (Rd.N./Tr.N.) – and the rod fractions in the longitudinal, oblique, and transverse directions – defined as the number of rods in each direction divided by the total number of trabeculae in the corresponding directions (L.Rd.N./L.Tr.N., O.Rd.N./O.Tr.N., and T.Rd.N./T.Tr.N.).
Statistical analyses were performed using Student’s t-test in Microsoft Excel 2003 and linear regression in JMP 7.0 (SAS Institute Inc., Cary, NC) with a significance level of p = 0.05. The normality of the parameters and of the regression residuals was verified using JMP.
Results
The bone samples were primarily composed of longitudinally oriented plates. When measured by tissue volume, 80 ± 10% (mean ± S.D.) of the tissue was plates, and over 70% of the plates were oriented along the longitudinal direction. In contrast, over 70% of the rods were oriented along the transverse direction. There was also a greater volume of tissue in trabeculae along the longitudinal direction than those along the transverse direction (Table 2).
Table 2.
Distribution of bone tissue among trabecular types and orientations (mean ± S.D.)
| Category | % (by tissue volume) | % (by number of each type) |
|---|---|---|
| Platesa | 80.44 ± 10.36 | |
| Longitudinalb | 87.59 ± 3.31 | 72.30 ± 4.97 |
| Obliqueb | 10.08 ± 2.99 | 19.80 ± 4.24 |
| Transverseb | 2.33 ± 0.81 | 7.90 ± 1.15 |
| Rodsa | 19.55 ± 10.35 | |
| Longitudinal | 20.35 ± 3.86 | 7.36 ± 1.91 |
| Oblique | 32.56 ± 3.74 | 20.24 ± 4.04 |
| Transverse | 47.09 ± 2.92 | 72.39 ± 4.48 |
Total plate vs. rod distribution was calculated by tissue volume only. Means sum to less than 100%, because a small amount of tissue could not be classified as either plates or rods.
Longitudinal: 0–30°; Oblique: 30–60°; Transverse: 60–90° relative to the axis of the samples, which was closely aligned with the principal trabecular orientation. Means sum to 100% within rounding error.
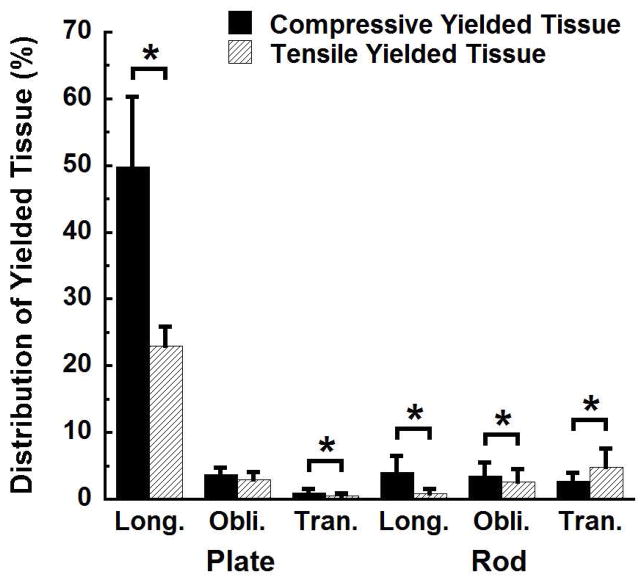
Most of the yielded tissue was found in longitudinally oriented plates (Fig. 1). At an apparent strain level of 1.2%, 73 ± 11% of the total yielded tissue was found in longitudinal plates. The remaining categories, including plates oriented in other directions and rods in all orientations, only contained from 2% to 8% of the total yielded tissue (p < 0.001).
Figure 1.
Distribution of the yielded tissue in the six trabecular type and orientation combinations at 1.2% apparent strain. The percentages in all twelve columns sum to 100%. Error bars are one standard deviation (n = 10). * p < 0.05.
The fraction of yielded tissue computed by the models did not correlate with the experimentally measured microdamage. None of the fraction of tissue yielded due to tensile strain, the fraction of tissue yielded due to compressive strain, or the total fraction of yielded tissue correlated with the measured Cr.Dn. (p > 0.20, Fig. 2a). Similarly, none of the predicted fractions of yielded tissue correlated with the measured Dx.Ar. (p > 0.44, Fig. 2b).
Figure 2.
The fraction of the tissue yielded due to tensile strain, compressive strain, and the total fraction of the tissue yielded vs. Cr.Dn. (a) and Dx.Ar. (b) at 1.2% apparent strain.
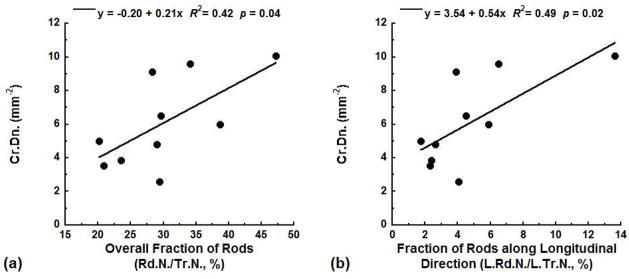
Measures of trabecular architecture using ITS were related to the microdamage measures. The experimentally measured Cr.Dn. increased with the overall fraction of rods Rd.N./Tr.N. (R2 = 0.42, p = 0.04, Fig. 3a). Inclusion of the trabecular orientation further improved the correlation. The fractions of rods along the longitudinal (L.Rd.N./L.Tr.N., R2 = 0.49, p = 0.02, Fig. 3b) and the transverse (T.Rd.N./T.Tr.N., R2 = 0.47, p = 0.03) directions both positively correlated with Cr.Dn., while the fraction of rods along the oblique direction (O.Rd.N./O.Tr.N.) showed no correlation (p > 0.05). Dx.Ar. was not correlated with any of these ITS-based architectural measures (p > 0.05).
Figure 3.
The experimentally measured Cr.Dn. was positively correlated with the overall fraction of rods Rd.N./Tr.N. (a) and the fraction of rods along the longitudinal direction L.Rd.N./L.Tr.N. (b).
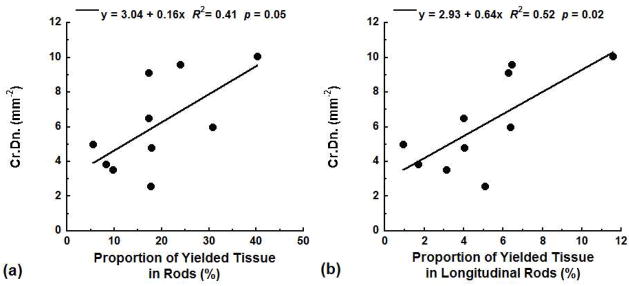
The experimentally measured microcrack density was also correlated to the distribution of the predicted yielded tissue. The proportion of the yielded tissue that occurred in rods was positively correlated with Cr.Dn. (R2 = 0.41, p = 0.05, Fig. 4a). When orientation was considered, the measured Cr.Dn. was more strongly correlated with the proportion of the yielded tissue in longitudinal rods (R2 = 0.52, p = 0.02, Fig. 4b). In contrast, there was no correlation between Cr.Dn. and the proportion of yielded tissue in rods oriented along other directions or with yielded tissue in trabecular plates of any orientation (p > 0.05). Dx.Ar. had no correlation with the distribution of tissue yielding in any trabecular type or orientation (p > 0.05).
Figure 4.
The experimentally measured Cr.Dn. was positively correlated with the proportion of the total yielded tissue found in rods (a) and the proportion of the total yielded tissue found in longitudinal rods (b) at 1.2% apparent strain.
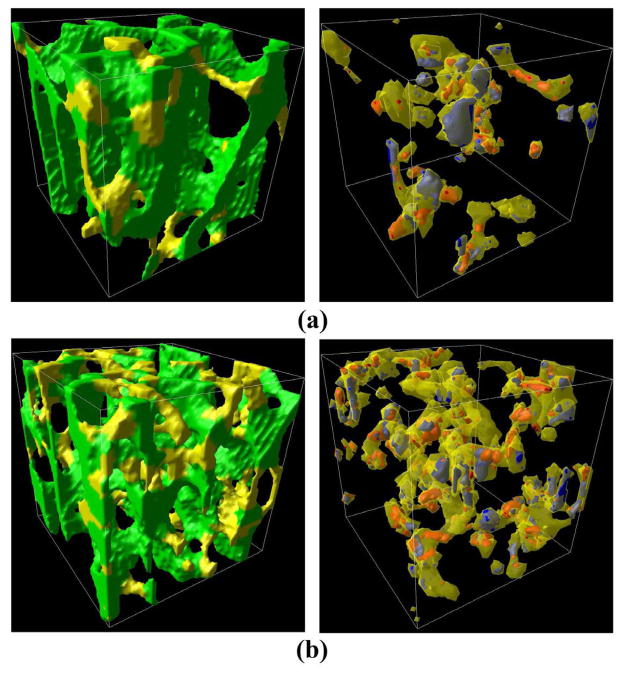
Three-dimensional visualization indicated that many rods contained both tensile and compressive regions of yielding (Fig. 5), indicative of bending. In trabeculae oriented along the loading axis, there was 5.20 ± 2.38 times as much tissue yielded due to compressive vs. tensile strain in rods, compared to 2.20 ± 0.59 times as much in plates (p = 0.001, Fig. 1). Only transversely oriented rods contained more tissue yielded in tension than in compression (p < 0.05).
Figure 5.
The left column shows renderings of a 2.5 mm cubic region of the samples that had the lowest (a) and highest (b) measured microcrack density. Rods are colored yellow, while plates are colored green. The right column shows the yielded tissue in the rods at 1.2% apparent strain. The tissue labeled red was loaded primarily in tension and that in blue was loaded primarily in compression. The loading direction is along the vertical axis in the images.s
Discussion
ITS and micro-FEA were used to gain insight into architectural contributions to microdamage susceptibility in trabecular bone. When trabecular samples were loaded along their principal trabecular orientation, although most of the predicted yielded tissue was found in longitudinal plates, the relative number of rods, especially the longitudinal rods, was the primary determinant of the whole structure’s susceptibility to microdamage formation. Longitudinal rods compose only a small fraction of trabeculae either by number or by volume, but appear to be a major factor in the damage susceptibility of trabecular architecture. When comparing among the longitudinal trabeculae, rods had a higher ratio of the amount of tissue yielded due to compressive strain vs. tensile strain, suggesting that the yielded rods are primarily in compression with superposed bending – a typical buckling scenario. Rods oriented in the transverse direction were also related to microdamage formation. The yielding mode of the transverse rods was bending with superposed axial tension. Since microdamage is considered to trigger bone remodeling [6, 7] and remodeling results in perforation of plates to rods in osteoporotic bone [3, 38], increasing the fraction of rods may result in an unstable feedback system that leads to continual degradation of the trabecular architecture.
The primary limitation of the study was the difference in boundary conditions between the experiments and the models. The maximum strain applied in the models was limited, because the tissue level constitutive model did not incorporate softening or damage, which is necessary for loading beyond the ultimate point [24, 25]. Hence, we assumed that the yielded regions at low strains will be predictive of the locations of damage initiation at higher applied strains [27]; however, there is not yet clear evidence that this is the case. Indeed, as loading progresses and microdamage forms in distinct trabeculae, the actual stresses will redistribute and the stress distribution at 1.2% apparent strain may differ from that at 2% strain. This redistribution of stress could cause the relative levels of yielded tissue in rods vs. plates to differ from that found here. To investigate the role of the apparent boundary conditions, we performed a parameter study varying the maximum applied apparent strain in the models. The proportions of tissue yielding at 0.6%, 0.8%, and 1.0% apparent strains all showed the same correlation with the measured microdamage as those for 1.2% apparent strain, suggesting that the conclusions are not sensitive to the simulated apparent strain level (data not shown).
If direct predictions of microdamage by modeling are to be made, improved tissue constitutive models that incorporate damage formation or material softening [25] and account for local matrix properties must be employed. Because even large microcracks are smaller than present finite element discretizations, damage must be modeled in a continuum manner. This normally requires a stress or strain threshold to be identified as the level at which a region of tissue transitions from yielding or ultrascale damage to microscale damage. An alternative procedure would be to employ a cohesive zone approach [39], which may soon be feasible for trabecular bone as computational power continues to increase.
The calculated tissue yielding, even when differentiated between rods and plates, provided only a moderately strong correlation with microdamage, indicating that other factors are also important. Bone matrix properties such as mineralization [40–42] and collagen cross-linking [14, 43] would be expected to affect the propensity for damage. However, microcracking has been associated with regions of both high [13] and low mineralization [10, 44], while in other studies there was no relationship between mineralization and damage susceptibility [15]. Given the conflicting data, incorporation of mineralization into the models was not attempted. Nonenzymatic glycation results in increased collagen cross-linking and increases trabecular bone damage susceptibility [14, 43, 45], although microdamage itself also affects measured cross-links [15]. At present, three-dimensional and non-destructive measurements of collagen cross-links are not possible, although such measures could theoretically be obtained using serial sectioning with Fourier transmission infrared spectroscopy [46]. As the samples in this study were from young animals, cross-link accumulation would not be expected to contribute to the damage accumulation.
The overwhelming proportion of the yielded tissue in longitudinal trabeculae agrees with the finding that axial loading is mainly sustained by axially aligned trabecular tissue [22]. This is also consistent with the fabric tensor based analysis of the evolution of yielded regions in the same samples [26]. However, the ITS decomposition allows a more direct analysis of trabecular type and orientation with respect to mechanics.
Microcrack density had a stronger correlation with the proportion of predicted yielding in rods than did diffuse damage area. This agrees with the finding that in vivo microcrack density, but not diffuse damage area, was related to the von Mises stress distribution found from computational simulations [47]. Diffuse damage occurs at a smaller scale, and may require less energy to form than linear microcracks [48]. As such, very small strains within trabecular plates may be sufficient to initiate diffuse damage. For both microdamage types, improved constitutive models are necessary to directly predict damage locations. Ideally, such constitutive models should account for variations in matrix composition [15].
The importance of trabecular rods in microdamage susceptibility is supported by the positive correlation between microcrack density and SMI [18] and the negative correlation between SMI and the toughness of trabecular bone [49]. SMI was also found to be the architectural parameter with the strongest correlation to in vivo microdamage burden in vertebral trabecular bone [19]. Our results further identified the importance of on-axis rods in microdamage susceptibility of trabecular bone during on-axis overloading. While transverse trabeculae are preferentially thinned and perforated over vertical trabeculae, leading to a more anisotropic structure [50–53], and there are more transversely oriented rods than vertically oriented rods in the samples studied, an increase in the fraction of transverse rods might render the whole structure more vulnerable to large bending deformations of rods along the principal trabecular orientation by removing stabilizing elements.
Computational models that specifically quantified the effects of finite deformations in trabecular bone models have shown that the effects are greatest in more rod-like and lower density bone [31]. In the context of the present results, this suggests that large bending deformations are associated with microcracking. However, the apparent strains that result in microcrack formation [18, 27, 36] and large bending deformation of rods generally exceed 1%, which is unlikely to occur in vivo. As such, although studies point to large bending deformation of rods as an important mechanism in microcrack formation during overloading, the in vivo mechanisms are likely to involve fatigue and crack propagation. While further studies are needed, the roles of strain gradients across bent trabeculae or the greater surface to volume ratio of rods in comparison to plates may be important for damage formation.
Acknowledgments
This study was supported by the National Institutes of Health (AR052008 and AR051376) and by an NSF MRI Grant (DBI-0420980).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Peck WA, Burkhardt P, Christiansen C. Consensus development conference: diagnosis, prophylaxis, and treatment of osteoporosis. Am J Med. 1993;94:646–50. doi: 10.1016/0002-9343(93)90218-e. [DOI] [PubMed] [Google Scholar]
- 2.Gibson LJ. Biomechanics of cellular solids. J Biomech. 2005;38:377–99. doi: 10.1016/j.jbiomech.2004.09.027. [DOI] [PubMed] [Google Scholar]
- 3.Wehrli FW. Structural and functional assessment of trabecular and cortical bone by micro magnetic resonance imaging. J Magn Reson Imaging. 2007;25:390–409. doi: 10.1002/jmri.20807. [DOI] [PubMed] [Google Scholar]
- 4.Bouxsein ML, Delmas PD. Considerations for development of surrogate endpoints for antifracture efficacy of new treatments in osteoporosis: a perspective. J Bone Miner Res. 2008;23:1155–67. doi: 10.1359/JBMR.080301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Turner CH. Biomechanics of bone: determinants of skeletal fragility and bone quality. Osteoporos Int. 2002;13:97–104. doi: 10.1007/s001980200000. [DOI] [PubMed] [Google Scholar]
- 6.Martin RB, Burr DB. A hypothetical mechanism for the stimulation of osteonal remodelling by fatigue damage. J Biomech. 1982;15:137–9. doi: 10.1016/s0021-9290(82)80001-8. [DOI] [PubMed] [Google Scholar]
- 7.Burr DB. Targeted and nontargeted remodeling. Bone. 2002;30:2–4. doi: 10.1016/s8756-3282(01)00619-6. [DOI] [PubMed] [Google Scholar]
- 8.Morgan EF, Yeh OC, Keaveny TM. Damage in trabecular bone at small strains. Eur J Morphol. 2005;42:13–21. doi: 10.1080/09243860500095273. [DOI] [PubMed] [Google Scholar]
- 9.Tang SY, Vashishth D. A non-invasive in vitro technique for the three-dimensional quantification of microdamage in trabecular bone. Bone. 2007;40:1259–64. doi: 10.1016/j.bone.2006.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Norman TL, Little TM, Yeni YN. Age-related changes in porosity and mineralization and in-service damage accumulation. J Biomech. 2008;41:2868–73. doi: 10.1016/j.jbiomech.2008.06.032. [DOI] [PubMed] [Google Scholar]
- 11.Boivin GY, Chavassieux PM, Santora AC, Yates J, Meunier PJ. Alendronate increases bone strength by increasing the mean degree of mineralization of bone tissue in osteoporotic women. Bone. 2000;27:687–94. doi: 10.1016/s8756-3282(00)00376-8. [DOI] [PubMed] [Google Scholar]
- 12.Mashiba T, Turner CH, Hirano T, Forwood MR, Jacob DS, Johnston CC, Burr DB. Effects of high-dose etidronate treatment on microdamage accumulation and biomechanical properties in beagle bone before occurrence of spontaneous fractures. Bone. 2001;29:271–8. doi: 10.1016/s8756-3282(01)00575-0. [DOI] [PubMed] [Google Scholar]
- 13.Wasserman N, Yerramshetty J, Akkus O. Microcracks colocalize within highly mineralized regions of cortical bone tissue. Eur J Morphol. 2005;42:43–51. doi: 10.1080/09243860500095471. [DOI] [PubMed] [Google Scholar]
- 14.Tang SY, Zeenath U, Vashishth D. Effects of non-enzymatic glycation on cancellous bone fragility. Bone. 2007;40:1144–51. doi: 10.1016/j.bone.2006.12.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruppel ME, Burr DB, Miller LM. Chemical makeup of microdamaged bone differs from undamaged bone. Bone. 2006;39:318–24. doi: 10.1016/j.bone.2006.02.052. [DOI] [PubMed] [Google Scholar]
- 16.Arthur Moore TL, Gibson LJ. Microdamage accumulation in bovine trabecular bone in uniaxial compression. J Biomech Eng. 2002;124:63–71. doi: 10.1115/1.1428745. [DOI] [PubMed] [Google Scholar]
- 17.Nalla RK, Stolken JS, Kinney JH, Ritchie RO. Fracture in human cortical bone: local fracture criteria and toughening mechanisms. J Biomech. 2005;38:1517–25. doi: 10.1016/j.jbiomech.2004.07.010. [DOI] [PubMed] [Google Scholar]
- 18.Wang X, Niebur GL. Microdamage propagation in trabecular bone due to changes in loading mode. J Biomech. 2006;39:781–90. doi: 10.1016/j.jbiomech.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 19.Arlot ME, Burt-Pichat B, Roux JP, Vashishth D, Bouxsein ML, Delmas PD. Microarchitecture influences microdamage accumulation in human vertebral trabecular bone. J Bone Miner Res. 2008;23:1613–8. doi: 10.1359/jbmr.080517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hildebrand T, Ruegsegger P. Quantification of Bone Microarchitecture with the Structure Model Index. Comput Methods Biomech Biomed Engin. 1997;1:15–23. doi: 10.1080/01495739708936692. [DOI] [PubMed] [Google Scholar]
- 21.Liu XS, Sajda P, Saha PK, Wehrli FW, Guo XE. Quantification of the roles of trabecular microarchitecture and trabecular type in determining the elastic modulus of human trabecular bone. J Bone Miner Res. 2006;21:1608–17. doi: 10.1359/jbmr.060716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu XS, Sajda P, Saha PK, Wehrli FW, Bevill G, Keaveny TM, Guo XE. Complete volumetric decomposition of individual trabecular plates and rods and its morphological correlations with anisotropic elastic moduli in human trabecular bone. J Bone Miner Res. 2008;23:223–35. doi: 10.1359/JBMR.071009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Niebur GL, Feldstein MJ, Yuen JC, Chen TJ, Keaveny TM. High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J Biomech. 2000;33:1575–83. doi: 10.1016/s0021-9290(00)00149-4. [DOI] [PubMed] [Google Scholar]
- 24.Kosmopoulos V, Keller TS. Finite element modeling of trabecular bone damage. Comput Methods Biomech Biomed Engin. 2003;6:209–16. doi: 10.1080/1025584031000149089. [DOI] [PubMed] [Google Scholar]
- 25.Verhulp E, Van Rietbergen B, Muller R, Huiskes R. Micro-finite element simulation of trabecular-bone post-yield behaviour--effects of material model, element size and type. Comput Methods Biomech Biomed Engin. 2008;11:389–95. doi: 10.1080/10255840701848756. [DOI] [PubMed] [Google Scholar]
- 26.Shi X, Wang X, Niebur GL. Effects of loading orientation on the morphology of the predicted yielded regions in trabecular bone. Ann Biomed Eng. 2009;37:354–62. doi: 10.1007/s10439-008-9619-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. J Biomech. 2005;38:707–16. doi: 10.1016/j.jbiomech.2004.05.013. [DOI] [PubMed] [Google Scholar]
- 28.Wang X, Liu X, Niebur GL. Preparation of on-axis cylindrical trabecular bone specimens using micro-CT imaging. J Biomech Eng. 2004;126:122–5. doi: 10.1115/1.1645866. [DOI] [PubMed] [Google Scholar]
- 29.Bevill G, Keaveny TM. Trabecular bone strength predictions using finite element analysis of micro-scale images at limited spatial resolution. Bone. 2009;44:579–84. doi: 10.1016/j.bone.2008.11.020. [DOI] [PubMed] [Google Scholar]
- 30.Niebur GL, Yuen JC, Hsia AC, Keaveny TM. Convergence behavior of high-resolution finite element models of trabecular bone. J Biomech Eng. 1999;121:629–35. doi: 10.1115/1.2800865. [DOI] [PubMed] [Google Scholar]
- 31.Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39:1218–25. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
- 32.Charras GT, Guldberg RE. Improving the local solution accuracy of large-scale digital image-based finite element analyses. J Biomech. 2000;33:255–9. doi: 10.1016/s0021-9290(99)00141-4. [DOI] [PubMed] [Google Scholar]
- 33.Hollister SJ, Brennan JM, Kikuchi N. A homogenization sampling procedure for calculating trabecular bone effective stiffness and tissue level stress. J Biomech. 1994;27:433–44. doi: 10.1016/0021-9290(94)90019-1. [DOI] [PubMed] [Google Scholar]
- 34.van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. J Biomech. 1995;28:69–81. doi: 10.1016/0021-9290(95)80008-5. [DOI] [PubMed] [Google Scholar]
- 35.Bayraktar HH, Morgan EF, Niebur GL, Morris GE, Wong EK, Keaveny TM. Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. J Biomech. 2004;37:27–35. doi: 10.1016/s0021-9290(03)00257-4. [DOI] [PubMed] [Google Scholar]
- 36.Wang X, Guyette J, Liu X, Roeder RK, Niebur GL. Axial-shear interaction effects on microdamage in bovine tibial trabecular bone. Eur J Morphol. 2005;42:61–70. doi: 10.1080/09243860500095570. [DOI] [PubMed] [Google Scholar]
- 37.O’Brien FJ, Taylor D, Lee TC. An improved labelling technique for monitoring microcrack growth in compact bone. J Biomech. 2002;35:523–6. doi: 10.1016/s0021-9290(01)00200-7. [DOI] [PubMed] [Google Scholar]
- 38.Liu XS, Huang AH, Zhang XH, Sajda P, Ji B, Guo XE. Dynamic simulation of three dimensional architectural and mechanical alterations in human trabecular bone during menopause. Bone. 2008;43:292–301. doi: 10.1016/j.bone.2008.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ural A, Vashishth D. Cohesive finite element modeling of age-related toughness loss in human cortical bone. J Biomech. 2006;39:2974–82. doi: 10.1016/j.jbiomech.2005.10.018. [DOI] [PubMed] [Google Scholar]
- 40.van Ruijven LJ, Mulder L, van Eijden TM. Variations in mineralization affect the stress and strain distributions in cortical and trabecular bone. J Biomech. 2007;40:1211–8. doi: 10.1016/j.jbiomech.2006.06.004. [DOI] [PubMed] [Google Scholar]
- 41.Bourne BC, van der Meulen MC. Finite element models predict cancellous apparent modulus when tissue modulus is scaled from specimen CT-attenuation. J Biomech. 2004;37:613–21. doi: 10.1016/j.jbiomech.2003.10.002. [DOI] [PubMed] [Google Scholar]
- 42.Harrison NM, McDonnell PF, O’Mahoney DC, Kennedy OD, O’Brien FJ, McHugh PE. Heterogeneous linear elastic trabecular bone modelling using micro-CT attenuation data and experimentally measured heterogeneous tissue properties. J Biomech. 2008;41:2589–96. doi: 10.1016/j.jbiomech.2008.05.014. [DOI] [PubMed] [Google Scholar]
- 43.Tang SY, Vashishth D. Non-enzymatic glycation alters microdamage formation in human cancellous bone. Bone. 2009;20:887–94. doi: 10.1016/j.bone.2009.09.003. PMID: 17329178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nagaraja S, Lin AS, Guldberg RE. Age-related changes in trabecular bone microdamage initiation. Bone. 2007;40:973–80. doi: 10.1016/j.bone.2006.10.028. [DOI] [PubMed] [Google Scholar]
- 45.Vashishth D, Gibson GJ, Khoury JI, Schaffler MB, Kimura J, Fyhrie DP. Influence of nonenzymatic glycation on biomechanical properties of cortical bone. Bone. 2001;28:195–201. doi: 10.1016/s8756-3282(00)00434-8. [DOI] [PubMed] [Google Scholar]
- 46.Paschalis EP, Verdelis K, Doty SB, Boskey AL, Mendelsohn R, Yamauchi M. Spectroscopic characterization of collagen cross-links in bone. J Bone Miner Res. 2001;16:1821–8. doi: 10.1359/jbmr.2001.16.10.1821. [DOI] [PubMed] [Google Scholar]
- 47.Yeni YN, Hou FJ, Ciarelli T, Vashishth D, Fyhrie DP. Trabecular shear stresses predict in vivo linear microcrack density but not diffuse damage in human vertebral cancellous bone. Ann Biomed Eng. 2003;31:726–32. doi: 10.1114/1.1569264. [DOI] [PubMed] [Google Scholar]
- 48.Fazzalari NL, Forwood MR, Manthey BA, Smith K, Kolesik P. Three-dimensional confocal images of microdamage in cancellous bone. Bone. 1998;23:373–8. doi: 10.1016/s8756-3282(98)00111-2. [DOI] [PubMed] [Google Scholar]
- 49.Garrison JG, Slaboch CL, Niebur GL. Density and architecture have greater effects on the toughness of trabecular bone than damage. Bone. 2009;44:924–929. doi: 10.1016/j.bone.2008.12.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McDonnell P, McHugh PE, O’Mahoney D. Vertebral osteoporosis and trabecular bone quality. Ann Biomed Eng. 2007;35:170–89. doi: 10.1007/s10439-006-9239-9. [DOI] [PubMed] [Google Scholar]
- 51.Homminga J, Van-Rietbergen B, Lochmuller EM, Weinans H, Eckstein F, Huiskes R. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “error” loads. Bone. 2004;34:510–6. doi: 10.1016/j.bone.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 52.Thomsen JS, Ebbesen EN, Mosekilde LI. Age-related differences between thinning of horizontal and vertical trabeculae in human lumbar bone as assessed by a new computerized method. Bone. 2002;31:136–42. doi: 10.1016/s8756-3282(02)00801-3. [DOI] [PubMed] [Google Scholar]
- 53.van Ruijven LJ, Giesen EB, Mulder L, Farella M, van Eijden TM. The effect of bone loss on rod-like and plate-like trabeculae in the cancellous bone of the mandibular condyle. Bone. 2005;36:1078–85. doi: 10.1016/j.bone.2005.02.018. [DOI] [PubMed] [Google Scholar]