Resolution of Crossing Fibers with Constrained Compressed Sensing using Traditional Diffusion Tensor MRI

Abstract

Diffusion tensor imaging (DTI) is widely used to characterize tissue micro-architecture and brain connectivity. Yet, DTI suffers serious limitations in regions of crossing fibers because traditional tensor techniques cannot represent multiple, independent intra-voxel orientations. Compressed sensing has been proposed to resolve crossing fibers using a tensor mixture model (e.g., Crossing Fiber Angular Resolution of Intra-voxel structure, CFARI). Although similar in spirit to deconvolution approaches, CFARI uses sparsity to stabilize estimation with limited data rather than spatial consistency or limited model order. Here, we extend the CFARI approach to resolve crossing fibers through a strictly positive, parsimonious mixture model. Together with an optimized preconditioned conjugate gradient solver, estimation error and computational burden are greatly reduced over the initial presentation. Reliable estimates of intra-voxel orientations are demonstrated in simulation and in vivo using data representative of typical, low b-value (30 directions, 700 s/mm²) clinical DTI protocols. These sequences are achievable in 5 minutes at 3 T, and the whole brain CFARI analysis is tractable for routine analysis. With these improvements, CFARI provides a robust framework for identifying intra-voxel structure with traditional DTI and shows great promise in helping to resolve the crossing fiber problem in current clinical imaging studies.

1. INTRODUCTION

Diffusion tensor imaging (DTI) provides non-invasive contrasts which are sensitive to in vivo cellular organization as modeled by local diffusivity, anisotropy, and tissue orientation. The tensor model represents one independent, dominant direction, so the estimated orientation may be ambiguous or misleading in voxels with complex fiber structure [1]. Substantial efforts have been made to address this “crossing fiber” problem. One fruitful approach has been to acquire more detailed information through additional scans (e.g., q-ball imaging [2]). Yet, scan time and hardware constraints limit widespread adaptation of these methods in clinical research. Here, we seek to characterize regions of crossing fibers using data acquired with traditional (i.e., low b-value, low angular resolution) DTI protocols.

Recently, there have been several indications that it is possible to resolve crossing-fibers from traditional DTI provided that sufficient a priori information is available. Independent component analysis can exploit spatial information to fit a prolate tensor mixture [3], while cylindrically constrained two-tensor models have been numerically amenable to fitting using regularization techniques [4, 5]. Direct deconvolution with a discrete tensor basis set has also been used [6]. As these approaches are highly sensitive to noise, authors typically suggest limiting application to areas of known fiber crossing (e.g., planar tensor estimates) to avoid erroneous detections. Although initially developed as an alternative to Nyquist sampling, compressed sensing [7] offers a simple and elegant solution to the problem of regularized fitting of tensor models which does not require explicit model selection. The recently presented Crossing Fiber Angular Resolution of Intra-voxel structure (CFARI) method can reproducibly extract multiple fiber orientations per voxel [8].

In this manuscript, we extend the CFARI approach to fit a strictly positive mixture of tensor basis functions and reduce the computational burden through an optimized a preconditioned gradient solver. Accuracy at low SNR is improved, and consistent resolution of three fibers is demonstrated in simulation and in vivo. With CFARI, one can conduct whole brain analyses on a single CPU in less than 3 hours. Both the original and improved CFARI methods are implemented in the JIST (Java Image Science Toolkit) framework and are available in open source (http://www.nitrc.org/projects/jist/). With these improvements, CFARI provides a robust framework for identifying intra-voxel structure with traditional DTI and shows great promise in resolving the crossing fiber problem.

2. METHODS

Each voxel is modeled as a finite mixture of discrete and independent compartments, and the diffusivity within each compartment is defined by the Stejskal-Tanner tensor formulation. The observed signal, S_k, along the k^th diffusion weighting direction (g_k) is determined by the exponential mixture model,

$$S_k=S_0{\sum }_i^N{f}_i{e}^{-b{\mathit{g}}_k^T{\mathbf{D}}_i{\mathbf{g}}_k}+\eta .$$ (1)

S₀ is a noise-free reference signal in the absence of diffusion weighting, N is the number of possible compartments (tensors) within each voxel, f_i is the (unknown) mixture component for each compartment, b is the diffusion sensitization parameter, D_i is the tensor associated with the i^th compartment, and η is a noise term that follows a Rician distribution. It is assumed that the reconstruction basis {D_i} — i.e., the set of possible diffusion tensors that may comprise a voxel — is fixed and known. Given this framework, the vector, y, of K observed attenuations, where each attenuation is defined as y_k = S_k/S₀, can be rewritten in matrix form as,

$${\mathbf{y}}_{K\times 1}={\mathbf{S}}_{K\times N}{\mathbf{f}}_{N\times 1}+{\stackrel{\sim }{\mathit{\eta }}}_{K\times 1},$$ (2)

where the matrix S comprises a set of exponential terms derived from Eq. (1) and η̃ is a scaled noise term. At an SNR of greater than 5:1, Rician noise is well approximated by a Gaussian distribution, so a least squares estimator is appropriate. With Eq.(2), we may immediately write the compressed sensing criteria,

$$\mathbf{f}={\text{argmin}}_{\mathbf{f}:{\mathbf{f}}_i\in [0,\infty )}{\left|\right|\mathbf{S}\mathbf{f}-\mathbf{y}\left|\right|}_{L2}+\beta {\left|\right|\mathbf{f}\left|\right|}_{L1},$$ (3)

where β is a strictly positive sparsity regularization parameter. Note that the positivity restriction on f_i is newly explored in this manuscript. Low β’s lead to least squares fitting of the observed signal with the specified basis, while high β’s force greater emphasis on a sparse model. There are efficient numerical methods to address optimization problems of the form of Eq. (3); in this work, we use the interior point method of Kim et al. [9] which includes the ability to enforce positivity constraints.

3. DATA

CFARI works with existing, traditional DTI data, so the sensing basis — i.e., the choices of b-values and diffusion encoding directions — is considered to be determined by external requirements (such as reliability of clinical contrasts). There are two remaining design choices that must be addressed: the reconstruction basis and the sparsity regularization parameter. In accordance with previous findings, the D_i’s are chosen to be cylindrically symmetric, of equal diffusivities, and regularly distributed on a sphere (fractional anisotropy of 0.71 and principle eigenvalue of 2×10⁻³ mm²/s, 241 symmetric orientations) while the regularization parameter β was selected to be 1 through empirical simulations to produce a tradeoff between minimal error and robustness against model mismatch. Monte Carlo simulations were performed using two repetitions of 30 diffusion weighting directions, b-value of 700 s/mm², five averaged unweighted reference acquisitions, and Rician distributed noise. The signal-to-noise (SNR) was defined as the ratio of the noise standard deviation on the complex coefficients and the (noise-free) unweighted signal intensity. In vivo data (acquired using an equivalent protocol) were analyzed with CATNAP (http://iacl.ece.jhu.edu/~bennett/catnap/).

4. RESULTS

4.1 SNR Simulations

For all simulations, Error was assessed as the mean angular difference between each estimated orientation and the closest orientation in the truth model, weighted by the estimated fraction:

$$E={\sum }_i{\mathbf{f}}_i{min}_{j\in \mathit{model}}\angle (v_i,v_j).$$ (4)

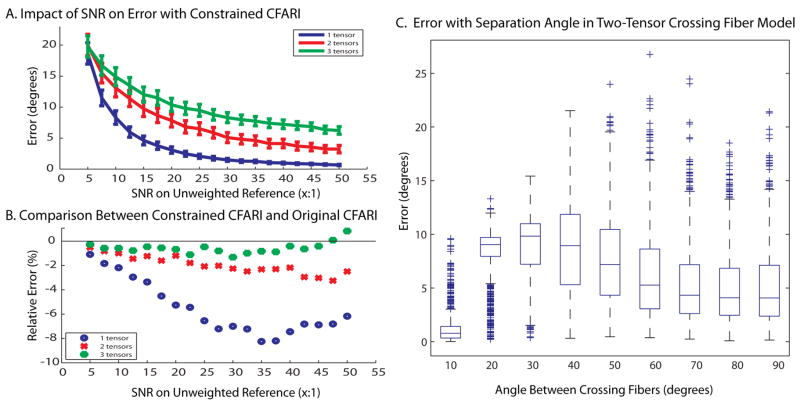
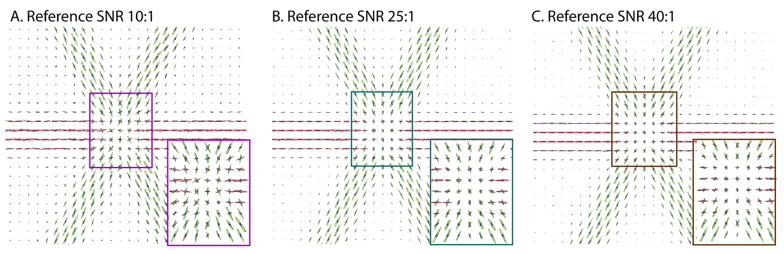
To explore the effect of SNR on multiple tensor crossings, 19 linearly spaced values of SNR from 5:1 to 50:1 in steps of 2.5 were evaluated with 1000 Monte Carlo iterations. To generate the tensors used, 1, 2, or 3 directions were randomly chosen from the reconstruction basis set. To compare the unconstrained CFARI with the constrained CFARI, the same simulated data was used with both CFARI estimators. To see the effect of angular separation, 2 tensors were generated at angles of 10° to 90° apart in 10° intervals. For each angle, the first tensor was randomly selected from the basis set. The second tensor was then chosen randomly from all the directions that were within 2° of the specified angle. An SNR of 25:1 was used. Fig. 1 illustrates that the constrained CFARI approach resulted in reduced error across a wide range of SNR. While benefits were concentrated for single tensor models, two-fiber crossing fiber models could be resolved to within 10° error across the range of possible separations. Fig. 2 shows three crossing fibers can be visually resolved when three tracts cross with a separation of 60° in a plane. Note that a fourth component was added to the simulation (but not the basis set) with an isotropic component (λ₁ =λ₂ =λ₃ =3×10⁻³ mm²/s).

Figure 1.

Impacts of SNR on CFARI intra-voxel direction estimation. Error increased with the presence of multiple true intra-voxel structures, but was within approximately 10° for an SNR of greater than 25:1 (A). The newly developed constrained CFARI approach resulted in lower error than the original approach at typical SNR (B). Median error for two-tensor models was less than 15° regardless of crossing angle (C).

Figure 2.

Increased SNR improves the consistency of estimated intra-voxel structure (compare A to B to C). However, three distinct crossing fibers are clearly apparent at a typical clinical SNR of 25:1.

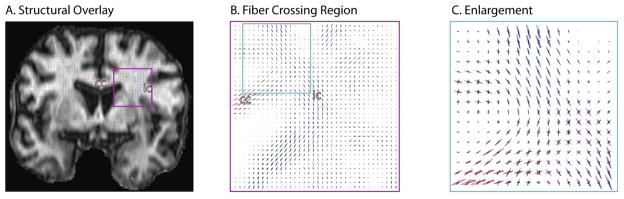
White matter fibers running lateral through the corpus callosum and superior through the internal capsule are visible (Fig. 3). On traditional tensor analyses, this region manifests as a “black hole.” With CFARI, the pattern of crossing fibers is clearly identified regions and the results are consistent with anatomical expectations. Mean analysis time was 62 ms per brain voxel on a 1.6 GHz notebook computer.

Figure 3.

Intra-voxel orientations estimated with in vivo data show patterns consistent with anatomy, which can be clearly appreciated in the region of the corpus callosum (cc) and internal capsule (ic).

5. CONCLUSION

CFARI provides a robust framework for identifying intra-voxel structure with traditional DTI and shows great promise in helping to resolve the crossing fiber problem. Although similar in spirit to existing deconvolution approaches, CFARI uses sparsity to stabilize estimation with limited data (rather than spatial consistency or a limited model order). As the current estimation process is driven only by information from individual voxels, one could exploit spatial regularization either in the subsequent fiber tracking or through direct incorporation of smoothing.