Role of spike-frequency adaptation in shaping neuronal response to dynamic stimuli

Abstract

Spike-frequency adaptation is the reduction of a neuron's firing rate to a stimulus of constant intensity. In the locust, the Lobula Giant Movement Detector (LGMD) is a visual interneuron that exhibits rapid adaptation to both current injection and visual stimuli. Here, a reduced compartmental model of the LGMD is employed to explore adaptation's role in selectivity for stimuli whose intensity changes with time. We show that supralinearly increasing current injection stimuli are best at driving a high spike count in the response, while linearly increasing current injection stimuli (i.e., ramps) are best at attaining large firing rate changes in an adapting neuron. This result is extended with in vivo experiments showing that the LGMD's response to translating stimuli having a supralinear velocity profile is larger than the response to constant or linearly increasing velocity translation. Furthermore, we show that the LGMD's preference for approaching versus receding stimuli can partly be accounted for by adaptation. Finally, we show that the LGMD's adaptation mechanism appears well tuned to minimize sensitivity for the level of basal input.

1 Introduction

The Lobula Giant Movement Detector (LGMD; O'Shea and Williams 1974) is a large visual interneuron found in the third optic neuropile of locusts and other Orthopterans. It is believed to receive input from an entire visual hemifield, with roughly equal synaptic input coming from each of the eye's ~7,500 ommatidia (Krapp and Gabbiani 2005). It is known to respond preferentially to stimuli on a collision course with the animal (or a two-dimensional simulation thereof: looming stimuli; Schlotterer 1977; Rind and Simmons 1992). During the presentation of a looming stimulus, the peak of the LGMD's firing rate occurs at a fixed delay after the stimulus exceeds a fixed threshold angle on the retina, independent of its size or approach velocity (Gabbiani et al. 1999, 2001). Such threshold angles are correlated to specific stages of jump escape behaviors (Fotowat and Gabbiani 2007). Because the firing rate time-course and the timing of spikes vary with stimulus velocity and size, it is unlikely that the LGMD conforms to traditional rate or timing coding schemes. Thus, the LGMD necessitates the approach to neuronal coding that Jose P. Segundo persistently advocated (e.g., Segundo 2000): a context-specific approach, without exclusive advocacy of a particular coding scheme.

Spike-frequency adaptation, a property of the LGMD's response to constant current injection (Gabbiani and Krapp 2006), affects its response to translating visual stimuli much more than to looming stimuli (Peron and Gabbiani 2009). Spike-frequency adaptation is an excellent example of a mechanism whose computational consequence must be understood in context—its ability to influence information transfer relates both to the nature of the inputs a neuron receives as well as the readout scheme employed by a neuron's postsynaptic targets. Adaptation in its most general sense is a ubiquitous neural process (Laughlin 1989). While it always involves the reduction of response over time to a fixed-amplitude stimulus, its time course and implementation vary widely. For instance, adaptation at the level of firing rate (i.e., spike-frequency adaptation) can arise due to intrinsic membrane properties of a neuron or due to processes taking place at input synapses. In the LGMD, spike-frequency adaptation is implemented via a calcium-sensitive potassium conductance located close to the spike initiation zone (Peron and Gabbiani 2009).

Two major interpretations of spike-frequency adaptation have been advanced in the literature: adaptation as a means for shifting the cell's dynamic range (e.g., forward masking: Sobel and Tank 1994) and adaptation as a mechanism to select for rapid over slow transients (i.e., high-pass filtering; Benda and Herz 2003; Benda et al. 2005; Glantz and Schroeter 2004; Ellis et al. 2007). Here, we explore an alternative interpretation: adaptation as a selectivity filter for specific temporal input profiles. In the context of time-varying stimuli, we argue that adaptation will be least effective at suppressing spikes in response to stimuli where not only the first, but also the second derivative of the input's intensity is positive. Looming stimuli exhibit precisely this property, and this may explain the insensitivity of the LGMD's looming response to spike-frequency adaptation.

Using a three-compartment LGMD model (Peron and Gabbiani 2009), we explore how spike-frequency adaptation tunes the firing rate response to input stimulus dynamics. Assorted temporal intensity profiles are employed to determine the sensitivity of various stimuli to spike-frequency adaptation. We show that the simulated adaptation is indeed least effective at suppressing stimuli rapidly increasing in intensity. This result is corroborated with additional experimental data showing that the LGMD's firing rate response is also sensitive to specific input temporal intensity profiles. Finally, we use the model to show that spike-frequency adaptation is likely to contribute to the previously observed preference of the LGMD for approaching versus receding stimuli (Rind and Simmons 1992; Simmons and Rind 1992).

2 Adaptation mechanisms

Adaptation can be implemented via local or global mechanisms. For instance, the LGMD can adapt globally—at the site of spike initiation—via spike-frequency adaptation (Peron and Gabbiani 2009), or locally—at individual excitatory inputs—via habituation (O'Shea and Rowell 1975). From the perspective of the adapting neuron and in the context of coding, this difference is important: local adaptation will only influence input coming from a particular subset of sources, while global adaptation will modulate all the input a neuron receives. Local adaptation is usually a consequence of synaptic or localized dendritic biophysics, whereas global adaptation, like spike-frequency adaptation, is often governed by mechanisms located close to the site of spike initiation. Activation of a slow (relative to spiking) hyper-polarizing conductance is often responsible for adaptation acting on the order of tens to hundreds of milliseconds, but other mechanisms such as gradual inactivation of the conductances underlying spike generation (Powers et al. 1999; Gorman et al. 2005; Miles et al. 2005) and depletion of the ions that subserve spiking (Höger and French 2005) may also contribute. However, this last type of adaptation is typically slower—with a time constant on the order of seconds.

From a sensory perspective, adaptation operating at a time scale on the order of seconds is more limited in its computational role than faster adaptation—with time constants ranging up to a few hundred milliseconds. Accordingly, the implementation of the latter type is far more diverse mechanistically. Perhaps the simplest example is the M-current, a depolarization-activated voltage-gated potassium conductance. The M-current has been shown to contribute in part to spike-frequency adaptation (Madison and Nicoll 1984; Gu et al. 2005), though other data suggests that it may sometimes contribute to increasing the firing rate (Yue and Yaari 2004). Changes in intracellular ion concentrations can also activate hyperpolarizing conductances, giving rise to spike-frequency adaptation. Specifically, sodium-sensitive potassium conductances (Bhattacharjee and Kaczmarek 2005), calcium-sensitive chloride conductances (Scott et al. 1995), and calcium-sensitive potassium conductances (Sah 1996; Sah and Davies 2000; Faber and Sah 2003) have been demonstrated to contribute to spike-frequency adaptation. Each of these has been observed in a variety of systems and subserves different computational roles. In the LGMD, spike-frequency adaptation is driven primarily by a calcium-sensitive potassium conductance (Peron and Gabbiani 2009).

Calcium-sensitive potassium conductances are classified on the basis of the unitary conductance of the underlying channels into BK, IK, and SK types (for big, intermediate, and small single-channel conductance, respectively). BK channels usually operate on a submillisecond timescale, narrowing the action potential and thereby allowing higher peak firing rates. They do not generally contribute to spike-frequency adaptation (Peron and Gabbiani 2009; Salkoff et al. 2006; but see Gu et al. 2007). IK channels remain poorly understood, and will not be discussed further. SK channels are present in many neurons, and are often responsible for adaptation with a timescale on the order of tens to hundreds of milliseconds (Stocker 2004; Bond et al. 2005). It is likely that they are responsible for spike-frequency adaptation in the LGMD (Peron and Gabbiani 2009). In most cases, SK channels can be identified by their sensitivity to apamin, a component of bee venom, though this is not the case in insects (Wicher et al. 2001). Calcium sensitivity in SK channels is due to the presence of calmodulin binding domains (Stocker 2004). The remainder of this study will employ a model of a calcium-sensitive potassium conductance that is similar in its properties to an SK conductance.

3 Adaptation model

To consider the impact of spike-frequency adaptation, a three-compartment model of the LGMD based on the two-compartment pyramidal cell model of Wang (1998) was employed. Three compartments were required to reproduce the visual responses and intrinsic properties of the LGMD, but adaptation with similar characteristics can be produced with two (Wang 1998) or even one (Benda and Herz 2003) compartment. We considered three, not necessarily mutually exclusive, roles of spike-frequency adaptation: shifting of a neuron's dynamic range—the “dynamic range hypothesis” (Sect. 3.1; e.g., Laughlin 1989), selectivity for high frequency over low frequency signals—the “high-pass filter hypothesis” (Sect. 3.2; Benda and Herz 2003), and selectivity for inputs that increase in intensity—the “temporal profile hypothesis” (Sects. 3.3 and 4; Peron and Gabbiani 2009). In each case, we looked at the potential capacity of the neuron to detect and discriminate changes in the amount of synaptic input, and the degree to which the basal level of input affected this discrimination.

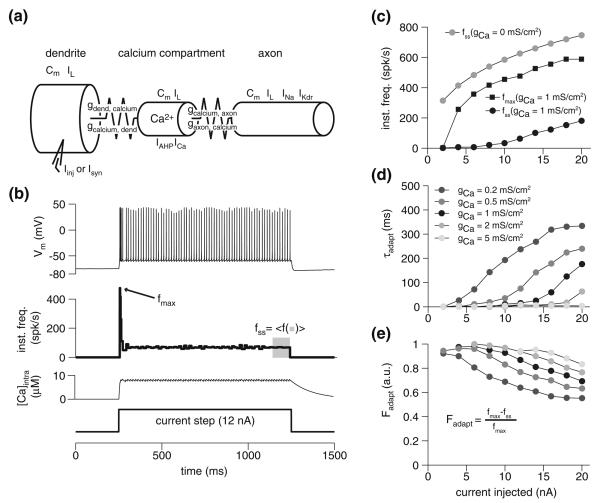
The model is illustrated in Fig. 1a. It consists of a “dendritic” compartment, a “calcium” compartment, and an “axon” compartment. The compartments areas were, respectively, 5×10⁻⁴ cm², 5×10⁻⁵ cm², and 9.5×10⁻⁴ cm². They were connected with the following coupling conductances: g_{dend, calcium} = 16.12 mS/cm², g_calcium,dend = 1.62 mS/cm², g_calcium,axon = 0.66 mS/cm², and g_axon,calcium = 12.30 mS/cm². Here g_a,b is the conductance from a to b, derived from the areas by assuming an axial resistivity, R_i, of 60 Ω cm and using eq. 6.30 of Dayan and Abbott (2001). All compartments had a leak current, I_L (g_L = 0.11 mS/cm², E_L = −75 mV) and a membrane capacitance (C_m = 1.5 μF/cm²) as in Peron et al. (2007). An implementation of the model is available at http://senselab.med.yale.edu/modeldb.

Fig. 1.

The spike-frequency adaptation model and its basic properties. a Schematic of the three-compartment model employed for simulations. C_m denotes membrane capacitance, I_x (x = L, stim, Ca, Na and Kdr) denotes the presence of a particular current (Sect. 3). The coupling conductance from compartment a to b, is denoted by g_a,b and is asymmetric (i.e., g_a,b ≠ g_b,a; see Sect. 3). b Response of the model to a 12 nA depolarizing current injection, with g_Ca = 1 mS/cm². From top to bottom, panels show the membrane potential response, instantaneous frequency, intracellular calcium concentration, and current step, respectively. c Peak (f_max) and steady-state (f_ss) response frequency during current injection. Black circles and squares show response in model with adaptation (g_Ca = 1 mS/cm²); grey circles show the steady-state for the model without adaptation (g_Ca = 0mS/cm²). Size of current step indicated on abscissa. d Adaptation time constant for various injection currents and levels of calcium conductance. e Adaptation ratios for the same current injection levels as in d

The Hodgkin–Huxley formalism was used to simulate voltage-dependent conductances, with the following equation governing the change in gating parameters:

$$\frac{\mathrm{d}q}{\mathrm{d}t}=\frac{{\varphi }_q[q_{\mathrm{ss}}\left(V_m\right)-q\left(t\right)]}{{\tau }_q\left(V_m\right)},$$ (1)

where ϕ_q is a temperature-dependent scaling factor always assigned a value of 4; q_ss is the steady state open probability of the gate and τ_q its time-constant of relaxation. A voltage-gated calcium conductance (I_Ca; g_max = 1 mS/cm²; E_Ca = 90 mV) and a calcium-sensitive potassium conductance (I_AHP; g_max = 50 mS/cm²; E_K = −80 mV) were placed in the calcium compartment. I_Ca was modeled with I_Ca(t) = g_max · k(t) · (V_m − E_Ca), with k(t) being the gating variable. The time constant and steady-state opening probability of the gating variable were governed by the equations τ_k(V_m) = 2.5 + 7.5/{1 + exp[V_m + 10)/ − 5])} and k_ss (V_m) = 1/{1 + exp[(V_m + 25)/ − 3]}, respectively. The change in intracellular calcium concentration, [Ca²⁺], was governed by the following equation:

$$\frac{d\left[{\mathrm{Ca}}^{2+}\right]}{\mathrm{d}t}=-\alpha I_{\mathrm{Ca}}-\frac{\left[{\mathrm{Ca}}^{2+}\right]}{\tau \mathrm{Ca}},$$ (2)

where τ_Ca (130 ms) is the time constant of calcium extrusion and α (0.12 μM(ms μA)⁻¹cm²) governs influx. I_AHP was modeled with I_AHP(t) = g_max · [[Ca²⁺/([Ca²⁺] + K_D)] · (V_m − E_K) where the dissociation constant, K_D, had a value of 35 μM. To generate action potentials, a fast inactivating sodium conductance (I_Na; g_max = 90 mS/cm²; E_Na = 70 mV) and a delayed-rectifier (I_KDR; g_max = 22 mS/cm²; E_K = −80 mV) were employed. Both conductances were identical to those described in Wang (1998), though their kinetics were accelerated to reproduce peak firing rates observed in the LGMD by scaling I_Na's activation, I_Na's inactivation, and I_KDR's activation time constants by factors of 0.25, 0.3, and 0.35, respectively.

The dendritic compartment received either current injections (I_inj; Sect. 3) or simulated synaptic currents (I_syn; Sect. 4). To simulate visual inputs, we used excitatory synapses described by an alpha-function (α = 0.3 ms, E_rev = 0 mV, g_max = 0.94 mS/cm²), and the uniform mapping (Peron et al. 2007) was employed to determine how many ommatidia the simulated object would activate. Feed-forward inhibition was not included in the simulations (Peron and Gabbiani 2009), since we were mainly interested in characterizing how adaptation affects excitatory visual inputs and its impact on neuronal firing. Visual stimuli were simulated by calculating the areas of the visual field experiencing a luminance change every 5 ms, the frame interval used in in vivo visual stimulation. A delay of 50 ms was employed between ommatidial and synaptic activation, to mimic the delay observed in vivo. A temporal jitter in synaptic activation drawn from a normal distribution (μ = 0 ms, σ = 5 ms) and a spatial angular jitter of visual axes also drawn from a normal distribution (μ = 0°, σ = 10°) introduced variability to our simulations. Twenty-five runs were averaged for each simulation condition. We simulated background synaptic noise by firing each of 15,000 synapses at a rate of 0.05 Hz with uniform probability. These events were generated with the same alpha-function, except that g_max was set to 0.0047 mS/cm² to simulate spontaneous vesicular fusion.

The amount of spike-frequency adaptation was varied by adjusting the peak conductance of the calcium current, g_Ca (Sect. 3). To mimic the effect of intracellular BAPTA iontophoresis, the method employed to pharmacologically interfere with adaptation in vivo (Peron and Gabbiani 2009), we increased the rate of calcium efflux by reducing τ_Ca to 20 ms (Sect. 4). As established by Wang (1998), other parameters (e.g., the peak conductance of the AHP current, g_AHP) can achieve the same effect. Because we were interested in the generic role of spike-frequency adaptation in the context of coding, the specific mechanism that was adjusted to modulate adaptation was not important. The basal value employed for g_Ca was 1 mS/cm²; all the base model parameters were obtained from fitting the model to the LGMD's physiological response to current injections (see Peron and Gabbiani 2009, for details).

Figure 1b illustrates the membrane potential, instantaneous frequency, and calcium concentration responses of the model to a 12 nA step current lasting 1 s. First, it should be noted that since the amount of calcium entry per action potential is essentially fixed (Wang 1998), it usually takes at least a few spikes for [Ca²⁺]_intra, and hence I_AHP, to reach steady state. For this reason, there is an initial burst of spikes followed by a decline in firing rate. Adaptation causes a large drop in firing frequency from the maximal value, f_max, to its steady state value, f_ss (Fig. 1c). The effect of adaptation is nonetheless felt immediately, as may be seen by comparing the maximal frequency and the steady state frequency without adaptation (g_Ca = 0 mS/cm²; gray points). This effect is due to calcium entry during the first spike, which influences f_max. The time constant of adaptation, τ_adapt, obtained by fitting the instantaneous frequency response during the current step to an exponential, is sensitive to the parameter g_Ca (Fig. 1d); as the amount of calcium conductance increases, the adaptation becomes faster for all levels of current injected. This fact will be important later on, when we consider the way neurons can employ variability in the speed of adaptation to shape selectivity for specific stimulus classes. The adaptation ratio,

$$F_{\text{adapt}}=\frac{f_{\max }-f_{\mathrm{ss}}}{f_{\max }},$$ (3)

is defined as the change in firing frequency from the peak (f_max) to steady state (f_ss), divided by the maximal response and increases with higher g_Ca (an F_adapt of 1 implies full adaptation, with f_ss = 0, while a value of 0 implies no adaptation, with f_ss = f_max; see Fig. 1e). A more detailed discussion of the general properties of this spike-frequency adaptation model can be found elsewhere (Wang 1998; Liu and Wang 2001; Gabbiani and Krapp 2006).

3.1 Adaptation as dynamic range control

One of the demonstrated functions of adaptation is regulation of dynamic range. For instance, early visual processing employs a diversity of adaptation mechanisms to allow the visual system to report relative luminance changes independent of the basal luminance of a scene (Laughlin 1989). We examined this effect in our model by injecting a baseline current—I_base—for a period sufficient to allow for firing rate stabilization, and then depolarizing the model with a step current injection—I_step.

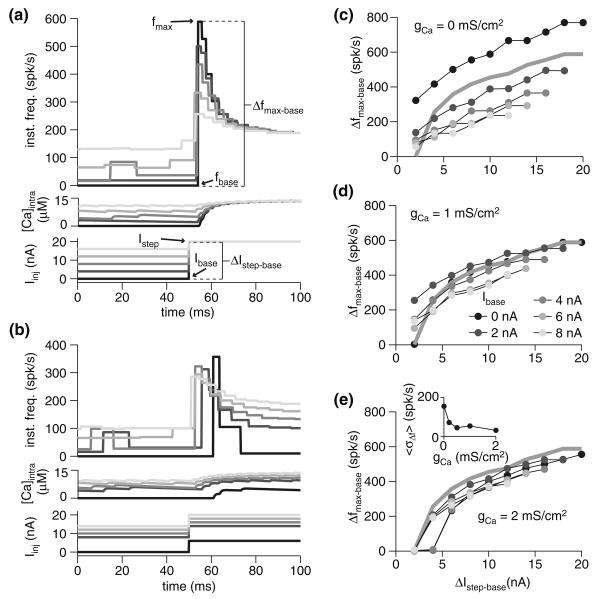
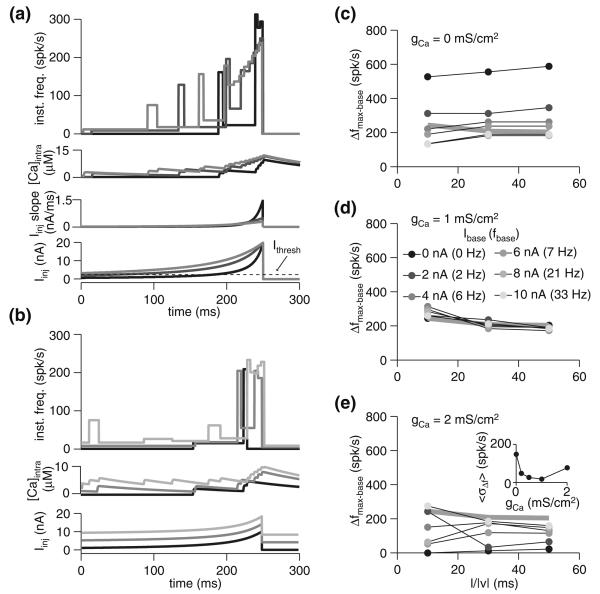
Because adaptation reduces the overall responsiveness of the neuron, stepping to a fixed I_step from increasing baseline current levels resulted in a decline in the maximal firing frequency (Fig. 2a). However, the difference in maximal firing frequency for identical current steps (ΔI_step−base = 10 nA) from varied baseline currents was much smaller (Fig. 2b). Adaptation therefore causes the cell to more similarly encode identical changes in input current, since the maximal change in firing rate, Δf_max−base, for a given amplitude current step, ΔI_step−base, becomes less dependent on I_base as g_Ca increases (Fig. 2c–e). This can be quantified by measuring the standard deviation (SD) of the Δf_max−base response across different I_base values, and taking the mean SD across ΔI_step−base for a given g_Ca. The resulting metric, 〈σΔ_f〉 (in spk/s), declines as g_Ca increases, though the majority of the decline occurs for g_Ca ≤ 1 mS/cm². Though the variability of the Δf_max−base versus ΔI_step−base curves across I_base values declined with increasing adaptation, the slope of the individual curves was fairly insensitive to g_Ca. Thus, while adaptation does enhance the fidelity of the code for ΔI_step−base, it does not appear to contribute much to improving the actual dynamic range of the neuron for a given baseline current injection. We observed similar results when we looked at the maximal frequency, f_max, attained as a function of ΔI_step−base. The consequences of these facts will depend on the postsynaptic readout scheme applied to the adapting neuron's spike trains.

Fig. 2.

Spike-frequency adaptation as a mechanism for dynamic range modulation. a Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various baseline currents and steps to 20 nA. Injected current is depicted at bottom. b Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various baseline currents and steps of 10 nA. c–e Maximal change in firing frequency (Δf_max−base) for various baseline currents (I_base; gray scale, as indicated in panel d) and current step size (ΔI_step−base). Baseline frequency (f_base) was measured as the mean frequency over the last 100 ms of injection with baseline current. The three panels show the response of the model with varying degrees of spike-frequency adaptation: none (g_Ca = 0 mS/cm²; c), fit to the underlying physiology (g_Ca = 1 mS/cm²; d), and above the physiological-fit value (g_Ca = 2 mS/cm²; e). The gray line denotes the response with I_base = 0 nA and g_Ca = 1 mS/cm². The inset in panel e shows response variability as a function of g_Ca. For each ΔI_step−base, the standard deviation of the Δf_max−base responses across various I_base values was obtained, and the mean of these (〈σ_Δf〉) is given for each g_Ca

Of course, other readout schemes are possible: as should be clear from Fig. 2b, the timing of the peak varied somewhat based on the baseline current. Higher baseline currents resulted in a faster peak time, though the overall range of peak timings was restricted to about 10 ms (Fig. 2b). Changing I_base substantially altered the spike count in the first 100 ms of response to the step current, meaning that a code employing spike number would be highly sensitive to I_base. Thus, f_max and Δf_max−base were relatively insensitive to I_base compared to peak time or spike count.

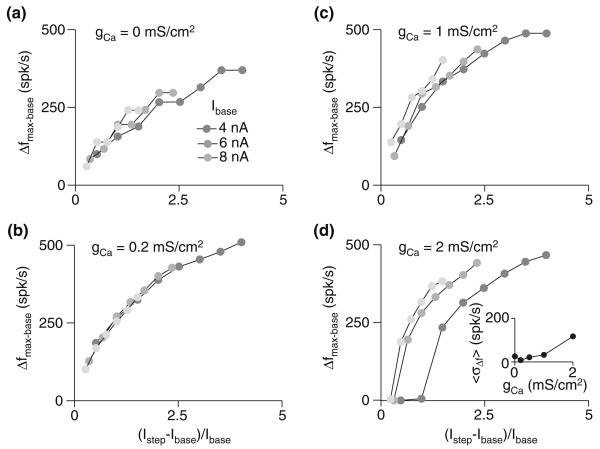
Interestingly, using changes in firing rate to encode relative changes in input intensity (i.e., (I_max − I_base)/I_base) provided a signal with an even lower sensitivity to baseline input intensity (Fig. 3). This was especially true for g_Ca = 0.2 mS/cm²: with the exception of the lowest I_base levels tested, the points for various baselines fell on the same curve (Fig. 3b). With the exception of the no-adaptation case (Fig. 3a), the dependence of cross-I_base response variability, 〈Δ_f〉, on g_Ca showed opposite trends for relative and absolute input intensity: increased g_Ca reduced response variability across I_base as a function of absolute current step size (ΔI_base−step), while increasing sensitivity to the size of relative intensity change ((I_max − I_base)/I_base; compare SD variability shown in insets of Figs. 2e and 3d). These results show that the right amount of adaptation enhances the ability of a cell to encode both absolute and relative changes in stimulus input intensity given variable levels of background input. However, the optimal level of adaptation depends on the variable that is to be detected, with greater adaptation enhancing sensitivity to absolute change but degrading sensitivity to relative change. Interestingly, the model using the g_Ca value fit to the physiological data (g_Ca = 1 mS/cm²) yielded fairly low response variability levels for both relative and absolute intensity change responses.

Fig. 3.

Spike-frequency adaptation renders a cell's response to relative input intensity changes largely invariant to baseline input. a–d Maximal change in firing frequency (Δf_max−base) for various baseline currents (I_base; gray scale, as indicated in panel a) and relative current step sizes ((I_step − I_base)/I_base). The four panels show the response of the model with varying degrees of spike-frequency adaptation: none (g_Ca = 0 mS/cm²; a), below the physiological-fit value (g_Ca = 0.2 mS/cm²; b), fit to the underlying physiology (g_Ca = 1 mS/cm²; c), and above the physiological-fit value (g_Ca = 2 mS/cm²; d). The inset in panel d shows response variability (〈σ_Δf〉; see Fig. 2) as a function of g_Ca; in this case, the mean was computed across (I_step − I_base)/I_base

3.2 Adaptation as high-pass filter

In addition to adjusting a neuron's dynamic range, spike-frequency adaptation has been demonstrated to endow neurons with high-pass filtering properties (Benda and Herz 2003; Benda et al. 2005; Benda and Hennig 2008). That is, a stimulus with a higher frequency—or, a larger temporal derivative—will elicit a stronger response in an adapting neuron than a stimulus of equal amplitude but lower frequency—or smaller temporal derivative. This is because faster stimuli can more effectively outrun adaptation. The time constant of adaptation plays an important role in determining the frequency beyond which adaptation is ineffective (see Benda and Herz 2003 for detailed treatment).

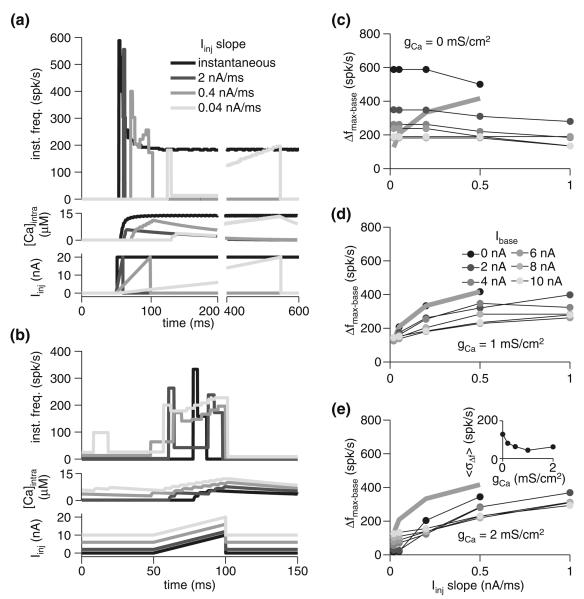
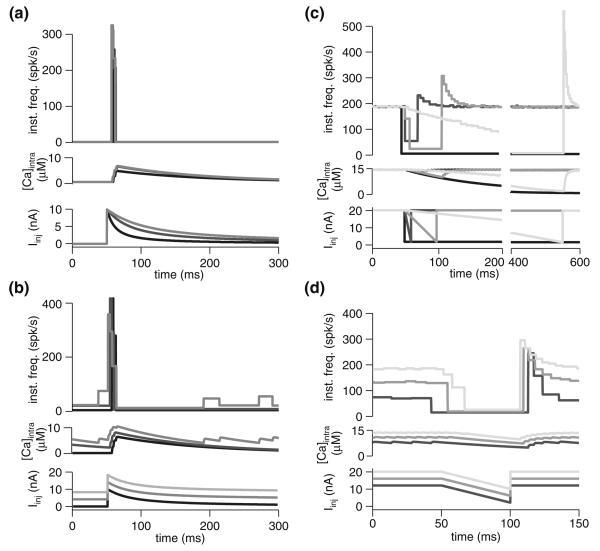
To explore this effect in our model, we employed simulated ramp current injections of identical amplitude but varied duration, resulting in different temporal derivatives (ΔI/Δt; units of nA/ms). Since the adaptation time constant, τ_adapt, increases with the level of current injected (Fig. 1d), higher temporal derivatives result in higher τ_adapt, averaged over the duration of the current ramp, and, therefore, less adaptation. In comparison to an instantaneous current step (i.e., ΔI/Δt = ∞), ramps from 0 to 20 nA resulted in lower peak firing rates as the ramp duration increased and the derivative, ΔI/Δt, declined (Fig. 4a). Indeed, for the lower slopes tested, the peak frequency barely exceeded the steady state frequency of an instantaneous 20 nA step (shown in black, Fig. 4a). The effect of the baseline current, I_base, was also examined in the context of 10 nA ramps lasting 50 ms, revealing a greater degree of sensitivity to baseline current than for instantaneous current steps (compare Figs. 4b and 2b). The degree of sensitivity to baseline declined with higher ramp derivatives. Moreover, with greater adaptation due to elevated g_Ca, the dependence of the change in response firing rate (Δf_max−base) on I_base declined (i.e., the SD in Δf_max−base across the different I_base values averaged across slopes, 〈σ_Δf〉, declined; Fig. 4e, inset). Beyond a certain g_Ca, however, adaptation abolishes the response altogether, with lower current injection responses abolished first. Thus, it appears that in this particular context, adaptation is limited in its ability to induce invariance to the basal level of input. Nevertheless, the g_Ca value fit to the physiological data (1 mS/cm²) yielded the lowest response variability relative to basal input level.

Fig. 4.

Spike-frequency adaptation reduces responses to stimuli with low derivatives without much effect on high derivative stimuli. a Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various current ramp slopes. All steps were from 0 to 20 nA. The ramp slope was varied by modulating current injection duration. The black response is to an instantaneous step to 20 nA. Injected current is depicted below. b Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various baseline currents and steps 50 ms long to 10 nA above baseline (slope of 0.2 nA/ms; I_base of 0, 2, 6, and 10 nA). c–e Maximal change in firing frequency (Δf_max−base) for various baseline currents (I_base; gray scale, as indicated in panel d) and current ramp slopes. All steps were 10 nA in amplitude at their maximum. The three panels show the response of the model with varying degrees of spike-frequency adaptation: none (g_Ca = 0 mS/cm²; c), fit to the underlying physiology (g_Ca = 1 mS/cm²; d), and above the physiological-fit value (g_Ca = 2 mS/cm²; e). The gray line denotes the response with I_base = 0 nA and g_Ca = 1 mS/cm². The inset in panel e shows response variability (〈σ_Δf〉; see Fig. 2) as a function of g_Ca

While increased adaptation slightly increased the dynamic range of the response (i.e., the slope of the Δf_max−base versus I_inj slope plot increased), it was a smaller increase than that observed with instantaneous current steps (compare Fig. 4c–e to Fig. 2c–e). Indeed, the majority of the dynamic range of the response is confined to the lower stimulus slopes, which adaptation filters most. For any given I_base, simulations with adaptation (g_Ca > 0 mS/cm²; Fig. 4d, e) typically yielded declining dynamic range with increasing I_inj slope. That is, individual Δf_max−base versus I_inj curves saturated. This suggests that, for a given I_base, the change in firing rate (Δf_max−base) can signal that a critical input slope was exceeded, but cannot report its precise slope value. A more reliable signal of slope value may be the timing of the firing rate peak (Fig. 4a), though this was quite susceptible to the level of background input (Fig. 4b). From an ethological perspective, however, rapid transients often signal specific events, suggesting that a binary readout based on a threshold firing rate change could suffice behaviorally. Indeed, the important feature of the response curves with adaptation (Fig. 4d, e) compared to those without (Fig. 4c) is the fact that lower slopes elicit far lower responses, making threshold-based detection possible. Without adaptation, the response is far less sensitive to the input slope, with even the lowest slope values yielding robust responses. Indeed, as Fig. 4c illustrates, removing adaptation results in an essentially flat Δf_max−base versus I_inj slope curve.

3.3 Adaptation and temporal profile selectivity

So far, we have considered adaptation's influence on the processing of constant current steps, as well as linear current ramps. The dynamics of adaptation, however, should also influence a neuron's response to more complex stimuli. For instance, if stimulus intensity increases supra-linearly (with a positive second derivative), it may be able to overwhelm adaptation even more effectively than step or ramp transients. To see this, let us approximate an accelerating stimulus as a succession of ramps of increasing slope that lead to successively higher base currents. For such a stimulus, Fig. 4d suggests that as I_base increases, it will take a slightly greater slope to achieve the same Δf_max−base. Thus, one may expect a stimulus that is increasing in slope to most effectively produce an increase in firing rate. Conversely, adaptation in the case of a rapidly decelerating stimulus would be expected to produce a sharply reduced response, after an initial onset transient. Recent work in the LGMD has shown that spike-frequency adaptation substantially reduces the response to translating visual stimuli, while having minimal effect on looming stimuli (Peron and Gabbiani 2009), corroborating the notion that looming stimuli are fairly insensitive to adaptation because of their supra-linear increase in intensity.

The angular size, θ(t), subtended at the eye at time t, where t < 0 is time to collision, by a looming disc having a constant approach velocity v (<0 for approaching objects), and radius l is given by (Gabbiani et al. 1999):

$$\theta \left(t\right)=2\cdot {\tan }^{-1}\frac{l}{\nu t}.$$ (4)

That is, the angle subtended at the retina depends on the size-to-speed ratio, l/|ν| (in units of ms). Thus, a larger object approaching at a fixed velocity is equivalent to a smaller object moving at proportionally slower velocity. The angular velocity of an edge of the looming stimulus, ψ(t), is simply half of the derivative of Eq. 4:

$$\psi \left(t\right)=\frac{1}{2}\frac{\mathrm{d}\theta }{\mathrm{d}t}=-\frac{l∕\nu }{t^2+{(l∕\nu )}^2}.$$ (5)

We tested the impact of adaptation on our model's response to temporal intensity profiles that mimic those expected for looming stimuli. Specifically, we implemented loom-like current ramps going from 0 to 20 or 0 to 10 nA by using the same temporal intensity profile as the size of a looming stimulus (I_inj(t) ∝ θ(t)) over the approach ranging from θ/2 = 2° to 62°, with 3 l/|ν| values: 10, 30, and 50 ms. In Sect. 4.2, we also consider the more realistic situation where ψ(t) (Eq. 5) dictates input conductance amplitude.

The peak firing frequency in the base model (g_Ca = 1 mS/cm²) was relatively insensitive to l/|ν| (Fig. 5a, d). In all cases, the loom-like stimuli attained comparable spike counts to ramp stimuli, despite having lower mean input slopes (based on comparison of the responses shown in Figs. 4a and 5a). Specifically, in the last 10 ms of the fastest loom-like stimulus (l/|ν| = 10 ms), four spikes are elicited with a mean injection slope of 0.93 nA/ms (for the last 10 ms; maximal slope of 1.43 nA/ms), which is the same number of spikes elicited by the 10 ms, 2 nA/ms ramp slope. Similarly, both of the slower stimuli (l/|ν| = 30 and 50 ms) elicited nine spikes in the last 50 ms, as did the 50 ms long 0.4 nA/ms ramp stimulus, despite having lower mean slopes over the last 50 ms (0.24 and 0.19 nA/ms, respectively; maximal slopes of 0.48 and 0.29 nA/ms, respectively). Thus, the loom-like current injection shape elicited a comparable spike count with a lower mean slope than analogous ramps. This is despite the fact that the loom-like injection resulted in some firing, and therefore adaptation, before the time window employed for analysis, whereas comparable ramp data started with I_inj = 0 nA, and therefore no adaptation. In contrast to spike count, the peak frequency change (Δf_max−base) observed with ramp stimuli was generally larger than that observed for loom-like stimuli. This was because ramp stimuli reached peak stimulus derivative instantly, while loom-like stimuli reached peak derivative towards the end of the stimulus, after some spikes had been fired, activating g_Ca. When various levels of baseline currents were used with 10 nA current steps and an l/|ν| of 10 ms, the peak frequency attained was less sensitive to I_base than for either instantaneous or fixed-slope current injections (Fig. 5b).

Fig. 5.

Spike-frequency adaptation reduces the range of responses to current injections with intensity profiles mimicking visual looming. a Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for current injections mimicking looming stimuli with various l/|ν| values. (I_inj(t) governed by θ(t), Eq. 4). All steps were from 0 to 20 nA (i.e., I_base = 0). From lightest to darkest, simulated l/|ν| was 50, 30, and 10 ms. The temporal profile of injected current is depicted below, with the dotted line indicating the threshold current (I_thresh; ~3 nA). b Instantaneous frequency response of the model with g_Ca = 1 mS/cm² for various baseline currents (0, 4, and 8 nA) and steps to 10 nA above baseline mimicking an l/|ν| value of 30 ms. c–e Maximal change in firing frequency (Δf_max−base) for various baseline currents (I_base; gray scale as indicated in panel d) and simulated l/|ν|. All steps were 10 nA in amplitude at their maximum. The three panels show the response of the model with varying degrees of spike-frequency adaptation: none (g_Ca = 0 mS/cm²; c), fit to the underlying physiology (g_Ca = 1 mS/cm²; d), and above the physiological-fit value (g_Ca = 2 mS/cm²; e). The gray line denotes the response with I_base = 0 nA and g_Ca = 1 mS/cm². The inset in panel d shows response variability (σ_Δf; see Fig. 2) as a function of g_Ca

The primary reason why loom-like stimuli are so effective at eliciting spikes can be observed by contrasting the calcium response in Fig. 5 to that in the ramp responses of Fig. 4. Since the AHP conductance responds instantaneously to calcium, the rate of calcium influx and efflux are the main determinants of adaptation. Because a roughly fixed quantity of calcium enters the cell for each action potential, it usually takes several spikes to reach steady state (e.g., Fig. 4a, darkest trace). In all but the steepest fixed current ramps, this results in a situation where adaptation lowers the firing rate sufficiently for any subsequent increases in current injection to be compensated for by the calcium influx of a single spike, thus maintaining the steady-state [Ca²⁺]_intra. With supralinear stimuli, even those having slopes lower than those necessary for fixed ramp stimuli to prevent the attainment of steady-state [Ca²⁺]_intra, the increase in current injection slope means too few spikes take place at any given current level for steady-state [Ca²⁺]_intra to be attained.

Though adaptation had a minimal effect on the timing of the firing rate peak in the model and our previous experimental results (Peron and Gabbiani 2009), the strength of adaptation in the model was quite important in determining the degree of sensitivity of the change in frequency, Δf_max−base, to I_base. Specifically, the model without adaptation (Fig. 5c) responded over almost a threefold range of Δf_max−base values, when I_base was varied. The level of adaptation fitted to physiological data – g_Ca = 1 mS/cm² – gave rise to a much higher degree of invariance to I_base at each l/|ν| value (Fig. 5d). Greater adaptation resulted in a re-emergence of I_base sensitivity (Fig. 5e). This shows that an appropriate level of adaptation can also implement invariance to basal input in the context of temporally complex input patterns. Again, the physiologically fit g_Ca value yielded the best results in terms of minimizing response variability (〈σ_Δf〉; Fig. 5e, inset).

A notable feature of the response to loom-like current injections was the invariance of the response to the value of l/|ν|. That is, one cannot infer l/|ν| from Δf_max−base because the Δf_max−base versus l/|ν| curve is relatively flat. This suggests that, as with transients, the maximal change in firing rate can only indicate the presence of a stimulus, not its l/|ν| value. In the case of a collision-detecting neuron like the LGMD, this may be ideal since a postsynaptic threshold detector will be able to signal impending collision independent of stimulus characteristics.

To further emphasize the role of adaptation in temporal profile selectivity, we performed simulations where we inverted the temporal intensity profile of the stimulus, mimicking a receding stimulus (Fig. 6a, b). These stimuli gave rise to a burst of spikes followed by silence. In a cell without adaptation, reversing the stimulus temporally should simply reverse the response; with adaptation, when the stronger currents come first, the overall response (in terms of spike count) is diminished. Thus, although the peak frequencies produced by these stimulations were similar to those obtained with currents mimicking approaching stimuli (compare Figs. 5a, b and 6a, b), the number of spikes produced was typically reduced by ~50%.

Fig. 6.

Spike-frequency adaptation results in sharply reduced responses to stimuli of decreasing strength. a Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for current injections mimicking receding stimuli with various l/|ν| values. (I_inj(t) governed by θ(t),Eq. 4). All steps were from 0 to 10 nA. From lightest to darkest, simulated l/|ν| was 50, 30, and 10 ms. The temporal profile of injected current is depicted below. b Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various baseline currents (0, 4, and 8 nA) and steps to 10 nA above baseline mimicking an l/|ν| value of 30 ms. c Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various negative current ramp slopes. All steps were from 20 to 0 nA (i.e., I_base = 20). d Instantaneous frequency and calcium response of the model with g_Ca = 1 mS/cm² for various baseline currents and steps taking 50 ms to 10 nA below baseline (slope of −0.2 nA/ms)

Similarly, inverting the intensity profile of the current ramps yielded rapidly declining responses (Fig. 6 c, d). This is because the cell was already in an adapted state, having been subject to sustained current injection. Only the response to the gentlest slope (Fig. 6c, lightest shade) was able to sustain firing with the declining stimulus, because in this case recovery from adaptation (governed by the fairly slow τ_Ca = 130 ms) kept pace with the injection amplitude decline.

4 Adaptation and the LGMD visual response

In the LGMD, spike-frequency adaptation appears to serve a fairly specific role: by suppressing the response to translating stimuli, while not affecting the response to looming stimuli, it effectively acts as a filter for a specific stimulus class (Peron and Gabbiani 2009). In the previous section, we employed a model of LGMD adaptation based on in vivo current injection experiments and pharmacology. That model, combined with information regarding the sampling of visual space by the locust eye (Krapp and Gabbiani 2005) and the projection of visual inputs onto the LGMD (Peron et al. 2007) allowed us to reproduce the LGMD's response to translating stimuli before and after pharmacological suppression of spike-frequency adaptation (Peron and Gabbiani 2009). We wished to extend this model to examine the effect of adaptation on the LGMD's selectivity for velocity profiles of translating stimuli, as the results from the previous section suggested that adaptation should be incapable of suppressing the response to loom-like translation (Fig. 5). Moreover, we wished to examine the possibility that spike-frequency adaptation may in part account for the LGMD's observed preference for approaching versus receding stimuli (Rind and Simmons 1992).

4.1 Response to translating squares

Though the locust eye does not sample visual space uniformly (Krapp and Gabbiani 2005), a comparison of electro-physiological and modeling data suggests that the LGMD compensates to some extent for this sampling anisotropy (Peron et al. 2007). Thus, we assumed that sampling of visual space was effectively uniform. Under such a scheme, translating squares will produce responses that resemble those to current injections matching the velocity profile of the visual stimulus. Noise was introduced by slightly randomizing the sampling of visual space between simulation trials, as well as introducing jitter into the arrival of synaptic input (see Sect. 3).

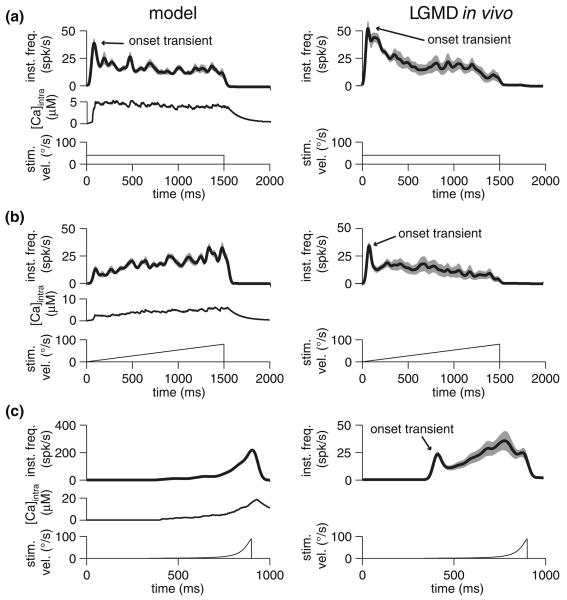
As observed previously, constant velocity motion produced an onset transient—i.e., an initial burst of firing—in the model followed by a low steady firing rate, much like the response to step current injections (Fig. 7a). This was due to strong, calcium-mediated adaptation in a fashion analogous to that observed with step current injection (Fig. 1c). Visual stimulation with constant velocity motion in vivo produced a similar response (n = 6 animals) in the LGMD's firing rate, namely, an onset transient followed by sustained firing at low rate, presumably due to strong adaptation (Peron and Gabbiani 2009). Interestingly, a similar response was observed in vivo to a linearly accelerating square, even though the model responded with a gradually increasing firing rate (Fig. 7b), as expected from the current ramp responses. This difference is not a result of the eye's anisotropy—motion in all four cardinal directions yielded similar responses. More likely, accelerating stimuli triggered other processes, like feed-forward (Gabbiani et al. 2005) or lateral inhibition presynaptic to the LGMD (Rowell et al. 1977), that were not included in the model but which further suppressed the cell's response. The response to a loom-like velocity profile, where the square's velocity was governed by ψ(t) (Eq. 5), resulted in a gradually increasing firing rate both in vivo and in the model (Fig. 7c). In vivo, the response to this stimulus led to stronger peak rates than to a linearly increasing velocity stimulus, in spite of a shorter stimulation time at comparable velocities (Figs. 7b vs. c). One notable difference in the model and in vivo responses was the presence of a sharp onset transient in vivo (Fig. 7c). Additionally, the peak frequency for the loom-like velocity profile was much higher in the model than in vivo, which again suggests that other processes such as feed-forward and lateral inhibition play a role in response suppression. Thus, while adaptation is not the only process affecting synaptic integration in the LGMD, the cell does show some features predicted by our model. Namely, translating squares with a loom-like velocity profile are able to elicit robust responses, even if they do not match those elicited by expanding squares or circles. This supports the notion that adaptation's primary function in the LGMD is to mitigate the response to non-accelerating stimuli.

Fig. 7.

Instantaneous frequency and calcium response in model (left), and instantaneous frequency response in the LGMD in vivo (right) to translating squares having various velocity profiles (indicated at the bottom of each panel). All responses are Gaussian-convolved (σ = 20 ms) mean instantaneous frequency responses, with SEM shown in grey. Model data was obtained by simulating ten presentations; in vivo data was obtained by taking the mean of the averaged responses for each animal (n = 6 animals). All stimuli consisted of 10° by 10° squares moving across 60° of real or simulated visual space, at fixed azimuth (90°) starting and ending at elevations of 30° and −30°, respectively (0° azimuth corresponds to the animal's front, and 0° elevation is the equator of the eye; see Krapp and Gabbiani 2005 for detailed description of coordinate system). a Response to stimulus having fixed velocity of 40°/s. b Response to stimulus with starting velocity of 0°/s and ending with velocity of 80°/s. c Response to square with a loom-like velocity profile, with velocity governed by ψ(t) (Eq. 5) for a looming object's edge where l/|ν| = 50 ms

4.2 Response to receding versus approaching stimuli

One experimentally demonstrated functional consequence of spike-frequency adaptation that has been replicated in a calcium dependent adaptation model is forward masking (Sobel and Tank 1994; Wang 1998). In this situation, a weak stimulus preceded by a stronger one produces a lower response than when the weak stimulus is presented alone. A similar situation arises when the LGMD is presented with a receding versus an approaching stimulus moving at constant velocity: during approach, the number of activated ommatidia, and hence synaptic input, increases with time. During recession, the majority of the motion occurs at the beginning, with synaptic input declining over the course of the stimulus. Based on our decreasing amplitude current injection results (Fig. 6), one would expect such receding stimuli to produce weaker responses.

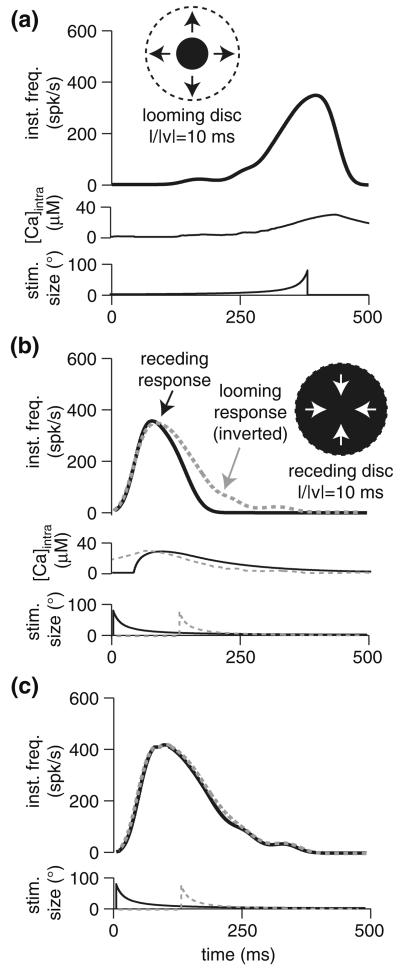
Indeed, in the LGMD, the response to approaching stimuli is far more robust, producing many more spikes than receding stimuli (Rind and Simmons 1992). Feed-forward inhibition is known to play a prominent role in this difference (Gabbiani et al. 2005), but spike-frequency adaptation could contribute as well. To test this idea, we simulated the response to approaching and receding discs in a model having regular (τ_Ca = 130 ms) and reduced (τ_Ca = 20 ms) adaptation (Fig. 8). In the model with regular adaptation, comparison of the receding response to the inverted approaching response (Fig. 8b) showed a larger response to the latter. When adaptation was reduced, the two responses overlapped perfectly (Fig. 8c), suggesting that the selectivity observed in the LGMD may be partly accounted for by spike-frequency adaptation. To confirm this result, we repeated the same simulations in a model including feed-forward inhibition (Peron and Gabbiani 2009). Although the effect of adaptation was diminished, causing ~15% less spikes rather than ~30%, it still substantially decreased the width of the transient response (from 102 to 86 ms, width at half-height).

Fig. 8.

Role of spike-frequency adaptation in selectivity for approaching versus receding stimuli. a Response of model with full spike-frequency adaptation (τ_Ca = 130 ms) to approach by a looming stimulus with l/|ν| = 10 ms. b Response of model with full spike-frequency adaptation to receding stimulus with l/|ν| 10 ms; the response from a is superimposed with grey dotted line after inverting the time axis and aligning the peaks. c Response of model with reduced spike-frequency adaptation (τ_Ca = 20 ms) to approaching (dotted grey line) and receding (black) stimulus with l/|ν| = 10 ms

5 Discussion

Spike-frequency adaptation is a common property of many neurons. In the LGMD, adaptation explains the weak response to constant-velocity translating squares relative to looming stimuli (Peron and Gabbiani 2009), and may contribute to the asymmetry in response to approaching versus receding stimuli. In addition, translating stimuli with a loom-like velocity profile elicit stronger responses than those with linear profiles, consistent with the combined stimulus and spike-frequency adaptation dynamics in the LGMD model. Specifically, the simulated current injection results suggest that loom-like velocity profiles should elicit greater spike counts for the same mean stimulus intensity relative to linear velocity profiles. It appears that the presence of additional inhibitory mechanisms in vivo further enhances the difference between these two stimulus classes. Together, these results support the notion that spike-frequency adaptation endows the LGMD with selectivity for stimuli on a collision course with the animal.

5.1 Adaptation's computational roles

Adaptation on the time scale studied here—τ_adapt of tens to hundreds of milliseconds—can perform several important computational tasks. While the specific implementations are diverse, we highlight three functional classes of computations carried out by spike-frequency adaptation: dynamic range modulation, high-pass filtering, and temporal profile selectivity.

Dynamic range modulation is important, especially in early sensory processing, since shifting tuning curves to account for the basal level of sensory input allows sensitivity to be optimized to the environmental context (Laughlin 1989). Such adaptation is necessary because neurons have a physiological limit on peak firing rates—firing rates above ~1 kHz cannot be supported by action potentials having a typical width of ~1 ms. One way of maintaining dynamic range is to keep a low basal firing level. Both contrast-adaptation in cat V1 cells (Sanchez-Vives et al. 2000) and forward masking in the cricket Omega neuron (Pollack 1988; Sobel and Tank 1994) can be understood in this context: though the response to a fixed stimulus intensity is diminished in the adapted state, it is likely that the response to intensity change remains fairly invariant to basal input. As shown here, this is true for both the same absolute (Fig. 2) and relative change (Fig. 3). Other systems where dynamic range modulation is believed to be the primary role of spike-frequency adaptation include, e.g., phase-disparity sensing neurons of the guinea pig inferior colliculus (Ingham and McAlpine 2004) and the proprioceptive anterior gastric receptor of the crab (Smarandache and Stein 2007).

Another proposed role for spike-frequency adaptation is high-pass filtering (Benda and Herz 2003). Lower frequency stimuli are less effective at overcoming adaptation than those of higher frequency. Intuitively, this can be explained by the fact that higher frequency stimuli have higher derivatives. A stimulus that reaches peak intensity faster than the cell can adapt will elicit higher firing rates than stimuli which reach that peak after the cell has had time to adapt (Fig. 4). The original phenomenological model of Benda and Herz (2003) explains frequency selectivity in the response of electrosensory neurons of weakly electric fish (Benda et al. 2005). These cells respond more strongly to identical-amplitude stimuli of high versus low frequencies. Additionally, the same model explains intensity invariance above a given cutoff frequency in cricket auditory AN1 neurons (Benda and Hennig 2008). Finally, it has been proposed that adaptation sharpens sensitivity to the input derivative in dimming and sustaining fibers of crayfish (Glantz and Schroeter 2004). In agreement with the AN1 results, our data using current ramps suggest that beyond a certain input derivative, the response will be fairly insensitive to the relative change in input for a given basal level of input (Fig. 4d, e). This is because spike-frequency adaptation results in individual Δf_max−base versus I_inj slope curves that saturate, implying that thresholding near the curve's saturation point endows cells with the ability to detect an input derivative threshold. In contrast to its role in dynamic range modulation, spike-frequency adaptation does not seem to enhance a cell's ability to discriminate stimulus derivative along a continuous scale. That is, the slope of the response curve is not steep enough to encode input stimulus derivative. Instead, it allows prospective decoding via a threshold—stimuli below a certain derivative will elicit minimal responses, whereas those above it will result in a robust response. Though such a coding scheme carries limited information, it is adequate in situations where all-or-none stimulus detection suffices.

Finally, we considered the role of adaptation in shaping selectivity for specific temporal input profiles. Our results suggest that a stimulus with a supra-linear intensity profile (i.e., having a positive second temporal derivative) will most effectively overwhelm spike-frequency adaptation. Thus, adaptation can be used to effectively detect accelerating stimuli, even if the mean change in stimulus strength—i.e., the average intensity slope—is less than that of a ramp stimulus having a similar peak input intensity slope. Our results suggest that this type of discrimination requires the use of spike count information, as sloped stimuli did elicit larger peak frequency changes than loom-like stimuli. The selectivity of this mechanism for specific accelerating profiles is limited, but it results in greater response fidelity than for ramp stimuli (compare the sensitivity of response to I_base in the insets of Figs. 5e and 4e). It is likely that many naturalistic stimuli follow such nonlinear input profiles—in addition to visual object approach, similar profiles can be expected from auditory object approach, as well as many communication signals (e.g., frequency sweeps in bird calls or human speech).

Interestingly, in all three cases, the LGMD model exhibited either minimal or near-minimal response variability with respect to I_base when the physiologically fit level of adaptation was employed (g_Ca = 1 mS/cm²). This effect was especially pronounced for ramp and loom-like stimuli (Figs. 4e and 5e, insets). In both cases, the physiologically fit g_Ca value yielded the minimal amount of response sensitivity to I_base observed, as measured by response SD (〈σ_Δf〉). This suggests that adaptation in the LGMD may be exquisitely tuned to minimize sensitivity to background activity levels, a strategy that would be quite useful in the context of a combined threshold and spike count based readout scheme.

5.2 Conclusions

The three computational roles of adaptation we describe are not mutually exclusive; all three simulation sets were, after all, carried out using the same model. Thus, to understand the function of spike-frequency adaptation from a neural coding perspective, a systems approach is crucial. For instance, though adaptation in the LGMD may allow for modulation of dynamic range, it appears unlikely that this feature is exploited in vivo. Clearly, different speeds (τ_adapt) and degrees (F_adapt) of adaptation will be better suited to particular tasks: for example, maintaining a large dynamic range in the firing rate response to stimuli of similar strength relative to different baselines can be achieved by a strong adaptation that keeps τ_adapt appropriately tuned so as not to degrade the ability to respond to relevant stimuli. To impose specific cutoff frequencies in the high-pass filtering context, adaptation must also be specifically tuned (see Benda and Herz 2003). For instance, a faster τ_adapt will lead to a higher cutoff frequency. Finally, the more complex relationship between the intensity of input and the parameters of adaptation (F_adapt, τ_adapt) is crucial in shaping selectivity for specific input stimulus profiles such as accelerating ones. Due to the diversity of biophysical mechanisms that can give rise to spike-frequency adaptation (Sect. 2), and the range of computational functions it can perform, it is likely that evolution has exploited it in a large number of roles. Because of its complex influence on neuronal firing, however, it will be important to take a context-specific approach—like the one advocated by J. P. Segundo—in considering its impact on neuronal coding.