Feature Space Resampling for Protein Conformational Search

Abstract

De novo protein structure prediction requires location of the lowest energy state of the polypeptide chain among a vast set of possible conformations. Powerful approaches include conformational space annealing, in which search progressively focuses on the most promising regions of conformational space, and genetic algorithms, in which features of the best conformations thus far identified are recombined. We describe a new approach that combines the strengths of these two approaches. Protein conformations are projected onto a discrete feature space which includes backbone torsion angles, secondary structure, and beta pairings. For each of these there is one “native” value: the one found in the native structure. We begin with a large number of conformations generated in independent Monte Carlo structure prediction trajectories from Rosetta. Native values for each feature are predicted from the frequencies of feature value occurrences and the energy distribution in conformations containing them. A second round of structure prediction trajectories are then guided by the predicted native feature distributions. We show that native features can be predicted at much higher than background rates, and that using the predicted feature distributions improves structure prediction in a benchmark of 28 proteins. Our approach allows generation of successful models by recombining native-like parts of first-round conformations. The advantages of our approach are that features from many different input structures can be combined simultaneously without producing atomic clashes or otherwise physically unviable models, and that the features being recombined have a relatively high chance of being correct.

1 Introduction

Ab initio structure prediction remains a fundamental unsolved problem in computational biology. Since proteins fold to their lowest free energy states, the challenge, given a sufficiently accurate energy function, is to locate the global energy minimum. This is a difficult problem because the search space is very high-dimensional and riddled with local minima. Indeed, locating the global minimum is the primary bottleneck to consistent and accurate structure prediction using current methods such as Rosetta [1].

One promising approach is to build up a map of the energy landscape by carrying out an initial set of searches to identify a large number of local energy minima, and then to utilize this information to guide a second set of searches towards the regions of the landscape likely to contain the global minimum. Several methods have been proposed to integrate information from a first round of sampling. On one end of the spectrum are methods that concentrate resampling around low-scoring structures from initial sampling rounds. In conformation space annealing [2], a pool of random starting structures is gradually refined by local search, with low energy structures giving rise to children that eventually replace the higher energy starting structures. In [3], a Rosetta-based resampling method is presented that operates by identifying “funnels” in conformation space and concentrating sampling on the low-energy funnels. Similar resampling strategies have been developed for general-purpose global optimization. These include fitting a smoothed response surface to the local minima already gathered [4] and using statistical methods to identify good starting points for optimization [5]. Methods of this kind do not aim to guide search outside previously explored regions, but rather to exploit the lowest-energy regions discovered through ordinary search. They will succeed when near-native regions have already been explored and identified as native-like by the energy function, but not otherwise. On the other end of the spectrum, genetic algorithm approaches [6, 7, 8] recombine features of successful structures to create new structures. Although genetic algorithms do explore new regions of conformation space by feature recombination, they do so in an undirected fashion—no attempt is made to identify those features most responsible for the success of low-energy structures and to recombine these. A third class, generalized ensemble methods such as multicanonical sampling [9], metadynamics [10], and the Wang-Landau algorithm [11], use initial samples to modify the energy function to improve sampling of low-energy regions.

In this paper we present a method designed both to avoid the limitations of concentration-style methods by recombining structural features to explore new regions of conformation space and to avoid the limitations of genetic algorithms by carefully selecting which features to recombine. Typically, no single local minimum computed in the first round of search has all the native feature values, but many or all features assume their native values in at least some of the models—for instance, in a beta sheet with three strands and hence two beta pairings, the proper registers for the beta pairings may both be present in some models, but never together. If we can identify these native feature values and recombine them, sampling can be improved. Related work [12] indicates that constraining a few native “linchpin” features can dramatically improve sampling. We hypothesize that many native feature values can be identified using information derived from an initial round of Rosetta models, most significantly the enrichment of native values in lower-energy models. We develop a statistical model that predicts the probability that each feature value is native by incorporating a variety of statistics, both energy-based and otherwise, from the pool of initial-round models. The output of the predictor is a distribution over features that corrects inefficiencies in the distribution sampled by plain Rosetta search. In the resampling round, we use this improved distribution to guide Rosetta search. In contrast to generalized ensemble methods, the energy function is not modified in the resampling round; instead, the sampling distribution is modified directly by means of fragment repicking, which involves changing the fragment pool available to Rosetta, and stochastic constraints to enforce beta sheet topology. Our resampling method explicitly promotes feature recombination by independent enrichment of native feature values, producing strings of native feature values never observed together in the initial round.

2 Methods and Materials

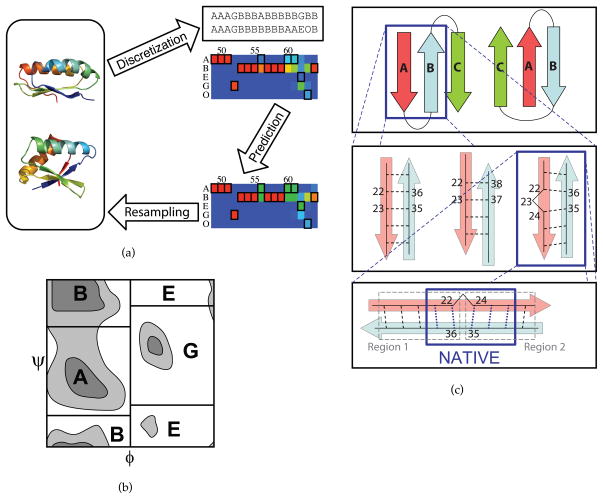
Our resampling algorithm has three steps (Figure 1(a)). In the first, “discretization” step, we project an initial set of Rosetta models for the target protein from conformation space into a discretized feature space. In the second, “prediction” step, we use the energies and frequencies associated with the different feature values in the initial set of models to estimate the probability that each is native. In the third, “resampling” step, we use the predicted native feature probabilities to guide Rosetta structure prediction calculations.

Figure 1. Feature space representation of protein structures.

(a) Flow-chart outline of the new resampling method. Each model from the initial round of Rosetta search (shown in the leftmost oval) corresponds after discretization to a string of feature values (shown here as strings of letters representing torsion feature values). The colored grid below represents frequencies of torsion feature values among feature strings from the initial round. Here, residues 49–64 of protein 1dcj are depicted (blue, frequencies near 0%; green, frequencies near 50%; red, frequencies near 100%). Each column represents the distribution over a single feature. A black outline indicates the native feature value. The grid in the lower right depicts the predicted native probabilities, which are used as targets in the resampling round of search. Rare feature values at residues 56, 69, 61, and 62 are enriched over the initial round. (b) Torsion feature values represent discrete regions of the Ramachandran plot. (c) Beta topology, pairing, and contact features. At the top level is a single topology feature, with each value a possible topology. One such topology consists of several pairings, each of which has an associated pairing feature. Pairing AB of the native topology is shown in the middle level. The values of the pairing feature are all possible registers. Each register is associated with a set of contact features, shown in the bottom level. In this example, 1di2, the native register has two bulge-free regions, each associated with a contact feature circled in gray. The values of a contact feature are all possible contacts within the region. Contact features differ from other types in that multiple values might be native. The contacts present in the native structure are circled in blue. To constrain the native register, one native constraint must be chosen from each contact feature.

2.1 Discretization

The discretization step significantly reduces the search space while preserving essential structural information. A “feature” is a structural property that can take on one of a discrete set of values. Conformations are represented by strings of feature values. Our features fall into three classes: torsion features, secondary structure features, and beta sheet features, with the latter class further subdivided into three subclasses.

Torsion features are residue-specific. In order to discretize the possible torsion angles for each residue, we divide the Ramachandran plot into four regions, referred to as “A,” “B,” “E,” and “G” (Figure 1(b)) roughly corresponding to clusters in the PDB. A fifth label, “O,” indicates a cis peptide bond and does not depend on φ or ψ. Labels were chosen to correspond to those used in related work [12].

Secondary structure features are also associated with single residues. They take values in the standard alphabet “E,” “H,” and “L,” indicating sheet, helix, and loop.

The beta structure of a protein conformation can be parsed at three different levels, illustrated for protein 1di2 in Figure 1(c). At the top level is a single topology feature. The native topology (depicted on the left) includes a beta sheet with three strands, strand A running from residue 19 to residue 25, strand B running from residue 33 to residue 39, and strand C running from residue 43 to residue 48. Strands A and B pair, as do strands B and C, so this topology has two associated pairing features, AB and BC. Pairing feature AB is examined in detail. The possible values for a pairing feature are registers, defined as sets of beta contacts, each denoted by a pair (i, j) of residue numbers. The possible registers for pairing AB include, from left to right, {(18, 40), (19, 39), …, (27, 31)}, {(20, 40), (21, 39), …, (27, 33)}, and {(18, 40), (19, 39), …, (22, 36), (24, 35), …, (27, 32)}. The third register has a beta bulge at residue 23. The beta contacts in these registers extend slightly outside the areas designated strand in the native structure, because they include all beta contacts ever observed in the initial sampling round. Each register brings with it one or more contact features, one for each bulge-free region in the register. The number of such features is therefore one greater than the number of bulges in the register. The chart shows the two contact features associated with register {(18, 40), (19, 39), …, (22, 36), (24, 35), …, (27, 32)}, one with possible values {(18, 40), (19, 39), (20, 38), (21, 37), (22, 36)}, and one with possible values {(24, 35), (25, 34), (26, 33), (27, 32)}. In order to constrain this register, two beta contact constraints must be chosen to be enforced, one from each of these two contact features.

Beta features are hierarchical; each pairing feature is associated with the topology value from which it derives, and each contact feature is associated with the register from which it derives. If two different topologies both contain the same pairing, a copy of the pairing feature is created for each. This distinction is important for the prediction step, in which the predicted distribution over registers may depend on the topology. However, due to the partially independent energetic contributions of different features, models with a non-native topology that nonetheless includes a native strand pairing can in fact be informative about the correct register for that pairing; if a given register is energetically favorable even in models with incorrect global topology, it is more likely to be the native register. Therefore, in predicting which register is the native value for a pairing feature, we collect energy and feature frequency statistics both for models within the parent topology and for all models with the pairing. Beta contact features also give rise to these two classes of statistics.

We denote the i^th feature for a given protein by X_i, and its possible values by $x_i^1,x_i^2,\dots ,x_i^{m_i}$, with one of these, denoted by $x_i^{\ast }$, being the native one. A single model is represented by a string (x₁, x₂, …, x_k) of values, one for each feature from (X₁, X₂, …, X_k).

2.2 Native feature value prediction

In the second, prediction step of our method, we attempt to predict the native value of each feature using statistics, or “properties,” collected from an initial population of models generated by Rosetta. These statistics include the frequencies of different feature values and the energies of models which contain them.

Since the energy of a structure is a sum of physically local interactions, we hypothesized that native feature values would generally be associated with lower energies even when paired with non-native features. In order to take advantage of this association, the predictor incorporates two energy statistics associated with a feature value: minE is the minimum energy over all models with that feature value and lowE is the 10th percentile energy of models with that feature value. The expected value of lowE does not depend on the sample size, so this is a fairer measure than minE of energy for promising feature values which are sampled rarely and hence do not have a chance to appear in a low energy structure. Sampling frequency in the initial set of models is also informative about native feature values. The frequency of feature values for a feature X_i, denoted P_samp(X_i), can be regarded as an initial belief about which of { $x_i^1,x_i^2,\dots ,x_i^{m_i}$} is native; if a torsion or secondary structure feature value is sampled by Rosetta in p proportion of models, it has about p chance of being native (as illustrated in the central bars of Figure 2(b) in the next section). The predictor therefore incorporates sampling frequency as a predictive statistic. In addition to energy and frequency statistics, each feature class also brings with it one or more additional class-specific feature value properties. Many of these address common modeling pathologies. For topologies, contact order [13] proves very useful in this regard. Rosetta sampling is biased toward short-range pairings, as these are easier to form, and inclusion of the contact order gives the predictor the ability to reduce this bias.

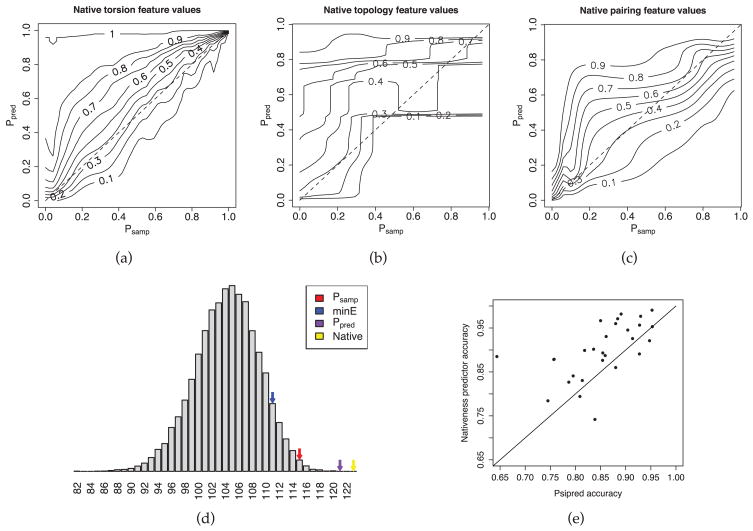
Figure 2. Predictor accuracy.

(a) Contours of the smoothed cumulative distribution function (CDF) of P_pred conditioned on P_samp for native torsion feature values. Examining the vertical strip above a value f of P_samp gives a portrait of the distribution of P_pred among those native feature values x^* with P_samp(x^*) near f; P_pred(x^*) can be expected to be less than the level labeled p for a fraction p of native torsion feature values with P_samp(x^*) = f. For instance, the median value of P_pred for feature values with P_samp(x^*) = f lies at the level labeled 0.5, and 20% of feature values with P_samp(x^*) = f will have P_pred(x^*) less than the level labeled 0.2. (b) Contours of the cdf for native topologies. The fit is noisy due to limited training data (one native topology per protein). (c) Contours of the cdf for native registers. (d) Number of native feature values for 1acf identified by several different feature value properties. Red arrow: number of native feature values identified by P_samp. Blue arrow: minE. Purple arrow: P_pred. Yellow arrow: native. Each column of the histogram shows the number of 1acf models from a pool of 20000 generated by Rosetta that had the indicated number of native torsion feature values. (e) Secondary structure predictor accuracy on 28-protein benchmark.

Our native feature value predictor takes the form of a modified logistic regression model, parametrized by a weight vector β with terms for each feature value property and each pairwise combination of properties (in order to take joint effects into account). The input to the predictor, for a feature value $x_i^j$ of feature X_i, is a vector of properties $\left[\mathit{minE}(x_i^j),\mathit{lowE}(x_i^j),P_{\mathit{samp}}(x_i^j),\dots \right]$ computed from those first-round models that have $X_i=x_i^j$. The output of the predictor is a new probability $P_{\mathit{pred}}(x_i^j)$. In advance of making predictions for any new target proteins, the predictor must be trained offline. This need only be done once. Afterward, the same predictor is used for all future targets. We use a training set of Rosetta models for 28 small alpha/beta proteins. For testing purposes, we employ leave-one-out training to train a separate predictor for each protein in the benchmark from data for the other proteins. Each of the five classes of features (torsion, secondary structure, topology, pairing, and contact) has a different set of associated statistics, so we train a different native feature value predictor for each class. The weight vector β is fitted to the training data by maximizing an objective function measuring the estimated effectiveness of the output of the native feature value predictor when used for Rosetta sampling. The maximization is performed with the standard BFGS variant of Newton’s method [14].

Brief descriptions of all of the feature value properties we use for native feature prediction are given in Table I, along with the predictive power of each by itself, as measured by the information gain per residue of a predictor including each property individually. The information gain of a predictor $P_{\mathit{pred}}^{\prime }$ for a particular feature type is estimated by

Table 1.

Properties used by the predictor, organized by feature class.

Feature value properties
Torsion meta-feature		Accuracy	IG
Psamp	Rosetta sampling rate	88.9%
lowE	10th percentile energy of models with the feature value	76.4%	0.016
minE	minimum energy of models with the feature value	87.7%	0.040
frag	rate of occurence of the feature value in the fragments	86.2%	0.039
loop	indicates either an E or O torsion feature value
Ppred	output of nativeness predictor	91.1%	0.081
Secondary structure meta-feature		Accuracy	IG
Psamp	Rosetta sampling rate	87.2%
lowE	10th percentile energy of models with the feature value	72.8%	0.018
minE	minimum energy of models with the feature value	86.2%	0.023
psipred	secondary structure prediction from Psipred	87.7%	0.034
jufo	secondary structure prediction from JUFO	80.9%	0.010
Ppred	output of nativeness predictor	91.8%	0.055
Topology meta-feature		Accuracy	IG
Psamp	Rosetta sampling rate	21.4%
lowE	10th percentile energy of models with the feature value	21.4%	0.032
minE	minimum energy of models with the feature value	46.4%	0.023
co	approximate contact order of a structure with the given topology
Ppred	output of nativeness predictor	60.7%	0.036
Register meta-feature		Accuracy	IG
Psamp	Rosetta sampling rate	54.0%
lowE	10th percentile energy of models with the feature value	44.7%	0.065
minE	minimum energy of models with the feature value	61.2%	0.057
bulge	indicates the presence of at least one beta bulge in the register
Ppred	output of nativeness predictor	57.6%	0.066
Contact meta-feature		Accuracy	IG
Psamp	Rosetta sampling rate	85.4%
lowE	10th percentile energy of models with the feature value	68.9%	0.002
edgedist	distance (in residue numbers) of a contact from either end of a pairing
oddpleat	indicates an anomaly in the pleating pattern
Ppred	output of nativeness predictor	88.3%	0.005

A native feature value is correctly identified by a property if the property is higher (or lower, in the case of energy properties) for the native feature value than for any other values of the associated feature. The “Accuracy” column indicates the percentage of features from our benchmark whose native values were correctly identified by each property. Accuracy values have been omitted for properties that are only informative in conjunction with others and so have no predictive value on their own. P_pred, the output of the native feature value predictor, is included here for comparison. Predictors were trained using leave-one-out training on the benchmark set of 28 proteins. Accuracy measures were computed on the left-out protein and averaged across the set. The “IG” column indicates the average information gain for a predictor $P_{\mathit{pred}}^{\prime }$ based only on P_samp and the indicated property, versus the baseline predictor P_samp, in units of bits per residue—total gain for features in each class for a given protein is divided by the number of residues in the protein. Results are averaged across proteins in our benchmark. Note that information gain can be large even for properties which do not yield accuracy increases if rare native feature values are often substantially enriched. The information gain given for P_pred is the gain when all properties are included in the predictor.

$$IG(P_{\mathit{pred}}^{\prime })=\frac{1}{\#\text{res}}\sum _{i=1}^n{log}_2(P_{\mathit{pred}}^{\prime }(x_i^{\ast })/P_{\mathit{samp}}(x_i^{\ast })),$$

where #res is the number of residues in the protein. Information gain is calculated with respect to the baseline predictor P_samp.

Rosetta’s prior beliefs P_samp (its feature sampling rates) are largely derived from the fragments, which are chosen using secondary structure predictors like Psipred [15], JUFO [16], and SAM [17] that only make use of sequence information. Native feature value prediction can be regarded as updating Rosetta’s prior beliefs by incorporating energy information to arrive at a more useful belief distribution. Details about the exact mathematical form of the native feature value predictor and the fitted weight vectors for each feature class can be found in the supplementary material (Section 5.1).

2.3 Resampling

In the third step, we use the predicted native feature values to guide a new round of Rosetta model generation. We use two approaches to guide Rosetta trajectories using the predicted feature values: (1) local secondary structure and torsional feature values are favored by selecting fragments for Rosetta model building that are enriched in predicted native feature values, and (2) predicted beta contact features are favored by enforcing the predicted non-local pairings using Rosetta broken chain folding [18].

An interesting and important question which must be resolved first is the ideal target sampling frequencies P_resamp for different feature values given the predicted probabilities P_pred that each is native. The optimal strategy can be determined by solving a constrained optimization problem (details in Section 5.2 of the supplementary material). Optimal strategies lie on a spectrum between two extremes. If only a single sample is permitted, the optimal strategy is to deterministically choose the single best guess for the native string—for each feature, the single value most likely to be native is chosen. If, on the other hand, sufficient samples are permitted to try every possible feature string at least once, the optimal strategy is to spread sampling as evenly as possible. The tension between concentration (placing all bets on the best guess) and diversification (spreading bets equally among all guesses) represents a typical tradeoff in resampling methods. For intermediate numbers of samples, neither extreme is very successful. The concentration strategy samples the same string over and over, so will very likely never find the native. The diversification strategy succeeds eventually, but requires enormous numbers of samples. The strategy of setting P_resamp equal to P_pred, similar in spirit to sampling from an approximation of the Boltzmann distribution, interpolates between these extremes by minimizing the expected log number of samples required to sample a single native string (proof in Section 5.2 of the supplementary material). For intermediate numbers of samples, it is far more successful than diversification. For instance, 77 distinct beta topologies for 1ctf appear with non-zero probability in P_samp, with the native topology sampled at rate 0.55%. A diversification strategy would place equal weight on all 77 topologies, resulting in a native sampling rate of 1/77 = 1.3%, a 2.4-fold increase in sampling efficiency. By contrast, P_pred places a probability of 73.7% on the native topology, a 135.2-fold increase. Clearly far fewer samples will be required to find the native structure if we use P_resamp = P_pred. In 1acf, P_samp contains 1233 distinct topologies and places probability 7.5% on the native one; diversification results in a 92.7-fold decrease in sampling efficiency, while setting P_resamp = P_pred results in a 5.3-fold increase to 39.5%.

2.3.1 Stochastic constraints

In order to effect a desired feature distribution, models are generated using different sets of beta contact constraints. Each Rosetta search trajectory for the target protein begins with a random draw of constraints. First a topology is drawn from the topology distribution in P_pred, then registers are drawn for each of the pairings that compose that topology, and finally the contacts to enforce are chosen for each register.

A residue–residue beta contact can be enforced by means of a rigid-body transformation constraint between the two residues [18] with an attendant chainbreak introduced in a nearby loop to allow for chain mobility. In general, b+1 constraints will be required to constrain a register with b bulges, one in each bulge-free segment.

Values are drawn from P_pred independently for each feature in order to promote feature recombination.

2.3.2 Fragment repicking

Rosetta sampling rates for torsion features are closely correlated with rates of occurrence of those features in the set of fragments used for Rosetta sampling. We can therefore change Rosetta sampling rates significantly by repacking fragments. If P_pred is our target distribution, with marginal distribution P_pred(X_i) for each torsion feature X_i, then we repick fragment files in such a way that the rate of occurrence of each value for feature X_i in the fragment file closely matches the rate given by P_pred(X_i). The fragment files are picked using a simple greedy quota-satisfaction method.

The fragment-picking method of distribution enforcement has several important advantages over the stochastic torsion constraint method used in our previous work [19]. First, it provides more fragments for rare native features, increasing the likelihood that one of them will be near the native geometry. Second, and most significantly, it sidesteps some of the inadequacies of the independence model. When the marginal distributions in P_pred are matched, correlations between nearby torsion features come along for free within the fragments. Rather than a combination of helical and strand residues, fragments will generally consist of all helical or all strand residues.

3 Results and Discussion

As described in detail in the Methods section, our approach has three steps. First, an initial set of Rosetta models are projected onto a discrete feature space to reduce the dimensionality of the sampling problem. Second, we estimate the probability that each feature value (secondary structure type, torsion angle bin, beta strand pairing, etc.) is present in the native structure. Third, we use these native feature probability distributions to guide another round of Rosetta structure prediction calculations into the regions of the energy landscape most likely to contain the native structure.

Each step in the approach can be evaluated independently. The first step is trivial since the feature values (torsion bins, beta contacts, etc) can be computed directly from the input structures. In the next two sections we evaluate (1) the extent to which native feature values can be predicted, and (2) the use of these predictions to improve conformational sampling close to the native structure. All results are from a benchmark set of 28 proteins ranging in size from 51 to 128 residues. The benchmark PDBs were chosen from a set in common use for Rosetta benchmarking in order to allow comparison of these methods to other Rosetta developments, such as recent work on linchpin features [12]. PDBs were selected to contain a variety of beta topologies, since beta sheet features are central to our method; our tests (discussed below) indicate that predictor weights are not heavily dependent on the choice of training set. In order to avoid testing on training data, we trained 28 separate sets of topology, pairing, contact, and torsion predictors, one for each test protein, from training models for the other 27 proteins.

3.1 Native feature value prediction accuracy

As discussed in Section 2.2, native torsion angle and secondary structure features are generally sampled with high frequency in standard Rosetta structure prediction runs. Combining sampling frequency with energy statistics associated with the feature values and the other feature value properties described in Table I yields quite accurate predictions of native feature values.

Since our goal in this paper is to use the predicted native feature value distributions to improve Rosetta sampling, it is most instructive to compare the probabilities predicted for native feature values with the frequencies observed for the native feature values in standard Rosetta runs: if the former are significantly greater than the latter, it should be possible to improve structure prediction by using the predicted frequencies to guide sampling. Contours of the cumulative distribution function (CDF) of P_pred conditioned on P_samp for native feature values are shown in Figure 2(a,b,c) for torsion, topology, and pairing features. Smoothed CDFs were fitted using kernel density estimation on features from the 28-protein benchmark, with leave-one-out training of P_pred. These plots demonstrate that P_pred is greater than P_samp for a majority of native feature values, particularly at lower values of P_samp, where the potential sampling gains are greatest. Potential sampling improvements are most evident for topology features. The height of the 0.7-level at P_samp = 0 shows that 30% of native topologies with P_samp ≈ 0 have P_pred higher than about 0.75.

As illustrated for protein 1acf in Figure 2(d), our native feature value predictor typically improves not only over the initial feature value frequencies, but also over predictions using energy information alone—the feature value for which P_pred is highest is more likely to be native than the feature value for which individual properties are highest (or lowest, in the case of energy-based properties). By incorporating multiple properties using fitted weights, the native feature value predictor P_pred performs better than any individual property.

In order to compare the accuracy of our native feature value predictor methodology against a standard benchmark, we specialized to secondary-structure prediction and trained a secondary structure predictor for comparison against Psipred [15], a standard sequence-based predictor, with accuracy defined as the fraction of residues for which the native value was given the highest probability. Psipred’s prediction was used as a feature value property in this predictor, so training could have recapitulated Psipred by placing all weight on this property to the exclusion of all others. Instead, it distributed weight between Psipred, P_samp, and various energy terms. Mean prediction accuracy is 88.4% on our benchmark set, as compared to 84.5% for Psipred (Figure 2(e)), echoing previous results indicating that low-resolution tertiary structure prediction can inform secondary structure prediction [20].

The total improvement in sampling using P_pred compared to P_samp can be measured using the sampling efficiency, the chance of producing an all-native feature string in a single Rosetta search trajectory. Under the assumption that features are independent, this can be estimated as the product of the probabilities of all native feature values. The ratio between the sampling efficiency of P_pred and of P_samp is also an estimate of the ratio between the number of samples required to find a native conformation under ordinary Rosetta sampling and under resampling with P_pred. Its logarithm to base 2 is an estimate of the total information gain of P_pred over P_samp for a single protein. The ratio of sampling efficiencies, estimated with leave-one-out training, is shown on a log scale for torsion features in Figure 3(a) and for topology and pairing features in Figure 3(b). The fully native torsion feature string had a median 11.3 times higher probability in P_pred than in P_samp; for seven proteins, the native string was more than 100 times as likely, implying that 100 times fewer samples would be required. These expected efficiency gains for torsion features are rough estimates, since some native torsion feature values are in fact highly correlated. The efficiency increases for beta topology features are more realistic, since there is only one topology feature per protein and hence no correlation effect. The hashed bars in Figure 3(b) indicate the additional expected efficiency gain from resampling of pairing features. The median sampling rate of native topologies under P_samp was 7.4%; under P_pred, it was 47.7%. P_pred further placed a median 2.25-fold higher joint probability on the co-occurence of all the native registers within the native topology.

Figure 3. Sampling efficiency gain.

Predicted gain in sampling efficiency (ratio between the likelihood of the native feature string under P_pred and under P_samp) by protein for (a) torsion features and (b) beta pairing features. Gain is given on a log scale. In (b), gray bars indicate sampling efficiency gain due to topology resampling and clear hashed bars indicate gain due to register resampling. The register bars begin where the topology bars end and occasionally go in the opposite direction, in which case gray and hashed overlap.

For several proteins, there were enough native values given lower probability by P_pred to outweigh the gains on other features; these are the ones for which the predicted sampling efficiency in Figure 3 is negative. The aggressiveness of our predictor training means a few cases like this are inevitable. The size of the gains in other cases comes at the expense of a few failures.

As a rough measure of the effect of different data sets on sampling efficiency, we performed 100 trials of dividing the benchmark in half and training torsion feature predictors on each half for testing on the other. Because this decreases training data significantly, some loss in predictor accuracy is to be expected; however, the change was not dramatic. Compared to leave-one-out training, total log sampling efficiency decreased by an average 10.3%, with a standard deviation of 12.1% of the mean. By inspection, predictor weights were very similar between the predictors trained on each half of the data set.

3.2 Resampling

For each of the 28 benchmark proteins, ranging in size from 51 to 128 residues, we generated 20000 first-round models. Fragments for each protein were repicked according to the output distribution of the torsion predictor. We then generated a resampled set of 10000 new models using the repicked fragments and stochastic beta constraints drawn from the output distributions of the topology, pairing, and contact predictors. We refer to this data set as frag+beta. At the same time, we generated a control set of 10000 regular Rosetta models for each protein. In order to pick apart the contributions of the repicked fragments and the stochastic constraints, we also generated data sets with repicked fragment files only (frag) and stochastic beta sheet constraints only (beta). Each Rosetta model takes on the order of one hour of CPU time to compute, so results were approximately normalized for CPU time by normalizing for number of samples (the discretization and prediction steps take a negligible amount of CPU time).

Rosetta predictions were generated according to methods similar to those used by Rosetta for CASP [21]. For each sampling round, we clustered the lowest-energy 10% of models and used as predictions the minimum-energy models from each of the five largest clusters. We noted both the RMSD of the first prediction (from the largest cluster) and the best (lowest RMSD) prediction. Because the energy function is not always accurate, we also noted the first percentile RMSD (1% RMSD), which measures the RMSD of the best conformations produced in a sampling round even if they are not identifiable by energy.

Full results of the resampling rounds are given in Table II. The RMSD of the first prediction improved by an average 1.77Å (from 6.52 Å to 4.75 Å), a significant decrease. A sign test on the null hypothesis that the RMSD of the first prediction does not improve under resampling yielded a p-value of 0.018. The RMSD of the best prediction improved by an average 0.42 Å (from 4.13 Å to 3.71 Å). The predicted sampling efficiency gain, shown in Figure 3, which measures the success of the predictors in identifying native feature values, was, as expected, a strong indicator of resampling success. For the 22 of 28 target proteins in which sampling gains were greater than 0.5 for both the torsion feature and beta sheet feature predictors, the RMSD of the first prediction improved by an average 2.23 Å; for the remaining 6 targets, the improvement was a negligible 0.06 Å. This result serves as confirmation that increased sampling of native features does indeed lead to lower RMSDs. However, for certain targets (such as 1mkyA) with high predicted gains in sampling efficiency, resampling yielded higher-RMSD predictions. This suggests room for improvement in the Rosetta broken chain folding protocol.

Table 2.

Results from a 28 protein benchmark.

Benchmark results
	RMSD of first pred.		RMSD of best pred.		1% RMSD		1% Energy
	Cont	Resamp	Cont	Resamp	Cont	Resamp	Cont	Frag	Resamp
1di2	6.03	4.26	1.50	3.58	2.65	2.16	− 138.68	−138.80	−132.45
1dtj	10.37	2.79	2.47	2.08	2.93	2.09	−144.73	−149.70	−145.95
1dcj	5.22	2.50	4.99	2.50	4.13	2.44	−131.90	−134.96	−122.43
1ogw	4.67	3.46	3.06	3.21	3.11	3.14	−152.25	−152.97	−146.72
2reb	1.33	1.27	0.74	1.07	1.23	2.04	−134.20	−134.89	−125.89
2tif	4.18	3.98	4.05	3.98	3.15	3.68	−118.01	−114.54	−105.25
1n0u	10.56	3.73	3.14	3.73	3.76	3.11	−129.61	−132.85	−127.63
1hz6A	3.15	3.50	3.12	2.53	2.41	2.08	−132.58	−135.33	−127.00
1mkyA	5.08	6.21	3.64	4.88	3.75	4.04	−152.32	−155.47	−145.47
1a19A	3.60	11.34	3.60	11.16	3.47	5.99	−176.04	−179.58	−168.98
1a68	15.01	7.76	8.80	6.94	6.37	6.80	−170.08	−177.38	−169.37
1acf	11.18	4.11	11.18	2.40	6.75	4.38	−233.91	−241.46	−222.27
1aiu	1.60	1.50	1.60	1.50	1.72	1.62	−208.86	−215.75	−205.03
1bm8	12.13	13.53	5.27	5.00	5.61	5.48	−197.36	−203.51	−189.84
1cc8A	3.94	4.63	2.52	3.52	2.73	2.60	−138.04	−139.63	−124.08
1bq9A	5.83	7.78	3.58	3.17	4.77	3.77	−83.03	−84.54	−82.59
1ctf	8.97	4.13	6.08	2.67	4.20	3.03	−141.52	−144.24	−135.21
1ig5A	3.73	2.82	3.73	2.71	3.01	2.32	−156.67	−159.15	−157.16
1iibA	10.12	4.66	3.54	4.56	3.19	3.54	−203.45	−204.30	−190.95
2ci2I	9.42	6.65	6.50	6.34	4.51	5.44	−123.48	−127.99	−111.98
2chf	3.96	3.06	3.08	3.06	3.59	3.00	−264.57	−266.76	−251.24
1opd	4.27	3.08	3.82	1.52	3.65	2.36	−166.97	−171.71	−165.78
1pgx	3.10	3.66	0.867	1.71	1.61	1.34	−118.16	−118.70	−111.27
1scjB	2.66	6.36	2.61	6.06	2.89	3.41	−132.38	−136.47	−124.93
1tig	11.66	4.17	11.14	3.06	3.91	3.04	−179.02	−179.10	−167.46
1ubi	9.23	3.81	3.27	3.56	3.02	2.75	−141.45	−143.57	−138.16
5croA	6.36	4.22	2.92	3.37	3.26	2.96	−110.43	−111.41	−107.56
4ubpA	5.20	4.10	4.92	4.10	4.26	4.41	−198.71	−201.91	−195.62
Mean	6.52	4.75	4.13	3.71	3.56	3.32	−156.37	−159.17	−149.94

The results in the initial four columns show the RMSD of the first and best-of-five predictions for control (control) and resampled (P_resamp) populations. Top five predictions were made by selecting the lowest-energy structures from the five largest clusters. In resampling, fragments were repicked according to the output of the torsion predictor. Beta topology, registers, and contacts were stochastically constrained according to the output of the beta sheet feature predictors. The results in the next two columns show first percentile RMSD for control and resampled populations. The final three columns show first percentile energy for these populations, in addition to models generated using repicked fragments but no beta constraints.

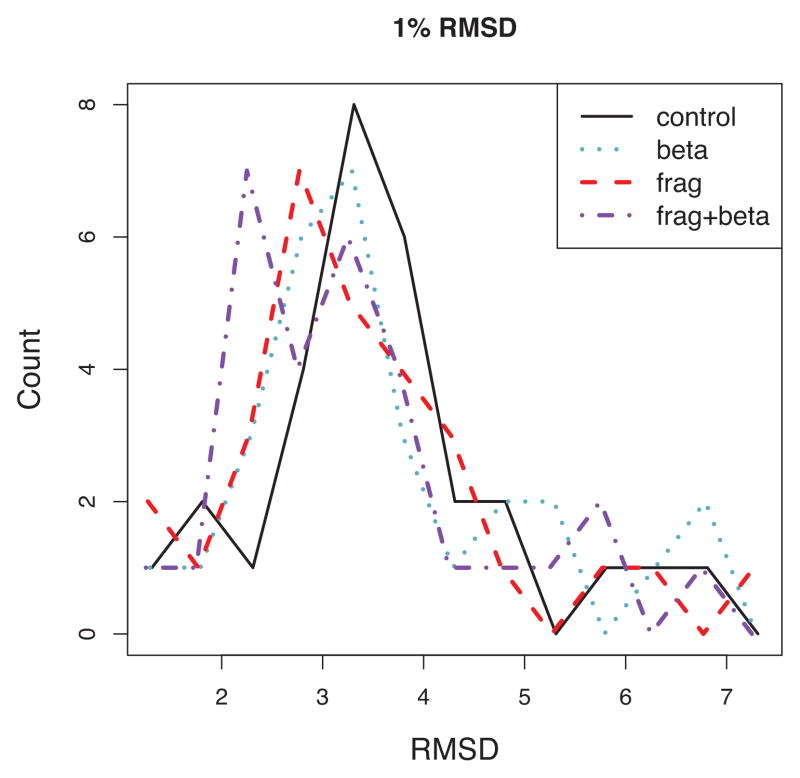
We can distinguish the contributions from fragment repicking and stochastic beta sheet constraints by examining the histogram of 1% RMSD over all targets for the various resampling methods (Figure 4). The modes of the distributions suggest the advances in frag (red) and beta (blue) are cumulative in frag+beta (purple); each component pushes the lower limit of achievable RMSDs a bit further.

Figure 4.

Histogram of 1^st percentile RMSD for a benchmark set of 28 alpha/beta proteins among models generated by fragment repicking (“frag”), beta topology resampling (“beta”) and both (“frag+beta”), compared with a control set with no constraints.

There were several clear cases where resampling recombined features to explore previously inaccessible regions of conformation space near the native structure. In the case of 1bq9, the native conformation has three beta pairings, each of which was present in the initial round of Rosetta search—one in 96.9% of models, one in 3.9%, and one in 0.5%—but all three were never present together in the same model. The minimum observed RMSD among the 20000 initial round models was 2.81 Å. In the resampling round, all three native pairings were present together in 61 of the 10000 models, a rate of 0.6%, and the minimum RMSD was 2.05 Å. Other proteins showed similar evidence of exploration in new, near-native regions. The minimum RMSD achieved in the resampling round was 1.14 Å for 1opd, as compared to 2.51 Å in the controls. The minimum RMSD for 1acf improved from 4.84 to 3.41; for 1ctf, from 3.15 Å to 2.39 Å; and for 1n0u, from 2.71 Å to 1.98 Å.

Features chosen for enrichment by the native feature value predictors are those associated with lower energies, so resampling should generally result in lower energies. The 1^st percentile energy (1% energy) of the control, frag, and P_resamp data sets are given in Table II. As expected, 1% energy is lower for 26 of 28 proteins in frag than in control, with a mean difference of −2.53. However, 1% energy is higher in P_resamp than in control, with a mean difference of 6.70. This suggests that Rosetta has a difficult time reaching low energies in broken-chain folding, even while achieving lower RMSDs, and further suggests room for improvement in the broken-chain folding protocol.

4 Conclusion

We have developed a new method for improving structure prediction methods like Rosetta by using information extracted from the discretized feature-space representation of an initial set of generated models to guide a new “re-sampling” round of search. The discretization step dramatically reduces the search space while preserving essential structural information, as in the reduction of conformation space to principal components of structural variation [22]. The prediction and resampling steps interpolate between the extremes of concentration-style methods, which exploit promising regions already explored, and genetic algorithms, which recombine structural features in an unguided fashion to explore new regions. There is also a close kinship between resampling methods and generalized ensemble methods such as multicanonical sampling [9] and the Wang-Landau algorithm [11], which use an initial round of sampling to modify the energy function in a subsequent round in order to yield a more advantageous sampling distribution (other methods such as metadynamics[10] use progressive modifications). However, the connection between energy and sampling distribution in Rosetta is complex; even if the energy function perfectly reflected physical free energy, Rosetta would not draw conformations from the Boltzmann distribution due to a non-uniform proposal distribution. Rather than adjust the energy function, we directly adjust the sampling distribution over features. In contrast to generalized ensemble methods, which perturb this distribution away from the canonical ensemble, we train a native feature value predictor to correct for the difference between the observed Rosetta sampling distribution and an estimate of the desired, canonical one.

In experiments, the predictive distribution P_pred showed significantly improved accuracy over the Rosetta sampling rate P_samp for all feature classes, though most significantly for beta topology. Resampling was quite successful on targets for which the lowest-energy models in the initial round were far from the lowest-RMSD models, suggesting our methods are resistant to energy function inaccuracies (details in Section 5.3 of the supplementary material). Several proteins also demonstrated clear evidence of recombining native feature values never observed together in the initial round in order to explore new regions of conformation space closer to the native. These results suggest the present method sits in a happy medium between conformation-space resampling methods, which focus on previously seen low-energy regions, and genetic algorithms, in which new feature combinations are explored in an unguided fashion. However, its relative advantages in practice must be tested by future side-by-side comparisons. The only similar Rosetta-based method [3] operates in a regime of many fewer samples than our method, so current results are incomparable.

Average improvements over plain Rosetta were significant. Our primary success measures, the RMSD of the first and best-of-five predictions, improved by an average 1.77Å and 0.42 Å, respectively. These results, though strong, may not reach the potential suggested by the accuracy of the native feature value predictors. Some targets with very high predicted gains in sampling efficiency showed moderate or nonexistent improvements under resampling. Improvements in the Rosetta broken chain folding protocol would likely have a significant effect on our method.

Although in this paper we concentrate our efforts on ab initio modeling, the application of our resampling method to homology modeling would be straightforward. The principle is very much the same—from an initial pool of candidate conformations, perhaps derived from a set of different templates, native-like feature values would be identified using predictors and enriched in a subsequent resampling round. Native feature value predictors for homology modeling might take into account feature value properties relating to template information, for instance the proportion of templates which have the feature value. New feature types specific to homology modeling might also be developed. One particularly promising possibility is to create a set of local alignment features, one for each residue (or gap-free block of residues). The alignment feature for a residue would take values in the possible template residues to which the target residue might be aligned. An initial sampling round in which models are generated for many possible alignments would give energy information that could be used in a predictor to identify the correct alignment. More generally, the core principle of our resampling work—that statistics derived from an initial sampling round are informative about local structural features—has the potential to be a powerful and broadly applicable tool in protein structure prediction.