Homogeneity computation: How interitem similarity in visual short-term memory alters recognition

Abstract

Visual short-term recognition memory for multiple stimuli is strongly influenced by the study items’ similarity to one another—that is, by their homogeneity. However, the mechanism responsible for this homogeneity effect has remained unclear. We evaluated competing explanations of this effect, using controlled sets of Gabor patches as study items and probe stimuli. Our results, based on recognition memory for spatial frequency, rule out the possibility that the homogeneity effect arises because similar study items are encoded and/or maintained with higher fidelity in memory than dissimilar study items are. Instead, our results support the hypothesis that the homogeneity effect reflects trial-by-trial comparisons of study items, which generate a homogeneity signal. This homogeneity signal modulates recognition performance through an adjustment of the subject’s decision criterion. Additionally, it seems the homogeneity signal is computed prior to the presentation of the probe stimulus, by evaluating the familiarity of each new stimulus with respect to the items already in memory. This suggests that recognition-like processes operate not only on the probe stimulus, but on study items as well.

Homogeneity computation: How interitem similarity in visual short-term memory alters recognition

Visual short-term memory (VSTM) actively maintains information about stimuli that recently disappeared from view. A new, incoming stimulus can automatically interact with items already in VSTM. These interactions, which are sensitive to a new stimulus’ similarity to the items in memory, can occur even when a new stimulus is task irrelevant (Grill-Spector, Henson, & Martin, 2006; Huang, Kahana, & Sekuler, 2009; Magnussen, 2000; Miller & Desimone, 1994). Here we tested competing accounts of how the similarity between multiple, sequentially presented items influences recognition performance.

Our test used a variant of Sternberg’s recognition paradigm (Sternberg, 1966). On each trial, a subject saw a sequence S of multiple stimuli (study items). Then, following a brief delay, a single probe stimulus p was presented, and the subject judged whether p replicated one of the studied items in S, responding YES if this was the case or NO otherwise. Since stimuli in S as well as p varied across trials, subjects had to maintain each of that trial’s items in memory, then compare p to these remembered items in order to make a recognition judgment.

The similarity of the probe to each of the study items strongly influences recognition, a phenomenon well explained by global matching models (Clark & Gronlund, 1996; Lamberts, Brockdorff, & Heit, 2003; Nosofsky, 1991; Zaki & Nosofsky, 2001). Such models postulate a global matching process whereby the probe, p, is compared to the memory representation of each study item, with each comparison yielding a scalar similarity signal. These separate signals are combined into a single familiarity signal, which is compared with a decision criterion to produce a recognition judgment. These models predict that the probability of a YES response—hereafter, P(YES)—will tend to be higher when p is simultaneously similar to multiple study items rather than to just one study item.

Studies of VSTM with the Sternberg paradigm have revealed another, independent effect of stimulus similarity that putatively reflects the similarity of the study items to one another (Kahana & Sekuler, 2002). Specifically, when the study items in VSTM are similar (i.e., “homogeneous”), subjects tend to make fewer false recognitions than standard similarity-based recognition models would predict. This effect of study-item similarity, which we will refer to as the homogeneity effect, has been confirmed with diverse stimuli, both visual (Kahana & Sekuler, 2002; Kahana, Zhou, Geller, & Sekuler, 2007; Nosofsky & Kantner, 2006; Yotsumoto, Kahana, Wilson, & Sekuler, 2007) and auditory (Visscher, Kaplan, Kahana, & Sekuler, 2007), and has been subjected to detailed, model-based analysis (Kahana & Sekuler, 2002; Kahana et al., 2007; Nosofsky & Kantner, 2006; Visscher et al., 2007). Despite the attention the homogeneity effect has attracted, its underlying mechanism has remained unclear. In this study, we empirically evaluated two competing explanations of the homogeneity effect.

The first of these possible explanations was suggested by behavioral and physiological evidence that the similarity of sequentially presented stimuli systematically influences the fidelity with which the stimuli are represented in memory (Bennett & Cortese, 1996; Magnussen, 2000; Magnussen, Greenlee, Asplund, & Dyrnes, 1991; Spitzer, Desimone, & Moran, 1988). According to this hypothesis, study items whose feature values are similar are each maintained in memory with higher fidelity than dissimilar study items would be. The heightened fidelity of memory representations would reduce the likelihood of a false recognition when the study items were highly similar to each other. We refer to this account of the homogeneity effect as the memory precision hypothesis.

A second hypothesis, proposed by Kahana and Sekuler (2002), asserts that the familiarity signal postulated by global matching models is supplemented by a second, homogeneity-dependent signal; and that recognition depends on both signals. To generate this second signal, scalar similarity values are obtained from pairwise comparisons of the study items. These interitem similarity values are then averaged to produce a scalar measure of homogeneity, which represents the degree of similarity of the study items in S to one another. This homogeneity signal subsequently influences the recognition judgment by modulating the familiarity signal. Nosofsky and Kantner (2006) proposed an alternative: that the homogeneity signal is used adaptively to adjust the decision criterion. This adjustment would offset the reduced accuracy in rejecting lures that global matching models predict for highly homogeneous study lists. As both these interpretations impute an independent computation of study set homogeneity, we refer to these two possibilities together as the homogeneity computation hypothesis.

To select between the two competing hypotheses, we used the Sternberg paradigm with lists of three study items. We identified critical configurations of study items and probes for which the two competing hypotheses make conflicting predictions. This allowed us to directly select between these hypotheses. The configurations we identified and the predictions of the two hypotheses are described next. As our empirical test required careful control over the similarity of each trial’s study items and their associated probes, we used Gabors—vertical sinusoidal luminance gratings windowed by a circular Gaussian—that could vary in spatial frequency. The metric properties of these stimuli provided a common measure with which to compare trials, and stimuli could be adjusted to control for differences in subjects’ perceptual performance (Zhou, Kahana, & Sekuler, 2004).

Experiment Design and Predictions

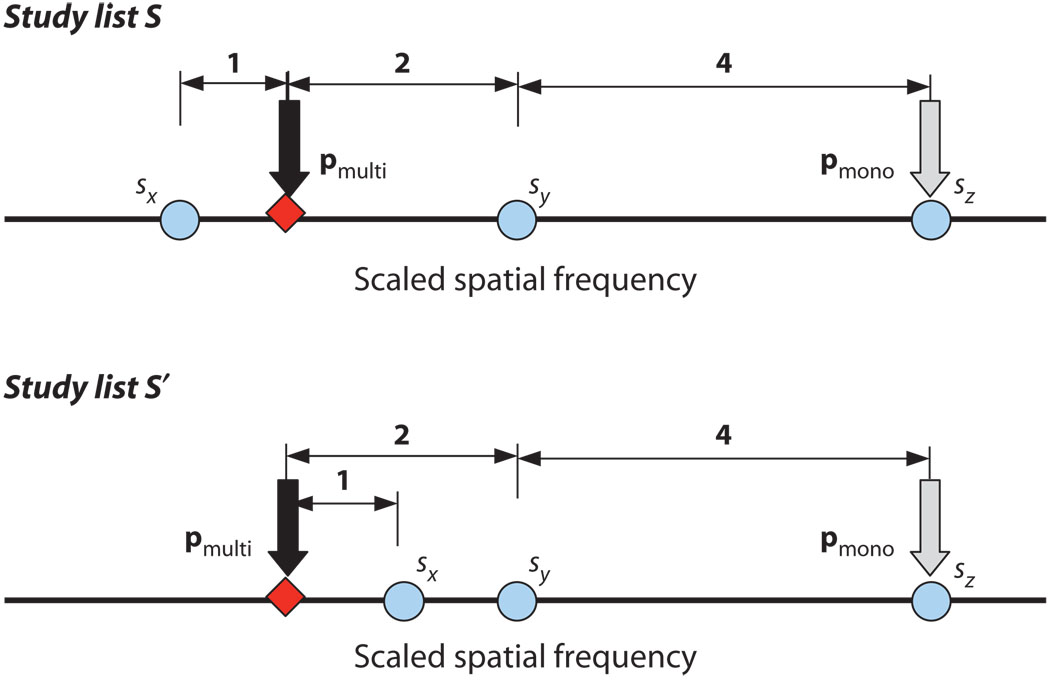
Figure 1 depicts schematically the design of the study lists and probe stimuli. The figure’s panels illustrate the relative spatial frequencies of the study items and the critical probes of interest for two types of study lists, S (upper panel) and S′ (lower panel). In each panel, the thick horizontal line represents spatial frequency scaled to units that are integer multiples of each subject’s discrimination threshold or just noticeable difference (JND; see the Method section for details of the scaling procedure). The three discs on each horizontal line represent the spatial frequencies of a trial’s study items, which we label s_x, s_y, and s_z. The thick vertical arrows indicate the spatial frequencies of the critical probes in relation to the study items. As is customary, we use the term target for a probe that matches one of the study items, and the term lure for a probe that does not. In Figure 1, a lure is represented by a diamond.

Figure 1.

The study lists S (upper panel) and S′ (lower panel) differ in their degrees of homogeneity. For both lists, the probe p_multi is similar to s_x and to s_y, and p_mono is very similar to s_z but far less similar to the other study items. Note that the similarity of p_multi and p_mono to each of the study items is maintained on both lists, for reasons explained in the text.

For purposes of describing the experiment design, we treat the absolute difference in scaled spatial frequency between two stimuli on this one-dimensional continuum as a measure of the perceptual similarity of these two stimuli via a nonlinear monotonic relationship (see Shepard, 1987). Note that the degree of similarity among study items in list S′ is greater than in S because the absolute difference (or distance) between s_x and s_y is smaller in S′ than in S. Consequently, the baseline prediction is that the homogeneity effect should have a larger influence on recognition judgments with study lists of type S′ than on lists of type S. To measure how recognition judgments are influenced by this difference in the two lists’ homogeneity values, we used two types of probes, referred to as MULTI-probes and MONO-probes. These are described next.

p_multi, the probe represented by the black arrows in both panels, is a lure that is 1 JND away from s_x, 2 JNDs from s_y, and 6 JNDs from s_z. This probe is referred to as a MULTI-probe since, in both types of study lists, it is at a relatively small distance from both s_x and s_y; that is, it is simultaneously similar to multiple study items. p_mono, the probe indicated by the gray arrow in both panels, is a target probe that replicates study stimulus s_z. This probe is referred to as a MONO-probe, since it is very similar to one of the study items but dissimilar to the other study items. As Figure 1 shows, the distance of p_mono to item s_z is zero, but its distance to the other two study items is relatively “large”—that is, at least 4 JNDs.

These interstimulus distances were chosen to ensure that p_multi’s distance to each study item in S would be preserved in the other type of list, S′ (see also Visscher et al., 2007). This constraint is approximately true for p_mono as well. In both S and S′ list types, p_mono is equally similar to s_y and s_z, but is extremely dissimilar from s_x (7 and 5 JND units different, respectively). So, in terms of perceptual similarity, p_mono is effectively equally similar to s_x on lists S and S′. Thus, the two list types are very different in their study items’ homogeneity, but the respective similarities between the probes and the study items are equivalent on both study lists. As a result, any differences in recognition performance between the two study lists would be attributable to the difference in the study lists’ homogeneity. The competing hypotheses introduced earlier make conflicting predictions on exactly how the recognition judgments might differ on the probes p_multi and p_mono. These predictions, which are the focus of our data analysis, are presented below. The probability that subjects respond YES on a particular condition [P(YES)] is the dependent variable.

The memory precision hypothesis asserts that the noise associated with a study item’s memory representation is reduced when that study item is very similar to other study items. If this were the case, the variance in the memory representations of s_x and s_y on list S′ should be lower than for the corresponding study items on list S.

The behavioral consequence of this “sharpening” in the memory representations with increased homogeneity is that lures should be endorsed less often on S′ than on S. Therefore, for the lure probe p_multi, this hypothesis predicts that

$$P(\text{YES}|{\mathbf{p}}_{\text{multi}},{\mathbf{S}}^{\prime })<P(\text{YES}|{\mathbf{p}}_{\text{multi}},\mathbf{S}).$$ (1)

Additionally, because memory representations for s_x and s_y are “sharper,” targets should be endorsed more often on S′ than on S. This hypothesis predicts no difference in the memory representation of s_z between the two lists, because study item s_z is dissimilar to s_x and s_y on both S and S′. However, there is the possibility that the memory representations of all the study items, including that of s_z, may be “sharpened” with an increase in the overall homogeneity of the study list. If so, p_mono should be deemed more similar to the memory representation of s_z on S′, hence predicting an increased value of P(YES). Combining these possibilities, the prediction for the target probe, p_mono, is

$$P(\text{YES}|{\mathbf{p}}_{\text{mono}},{\mathbf{S}}^{\prime })\ge P(\text{YES}|{\mathbf{p}}_{\text{mono}},\mathbf{S}).$$ (2)

Thus, the memory precision hypothesis predicts that if P(YES) did differ between S and S′, their differences should be of opposite sign for the two probe types.

The homogeneity computation hypothesis asserts that a computation of study-list homogeneity influences recognition judgments on all probes, and does so independently of the degree of similarity of the probe to the study items. Therefore, this hypothesis predicts that the change in P(YES) value on both p_multi and p_mono between the two lists would have the same sign; that is,

$$P(\text{YES}|{\mathbf{p}}_{\text{multi}},{\mathbf{S}}^{\prime })<P(\text{YES}|{\mathbf{p}}_{\text{multi}},\mathbf{S}),$$ (3A)

$$P(\text{YES}|{\mathbf{p}}_{\text{mono}},{\mathbf{S}}^{\prime })<P(\text{YES}|{\mathbf{p}}_{\text{mono}},\mathbf{S}).$$ (3B)

METHOD

Stimuli

Each Gabor stimulus subtended 5.6° at a viewing distance of 114 cm. A Gabor’s mean luminance was 50 cd/m², and its sinusoidal component had a peak contrast of 0.20. Different stimuli were generated by varying f, the spatial frequency of the Gabor’s sinusoidal component (described below). On each presentation of a stimulus, the phase of its sinusoidal component was varied randomly over the range [0, π/2], which forced subjects to make judgments on spatial frequency rather than on any local, retinotopic detail. Stimuli were generated and displayed using MATLAB and the Psychophysics Toolbox (Brainard, 1997) on a 32 cm × 24 cm CRT monitor with a screen resolution of 1,152 × 864 pixels.

Stimulus Scaling

The stimulus set for each subject was generated by a subject-specific scaling procedure (Zhou et al., 2004). A subject’s stimulus set consisted of spatial frequencies defined by the relation f = f₀(1 + K_subject)ⁿ where f₀ is a fixed base frequency. K_subject was the subject’s own Weber fraction providing an estimate of the smallest difference in spatial frequency that the subject discriminates correctly 85% of the time (i.e., the JND). The variable n defines the difference between f and f₀ in JND units. In our experiment, n assumed integer values in the range [−6, +7]. This defined a set of 14 stimuli for which spatial frequencies in stimulus pairs differed by an integer number of JND units. The base frequency was set to f₀ = 1.43 cycles/deg. To prevent subjects from memorizing these individual stimuli, a second set of 14 stimuli was generated with a slightly different base frequency obtained by incrementing f₀ by 0.5 JNDs. This “jittered” stimulus set was used on half the trials, chosen randomly. All stimuli on a particular trial were drawn from only one of these 2 stimulus sets. Our data analysis aggregated trials from the 2 stimulus sets.

Study Lists

Three types of study lists, each with three items, were used. Each list type was defined only by the absolute distances (in JND units) between study items. The two list types needed to select between the competing hypotheses are shown graphically in Figure 1. A third list type was introduced to keep subjects from adopting a strategy specifically tuned to these two lists. In this third list, the distance between s_x and s_y was constrained to be 4 JNDs, whereas the distance between s_y and s_z was 4 JNDs, as in the two lists shown in Figure 1.

Since differences in homogeneity among these three lists are governed by the distance between s_x and s_y, we adopt the following nomenclature: Lists in which the distance between s_x and s_y was 1 JND—that is, highly homogeneous lists—will be referred to as the HIGHHOM type; when the distance was 3 JNDs, as the MEDHOM type; and when 4 JNDs, as the LOWHOM type. The two study lists S and S′ shown in Figure 1 correspond to the MEDHOM and HIGHHOM list types, respectively. We will also refer to s_y as the MIDDLE study item, because it lies between the other two study items; s_x as the CLOSE study item due to its variable distance to MIDDLE; and s_z as the FAR study item due to its larger (and constant) distance of 4 JNDs to MIDDLE.

Individual lists for each of the list types were defined only by the absolute distances (in JND units) between the study items, as described above. We generated every triple of spatial frequencies that satisfied these list-specific constraints. These spatial frequency triples occurred with equal probability on trials of each of the list types. Hence, there was no preferred spatial frequency relationship between the CLOSE, MIDDLE, and FAR study items. For example, one list of the HIGHHOM type could be such that f_Close < f_Middle < f_Far, where f_i is the spatial frequency of stimulus i, and another could be such that f_Close > f_Middle > f_Far. Consequently, a stimulus having a particular spatial frequency could not be used to predict the list type being tested. The sequential presentation order of the CLOSE, MIDDLE, and FAR study items for each list type was randomized, with each of the six possible unique presentation orders being equally likely.

Probes

Each subject performed 1,620 trials (50% target trials, 50% lure trials). An equal number of trials (540) were devoted to each of the three list types, HIGHHOM, MEDHOM, and LOWHOM. Within each type of list, target and lure trials occurred with equal frequency. For each list type, the target probes matched the study item at each of the three serial positions on one third of the target trials. The target matching the FAR study item on lists HIGHHOM and MEDHOM was the critical probe p_mono. The lure set contained the critical probe p_multi. To prevent subjects from overtly using the perceived similarity of the study items as a cue to predict the “difficulty” in judging the probe, we ensured that the lure trials for each list type were (approximately) equivalent in difficulty. The set of possible lures was constrained to always lie within the range s_low − 3 and s_high + 3 on each list, where s_low is the study item having the lowest spatial frequency on a trial, and s_high is the one with higher spatial frequency. The lure set for each list type was divided equally into two groups: “hard” and “easy.” Lures in the “hard” group were 1 JND away from the nearest study-item on the list, and lures in the “easy” group had a distance >1 JND. On list types MEDHOM and HIGHHOM, the “hard” lures contained the MULTI-probe p_multi. This lure was presented on 90 trials for each of these two list types.

The ordering of list types across trials was randomized, and an approximately equal number of trials was presented for each type in each session of the five that comprised the experiment.

Subjects

Ten subjects (3 male, 7 female) recruited from the Brandeis University student population participated in the experiment. All subjects were paid and were between 18 and 23 years old (mean, 20 years). The experiment comprised five sessions of about 50 min each. Successive sessions were separated by at least 3 h; all sessions were completed within 2 weeks.

Procedure

Before the first experimental session, subjects underwent a vision screening that ensured that their Snellen acuity was normal or corrected-to-normal. After this screening, each subject’s Weber fraction for spatial frequency was estimated using an adaptive psychophysical procedure (Watson & Pelli, 1983). Figure 2 summarizes the sequence and timing of events on a trial in the main experiment. Trials were self-paced, with subjects pressing a key to start a trial. Subjects received 30 practice trials prior to each session, and were instructed to be accurate and quick with their responses.

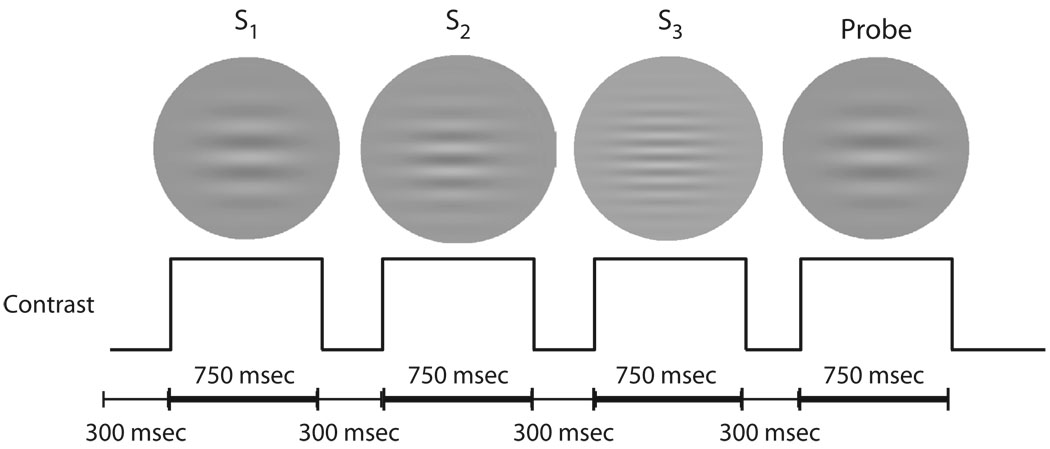
Figure 2.

The sequence and timing of events on a trial. On each trial of the experimental task, subjects first fixated on a “+” at the center of a computer screen for 750 msec. After this, each of the study items was presented for 750 msec with a 300-msec interval, during which a blank screen was presented. After the last item from a list was presented, a short beep sounded, and an ellipsis (…) was displayed for a 300-msec retention interval, indicating that the subject should wait for the probe. This was followed by the display of the probe for 750 msec. The trial ended when the subject responded by pressing either of two predesignated keys. Feedback was provided using distinctive tones that indicated whether their response had been correct or incorrect. Between trials, the screen indicated the percentage of correct trials.

RESULTS

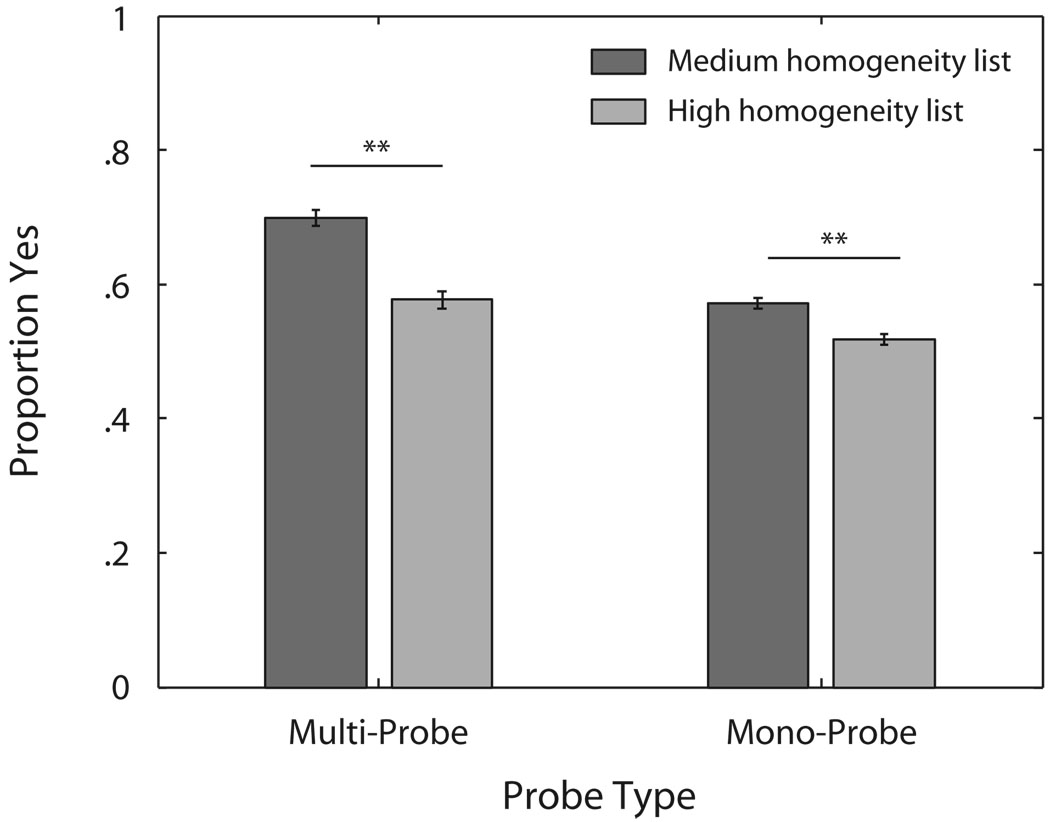
Figure 3 shows the mean P(YES) values with the MULTI-probe p_multi and the MONO-probe p_mono, on MEDHOM and on HIGHHOM lists. For the probe p_multi, subjects were significantly less likely to respond YES on the HIGHHOM list [mean P(YES) = .57] than on the MEDHOM list [mean P(YES) = .69] [t(9) = −4.99, p < .0001]. Furthermore, P(YES) for p_mono on the HIGHHOM list [mean P(YES) = .52] was significantly lower than on the MEDHOM list [mean P(YES) = .57], although by a smaller amount [t(9) = −3.29, p < .01]. Notably, only 1 subject failed to show both of these effects.

Figure 3.

P(YES) values for p_multi (left bars) and p_mono (right bars) for list types MEDHOM (dark bars) and HIGHHOM (lighter bars). Error bars are within-subjects standard errors of the means (Cousineau, 2005). **p < .01.

With increased list homogeneity, P(YES) values on both p_multi and p_mono were reduced. This rules out the possibility that the homogeneity effect arises solely from a change in the precision of representations in memory, as proposed by the memory precision hypothesis. This hypothesis predicted that the P(YES) value for p_multi would be lower on the HIGHHOM list as compared to the MEDHOM list (Equation 1), and that the P(YES) value for p_mono would be equal or higher on the HIGHHOM list as compared to the MEDHOM list (Equation 2). The first of these two predictions is satisfied but the second is not. The data are, however, consistent with the predictions of the homogeneity computation hypothesis, as described in Equations 3A and 3B.

Both the memory precision and homogeneity computation hypotheses explicitly assume that the similarity of the probe to each of the study items plays no role in the origin of the homogeneity effect. If the probe’s similarity to the study items were indeed entirely responsible for the homogeneity effect, then there should have been no difference in the P(YES) values for p_multi and p_mono between MEDHOM and HIGHHOM, as the similarity of these probes to each of the study items was equalized across MEDHOM and HIGHHOM.

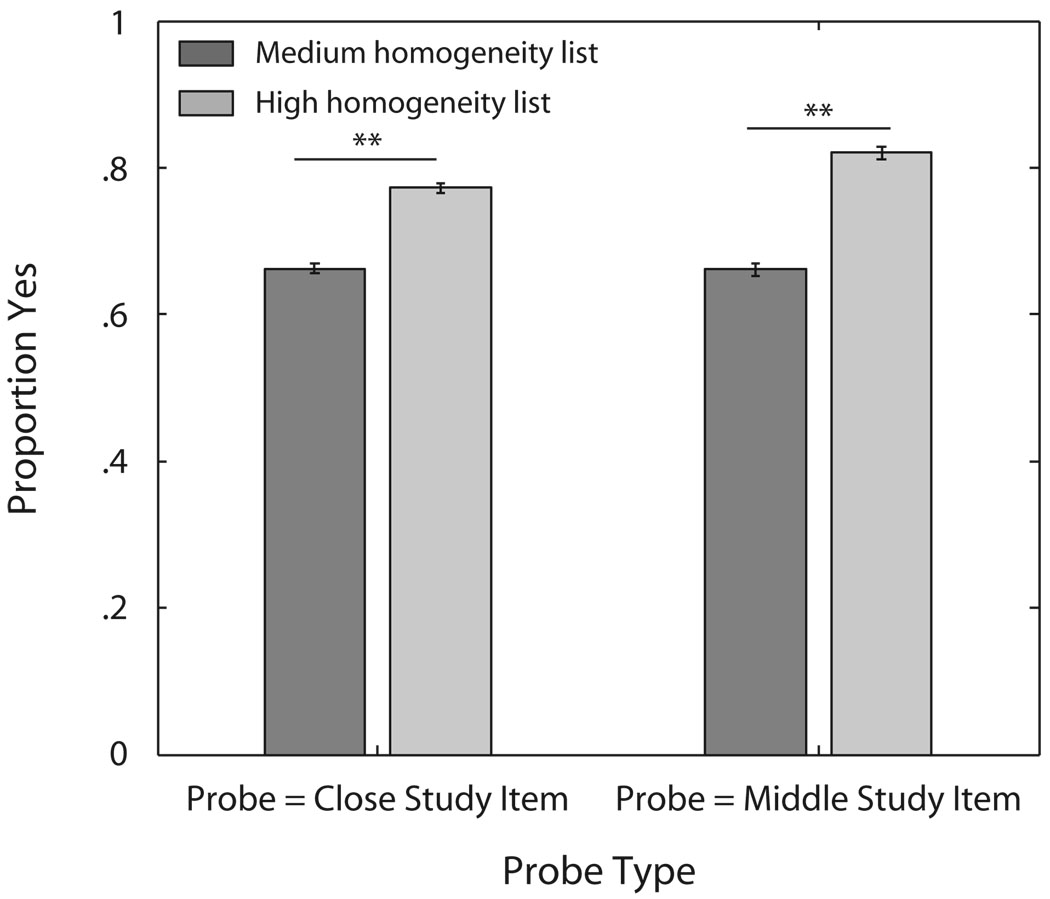
However, this prediction is clearly not true, as shown in Figure 3. To further confirm this reasoning, Figure 4 shows the P(YES) values for two probes whose similarity to the study items is not equalized across lists. Unlike p_mono and p_multi, the target that matched the CLOSE study item was more similar to MIDDLE on list HIGHHOM than on MEDHOM; and the target that matched the MIDDLE study item was more similar to CLOSE on list HIGHHOM than on MEDHOM. Consistent with the predictions of the global matching models, the P(YES) values for both these probes is indeed higher on HIGHHOM as compared to MEDHOM. These data show that the homogeneity effect cannot solely be due to the probe-item computations involved in evaluating the familiarity of the probe stimulus.

Figure 4.

P(YES) for target probes that match the CLOSE study item (left pair of bars) and for target probes that match the MIDDLE study item (right pair of bars). The target that matched the CLOSE study item produced P(YES) values that were significantly greater on HIGHHOM lists (M = .77) than on MEDHOM lists (M = .66) [t(9) = 8.69, p < .0001]. Similarly, the mean P(YES) value for the target matching the MIDDLE study item was significantly greater on HIGHHOM lists (M = .82) than the corresponding value on MEDHOM lists (M = .66) [t(9) = 9.40, p < .0001]. Error bars are within-subjects standard errors of the means (Cousineau, 2005). **p < .01.

DISCUSSION

Our data provide evidence for the homogeneity computation hypothesis (Kahana & Sekuler, 2002; Nosofsky & Kantner, 2006); specifically, the data support the idea that a comparison process operates on the similarities of the study items, generating a signal that influences recognition judgments independently of the probe’s similarity to the study items.

We must note one potential confound in the design of our experiment: On MEDHOM study lists, p_multi lies between the CLOSE and MIDDLE study items, but on HIGHHOM study lists, p_multi lies outside these two items (as shown in Figure 1). Even though p_multi has the same distance to the CLOSE, MIDDLE, and FAR study items on both lists, it might be that this difference in its location could have influenced subjects’ judgments, perhaps because of what have been called “edge effects” (Braida et al., 1984). As the CLOSE and FAR study items define the boundaries (“edges”) of the interval within which the spatial frequencies of all the study items lie on each trial, it is possible that there may have been differences in how subjects evaluated p_multi on the MEDHOM and HIGHHOM lists. However, the confound caused by such “edge effects” can be ruled out as they do not account for the observed difference in P(YES) for the probe p_mono between the MEDHOM and HIGHHOM lists, as this probe matches the FAR study item that lies on the “edge” of both lists.

Note that on both lists, P(YES) values for lure p_multi are higher than those for target p_mono. This pattern is not an anomaly but is predicted by global matching models. Since p_multi is very similar to multiple study items, the summation of these probe-item similarity values is predicted to produce a high P(YES) value. In contrast, even though p_mono is a target with a high similarity value to the FAR study item, it is nonetheless dissimilar to the other study items, so the summation of probe-item similarity values would not produce an increased familiarity of the probe.

In conclusion, the homogeneity computation hypothesis suggests that recognition actually begins prior to the presentation of the probe, with the comparison of the study items. We propose that the homogeneity signal is computed during the encoding of the study items. When the first item of the sequence, s₁, is seen, it is represented and held in memory. When the second item in the sequence, s₂, is presented, it is automatically compared with the memory representation of s₁ to produce a similarity signal, which is held in memory. When the third item, s₃, is presented, it is automatically compared with the memory representations of s₁ and s₂. The two resulting similarity signals are added to the first similarity signal, and the sum is scaled to produce a single value representing the study list’s degree of “homogeneity.” Note that with this process, the computation of the homogeneity signal would be completed with the presentation of the last study item. If this is indeed the case, the generation of the homogeneity signal would not depend strongly on the length of the delay between the presentation of the last study item and the probe. However, such a process imposes an additional memory requirement, that of maintaining the partially computed homogeneity signal until the final study item is presented. This value may be stored in memory buffers related to the monitoring of trial difficulty. It is remarkable that the homogeneity signal would be based on comparisons of this form. Since the number of interitem comparisons increases as a polynomial function of list length, assessing homogeneity could impose a greater computational burden than evaluating the familiarity of the probe.