Toward a Unified Timestamp with explicit precision

Abstract

Demographic and health surveillance (DS) systems monitor and document individual and group-level processes in well-defined populations over long periods of time. The resulting data are complex and inherently temporal. Established methods of storing and manipulating temporal data are unable to adequately address the challenges posed by these data. Building on existing standards, a temporal framework and notation are presented that are able to faithfully record all of the time-related information (or partial lack thereof) produced by surveillance systems. The Unified Timestamp isolates all of the inherent complexity of temporal data into a single data type and provides the foundation on which a Unified Timestamp class can be built. The Unified Timestamp accommodates both point- and interval-based time measures with arbitrary precision, including temporal sets. Arbitrary granularities and calendars are supported, and the Unified Timestamp is hierarchically organized, allowing it to represent an unlimited array of temporal entities.

1. Introduction

With this paper we wish to address two potentially quite different audiences. First, demographers who need to work with concepts of time, and second, programmers and database managers who have to design and maintain the systems that can store the resulting data and provide the functionally for their appropriate analysis. While we found it difficult in places to address both audiences equally, we see mutual understanding of the other party’s perspective, concerns and limitations as a precondition for any satisfying solutions. This paper wants to contribute to such mutual understanding.

Whereas we have conceived the representation of time described in this paper with a wider range of applications in mind, it is based largely on our experiences developing information systems for Demographic and Health Surveillance (here abbreviated DS rather than DHS, which might easily be mixed up with cross-sectional Demographic and Health Surveys).

DS systems (covered in detail in the following section) collect data continuously from defined populations over considerable periods³ of time. The conceptual framework common to most of them is described in Ngom et al. 2002. Both of us have worked on data management systems for several DS sites during the past ten years, and have contributed to INDEPTH, the International Network for the continuous Demographic Evaluation of Populations and Their Health in developing countries.

Despite recent efforts toward the specification of a standard data model for core entities of demographic surveillance (Benzler, Herbst, and MacLeod 1998, Wontuo, Kiwanuka, and Phillips 2002), member sites of INDEPTH still use a variety of data models, making comparisons of the data generated by different sites dependent on tedious ‘harmonization’ procedures.

Whereas the time dimension of DS data is central to their evaluation, there is no systematic and consistent management of temporal data in most sites. Even the standard data model mentioned above offers only rudimentary temporal support.

Partly in response to such limitations, Clark proposes an abstract, multi-purpose, flexible, self-documenting, temporal data model, the Structured Population Event History Register (SPEHR; Clark 2001, Clark 2002).

Recently, we have focused our design efforts on temporal aspects of data models appropriate for demographic surveillance.

DS systems describe the current state and past dynamics of the population under observation through various regularly calculated indicators. These are typically measures of incidence, point prevalence, and interval prevalence, as defined in subsection ‘Temporal indicators.’ All three indicators are inherently temporal, requiring the extraction of current states at specified timepoints, or the counts of events and summation of durations of exposure over specified intervals. Accordingly, the source data must be fully time-referenced, and flexible, consistent concepts, terminology and tools must be available to describe and handle time.

At a minimum, this requires support for valid time (see Jensen et al. 1998), i.e. the time over which a fact is true or an entity or condition persists in the modeled reality (see subsection ‘Valid time and transaction time’). A timestamp is a record of valid time, and a timestamped fact is a record consisting of the fact and its valid time. Although many data are not explicitly timestamped, all data are associated with a valid time, and it is the explicit representation and management of this valid time attribute that is the focus of this work.

1.1 Timestamp

The term ‘timestamp’ is commonly used to refer to only one type of time metric; namely the specification of timepoints with high precision. Because of the range of temporal types that we encounter in demographic surveillance and for the sake of generality, we prefer a broader meaning of ‘timestamp,’ described by Jensen (e.g. Jensen and Snodgrass 1996) and used in conceptual models like MADS (Spaccapietra, Parent, and Zimanyi 1998), to include points, intervals and sets of time.

Events are facts that are true at their corresponding valid timepoints, but false immediately before and after. Episodes are facts that are true during all and only their corresponding valid time intervals between a starting and ending event. And patterns are events or episodes that repeat either regularly (periodically) or irregularly as time progresses. We will carefully discuss these concepts and the accompanying terminology in section 5, after having shared our general understanding of time in section 4.

DS systems typically acquire data through interviews with members of the population (respondents) who are not always able to provide perfectly accurate information. In particular, the temporal accuracy and precision of the data are often poor resulting in the need to represent and store some measure of temporal uncertainty. We aim to faithfully store all of the temporal information provided by respondents including its precision and potentially its relationship(s) with other temporal data. Most of section 6 and 7 is devoted to this main objective. Correspondingly, we strive to remove all implicit temporal information from our temporal representation to avoid inadvertently storing more temporal information than the respondent is able to provide. A sample narrative is provided in section 3 to illustrate these points.

Moreover, during and after the faithful storage of data, we need to work with them in at least three general ways: validation, modification and calculation. Temporal data validation includes ensuring temporal entity integrity and temporal referential integrity. Temporal entity integrity refers to the condition where all facts are associated with well-formed timestamps; taking an interval for example, the start must precede the end. Temporal referential integrity adds time to the constraints governing foreign key relationships. (For a formal approach to temporal integrity constraints in the relational model see Date, Darwen, and Lorentzos 2002, chapters 11 and 12.)

Temporal data modification includes all of the procedures necessary to shift, split, and merge timestamps, and to transform their type, granularity, and precision. Calculation on temporal entities takes many forms including the arithmetic resulting in aggregate indicators for events and episodes. Most importantly, all calculations must have access to and utilize the varying precision of timestamps in a standardized way. Section 9 explores these topics in detail.

1.2 Unification

Consistent and accurate management of temporal data is a central requirement of DS systems. However, due to the lack of standardized, flexible and easy-to-use tools, a large number of unsatisfying ad hoc solutions has been built over the past decade. A serious problem with many of these is their inappropriate use of ‘timeless’ data models (within ‘conventional’ RDBMSs) that either ignore the temporal nature of the data they manage, or make implicit assumptions about it. As well as being fundamentally inappropriate, they often become very complicated and unwieldy. The proliferation of once-off approaches also leads to critical inconsistencies between (and even within) systems and to overall inefficiency, as solutions to similar problems are reinvented by each team. To begin addressing these problems, we have been working on the nature of time in demographic surveillance and presenting our progress to our colleagues at regular intervals (Benzler and Clark ​2000​, ​2001​, ​2002).

As part of this effort we have searched the literature for existing concepts and discovered a wide range of papers on temporal topics: The ISO 8601 (1988 and 2000) standard for representing time values (ISO 2000, summarized by Kuhn 2001), and various profiles (i.e. subsets) of the ISO 8601 standard such as suggestions concerning its implementation for Internet protocols (Klyne and Newman 2001) or websites (W3C; Wolf and Wicksteed 1997), are promoting uniform notations for determinate time. We will explain this standard in section 4 and extend it in sections 6 and following.

Temporal extensions to SQL3 (SQL 1999), the temporal DBMS TSQL2 (Snodgrass et al. 1998), the Consensus Glossary of temporal terminology (Jensen et al. 1998), and various sources describing temporal modeling and logic; for example Snodgrass’ book (Snodgrass 1999) and Lorentzos’ and Jensen’s theses (Lorentzos 1988, Jensen 2000), translate common understanding and usage of time into conceptual frameworks and experimental implementations. Others again present custom-built information systems with emphasis on temporal query support (e.g. Dorda, Gall, and Duftschmid 2002).

What strikes us most powerfully about this literature is its clear fragmentation into different camps. Many authors appear unaware of or unwilling to acknowledge the work of others leading to a lack of cohesiveness, minor variations on similar principles, and inconsistencies in various areas.

Given the lack of a clear core consensus around temporal topics, we feel justified in proposing our own temporal framework motivated strongly by the needs of demographic surveillance. We adhere to established models and standards where they exist and appear useful, and we add new concepts as necessary. Although we are inspired by demographic surveillance, our temporal framework is general and may be applied in other areas as well.

Here we present our underlying model of time, the terminology we have developed to describe and manipulate it, and finally a broad classification of timestamps. The overall aim is to isolate the inherent complexity of representing and manipulating time in a single place, a ‘Timestamp class’ that can be easily used within most available database management systems. The Timestamp class consists of a complex timestamp data type and methods necessary to manipulate it. Here we focus attention on the definition of concepts and terminology and the specification of the Timestamp class rather than the details of its implementation.

2. Demographic and health surveillance systems

A demographic surveillance system records information describing a well-defined population over a period of time. Geographical, genealogical and social criteria are used to define the population and to specify individual inclusion eligibility. Because individuals are mobile on both geographic and social dimensions, their eligibility often changes with time resulting in episodes during which they are included in the surveillance system. These episodes of eligibility are initiated and terminated through carefully defined events that correspond to the definition of the population under surveillance. Data describing the eligible individuals are collected on a continuous basis through repeated visits to their place(s) of residence.

Demographic and health surveillance (DS) systems are used to address a range of demographic, social and health-related questions. Of primary importance to most of these is the temporal or dynamic nature of the underlying processes and of the interconnected influences that various processes have on one another. Most DS systems minimally address fertility, mortality and the burden of disease, migration and social dynamics.

Questions relating to fertility minimally require recording the marital or conjugal status of women, pregnancy histories and registration of all births. Studying the burden of disease minimally requires the registration of all deaths and wherever possible their causes, for instance through verbal autopsies. It often also involves monitoring the general health of individuals in the population and particularly the degree to which they are debilitated by disease. Social dynamics are very complicated and are addressed to varying degrees by different DS systems. Most minimally monitor migration and household membership, and some also record marital histories. Monitoring migration is critical in an operational sense because residence within a geographic area is often one of the key eligibility requirements for individuals.

2.1 Temporal indicators

All of the indicators calculated from the data collected by a demographic surveillance system are defined over time. Some describe reality at a defined point in time whereas others reflect reality over a specified interval of time.

Measures of incidence reflect the number of events of a given type experienced by individuals divided by their total duration of exposure over a given interval of time.

Measures of prevalence reflect the proportion of individuals in a given state and can refer either to a specific timepoint or to an interval of time. Point-prevalence is the proportion of individuals in a given state at a given timepoint. Interval prevalence is the total time spent in a given state by all individuals in the population divided by their total time in an eligible state - the most common of which is simply ‘alive’ - over a given interval of time.

3. Time in natural language

References to past timepoints and intervals are omnipresent in the kind of information collected in DS systems. Structured questionnaires are full of date fields regarding the occurrence of specific events, e.g. dates of birth, death, marriage, divorce, or last change e.g. of residence, employer or contraceptive method. But also semi- or unstructured interviews yield an immense richness of narrative temporal information as the following example of a typical verbal autopsy demonstrates.

Verbal autopsies are usually conducted with the immediate caregivers of deceased persons by medically trained staff in order to establish causes and circumstances of death in the absence of well-maintained medical records and a reliable diagnosis.

This is the fictional transcript of an interview held with a neighbor’s son in May or June 2001 after the death of an elderly woman.

“Maria was a fairly old woman, born sometime in the 1920s. She had never been seriously ill until 3 or 4 years ago.

Then she developed sores on her legs that wouldn’t heal, and her eyesight deteriorated. She went to hospital for the first time in November 1998, where advanced Diabetes was diagnosed. She was treated and released after 2 weeks.

She was re-admitted on February 3^rd, 2000 at 5 PM in very bad condition and stayed in the hospital until February 29^th. During that time her left foot had to be amputated.

She was admitted again for 6 days in April. I saw her for the last time on Christmas Day 2000, and she was already blind by then. I heard she died 3 months later.”

We have highlighted the temporal information contained in this text, and will analyze it in detail when discussing the corresponding timestamps. But first we want to describe and comprehend time in a more general and abstract manner.

4. A model of time

When it comes to a definition of the phenomenon ‘time’, one is quickly drawn into philosophical discussions or theoretical physics well beyond the scope of what we want to present here. For the purposes of temporal data management in DS, and most other contexts, a much simpler model provides a workable foundation.

We consider the time domain to be universal, one-dimensional, dense and unbounded. This implies that a single time domain applies to all locations and a general notion of concurrence exists (universal), that its constituting elements are unambiguously identified, described and ordered by unique values of a single numeric attribute, which we call ‘position’ (one-dimensional), that it is possible at any level of resolution to define additional elements between two consecutive elements (dense), and that it is also always possible to define additional elements ‘before’ the first and ‘after’ the last element (unbounded).

We further assume that distances between the constituting elements of the time domain can be compared, making statements like “the time distance from A to B is twice that of B to C” meaningful.

4.1 TAI64 (and its limitations)

The standard that best reflects this model of time is TAI64 with its extensions, TAI64N and TAI64NA (Bernstein 2002). TAI64 defines a 64-bit integer format where each value identifies a particular SI second.⁴ The duration of SI seconds is defined through a count of state transitions of the cesium atom and understood as constant. Time is structured as a sequence of seconds anchored on the start of the year 1970 in the Gregorian calendar, when atomic time (TAI) became the international standard for real time. The standard defines 2⁶² seconds before the year 1970, and another 2⁶² from this epoch onward, thus covering a span of roughly 300 billion years, enough for most applications.

The extensions TAI64N and TAI64NA allow for finer time resolutions by referring to particular nanoseconds and attoseconds (10⁻¹⁸s), respectively, within a particular second.

While TAI64 is compellingly simple and consistent, it has to be extended not only with regard to fine resolutions, but in other ways as well. First, it is only concerned with timepoints, but a complete model of time needs to address the interrelation of timepoints and intervals as well. Most models conceive intervals as sets of consecutive timepoints. This creates the obvious transformation problem - assuming a dense time domain - that no amount of timepoints with a postulated duration of 0 can yield an interval with a duration larger than 0, and that even the shortest interval is a set of an infinite number of timepoints.

We bypass this problem by handling points and intervals as distinct types of time, which may define each other, but are not equivalent to sets or elements, respectively, of each other (see section 5).

Second, TAI64 does not address uncertainty with respect to time. We will explore this area later in section 6.

Third, it emphasizes regularity of time measurement. Human perception of time, however, is shaped by less regular astronomical phenomena, as discussed in the following subsection.

4.2 Date and time

In the beginning of this section we have described the time domain as one-dimensional. While this view may be shared by most scientists, most farmers (and hunters, gatherers and herdsmen) would add a second aspect and describe the time domain as cyclic. Through most of its history, mankind has experienced the influence of recurrent phenomena, namely the daily revolution of Earth and the yearly orbit of Earth around the sun, as much more powerful than any steady long-term progress. Fortunately so, as without these fundamental daily and yearly cycles we might never have developed the motivation and ability to count and measure time and calculate with it.

Unfortunately though, the duration of the astronomical year is not an integral multiple of the duration of the astronomical day, and all historic and contemporary calendars, developed around these common concepts of days, seasons and years, give proof of the fundamental difficulty of handling the asynchrony of these basic time granularities. (For a detailed account see Doggett 1992.)

The same applies to the third astronomical phenomenon widely reflected in calendars, the phases of the moon. Date calculations could have been so much simpler, if only years lasted an integral number of lunar cycles, and the latter of days. Unfortunately none of this is the case, and as a result the duration in days of both Month and Year varies in our established date management system, the Gregorian calendar.

Finer granularities, i.e. subdivisions of days into hours, minutes and seconds, have in the absence of reliable clocks during most of time-keeping history been calibrated through the observed position of the sun in the sky. Civil time, that is the shared notion of time in society, has been refined from humble beginnings to the sophisticated Mean Solar Time, and local times have been abstracted to a global time, UTC. (For a detailed account see McCarthy 1991 and Husfeld 1996.)

We are so accustomed to this established combination of the Gregorian calendar and UTC (albeit with its applicable zone and season-dependent offset, e.g. daylight saving Central European Summer Time), that we take its structure as time-immanent rather than perceiving it as an arbitrary representation projected onto the underlying time domain. But due to leap seconds, inserted or deleted at irregular intervals and at unpredictable times, no common granularity larger than the Second is of constant duration, and due to the protracted introduction of the Gregorian calendar and its leap year rules from the 17^th century onward, the same historic day may be associated with different dates, even within the western world. Astronomers (and others) use Julian day numbers (Meyer 2002) to avoid this confusion.

While the Gregorian calendar’s rules governing the mapping of year, month and day counts onto each other and - through its epoch, the start of year one - onto the underlying time domain, and the standard rules subdividing days into hours, minutes and seconds are deeply entrenched in the contemporary Western world, the same can not be said of their textual representation. The order of the elements of a timestamp changes from country to country and so do the characters separating and formatting them. This together with the widespread two-digit shorthand representation of the year part makes the textual representation of dates notoriously ambiguous, like ‘10/11/12’.

4.3 ISO 8601

ISO 8601 (ISO 2000) is an existing - and in theory widely accepted (see e.g. Galpin 1998) - standard regarding the ‘Representation of Dates and Times’. Surprisingly it is little adhered to in daily practice, even within the expert community. Most of the specific literature on temporal issues simply ignores it.

In contrast, we support ISO 8601 and have chosen to build our unified portable timestamp on this standard, even while we think that some of its provisions are sub-optimal. To accommodate several of the currently used notations, ISO 8601 sometimes allows alternative notations in parallel. Of these we have chosen to adhere to a particular subset, that is, its profile suggested by Klyne and Newman 2001.

Central attributes of a timestamp notation according to this profile are:

• - composed of 4-digit year, 2-digit month, 2-digit day, 2-digit hour (00 - 23), 2-digit minute, 2-digit second, and any number of digits for fractions of seconds, all in descending order from most significant (and least precise) to least significant (and most precise) element

• - the three date elements separated by hyphens (‘-’), the three time-of-day elements separated by colons (‘:’), and a decimal point between entire seconds and fractions of seconds

• - the date part and the time-of-day part separated either by ‘T’ or a space character

• - terminated by the time zone, either indicated by its offset from UTC, or, in case of UTC itself, by ‘Z’.

The timestamp of Maria’s second admission to hospital could thus be represented as ‘2000-02-03T16:58:27.9-04:00’, provided it had been recorded with such inappropriately high precision and attributed to the −4:00 time zone ranging from Canada to Chili.

Beside it being unambiguous, Kuhn 2001 states (among others) the following advantages of the ISO 8601 notation:

• - language independence

• - easy machine readability

• - constant string length (of expressions of equal granularity due to leading zeros)

• - equivalence of alphanumerical and chronological order.

All advantages apply to the profile suggested by Klyne and Newman as well, the latter three even more. Klyne and Newman state two more: simplicity and easy human readability.

The ISO 8601 standard allows the omission of trailing components, for ‘reduced precision’, without further developing this concept. Wolf and Wicksteed 1997 suggest a profile similar to Klyne and Newman, but allow six different ‘levels of granularity’, also implemented as omission of trailing components.

We adopt this modification, which enables us to represent the timestamp of Maria’s second hospital admission as ‘2000-02-03T16:58-04:00’, and her first one as ‘1998-11’.⁵

In addition to timepoints, ISO 8601 also covers periods and durations, that is, unanchored intervals. This section of the standard is even less adhered to (and not part of the profiles mentioned above), but we want to introduce its ‘Representation of duration of time’, because we will refer to it later.

ISO 8601 designates durations through the prefix ‘P’, followed by a string of counts and designators for the time units used, the basic format being ‘PnYnMnDTnHnMnS’. The standard gives the example of a duration of two years, 10 months, 15 days, 10 hours, 30 minutes and 20 seconds, represented as ‘P2Y10M15DT10H30M20S’. In our view this format has a number of disadvantages - limited human readability, introduction of an extended set of unit codes, ambiguity of the ‘M’ - and we wonder why the ISO 8601 date and time format, extended by the ‘P’-prefix has not been applied to durations as well. The example would then read ‘P0002-10-15T10:30:20’. We support ISO 8601’s provision, that the part between ‘P’ and ‘T’ can be omitted, if it is zero. Two minutes and 30 seconds would thus read ‘PT00:02:30’.

To conclude, ISO 8601 also allows a format including weeks, both for calendar weeks and durations. In both cases the designator ‘W’ is used, like in ‘2000-W07’⁵ or in ‘P2Y26W’.

5. Timestamped facts

Before we expand our ISO 8601 derived profile for timestamp notation further (in the next section), we want to explore its place in temporal information systems. C.J. Date states in his ‘Introduction to Database Systems’ (Date 2000): “A database is a collection of true propositions.” In our ever-changing world, we can assume that few propositions are always true, and that even these have not always been stored in a particular database. Thus all facts stored in a database have at least two aspects of temporal restriction: when they were true in the outside world, and when they were stored in the database or otherwise known to the system as being true.

5.1 Valid time and transaction time

Jensen and Snodgrass 1994, who have extensively studied the interdependencies of these two time dimensions, call them valid time (vt) and transaction time (tt), respectively. Thompson 1991 calls them logical time and physical time. Systems apt to manage both dimensions are termed ‘bitemporal’.

Different temporal constraints apply to vt, tt and their relationship depending on the relationship between the model and the modeled reality. In the typical case of a database retrospectively monitoring processes in the real world with less or more delay, vt must always be prior to tt. And as there is no future tt, there is also no future - and no present - vt. On the other hand, one can also conceptualize situations, where the database content precedes and determines the modeled reality, e.g. for complex process management in a chemical plant, or - less complex - payroll data to be implemented at month end. Such a database may well contain future vt. Any meaningful distinction between vt and tt is obviously only possible if the model is not considered part of the modeled reality.

In the DS databases we work with, vt invariably precedes tt, and deviating from a true bitemporal model where vt and tt are orthogonal dimensions of a static proposition, we implement tt as a meta timestamp wrapped around a time-dependent fact consisting of a static proposition associated with a vt timestamp.

While propositions in a database are always associated with vt and tt, one may not always chose to store this information, because it comes at a considerable cost in terms of complexity, storage capacity and performance. tt is often discarded altogether, where the re-constitution of a past database state is not regarded as important functionality. vt is usually selectively attributed to entities with a relevant history.

Timestamping, i.e. association of propositions with vt or tt, can occur at different levels, and not always explicitly. Implicit timestamping is common at database and - here we focus on relational databases - table level, for instance where a database or table has been created and filled at a particular point in time, or is meant to represent a past snapshot or the current state. Explicit timestamping is rather implemented at record (tuple) or even attribute level. Conceptually both are equivalent, but databases with attribute-timestamping are not normalized. Normalization would require such tuples to be broken up into synchronic entities, i.e. into smaller tuples, where one timestamp applies to all attributes. Date, Darwen, and Lorentzos 2002 suggest a process of vertical decomposition resulting in a sixth Normal Form (6NF). In terms of SQL, delete and insert statements are best implemented with tt timestamps at tuple level, while attribute level tt timestamps are the most efficient way to deal with update statements.

Ignoring differences in their precision for now, timestamps can be classified into four types: durations (that is, unanchored intervals), timepoints, (anchored) intervals, and sets of points or intervals. Intervals are determined by two timepoints, or one timepoint and a duration. Valid time sets⁶ must not contain intervals that overlap or meet (in the sense of Allen’s operators; Allen 1983), or timepoints that are equal. Durations are timestamps themselves, but also attributes of timestamps. By definition, timepoints have a duration of 0, intervals a duration > 0, and valid time sets a duration, which is the sum of the durations of its elements (0 in the case of timepoint sets).

5.2 Event, episode, pattern

The type of a timestamped fact is determined by its vt timestamp. Facts are events if timestamped by timepoints, episodes if timestamped by intervals (or durations), and patterns if timestamped by time sets.

We are aware that some authors use the concept ‘event’ in a more general way, embracing all kinds of timestamped facts. Allen 1994 for instance calls events ‘relevant patterns of change’, which ‘may be instantaneous’, but mostly ‘occur over an interval of time’. However, we believe that the distinction between event, episode and pattern enhances our ability to communicate about the temporal dimension of objects.

In the same way as two timepoints determine an interval, episodes are determined by two events, one start event and one end event. For episodes, which were ongoing at the time of their last observation, a temporary end event ‘last observation’ is used, which at the time of a future observation is replaced by either another (later) ‘last observation’ or a definite end event. Thus we take the unavoidable delay between events occurring in the real world and being known to the database into account and restrict the vt of episodes to the interval for which we have explicit knowledge rather than making implicit assumptions.

Additional events can be associated with episodes or patterns, for instance as transition events between states. In our example, the episode of Maria’s second stay in hospital is subdivided in a pre- and a post-operative phase by the event of her foot amputation.

Finally, different episodes can share events. The following examples illustrate the two forms of event-sharing we distinguish:

• - Maria’s foot amputation is at the same time the end event of her pre- and the start event of her post-operative phase in hospital.

• - Her release on 2000-02-29 is at the same time the end event of her second hospital stay and of its post-operative phase.

Our terminology stems from the conventional representation of temporal relationships in diagrams, where the time scale is associated with the horizontal axis. There, consecutive intervals would be drawn next to each other, from left to right, and concurrent ones on top of each other. Thus, if two consecutive episodes share the same event, we call it a horizontally shared event. And if two episodes, of which one is a sub-episode of the other, share the same event, we call it a vertically shared event.

6. Temporal primitives

In this and the following section we introduce our concepts and suggest a textual and - as a precursor to a database implementation - relational representation. We start with simply structured timestamp types, so-called ‘temporal primitives’, and progress to more complex types that can be built from these primitives. The textual representation conforms to the ISO 8601 standard wherever possible, and extends it where we see strong reasons to go beyond its limitations. A summary table of this is provided in the ‘Conclusions’ section.

For most applications, including DS, a set of railway tracks stacked on top of each other provides a good illustration of a working model of time. The multilayered stack of tracks represents a calendar in which each track represents one defined granularity. Each track is structured by sleepers (or ties), which support it at more or less regular intervals. However, the distance between sleepers varies widely from track to track. Occasionally the sleepers of two or more tracks are exactly on top of each other, but most sleepers on the tracks with ‘fine’ spacing have no equivalent on the tracks with ‘coarse’ spacing.

On each track all sleepers are uniquely labeled (or at least countable starting with an ‘epoch’ sleeper, which anchors the system) and the only way to indicate a particular position on the rail is by referring to the label (or count) of the preceding or the nearest sleeper. Distances between positions are indicated by the count of sleepers between them.

Our interpretation of the sections between the sleepers - e.g. as years, seconds, or days - defines the granularity of the track. In our model of time we call the sleepers ticks, the sections of the rail between them granules, and arbitrary positions on the rail instants.

6.1 Textual representation

A serious limitation of ISO 8601 is that it does not distinguish between tick, granule and instant. The same literal, e.g. ‘2000-02-03T16:58-04:00’, can represent the tick that starts this particular minute, or the minute as such (the granule), or a timepoint at an undefined position within the minute (an instant).

The first step toward a comprehensive timestamp notation is to distinguish these three temporal primitives, tick, granule and granule instant⁷. We propose to reserve the original ISO 8601 notation, which we call the ‘core’, for instants, because this is by far the most commonly used type. As the width of the sleepers in our model is infinitely small compared to the distance between them, only an infinitely small proportion (indeed none) of randomly distributed events falls exactly on a tick. While instants are thus appropriate timestamps for ‘naturally occurring’ events beyond a passive observer’s control, ticks are needed as timestamps for events that are actively positioned⁸, usually along an existing temporal grid, for instance the start of an insurance policy at noon exactly.

For the designation of ticks, we propose the introduction of a tick-prefix, and our intuitive choice is the exclamation mark (‘!’). ‘!2000-02-03T16:58Z’⁹ would thus indicate the tick starting this particular minute, while ‘2000-02-03T16:58Z’ would indicate an instant at an undefined position between ‘!2000-02-03T16:58Z’ and ‘!2000-02-03T16:59Z’.

According to widely adopted conventions, we use a hyphen with spaces (‘ - ’) instead of the solidus (‘/’) introduced for this purpose by ISO 8601, to connect the start and end points of intervals, and we use square brackets (‘[‘, ’]’) and rounded parentheses (‘(‘, ’)’), respectively, to indicate whether these timepoints are included in or excluded from the interval. Granules are so-called closed-open¹⁰ intervals. They include their starting tick, but not the consecutive one, because the latter is already part of the consecutive granule, and granules of the same granularity must not overlap, not even at a single point.

The complete (and redundant) textual representation for the granule (of ‘minute’ granularity) started by ‘!2000-02-03T16:58Z’ is thus ‘[!2000-02-03T16:58Z - !2000-02-03T16:59Z)’, but we would also allow (and actually prefer) the shorter notation ‘[2000-02-03T16:58Z)’.

We apply the convention of expressing different granularities or levels of precision by adding or omitting trailing components to all temporal primitives. The instant of Maria’s first hospital admission is thus ‘1998-11Z’, which is a timepoint at an undefined position between the ticks ‘!1998-11Z’ and ‘!1998-12Z’, and thus within the granule ‘[1998-11Z)’.

It is obvious that ‘1998-11Z’, ‘1998-11-01Z’ and ‘1998-11-01T00:00:00.000Z’ are different instants. They are timepoints at an undefined position in the granules ‘[1998-11Z)’, ‘[1998-11-01Z)’ and ‘[1998-11-01T00:00:00.000Z)’, which are different as well, spanning a month, a day, and a millisecond, respectively.

The ticks ‘!1998-11Z’, ‘!1998-11-01Z’ and ‘!1998-11-01T00:00:00.000Z’ are chronologically identical. They all indicate the same timepoint with the same - infinite - precision. However, they belong to different granularities and thus have different successors: ‘!1998-12Z’, ‘!1998-11-02Z’ and ‘!1998-11-01T00:00:00.001Z’.

As stated earlier, we apply time zone designators to all anchored timestamps, in deviation from ISO 8601 and its profiles, which apply them to times, but not to dates. Given that ticks of different granularities have the same infinite precision and may be chronologically identical, it would not be consistent to specify a time zone for some but not for all. As other timestamp types are derived from ticks, this holds in general. Only where time zone information is irrelevant, because all temporal data apply to the same time zone, it may be omitted. We assume this from here onward for the sake of simplicity.

Where calendars other than the Gregorian calendar are used, this has to be indicated by an appropriate code, e.g. ‘JC’ for dates following the rules of the Julian calendar. The tick ‘JC !1582-10-04’ is thus chronologically identical with ‘GC !1582-10-14’ or ‘JD !2299160’ (JD = Julian day number).¹¹ The code ‘GC’ for the (proleptic) Gregorian calendar is regarded as the default and thus may be omitted.

In summary, the textual representation for instants is the ISO 8601 core, for ticks the core with a tick-prefix, and for granules with interval bracketing.

6.2 Timestamp attributes

Four attributes can be derived from this notation, which unambiguously identify each temporal primitive. Two of these depend only on the core literal: granularity and position, i.e. the count of ticks of the given granularity since a defined epoch. The other two depend on the type of the temporal primitive: duration, which (in terms of the given granularity) is 0 for ticks and instants, and 1 for granules, and precision, which (again in terms of the given granularity) is infinite for ticks and granules, and 1 for instants.

There is an important distinction to be made between duration as a timestamp’s attribute, which is merely a numeric value, and duration as a type of timestamp, that is, an unanchored interval. The latter has all the attributes of a timestamp - granularity, duration, precision - except position, and it has a defined textual representation.

As a means for calculating precision and the related concept of uncertainty, we introduce the notion of a ‘base timestamp’. Each timestamp has a base timestamp, which is (for temporal primitives except durations) defined as the aggregate of all times that are possibly covered by the index timestamp. The base timestamp of precise timestamps like ticks or granules is equal to the index timestamp. The base timestamp of an instant is the granule with the same granularity and position.

As a next step, we describe uncertainty as the excess of the base timestamp over the index timestamp. It can be calculated as the duration of the base timestamp minus the duration of the index timestamp, in units of their common granularity. Finally, we calculate a timestamp’s precision as the reciprocal of its uncertainty.¹² For technical reasons we prefer storing the attribute uncertainty (a non-negative integer value in most common situations) instead of the attribute precision (often a fraction or infinite).

Extending the collection of timestamps at our disposal, we propose a fourth and fifth temporal primitive, the tixel and tixel instant, respectively. ‘Tixel’ stands for ‘tick element’ (similar to ‘pixel’ for ‘picture element’) and designates the section of the timeline that shares the same nearest tick (in the given granularity). Compared to granules - sections, which share the same preceding tick - tixels are left-shifted by half a granule. Like granules they have a duration of 1 and infinite precision. Tixel is an abstract type insofar as we do not know of any established direct application, that is, other than defining the tixel instant. Tixel instants are for tixels, what granule instants are for granules: timepoints at an undefined position within. Like granule instants they have duration 0 and precision 1.

In order to distinguish tixels and tixel instants from granules and granule instants, a fifth, boolean attribute is needed, which is true for the former and false for the latter, and which we call ‘isShifted’.

Tixels and tixel instants are an important addition to the collection of temporal primitives, because they capture a common usage of time, particularly in ‘hour’ granularity, which cannot easily be implemented with the other types. The time of Maria’s second hospital admission for instance, expressed as ‘on February 3^rd, 2000 at 5 PM’ does not mean, between ‘!2000-02-03T17’ and ‘!2000-02-03T18’, but closer to ‘!2000-02-03T17’ than to ‘!2000-02-03T16’ or ‘!2000-02-03T18’.

They are indispensable again, when typical durations or relative times are expressed. Maria’s death ‘3 months later’ for instance does not mean, ‘between exactly 3 and 4 months later’, but ‘closer to 3 months later than to 2 months later or to 4 months later’.

Our intuitive choice for a tixel-prefix is the solidus (‘/’). It indicates the half-a-granule left-shift. ‘/[2000-02-03T17)’ is the textual representation of the tixel around February 3rd, 2000, 5 PM, and ‘/2000-02-03T17’ is the corresponding tixel instant.

If temporal primitives are defined as timestamps that are fully described by the five attributes granularity, position, duration, uncertainty, and isShifted, then sequences and sequence instants are the last anchored timestamp types to be introduced here.

Granule sequences are intervals of consecutive granules, e.g. three consecutive months starting with November 1998. They have the same granularity, position and precision as their starting granule, and an integer duration > 1. Our example has the duration 3 and the textual representation ‘[!1998-11 - !1999-02)’. Its tuple representation (i.e. its values for the five attributes stated above, in that order) is {month, n, 3, 0, false}, where n is the count of elapsed months since some epoch according to the underlying calendar. (We spared the effort of setting the epoch and calculating n.)

Accordingly, tixel sequences are intervals of consecutive tixels, e.g. the five minutes ‘/[!2000-02-03T16:58 - !2000-02-03T17:03)’, or alternatively {minute, n, 5, 0, true}. Like tixels they would mainly serve for defining their corresponding instant.

In the same way as granule instants are timepoints at an undefined position within a confining granule, other instants can be confined by sequences. The granule-sequence instant ‘somewhen in the three-month interval starting with November 1998’ for instance is confined in ‘[!1998-11 - !1999-02)’. It has the same granularity and position as its confining sequence (which is also its base timestamp), but - being an instant - it has duration 0. As the duration of its base timestamp is 3, its uncertainty is 3 as well (and its precision 3⁻¹, i.e. 1/3).

The textual representation of sequence instants is derived from that of their base timestamps. The distinction is made through a colon (‘:’) replacing the hyphen as a connector of the start and end tick. Our previous example th us reads as ‘[!1998-11 : !1999-02)’ (tuple representation: {month, n, 0, 3, false}), and ‘/[!2000-02-03T16:58 :!2000-02-03T17:03)’ is a tixel-sequence instant of ‘minute’ granularity, duration 0 and uncertainty 5.

While timepoints without position are meaningless, intervals without position are durations. The duration ‘one year’ for instance is a ‘floating’ granule (or tixel) represented by the tuple {year, null, 1, 0, undefined} and the literal ‘P!0001’. The positionless equivalents of granule (or tixel) sequences are durations with integer duration > 1. Together they are the eighth temporal primitive; if we postulate their start points to be ticks, their end points are ticks as well. Thus we call them tick durations.

If a duration’s end point were a granule or tixel instant, respectively, its ‘real’ duration would be less precisely known. A typical example for the former, the granule instant duration, is a person’s age. ‘78 years old’ for instance means ‘between exactly 78 and 79 years old’. It is represented by the tuple {year, null, 78, 1, false} and the literal ‘P0078’. We already gave an example for the latter, the tenth and final temporal primitive: Maria’s death ‘3 months later’, where ‘3 months’ is a tixel instant duration ({month, null, 3, 1, true}, ‘P/0000-03’).

For durations, the base timestamp, which is a duration itself, is defined as the aggregate of all times that are possibly covered by the index timestamp’s end point, assuming a fixed start point (or vice versa). From this we derive an uncertainty of 1 for the two preceding examples, and of 2 for an even less precise duration like ‘two or three weeks’ ({week, null, 2, 2, true}, ‘P/[!0000-W02 : !0000-W04)’.

7. Complex timestamps

All timestamps that cannot be fully specified by any value combination of the five attributes introduced above can still be expressed as a combination of temporal primitives. We call them ‘complex timestamps’.

Here, the index timestamp is defined by a set of defining or constituting timestamps, each specified by one of six possible roles that it may have in relation to the index timestamp. Three of these roles are borrowed from Allen’s operators: starts, ends¹³ and contains; the fourth, centers, is a prerequisite for tixels, the fifth, anchors, allows for ‘relative’ time, and the sixth, isElement, the construction of sets.

This approach can also be applied to temporal primitives as an alternative way to expressing them, and we want to illustrate this with some of the temporal primitives already introduced before.

Granule sequences can be defined by their starting and ending ticks. ‘[!1998-11 - !1999-02)’ is (in an ‘extended’ tuple representation) thus {{month, n, 0, 0, false} starts, {month, n+3, 0, 0, false} ends}. And instants can be defined by their confining granules, e.g. ‘1998-11’ as {{month, n, 1, 0, false} contains}.

7.1 Relational representation

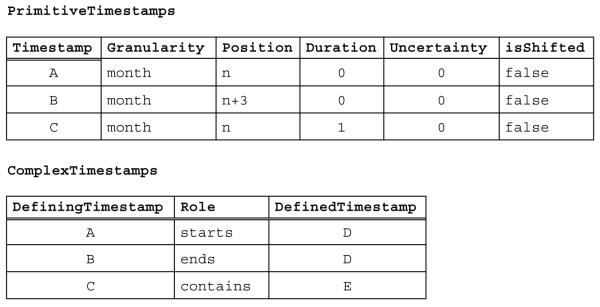
The nested structure of the list syntax used here for complex timestamps is best illustrated by one of its possible implementations in an RDBMS (see figure 1). This design stores the five attributes of temporal primitives in one table, called PrimitiveTimestamps, and the components of complex timestamps (and their roles) in a second table, called ComplexTimestamps.

Figure 1.

Each record in the first table needs a unique identifier for internal reference within complex timestamps and external reference from timestamped facts. We call this primary key field Timestamp and use characters as timestamp identifiers in our example.

The second table has three fields - two references to timestamp IDs and a role designator - and stores associations between timestamps, with predicates like “C contains E” or “A starts D”.

In our example, A and B are the ticks defining granule sequence D (‘[!1998-11 - !1999-02)’), and E is the instant (‘1998-11’) at an undefined position in granule C.

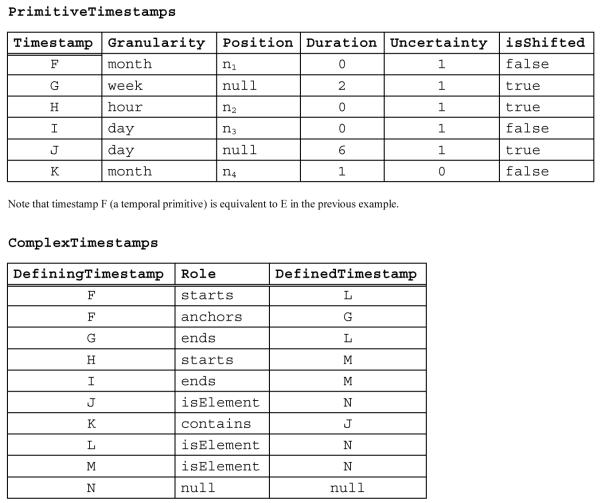
This system can be extended to form hierarchical trees allowing timestamps of any degree of complexity. The tixel-sequence instant ‘/[!2000-02-03T16:58 : !2000-02-03T17:03)’ for instant is {{{minute, n, 0, 0, true} starts, {minute, n+5, 0, 0, true} ends} contains}. Here, the instant is confined by the tixel sequence, which in turn is defined by two tixels.

Its ability to define timestamps through other timestamps applies to many real-world situations. The timestamp of Maria’s foot amputation for instance is only known in relation to her second hospital stay. It is an instant confined by the interval (timestamp M in figure 2) between her admission to and release from hospital, which are both instants as well. Its hierarchical tree structure is {{{hour, n1, 0, 1, true} starts, {day, n2, 0, 1, false} ends} contains}, and its literal ‘[/2000-02-03T17 : 2000-02-29)’.

Figure 2.

Other events may only be confined from one side. We know that they occurred before another event, but nothing more. Such an event is contained in an interval ended by another event, but without a starting event. Example: The inauguration of the hospital must have been before Maria’s first admission. That’s all we know from the narrative. Its timestamp is {{{month, n, 0, 1, false} ends} contains}, written as ‘[: 1998-11)’.

Not only timepoints, but also intervals may be confined by other intervals. Maria’s third hospital stay (timestamp J in figure 2) for instance, ‘for 6 days in April’, is a tixel instant duration of ‘day’ granularity confined in a granule of ‘month’ granularity, {{day, null, 6, 1, true}, {month, n, 1, 0, false} contains}. We propose the @-sign to express this relationship of the constituting timestamps: ‘P/0000-00-06@[2000-04)’.

In addition to being directly anchored on the underlying time domain (i.e. on its epoch), freely floating, or confined by other timestamps, a timestamp may also be anchored on another timestamp. This is very common in human time reference, and our verbal autopsy has several examples, e.g. Maria’s first release from hospital ‘after 2 weeks’, or her death ‘3 months later’. Such indirectly anchored timestamps are typically timepoints composed from an absolute and a relative position, that is, another timepoint and a duration.

Maria’s first release from hospital for instance is defined by her first hospital admission, ‘1998-11’, and the duration she stayed there, ‘P/0000-W02’. Its tuple representation is {{week, null, 2, 1, true}, {month, n, 0, 1, false} anchors}, and our intuitive choice to connect these components is a plus-sign, resulting in the literal ‘1998-11+P/0000-W02’.

Obviously, relative positions may be negative, like in ‘3 or 4 years ago’ (relative to the time of the interview, ‘in May or June 2001’). In this case, the plus-sign is replaced by a minus. The literal ‘[!2001-05 : !2001-07)-P/[!0003 : !0005)’ is unambiguous, although minus-sign and hyphen cannot be distinguished.

Frequently, intervals are defined by two timepoints, one of which is defined through its relative position to the other. Maria’s first hospital episode (timestamp L in figure 2) for instance is the interval started by her admission in November 1998 and her release two weeks later. For such cases we propose an abbreviated notation, e.g. ‘[1998-11 - +P/0000-W02)’ instead of ‘[1998-11 - 1998-11+P/0000-W02)’.

While the timestamp types introduced up to here allow timestamping of a wide range of events and episodes, we see also a need to cover patterns, that is, sets of regularly or irregularly repeated events or episodes. We may for instance want to refer to Maria’s pattern of hospitalization, which is composed from three episodes: {{month, n₁, 0, 1, false} starts, {{week, null, 2, 1, true}, {month, n₁, 0, 1, false} anchors} ends} isElement}, {{hour, n₂, 0, 1, true} starts, {day, n₃, 0, 1, false} ends} isElement}, {{day, null, 6, 1, true}, {month, n₄, 1, 0, false} contains} isElement}. Figure 2 shows its possible database implementation.

In their textual representation, sets are indicated by curly brackets and the constituting elements are separated by a comma: ‘{[1998-11 - +P/0000-W02), [/2000-02-03T17 - 2000-02-29), P/0000-00-06@[2000-04)}’.

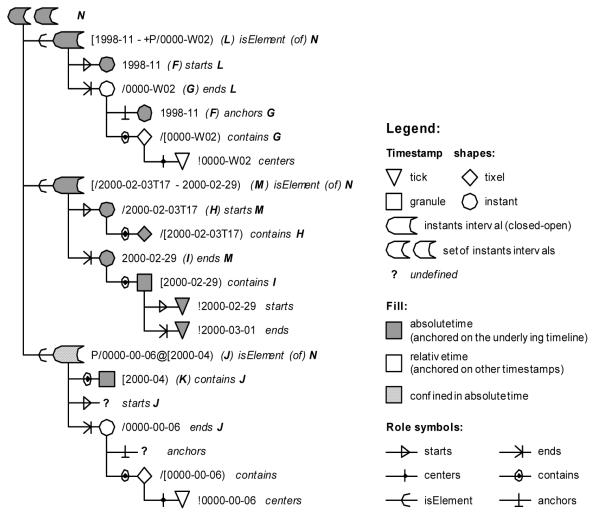
7.2 Graphical representation

In addition to a textual and a relational representation, a graphical representation may be helpful visualizing the structure of complex timestamps. Figure 3 shows our suggestion for this purpose, constituted from geometrical shapes forming the nodes and leaves of a hierarchical tree, and smaller symbols qualifying its branches, applied to the previous example, Maria’s pattern of hospitalization.

Figure 3.

The root, the nodes and the leaves of the tree are all timestamps. Their complexity usually decreases from the root to the periphery. Note, that the same timestamp may have multiple occurrences in the tree (e.g. F), and that not all nodes in figure 3 are expanded down to their final leaves, which would always be ticks, represented as triangles. Like all shapes used here, they are solid, if they are anchored on the underlying timeline, and hollow, if they are anchored on other timepoints.

Hollow symbols may be anchored on other defined timepoints, like G on F, or on undefined timepoints, like the end event of J, thus expressing durations.

Leaves and more peripheral nodes define more central nodes. Ticks define granules (squares) or tixels (diamonds), which in turn define instants (circles). Instants define intervals, e.g. F and G starting and ending L.

The shape representing closed-open instants intervals (L, M and J) visualizes a section of the timeline that includes its starting instant, but excludes its ending instant (both circles). L and M are solid, because they are anchored on the underlying timeline, while J is an unanchored duration, but confined within K.

Finally, timestamp N (Maria’s pattern of hospitalization) is a set of intervals (L, M and J); this again is reflected by its shape.

8. The Timestamp class

There are certainly many ways to implement the different timestamp types introduced above. The main objectives guiding our implementation choice are first to provide a single data type for all timestamping needs, second to isolate all temporal complexity, rules and calculations in this single place, and third to shield this complexity from the user. We have opted for the combination of a relational database with an object-oriented front end, because this achieves the objectives through an architecture already widely established in DS systems.

A possible two-table design for the database schema has already been introduced in figures 1 and 2. Additionally to the fields shown there, table PrimitiveTimestamps may need two more fields to indicate the calendar used and the time zone, if these are not constant within the system.

Both tables are accessed through objects of the Timestamp class, whose most important property - beside their ID - is the label, the textual representation of the temporal information stored for the timestamp. The timestamp class validates labels and translates them into attribute values and vice versa. It determines the timestamp type and exposes general properties like duration, which can directly be read from the attributes’ granularity and duration in the case of temporal primitives, or have to be calculated in case of complex timestamps. Many properties depend on the timestamp type. ‘Position’ for instance only applies to ticks, while other timestamp types may have pairs of positions: Start and end position in the case of precise intervals or min (i.e. earliest possible) and max (i.e. latest possible) position for imprecise timestamps.

Allen’s operators are implemented and extended through properties that require a second timestamp as parameter and perform comparisons with Boolean results, like ‘A.Before(B)’¹⁴, which may be true or false depending on the timestamps A and B and on the definition of ‘Before’ in the comparison of imprecise timestamps or time sets.

The centerpiece of the functionality of the timestamp class is a group of operators that take two (or more) timestamps and return a timestamp. They may be implemented as methods creating a new timestamp object or altering the timestamp that calls them.

The most basic and most powerful operators are the temporal equivalents to the logic operators AND (conjunction) and OR (disjunction). If two timestamps A and B are intervals that overlap (in Allen’s terminology), then ‘A.AND(B)’ returns the interval in which they overlap, while ‘A.OR(B)’ returns the interval from the earlier start to the later end. If A and B are intervals that do neither overlap nor meet, then ‘A.AND(B)’ returns an empty set, while ‘A.OR(B)’ returns the set of both intervals.¹⁵

These two operators are complemented by the temporal equivalent to the logic NOT (negation), which takes only one timestamp. ‘A.NOT’ returns all times except A. For overlapping intervals, ‘A.AND(B.NOT)’ returns the part(s) of A that do(es) not overlap B.

AND, OR and NOT may of course also apply to timepoints or sets, with more or less obvious results, which cannot be discussed in detail here. Particularly building a consistent framework for the evaluation of imprecise timestamps goes beyond the scope of this paper.

Another area of basic functionality is the transformation of timestamps. This includes changing a timestamp’s type, for instance from instant to granule, or from instants interval to granule sequence, or changing its granularity. Most calculations involving more than one timestamp require implicit or explicit temporal transformations as a preparatory step.

9. Working with timestamps

We have two main objectives when working with temporal information: increasing its quality and analyzing it in a meaningful way with regard to our study questions. A minimal quality requirement is temporal integrity, which ensures that the data are consistent within temporal business rules.

Temporal entity integrity ensures that all time-dependent facts are indeed timestamped and that their timestamps are ‘well formed’, that is, internally consistent. Date, Darwen, and Lorentzos 2002 identify three typical problems with temporal sets, namely redundancy, circumlocution and contradiction, that need to be overcome. They focus on interval timestamps (granule sequences in our classification), sets of which they expand to sets of ‘unit intervals’ (granules) and subsequently collapse to achieve well-formed sets.

Temporal referential integrity concerns consistency between the timestamps of related facts, for instance in foreign key relationships. While ‘conventional’ referential integrity enforces the existence of a record that is referred by the foreign key of another record, temporal referential integrity enforces that the timestamp of the independent record contains the timestamp of the dependent record.

Assuming the business rule that only existing people can be hospitalized, and that they can only be hospitalized while alive (and while the hospital is functional), Maria’s episodes of hospitalization for instance must all be contained in the episode of her lifetime (and the set of episodes of the hospital being functional).

Assuming further that she can only be hospitalized once at any time, we introduce the concept of temporal cardinal integrity, which in this case enforces that Maria’s episodes of hospitalization do not overlap (and thus form a valid time set).

We gave some examples for temporal indicators, which may be subjects of analysis, earlier. Many of them require summing up of durations within populations, for instance individual durations of exposure or durations spent in specific states of interest. Other typical operations are testing whether a particular event falls within a particular interval, or establishing the overlapping section of two (or more) intervals. The functionality needed for validation and analysis is basically the same.

And the central problem is the same as well: precise results of comparison of and calculation with timestamps are only guaranteed where precise timestamps - i.e. ticks, granules, granule sequences and sets of them - of the same granularity are involved. All other cases require either the transformation of timestamps as a first step before the operation can be done, or a differentiation of results.

In order to calculate the duration of Maria’s second stay in hospital for instance, we could first transform the timestamps of her admission and release into ticks, ‘!2000-02-03T17’ and ‘!2000-02-29’, and then coarsen the granularity of the admission timestamp from ‘hour’ to ‘day’, resulting in ‘!2000-02-03’ and a duration of exactly 26 days. This procedure is of course arbitrary. We could alternatively decide to transform ‘!2000-02-03T17’ into the nearest tick of ‘day’ granularity, resulting in ‘!2000-02-04’ and a duration of exactly 25 days, or to refine ‘!2000-02-29’ to a tick of ‘hour’ granularity, for instance ‘!2000-02-29T00’ or ‘!2000-02-29T12’, resulting in a duration of exactly 607 or 619 hours, respectively.

Differentiation of results means, for instance, calculating the minimal and maximal possible duration from the intervals of the earliest and latest possible ticks, ‘!2000-02-03T16:30’ and ‘!2000-03-01’, and ‘!2000-02-03T17:30’ and ‘!2000-02-29’, instead of a single duration. Useful parameters for analysis and further calculations are also a medium duration or a randomly assigned possible duration.

Additional uncertainty is introduced, where unanchored timestamps are used. The duration in days (and any finer granularity) of a particular month or year is defined, but less so of the duration ‘P!0001’ (one year) or ‘P!0000-01’ (one month).

Again, it is not the purpose of this article to propose rules for these transformations and calculations, but rather to show the potential of a unified timestamp to implement them in a transparent and consistent way.

10. Conclusions

Database design for DS systems that collect data describing a population over time must support storage, manipulation and analysis of various types of temporal data, which are observed or reported with different degrees of uncertainty.

Building on three distinct temporal primitives - tick, granule and instant - we suggest a unified timestamp with explicit precision and unambiguous textual representation emphasizing human readability as a single flexible data type for the faithful storage of valid time. We further suggest a related timestamp class encapsulating the inherent complexity of temporal logic and exposing useful temporal properties and methods for its management.

This paper focuses on the textual and internal representation of timestamps and gives some examples for useful class members. This is meant as a complement to the ISO 8601 standard, which largely ignores timestamps of variant precision, and to temporal DBMSs, where temporal functionality is a capability built into the database rather than into the data type, which makes it difficult to transfer data between systems. We think that the concepts introduced here can contribute a framework for an ongoing discussion of rules concerning operations with timestamps.

The following overview summarizes a selection of basic timestamp types and their literals, with T standing for ISO 8601 datetime in its various right-truncated forms indicating different precisions:

Table 1.

Type	Extended/Modified ISO 8601 representation		Natural language example
	Abstract	Example
1. ‘absolute’ time:
tick	!T	!2001-03-30T16 (or e.g. !2001-03-30T16:00:00, which is equivalent)	The new weekend fare applies from Friday, March 30th, 2001, 4 PM.
granule	[T)	[2001-03-30)	The ticket is valid on March 30th, 2001.
tixel	/[T)	/[2000-02-03T17)	(not applicable)
(granule) instant	T	1998-11	She went to hospital in November 1998.
tixel instant	/T	/2000-02-03T17	She was re-admitted on February 3rd, 2000 at 5 PM.
granule sequence	[!T1 - !T2)	[!2001-01-03 - !2001-01-06)	A 3-day mourning has been declared for January 3rd, 4th and 5th, 2001.
tixel sequence	/[!T1 - !T2)	/[!2000-02-03T16 - !2000-02-03T19)	(not applicable)
granule-sequence instant	[!T1 : !T2)	[!1998-11 : !1999-02)	He was last seen in the 3-month interval starting with November 1998.
(granule) instants interval	[T1 - T2)	[1998-07 - 1998-11)	She stayed with us from (her birthday in) July to (her marriage in) November 1998.
interval instant	e.g. [T1 : T2)	[1998-07 : 1998-11)	She bought her car between (her birthday in) July and (her marriage in) November 1998.
set of (granule) instants	{T1, T2}	{1998-07, 1998-11}	I saw her (at her birthday) in July and (at her marriage) in November 1998.
2. durations:
tick duration	P!T	P!T01	The ticket is valid for one hour.
(granule) instant duration	PT	P0078	He is 78 years old.
tixel instant duration	P/T	P/0000-03	She stayed for 3 months.
tixel-sequence instant duration	P/[!T1 : !T2)	P/[!0000-00-08 : !0000-00-12)	The symptoms may last 8 to 12 days.
3. ‘relative’ time:
right-constrained instant	e.g. [: T)	[: 1998-11)	She bought her car before (her marriage in) November 1998.
(granule) instant duration anchored on tick	!T1+PT2	!2001+P0000-04 (equivalent to 2001-05)	It was in the fifth month of the year 2001.
tixel instant duration anchored on tick	!T1+P/T2	!2001+P/0000-05 (equivalent to /2001-06)	It was 5 months after the start of the year 2001.
tixel instant duration anchored on (granule) instant	T1+P/T2	2000-12-25+P/0000-03	Maria died 3 months after I saw her last on Christmas Day 2000.
4. examples of more complex timestamps:
tixel instant duration contained in granule	P/T1@[T2)	P/0000-00-06@[2000-04)	Six days in April 2000.
set of (granule) instants intervals	{[T1 - T2), [T3 - T4)}	{[1998-11 - 1999-03), [2001-04-05 - 2001-04-12)}	I was in Paris from November 1998 to March 1999 and from the 5th to the 12th of April 2001.