Optimal Embedding for Shape Indexing in Medical Image Databases

Abstract

This paper addresses the problem of indexing shapes in medical image databases. Shapes of organs are often indicative of disease, making shape similarity queries important in medical image databases. Mathematically, shapes with landmarks belong to shape spaces which are curved manifolds with a well defined metric. The challenge in shape indexing is to index data in such curved spaces. One natural indexing scheme is to use metric trees, but metric trees are prone to inefficiency. This paper proposes a more efficient alternative.

We show that it is possible to optimally embed finite sets of shapes in shape space into a Euclidean space. After embedding, classical coordinate-based trees can be used for efficient shape retrieval. The embedding proposed in the paper is optimal in the sense that it least distorts the partial Procrustes shape distance.

The proposed indexing technique is used to retrieve images by vertebral shape from the NHANES II database of cervical and lumbar spine x-ray images maintained at the National Library of Medicine. Vertebral shape strongly correlates with the presence of osteophytes, and shape similarity retrieval is proposed as a tool for retrieval by osteophyte presence and severity.

Experimental results included in the paper evaluate (1) the usefulness of shape-similarity as a proxy for osteophytes, (2) the computational and disk access efficiency of the new indexing scheme, (3) the relative performance of indexing with embedding to the performance of indexing without embedding, and (4) the computational cost of indexing using the proposed embedding versus the cost of an alternate embedding. The experimental results clearly show the relevance of shape indexing and the advantage of using the proposed embedding.

1 Introduction

This paper is concerned with shape indexing of medical image databases containing two-dimensional shapes with landmarks. Shape indexing is relevant to medical image databases because shapes of organs are indicators of abnormality and disease.

There are many different notions of shape in the image processing literature. We adopt the notion developed by Kendall [26]. This is a very precise mathematical notion of shape in which two configurations of points have the same shape if they can be mapped onto each other by translation, rotation, and scaling. The shape of a configuration is defined as the equivalence class under this relation. Kendall showed that shapes defined in this manner belong to a shape space which is a high-dimensional curved manifold with many natural shape distances. Our goal is to index shapes in this manifold in order to carry out nearest–neighbor shape queries. Our indexing strategy may be used in any database that uses Kendall’s notion of shape space and is not restricted to our database. Our framework can be easily extended to index size-and-shape space [3, 10, 26, 29] when size carries critical clinical information.

Nearest–neighbor shape queries can be satisfied by a brute–force search through the database. Brute–force search is used in most of the existing research prototype image databases [11, 12, 17, 20, 52]. These databases handle at most a few thousand images and brute–force search is not too expensive. However, the computational cost of a brute–force search becomes prohibitive as the size of the database increases. To speed up the response – i.e. to get sub-linear complexity – brute–force search has to be replaced by indexing ¹.

Indexing in shape spaces is challenging because they are high dimensional as well as curved. Classical coordinate-based indexing trees - which work in flat vector spaces - cannot be easily used in these curved spaces. Although metric-based trees can be used in shape spaces, their performance degrades substantially because of the high dimension of shape spaces. Our innovation is to show how finite sets of shapes in shape spaces may be embedded into a vector space and how coordinate indexing trees can be used after embedding. Embedding a curved space into a vector space distorts the space (because the underlying metric must change) and we find the least distorting embedding. This is our main theoretical result. Using the least distorting embedding, it is possible to index shapes with coordinate-based trees. Our experiments show that these coordinate-based trees outperform metric trees in the original shape space.

The embedding idea has a second advantage as well. Indexing trees created with embedding allow efficient retrieval with respect to a weighted shape distance without re-indexing. The weights can be freely adjusted to emphasize only a portion of the organ shape. Thus, the same indexing tree can be used to retrieve images with respect to complete or partial shape. It is not possible to do this with the same metric tree.

1.1 NHANES II

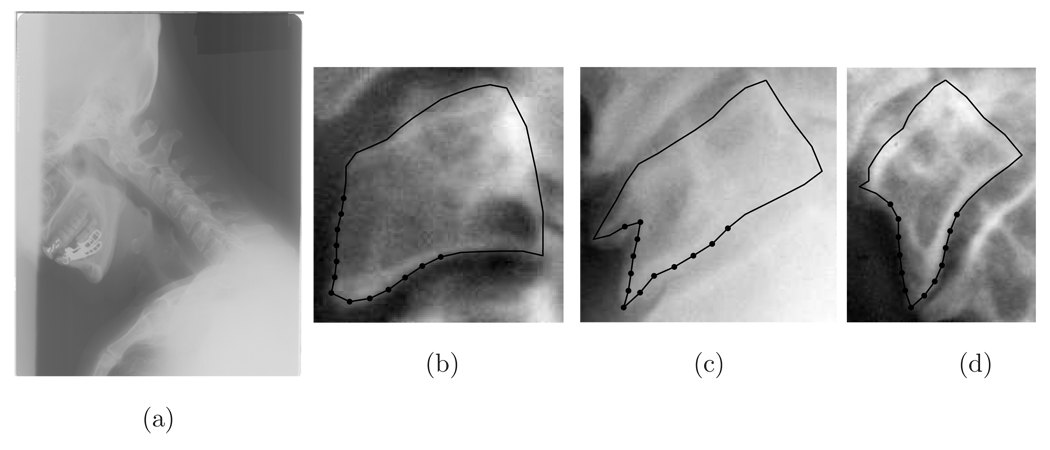
The database we use is the Second National Health and Nutrition Examination Survey (NHANES II) database maintained by the National Library of Medicine at the National Institutes of Health. NHANES II contains data about the health and nutrition of the U.S. population. Because of the prevalence of neck and back pain, the survey collected 17,000 images, approximately 10,000 of which are cervical spine x-rays and 7,000 are lumbar spine x-rays. Figure 1a shows an example image from NHANES II.

Figure 1.

One example image from NHANES II and several vertebrae with osteophyte severity increasing from left to right

One marker of spine disease is an osteophyte [32, 37]. Osteophytes are the outgrowth or excrescence of bone. They form in response to repetitive strain at the sites of ligamentous insertion [2, 36]. They usually develop as bony prominences along the anterior, lateral, and posterior aspects of the vertebral body. Two workshops held at the National Institutes of Health (NIH) and sponsored by the National Institute of Arthrtitis and Musculoskeletal and Skin Diseases (NIAMS) identified anterior osteophytes as the one of most important features of NHANES II images. Osteophtyes are the sharp prominences at the bottom left of the outlines in Figure 1 b to d. It is quite clear from these figures that the presence and severity of osteophytes affects the shape of the vertebral boundary. Thus retrieval by shape of the vertebral boundary is one means for retrieval by osteophyte severity.

1.1.1 Shape query in NHANES II

Given a query shape q we would like to retrieve images with k most similar shapes u according to a shape distance D(q, u). This is the k-nearest neighbor query. We expect the retrieved vertebrae to have osteophyte severity that is similar to the osteophyte severity in the query vertebra.

1.1.2 Boundaries and shapes in NHANES II

Boundaries of vertebrae in NHANES II images are already available as a result of a previous interactive segmentation which uses a dynamic programming template deformation algorithm [49]. The segmentation starts with an initial template placed close to vertebrae and segments vertebrae based on an active contour energy function. In this paper, the vertebral contours are represented by a set of 34 ordered landmarks sampled around the boundary in a homologous manner. Further, the landmarks are indexed such that the index i = 1 is located at the top right corner. The index increments counter-clockwise along the boundary. By the shape of a vertebra we mean the shape of the 34 ordered points in the plane obtained by the segmentation. The precise definition of shape and shape distance is given in section 3.

It might appear that the requirement of interactive segmentation of each image is limiting, but interactive segmentation is a common situation in many medical image databases. In medical databases, the images are often carefully acquired from previous research or historical teaching files, and the addition of images into the archive is subject to quality control. Also, because medical image databases are often used for future research, the creators of the database are quite willing to assist in segmentation and annotation of images as they are entered into the database. And in return, they expect retrievals that are precise enough for use in research. This is the situation that we address.

1.2 Organization of the paper

The paper is organized as follows: Section 2 reviews the literature on shape descriptors and indexing structures. Section 3 introduces shape space theory and identifies various spaces used in embedding. Section 4 describes our shape embedding algorithm and proves its optimality on minimizing metric distortion before and after embedding. Section 5 reviews indexing and how it is used after shape embedding. Section 6 reports experimental results. Section 7 concludes the paper.

2 Literature Review

Shape is commonly understood as a property of a figure that is independent of similarity transformations. Many shape descriptors of objects have been proposed and they can be loosely categorized as boundary or region based. Boundary based shape descriptors include Fourier and wavelet coefficients [6, 17, 44], scale space techniques [34], medical axis representations [25, 41] and shape matching methods [8]. Region based methods mainly uses moment descriptors, e.g., Zernike moments [18, 31, 44].

In this paper, we adopt shape space theory as proposed by Kendall [10, 26]. This theory is appropriate because in our case the boundary is available as a fixed set of points whose index begins at homologous locations. Shape analysis of continuous, closed planar curves has also been recently proposed in [28] but the distance calculation between shapes is computationally expensive.

Schemes for comparing partial shapes have also been proposed, e.g. [19, 35, 40, 43]. These schemes are based on a dynamic programming alignment of curve fragments, which is quite time-consuming when the number of points is large.

While shape descriptors abound, there are very few shape indexing algorithms [39]. Most of the current shape retrieval systems simply apply a brute-force search of all the images/shapes in the database (e.g. [11, 12, 17, 20, 52]). Brute-force search scales only linearly with the size of the database, and can be limiting as the database grows. A few researchers use kd-trees or R-trees to index other features, e.g. Fourier shape descriptors [15, 33] and quasi-invariants [45]. However, we are not aware of any serious indexing attempts to index shape in Kendall’s shape space.

Indexing has a rich history. For data in vector spaces, a variety of coordinate based indexing trees have been proposed in the literature, e.g., kd-tree [16], R-tree [21] and their extensions [1, 46]. There are also metric based indexing trees [5, 7, 43, 51] when data belongs to metric spaces. There are very few efficient indexing algorithms for similarity retrieval in non-Euclidean space [39]. Different embedding techniques have been proposed to speed up indexing by mapping non-Euclidean spaces to vector spaces, including FastMap [14], SparseMap [4], and MetricMap [50] as described in excellent surveys [23, 24]. These embedding algorithms are designed for a fixed distance metric in original spaces and their corresponding indexing techniques thereafter are also only effective for this metric. To our knowledge, there is no published research on embedding shape spaces for indexing. As mentioned earlier, we derive an embedding algorithm which allows efficient indexing and retrieval with user adjustable weighted shape distances.

The algorithms for shape embedding derived in this paper are similar to those used for general Procrustes analysis in statistical shape analysis [8, 10] and multi-view registration techniques in computer vision [9, 30, 38, 47]. The proof of optimality for our embedding algorithm is novel and our idea of embedding shape space for indexing is also novel.

3 Shape Space

This section is technical and tutorial. We begin with basic definitions of shape space which are critical to shape indexing. The essential idea of shape space theory is to define shape as what is left when one quotients out the action of a transformation group on an ordered set of n landmarks in the same space. In 3– or higher dimensional spaces, the calculations for shape distances involve eigen-system analysis and are usually complicated [10, 26, 27, 30]. For 2–d, calculations are based on complex numbers and are significantly simpler. In this paper, we focus on 2–d shape indexing. Our algorithms can be generalized to higher dimensional problems with increased complexity.

3.1 What is shape?

In shape space theory [26], shape is defined as all the geometric information that remains when location, scale, and rotational effects are filtered out. Hence, two sets of n ordered landmarks (contour points) in the plane have the same shape if they can be made to coincide exactly by some translation, rotation, and scale change of the plane. The idea is that translation changes the location of the set of points, rotation changes their orientation, and scale changes their size, thereas shape is a property that is independent of location, orientation, and size.

The plane is easily identified with 𝒞, the set of complex numbers taken as a complex vector space. This is done in the standard fashion by identifying the point x, y with the complex number z = x + iy. Any set of n points in the plane u = (z₁, ⋯, z_n) is similarly identified as an element of 𝒞ⁿ. The space 𝒞ⁿ has a natural Euclidean metric defined by

$$\parallel u{\parallel }_{{𝒞}^n}=\sqrt{u{u}^{*}},$$

where, u* is the complex conjugate transpose of u.

In general, one or more of the n points in u = (z₁, ⋯, z_n) may be coincident. The case where all n points are coincident is not very interesting and may cause problems in embedding by introducing discontinuity. Hence, this situation is deleted from consideration. We are only interested in configurations of n points where at most n − 1 of them are coincident.

Definition: The configuration space of n points in the plane is Cⁿ = 𝒞ⁿ − {(w, ⋯,w)∥w ∈ 𝒞}.

Translations, rotations, and scalings of the plane generate the similarity group. A similarity acts on the plane by z ↦ αz + t, where α and t are complex numbers with ∥α∥ ≠ 0. The translation is given by t, and the rotation and scaling given by α = ∥α∥e^iθ. The effect of a similarity on a configuration u = (z₁, ⋯, z_n) is

$$u=(z_1,\cdots ,z_n)\mapsto (\alpha z_1+t,\cdots ,\alpha z_n+t)=\alpha u+1_{n}t,$$

where 1_n = (1, ⋯, 1).

Now suppose G = {g} is a group whose elements act on a set S. That is, every g ∈ G gives a map g : S → S. Let ~_G be a relation between elements of S such that for u, v ∈ S the relation u ~_G v holds when u = g(v) for some g ∈ G. The relation ~_G is an equivalence relation on S and therefore partitions S into equivalence classes. The equivalence class of any u ∈ S is called the orbit of u and is denoted [u]_G. Thus, [u]_G = {v | v ~_G u}. The orbits in S can be used to create a new space called the quotient space, denoted S\ ~_G. Each element of the new space is an equivalence class of S, i.e. S\ ~_G= {[u]_G | u ∈ S}. A natural topology for the quotient space is the quotient topology derived from S.

For planar shapes, the above definitions manifest as follows:

Definitions: Denote the similarity group as s. Two configurations u, v ∈ Cⁿ have the same shape, denoted u ~_s v, if v is in the orbit of u under the action of the similarity group s, i.e., if v = αu + 1_nt for some ∥α∥ ≠ 0. Having the same shape is an equivalent relation, and each equivalence class under this relation is called a shape. The quotient space Cⁿ\ ~_s with the quotient topology is the shape space of Cⁿ. We denote the shape space by SSⁿ (SS^N = Cⁿ\ ~_s), and the map that takes a configuration u to its shape [u]_s by σ : Cⁿ → SSⁿ.

Kendall showed that SSⁿ with the quotient topology has a particularly simple structure – it is a complex projective space of complex dimensions n − 2 [10, 26] where n is the number of landmarks and a similarity transform has 2 complex degrees of freedom. Complex projective spaces are differentiable manifolds of constant sectional curvature. The reader is referred to [48] for details.

3.2 Pre-shape space

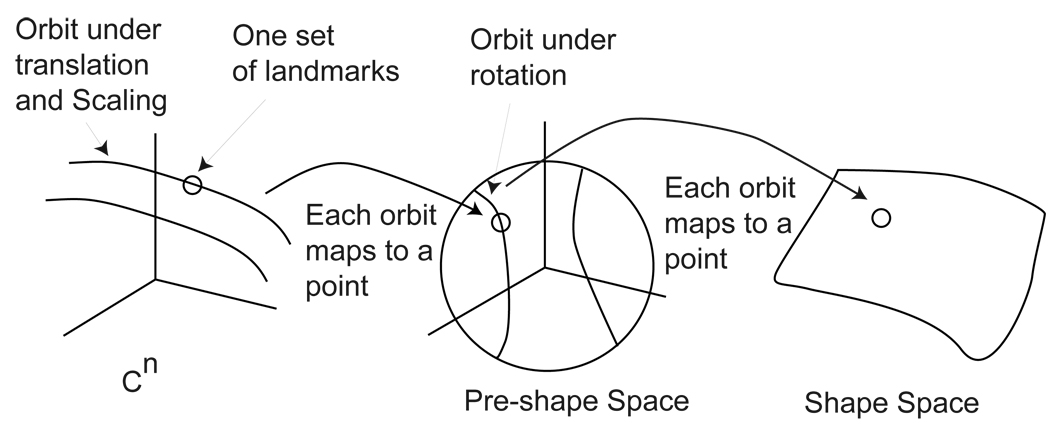
Although the above is a direct path to the definition of shape space, an alternate approach in which we obtain the shape equivalence class in two steps is more relevant to our work. First, an equivalence class is obtained only by considering translation and scaling. Then, a second equivalence class is obtained by rotation. Figure 2 illustrates the different steps, which we now elaborate.

Figure 2.

Pre-Shape and Shape spaces

3.2.1 Equivalence under translation and scaling

Two configurations u, v ∈ Cⁿ are equivalent under translation and scaling if v = αu + 1_nt, for some real number α > 0, and complex translation t.

Definitions: The set of translations and scalings (i.e. similarities with zero rotation) forms a subgroup of the similarity group. This is the pre-shape group. The action of the pre-shape group on Cⁿ partitions Cⁿ into equivalence classes. This equivalence relation is denoted ~_p. The equivalence class of u ∈ Cⁿ under the action of the pre-shape group is denoted [u]_p and is the pre-shape of u. The quotient space PSⁿ = Cⁿ\ ~_p is the pre-shape space. The map from the configuration space to its pre-shape is denoted ψ : Cⁿ → PSⁿ.

The pre-shape space PSⁿ is easily identified with the unit complex sphere in 𝒞ⁿ. To see this, consider the map

$$u\mapsto \overline{u}=(u-\frac{1}{n}{1}_n(u{1}_n^T))/\parallel u-\frac{1}{n}{1}_n(u{1}_n^T){\parallel }_{{𝒞}^n}.$$

This map has the following properties

1. It maps the configuration u to the configuration ū where the mean of the new configuration is at the origin and the scale (as measured by ∥u∥_𝒞ⁿ) is set to unity. The image of Cⁿ under this map is the unit sphere in 𝒞ⁿ.

2. All configurations that are equivalent under translation and scaling are mapped to the same ū. Thus, ū is identified with [u]_p and we can take the unit sphere in 𝒞ⁿ to be PSⁿ and set ψ : Cⁿ → PSⁿ to

   $$\psi (u)=(u-\frac{1}{n}{1}_n(u{1}_n^T))/\parallel u-\frac{1}{n}{1}_n(u{1}_n^T){\parallel }_{{𝒞}^n}.$$

Figure 2 illustrates this. The figure shows a configuration u in Cⁿ and the orbit of the configuration under translation and scaling. The map ψ takes this entire orbit to [u]_p which is a point in the pre-shape space PSⁿ; the pre-shape space itself being the unit sphere in 𝒞ⁿ.

3.2.2 Equivalence under rotation

Planar rotations form a group (the subgroup of similarities with zero translation and unit scaling) which we call the rotation group. The rotation group acts on the pre-shape space in the following manner: Rotation by θ maps [u]_p to [e^iθu]_p.

Definitions: The action of the rotation group on PSⁿ gives the equivalence relation ~_r. The equivalence class of [u]_p under this relation is denoted [[u]_p]_r. The quotient space under this relation is PSⁿ\ ~_r, and the map ρ : PSⁿ → PSⁿ\ ~_r takes [u]_p to [[u]_p]_r.

Of course, PSⁿ / ~_r is the shape space, i.e., PSⁿ / ~_r≡ SSⁿ. Equivalent ways of saying this are, (Cⁿ/ ~_p)/ ~_r= Cⁿ / ~_s, σ = ρ ○ ψ, and [[u]_p]_r = [u]_s.

In figure 2 equivalence classes in the pre-shape space under rotation are shown as curves on the sphere. The map ρ takes each equivalence class into the shape space SSⁿ.

As an aside, we note that scale (the size of object configurations) is an important property that carries critical information for applications in some medical image databases. There is in fact well established notion of size-and-shape space [3, 10, 26, 29] which is obtained by modifying the above definitions without factoring out scaling. In this paper, we do not address size-and-shape indexing. We only focus on indexing shape space. However, our framework can be easily extended to index size-and-shape space.

3.3 Shape space distances

Shape space has several natural shape distances, including full Procrustes distance, partial Procrustes distance, and Procrustes distance. These distances are topologically equivalent and have a simple monotonic functional relationship between them (page 64, [10]). When the shapes [u]_s and [v]_s ∈ SSⁿ are similar, the numerical values of the these distances are similar (page 73, [10]). The full Procrustes distance between two shapes [u]_s and [v]_s is the minimal Euclidean distance between the pre-shape [u]_p and the elements of the equivalence class of [v]_p under rotation and scaling:

$$d_F({[u]}_s,{[v]}_s)=\underset{\beta ,\theta }{\text{min}}\parallel {[u]}_p-\beta e^{i\theta }{[v]}_p{\parallel }_{{𝒞}^n},$$ (1)

where the real number β > 0 [10].

In this paper, we study shape embedding and indexing using the partial Procrustes distance d_P ([u]_s, [v]_s) between two shapes [u]_s and [v]_s, which is defined as the closest Euclidean distance between the pre-shape [u]_p and the elements of the equivalence class of [v]_p under rotation:

$$d_P({[u]}_s,{[v]}_s)=\underset{\theta }{\text{min}}\parallel {[u]}_p-e^{i\theta }{[v]}_p{\parallel }_{{𝒞}^n}.$$ (2)

This distance is symmetric and satisfies the triangle inequality [10].

4 Embedding Shape into a Vector Space

As we mentioned in Section 1, our goal is to embed shapes into a vector space and use coordinate trees for efficient indexing. By embedding, we search for a mapping of a finite set of shapes from the original shape space to a vector space so that the Euclidean distance in the vector space between embedded shapes is similar to the original shape distance.

Before deriving a new shape embedding, we first review a previously suggested embedding technique based on full Procrustes distance.

4.1 Equivariant embedding

For full Procrustes distance, there exists a distance preserving embedding of shape spaces called equivariant embedding [27], in which the Euclidean distance between embedded shapes is equal to the full Procrustes distance in the original shape space. The embedding is constructed as follows: the configuration u ∈ Cⁿ is mapped into a point in 𝒞^n×n by φ : Cⁿ → 𝒞^n×n defined by $\phi (u)=\frac{{[u]}_p^{*}{[u]}_p}{\sqrt{2}},\text{where}{[u]}_p^{*}{[u]}_p$ is a n × n complex matrix. The Euclidean distance in 𝒞^n×n gives $d_E^2(\frac{{[u]}_p^{*}{[u]}_p}{\sqrt{2}},\frac{{[v]}_p^{*}{[v]}_p}{\sqrt{2}})=\frac{1}{2}{\parallel {[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p\parallel }_{{𝒞}^{n\times n}}^2$, where ∥ ∥_𝒞^n×n is the usual Euclidean or Frobenius norm of the matrix. After some algebraic manipulations, it can be shown that $d_E^2(\phi (u),\phi (v))=d_F^2({[u]}_s,{[v]}_s)$ (see Appendix).

On the face of it, this embedding seems useful for shape indexing as coordinate-based trees can be used in 𝒞^n×n with well defined Euclidean distance, but as we show in section 6, it has severe computational limitations. The limitations arise from the fact that the embedding increases the dimension of the space from n to n × n. This significantly increases the computational cost of constructing the indexing tree and of retrieval.

In contrast, below we propose an embedding that does not increase the dimension of the space. The embedding is approximate in that it does not exactly preserve distance. However of all possible embeddings into the vector space, we find the one that least distorts the distance. Experimental results show that the approximation is very good and causes no significant change in k-nearest neighbor retrievals; and of course, the computational cost of using this embedding is much smaller.

4.2 The class of embeddings

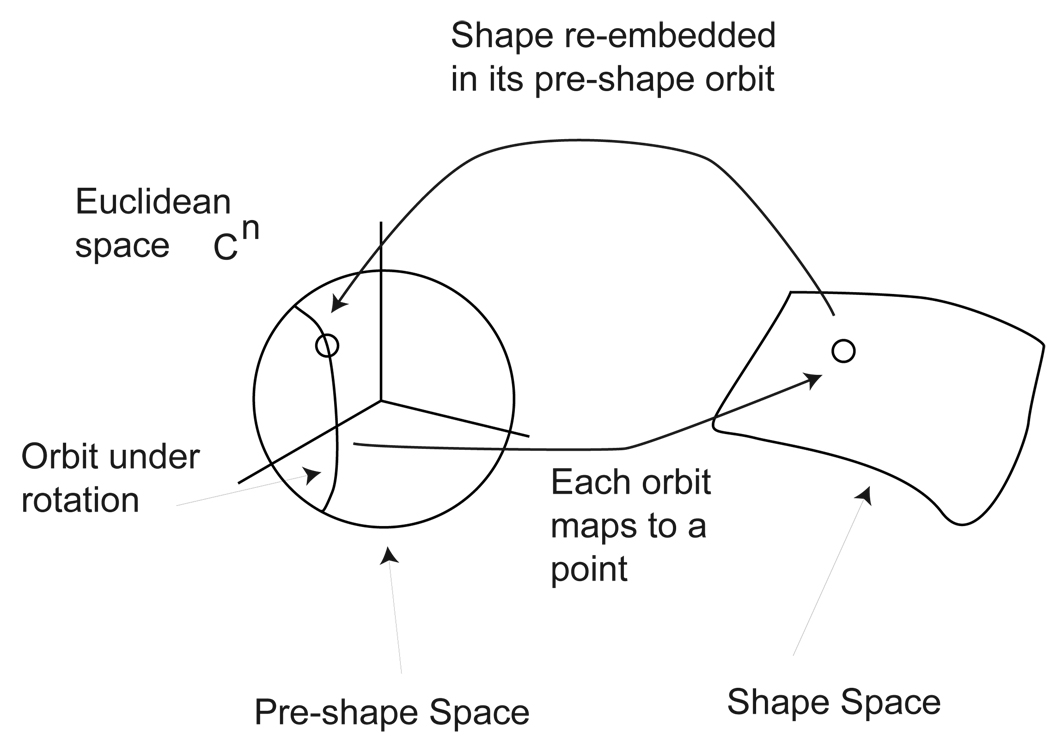
Recall that the pre-shape space PSⁿ is the unit sphere in 𝒞ⁿ (see fig. 2) and that the map ρ : PSⁿ → SSⁿ takes the entire equivalence class of pre-shapes [u]_p/ ~_r to the shape [u]_s = ρ([u]_p). One natural way to embed the shape space SSⁿ into the vector space 𝒞ⁿ is to “invert” the map ρ. That is, we re-embed the shape [u]_s in the orbit of the pre-shape [u]_p at some point e^iθ[u]_p (see fig. 3). We note here that it is generally not possible to find this “inverting” map from the full shape space to pre-shape space as established by the theory of fibre bundles [26, 27, 30, 48]. We focus on constructing such an optimal embedding for a finite set of shapes that are tightly clustered, which is the typical case in many medical applications.

Figure 3.

Embed shape space back in pre-shape space

Let u_k, k = 1, ⋯, N be the configurations in the database, and let [u_k]_p and [u_k]_s be their preshapes and shapes respectively. We embed [u_k]_s at the point in the pre-shape orbit given by e^iθ_k[u_k]_p for some θ_k. After embedding, the Euclidean distance between shapes [u_k]_s and [u_l]_s is

$$d_E({[u_k]}_s,{[u_l]}_s)=\parallel e^{i{\theta }_k}{[u_k]}_p-e^{i{\theta }_l}{[u_l]}_p{\parallel }_{{𝒞}^n},$$ (3)

where, ∥ ∥_𝒞ⁿ is the usual Euclidean norm in 𝒞ⁿ. In general, this shape distance is different from the partial Procrustes distance, and we would like to choose an embedding such that the difference between the distances is as small as possible.

One measure of the difference between the distances is

$$J={\displaystyle \sum _k{\displaystyle \sum _l|d_E^2({[u_k]}_s,{[u_l]}_s)}-d_P^2({[u_k]}_s,{[u_l]}_s)}|,$$ (4)

where d_E is the Euclidean distance and d_P is the partial Procrustes distance. We would like to choose the embeddings e^iθ₁ [u₁]_p, e^iθ₂ [u₂]_p, ⋯, e^iθ_N [u_N]_p, or alternatively, choose the angles Θ = (θ₁, θ₂, ⋯, θ_N) such that J is minimized as a function of Θ. From now on we will write J as J(Θ) explicitly showing dependence on Θ.

The next step is to note that we do not need to know the values of the partial Procrustes distances to find the minimizing Θ.

Proposition 1: A Θ minimizes J(Θ) if and only if it minimizes

$$J_1(\mathrm{\Theta })={\displaystyle \sum _k{\displaystyle \sum _l{d}_E^2({[u_k]}_s,{[u_l]}_s)}}.$$ (5)

Proof: For any given Θ, d_E([u_k]_s, [u_l]_s) is the Euclidean distance between two fixed point e^iθ_k [u_k]_p and e^iθ_l [u_l]_p in the pre-shape orbits of [u_k]_p and [u_l]_p. But the partial Procrustes distance d_P([u_k]_s, [u_l]_s) is the shortest distance between pre-shape orbits of [u_k]_p and [u_l]_p. Thus, d_E([u_k]_s, [u_l]_s) ≥ d_P([u_k]_s, [u_l]_s), and therefore $|d_E^2({[u_k]}_s,{[u_l]}_s)-d_P^2({[u_k]}_s,{[u_l]}_s)|=d_E^2({[u_k]}_s,{[u_l]}_s)-d_P^2({[u_k]}_s,{[u_l]}_s)$, giving

$$J(\mathrm{\Theta })={\displaystyle \sum _k{\displaystyle \sum _l{d}_E^2({[u_k]}_s,{[u_l]}_s)-d_P^2({[u_k]}_s,{[u_l]}_s).}}$$

Now, note that the $d_P^2({[u_k]}_s,{[u_l]}_s)$ term is independent of Θ and can be dropped from J(Θ), giving

$$J(\mathrm{\Theta })={\displaystyle \sum _k{\displaystyle \sum _l{d}_E^2({[u_k]}_s,{[u_l]}_s)=J_1(\mathrm{\Theta }).}}$$

This proves the proposition.

To proceed further, a simple algebraic manipulation of J₁(Θ) gives:

$$J_1(\mathrm{\Theta })={\displaystyle \sum _k{\displaystyle \sum _l{d}_E^2({[u_k]}_s,{[u_l]}_s)}}=2N{\displaystyle \sum _k\parallel }{e}^{i{\theta }_k}{[u_k]}_p-\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p{\parallel }_{{𝒞}^n}^2.$$ (6)

Now consider a second objective function

$$H_1(\mathrm{\Theta },\mu )=2N{\displaystyle \sum _k\parallel }{e}^{i{\theta }_k}{[u_k]}_p-\mu {\parallel }_{{𝒞}^n}^2.$$ (7)

We have:

Proposition 2: If H₁(Θ, μ), has a minimizer (Θ*, μ*), then Θ* also minimizes J₁(Θ).

Proof: The embedding points e^iθ_k [u_k]_p are in the vector space 𝒞ⁿ. Further, ∥ ∥_𝒞ⁿ is the usual Euclidean norm in this space. Consequently, for a fixed Θ, H₁(Θ, μ) is a quadratic function of μ. Hence (for a fixed Θ), the function H₁(Θ, μ) has a unique minimum with respect to μ. The minimum is given by ${\mu }^{*}=\frac{1}{N}{\displaystyle {\sum }_k{e}^{i{\theta }_k}{[u_k]}_p}$. The value of H₁ at the minimum is

$$\underset{\mu }{\text{min}}{H}_1(\mathrm{\Theta },\mu )=2N{\displaystyle \sum _k\parallel }{e}^{i{\theta }_k}{[u_k]}_p-\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p{\parallel }_{{𝒞}^n}^2=J_1(\mathrm{\Theta }).$$ (8)

Since H₁ is a continuous function of Θ and μ, if (Θ*, μ*) minimize H₁, then Θ* by itself minimizes the function H₁(Θ, μ*) = min_μ H₁(Θ, μ) = J₁(Θ), where the last step follows from (8). This proves the proposition.

4.2.1 Existence and uniqueness of μ*

The existence of solution for (7) is obvious since the problem is the minimization of a continuous function over a compact set. The μ that minimizes H₁ is known in the shape space literature as the Procrustean mean size-and-shape of the pre-shapes [u_k]_p. Conditions for a unique Procrustean mean size-and-shape are given in [29]. A unique mean exists if the distribution of the size-and-shape of u_k is contained in a geodesic ball of radius r centered at μ such that the larger geodesic ball of radius 2r centered at μ is regular. Loosely speaking, this means that a unique μ exists if the distribution of the size-and-shapes of u_k is not too broad. In practice, this condition almost always holds and a unique μ exists. We assume this to be the case.

4.2.2 Numerical algorithm

Algorithmically, we can find the minimizer of H₁(Θ, μ) by alternately minimizing with respect to Θ and μ as follows:

1. Set m = 1, and initialize Θ^[m] = (0, ⋯, 0), and ${\mu }^{[m]}=\frac{1}{N}{\displaystyle {\sum }_l{e}^{i{\theta }_l^{[m]}}{[u_l]}_p}$.

2. Set m = m + 1.

   Calculate Θ^[m] = arg_Θ min H₁(Θ, μ^[m−1]). The minimizer ${\mathrm{\Theta }}^{[m]}={\theta }_1^{[m]},\cdots ,{\theta }_k^{[m]},\cdots )$ is given by

   $${\theta }_k^{[m]}=\text{arg }{\mu }^{[m-1]}{[u_k]}_p^{*},$$ (9)

   where, ${[u_k]}_p^{*}$ is the complex conjugate transpose of [u_k]_p. Note that μ^[m−1] in the right hand side cannot be orthogonal to the pre-shape representing [u_k]_p in order to guarantee that ${\theta }_k^{[m]}$ is well defined. Otherwise there will be ambiguities, which may cause a problem if one tries to extend the embedding to the entire shape space.
   Calculate μ^[m] = arg_μ min H₁(Θ^[m], μ). This is given by

   $${\mu }^{[m]}=\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l^{[m]}}{[u_l]}_p,}$$ (10)

   where, ${\mathrm{\theta }}_l^{[m]}$ are components of Θ^[m] as given above.

3. Terminate if a fixed point is reached (i.e. if (Θ^[m], μ^[m]) = (Θ^[m−1], μ^[m−1])). Else, go to 2.

Upon termination Θ^[m] gives the optimal embedding angles. The shapes [u_k]_s are optimally embedded as $e^{i{\theta }_k^{[m]}}{[u_k]}_p$. We denote this embedding function by γ; and any shape [u]_s in a compact subspace can be optimally embedded in the pre-shape space as γ([u]_s) = e^iθ[m] [u]_p, where ${\theta }^{[m]}=\text{arg}{\mu }^{[m]}{[u]}_p^{*}$.

4.3 Embedded representation and distance

Using the optimal embedding, the shape of a configuration u can be represented as the vector γ([u]_s), and the Euclidean distance

$$d_E({[u]}_s,{[v]}_s)=\parallel \gamma ({[u]}_s)-\gamma ({[v]}_s){\parallel }_{{𝒞}^n}=\sqrt{(\gamma ({[u]}_s)-\gamma ({[v]}_s))(\gamma ({[u]}_s)-\gamma ({[v]}_s{)}^{*}}$$

can be taken as the shape distance between the configurations u and v.

It is also useful to consider a weighted Euclidean distance between configurations where the shape contribution of some subset of points in the configuration is more important. For this, we define a weighted Euclidean distance between two embedded shapes as

$$d_{\mathit{\text{WE}}}({[u]}_s,{[v]}_s)=\sqrt{(\gamma ({[u]}_s)-\gamma ({[v]}_s))W(\gamma ({[u]}_s)-\gamma ({[v]}_s{)}^{*}},$$

where, W is a real positive definite matrix of weights. We always take W to be a diagonal matrix with non-zero diagonal terms {w_kk}.

The main use for the weighted distance is to emphasize the contribution of a part of the shape. In NHANES II, for example, anterior osteophytes occur in a known subset of the boundary points (in figure 1, these points are marked with heavy dots). And to retrieve with respect to osteophyte severity, the shape of these points is more important than the shape of the rest of the boundary. To emphasize the shape of osteophyte, we set the diagonal terms w_kk in the region of the osteophyte to 1 and other diagonal terms to 0.01 ².

In principle, having defined a weighted partial Procrustes distance, the previous embedding framework should be extended to find the optimal embedding with respect to the weighted partial Procrustes distance. However, it is desirable to allow users to adaptively decide W in an interactive fashion. In this setting, recomputing the embedding every time for different users and images is time consuming for each possible weighting matrix W. Instead, we continue to use the indexing tree created without weights to retrieve weighted shapes. Our experiments show that this heuristic method is efficient.

4.4 Embedding with shape queries

Finally, before we discuss shape indexing, we address another implementation heuristic of our embedding algorithm that is relevant to shape indexing.

A k-nearest neighbor query asks for k-closest shapes to the query shape q. In the original shape space, the appropriate distance for defining these queries is the partial Procrustes distance. After embedding, the appropriate distance is either the Euclidean or the weighted Euclidean distance. Ideally, when a new query is being considered, similarity retrievals should be based on the original partial Procrustes distance. However, after embedding, we take the Euclidean distance in the embedding space to retrieve nearest neighbors. Theoretically, in order to preserve the ranking order of the retrieved results based on their proximity in the original shape space, we have to recompute the least distorting embedding taking this new query point into account. But it is clear from the above algorithm that adding one more shape to the calculation will have an extremely small effect (roughly $O\left(\frac{1}{N}\right)$, where N is the size of the database) on the calculation for μ and Θ. In addition, for many medical applications, the query shape comes from the same distribution as the shapes in the database and the recomputed embedding with the query point is very similar to the embedding without the query point. Hence, there is no real need to recalculate the embedding. The query shape [q]_s can be embedded as γ([q]_s) = e^iθ_q [q]_p, where, ${\theta }_q=\text{arg}{\mu }^{[m]}{[q]}_p^{*}$ and μ^[m] is the terminating mean in the algorithm given above.

5 Indexing

Having discussed optimal embedding of shape space into a vector space, we turn to discussing indexing.

5.1 Coordinate trees

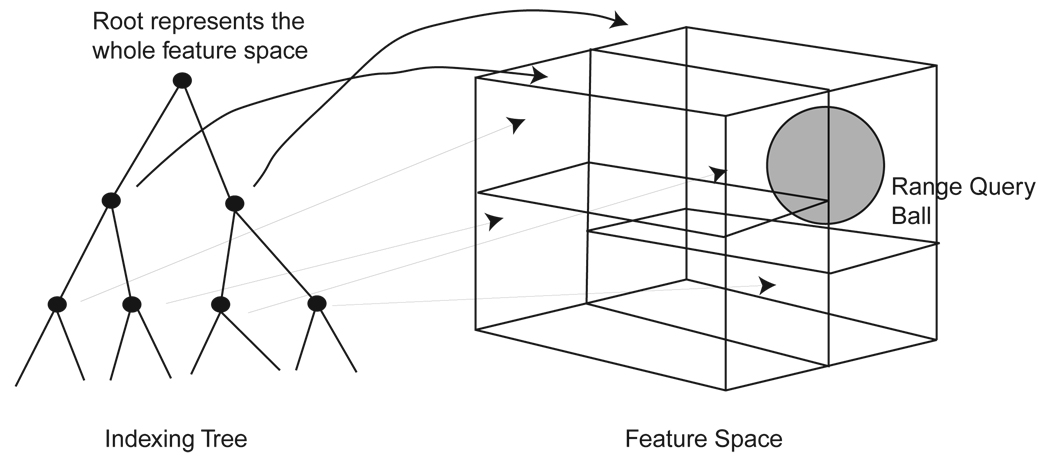
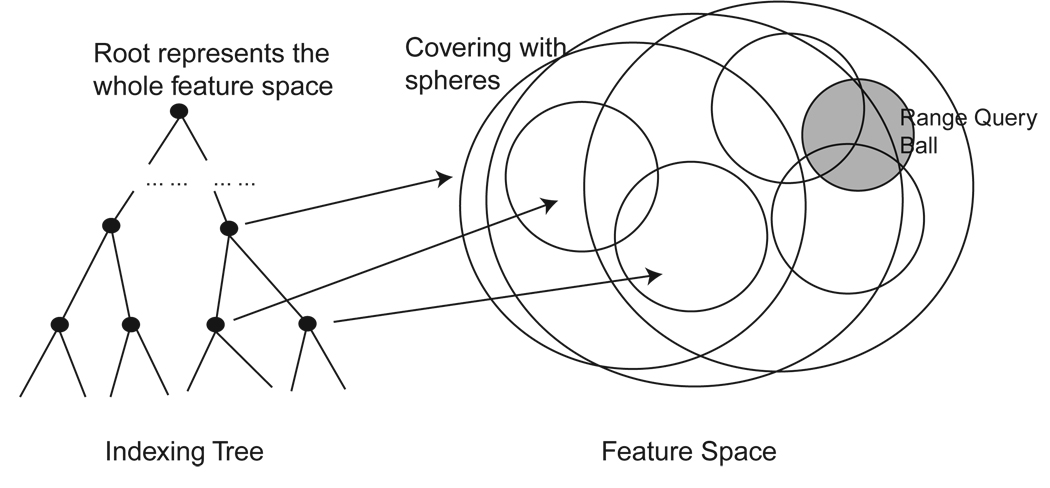
𝒞ⁿ has real dimension 2n and each embedded shape γ([u]_s) in the database can be represented by 2n real numbers. Coordinate indexing trees recursively partition 𝒞ⁿ into cubes whose sides are perpendicular to the coordinate system (fig. 4). The partitioning is arranged in a kd-tree, where each node of the tree represents a cube. The root node of the tree represents the largest cube and it contains all of the embedded shapes. The partitioning continues recursively till the size of the cubes (measured either by their longest side, by their volume, or by the number of database features in the cube) falls below a threshold. At that point, the node becomes a leaf node. Variants of this idea give R-trees, R⁺-trees, etc [46].

Figure 4.

Coordinate Tree

We call the cube at each node a cover, since it covers all of the data contained in the leaf nodes below the node. The cover at each node is defined by the set of inequalities

$$a_i\le x_i\le b_i,i=1,\cdots ,2n,$$ (11)

where, x_i are the 2n real coordinates in 𝒞ⁿ; x_i with odd index is the real part of complex number and x_i with even index is the imaginary part; a_i ≤ b_i are the bounds that define the cover.

The minimum Euclidean distance from a query shape γ([q]_s) in 𝒞ⁿ to the cover defined by equation (11) is

$$\sqrt{{\displaystyle \sum _{k=1}^{2n}{\delta }^2(q_k,[a_k,b_k])}}$$ (12)

where, ${\delta }^2(q_k,[a_k,b_k])=\{\begin{array}{ll}\hfill 0\hfill & \text{if}{q}_k\in [a_k,b_k]\hfill \\ \hfill \text{min}({(q_k-a_k)}^2,{(q_k-b_k)}^2)\hfill & \text{otherwise}.\hfill \end{array}$ Here, q_k is one of 2n real coordinates of the embedded shape γ([q]_s).

The minimum weighted Euclidean minimum distance from a query shape γ([q]_s) in 𝒞ⁿ to the cover is

$$\sqrt{{\displaystyle \sum _{k=1}^{2n}{\delta }^2(q_k,[a_k,b_k])}}$$ (13)

where, ${\delta }^2(q_k,[a_k,b_k])=\{\begin{array}{ll}\hfill 0\hfill & \text{if}{q}_k\in [a_k,b_k]\hfill \\ \hfill \text{min}(w_{\lceil \frac{k}{2}\rceil \lceil \frac{k}{2}\rceil }{(q_k-a_k)}^2,w_{\lceil \frac{k}{2}\rceil \lceil \frac{k}{2}\rceil }{(q_k-b_k)}^2)\hfill & \text{otherwise}.\hfill \end{array}$, where w_ij is the matrix entry at the i-th row and j-th column in W and $\lceil \frac{k}{2}\rceil$ is the smallest integer larger than $\frac{k}{2}$.

For a k-nearest neighbor query, the user provides a configuration q and asks for k images whose configurations u are most similar to the query. There is a standard retrieval procedure [22] that can satisfy this query. The procedure traverses the tree by visiting its nodes. At every visited node, it calculates the minimum distance to the node cover and compares it with a threshold. If the distance is greater than the threshold the entire subtree rooted at the node is discarded (i.e. its nodes are not visited). A key part of the procedure is to dynamically update the threshold such that the surviving leaf nodes are guaranteed to contain the k-nearest neighbors. The complete procedure is available in [22].

We call the test applied to each node to compare the minimum distance to the node with a threshold, a node test.

5.2 Metric trees

Since the shape space SSⁿ is endowed with the partial Procrustes distance - d_P ([u]_s, [v]_s), where u, v are configurations in the database, shapes can be indexed in SSⁿ using a metric tree.

A metric indexing tree has spheres as node covers, with the root node covering the entire data. Each node cover is a sphere (according to the metric d_P ) with a finite radius. Figure 5 illustrates the idea. The simplest way of constructing metric trees is to hierarchically cluster the features top-down or bottom-up [46, 53]. In this paper, the metric tree is constructed using bottom-up clustering.

Figure 5.

Metric Tree

The k-nearest neighbor retrieval procedure is exactly the same as before with the node test comparing the minimum distance from the query to the spherical node cover.

5.3 Indexing performance

The performance of coordinate and metric trees is evaluated by two criteria: Computational Cost and Disk Access Cost.

Computational cost refers to the computation incurred by the retrieval algorithm as it descends to find the surviving leaf nodes. One measure of this is the average number of node tests per query as a function of the size of the database.

Disk access cost refers to the amount of disk access carried out per query. The leaf nodes of indexing trees point to data. When a leaf node passes the node test, the retrieval procedure accesses this data. Thus, one measure of disk access cost is the average number of surviving leaf nodes per query as a function of the size of the database.

6 Experiments

In the experiments, we evaluated the main claims of this paper: (1) The shape of the vertebra captures the presence and severity of osteophytes, (2) Optimal shape embedding gives a good approximation to the partial Procrustes distance, (3) Indexing shape using embedding gives more efficient retrieval than metric tree indexing, (4) Optimal shape embedding gives more efficient retrieval than the equivariant embedding.

All experiments were done with a subset of NHANES II images. At the present, a total of 2812 vertebral boundaries are available. We used all boundaries in the experiments.

6.1 Shape distance and osteophyte severity

The first set of experiments determined how well the shape of the boundary captures the notion of osteophyte severity. Since there is no universally accepted standard for grading osteophyte severity, we asked an experienced neuro-radiologist to create osteophyte grades based on his clinical experience. The expert manually graded a subset of 169 vertebrae. The grading is from 0 to 5, where “0” represents normal vertebrae without osteophyte; “1” indicates sharp protuberance that is barely visible; “2” means a short osteophyte with length less than 1/2 disk spacing; “3” implies longer and thicker osteophyte with length greater than 1/2 disk spacing; “4” and “5” are rare cases of large osteophytes that can bridge or extend to the next vertebra but have osteophyte that are straight or bent respectively.

Five vertebrae of rank 0 and five vertebrae of rank 3 were chosen as query vertebrae. The rank 0 vertebrae simulate queries with normal vertebrae and rank 3 vertebrae simulate queries with osteophytes. For each query, different shape distances between the query and the 169 expert graded vertebrae were calculated and ranked according to increasing distance from the query shape. Since the closest neighbor of any query shape is the query itself, we excluded the closest neighbor from the following analysis.

Suppose q is the query vertebra and k = 1, ⋯, 169 are the ranked vertebrae. Let g(q) and g(k) refer to the expert grading of the query and k^th ranked vertebra. We expect g(k) to be similar to g(q) for low values of k. To measure this, we calculated the average grade up to rank i as $\mathit{\text{AG}}=\frac{1}{i-1}{\displaystyle {\sum }_{k=2}^{i}g(k)}$. We expect this number to be close to the grade of the query g(q). Of course, the grades of the ranked vertebrae are never exactly the same as the grade of query vertebra. To evaluate the difference, we calculated the average positive difference of the grades as ${\mathrm{\Delta }}^{+}=\frac{1}{i-1}{\displaystyle {\sum }_{k=2}^i{(g(k)-g(q))}^{+}}$, where (g(k) − g(q))⁺ = (g(k) − g(q)) if (g(k) − g(q)) > 0, else (g(k) − g(q))⁺ = 0. The average positive difference tells us the number of more severe grades up to i. We also calculated the average negative difference as ${\mathrm{\Delta }}^{-}=\frac{1}{i-1}{\displaystyle {\sum }_{k=2}^i{(g(k)-g(q))}^{-}}$, where (g(k) − g(q))⁻ = −(g(k) − g(q)) if (g(k) − g(q)) < 0, else (g(k) − g(q))⁻ = 0. The average negative difference should tell us the number of less severe grades up to i.

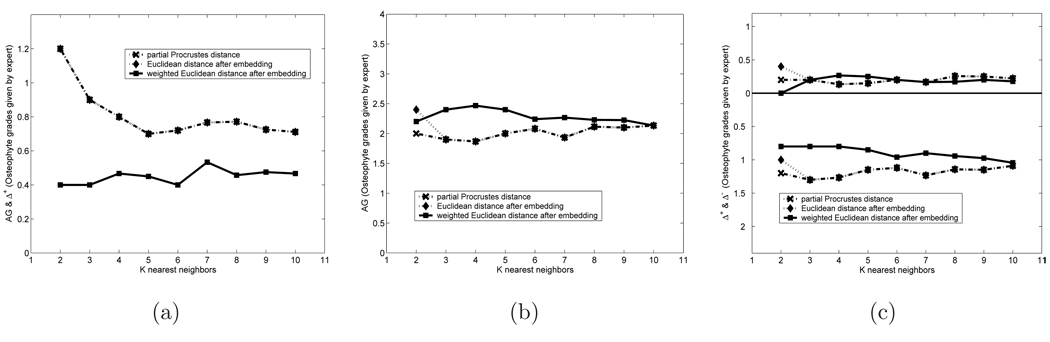
Figure 6 shows the average AG, Δ⁺, and Δ⁻ for the partial Procrustes distance, the Euclidean and weighted Euclidean shape distances after embedding for grade 0 and 3 queries. The grade 0 results are somewhat special. Because there is no grade lower than 0, it does not have any non-zero Δ⁻, hence its AG and Δ⁺ are identical. Thus we only plot the AG, which is shown in Figure 6(a) for grade 0. Figures 6(b) and (c) show the AG and the Δ⁺ and Δ⁻ for the grade 3 retrievals.

Figure 6.

Comparison the Efficacy of Different Distance Metrics: a) AG and Δ⁺ for Grade 0 Queries; (b) AG for Grade 3 Queries; (c) Δ⁺ and Δ⁻ for Grade 3 Queries

We can infer the following from the figure:

1. The partial Procrustes distance and the Euclidean distance are almost identical in behavior. This is not too surprising considering that the embedding is designed to keep these distances as close to each other as possible.

2. The grading obtained by the weighted Euclidean distance has a closer match to expert grades than the partial Procrustes or the Euclidean distance. The improvement is particularly obvious for grade 0 queries.

3. The grading obtained by the weighted Euclidean distance is very close to expert grading in all queries. For grade 0 queries the average grade is between 0.4 and 0.5 even for the 10^th nearest neighbor. For grade 3 queries the average grade is around 2.13 for the 10^th nearest neighbor.

This shows clearly that the weighted Euclidean distance mimics expert grading, and that shape can indeed be used to retrieve by osteophyte presence and severity.

6.2 Comparing embedding distance with partial Procrustes distance

Next, we evaluated the closeness of the Euclidean distance after embedding to the partial Procrustes distance. The results of section 4 indicate that our embedding is optimal but do not provide numerical estimates of how close the two distances are. We measured this experimentally.

To measure the similarity between the two distances we calculated fraction squared difference (FSD)

$$FSD=(d_E^2({[z_i]}_s,{[z_j]}_s)-d_P^2({[z_i]}_s,{[z_j]}_s))/d_P^2({[z_i]}_s,{[z_j]}_s)$$

as well as the fractional difference (FD)

$$\mathit{\text{FD}}=|d_E({[z_i]}_s,{[z_j]}_s)-d_P({[z_i]}_s,{[z_j]}_s)|/d_P({[z_i]}_s,{[z_j]}_s)$$

between pairs [z_i]_s, [z_j]_s from the database. A set of 1000 vertebrae were randomly chosen from the database and the FSD and FD was calculated for all pairs of vertebrae from this set ( total number of pairs = 1000 × 999 ≃ 10⁶).

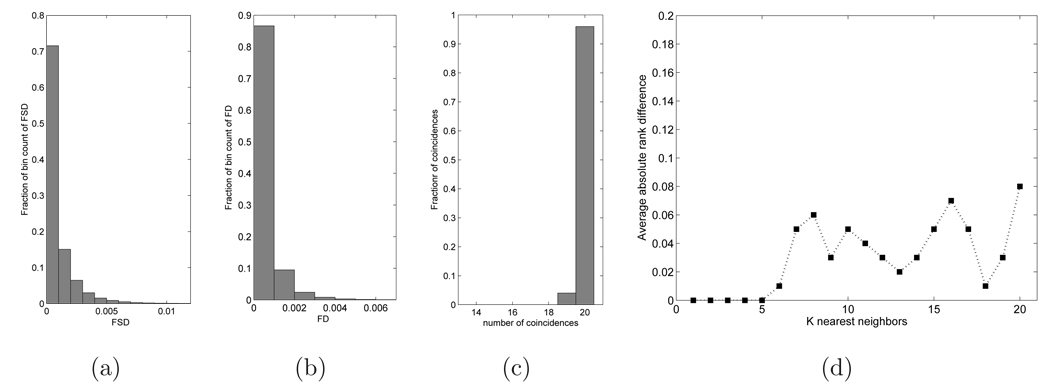
The average and standard deviation of the FSD and FD are given in Table 1 and histograms of FSD and FD are shown in figure 7(a), (b). From the table and the figures, it is clear that the Euclidean distance following optimal embedding is very similar to the partial Procrustes distance.

Table 1.

Mean and standard deviation (STD) of FSD and FD of pairs from a set of 1000 vertebrae

Quantity	Mean	STD
FSD	9.19 × 10−4	1.43 × 10−3
FD	4.59 × 10−4	7.22 × 10−4

Figure 7.

Metric distortion after optimal shape embedding: (a) Histogram of FSD of pairs from a set of 1000 vertebrae; (b) Histogram of FD; (c) Histogram of S_P ∩ S_E for 100 queries; (d) Average rank difference for 100 queries

This explains why the performance of partial Procrustes distance and Euclidean distance are virtually identical in the previous experiment.

Next, we compared the nearest neighbor structure of the data set before and after embedding. This was done as follows: From the set of 1000 vertebrae used in the above experiment, 100 vertebrae were randomly chosen as query vertebrae. For each query vertebra, the set of 20 nearest vertebrae was found according to the partial Procrustes distance d_P and the embedded Euclidean distance d_E. Let these sets be S_P and S_E respectively. Then S_P ∩ S_E is the set of vertebrae that are common to both retrievals in the query. The distribution of the number of elements in S_P ∩ S_E over the 100 queries is shown in figure 7(c). For 97 of 100 queries the sets S_P and S_E were identical, and for 3 queries they differed by a single image.

A more sensitive measure of nearest neighbor structure was also created. Elements of each set S_P and S_E were ranked in increasing distance from the query. Let r_P : S_P → {1, ⋯, 20} be the rank function of S_P, i.e. the rank of [z]_s ∈ S_P is r_P ([z]_s) (rank 1 is the nearest neighbor to the query and rank 20 is the 20^th-nearest neighbor), and let r_E : S_E → {1, ⋯, 20} be the rank function of S_E. For each i ∈ {1, ⋯, 20}, if $r_P^{-1}(i)\in S_P\cap S_E,\text{then}|r_E(r_P^{-1}(i))-i|$ is the difference in the rank of the vertebra that was in the i^th position in S_P. Figure 7(d) shows the average value of $|r_E(r_P^{-1}(i))-i|$ over the 100 queries as a function of i. The figure shows that the first 5 neighbors were identical over the 100 queries, and the average difference in the rank was ≤ 0.1 for the first 20 neighbors.

These experiments show that the embedded Euclidean distance is a very good approximation to the partial Procrustes distance and can be used in shape retrieval queries.

6.3 Indexing performance

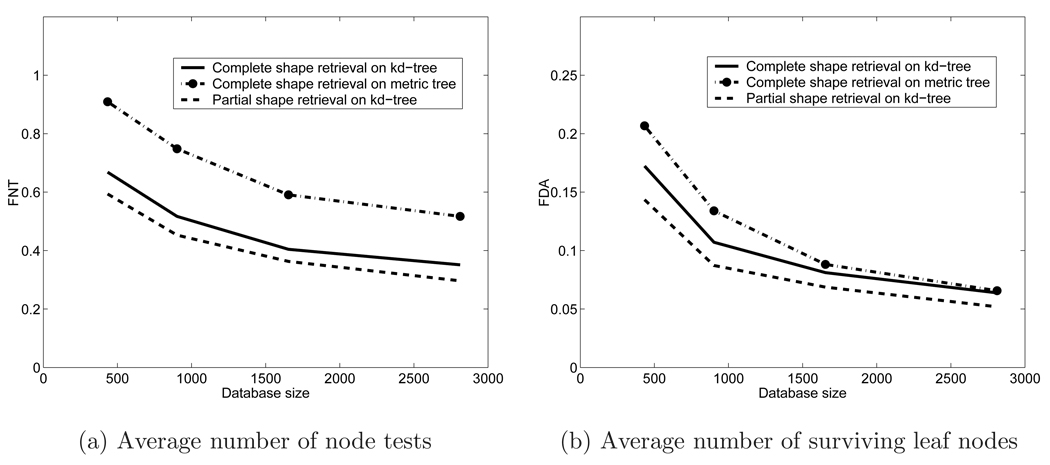
We also evaluated the efficiency of the indexing scheme using kd-tree after shape embedding and compared it to a metric tree in the original metric space. The 2812 shapes were randomly sampled into sets of size 434, 902, 1654 and 2812. Each set was indexed in the original shape space by a metric tree and after embedding by a kd-tree. Every shape in each database was used as a query shape and k-nearest neighbor vertebral images were retrieved using the Euclidean shape distance for k = 10 and 20 neighbors. The average number of node tests per query and the average number of surviving leaf nodes were recorded. Recall that the first measures the computational burden of indexing while the second measures the disk access performance.

Table 2 shows the performance measures as a function of the database size and k for kd- and metric trees. The performance measures are expressed as absolute numbers and as a fraction of the database size. The fractions should remain constant for an indexing scheme with linear complexity and should decrease with the size of the database for sub-linear complexity. Figure 8 shows the fractions FNT and FDA (defined in the caption of Table 2), for the k=10 nearest neighbors case, as a function of database size. It is clear from the figure that the indexing algorithms are sub-linear in complexity.

Table 2.

Indexing performance for the kd-tree and the metric tree. (k is the number of retrieved nearest neighbors, NT is the average number of node tests, $\mathit{\text{FNT}}=\frac{\mathit{\text{NT}}}{\mathit{\text{DBSize}}}$ is NT expressed as a fraction of database size, DA is the average number of disk accesses, $\mathit{\text{FDA}}=\frac{\mathit{\text{DA}}}{\mathit{\text{DBSize}}}$ is DA expressed as a fraction of database size.)

	DB	k = 10				k = 20
	Size	NT	FNT	DA	FDA	NT	FNT	DA	FDA
Kd-tree	434	289.9	0.67	74.8	0.17	351.3	0.81	104.6	0.24
	902	466.2	0.52	96.6	0.11	559.9	0.62	136.4	0.15
	1654	668.7	0.40	134.2	0.081	800.2	0.48	187.7	0.11
	2812	987.6	0.35	179.5	0.064	1172.0	0.42	248.7	0.09
Metric tree	434	394.6	0.91	89.7	0.21	446.5	1.03	119.7	0.28
	902	675.1	0.75	120.9	0.13	758.3	0.84	163.6	0.18
	1654	976.9	0.59	145.8	0.09	1093.3	0.66	198.3	0.12
	2812	1453.9	0.52	184.6	0.07	1615.0	0.57	251.1	0.09

Figure 8.

Comparison of indexing performance

Recall that the kd-tree can be used for retrieval with respect to weighted Euclidean distance. In a separate experiment we evaluated the relative performance of the kd-tree for this. We used a diagonal weight matrix W in which all entries were set to 0.01 except those corresponding to indices i = 14–24, which were set to 1.0. These indices are the ones that fall on an anterior osteophyte.

The average number of node tests and the average number of disk accesses for 10- and 20- nearest neighbor queries using the weighted Euclidean distance are shown in Table 3. A comparison with Table 2 shows that the performance of the kd-tree for weighted Euclidean distance is comparable to the performance for Euclidean distance. This is also clear in figure 8 where the fractions are plotted as a function of the database size.

Table 3.

Indexing performance for nearest neighbor queries using weighted Euclidean distances on kd-tree. (k is the number of retrieved nearest neighbors, NT is the average number of node tests, $\mathit{\text{FNT}}=\frac{\mathit{\text{NT}}}{\mathit{\text{DBSize}}}$ is NT expressed as a fraction of database size, DA is the average number of disk accesses, $\mathit{\text{FDA}}=\frac{\mathit{\text{DA}}}{\mathit{\text{DBSize}}}$ is DA expressed as a fraction of database size. )

DB	k = 10				k = 20
Size	NT	FNT	DA	FDA	NT	FNT	DA	FDA
434	257.7	0.59	62.3	0.14	318.4	0.73	89.8	0.21
902	408.5	0.45	78.7	0.09	498.6	0.55	114.1	0.13
1654	600.1	0.36	113.6	0.07	719.2	0.44	160.2	0.10
2812	833.2	0.30	146.0	0.05	996.8	0.36	204.5	0.07

We can draw several conclusions from this experiment:

1. All three indexing and retrieval strategies are sub-linear in complexity. That is, indexing with any of these strategies is effective and useful.

2. The kd-tree after embedding outperforms the metric tree. The average number of node tests for the kd-tree is only 2/3 of that of the metric tree. The reason for the difference is that the intermediate nodes in the metric tree overlap with each other while the kd-tree has disjoint nodes and has the better pruning capability.

3. The performance of the kd-tree with weighted Euclidean metric is similar to the performance with the Euclidean metric. This suggests that the same kd-tree is useful for retrieval in both cases.

6.4 Examples of retrievals

As an illustration of the use of the shape retrieval system, figure 9 (a)–(b) shows some retrievals using query images containing a lumbar (Fig. 9(a)) and cervical (Fig. 9(b)) vertebrate, respectively. In each row of figure 9 the leftmost image is the query image and the subsequent images are retrievals ranked by increased distance from the query image. The (a) and (b) parts of the figure show two queries. Within the (a) and (b) parts of the figure, the first row shows retrieval with respect to Euclidean metric and the second row shows retrieval with respect to the weighted Euclidean metric.

Figure 9.

Shape query samples

6.5 Comparison with equivariant embedding

Finally, we compared the efficiency of equivariant embedding (section 4.1) with optimal embedding. The comparison experiment used a set of 434 vertebral boundaries, and as before, kd-trees were used after the data was embedded using equivariant embedding (EE) and optimal embedding (OE).

The execution time on a P4 1.8GHz Dell desktop computer for indexing after equivariant embedding was 41.42 hours to construct the tree. On the other hand, it only took 2.11 minutes to construct the tree after optimal embedding. The difference in these timings reflects the additional computational cost of significantly higher dimension of equivariant embedding. Similarly, the average query time (all 434 images used one at a time for querying) for 10 nearest neighbor retrieval were 319.42 seconds and 0.29 seconds respectively for equivariant embedding and optimal embedding. From this it is clear that the optimal embedding is significantly faster than equivariant embedding.

This was also the reason for only using 434 boundaries in these experiments. The tree construction cost of equivariant embedding was prohibitive for equivariant embedding with the entire data set.

7 Conclusions

Efficient shape indexing for similarity retrieval is important in medical image databases. We report an optimal shape embedding procedure to index shapes for complete and partial shape similarity retrieval. The technique optimally embeds shapes back into pre-shape spaces. Experimental results show that (1) Shape retrieval is useful in retrieving vertebrae with expert grades similar to the query vertebra, (2) The optimal embedding gives distances that are very close to the original partial Procrustes distances, (3) Indexing with kd-tree after embedding outperforms indexing with metric tree while simultaneously supporting Euclidean and weighted Euclidean retrieval, (4) The optimal embedding gives significantly faster algorithms than equivariant embedding.

One alternative to the technique presented in this paper is to use density-based clustering methods to derive a piecewise embedding [13, 42]. We hope to investigate this and other possibilities in the future.

Appendix

Appendix A: Proof of $d_E^2(\phi (u),\phi (v))=d_F^2({[u]}_s,{[v]}_s)$ for the equivariant embedding φ

In this section, we prove that the equivariant embedding φ defined in Section 4.1 preserves full Procrustes distance after embedding for 2-d object configurations. We start with computing the full Procrustes distance between two shapes [u]_s and [v]_s. As given in Section 3.3, $d_F^2({[u]}_s,{[v]}_s)={\text{min}}_{\beta ,\theta }\parallel {[u]}_p-\beta e^{i\theta }{[v]}_p{\parallel }_{{𝒞}^n}^2$. We first compute the full Procrustes fit and distance through the procedure given in [10] by expanding $d_F^2({[u]}_s,{[v]}_s)$:

$$\begin{array}{ll}{d}_F^2({[u]}_s,{[v]}_s)\hfill & =\underset{\beta ,\theta }{\text{min}}({[u]}_p-\beta e^{i\theta }{[v]}_p)({[u]}_p-\beta e^{i\theta }{[v]}_p{)}^{*}\hfill \\ \hfill & =\underset{\beta ,\theta }{\text{min}}({[u]}_p{[u]}_p^{*}-\beta e^{i\theta }{[v]}_p{[u]}_p^{*}-\beta e^{-i\theta }{[u]}_p{[v]}_p^{*}+{\beta }^2{[v]}_p{[v]}_p^{*}).\hfill \end{array}$$

Denote ${[u]}_p{[v]}_p^{*}=\lambda e^{i\varphi }$ where the real number $\lambda =\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}>0$. We have ${[v]}_p{[u]}_p^{*}=\lambda e^{-i\varphi },{[u]}_p{[u]}_p^{*}=1\text{and}{[v]}_p{[v]}_p^{*}=1$ as these are pre-shapes. Hence,

$${[u]}_p{[u]}_p^{*}-\beta e^{i\theta }{[v]}_p{[u]}_p^{*}-\beta e^{-i\theta }{[u]}_p{[v]}_p^{*}+{\beta }^2{[v]}_p{[v]}_p^{*}=1-2\beta \lambda \text{cos}(\theta +\varphi )+{\beta }^2.$$ (14)

Clearly, to minimize (14), we need to maximize 2βλ cos (θ + ϕ) so that the minimizing θ* = − ϕ. For the minimizing β*, we need to minimize 1 + β² − 2βλ. Hence, ${\beta }^{*}=\lambda =\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}$. Substituting β* and θ* into (14), we have $d_F^2({[u]}_s,{[v]}_s)=1-\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}^2$.

We now prove $d_E^2(\frac{{[u]}_p^{*}{[u]}_p}{\sqrt{2}},\frac{{[v]}_p^{*}{[v]}_p}{\sqrt{2}})=\frac{1}{2}\parallel {[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p{\parallel }_{{𝒞}^{n\times n}}^2=1-\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}^2$. Using $\parallel {[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p{\parallel }_{{𝒞}^{n\times n}}^2=\mathit{\text{Tr}}(({[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p)({[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p{)}^{*})$ with Tr( ) as the matrix trace, we have $d_E^2(\frac{{[u]}_p^{*}{[u]}_p}{\sqrt{2}},\frac{{[v]}_p^{*}{[v]}_p}{\sqrt{2}})=\frac{1}{2}Tr(({[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p)({[u]}_p^{*}{[u]}_p-{[v]}_p^{*}{[v]}_p{)}^{*})=\frac{1}{2}Tr({[u]}_p^{*}{[u]}_p{[u]}_p^{*}{[u]}_p-{[u]}_p^{*}{[u]}_p{[v]}_p^{*}{[v]}_p-{[v]}_p^{*}{[v]}_p{[u]}_p^{*}{[u]}_p+{[v]}_p^{*}{[v]}_p{[v]}_p^{*}{[v]}_p)=\frac{1}{2}(Tr({[u]}_p^{*}{[u]}_p+{[v]}_p^{*}{[v]}_p)-2Tr({[u]}_p^{*}{[u]}_p{[v]}_p^{*}{[v]}_p)=1-Tr({[u]}_p^{*}{[u]}_p{[v]}_p^{*}{[v]}_p)\text{as}{[u]}_p{[u]}_p^{*}=1,{[v]}_p{[v]}_p^{*}=1$, Tr(A + B) = Tr(A) + Tr(B) and Tr(AB) = Tr(BA) for A,B ∈ 𝒞^n×n. While $\mathit{\text{Tr}}({[u]}_p^{*}{[u]}_p{[v]}_p^{*}{[v]}_p)=\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}^2\text{since}\mathit{\text{Tr}}({[u]}_p^{*}{[v]}_p)=\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}$, we finally have $d_E^2(\frac{{[u]}_p^{*}{[u]}_p}{\sqrt{2}},\frac{{[v]}_p^{*}{[v]}_p}{\sqrt{2}})=1-\parallel {[u]}_p{[v]}_p^{*}{\parallel }_{{𝒞}_n}^2=d_F^2({[u]}_s,{[v]}_s)$.

Appendix B: Proof of (6) in Section 4.2

Here we give the proof for $J_1(\mathrm{\Theta })={\displaystyle {\sum }_k{\displaystyle {\sum }_l{d}_E^2({[u_k]}_s,{[u_l]}_s)=2N}}{\displaystyle {\sum }_k\parallel e^{i{\theta }_k}{[u_k]}_p-}N\frac{1}{N}{\displaystyle {\sum }_l{e}^{i{\theta }_l}{[u_l]}_p{\parallel }_{{𝒞}^n}^2}$:

$$\begin{array}{ll}{J}_1(\mathrm{\Theta })\hfill & ={\displaystyle \sum _k{\displaystyle \sum _l{d}_E^2({[u_k]}_s,{[u_l]}_s)}}\hfill \\ \hfill & ={\displaystyle \sum _k{\displaystyle \sum _l({[u_k]}_p{[u_k]}_p^{*}-e^{i({\theta }_k-{\theta }_l)}{[u_k]}_p{[u_l]}_p^{*}-e^{i({\theta }_l-{\theta }_k)}{[u_l]}_p{[u_k]}_p^{*}+{[u_l]}_p{[u_l]}_p^{*})}}\hfill \\ \hfill & =N(2{\displaystyle \sum _k{[u_k]}_p{[u_k]}_p^{*}-{\displaystyle \sum _k{e}^{i{\theta }_k}}{[u_k]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}{[u_l]}_p^{*}+\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p{e}^{-i{\theta }_k}{[u_k]}_p^{*}}})\hfill \\ \hfill & =N(2{\displaystyle \sum _k{[u_k]}_p{[u_k]}_p^{*}-2N\frac{1}{N}{\displaystyle \sum _k{e}^{i{\theta }_k}}{[u_k]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}}{[u_l]}_p^{*})}\hfill \\ \hfill & =2N({\displaystyle \sum _k{[u_k]}_p{[u_k]}_p^{*}-2N\frac{1}{N}{\displaystyle \sum _k{e}^{i{\theta }_k}}{[u_k]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}}{[u_l]}_p^{*}+N\frac{1}{N}{\displaystyle \sum _k{e}^{i{\theta }_k}}{[u_k]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}}{[u_l]}_p^{*})}\hfill \\ \hfill & =2N{\displaystyle \sum _k({[u_k]}_p{[u_k]}_p^{*}-e^{i{\theta }_k}{[u_k]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}}{[u_l]}_p^{*}-\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p{e}^{-i{\theta }_k}{[u_k]}_p^{*}}\hfill \\ \hfill & +\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p\frac{1}{N}{\displaystyle \sum _l{e}^{-i{\theta }_l}}{[u_l]}_p^{*})\hfill \\ \hfill & =2N{\displaystyle \sum _k\parallel e^{i{\theta }_k}{[u_k]}_p-\frac{1}{N}{\displaystyle \sum _l{e}^{i{\theta }_l}}{[u_l]}_p{\parallel }_{{𝒞}^n}^2.}\hfill \end{array}$$