Abstract
Application of dynamical systems tools has recently revealed in surface ocean currents produced by a Hybrid-Coordinate Ocean Model (HYCOM) simulation the presence of a persistent large-scale Lagrangian coherent structure (LCS) on the southern portion of the west Florida shelf (WFS). Consistent with satellite-tracked drifter trajectories, this LCS constitutes a cross-shelf barrier for the lateral transport of passive tracers. Because of the constraints that the above LCS, as well as smaller-scale LCSs lying shoreside, can impose on pollutant dispersal and its potentially very important biological consequences, a study was carried out on the nature of the surface ocean Lagrangian motion on the WFS. The analysis is based on the same simulated surface ocean velocity field that has been able to sustain the aforementioned persistent cross-shelf transport barrier. Examination of several diagnostics suggests that chaotic stirring dominates over turbulent mixing on time scales of up to two months or so. More specifically, it is found on those time scales that tracer evolution at a given length scale is governed to a nonnegligible extent by coarser-scale velocity field features, fluid particle dispersion is spatially inhomogeneous, and the Lagrangian evolution is more irregular than the driving Eulerian flow.
1. Introduction
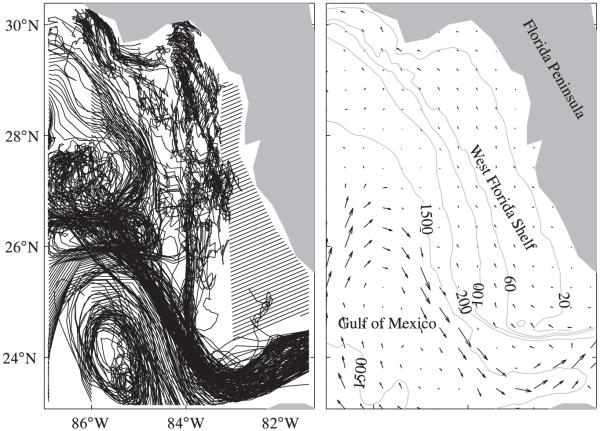
Recent analysis (Olascoaga et al. 2006) of surface ocean velocities produced by a Hybrid-Coordinate Ocean Model (HYCOM) simulation of the west Florida shelf (WFS) has revealed the presence of a cross-shelf transport barrier near the same location as the boundary of the so-called ‘forbidden zone,’ which is a triangular-shaped region on the southern portion of the WFS that was found not to be visited by satellite-tracked drifting floats deployed outside of the region (Yang et al. 1999). The ‘forbidden zone’ is indicated in the left panel of Fig. 1 along with trajectories for simulated drifting floats deployed outside of this region. The right panel of Fig. 1 shows a typical surface current snapshot as produced by HYCOM, which was used to produce the trajectories. Note the tendency of the simulated trajectories to avoid the forbidden zone. The cross-shelf transport barrier on the WFS was characterized in Olascoaga et al. (2006) as a large-scale Lagrangian coherent structure (LCS), a notion recently developed in the area of dynamical systems (Green et al. 2007; Haller 2001; Lekien and Coulliette 2007; Lekien et al. 2005, 2007; Mathur et al. 2007; Shadden et al. 2005, 2006). Loosely speaking, in an unsteady two-dimensional flow defined over a finite time interval, an LCS can be regarded as a material line such that initially nearby fluid particles straddling the line experience maximal forward-time divergence or convergence. Like invariant manifolds of steady or time-periodic flows, LCSs delineate the boundary between immiscible fluid domains with quite distinct advective characteristics. The large-scale LCS simulated by Olascoaga et al. (2006) was found to wobble with a complicated spatiotemporal structure, which is partly supported by the seasonal analysis of drifter trajectories presented by Morey et al. (2003). The cause of this wobbling may be related to the change in position of the southward flowing jet along the edge of the WFS, which has been argued (Hetland et al. 1999) to be induced by the pressure imposed on the WFS by the loop current. Possible physical explanations for the existence of the forbidden zone itself have been discussed by Yang et al. (1999). These emphasize the role of the above coastal jet, whose transport is primarily offshore as a result of the combined effects of the alongshore wind forcing, and the convergent coastal geometry and bottom topography.
Fig. 1.
(left) Trajectories on the period 1 Feb 2004 through 1 Apr 2004 for simulated drifting floats deployed outside the ‘forbidden zone’ on the WFS as identified by Yang et al. (1999), which is indicated by the cross-hatched region. (right) A snapshot on 1 Mar 2004 of surface ocean velocity field as produced by a HYCOM simulation of the WFS, which was used to produce the trajectories in the plot on the left. Maximum velocity magnitude is roughly 2 m s−1. Indicated bathymetry contours are in meters.
In addition to being consequential for the lateral transport of passive tracers on the surface of the ocean in the WFS, the transport barrier on the WFS has potentially very important implications for the transport of biologically active tracers. We have argued in Olascoaga et al. (2006) that this cross-shelf transport barrier provides favorable conditions for the development of harmful algal blooms caused by the toxic dinoflagellate Karenia brevis (e.g., Brand and Compton 2007; Walsh et al. 2006) by favoring substantial toxic dinoflagellate concentration and nutrient buildup on its shoreside. Using a population dynamics model, in Olascoaga et al. (2008) we studied the evolution of a harmful algal bloom that was detected using satellite imagery and in situ observations (Hu et al. 2005), and found that it was very strongly tied to small-scale LCSs on the shoreside of the large-scale LCS that characterizes the cross-shelf transport barrier on the WFS.
Motivated by the constraints on pollutant and plankton dispersal imposed by the cross-shelf transport barrier on the WFS, in this article we investigate in more detail than in Olascoaga et al. (2006) the nature of the Lagrangian motion on the surface of the ocean in this region. Our goal is to assess the importance of chaotic stirring and turbulent mixing over time scales of the order of a few months. By ‘chaotic stirring’ we here refer to a situation wherein the advection field is spatially quasicoherent and temporally quasiregular on time scales over which the fluid particle motion is predominantly irregular (Brown and Smith 1991; Swanson and Pierrehumbert 1997). By ‘turbulent mixing’ we refer to the situation wherein both the velocity field is spatiotemporally incoherent and the Lagrangian motion is irregular. Our focus on Lagrangian motion over time scales of the order of a few months is justified by the fact that the characteristic blooming time scale of harmful algae in the WFS is about a month (Brand and Guillard 1981), and the estimated residence time for passively advected particles on the shoreside of the cross-shelf transport barrier on the WFS is two months or so (Olascoaga et al. 2006). To achieve our goal, in addition to computing LCSs as in Olascoaga et al. (2006), in this article we consider several passive tracer evolution diagnostics. These diagnostics are kinetic energy, tracer variance, and velocity gradient spectra; probability distribution functions (PDFs) of finite-time Lyapunov exponents (FTLEs); and Eulerian and Lagrangian autocorrelation times of velocity gradient components. The tracer transport characterization presented here is based on a surface velocity field produced by the same HYCOM simulation considered in Olascoaga et al. (2006), which was able to sustain a cross-shelf transport barrier on the WFS with similar characteristics as those suggested by the trajectories of satellite-tracked drifters (Yang et al. 1999). Several spatiotemporal truncations of these simulated surface currents are considered to examine the sensitivity of the modeled LCSs to the truncations, thereby allowing us to determine the extent to which tracer evolution at a given length scale is controlled by velocity features at comparable or much larger length scale. The above Lagrangian motion diagnostics were considered by Shepherd et al. (2000) in their study of the nature of Lagrangian dynamics in the middle atmosphere; our analysis closely follows that of those authors. Similar diagnostics have been considered in many studies of tracer evolution in the atmosphere (e.g., Bartello 2000; Hu and Pierrehumbert 2001; Lukovich and Shepherd 2005; Ngan and Shepherd 1999a,b; Norton 1994; Pierce and Fairlie 1993; Pierrehumbert 1991, 1994; Pierrehumbert and Yang 1993; Waugh and Plumb 1994; Waugh and Rong 2002). LCSs and/or some of the above or other similar diagnostic tools have been also employed in the study of the nature of Lagrangian surface ocean dynamics, albeit more recently (e.g., Abraham and Bowen 2002; d’Ovidio et al. 2004, 2008; Garcia-Olivares et al. 2007; LaCasce and Ohlmann 2003; Lacorata et al. 2001; Lehahn et al. 2007; Lekien and Coulliette 2007; Lumpkin and Flament 2001; Marshall et al. 2006; Waugh and Abraham 2008; Waugh et al. 2006).
The plan of the article is as follows. In section 2 the various HYCOM output versions considered in our passive tracer evolution study are discussed along with some details of the Lagrangian calculation techniques used in this paper. Section 3 presents the results of the analysis of the several computed passive tracer transport diagnostics. A discussion is offered in section 4. Finally, a summary and conclusions are presented in section 5.
2. Methods
Numerical model output provides a surface flow description that is suitable for use to study passive tracer evolution. Also, it has the advantage of allowing for a spatiotemporal coverage that is impossible to be attained with existing observational systems. Thus, as in Olascoaga et al. (2006), we consider surface velocities produced by an HYCOM simulation of the WFS for the year 2004.
The simulated surface currents consist of surface velocity fields extracted in the WFS domain from a 0.04° horizontal-resolution (roughly 8-km longitude × 3-km latitude), free-running HYCOM simulation of the Gulf of Mexico, itself nested within a 0.08° horizontal-resolution Atlantic basin data-assimilative nowcast, which was generated at the Naval Research Laboratory as part of a National Oceanographic Partnership Program in support of the Global Ocean Data Assimilation Experiment (Chassignet et al. 2006, 2007). The Atlantic nowcast was forced with realistic high-frequency forcing obtained from the U.S. Navy Operational Global Atmospheric Prediction System (NOGAPS) operational atmospheric model. It assimilated sea surface temperature and anomalous sea surface height from satellite altimetry with downward projection of anomalous temperature and salinity profiles. The nested Gulf of Mexico model was driven by the same high-frequency atmospheric forcing. The topography used in both models was derived from the ETOPO5 5-Minute Gridded Global Relief Data Collection, with the coastline in the Gulf of Mexico model following the 2-m isobath. Both models included river runoff.
Four surface velocity sets, denoted R4D, R4W, R28D, and R28W, consisting of several spatiotemporal truncations of surface velocities produced by the above described HYCOM simulation are considered here. Set R4D has daily archived surface velocity fields and full 0.04° horizontal resolution. Surface velocities in set R4W also have full 0.04° horizontal resolution, but numerical values are stored weekly. Sets R28D and R28W are composed of coarser-grained 0.28° horizontal-resolution surface velocities archived daily and weekly, respectively. Note that, to make a fair comparison of the sensitivity of Lagrangian calculations with respect to spatial and temporal velocity truncations, the spatial (temporal) resolution of R28D and R28W (R4D and R28D) velocities has been chosen to be 7 times coarser than that of R4D and R4W (R4W and R28W) velocities. We note in passing that the spatiotemporal resolution of surface velocities in set R28W, the coarsest-grained set considered here, is comparable to that of altimetry-derived gridded surface velocities, which have been recently employed in Lagrangian surface ocean circulation studies (Beron-Vera et al. 2008; Marshall et al. 2006; Waugh and Abraham 2008; Waugh et al. 2006).
For the study reported here we have chosen to concentrate on tracer evolution around 1 March 2004. As our interest relies on time scales of the order of a few months, a time interval around this reference date that is no longer than 120 days was considered in our calculations (e.g., some Lagrangian trajectory integrations were carried out forward in time during 60 days starting on 1 March 2004, other integrations were performed backward in time for 60 days starting on this date, and other integrations were produced forward in time during 30 days starting 15 days before 1 March 2004). The Lagrangian integrations were carried out offline using the standard fourth-order Runge–Kutta method with a fixed 1-h time step. Velocity values at each time step were obtained by linearly interpolating in space and time stored values. The results presented below were found to be fairly insensitive to the above reference date, integration time step, and interpolation scheme choices. Indeed, results of computations (not shown) carried out for reference dates 1 June 2004, 1 August 2004, and 1 October 2004 produced no significant differences with respect those presented in this paper. Also, some calculations were repeated using a time-step-adapting integrator along with a tricubic interpolation scheme, which produced only minor differences with respect to those reported here. Finally, because the variance of the distance between adjacent grid points in the WFS model domain considered is small, we have assumed a Cartesian geometry, with coordinates x and y, in all of the calculations presented here. Because the direction of the flow is predominantly southward and along the edge of the WFS, instead of considering (x, y) as being the traditional eastward–northward frame, it is convenient to choose the frame rotated clockwise by a 60° angle, so that x and y roughly represent along- and across-shelf coordinates, respectively.
3. Results
a. Lagrangian coherent structures
Theoretical, numerical, and experimental work has demonstrated that computation of FTLEs constitutes a practical and robust means of identifying LCSs (Green et al. 2007; Haller 2002; Haller and Yuan 2000; Lekien and Coulliette 2007; Lekien et al. 2005, 2007; Mathur et al. 2007; Shadden et al. 2005, 2006). The FTLE is a scalar measure of the finite-time separation rate of initially nearby fluid particles. More precisely, let x0 = (x0, y0) denote the position on the sea surface of a fluid particle at time t0. Its position at any time t, denoted x(t; x0, t0), follows by integrating the trajectory equation
| (1) |
where the overdot stands for time differentiation, and u = (u, v) is the sea surface velocity with u(v) being southeastward (northeastward), roughly along (across) the WFS. The FTLE can then be defined as
| (2a) |
where spec denotes matrix spectrum (eigenvalues) and
| (2b) |
Regions of maximum separation rates produce ridges in the FTLE field, which approximate LCSs. Because fluid particles that diverge in backward (forward) time converge in forward (backward) time, when the FTLE is computed by integrating particle trajectories backward (forward) in time, τ < 0 (τ > 0), a ridge in the FTLE field corresponds to an attracting (a repelling) LCS. Repelling and attracting LCSs delineate the boundary between immiscible fluid regions with quite distinct advective characteristics, and constrain, respectively, past and future path histories of passively advected fluid particles.
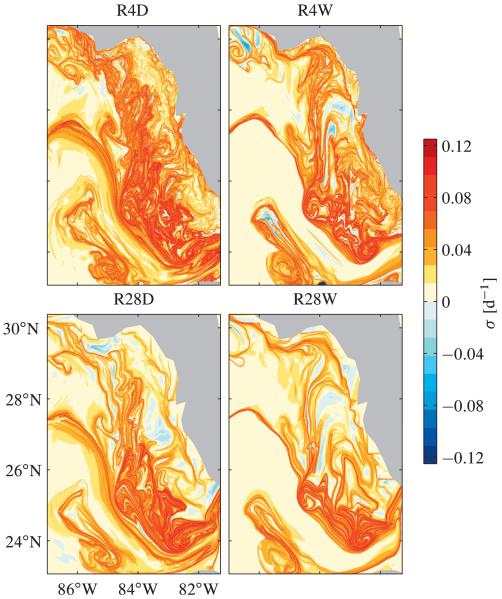
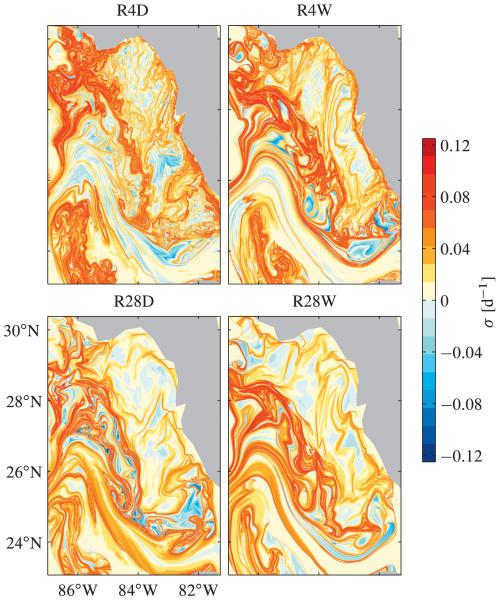
Figures 2 and 3 show FTLE fields1 on 1 March 2004 computed backward and forward in time for 60 days, respectively, based on the various spatiotemporally truncated simulated surface velocities R4D, R4W, R28D, and R28W described above. The FTLE fields shown were computed by evaluating (2) upon estimation of ∂x0 x(t0 + τ; x0, t0) using direct finite differentiation of fluid particle trajectories with initial positions distributed on a regular 0.007° resolution lattice. This allowed us to extract LCSs from these fields with a horizontal resolution about 6 times finer than that of R4D surface velocities, which have the full spatial resolution of the HYCOM simulation considered here. The regions of most intense red tones in Figs. 2 and 3 roughly indicate ridges of FTLE field. These regions, which are seen to form seemingly smooth (albeit highly structured) curves, constitute attracting and repelling LCSs, respectively. These LCSs are present year-round while undergoing a seasonal wobbling and exhibit nearly the same amount of complexity as those shown in Fig. 1 of Olascoaga et al. (2006). As pointed out above, their year-round persistence suggests the presence of a relentless cross-shelf transport barrier on the WFS in accordance with the analysis of year-long trajectories of satellite-tracked drifters (Yang et al. 1999). It is important to emphasize that the LCSs shown in Figs. 2 and 3 cannot be guessed visually from the inspection of velocity field snapshots (cf. upper-left panels in Figs. 2 and 3 and the right panel in Fig. 1).
Fig. 2.
FTLE field snapshots of 1 Mar 2004 computed backward in time for 60 days based on each of the four different surface velocity sets, denoted R4D, R4W, R28D, and R28W, consisting of various spatiotemporal truncations of surface velocities produced by an HYCOM simulation of the WFS. Set R4D has daily archived surface velocity fields and full 0.04° horizontal resolution. Surface velocities in set R4W also have full 0.04° horizontal resolution, but numerical values are stored weekly. Sets R28D and R28W are composed of coarser 0.28° horizontal-resolution surface velocities archived daily and weekly, respectively. Regions of most intense red tones roughly indicate ridges of FTLE field, which approximate attracting LCSs.
Fig. 3.
Same as in Fig. 2, but 60 days forward in time. Ridges roughly constitute repelling LCSs.
Before considering the sensitivity of the LCSs to spatiotemporal truncations, it is insightful to inspect the qualitative aspects of the attracting LCSs shown in the upper-left panel of Fig. 2, which were computed using unfiltered R4D velocities. Fluid particle trajectories that stretch relative to each other when integrated backward in time converge in forward time, which is analogous to passively advected tracers collecting in coherent structures obtained from flow visualization (Green et al. 2007). Furthermore, Shadden et al. (2005) have demonstrated that the FTLE field is exactly advected as a passive tracer in the long-time integration limit. Thus, the backward-time FTLE field distribution shown in the upper-left panel of Fig. 2, where the ridges approximate attracting LCSs, can be regarded as that one achieved by a passive tracer (the numerical FTLE values representing tracer concentration) on 1 March 2004 after being passively advected during 60 days by the full-resolution model velocity field from some suitably chosen initial inhomogeneous distribution. Rather than exhibiting excessive small-scale wiggling, the tracer distribution depicted in the upper-left panel of Fig. 2 shows long thin filaments that wrap around each other in typically large smooth patterns. These large-scale organized structures are characteristic of chaotic stirring, and thus it is tempting to conclude that the latter dominates over turbulent mixing on the time scales of interest. However, one should first check that these organized coherent structures do not dependent too strongly on the spatiotemporal resolution of the advection field.
Consider then all the FTLE distributions shown in Figs. 2 and 3. Comparison of the four panels in each of these figures reveals that the large-scale traits of both simulated attracting and repelling LCSs are indeed quite insensitive to spatiotemporal truncations of the surface velocity field. The simulated LCSs in all four panels in each of these figures present fairly the same large-scale features, in nearly the same location and with similar amount of complexity. Only details of the filamentary structure of both attracting and repelling LCSs computed using the most finely resolved R4D surface velocities are lost when these are computed using the more coarsely resolved surface velocities R4W, R28D, and R28W. Comparison of the upper with the lower panels and the left with the right panels reveals that the smoothing effect of the velocity truncation is somewhat more effective when the truncation is performed in space than when it is performed in time. This may be only an indication of the fact that 0.04° resolution in space is in some sense ‘finer’ than 1-day resolution in time (the result is expected to depend on the temporal-to-spatial grid spacing of the original—i.e., untruncated—velocity field).
The above analysis of LCSs demonstrates that the large-scale LCS identified in Olascoaga et al. (2006) with the cross-shelf transport barrier on the WFS suggested by satellite-tracked drifter trajectories (Yang et al. 1999) constitutes a fairly robust feature (sensitivity of only small-scale LCS features to velocity truncations indicates that leakage through the barrier may possibly be expected over a time scale longer than a few months). The above analysis also indicates that passive tracer evolution on a time scale of a few weeks to a few months is influenced to a nonnegligible extent by the large-scale low-frequency component of the surface ocean circulation, suggesting that chaotic stirring, rather than turbulent mixing, plays a predominant role. The analyses that follow aim to provide further support to these conclusions.
b. Spectra of kinetic energy, tracer variance, and velocity gradient
According to Bennett (1984) and Babiano et al. (1985), for a two-dimensional nondivergent flow with a wavenumber spectrum of kinetic energy of the form
| (3) |
where k is the total horizontal wavenumber, passive tracer evolution at a given scale is governed by velocity features at a comparable scale when 1 < α < 3 (local dynamics), whereas it is governed by velocity features at a larger scale when α ≥ 3 (nonlocal dynamics). When α = 1 transport is described by diffusion. The spectrum of the variance of passive tracer concentration is (Obhukov 1949)
| (4) |
where τc(k) is the characteristic time scale of tracer variance transfer at wavenumber k. This time scale is related to E(k) according to (Kraichnan 1971)
| (5) |
where is the integral turbulence (energy containing) length scale. In the nonlocal case, τc(k) ~ const as k → ∞; that is, there is a single characteristic time scale set by the large-scale components of the flow [when α = 3, τc ~ (lnk/ki)−1/2, which effectively approaches a constant at large k]. Accordingly, T(k) ~ k−1 as k → ∞. Assuming that both velocity and tracer variance dissipate at similar length scales, in the local case, τc(k) ~ k(α−3)/2 as k → ∞ so the characteristic time scale decreases as the horizontal scale decreases. In this case, T(k) ~ k(α−3)/2−1 as k → ∞, which is steeper than in the nonlocal case. Thus, while turbulent mixing may be identified with local dynamics, chaotic stirring may be associated with nonlocal dynamics. A further means (e.g., Haynes 2003; Lekien and Coulliette 2007) of assessing the importance of chaotic stirring and turbulent mixing consists of inspecting the scale dependence of the velocity gradient, which is responsible for controlling fluid particle relative dispersion (i.e., for initially nearby fluid particle pairs). If the spectrum G(k) of velocity gradient is larger at small k than at large k, then the time it takes to develop sufficiently thin passive tracer filaments that can be spread via turbulent mixing is much larger than the characteristic time scale for transport by the large-scale flow components. It must be noted that E(k) and G(k) are not independent quantities. Indeed, Lekien and Coulliette (2007) have shown that associated with a kinetic energy spectrum E(k) ~ k−3 is a velocity gradient spectrum G(k) ~ const.
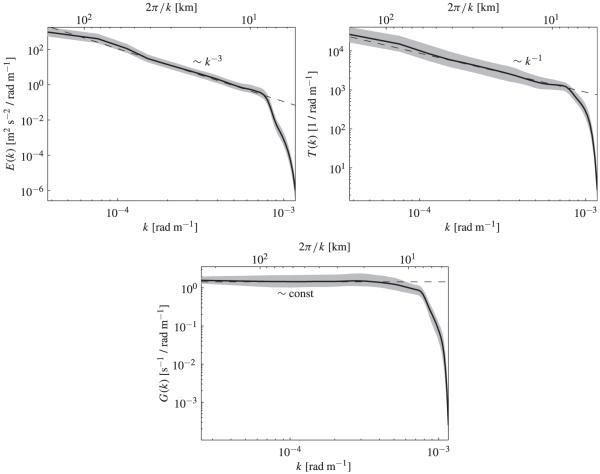
The top left, top right, and bottom panels of Fig. 4 show estimates of E(k), T(k), and G(k), respectively. These spectra were estimated as in Errico (1985) using the fast Fourier transform (FFT). This involves choosing the largest rectangular region included in the WFS model domain, and removing linear trends inside the region from the two components of the simulated surface velocity and backward-time FTLE field distributions computed using these velocities. The backward-time FTLE field distributions are considered here as proxy for passive tracer field distributions, with the numerical FTLEs values taken as nondimensional tracer concentration values. Removal of linear trends renders the simulated surface velocity components and backward-time FTLE field distributions periodic within the domain, and formally allows one to employ the FFT. This also prevents the smaller resolved scales to be aliased by larger unresolved scales. One-dimensional spectra are determined by first computing the corresponding two-dimensional spectra using the FFT, and then summing these densities within discrete annuli in the two-dimensional wavenumber space where k is defined as the central radii of those annuli. The one-dimensional spectra shown in Fig. 4 (solid curves) are the result of averaging 60 spectra computed in this manner using R4D surface velocities and FTLE fields in a 60-day time window centered on 1 March 2004 (the FTLEs are evaluated on the same grid as that of R4D velocities to allow a comparison of the various spectra with the above phenomenological results). The shaded band around the solid curve in each panel of this figure represents a one-standard-deviation uncertainty. The dashed line in each panel, which is plotted for reference, has indicated its corresponding k dependence. An alternative method for estimating kinetic energy spectra in domains with nonperiodic boundary conditions is provided by the modified Fourier transform derived in Lekien et al. (2004).
Fig. 4.
(top left) Kinetic energy, (top right) passive tracer variance, and (bottom) velocity gradient spectra estimates as a function of total horizontal wavenumber based on R4D surface velocities. Solid curves are 60-day averages while shaded bands around these curves represent one-standard-deviation uncertainties. Dashed lines, shown for reference, are labeled with their wavenumber dependencies.
The estimated E(k) (Fig. 4, top-left panel), T(k) (Fig. 4, top-right panel), and G(k) (Fig. 4, bottom panel) show power laws roughly adhering to the forms E(k) ~ k−3, T(k) ~ k−1, and G(k) ~ const, respectively, between 2π/k ≈ 8 km which roughly corresponds to the energy containing scale, and which is close to the spatial resolution of the R4D model velocities. The power-law forms of E(k) and T(k), which are consistent with the above passive tracer phenomenology, indicate that passive tracer evolution on the ocean surface in the WFS is governed by (weakly) spectrally nonlocal dynamics, consistent with chaotic stirring but not with turbulent mixing. The estimated form of G(k) is also consistent with those estimated for E(k) and T(k), and suggests that the development of patchy stretching regions that may be subject to turbulent mixing are only marginally favored.
c. Probability density functions of finite-time Lyapunov exponents
Chaotic stirring is characterized by substantial spatial inhomogeneity in the dispersion of fluid particles, while turbulent mixing by a rather spatially homogeneous fluid particle dispersal. The degree of spatial inhomogeneity in the dispersion of fluid particles can be studied by inspecting the PDF of FTLEs, P(σ), where the FTLEs are computed for initial conditions on the domain of interest. For a system with a single chaotic region, P(σ) is Gaussian-like, centered at the infinite-time Lyapunov exponent value. For a system with a mixed-phase space structure wherein regions of regular (periodic or quasiperiodic) and irregular (chaotic) motion are complexly interwined, P(σ) is multimodal where each extremum corresponds to the motion in a particular chaotic region (Harle and Feudel 2007; Szezech et al. 2005). Clearly, the spatially inhomogeneous particle dispersion characteristic of chaotic stirring cannot be described by a system with a single chaotic region; rather, it requires of a system capable of exhibiting a mixed phase space structure. Thus, in general, the more narrow (broad) P(σ), the more spatially homogeneous (inhomogeneous) the fluid particle dispersal.
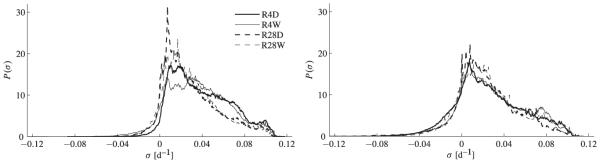
The left and right panels of Fig. 5 depict PDFs of FTLEs computed in backward and forward time, respectively, for initial particle positions on 1 March 2004 computed using each of the four spatiotemporally truncated model velocity sets discussed above. The FTLE integration time in each case was |τ| = 60 days. The PDFs depicted are normalized histograms constructed by binning each FTLE field in the interval σ = ±15 day−1 into 500 equally spaced containers, counting the number of elements within each container, and normalizing such that the probability in this interval equals unity. Independent of the amount of spatiotemporal truncation of the velocity field, the PDFs shown in the figure exhibit Gaussian cores and long tails, including various extrema, that fall more slowly than Gaussian toward large stretching rates. This is indicative of spatially inhomogeneous fluid particle dispersal. It is worthwhile mentioning that the somewhat stronger sensitivity reported above of small-scale LCS features to spatial velocity truncations than to temporal velocity truncations is reflected in the FTLE distributions shown in the present figure. Indeed, the differences between the PDFs of FTLEs based on R4D and R4W velocities or R28D and R28W velocities are in general somewhat smaller than the differences between the PDFs of FTLEs based on R4D and R28D velocities or R4W and R28W velocities.
Fig. 5.
PDFs of FTLEs computed in (left) backward and (right) forward time during 60 days using the various spatiotemporally truncated surface model velocities described in the caption of Fig. 2.
It must be noted that if the velocity field u(x, t) in (1) were nondivergent, then area preservation would imply that the FTLE as defined in (2) be nonnegative. Consequently, in addition to reflecting inaccuracies associated with the numerical integration of fluid particle trajectories, the presence of nonzero PDF values at negative FTLE values in Fig. 5 indicates that the modeled surface velocity field has a divergent component. The degree of horizontal divergence, and ensuing vertical motion, may be quantified by the degree of biasing toward negative FTLE values, which is not found to be too large. It must be remembered, however, that a nonnegative FTLE is only a necessary condition for u(x, t) being nondivergent. A necessary and sufficient condition is that the determinant of the deformation matrix ∂x0 x(t0 + τ;x0, t0) in (2) be unity, which has been found to be nearly so everywhere except where the FTLE takes negative values. Thus, negativeness of the FTLE appears to be an appropriate indicator of nonvanishing horizontal divergence in the case of study.
d. Eulerian and Lagrangian correlation times
The temporal persistence of the strain field may assessed by computing temporal autocorrelations of velocity gradient components, which control relative dispersion of fluid particles. Given a series {q1, … , qN} at h equispaced times {t1, … , tN} of a certain variable q, the lag-m autocorrelation rm is given by
| (6) |
where . Two types of autocorrelations may be computed, one in which q is evaluated at a fixed location (Eulerian autocorrelation) and another one in which q is evaluated along a fluid particle trajectory (Lagrangian autocorrelation).
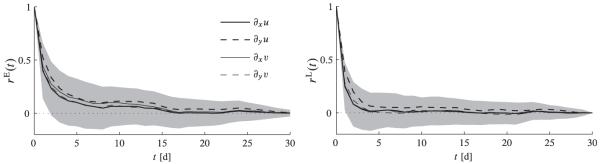
The left and right panels of Fig. 6 show Eulerian, rE(t), and Lagrangian, rL(t), autocorrelation curves for each of the four components of the velocity gradient (i.e., ∂xu, ∂yu, ∂xv, and ∂yv), respectively, as a function of the dimensional time tm = mh where h = 1 day. The computations presented are based on R4D velocities on the 30-day interval about 1 March 2004. Each curve shown in the figure corresponds to an average over an ensemble of roughly 25 000 autocorrelation curves computed by evaluating the velocity gradient component in question on the model grid points (left panel) or along fluid particle trajectories initially located on those points (right panel). In the latter case the roughly 25 000 points correspond to initial positions corresponding to trajectories that remain within the numerical model domain during a 30-day period. The shaded band around the curves in each panel of the figure represents an uncertainty of one standard deviation. Both Eulerian and Lagrangian autocorrelation curves of each individual velocity derivative exhibit a nearly exponential decay with time. The autocorrelation curves of ∂yu decorrelate a bit slower than those of the rest of the velocity gradient components, which are very similar to one another. The somewhat slower decorrelation of ∂yu can be related to the important southeastward (roughly along the WFS) component of the surface flow. As a consequence, random-strain theory (Batchelor 1959; Kraichnan 1974), which is an often-used simplified description of turbulent mixing wherein the velocity derivatives are assumed to be zero-mean random functions with constant decorrelation time, is not applicable. Consistent with this observation much larger differences are seen when each individual velocity-derivative Eulerian autocorrelation curve is compared with its Lagrangian counterpart. In all cases the Eulerian autocorrelations decay more slowly than the Lagrangian autocorrelations. The Eulerian autocorrelation decay time scale may be estimated to be about 15 days, which is longer than the Lagrangian autocorrelation decay time scale, estimated to be of the order of 5 days. This suggests that the Lagrangian evolution is more irregular than the driving Eulerian flow, which in turn suggests that chaotic stirring provides a more appropriate description of the surface ocean Lagrangian evolution on the WFS than turbulent mixing. However, the large uncertainty (spread) associated with the above autocorrelation time-scale estimates does not allow us to place too much trust in the conclusion drawn from the present diagnostic analysis. Nevertheless, this conclusion is consistent with those obtained from the previously considered diagnostics, which had smaller associated uncertainties.
Fig. 6.
(left) Eulerian and (right) Lagrangian autocorrelations of velocity gradient components assuming R4D full-model surface velocities. The velocity component u (v) is in the direction of the Cartesian coordinate x (y), which is southeastward (northeastward), roughly along (across) the WFS. Each curve corresponds to an average over an ensemble of roughly 25 000 autocorrelation curves computed by evaluating (left) the velocity gradient component in question on the model grid points or (right) along fluid particle trajectories initially located on those points. The shaded band around the curves in each panel represents an uncertainty of one standard deviation.
4. Discussion
LaCasce and Ohlmann (2003) have recently studied relative dispersion statistics of a subset of the satellite-tracked drifter trajectories considered by Yang et al. (1999), which provide observational support to the model-derived results presented above. Most of the trajectories in that subset lay on the northernmost part of the Gulf of Mexico, outside the WFS, so the results of LaCasce and Ohlmann (2003) may not be directly compared with those of the present article. However, and despite the difficulties associated with relative dispersion studies based on observed Lagrangian trajectories, LaCasce and Ohlmann (2003) found evidence of exponential dispersion consistent with a tracer evolution regime characterized by marginally nonlocal dynamics below the baroclinic deformation scale (roughly 50 km), which is consistent with the results presented here.
It is important to compare the results of the present work with those from studies in other locations of the world’s oceans. Using surface currents inferred from high-frequency radar measurements made in the Monterey Bay, Lekien and Coulliette (2007) found evidence of a near k−3 surface kinetic energy spectrum, implying marginally nonlocal dynamics in the Monterey Bay in a similar manner as on the WFS. It is interesting to note that the observational result for the Monterey Bay and the model-derived result obtained here for the WFS show consistence with altimetric measurements of sea surface height in open ocean locations, which provide evidence of a near k−3 kinetic energy spectrum at length scales of the order of 10–500 km (Stammer 1997; Stewart et al. 1996). The validity of this result, however, is a subject of debate (Le Traon et al. 2008).
Using altimetry-derived surface ocean velocities, PDFs of ensemble averages of forward-time FTLEs were computed and found to exhibit long tails toward large FTLE values in the Tasman Sea (Abraham and Bowen 2002; Waugh et al. 2006) and other locations of the world’s oceans (Waugh and Abraham 2008), suggesting spatially inhomogeneous fluid particle dispersal as on the WFS. It must be noted, however, that rather than calculating the deformation matrix ∂x0 x(t0 + τ;x0, t0) directly by finite differentiating trajectories on a grid as in this work, in Abraham and Bowen (2002), Waugh et al. (2006), and Waugh and Abraham (2008), ∂x0 x(t0 + τ;x0, t0) was obtained by integrating the so-called variational equations along trajectories (cf. Parker and Chua 1989). Although the full divergent velocity field was used to integrate the trajectory Eq. (1), only the traceless component of ∂xu(x, t) was integrated to obtain ∂x0 x(t0 + τ;x0, t0), which resulted in nonnegative FTLEs. The PDFs of ensemble averages of forward-time FTLEs so computed were found to exhibit universal shape, well-fitted by a Weibull distribution. The PDFs of both the forward- and backward-time FTLEs computed here, which are not enforced to be nonnegative, are found to be better fitted by log–Weibull distributions once the various extrema included in these PDFs are smoothed out. It is interesting to note that good fits to log–Weibull distri-butions are also attained when forward- and backward-time FTLEs are computed as in this article but are based on altimetry-derived surface currents in open ocean regions lying away from major currents (Beron-Vera et al. 2008). It must be noted, however, that in those open ocean regions the PDFs are narrower and do not exhibit multiple extrema, which is consistent with the absence of persistent organized structures.
5. Summary and conclusions
In this paper we have examined in some detail the character of the Lagrangian motion on the surface of the ocean in the west Florida shelf (WFS) by employing surface ocean velocities produced by an Hybrid-Coordinate Ocean Model (HYCOM) simulation. This investigation was motivated by the desire to better understand the nature of the peculiar cross-shelf transport barrier revealed on the WFS in prior analyses of satellite-tracked drifter trajectories (Yang et al. 1999) and simulated surface currents (Olascoaga et al. 2006). The presence of such a transport barrier on the WFS is consequential for pollutant dispersal, and also has potentially very important implications for the dispersion of plankton, particularly toxic algae, which lead to the development of harmful algal blooms.
We first computed Lagrangian coherent structures (LCSs) using several spatiotemporal truncations of the simulated surface velocities that were able to sustain a cross-shelf transport barrier on the WFS to investigate the sensitivity of the LCSs to the truncations. The large-scale traits of the simulated LCSs resulted largely insensitive to the spatiotemporal truncations considered; only the small-scale details of the LCSs were found to exhibit sensitivity to truncations of the surface velocity field. The performed analysis of the LCSs lead us to conclude that our prior characterization of the cross-shelf transport barrier on the WFS was indeed robust, and that chaotic stirring may dominate over turbulent mixing on time scales of up to two months. Significant leakage through the barrier may be only expected over longer time scales.
We also considered various other passive tracer evolution diagnostics to complement the above analysis. These diagnostics were kinetic energy, tracer variance, and velocity gradient spectra; probability distribution functions (PDFs) of finite-time Lyapunov exponents (FTLEs); and Eulerian and Lagrangian autocorrelation times of velocity gradient components. The kinetic energy was found to be characterized by a rather steep spectrum with a nearly −3 spectral slope; the tracer variance spectrum was found to be shallow with an approximately −1 spectral slope; and the velocity gradient spectrum was found to be essentially constant. These results consistently implied marginally spectrally nonlocal dynamics (passive tracer evolution at a given length scale is governed to a nonnegligible extent by velocity field features at a larger scale). The PDFs of FTLEs were found to exhibit Gaussian cores and long tails, including several extrema, that fall more slowly than Gaussian toward large stretching rates, which was indicative of spatially inhomogeneous dispersion of fluid particles. The Eulerian autocorrelation decay time scale of velocity gradient components was found to be generally longer than the Lagrangian autocorrelation decay time scale, which suggested that the Lagrangian evolution was more irregular than the driving Eulerian flow. These diagnostics all suggested that the ocean surface advection field produced by the HYCOM simulation of the WFS considered here is spatially quasicoherent and temporally quasiregular on time scales over which the associated fluid particle motion is predominantly irregular. These characteristics define a Lagrangian motion regime wherein chaotic stirring dominates over turbulent mixing, thereby providing support to the results of the sensitivity analysis of LCSs under spatiotemporal truncations of the velocity field.
The results reported in this article help explain why the evolution of observed harmful algal blooms on the southern portion of the WFS was found (Olascoaga et al. 2008) to be so strongly tied to LCSs. These results also highlight that LCSs are key kinematical elements to be considered in developing harmful algal bloom predictability strategies for the WFS.
Acknowledgments
We thank T. Shepherd for calling our attention to Shepherd et al. (2000), which motivated this work. We also thank M. Brown, H. Koçak, I. Rypina, and I. Udovydchenkov for the benefit of many helpful discussions on dynamical systems theory. The constructive criticism of two anonymous reviewers contributed to improve the paper. Support for this work was provided by NFS under Grants CMG0417425, CMG0825547, and OCE0432368, and by NIEHS under Grant P50ES12736.
Footnotes
A factor 2|τ|−1 was unintentionally omitted in the FTLE computations presented in our prior work (Olascoaga et al. 2006, 2008), which explains the differences in numerical values among the FTLEs reported here and those reported in our prior work. Omission of this factor, however, does not change the conclusions from our prior work.
REFERENCES
- Abraham ER, Bowen MM. Chaotic stirring by a mesoscale surface-ocean flow. Chaos. 2002;12:373–381. doi: 10.1063/1.1481615. [DOI] [PubMed] [Google Scholar]
- Babiano A, Basdevant C, Sadourny R. Structure functions and dispersion laws in two-dimensional turbulence. J. Atmos. Sci. 1985;42:941–949. [Google Scholar]
- Bartello P. Using low-resolution winds to deduce fine structure in tracers. Atmos.–Ocean. 2000;38:303–320. [Google Scholar]
- Batchelor GK. Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 1959;5:113–133. [Google Scholar]
- Bennett AF. Relative dispersion: Local and nonlocal dynamics. J. Atmos. Sci. 1984;41:1881–1886. [Google Scholar]
- Beron-Vera FJ, Olascoaga MJ, Goni GJ. Oceanic mesoscale vortices as revealed by Lagrangian coherent structures. Geophys. Res. Lett. 2008;35:L12603. doi:10.1029/2008GL033957. [Google Scholar]
- Brand LE, Guillard RRL. The effects of continuous light and light intensity on the reproduction rates of twenty-two species of marine phytoplankton. J. Exp. Mar. Biol. Ecol. 1981;50:119–132. [Google Scholar]
- Brand LE, Compton A. Long-term increase of Karenia brevis abundance along the southwest Florida coast. Harmful Algae. 2007;6:232–252. doi: 10.1016/j.hal.2006.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown MG, Smith KB. Ocean stirring and chaotic low-order dynamics. Phys. Fluids. 1991;3:1186–1192. [Google Scholar]
- Chassignet EP, Hurlburt HE, Smedstad OM, Halliwell GR, Hogan PJ, Wallcraft AJ, Bleck R. Ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM) In: Chassignet EP, Verron J, editors. Ocean Weather Forecasting: An Integrated View of Oceanography. Springer; 2006. pp. 413–436. [Google Scholar]
- Chassignet EP, Hurlburt HE, Smedstad OM, Halliwell GR, Hogan PJ, Wallcraft AJ, Baraille R, Bleck R. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007;65:60–83. [Google Scholar]
- d’Ovidio F, Fernández V, Hernández-Gracía E, López C. Mixing structures in the Mediterranean Sea from finite-size Lyapunov exponents. Geophys. Res. Lett. 2004;31:L17203. doi:10.1029/2004GL020328. [Google Scholar]
- d’Ovidio F, Isern-Fontanet J, López C, Hernández-García E, Garcí-Ladona E. Comparison between Eulerian diagnostics and finite-size Lyapunov exponents computed from altimetry in the Algerian basin. Deep-Sea Res. I. 2008;56:15–31. [Google Scholar]
- Errico RM. Spectra computed from a limited area grid. Mon. Wea. Rev. 1985;113:1554–1562. [Google Scholar]
- Garcia-Olivares A, Isern-Fontanet J, Garcia-Ladona E. Dispersion of passive tracers and finite-scale Lyapunov exponents in the Western Mediterranean Sea. Deep-Sea Res. I. 2007;54:253–268. [Google Scholar]
- Green MA, Rowley CW, Haller G. Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 2007;572:111–120. [Google Scholar]
- Haller G. Distinguished material surfaces and coherent structures in 3D fluid flows. Physica D. 2001;149:248–277. [Google Scholar]
- Haller G. Lagrangian coherent structures from approximate velocity data. Phys. Fluids. 2002;14:1851–1861. [Google Scholar]
- Haller G, Yuan G. Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D. 2000;147:352–370. [Google Scholar]
- Harle M, Feudel U. Hierachy of islands in conservative systems yields multimodal distributions of FTLEs. Chaos Solitons Fractals. 2007;31:130–137. [Google Scholar]
- Haynes PH. Encyclopedia of the Atmospheric Sciences. Elsevier; 2003. Turbulence and mixing; pp. 2446–2450. [Google Scholar]
- Hetland RD, Ya Hsueh RRL, Niiler P. A loop current-induced jet along the edge of the West Florida Shelf. Geophys. Res. Lett. 1999;26:2239–2242. [Google Scholar]
- Hu C, Muller-Karger FE, Taylor C, Carder KL, Kelbe C, Johns E, Heil CA. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005;97:311–321. [Google Scholar]
- Hu Y, Pierrehumbert RT. The advection–diffusion problem for stratospheric flow. Part I: Concentration probability distribution function. J. Atmos. Sci. 2001;58:1493–1510. [Google Scholar]
- Kraichnan RH. Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 1971;47:525–535. [Google Scholar]
- Kraichnan RH. Convection of a passive scalar by a quasi-uniform random straining field. J. Fluid Mech. 1974;64:737–762. [Google Scholar]
- LaCasce JH, Ohlmann C. Relative dispersion at the surface of the Gulf of Mexico. J. Mar. Res. 2003;61:285–312. [Google Scholar]
- Lacorata G, Aurell E, Vulpani A. Drifter dispersion in the Adriatic Sea: Lagrangian data and chaotic model. Ann. Geophys. 2001;19:121–129. [Google Scholar]
- Lehahn Y, d’Ovidio F, Lévy M, Heifetz E. Stirring of the northeast Atlantic spring bloom: A Lagrangian analysis based on multisatellite data. J. Geophys. Res. 2007;112:C08005. doi:10.1029/2006JC003927. [Google Scholar]
- Lekien F, Coulliette C. Chaotic stirring in quasiturbulent flows. Philos. Trans. Roy. Soc. 2007;365A:3061–3084. doi: 10.1098/rsta.2007.0020. [DOI] [PubMed] [Google Scholar]
- Lekien F, Coulliette C, Bank R, Marsden J. Open-boundary modal analysis: Interpolation, extrapolation, and filtering. J. Geophys. Res. 2004;109:C12004. doi:10.1029/2004JC002323. [Google Scholar]
- Lekien F, Coulliette C, Mariano AJ, Ryan EH, Shay LK, Haller G, Marsden JE. Pollution release tied to invariant manifolds: A case study for the coast of Florida. Physica D. 2005;210:1–20. [Google Scholar]
- Lekien F, Shadden SC, Marsden JE. Lagrangian coherent structures in n-dimensional systems. J. Math. Phys. 2007;48:065404. doi:10.1063/1.2740025. [Google Scholar]
- Le Traon PY, Klein P, Hua BL, Dibarboure G. Do altimeter wavenumber spectra agree with interior or surface quasi-geostrophic theory? J. Phys. Oceanogr. 2008;38:1137–1142. [Google Scholar]
- Lukovich JV, Shepherd TG. Stirring and mixing in two-dimensional divergent flow. J. Atmos. Sci. 2005;62:3933–3954. [Google Scholar]
- Lumpkin R, Flament P. Lagrangian statistics in the central North Pacific. J. Mar. Syst. 2001;29:141–155. [Google Scholar]
- Marshall J, Shuckburgh E, Jones H, Hill C. Estimates and implications of surface eddy diffusivity in the Southern Ocean derived from tracer transport. J. Phys. Oceanogr. 2006;36:1806–1821. [Google Scholar]
- Mathur M, Haller G, Peacock T, Ruppert-Felsot JE, Swinney HL. Uncovering the Lagrangian skeleton of turbulence. Phys. Rev. Lett. 2007;98:144502. doi: 10.1103/PhysRevLett.98.144502. doi:10.1103/PhysRevLett.98.144502. [DOI] [PubMed] [Google Scholar]
- Morey SL, Martin PJ, O’Brien JJ, Wallcraft AA, Zavala-Hidalgo J. Export pathways for river discharged fresh water in the northern Gulf of Mexico. J. Geophys. Res. 2003;108C:3303. doi:10.1029/2002JC001674. [Google Scholar]
- Ngan K, Shepherd TG. A closer look at chaotic advection in the stratosphere. Part I: Geometric structure. J. Atmos. Sci. 1999a;56:4134–4152. [Google Scholar]
- Ngan K, Shepherd TG. A closer look at chaotic advection in the stratosphere. Part II: Statistical diagnostics. J. Atmos. Sci. 1999b;56:4153–4166. [Google Scholar]
- Norton WA. Breaking of Rossby waves in a model stratosphere diagnosed by a vortex-following coordinate system and a technique for advecting material contours. J. Atmos. Sci. 1994;51:654–673. [Google Scholar]
- Obhukov AM. Structure of the temperature field in turbulent flows. Isv. Geogr. Geophys. Ser. 1949;13:58–69. [Google Scholar]
- Olascoaga MJ, Rypina II, Brown MG, Beron-Vera FJ, Koçak H, Brand LE, Halliwell GR, Shay LK. Persistent transport barrier on the West Florida Shelf. Geophys. Res. Lett. 2006;33:L22603. doi: 10.1029/2006GL027800. doi:10.1029/2006GL027800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olascoaga MJ, Beron-Vera FJ, Brand LE, Koçak H. Tracing the early development of harmful algal blooms with the aid of Lagrangian coherent structures. J. Geophys. Res. 2008;113:C12014. doi: 10.1029/2007JC004533. doi:10.1029/2007JC004533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker TS, Chua LO. Practical Numerical Algorithms for Chaotic Systems. Springer; 1989. p. 348. [Google Scholar]
- Pierce RB, Fairlie TD. Chaotic advection in the stratosphere: Implications for the dispersal of chemically perturbed air from the polar vortex. J. Geophys. Res. 1993;98:18 589–18 595. [Google Scholar]
- Pierrehumbert RT. Large-scale horizontal mixing in planetary atmospheres. Phys. Fluids. 1991;3:1250–1260. [Google Scholar]
- Pierrehumbert RT. Tracer microstructure in the large-eddy dominated regime. In: Aref H, El Naschie MS, editors. Chaos Applied to Fluid Mixing. Pergamon; 1994. pp. 347–366. [Google Scholar]
- Pierrehumbert RT, Yang H. Global chaotic mixing on isentropic surfaces. J. Atmos. Sci. 1993;50:2462–2480. [Google Scholar]
- Shadden SC, Lekien F, Marsden JE. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D. 2005;212:271–304. [Google Scholar]
- Shadden SC, Dabiri JO, Marsden JE. Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids. 2006;18:047105. doi:10.1063/1.2189885. [Google Scholar]
- Shepherd TG, Koshyk JN, Ngan K. On the nature of large-scale mixing in the stratosphere and mesosphere. J. Geophys. Res. 2000;105:12 433–12 466. [Google Scholar]
- Stammer D. Global characteristics of ocean variability estimated from regional TOPEX/POSEIDON altimeter measurements. J. Phys. Oceanogr. 1997;27:1743–1769. [Google Scholar]
- Stewart RH, Shum CK, Tapley B, Li L. Statistics of geostrophic turbulence in the southern ocean from satellite altimetry and numerical models. Physica D. 1996;98:599–613. [Google Scholar]
- Swanson KL, Pierrehumbert RT. Lower-tropospheric heat transport in the Pacific storm track. J. Atmos. Sci. 1997;54:1533–1543. [Google Scholar]
- Szezech JD, Jr., Lopes SR, Viana RL. Finite-time Lyapunov spectrum for chaotic orbits of non-integrable Hamiltonian systems. Phys. Lett. 2005;335A:394–401. [Google Scholar]
- Walsh JJ. Red tides in the Gulf of Mexico: Where, when, and why? J. Geophys. Res. 2006;111:C11003. doi: 10.1029/2004JC002813. Coauthors. doi:10.1029/2004JC002813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waugh DW, Plumb RA. Contour advection with surgery: A technique for investigating finescale structure in tracer transport. J. Atmos. Sci. 1994;51:530–540. [Google Scholar]
- Waugh DW, Rong PP. Interannual variability in the decay of lower stratospheric Arctic vortices. J. Meteor. Soc. Japan. 2002;80:997–1012. [Google Scholar]
- Waugh DW, Abraham ER. Stirring in the global surface ocean. Geophys. Res. Lett. 2008;35:L20605. doi:10.1029/2008GL035526. [Google Scholar]
- Waugh DW, Rong PP, Bowen MM. Spatial variations of stirring in the surface ocean: A case study of the Tasman Sea. J. Phys. Oceanogr. 2006;36:526–542. [Google Scholar]
- Yang H, Weisberg RH, Niiler PP, Sturges W, Johnson W. Lagrangian circulation and forbidden zone on the West Florida Shelf. Cont. Shelf Res. 1999;19:1221–1245. [Google Scholar]