Abstract
A new approach to species distribution modelling based on unsupervised classification via a finite mixture of GAMs incorporating habitat suitability curves is proposed. A tailored EM algorithm is outlined for computing maximum likelihood estimates. Several submodels incorporating various parameter constraints are explored. Simulation studies confirm, that under certain constraints, the habitat suitability curves are recovered with good precision. The method is also applied to a set of real data concerning presence/absence of observable small mammal indices collected on the Tibetan plateau. The resulting classification was found to correspond to species-level differences in habitat preference described in previous ecological work.
Keywords: finite mixture models, EM algorithm, generalised additive models, habitat suitability curves, logistic regression, over-dispersion
1. Introduction
Understanding variations in species distribution has remained one of the key challenges in ecology since its conceptualisation as a discipline (Guisan and Zimmerman, 2000). It has been natural that ecologists should seek to model species distribution and early models date from the nineteen twenties (Guisan and Thuiller, 2005). Uses of species distribution models (SDMs) in conservation biology include (Guisan and Thuiller, 2005): quantification of environmental niches for species; testing biogeographical, ecological and evolutionary hypotheses; invasive species monitoring; impact assessment for climatic change; prediction of unsurveyed sites for rare species; management support for species reintroduction and recovery; conservation planning; species assemblage modelling; classification of biogeographic or ecogeographic regions; calibration of ecological distance between patches in meta population or gene flow models.
Several techniques have been employed for SDMs including: generalised linear models (GLMs) and their flexible extension generalised additive models (GAMs) (Guisan et al. (2002), Greaves et al. (2006) and Segurado et al. (2006)); tree based classification techniques (Franklin, 1998); ordination (Schenková et al., 2001); eco-niche factor analysis (Hirzel et al., 2002); Bayesian approaches (Gelfand et al., 2006); neural networks (Bessa-Gomes and PetrucciFonseca, 2003) and support vector machines (Drake et al., 2006). Ecologists have long recognised the bias introduced into SDMs when data are overdispersed with respect to a simple parametric model such as can arise when strong spatial dependence exists between observations for example (Guisan and Thuiller (2005), Barry and Elith (2006) and Segurado et al. (2006)) but the proportion of articles published in ecological journals in which these biases are reasonably corrected for remains low. One problem, particularly in the spatial context, has been the lack of available tools for analysing overdispersed binary or Poisson data. This situation has been slowly changing since the seminal work of Diggle et al. (1998) who introduced the geostatistical concept of Gaussian random fields to the GLM literature to account for spatially smooth sources of overdispersion. Since then appropriate tools have become increasingly more available: the geoRglm library (Christensen and Ribeiro Jr, 2002) for Bayesian analysis of GLMs with geostatistical priors and the mgcv library for fitting generalised additive mixed models with either geostatistical or spline based random effects using penalised likelihood (Wood, 2006) are just two examples of what is now available for R (R Development Core Team, 2007).
A recent review (with online R code) of available techniques for the estimation of Gaussian random fields within a GLM for spatially dependant Bernoulli data (Paciorek and Ryan, 2005) suggested that the estimation of spatially structured random effects could be reasonable if the underlying spatial structure was simple relative to the sampling density of observation points. However when each curve and bend in a complex hidden surface was sparsely sampled then attempts to estimate the hidden surface proved less successful. The estimation of complicated hidden spatial structure from Bernoulli samples is now recognised to be highly data demanding suggesting that these models might be unreasonable in certain practical situations where logistical constraints limit the quantity of available data. We could ask the question “is it always necessary to estimate continuous spatial random effects plus three or four variogram parameters for binary ecological data sets?” or even “are hidden spatial structures in ecological data sets always smooth?”. If the answers to these questions is “no” then perhaps we can simplify and reduce the number of random effects and parameters that we expect to estimate, thereby reducing the demands we place on our datasets. In this paper we attempt to do this using a mixture model approach where the usual single GAM with n continuous random effects might be replaced by say K GAMs. Such a simplification would require a small number of parameters relative to n, especially when further constraints between the mixture components are imposed.
Note that here we do not attempt to explicitly model the sources of overdispersion. The mixture model approach simply provides a general solution to account for various overdispersion sources. According to Robert (1996) mixture components “correspond to particular zones of support of the true distribution” and thus provide local representations of the likelihood function. While these local supports “do not always possess an individual significance or reality for the particular phenomenon modelled”, interpretability can be possible in situations such as discrimination or clustering. This is the case for our model and a real data example is Section 5 is found to provide a very natural ecological interpretation.
It is worth noting that the simplification we propose is not necessarily made at the expense of physical interpretation. In a given ecological context a small number of discrete random effects could be a reasonable model for hidden spatial structure or other sources of overdispersion. For example, if the species in question is known to form colonies, one GAM might represent colony formation as a function of habitat suitability under relatively ideal conditions while a second GAM could account for possible absence of colonies in otherwise favourable habitat arising from a complex history of unobserved factor. Similarly, if the observations in question materialised from numerous different processes then a mixture model approach could be expected to outperform it's K = 1 counterpart. The most pertinent number of random effects K could then be identified using model selection techniques. Herein lies an additional advantage of our approach, our GAM utilises a simple transformation on covariates and so the parameters for our mixture model can be estimated by maximum likelihood. For highly flexible models such as GAMs with splines or random fields ML is known to be prone to over fitting and penalisations are often imposed to compensate. Since we use a mixture of simple GAMs with relatively limited flexibility we can use maximum likelihood directly without penalisation. For model comparison statistics such as Akaike Information Criterion (AIC) (Burnham and Anderson, 2002) are therefore readily available.
In the current paper we implement this proposed model simplification in a habitat suitability identification context. Habitat suitability curves are used to identify non-linear species responses along environmental gradients (see for example Jowett et al. (1991), Roussel et al. (1999) and Mäki-Petäys et al. (2002)). The concept is to identify a curve which transforms a continuous environmental variable to a scale more relevant to the distribution of the species in question thereby giving an index of habitat suitability.
2. A generalised additive model for habitat suitability identification
2.1. Habitat suitability curves in a GAMs framework
Generalised additive models (GAMs) have become popular tools in ecology due to their ability to detect non-linearities. A recent review of GAMs can be found in Wood (2006). The usual approach, when modelling an n length vector Y = Y1, … , Yn, where Y follows some distribution of the exponential family, is to modify the linear predictor of a generalised linear model (McCullagh and Nelder, 1989) via the inclusion of smooth functions of covariates Wood (2006). Here we take the simple case,
| (1) |
where i provides an index on observations, μi ≡ E[Yi], g(·) is a link function, β are coefficients and ℋ is a smooth function of covariate x. Commonly ℋ is chosen from a class of spline functions such as B-splines, P-splines, thin plate splines etc (Wood, 2006). Such choices offer highly flexible solutions but the large number of parameters involved requires that practitioners remain cautious to problems of over fitting. Here, we depart from standard practice and adopt a much simpler two-parameter habitat suitability curve based on power functions for modelling ℋ. Our proposed habitat suitability curve (HSC) is designed to detect a single region within a bounded environmental gradient within which a given species is found in greatest abundance. This approach is related to that of niche modelling, although we avoid the term “niche” since here we work exclusively in the univariate case in the interest of maintaining simplicity. The HSC ℋ used in our GAMs is defined as the unimodal transformation
| (2) |
where x is a bounded covariate that can take values in the range [l, u], m is the value of x that corresponds to the mode of ℋα1, α2(x) and α1 and α2 are parameters governing curvature. The numerator of ℋα1, α2(x) (2) is a product of two power functions, the first of positive gradient with an x-intercept corresponding to l, the second of negative gradient and x-intercept corresponding to u. The product of these two simple power curves provides a flexible uni-modal mapping from the range [l, u] ⊂ ℝ to [0, D(ℋ)], where D(ℋ) represents the denominator of (2) which is equivalent to the numerator evaluated at x = m. The denominator of (2) ensures ℋ is consistently scaled to the range [0, 1] which greatly facilitates biological interpretation. Our HSC (2) is intended to be flexible enough to identify the most pertinent subset of x corresponding to those areas where a species may be found in greatest density. The parameters α1 and α2 may take values in (0, ∞) and ℋα1, α2(l) = Hα1, α2(u) = 0. The mode is located at m = (uα1 + lα2)/(α1 + α2) and ℋα1, α2(x = m) = 1. As {α1, α2} → (0, 0) then ℋα1, α2(x) → 1 ∀ x ∈ (l, u) giving a uniform mapping in the limit. As {α1, α2} → (∞, ∞) then .
A priori out HSC assumes that optimal habitat does not correspond to the extremes of the range [l, u]. However, provided min(x) > l and max(x) < u this unlikely to prove problematic. Our HSC (2) also makes the a priori assumption that habitat suitability is adequately modelled by a uni-model curve. However, if in a given application this choice of ℋ proves insufficiently flexible, as proved the case in our ecological example in Section 5, multi-modality can easily be introduced using the mixture model approach outlined below in Section 2.2.
Transformation (2) can be re-parameterised in terms of α1 (α from here on) and mode location m. This has the advantage over (2) of greater orthogonality between parameters plus a more intuitive interpretation of m. The new parameterisation is thus
| (3) |
In what follows x represents a continuous index of some environmental gradient such as vegetation biomass, soil moisture, mean daily temperature etc. In practice such an index might be mapped across the study area in raster format.
2.2. The mixture of GAMs model
We will now introduce our mixture of GAMs. We will assume that given the vector (ℋ(x1), …, ℋ(xn)) each observation yi ∈ {1, 0} corresponding to presence/absence, is sampled from the distribution
| (4) |
where
| (5) |
and
| (6) |
The unknowns in this model which we will have to estimate for each k ∈ {1,…, K} are,
the probability weights pk s.t. ,
the reals β0k ∈ ℝ and β1k ∈ ℝ+, the positivity restraint, imposed for reasons of biological interpretation, ensures ℋ remains positively associated with habitat suitability and not unsuitability,
the parameters (αk, mk) of the functions ℋαk,mk which map [l, u] to [0, 1] and linearise the influence of x, a bounded continuous index of environmental variation.
The goal of this model is to split the sample into K classes of data with similar statistical properties. It is expected that these classes will reflect to a certain extent the sources of overdispersion within the observed phenomenon at a reasonable computational cost, i.e. without being over demanding of the information available in the data. This formulation is clearly not spatially explicit and so prediction of hidden spatial structure at unsampled locations is not a feature of our model. This is a further step that we will investigate in future work.
3. Estimation and EM algorithm
We now address the question of estimating the unknown parameters of our mixture model. The estimation of the parameters can be obtained using the maximum likelihood approach for which the EM algorithm is well tailored.
3.1. Maximum likelihood
We now provide details of the maximum likelihood approach we adopt for parameter estimation under our finite mixture model.
3.1.1. Description
The observed data are couples (yi, xi), i = 1, …, n. To this sample, we associate a sequence of couples (Yi, Xi) of independent random variables, i = 1,…, n such that the value of the conditional likelihood taken at (y1, …, yn) given the event {X1 = x1, …, Xn = xn} may be written as
| (7) |
with the fik given by formula (5) and where θ is the vector of unknown parameters, i.e.
| (8) |
The vector of parameters θ can be estimated using the maximum likelihood procedure, i.e.
| (9) |
where Θ is the domain of the likelihood function satisfying
| (10) |
The domain may also incorporate various additional restrictions on the model such as the possible equalities of certain parameters between classes.
3.2. The questions of non-convexity and possible non-identifiability
The question of identifiability in this model is open at present time. This problem has been studied in Follmann and Lambert (1991) in a simpler framework but Theorem 1 in that paper does not directly apply to mixtures of logistic regressions and a fortiori to our mixture of GAM's (since their theorum requires the number of mixture components to be lower than one). It would be very interesting to pursue their analysis in the case of our model but this is beyond the scope of the present paper. One objective of our simulation studies below is to show that in practice empirical mean squared convergence was observed in the case where the optimization algorithm could reach the pertinent root of the likelihood equation, which is encouraging with respect to the possibility of mathematically proving this property. The paper Zhu and Zhang (2006) proposes however a very nice theoretical framework for dealing with the loss of identifiability in case it should happen to be a problem with the model introduced in this paper.
Another problem is that the log-likelihood cannot be convex as is well known for mixture models. However, another source of difficulty concerning the geometry of the likelihood surface is that the function Hα,m(x) is also not convex in (α, m) at any x as can easily be verified. Moreover, the product β1h is not convex in (β1, h) inducing another technical problem when dealing with the product β1Hα,m(x). However, our simulations results show that the optimization procedure still behaves reasonably well despite these difficulties.
3.3. The EM algorithm
It is easy to notice that a vector θML maximising the conditional likelihood cannot be obtained via a closed form formula. Thus, an iterative algorithm has to be used and in the following section we describe a version of the well known EM algorithm for this purpose.
3.3.1. Description of the method
The EM algorithm is a well known conceptual scheme allowing to build recursive procedures that converge towards a set of vectors maximising the likelihood, or more appropriately here, the conditional likelihood over the domain Θ. EM has been proposed in its present general form by Dempster, Laird and Rubin in Dempster et al. (1977), hence encompassing several specialised procedures that had been developed in various applications of the maximum likelihood principle. The main reference on EM algorithms, their variants and their applications is the book of McLachlan and Peel (2000).
The idea underlying the EM algorithm is the following. It is expected that if more information on the observations were available, then optimising the likelihood could be performed easily. The main additional information that we could have in the ecological setting is the class of the mixture to which each observation belongs.
If we denote by Zi the random index of the mixture component from which observation Yi was drawn, the so-called complete data is actually given by the triples (Y1, Z1, X1), …, (Yn, Zn, Xn). One still has to keep in mind that the Zi's are actually unobserved and that their only contribution is to provide the right framework underlying the EM procedure. The complete likelihood associated to the complete data is given by
| (11) |
where πiZi is given by (6) above. One of the main features of the complete likelihood is that it can usually be optimised in an easier fashion than the plain likelihood. This is the exact reason why statisticians have been using the EM approach.
E Step
Assume that we have a current value of θ, denoted hereafter by θ̃. Then, one unreachable but tempting goal would be to optimise the complete likelihood. Now here is the crux: the Zi's are not observed. One sensible way to approximate log (θ) then is to take its minimum mean squared error estimator among functions of the Yi's only. It is well known that the minimum mean squared error estimator is given by the conditional expectation given the Yi's assuming that the underlying probability is specified by θ̃, i.e.
| (12) |
In the case of our model, this conditional expectation is quite simple to obtain. Indeed, one only needs to know the values of the conditional probabilities for each possible value of Zi, i = 1, …, n given Y1, …, Yn under the model specified by θ̃. Using Bayes' rule, one obtains
| (13) |
where fik(yi;θ̃) corresponds to fik(yi) parameterised by θ̃. Therefore, we obtain that
| (14) |
M Step
The next step is the choice of the next iterate, θnext. The idea for obtaining a sensible candidate is quite simple: just maximise the approximation of the complete log-likelihood conditionally on the observations y1, …, yn, i.e.
| (15) |
Finally the EM algorithm consists of repeating these two steps recursively until the increase of the likelihood obtained between two successive iterates is judged sufficiently small. In the following, we will write the sequence of EM iterates (θ(ν))ν∈2ℕ.
One important point to notice is that the function Q is convex with respect to the regression variables β0,k and β1,k as is well known in logistic regression theory; see (Boyd and Vandenberghe, 2004, Section 7.1) for details. However, as already noticed in subsection 3.2, the products β1,k Hαk,mk(x) are not convex with respect to (β1,k, αk, mk) and the optimization of Q cannot be guarantee achieving a global optima.
3.3.2. Implementation details
Given iterate θ(ν) at step ν, the computation of the next iterate is obtained by solving the first order optimality condition
| (16) |
where ∇ is the gradient with respect to the vector of variables θ. Cancelling the partial derivatives with respect to the pk's is easy and gives the same result as in any mixture model of this type, i.e.
| (17) |
where is the posterior probability that Zi = k given Yi = yi under the model parametrised by the current estimate θ̃. More explicitly,
| (18) |
The computation is less straightforward for other components of θ. The gradient of Q with respect to all the other components has been calculated and is given in the Appendix below. The expression for the gradient (16) should convince that no closed form formula can be obtained as a solution. With this respect, our situation is different from the case of Gaussian mixtures for instance where the successive iterations can be computed by hand. Therefore, a computational approach has to be chosen. We used the L-BFGS-B version of function optim in the software R to perform this task.
3.4. Parameter equality constraints
The model described thus far is highly flexible. Depending on the application it can be desirable to impose further constraints. Here we consider the modifications required to ensure that certain elements of the parameter vector θ are constrained to be equal. For example, adopting the notation θk = (pk, β0k, β1k, αk, mk) such that , a user might impose that the parameter vectors θ1, …, θK are equivalent with the exception that β01 ≠ … ≠ β0K. This would provide a mixture model representation of a random effect on intercept model. Alternatively, a user might impose that vectors θ1, …, θK are equivalent with the exception that β11 ≠ … ≠ β1K, thus providing a random effects on β1 model, otherwise known as a variable coefficient model.
Let θe represent a subset of θ for which all elements, θek, are constrained to be equal. To impose this equality among elements of θe throughout the estimation process it is sufficient to: first, impose equality between elements of the vector of starting values ; and thereafter, present the L-BFGS-B with a gradient vector in which (see Appendix) is replaced by , the mean of the derivatives w.r.t each element of θe, i.e.
| (19) |
where |θe| represents the cardinality of set θe. In what follows below we denote θfree ⊂ θ to be the subset of free parameters, i.e. the subset of θ with elements rendered redundant under model constraints, pK and non-free elements of any set θe, removed.
We now describe two simulation studies and a real data application of our model. The first simulation study in Section 4.1 investigates identifiability under the random effect on intercept parameterisation. The second simulation study in Section 4.2 investigates the effect of sample size on the precision of parameter estimates under the random effect on β1 parameterisation. The real data analysis in Section 5 compares four different parameterisations in the analysis of small mammal indices data collected on the Tibetan plateau, Sichuan Province, China.
4. Simulation studies
4.1. First study
4.1.1. Description
A dataset was simulated under the following parameters: K = 2, n = 1000,, β {β0, β1}, β0 = {β01, β02} = {−4, −2}, β1 = {β11, β12} = {2, 2}, l = −1, u = 1, α = {10, 10}, m = {0.1, 0.1}. The covariate x was simulated over a 100 × 100 pixel raster grid using a zero-mean Gaussian Random Field (GRF) (Cressie, 1993), that is, pixel values were drawn from a multivariate Gaussian distribution with covariance between any two pixels si and sj defined as a function of the vector . We used the so called Gaussian covariance function
| (20) |
with nugget , sill and range (a) set to 0, 5 and 15 (pixels) respectively. This simulation was performed in R using the RandomFields library (Schlather, 2007). The simulated GRF was subjected to a linear rescaling so that it was bounded by l and u (Fig. 1 (a)).
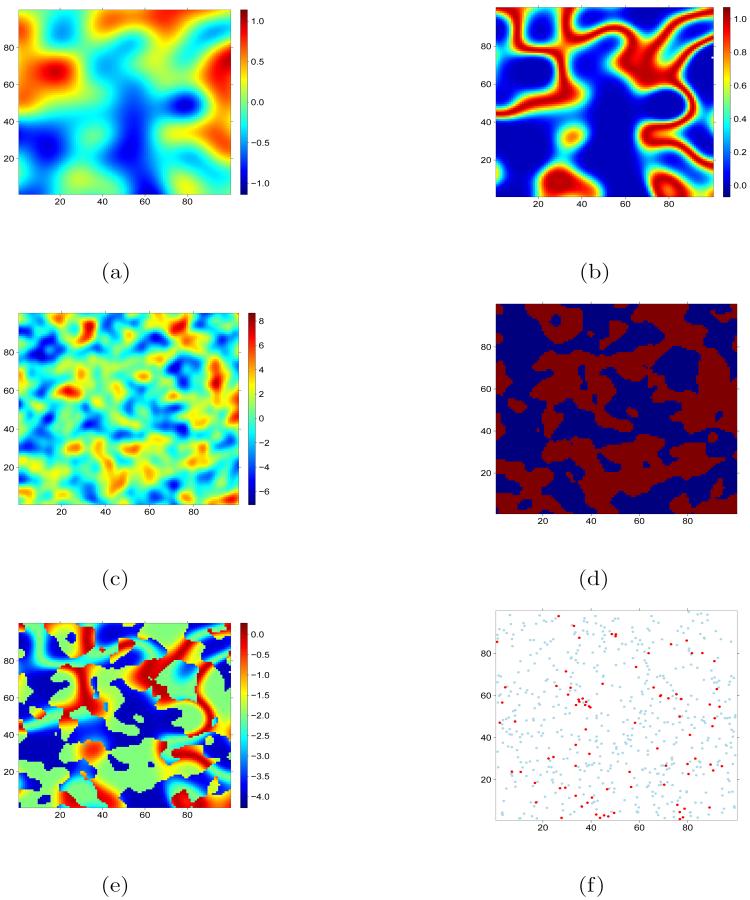
Figure 1.
Dataset generated for simulation study 1. The first GRF (a) was transformed by the HSC to derive habitat suitability (b). The second GRF (c) was split at the 50% quantile to provide and indicator map of where model 1 (blue) and model 2 (red) operate. A map of g(μ) (e) was derived from (b) and (d) and used to simulate observed data (f).
To simulate localised clustering of the “hidden” random effect a second GRF was simulated as above but with a = 5 (Fig. 1 (c)). The 50% quantile of this GRF was used to partition the grid into two classes Z = 1 and Z = 2 (Fig. 1 (d)). A stratified sampling was then implemented with n/K sampling locations simulated at random within each of the two classes. An observation yi was simulated at each location i in the knowledge of the parameters, covariate and z (Fig. 1 (f)). For the purpose of parameter estimation zis were assumed unknown and all parameters were constrained to be shared by models 1 and 2 with the exception of the intercepts and mixing probabilities.
The EM algorithm was used to try to re-capture the true parameter values. This was performed using fifty sets of starting values obtained at random under the following rules: pstart ∝ Unif(0, 1); ; ; β01 = β02; α ~ Unif(10−2, 102 and m ~ Unif(l, u). In order to maintain the interpretation that ℋ provides an index of habitat suitability a lower bound of β1 = 0 was imposed in the M-step. The EM was run until the l2 norm difference in θfree between successive iterates became lower than a threshold, i.e. .
4.1.2. Results
Solutions provided by the EM algorithm were clearly clustered in parameter space. This clustering indicates dependency between starting values and the local optima to which the algorithm converges, a characteristic of mixture models that is widely recognised (Biernacki et al., 2003). Table 1 shows cluster means and variances of parameter estimates and maximised log likelihoods. The optima closest to the true parameter values was optima 3. The HSC mode m was consistently estimated with precision. The algorithm also detected areas of the likelihood which returned more erroneous parameter estimates and yet higher likelihoods than those obtained using the original parameters, i.e. optima 1 and optima 2. In these solutions β01 was under estimated and p1 over estimated. These solutions appear to correspond to degenerate solutions since lowering both the threshold for the stopping rule and the lower bound of β0 in the L-BFGS-B algorithm resulted in even lower estimates of β01 (not shown). The lowest likelihood corresponded to optima 4 where β02 becomes over estimated and β1 underestimated. These solutions arose when the estimates for α became large causing excessive narrowing of the HSC thus increasing the proportion of observations for which ℋ(x) ≈ 0. The proportion of observations being significantly influenced by variation in the covariate x was thus reduced and β02 grew in order to compensate.
Table 1.
Summarised results for simulation study 1 in which EM was run from fifty sets of starting values. Solutions were clustered in four sets and cluster means and variances (in brackets) of parameter estimates and the observed data log likelihood are reported here. freq. is the number of times the algorithms stopped close to the reported cluster means. The algorithm returned NAs 32 times in 50.
| freq. | l̄y1,…,yn(θ) | p̄1 | β̄01 | β̄02 | β̄1 | ᾱ | m̄ | |
|---|---|---|---|---|---|---|---|---|
| EM | 50 | |||||||
|
| ||||||||
| Optima 1 | 11 | −467.55 | 0.67 | −13.89 | −1.21 | 6.40 | 20.22 | 0.11 |
| (4.5E-3) | (1.1E-3) | (0.91) | (0.010) | (0.20) | (0.48) | (1.1E-4) | ||
|
| ||||||||
| Optima 2 | 1 | −468.80 | 0.93 | −15.00 | 6.32 | 14.21 | 1.16 | 0.11 |
|
| ||||||||
| Optima 3 | 3 | −469.38 | 0.88 | −2.91 | −1.49 | 2.17 | 8.31 | 0.10 |
| (1.4E-3) | (0.021) | (0.065) | (0.026) | (0.024) | (0.026) | (6.5E-5) | ||
|
| ||||||||
| Optima 4 | 3 | −507.22 | 0.89 | −2.11 | 7.55 | 0.43 | 186.32 | 0.76 |
| (0.047) | (6.2E-3) | (0.051) | (4.90) | (0.36) | (130.00) | (4.7E-3) | ||
|
| ||||||||
| Returned NAs | 32 | - | - | - | - | - | - | - |
| (−) | (−) | (−) | (−) | (−) | (−) | (−) | ||
|
| ||||||||
| θ true | −472.78 | 0.5 | −4 | −2 | 2 | 10 | 0.1 | |
4.2. Second study
4.2.1. Description
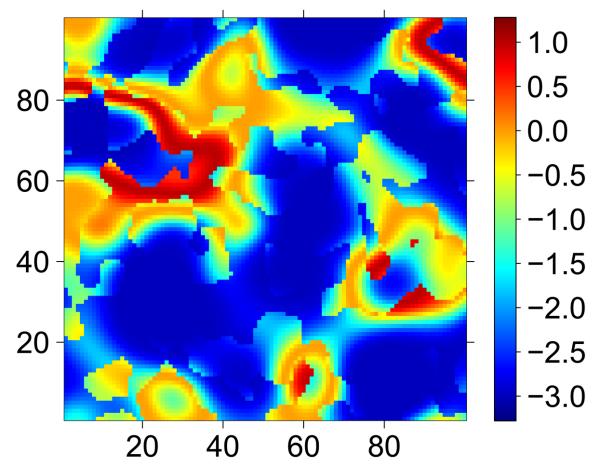
Data was generated according to the method outlined above (Section 4.1) but with β = {β0, β1} = {−3, −3, 3, 4} and m = {m1, m2} = {0.1, 0.4}. An image of the resulting g(μ) is shown in Fig. 2. A range of sample sizes was considered with n ∈ {5000, 4000, 3000, 2000, 1000, 500, 400, 300, 200, 100}. For each sample size n one hundred realisations of Yn were generated with x fixed. True parameter values were used as starting values and the EM algorithm was used to maximise the likelihood. The EM was stopped after the first iterate within which the square of the l2 norm of the difference between successive parameter estimates was smaller than a threshold, i.e. , this higher (than in Study 1) threshold being adopted in the interest of computation time.
Figure 2.
g(μ) used for simulation study 2.
4.2.2. Results
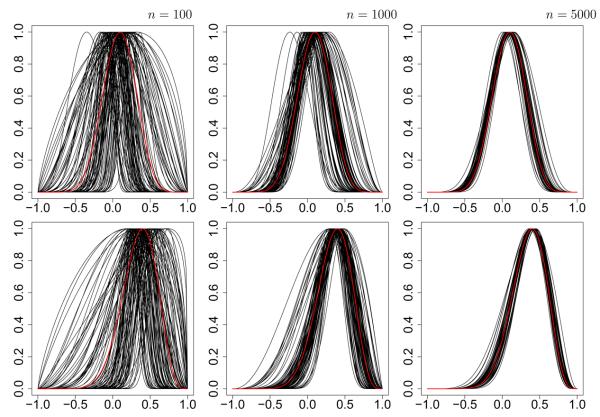
The mean, variance and l2 norm of the discrepancy between true and fitted values are reported in Table 2. In general the fitted values successfully recapture the original parameter values. The largest discrepancies between original and fitted values appear to be for the α parameter which is not surprising since this parameter might realistically take values across several orders of magnitude. The effect of variance in (α̂, m̂) on the fitted HSC is shown in Figure 3 where it is clear that with larger data sets the fitted HSC in general bears greater resemblance to the original (marked in red). The largest outliers clearly correspond to those estimates derived from the smallest samples where n = 100. Otherwise θ is consistently estimated with a satisfactory degree of precision, the precision in m̂ being particularly striking.
Table 2.
Results from simulation study 2. 100 Monte Carlo simulations were performed at each sample size and parameters were fitted with EM. Absolute errors for each parameter and the l2 norm of errors in all free parameters were calculated and their MC means and variances are reported here.
| n | | p̂1 − P1 | | | β̂0 − β0 | | | β̂11 − β11 | | | β̂12 − β12 | | | α̂ − α | | | m̂1 − m1 | | | m̂2 − m2 | | ∥ ∊ ∥ 2 | |
|---|---|---|---|---|---|---|---|---|---|
| 5000 | μ | 6.97e−03 | 1.04e−01 | 1.52e−01 | 2.02e−01 | 1.19e+00 | 2.06e−02 | 1.43e−02 | 1.37e+00 |
| σ 2 | 6.28e−05 | 8.30e−03 | 1.42e−02 | 2.62e−02 | 1.16e+00 | 3.34e−04 | 1.30e−04 | 9.77e−01 | |
|
| |||||||||
| 4000 | μ | 6.99e−03 | 1.58e−01 | 1.92e−01 | 2.37e−01 | 1.55e+00 | 2.36e−02 | 1.48e−02 | 1.75e+00 |
| σ 2 | 4.58e−05 | 1.81e−02 | 2.06e−02 | 3.02e−02 | 2.12e+00 | 3.71e−04 | 1.09e−04 | 1.80e+00 | |
|
| |||||||||
| 3000 | μ | 7.40e−03 | 1.18e−01 | 1.88e−01 | 3.13e−01 | 1.78e+00 | 2.68e−02 | 1.76e−02 | 1.96e+00 |
| σ 2 | 4.51e−05 | 9.35e−03 | 2.26e−02 | 1.63e−01 | 3.17e+00 | 7.07e−04 | 2.25e−04 | 3.00e+00 | |
|
| |||||||||
| 2000 | μ | 1.22e−02 | 2.18e−01 | 2.39e−01 | 4.47e−01 | 2.15e+00 | 3.46e−02 | 1.98e−02 | 2.38e+00 |
| σ 2 | 1.74e−04 | 2.79e−02 | 3.77e−02 | 5.16e−01 | 3.77e+00 | 1.45e−03 | 2.32e−04 | 3.77e+00 | |
|
| |||||||||
| 1000 | μ | 2.03e−02 | 2.78e−01 | 3.89e−01 | 1.16e+00 | 4.11e+00 | 6.34e−02 | 3.53e−02 | 4.50e+00 |
| σ 2 | 5.20e−04 | 8.13e−02 | 9.82e−02 | 5.17e+00 | 2.09e+01 | 3.58e−03 | 8.60e−04 | 2.46e+01 | |
|
| |||||||||
| 500 | μ | 3.80e−02 | 5.63e−01 | 1.07e+00 | 1.87e+00 | 7.42e+00 | 7.92e−02 | 5.70e−02 | 8.23e+00 |
| σ 2 | 2.07e−03 | 1.21e+00 | 3.11e+00 | 8.67e+00 | 5.69e+01 | 5.78e−03 | 2.16e−03 | 6.22e+01 | |
|
| |||||||||
| 400 | μ | 3.89e−02 | 4.78e−01 | 9.73e−01 | 2.13e+00 | 9.52e+00 | 8.03e−02 | 5.85e−02 | 1.03e+01 |
| σ 2 | 2.43e−03 | 4.99e−01 | 2.19e+00 | 1.02e+01 | 1.31e+02 | 4.55e−03 | 4.34e−03 | 1.35e+02 | |
|
| |||||||||
| 300 | μ | 4.94e−02 | 9.25e−01 | 1.68e+00 | 3.22e+00 | 1.35e+01 | 1.04e−01 | 7.85e−02 | 1.48e+01 |
| σ 2 | 2.28e−03 | 2.52e+00 | 5.90e+00 | 1.30e+01 | 3.24e+02 | 6.80e−03 | 8.00e−03 | 3.20e+02 | |
|
| |||||||||
| 200 | μ | 7.41e−02 | 1.07e+00 | 3.13e+00 | 4.52e+00 | 2.03e+01 | 8.71e−02 | 7.76e−02 | 2.24e+01 |
| σ 2 | 4.84e−03 | 2.95e+00 | 1.31e+01 | 1.96e+01 | 2.83e+02 | 5.44e−03 | 5.00e−03 | 2.61e+02 | |
|
| |||||||||
| 100 | μ | 8.47e−02 | 2.49e+00 | 5.29e+00 | 5.80e+00 | 2.47e+01 | 9.74e−02 | 1.04e−01 | 2.85e+01 |
| σ 2 | 6.15e−03 | 8.60e+00 | 1.99e+01 | 1.77e+01 | 7.99e+02 | 6.33e−03 | 5.53e−03 | 7.11e+02 | |
Figure 3.
Habitat suitability curves from simulation study 2. The data-generating mixture model possessed two HSCs with modes at 0.1 and 0.4 (top and bottom rows respectively). This model was used to generate 100 datasets with sample sizes of 100, 1000 and 5000 (left, center and right respectively). The true HSCs are indicated in red. Fitted HSCs from the 100 Monte Carlos iterations are shown in black.
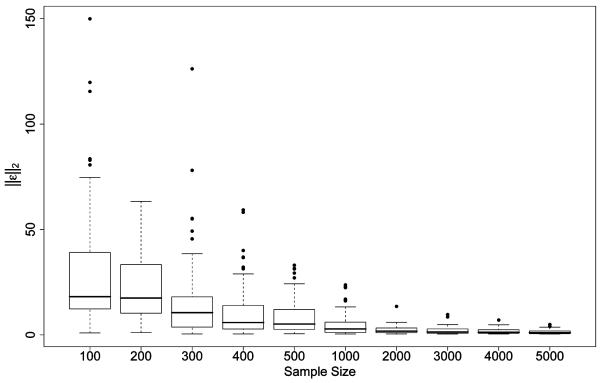
It is important to note that, as indicated by Figure 4 , the l2 norm of the error tends to zero as sample size increases. So at the same time the proportion of estimators which are consistent to the true parameter values tends to one and the proportion of meaningless estimators such as those encountered in simulation study 1 tends to zero as sample size grows.
Figure 4.
Effect of sample size on the l2 norm of the six parameters estimated from 100 Monte Carlo simulations at each sample size in simulation study 2.
5. Small mammal index example
5.1. The data
The data analysed here were from transect surveys conducted in the vicinity of Tuanji, a town situated at 4250m altitude on the Tibetan plateau, Serxu County (or Shiqu County in Chinese pinyin), Sichuan Province, China. All transects were made in July 2001 and 2002. Investigators walked straight lines and recorded locations of start, stop and turn points with hand held GPS receivers. After each ten pace interval volunteers stopped and recorded presence or absence of holes belonging to Microtus limnophilus, Microtus leucurus, Microtus irene or Cricetulus kamensis. Holes of these species are very similar so no attempt was made to identify holes at the species level. A full account of this data can be found in Raoul et al. (2006). The aim here was to present a regression analysis of this presence / absence data with respect to the normalised difference vegetation index (NDVI) derived from a Land-sat Enhanced Thematic Mapper (ETM) image acquired on 3rd July 2001. The NDVI here is assumed to provide a suitable proxy index for vegetation biomass for the study area and was derived from ETM's red R and infra-red NIR wave bands as follows.
| (21) |
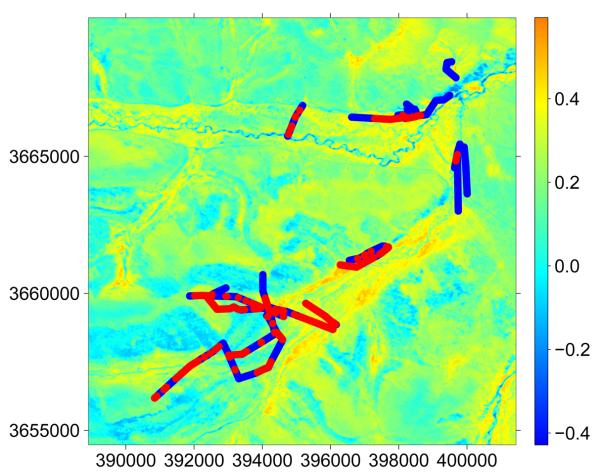
A map of NDVI across the study area, overlayed with the pressence / absence of small mammal activity indices data, is presented in Figure 5.
Figure 5.
Normalised difference vegetation index (NDVI) for the Tuanji study area overlayed with transect data on small mammal indices. Red and blue points repressent pressence and absence of observable small mammal indeced respectively. Coordinates are in UTM projection.
We applied our mixture of HSC GAMs to this data set in the interest of identifying the range of NDVI within which small mammal indices were observed in greatest number. In our analysis we consider the two types of parameter constraints mentioned in Section 3.4. We will refer to these two models as ℳ1 and ℳ2 and define these two models as ℳ1 ≡ {K = 2, β01 ≠ β02, β11 = β12, α1 = α2, m1 = m2} and ℳ2 ≡ {K = 2, β01 = β02, β11 ≠ β12, α1 = α2, m1 = m2}. We also consider two more flexible models defined as ℳ3 ≡ {K = 2, β01 = β02, β11 ≠ β12, α1 = α2, m1 ≠ m2} and ℳ4 ≡ {K = 2, β01 = β02, β11 ≠ β12, α1 ≠ α2, m1 ≠ m2}.
5.2. Results
AIC values and maximum likelihood estimates of parameters under ℳ1, ℳ2, ℳ3 and ℳ4 are presented in Table 3. ℳ3 was identified as the best parsimonious fit to the data w.r.t. estimated AIC. Under ℳ3 two different modes of the HSC were identified. The component with the m-value equal to 0.58 apparently corresponds to areas of greatest biomass since the maximum NDVI within the study area was 0.53. By comparison with ℳ2 there appears to be evidence of a bimodal response in small mammal indices with respect to the NDVI gradient. The inclusion of an additional model component, i.e. K = 3, was observed not to improve upon the data description provided by ℳ3. Specifically, the mixture probability of this third component was observed to converge to zero effectively reducing the model to ℳ3 (data not shown).
Table 3.
Estimates of parameters in θfree, under four different sets of constraints, for the small mammal index example. In ℳ1 β02 reached the lower bound used in the L-BFGS-B algorithm, which resembles the behaviour observed in study 1 associated with degenerate solutions. In ℳ2 the fitted HSC is clearly not degenerate and corresponds to approximately 24% of the observations y. The AIC is reduced when more than one mode is allowed as in ℳ3 although there is little evidence of the need for relaxing the equality constraint on α as in ℳ4.
| model | AIC | l | p | β 0 | β 1 | α | m |
|---|---|---|---|---|---|---|---|
| ℳ 1 | 3565.3 | −1776.7 | {0.30,0.70} | {−1.33,−15.00} | 8.94 | 56.11 | 0.41 |
| ℳ 2 | 3563.7 | −1775.8 | {0.76,0.24} | −2.52 | {0.00,13.32} | 76.45 | 0.38 |
| ℳ 3 | 3556.7 | −1771.4 | {0.36,0.64} | −2.68 | {3.72,3.87} | 80.1 | {0.30,0.53} |
| ℳ 4 | 3558.6 | −1771.3 | {0.35,0.65} | −2.68 | {3.76,3.85} | {80.10,80.11} | {0.30,0.53} |
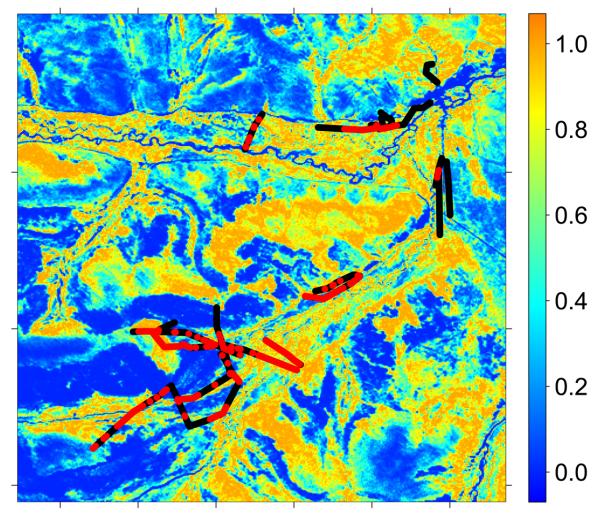
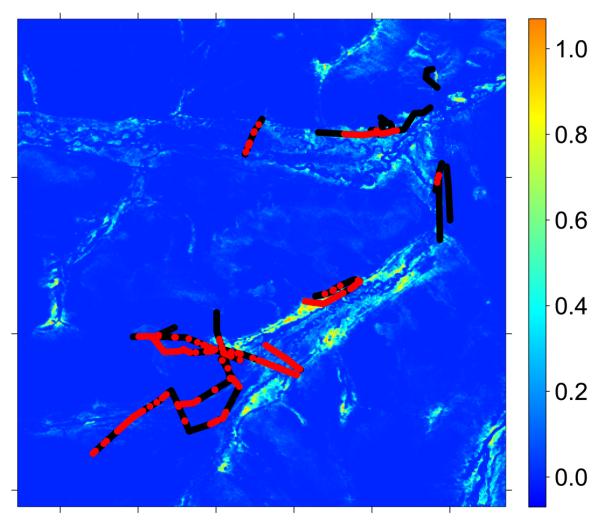
Our results may be better interpreted using Table 4 and Figure 4 in Raoul et al. (2006) which show trapping frequencies of the four species in various classes of habitat. Microtus limnophilus and Cricetulus kamensis were the most frequently trapped species. It is clear from Raoul et al. that Microtus limnophilus and Microtus leucurus were more abundant in areas subjected to relatively low grazing pressure where vegetation biomass was greater. The two other species, Cricetulus kamensis and Microtus irene were more abundant in areas of relatively low vegetation biomass. It can be safely ascertained that the first component in our mixture with β11 = 2.96 and m1 = 0.31 corresponds to indices of Cricetulus kamensis and Microtus irene whereas the second mixture component with β12 = 8.01 and m2 = 0.58 corresponds to indices of Microtus limnophilus and Microtus leucurus. Figures 6 and 7 map the derived HS indices for these two groups of species.
Figure 6.
Habitat Suitability Index derived from the NDVI using ML estimates of α̂ and m̂1 from ℳ3 overlayed with transect data on small mammal indices. Red and black points repressent pressence and absence of observable small mammal indeced respectively.
Figure 7.
Habitat Suitability Index derived from the NDVI using ML estimates of α̂ and m̂2 from ℳ3 overlayed with transect data on small mammal indices. Red and black points represent presence and absence of small mammal indices respectively.
6. Discussion
This paper proposes a species distribution model that performs unsupervised classification via a finite mixture of GAMs where the traditional spline function has been replaced with a unimodal habitat suitability curve. An EM algorithm has been proposed for deriving maximum likelihood estimates. Several submodels were studied in which the mixture components were assumed to share certain parameter values. Not all of submodels were satisfactorily identifiable. For instance using different intercepts in two components led to several possible stationary points, moreover, the estimated parameter set retaining the highest likelihood was far from the vector of true values. On the other hand accurate parameter estimates were obtained when the constraint of equal intercepts was imposed as shown in Table 2 and Figure 3.
The method was also applied to a set of real data concerning presence/absence of observable small mammal indices collected on the Tibetan plateau. The AIC was used to determine the best submodel among 4 candidates and the resulting classification was found to confirm trapping results given in Raoul et al. (2006) about the common response to vegetation biomass of Microtus limnophilus and Microtus leucurus on the one hand and Cricetulus kamensis and Microtus irene on the other.
Our proposed model bears much in common with the vector generalised additive model (VGAM) of Yee and Wild (1996). In that paradigm K linear predictors are used to model q-dimensional response vectors where q ≥ 1. For this purpose Yee and Wild use the “vector spline” of Fessler (1991) and estimate parameters by minimising a generalised least squares criterion that included a smoothness penalisation term. This flexible paradigm includes mixture models as a sub-class and Yee and Wild discuss parameter constraints similar to those discussed here. However, while the vgam R package does contain functions for modelling mixtures of Poissons, normals and exponentials, functionality for mixtures of binomial glms is currently not provided. Moreover, our approach differs from the VGAM paradigm in that we choose a much simpler non-linear transformation function which advantageously permits to forego the smoothness penalisation term in the likelihood required to avoid overfitting of splines. We believe the simplicity of our habitat suitability curve can advantageously aid biological interpretation since likelihood based model selection techniques can be used to penalise against overfitting. Identification of redundant model components can also be inferred from very low mixture probabilities as illustrated in our real data example.
Current work seeks to address several short-comings of our proposed model. In its present state, our model makes the strong scale assumption that species presence / absence at an observation point is most pertinently modelled using a habitat index calculated at the corresponding single pixel. However, the ROMPA (Ratio of Optimal to Marginal Patch Area) hypothesis of Lidicker (2000) describes how population dynamics can change as a function of the proportion of their preferred habitat within a landscape. There lies hidden here a question of scale since, in addition to habitat quality itself, the distribution or abundance of a given species may respond to the spatial arrangement of preferred habitat (Riitters et al., 1997). The species Arvicola terrestris (Fichet-Calvet et al., 2000), Microtus arvalis (Delattre et al., 1999), Tetrao urogallus (Graf et al., 2005) and the cestode Echinococcus multilocularis (Giraudoux et al., 2003) are just some examples of species who's populations appear to respond to landscape level effects. Scale has become an important issue in ecology and the paper of Dungan et al. (2002) reviews it's multifaceted nature. In order to derive a landscape index such as ROMPA the area over which it is to be calculated must be defined. A commonly adopted approach is to calculate the metric in a circular buffer centerred at each observation. There are two problems. First, a suitable buffer size is not always a priori apparent. Secondly, the abrupt cutoff and the indicator weighting scheme that such a buffer imposes is most likely an unrealistic representation of reality. With these ecological considerations in mind, a suitable modification of our model might include the additive component
| (22) |
where ℬi denotes the subset of pixels falling within a buffer centerred at location i, 𝒩ℬi is its cardinal and weights ωij are some function of distance s.t. Σj∈ℬiωij = 1. The terms therefore introduces into the regression equation the spatially weighted mean habitat suitability within an area surrounding each observation. Preliminary experience with this type of enrichment indicates that our EM algorithm (written in R) becomes impractically slow as buffer size increases. Evidently there is a need for faster algorithms and building such improved methods will be the subject of our next efforts. Finally future work will also be undertaken on the crucial and exciting question of incorporating spatial dependence into our model via using a discrete random field as a prior for Z.
A. Gradients
In this section, we provide the formulas for the gradient of Q(θ, θ̃) in order for the reader to be able to implement our EM algorithm. As described in Section 3.1, the vector θ is composed of the K mixture probabilities pk's, the K intercepts β01, … , β0K, the K coefficients β11, … , β1K, the shape parameters α1, … , αK's and the mode points m1, … , mK. The derivative with respect to any variable Vk ∈ {β0k, β1k, αk, mk} is given by
| (23) |
with
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
and
| (29) |
7. Acknowledgements
The research described was supported by Grant Number RO1 TW001565 from the Fogarty International Center. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Fogarty International Center or the National Institutes of Health.
Small mammal indices data we collected by Patrick Giraudoux, Nadine Bernard, Renaud Scheifler, Dominique Rieffel and Francis Raoul, all of whom are affiliated to the Department of Chrono-Environment, University of Franche-Comté, France.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Data and scripts used in the current paper are available for download from https://sites.google.com/site/drjpleydell/
References
- Barry S, Elith J. Error and uncertainty in habitat models. JAE. 2006;43:413–423. [Google Scholar]
- Bessa-Gomes C, Petrucci-Fonseca F. Using artificial neural networks to assess wolf distribution patterns in portugal. Animal Conservation. 2003;6:221–229. [Google Scholar]
- Biernacki C, Celeux G, Govaert G. Choosing starting values for the em algorithm for getting the highest likelihood in multivariate Gaussian mixture models. CSDA. 2003;41(3-4):561–575. [Google Scholar]
- Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- Burnham K, Anderson D. Model selection and multi-model inference. 2nd Edition Springer; London: 2002. [Google Scholar]
- Christensen OF, Ribeiro PJ., Jr georglm - a package for generalised linear spatial models. R News. 2002;2(2):26–28. [Google Scholar]
- Cressie N. Statistics for spatial data. revised edition. Wiley; New York: 1993. tHE key reference for spatial statistics throughout the 1990s and beyond. [Google Scholar]
- Delattre P, De Sousa B, Fichet-Calvet E, Quéré J, Giraudoux P. Vole outbreaks in a landscape context: evidence from a six year study of microtus arvalis. Landscape Ecology. 1999;14(4):401–412. [Google Scholar]
- Dempster A, Laird N, Rubin D. Maximum-likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society B. 1977;39(1):1–38. [Google Scholar]
- Diggle PJ, Tawn JA, Moyeed Model-based geostatistics. with discussion and a reply by the authors. J. Roy. Statist. Soc. Ser. C. 1998;47(3):299–350. [Google Scholar]
- Drake J, Randin C, Guisan A. Modelling ecological niches with support vector machines. J. Appl. Ecol. 2006;43:424–432. [Google Scholar]
- Dungan J, Perry J, Dale M, Legendre P, Citron-Pousty S, Fortin M, Jakomulska A, Miriti M, Rosenberg M. A balanced view of scale in spatial statistical analysis. Ecography. 2002;25(5):626–640. [Google Scholar]
- Fessler J. Nonparametric fixed-interval smoothing with vector splines. IEEE Transactions on Signal Processing. 1991;39(4):852–859. [Google Scholar]
- Fichet-Calvet E, Pradier B, Quéré J, Giraudoux P, Delattre P. Landscape composition and vole outbreaks: evidence from an eight year study of arvicola terrestris. Ecography. 2000;23(6):659–668. [Google Scholar]
- Follmann D, Lambert D. Identifiability of finite mixtures of logistic regression models. Journal of Statistical Planning and Inference. 1991;27(3):375–381. [Google Scholar]
- Franklin J. Predicting the distribution of shrub species in southern california from climate and terrain-derived variables. J. Veg. Sc. 1998;9(5):733–748. [Google Scholar]
- Gelfand A, Silander JA, Wu S, Latimer S, O. Lewis P, Rebelo A, Holder M. Explaining species distribution patterns through hierarchical modeling. Bayesian Analysis. 2006;1:41–92. [Google Scholar]
- Giraudoux P, Craig P, Delattre P, Bao G, Bartholomot B, Harraga S, Quéré J, Raoul F, Wang Y, Shi D, Vuitton D. Interactions between landscape changes and host communities can regulate Echinococcus multilocularis transmission. Parasitology. 2003;127:S121–31. [PubMed] [Google Scholar]
- Graf RF, Bollmann K, Suter W, Bugmann H. The importance of spatial scale in habitat models: Capercaillie in the swiss alps. Landscape Ecol. 2005;20(6):703–717. [Google Scholar]
- Greaves G,J, Mathieu R, Seddon PJ. Predictive modelling and ground validation of the spatial distribution of the new zealand long-tailed bat (Chalinolobus tuberculatus) Biol. Conserv. 2006;132:211–221. [Google Scholar]
- Guisan A, Edwards TC, Hastie T. Generalised linear and generalised additive models in studies of species distributions: setting the scene. Ecol. Model. 2002;157:89–100. [Google Scholar]
- Guisan A, Thuiller W. Predicting species distribution: offering more than simple habitat models. Ecological letters. 2005;8:993–1009. doi: 10.1111/j.1461-0248.2005.00792.x. [DOI] [PubMed] [Google Scholar]
- Guisan A, Zimmerman NE. Predictive habitat distribution models in ecology. Ecol. Model. 2000;135:147–186. [Google Scholar]
- Hirzel A,H, Hausser J, Chessel D, Perrin N. Ecological-niche factor analysis: how to compute habitat-suitability maps without absence data? Ecology. 2002;83(7):2027–2036. [Google Scholar]
- Jowett I, Richardson J, Biggs B, Hickey C, Quinn J. Microhabitat preferences of benthic invertebrates and the development of generalised Deleatidium spp. habitat suitability curves, applied to four new zealand rivers. New Zealand Journal of Marine and Freshwater Research. 1991;25:187–199. [Google Scholar]
- Lidicker JW. A food web/landscape interaction model for microtine rodent density cycles. Oikos. 2000;91(3):435–445. [Google Scholar]
- Mäki-Petäys A, Huusko A, Erkinaro J, Muotka T. Transferability of habitat suitability criteria of juvenile atlantic salmon (Salmo salar) Can. J. Fish. Aquat. Sci./J. Can. Sci. Halieut. Aquat. 2002;59(2):218–228. [Google Scholar]
- McCullagh P, Nelder J,A. Generalised linear models. 2nd Edition Chapman and Hall/CRC; London: 1989. [Google Scholar]
- McLachlan G, Peel D. Finite mixture models. Wiley-Interscience; New York: 2000. [Google Scholar]
- Paciorek C, Ryan L. Computational techniques for spatial logistic regression with large datasets; Harvard University Biostatistics Working Paper Series 32; Harvard University. 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2007. ISBN 3-900051-07-0. URL http://www.R-project.org. [Google Scholar]
- Raoul F, Quéré J, Rieffel D, Bernard N, Takahashi K, Scheifler R, Ito A, Wang Q, Qiu J, Yang W, Craig P, Giraudoux P. Distribution of small mammals in a pastoral landscape of the tibetan plateaus (western sichuan, china) and relationship with grazing practices. Mammalia. 2006;70(3/4):214–225. [Google Scholar]
- Riitters K, O;Neill R, Jones K. Assessing habitat suitability at multiple scales: a landscape-level approach. Biological Conservation. 1997;81:191–202. [Google Scholar]
- Robert C. In: Mixtures of distributions: inference and estimation. Gilks W, Richardson S, Spiegelhalter D, Markov chain Monte Carlo in practice, editors. Chapman and Hall/CRC; Boca Raton: 1996. chap. 24. [Google Scholar]
- Roussel J, Bardonnet A, Claude A. Microhabitats of brown trout when feeding on drift and when resting in a lowland salmonid brook: effects on weighted usable area. Arch. Hydrobiol. 1999;146(4):413–429. [Google Scholar]
- Schenková J, Komárek O, Zahrádková S. Oligochaeta of the morava and odra river basins (czech republic): species distribution and community composition. Hydrobiologia. 2001;463:235–240. [Google Scholar]
- Schlather M. RandomFields: Simulation and Analysis of Random Fields. 2007 Version 1.3.30. URL http://www.R-project.org.
- Segurado P, Araújo MB, Kunin WE. Consequences of spatial autocorrelation for niche-based models. J. Appl. Ecol. 2006;43:433–444. [Google Scholar]
- Wood S. Generalised additive models: An introduction with R. Chapman and Hall/CRC; Boca Raton: 2006. [Google Scholar]
- Yee T, Wild C. Vector generalized additive models. Journal of the Royal Statistical Society, Series B Methodological. 1996;58:481–493. [Google Scholar]
- Zhu H, Zhang H. Asymptotics for estimation and testing procedures under loss of identifiability. Journal of Multivariate Analysis. 2006;97:19–45. [Google Scholar]