In Vivo Penetration Mechanics and Mechanical Properties of Mouse Brain Tissue at Micrometer Scales

Abstract

Substantial advancement in the understanding of the neuronal basis of behavior and the treatment of neurological disorders has been achieved via the implantation of various devices into the brain. To design and optimize the next generation of neuronal implants while striving to minimize tissue damage, it is necessary to understand the mechanics of probe insertion at relevant length scales. Unfortunately, a broad based understanding of brain-implant interactions at the necessary micrometer scales is largely missing. This paper presents a generalizable description of the micrometer scale penetration mechanics and material properties of mouse brain tissue in vivo. Cylindrical stainless steel probes were inserted into the cerebral cortex and olfactory bulb of mice. The effects of probe size, probe geometry, insertion rate, insertion location, animal age and the presence of the dura and pia on the resulting forces were measured continuously throughout probe insertion and removal. Material properties (modulus, cutting force, and frictional force) were extracted using mechanical analysis. The use of rigid, incompressible, cylindrical probes allows for a general understanding of how probe design and insertion methods influence the penetration mechanics of brain tissue in vivo that can be applied to the quantitative design of most future implantable devices.

I. INTRODUCTION

Techniques to measure and modify the activity of neuronal ensembles in awake-behaving animals make it possible to study the neural basis of behavior. Current technology relies mainly on implantable electrodes that permit the measurement of neuronal ensemble activity in anaesthetized primates and conscious humans undergoing neurosurgery [1]-[5] as well as in awake-behaving rats or guinea pigs, albeit with progressive degradation of the signal [6]-[10]. Taken together with drug infusion and microstimulation experiments, recordings of neuronal ensemble activity in awake-behaving animals have yielded substantial advances in our understanding of the neuronal basis for behavior in the sensory and motor systems. However, to date, the approach to understanding the mechanical interaction of small neuronal implants (e.g. microelectrodes and cannulae) in brain tissue has been primarily empirical without understanding the fundamental mechanics of probe insertion. In order to develop and optimize the next generation of neuronal probes, it is necessary to understand the mechanics of in vivo probe insertion at relevant length scales. Moreover, knowledge of key material properties of brain tissue in vivo at these dimensions is useful for a sound base upon which future probes can be designed.

While non-penetrating indentation studies have aided in the attainment of elastic properties of brain tissue [11]-[15], neuronal probe implantation requires information on the elastic and inelastic behavior of the tissue during penetration, beyond what is ascertained from near surface indentation. The penetration mechanics and mechanical interaction of millimeter scale probes in brain tissue has been studied to some extent [16]-[18], but can be difficult to translate quantitatively to state of the art neuronal probes, which are an order of magnitude smaller in size. Studies on the penetration mechanics and mechanical interaction of micro-scale probes in brain tissue include looking at stresses developed in probes during penetration [19], modeled interaction of probes and tissue post-implantation [20], the dimpling and compression of tissue during implantation of silicon arrays [21] and the force required to penetrate human cochlear nuclei in vitro [22]. Recently, Jensen et al. [23] looked at the forces seen during micro-scale probe implantation and removal in the cerebral cortex of rats in vivo as a function of parameters such as probe size, tip angle, shaft number, and cleaning method and Bjornsson et al. [24] studied the effects of probe shape and insertion rate on tissue strain.

The purpose of this study is to add to the limited knowledge of the penetration mechanics of micro-scale probes into brain tissue in vivo. We demonstrate how common parameters (probe size, tip geometry, insertion rate, insertion location, and presence of dura/pia) affect the resulting penetration mechanics such as magnitude of forces encountered during penetration and removal as a function of time and distance. By using rigid, incompressible, cylindrical probes, we are able to extract key properties of the tissue (modulus, frictional forces between the probe and surrounding tissue, and cutting force) from the data using basic mechanics models. These characteristics provide information on the forces and material properties probes must be designed to withstand during implantation and/or removal and how basic design parameters may be used to optimize probe insertion into brain tissue in vivo from a mechanical point of view. It should also be noted that probe design and insertion optimization could reduce negative effects on tissue in both the short and long terms [23]-[25].

II. MATERIALS AND METHODS

A total of 22 mice of mixed backgrounds (129SVJ, C57, BL/6J and FVB) were used in this study. Mice ranged in weight from 28-50 g and in age from approximately 2 months to 2.5 years. The weight, age, strain and gender of the mice were not controlled and were selected randomly. All animal procedures were approved by the Institutional Animal Care and Use Committee at UCDHSC.

A. Surgery

Initially, mice were anesthetized deeply with a combination of ketamine and xylazine (10% and 2% respectively) in sterile physiological saline (145 mM NaCl, 5 mM KCl, 20 mM Hepes, 1 mM MgCl₂, 1 mM CaCl₂, 1 mM Na pyruvate, and 5 mM D-glucose, pH 7.2) (0.01 ml/g). Then the mice were placed in a stereotaxic apparatus (SR-5M, Narashigi International USA, Inc., East Meadow, N.Y.) to stabilize their head during surgery and probe insertion and placed under a flow of an isoflourane/oxygen mixture (2%) to maintain anesthesia throughout the surgery and insertion measurements. The anesthetized state of the mice was monitored closely during the entire procedure. Once the mice were secured in the stereotaxic apparatus, the skin was incised along the medial aspect of the skull and retracted. A small hole was drilled in the skull with a dental drill, exposing the olfactory bulb (center of the olfactory bulb) or cerebral cortex (1.8-2.2 mm caudal to bregma and 1.8-2.2 mm lateral of the sagittal suture), depending on which area was to be tested. The dura was then carefully removed (if desired) with a pair of sharp forceps. The surface of the brain was then carefully cleaned with a cotton swab dampened in physiological saline to remove any clots or other debris. This process generally removes the pia from the surface of the brain. Surface blood vessels were avoided when possible. Prior to long insertion tests, a thin layer of physiological saline solution was applied to the brain surface to prevent drying. Cortical placement was into the secondary visual cortex, lateral parietal cortex or primary somatosensory cortex and continued through the corpus callosum and dorsal hippocampal commissure terminating in the hippocampus.

B. Insertion Measurements

Probes were manufactured from stainless steel wire with diameters of 0.004 inches (101.6 μm which will be referred to as the 100 μm probe) and 0.008 inches (203.2 μm which will be referred to as the 200 μm probe) with an exposed length of 3 mm (Point Technologies, Inc, Gibbon, MN; Boulder, Colorado). Two probe-tip geometries were used; a cylindrical flat punch tip and a cylindrical probe with a sharpened tip (Fig. 1(a-c)). The stainless steel wires were cut flat (and de-burred) to produce the flat punch geometry. The sharpened probes were produced by chemically etching the stainless steel wire to a total tip angle of 20°. The wires were epoxied into a stainless steel base, which was attached to a precision gram load cell (GSO series, 10g maximum force, Transducer Techniques, Temecula, CA). The load cell was secured to an electronically controlled micromanipulator (MP-285, Sutter Instruments, Novato, CA), which drove the load cell and probe assembly vertically a set distance at a preprogrammed rate. Fig. 1(d-e) shows a schematic of the instrument setup and an image of the actual load cell and stereotaxic apparatus.

Fig. 1.

Experimental setup used in this study. (a-c) Scanning Electron Microscopy (SEM) images of the stainless steel cylindrical probes used in this study, scanned after use in insertion tests. (a) The flat punch probe with a 100 μm diameter. (b) The flat punch probe with a 200 μm diameter. (c) The sharpened probe with a 20° tip angle and a 200 μm base diameter. (d) Schematic of the experimental setup. (e) Photograph of load cell and stereotaxic apparatus.

The sequence of steps in a given insertion test was as follows: once in contact, the manipulator drove the probe (positioned perpendicular to the brain surface) a vertical displacement of 1.5mm, paused for 0.2 sec, and returned the probe to its initial position to remove it from the tissue. The surface of the brain was determined by manually lowering the probe until a small force was registered on the load cell. The probe was then raised slightly just until the load on the probe returned to zero. Three average insertion and removal rates were used, 822 μm/s, 104 μm/s and 11 μm/s (actual velocities determined from the time it took to move 1.5 mm at settings of 1.0, 0.1 and 0.01 mm/s respectively and assuming constant velocity). Data were collected continuously throughout insertion and removal of the probe as corresponding sets of force and time. The probe depth at a given time was determined from the time data and the known insertion rate. Data for initial tests (ten out of 68 tests) were collected using the RS-232 serial communication interface option that came with the load cell (18 Hz and 1 Hz sampling rate) (Transducer Techniques, Temecula, CA). Data obtained from the RS-232 serial communication interface option was autofiltered during collection. For the remaining tests (58 out of 68 tests), data were collected with a Digidata 1322A using pClamp 8 software due to the faster sampling rate capabilities (100 Hz sampling rate, unfiltered) (Axon Instruments, Inc. Union City, CA). The affect of filtering on the initial ten tests was less than the sample to sample variability encountered during testing. The probes were rinsed with water and manually wiped clean between each insertion. Care was taken to prevent deflection of the probes during cleaning. All data were from single insertions into an olfactory bulb or hemisphere of the cortex. A minimum of two tests were done for each given set of parameters (n ≥ 2).

C. Derivation of Material Properties

The Young’s modulus (E) of the tissue was calculated from the slope (K₁) of the force-displacement response of the flat probes prior to penetration using a load-displacement relation developed for indentation of a rigid, flat, cylindrical punch [26]:

$$E=\frac{\Delta F(1-{\nu }^2)}{\Delta u2a}=\frac{K_1(1-{\nu }^2)}{d}$$ (1)

where F is the applied force, ν is Poisson’s ratio (which is the negative of the ratio of lateral strain to uniaxial strain) of the material being indented, a is the radius of the flat punch, d is the diameter of the flat punch, u is the indentation depth, and K₁ is assumed linear with indentation depth. Brain tissue is commonly treated as an incompressible material, thus a Poisson’s ratio of 0.5 was used [11], [14]. The relation for modulus stated in Eq. 1 is for linear elastic materials. While brain tissue is considered a nonlinear, viscoelastic material [15], the force-displacement response obtained prior to penetration included a region of linearity and Eq. 1 was only used in this region.

The rates of change of frictional force acting on the probe with respect to penetration depth or probe displacement (δ) were calculated as follows:

$$\frac{\Delta F_f}{\Delta \delta }=\mid K_2\mid$$ (2)

where F_f is the frictional force and K₂ is the slope of the linear portion of the force-displacement curve during the retraction phase.

The rates of change of the cutting force (F_cut) of the in vivo brain tissue with respect to the penetration depth or probe displacement (δ) was determined from the loading slope of the sharpened probe (K₃) by the relation in Eq. 3.

$$\frac{\Delta F_{\text{cut}}}{\Delta \delta }=\frac{\Delta F_{\text{total}}}{\Delta \delta }-\frac{\Delta F_f}{\Delta \delta }=K_3-\mid K_2\mid$$ (3)

ΔF_total/Δδ is the rate of change of the force read from the load cell with respect to penetration depth and ΔF_f/Δδ is the rate of change of frictional force between the probe and tissue with respect to penetration depth as previously defined (Eq. 2).

D. Statistical Analysis

The slopes of linear portions of the force-probe displacement response were determined by finding a straight-line best fit to the force-displacement data using the method of least squares. The effect of tissue type, probe geometry, insertion rate and age on the average values of maximum force, modulus, frictional force, and cutting force were analyzed by ANOVA in SAS (SAS Institute Inc., Carey, NC). Since mistaken null hypothesis rejections are more likely to occur when dealing with multiple comparisons, a false discovery rate procedure was employed subsequent to the ANOVA analysis to control for the multiple comparisons and reduce the occurrence of Type I errors [27]. It was not possible to control for effects due to changes in modulus that could account for changes in properties such as frictional force and maximum force and still make comparisons to the sharpened probe data. This is due to the fact that modulus can only be determined for the flat punch experiments. Post-hoc comparisons for specific affects were determined using the least squares method. In the statistical analysis an error rate and false discovery rate of 0.05 were used.

III. RESULTS

Here we present load-displacement data from in vivo penetration measurements. Data are mostly presented as averages of multiple runs in interest of space. Pairs of representative runs can be found at the following website: www.siumed.edu/anatomy/asharp.htm. All tests were performed with the dura and pia removed unless otherwise stated. Also, material properties of the brain tissue useful for future probe engineering are derived from these data.

A. Flat Punch Probe Insertion

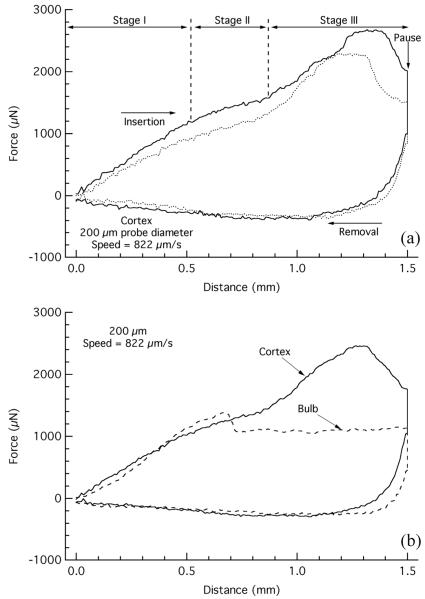
Two representative load-displacement curves for the insertion and removal of the 200 μm diameter flat punch probe in the cerebral cortex, at an insertion rate of 822 μm/s are shown in Fig. 2(a). As the flat probe tip began to move downward on the tissue, it initially compressed the tissue beneath it resulting in a near linear increase in force as a function of probe displacement (Stage I). At a critical force, the probe penetrated the tissue, leading to a decrease in the loading slope of the force-displacement curve (Stage II). A third loading stage, which began approximately 0.8-0.9 mm below the surface, consisted of a bump or increase in loading slope that began to decrease again just before the final insertion depth. This third stage likely represents the interface between the cortex and underlying mylenated fiber tracts. The mylenated axons of the fiber tracts could present higher resistance to the probe and a commensurate increase in loading. The rapid drop in force in the last 100-200 μm likely represents the cutting of the probe through the corpus callosum and the entry of the probe into the hippocampus. At the final insertion depth, the probe paused for 0.2 s at which point there was a noted decrease in force due to tissue relaxation. As the probe began to be withdrawn (at the same rate it was inserted), the forces on the probe turned from compressive (positive) to tensile (negative) as the forces acting on the tip of the probe began to be released and frictional forces developed. Finally, a near linear relation between force and displacement resulted primarily due to the frictional forces between the probe and tissue, which approached zero as the probe was removed from the tissue.

Fig. 2.

Load-displacement response for insertion and removal of the 200 μm diameter flat punch probe with an insertion rate of 822 μm/s. (a) Duplicate load-displacement curves for insertion into the cerebral cortex. (b) Average load-displacement curves comparing the response of insertion into the cortex and olfactory bulb (n_CortexLoad=2, n_CortexUnload=3, n_Bulb=3).

The penetration of soft solids, such as rubber, by a cylindrical flat punch has been noted as producing a similar force-displacement response upon probe insertion [28]. The mode of flat probe penetration in these soft solids has been shown to be by the formation and propagation of a mode II ring crack. The plateau (and occasional oscillation) in force following the initial compression and subsequent penetration of the soft solid is linked to the propagation of the crack just ahead of the penetrating probe.

Since different locations in the brain differ in the underlying structures (i.e. variation in blood vessel density or laminar structures), insertion measurements were also taken from the olfactory bulb (Fig. 2(b)). Responses were similar to those from the cortex, however, the responses consisted only of the first two stages. This is consistent with the lack of an underlying fiber tract in the olfactory bulb. Comparison of the average load-displacement curves of the 200 μm flat punch probe inserted at a rate of 822 μm/s into the olfactory bulb and the cortex (Fig. 2(b)) show that while the initial loading slopes for the first 600-700 μm were similar, the maximum penetration forces were significantly higher in the cortex than in the bulb tissue (p<0.0001).

Since the physical structure of tissue is known to change as an animal ages, we analyzed the data to determine if there was an affect of age on the values measured or calculated in this study. Interestingly, there was no significant affect of age on maximum forces reached during probe insertion or the calculated modulus and frictional force values (p>0.47) unlike a previous study [14] that showed an affect of age on the modulus of rat brain. We can only conclude that this is the result of species differences or differences in the size of probes used in these two studies.

B. Modulus of Brain Tissue

Analysis of the entire load-displacement relationship allows for basic material properties of the brain to be determined from these data. For example, the load-displacement slope that occurred in Stage I (K₁, Fig. 2(a)) prior to the probe penetrating the tissue, is a function of the modulus (E) of the tissue and the diameter of the probe (d). The modulus is a measure of the tissue’s stiffness, with a larger modulus indicating a stiffer material. The Young’s modulus of the tissue was calculated using a load-displacement relationship developed for indentation for a rigid, flat, cylindrical punch (Eq. 1, [26]). The average modulus values of the olfactory bulb and cortex tissue (Table 1) were not determined to be statistically different.

TABLE I.

In vivo mechanical and material properties of brain tissue

Punch Type	100 μm Ø flat punch			200 μm Ø flat punch			200 μm Ø sharp
Insertion Rate	822 μm/s	104 μm/s	11 μm/s	822 μm/s	104 μm/s	11 μm/s	822 μm/s
Fmax bulb (μN)	732.4±244.1 (n = 9)	323.3±67.1 (n = 4)	427.0±74.9 (n = 6)	1609.0±174.1 (n = 3)	1091.1±62.8 (n = 2)	1024.3±124.1 (n = 3)	790.8±10.1 (n = 3)
Fmax cortex (μN)	833.7±55.1 (n = 6)	564.4±58.7 (n = 4)	519.4±52.7 (n = 7)	2481.7±193.1 (n = 2)	1700.9±142.4 (n = 3)	1270.8±105.2 (n = 3)	1358.6±107.7 (n = 3)
Fcrit bulb * (μN)	605.0±70.9 (n = 9)	201.5±60.0 (n = 4)	317.9±105.2 (n = 6)	1344.6±293.9 (n = 3)	794.8±38.9 (n = 2)	590.2±31.4 (n = 3)	-----
Fcrit cortex * (kPa)	464.0±63.6 (n = 6)	321.0±55.0 (n = 4)	328.0±68.2 (n = 7)	1092.6±166.2 (n = 2)	1235.8±227.9 (n = 3)	1174.9±104.8 (n = 3)	-----
E bulb (kPa)	13.0±3.6 (n = 9)	5.5±1.1 (n = 4)	5.2±0.9 (n = 6)	10.4±1.8 (n = 3)	4.6±0.2 (n = 2)	3.4±0.8 (n = 3)	-----
E cortex (kPa)	10.5±0.9 (n = 6)	6.1±0.3 (n = 4)	4.9±0.7 (n = 7)	7.4±0.7 (n = 2)	5.4±0.8 (n = 3)	5.2±0.2 (n = 3)	-----
ΔFf/Δδ bulb (μN/mm)	191.9±43.7 (n = 3)	58.2±23.6 (n = 2)	172.7±68.8 (n = 3)	168.2±10.2 (n = 3)	154.1±22.6 (n = 2)	461.4±143.7 (n = 2)	194.3±8.9 (n = 3)
ΔFf/Δδ cortex (μN/mm)	213.9±38.9 (n = 3)	279.3±28.3 (n = 3)	300.8±110.8 (n = 3)	269.7±65.4 (n = 3)	473.2±37.2 (n = 3)	721.0±250.4 (n = 3)	556.3±77.9 (n = 3)
ΔFcut/Δδ bulb (μN/mm)	-----	-----	-----	-----	-----	-----	349.4±23.4 (n = 3)
ΔFcut/Δδ cortex (μN/mm)	-----	-----	-----	-----	-----	-----	321.8±43.0 (n = 3)

Average values and standard errors are presented. (Ø = diameter, bulb = olfactory bulb, cortex = cerebral cortex, F_max = maximum force, E = tissue modulus, F_crit = force at which probe penetrates the tissue, ΔF_f/Δδ = rate of change frictional force with respect to penetration depth, and ΔF_cut/Δδ = rate of change of cutting force of the tissue with respect to penetration depth).

^*Not included in statistical analysis

C. Frictional Forces

The slope of the linear portion of the unloading path of the force-displacement curve (K₂) is a function of the tissue modulus, probe diameter, and the coefficient of friction between the probe and surrounding tissue. Since ideally the only forces acting on the probe during its removal are that due to friction, the rate of change of frictional force acting on the probe with respect to penetration depth or probe displacement (ΔF_f/Δδ) was determined from K₂ as shown in Eq. 2. Insertion location was determined to have a significant effect on the rate of change of frictional force with respect to insertion depth, (p=0.0007) with the tissue in the cortex resulting in larger average values than in the olfactory bulb (Table 1). The rate of change of frictional force acting on the probe with respect to penetration depth will be referred to as “frictional forces” throughout the remainder of the text for the sake of simplicity.

D. Effects of Changing the Insertion Rate

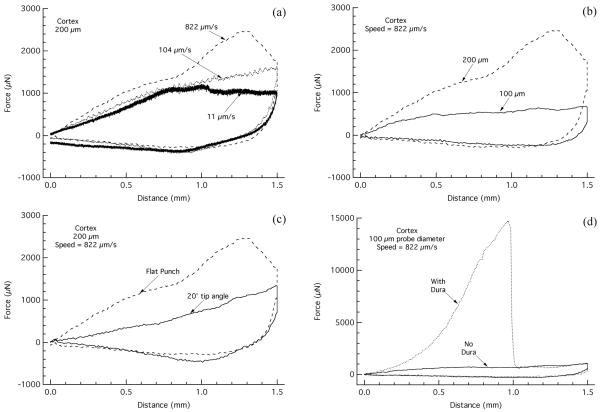
Due to the viscoelastic and/or viscoplastic nature of brain tissue, it is reasonable to assume that the penetration mechanics, as well as key properties of the material, such as stiffness, are affected by the rate at which the tissue is penetrated. For this study we selected three insertion rates that spanned part of the range typical for electrode insertion into the brain (822 μm/s, 104 μm/s, and 11 μm/s). Fig. 3(a) presents the average load-displacement curves of the 200 μm flat punch probe inserted into the cortex at these rates. A number of features of the force-displacement response of probe insertion and removal were affected by the rate at which the probe was inserted. Rate was determined to have a significant effect on the modulus of the tissue (p=0.0004) and the average modulus decreased with slowing insertion rate (Table 1). Post-hoc analysis determined that there was a significant difference in modulus values between the fast and medium rate (p=0.0027) as well as between the fast and slow insertion rate (p=0.0002). The maximum forces developed upon probe insertion were also affected by the rate of insertion, as was the load-displacement hysteresis. Both of these features generally decreased with decreasing insertion rate (Fig. 3(a), Table 1), and rate was determined to have a significant effect on the maximum force (p<0.0001). Post-hoc analysis determined there was a significant difference between the maximum forces developed between the fast and medium insertion rate (p<0.0001) and the fast and slow insertion rate (p<0.0001). The critical force of penetration (F_crit) of the flat punch probe seems to be affected by insertion rate in the olfactory bulb, yet seems less dependent on rate in the cortex. Additionally, insertion rate was determined to have a significant effect on the frictional force between the probe and tissue (p=0.0200) and post-hoc analysis showed that the frictional forces were statistically different between the fast and slow rates (p=0.0079) and the medium and slow rates (p=0.0354). Increased adhesion at the slowest rate during probe removal made it difficult to find linear portions of the corresponding force-displacement response and the extent of adhesion varied between runs, leading to large variances in the frictional forces.

Fig. 3.

The effect of parameter changes on the load-displacement relationship. (a) The effect of rate on the load-displacement response for insertion and removal of the 200 μm diameter flat punch probe in the cortex. Average load-displacement curves comparing the response of insertion at the three different insertion rates (n_FastLoad=2, n_FastUnload=3, n_Medium=3, n_Slow=3). (b) The effect of probe size on the load-displacement response for the insertion and removal of the flat punch probe. Average load-displacement curves comparing the response of the 100 and 200 μm diameter probes inserted into the cortex at a rate of 822 μm/s (n_200Load=2, n_200Unload=3, n_100Load=6, n_100Unload=3). (c) Average load-displacement curves comparing the response of the 200 μm diameter probe with a flat punch and sharpened tip into the cortex (n_FlatLoad=2, n_FlatUnload=3, n_Sharp=3). (d) Effect of dura and pia on the load-displacement response to probe insertion and removal. Representative load-displacement curves for the insertion of the 100 μm diameter flat punch probe into the cortex at insertion rates of 822 μm/s with and without the dura and pia present prior to insertion.

E. Effect of Changing Probe Size

In Fig. 3(b), the average load-displacement curves for the insertion of the flat punch probe into the cortex at an insertion speed of 822 μm/s are shown for the 100 μm and 200 μm probe diameters. The responses to insertion and removal of the 100 μm diameter flat punch probe in the cortex for all insertion rates showed a similar trend in the loading path to that of the 200 μm diameter probe (data not shown). However, the larger probe resulted in larger penetration forces and load-displacement hysteresis upon insertion (Fig. 3(b), Table 1). This would be expected due to the larger amount of tissue that is compressed and displaced upon insertion and the larger radial displacement caused by the larger probe diameter. Post-hoc analysis did show a significant difference in maximum force upon insertion between the 100 μm and 200 μm flat punch probes (p<0.0001). F_crit was also notably reduced when the 100 μm probe was used compared to the 200 μm probe (Table 1). The average modulus of the tissue (Table 1), as expected, was not determined to be dependent on the probe size. The average frictional forces were smaller for the 100 μm than the 200 μm probe and post-hoc analysis showed that these differences were significant (p=0.0057).

F. Sharpened Probe Insertion

To gain a better understanding of the effect that probe shape has on the penetration mechanics of brain tissue at the micrometer scale, the penetration of a sharpened probe was studied in comparison to the flat probe. In Fig. 3(c), the average force-displacement curves for the 200 μm probe inserted into the cortex at a rate of 822 μm/s are shown for the flat punch and the sharpened probe. In contrast to the two-stage response to the flat punch probe, insertion of the sharp probe resulted in a constant loading slope up to the final insertion depth. The penetration mechanism of a sharpened probe into soft solids (i.e. rubber) is the formation and opening of a mode I crack, in contrast to the mode II crack produced by the flat punch probe [28]. With this penetration mechanism, the load on the sharpened probe shows a steady increase once the crack has initiated and the probe has penetrated the soft solid.

The sharpened probe tip typically led to lower penetration forces than that of the flat punch probe with the same base diameter (Fig. 3(c), Table 1), and post-hoc analysis showed that there was a significant difference in the maximum force reached upon insertion between the flat and sharp 200 μm probe (p<0.0001). Also, it was determined that probe tip geometry did not have a significant effect on the frictional forces developed during probe removal.

The force acting on the sharpened probe after initial penetration is composed of the cutting force of the tissue and the frictional force acting on the probe [29], thus the loading slope (K₃) is a function of the tissue modulus, probe diameter, the coefficient of friction, and the cutting force of the tissue (F_cut). The rate of change of the cutting force of the in vivo brain tissue with respect to the penetration depth or probe displacement (δ) was thus determined from the loading slope K₃ by the relation in Eq. 3. As determined here, the cutting force of the material consists of both the force it takes to actually cut the tissue as well as the forces acting at the tip of the probe [29]. The rate of change of the cutting force with respect to the penetration depth (ΔF_cut/Δδ) of the tissue in the cortex and olfactory bulb are listed in Table 1 and will be referred to as the “cutting force” throughout the remainder of the paper for the sake of simplicity. There was not a statistical difference in the cutting force between these two insertion locations. The force required to cut a tissue should ideally be constant [29] unlike the displacement dependent response of the cutting force observed here (also observed for the insertion of a needle into liver tissue ex vivo [29]). The increase in cutting force with insertion depth is possibly due to internal substructures that result in local areas of increased stiffness [29] or due to the forces acting at the probe tip during insertion as it compresses the tissue beneath it.

The response of insertion of the sharpened probe in both the cortex and olfactory bulb was affected by the rate of insertion. At an insertion rate of 11 μm/s, a two-stage loading path sometimes occurred (data not shown). It should be noted that at least one insertion in the olfactory bulb and cortex, at the insertion rate of 11 μm/s, resulted in a more constant, linear increase in force as a function of probe displacement up to the final insertion depth. The lack of a consistent linear response upon the insertion of the sharpened probe at the slowest rate prevented the calculation of a cutting force.

G. Dura and Pia Mater

Representative load-displacement curves for the insertion of the 100 μm flat punch probe into the cortex at 822 μm/s, with and without the dura and pia present, are shown in Fig. 3(d). With dura and pia present, the forces developed upon insertion were orders of magnitude larger than when the dura and pia were removed prior to insertion. A number of runs were completed with the dura and pia left intact and while there was variation in the maximum load reached and at what depth it was reached, all the tests resulted in forces significantly higher than when the dura and pia were removed. These tests included the insertion of the 100 μm flat punch probe into the olfactory bulb at a rate of 822 μm/s (average F_max = 11594 μN, standard deviation = 1925 μN, n = 3), the cortex at a rate of 822 μm/s (average F_max = 10886 μN, standard deviation = 8104 μN, n = 3), the cortex at a rate of 11 μm/s (average F_max = 7258 μN, standard deviation = 4510, n = 3), the olfactory bulb at a rate of 11 μm/s (F_max = 4728 μN, n = 1), and the cortex at a rate of 104 μm/s (F_max = 1510, n = 1).

IV. DISCUSSION

Future optimization of neuronal implants of any nature necessitates a minimization of tissue damage by engineering the shape and material properties of the implant [23]-[25]. An understanding of the interaction of micro-scaled probes with brain tissue is required for this design effort. Our study utilized micro-scaled, cylindrical probes that did not compress or deflect during insertion and removal. This allowed us to make directly relevant measurements of force vs. displacement and to use these measurements in simple models to calculate mechanical and material properties of the brain tissue. Our study is in contrast to previous efforts that have used larger probes [16-18] or probes of more complex shape [19-24] that do not allow for direct calculation of mechanical and material properties for use in the design of arbitrary probes. Our data is suitable for use in first generation finite element models for designing probes complying with specific probe use, shape and material considerations. Additionally, our experiments along with prior studies provide a framework for understanding how the properties of an implant impact the mechanics of insertion into the brain and suggest strategies for implant design and insertion.

A. Material Properties

The modulus values of rat and porcine brain tissue have been determined in previous studies in vivo, in situ, and in vitro by the method of indentation [14], [15], [20] and are similar (although typically lower for comparable speeds) to those determined in the current study for mouse brain tissue in vivo, despite differences in testing parameters such as indenter size, geometry, indentation depth, and animal species. The average tissue modulus in this study is affected most by insertion rate and decreases with decreasing rate. This could indicate that the modulus would reach a plateau in value as insertion rate continued to decrease. It is also possible that a plateau in modulus value would occur if the insertion rate became fast enough. However, the rate at which either of these would occur, or if they even would occur, is not known and would require further study.

For applications involving the penetration of the brain tissue, information on viscoplastic properties of the tissue are needed in addition to viscoelastic properties (e.g. modulus). The cutting force of the tissue as well as frictional forces between the probe and tissue are useful properties for the design of probes and the modeling of probe insertion. The cutting force of the tissue is independent of insertion location and was only able to be calculated for the fastest insertion rate, due to the nonlinear response seen from penetration of the sharp probe at the slowest insertion rate. Frictional forces are significantly affected by the rate of insertion (due to adhesion), size of the probe base (not tip geometry), and location of insertion.

Underlying assumptions of the mechanical model used in this study to determine the modulus of in vivo brain tissue from indentation measurements should be noted and considered as part of this analysis, as well as some of the limitations of this model as used in the current study. Assumptions made with the use of Eq. 1 include that the material being indented is linear elastic, homogeneous, and isotropic, the indented material is an elastic half-space [26], and the contact between the indenter and tissue is frictionless [26]. While the influences of friction and finite tissue thickness on modulus values calculated with such a model have been shown to increase as Poisson’s ratio and relative indentation depth (ratio of indentation depth to tissue thickness) increase, both have been shown to decrease as the aspect ratio (ratio of the indenter radius to tissue thickness) decreases [30]. Thus, the small aspect ratio used in this study should help to reduce this source of error. The model was used with regions of the force-displacement data that demonstrated a linear relationship due to the underlying assumption of linear elasticity. It is not possible to separate the effects of intrinsic material properties and effects of constraints (due to the surrounding pia, dura, and skull), especially when comparing the calculated properties of the cortex and olfactory bulb. In previous studies [14], [15], it was concluded that, compared to unconfined in vitro indentation, confinement of the brain within the skull during in situ indentation did not effect the calculated modulus values for 1mm deep indentations of rat brain tissue, but did effect the calculated modulus values for 4mm deep indentations of porcine brain tissue resulting in a stiffening effect. The material properties obtained in the current study are presented solely as apparent values to demonstrate the relative change in properties that occur with modifications to key testing parameters using testing conditions that most closely mimic actual probe implantation.

B. Probe Design Considerations

When designing a probe for insertion into the brain it is paramount to try to reduce damage to the tissue, but it is still necessary to construct a probe that can withstand the force required to implant it. The penetration forces measured in this study are comparable to those of the penetration of the cerebral cortex of rats by sharpened tungsten electrodes [23]. Additionally, our results confirmed the trend reported by Jensen et al. [23] that penetration forces decrease with a decrease in probe cross-sectional area, as expected based on the mechanics of insertion. However, a decrease in insertion force due to smaller probe diameter does not ensure better probe stability during insertion since a reduction in diameter reduces the probe’s resistance to buckling. A reduction in cross-sectional area may however be associated with a decrease in the amount of initial tissue damage upon insertion [31] and is therefore desirable.

It may be possible to gain a qualitative understanding of the relative amount of tissue damage induced by probe implantations from the hysteresis of the force-displacement response of probe insertion and removal. The area under the loading portion of the force-displacement curve is an indication of the energy absorbed by the tissue, which consists in part of energy required to tear (damage) the tissue upon insertion, along with other energy contributions. So, for example, the difference in force-displacement hysteresis between the 100 μm and 200 μm diameter probes (Fig. 3(b)) could be an indication that the larger probe is inducing more damage (tissue tearing) than the smaller probe. Thus, with further study, the force-displacement hysteresis may be able to provide information on relative amounts of tissue damage occurring during the implantation process.

The complete force-displacement curves presented in this study for sharpened probes demonstrate a more gradual increase in force during insertion relative to the flat punch, with largest forces occurring near the final insertion depth (at the fastest insertion rate). This is due to the flat probe initially compressing the tissue beneath it prior to penetration (Stage I) and should increase the flat probe’s propensity to bending compared to the sharpened probe. This is an important design consideration since it could facilitate the use of a compliant material for the probe body, as long as the probe was shaped properly and inserted at the correct speed to circumvent compression (and thus the rapid increase in force) of the tissue prior to probe penetration.

It has previously been shown that slow probe insertion rates can decrease tissue damage [25]. Therefore, it is particularly important to consider the relative merits between stiffness (modulus) reduction and increased adhesion with decreasing insertion rate. For example, based on the results of this study, it could be advantageous to insert the probe into the tissue at a rate of 104 um/s. At this rate, the average modulus is lower than at the fastest insertion rate, as are the overall penetration forces, and adhesion was not a problem. Also, methods to prevent adhesion during implantation could be beneficial and allow for the use of slower insertion rates without the drawback of increased adhesion. Thus balancing the effect of rate on tissue stiffness and probe adhesion can be critical in probe design and insertion procedure to ensure an ideal insertion methodology.

Together, the force-displacement data presented here and the material properties of the brain derived from them provide key information for designing neuronal probes, single or multi-tined, using advanced analytical or computational tools for optimal penetration mechanics.