Identification of synthetic vowels based on a time-varying model of the vocal tract area function

Abstract

The purpose of this study was to conduct an identification experiment with synthetic vowels based on the same sets of speaker-dependent area functions as in Bunton and Story [(2009) J. Acoust. Soc. Am. 125, 19–22], but with additional time-varying characteristics that are more representative of natural speech. The results indicated that vowels synthesized using an area function model that allows for time variation of the vocal tract shape and includes natural vowel durations were more accurately identified for 7 of 11 English vowels than those based on static area functions.

Introduction

The vocal tract area function is a representation of the collective effect of the positions of the articulators at some instant in time, and is a primary component in the development of certain types of speech production models and speech synthesizers. The typical aim in using such models is to compute the acoustic characteristics of various structural and kinematic variations of the vocal tract, and compare them to similar measurements of natural speech. An equally important, but less common aim is to assess the perceptual relevance of speech sounds produced by such models. Toward this goal, a vowel identification experiment was reported by Bunton and Story (2009) in which synthetic vowel samples were based on vocal tract area functions of eight different speakers. A particular vowel was generated by specifying a static area function that had been derived from previously published measurements based on magnetic resonance imaging (MRI) (Story et al., 1996, 1998; Story, 2005a, 2008). Vowels were synthesized with a one-dimensional wave-reflection type of vocal tract model coupled to a voice source. Considerable variability was noted in the identification accuracy of individual vowels based on the simulated productions. These results were not surprising given the large body of research that has suggested that vowel inherent spectral changes, such as time-varying formant transitions and vowel duration, are important for identification accuracy (Nearey and Assmann, 1986; Nearey, 1989; Hillenbrand and Nearey, 1999; Hillenbrand et al., 2000; Nittrouer, 2007). Thus, it is hypothesized that identification accuracy of synthetic vowels based on vocal tract area functions would be enhanced if the shape defined by the area function was allowed to change over the duration of each vowel, and that duration was vowel dependent.

Method

Acoustic analysis of recorded vowels

To obtain spectro-temporal information for the vowel synthesis, time-varying formant frequencies were obtained from productions of 11 American English vowels ([i, ɪ, e, ε, æ, Λ, ɑ, ɔ, o, ʊ, u]) spoken in citation form by an adult male speaker. The vowels were digitally recorded with a Kay Elemetrics CSL4400 using an AKG CS1000 microphone. The first two formant frequencies were estimated over the time course of each vowel with the formant analysis module in PRAAT (Boersma and Weenink, 2009). Formant analysis parameters were manually adjusted so that the formant contours of F1 and F2 were aligned with the centers of their respective formant bands in a simultaneously displayed wide-band spectrogram. Fundamental frequency and intensity contours for each vowel were also extracted with the appropriate PRAAT modules and were transferred to vector form in MATLAB (The Mathworks, 2008) for further processing. This collection of trajectories was not intended to be representative of American English in general, but rather to capture the natural temporal variation of formant frequencies for one speaker that could be emulated in synthetically generated vowels.

Formant-to-area function mapping

A technique for mapping area functions to formant frequencies, and vice versa, was developed by Story and Titze (1998) and further described in Story (2005a, 2005b, 2009). With this technique a time-varying area function can be generated by

$$A\left(x,t\right)=\frac{\pi }{4}{\left[\Omega \left(x\right)+q_1\left(t\right){\varphi }_1\left(x\right)+q_2\left(t\right){\varphi }_2\left(x\right)\right]}^2,$$ (1)

where x is the distance from the glottis and t is time. The Ω(x), ϕ₁(x), and ϕ₂(x) are the mean vocal tract diameter function and shaping functions (referred to as “modes”) as obtained from principal component analysis (PCA) of a speaker-specific set of static area functions. The q₁(t) and q₂(t) are scaling coefficients that determine the vocal tract shape at a given instant of time. As shown in Story and Titze (1998), within a limited range any given pair of [q₁,q₂] coefficients corresponds to a unique pair of [F1,F2] formants, thus forming a one-to-one mapping.

Eight different coefficient-to-formant mappings were generated based on the same sets of area functions for the eight speakers studied in Bunton and Story (2009). These included four male (mean age 33 years; range 29–40 years) and four female (mean age 26 years; range 23–39 years) speakers. Speakers will be identified in this study as they were previously as SF0, SF1, SF2, SF3, SM0, SM0-2, SM1, SM2, and SM3, where “F” denotes female and “M” male. The SM0-2, SM1, SM3, SF1, SF2, and SF3 contained area functions for the 11 American English vowels ([i, ɪ, e, ε, æ, Λ, ɑ, ɔ, o, ʊ, u]), whereas the SM0 and SF0 sets do not have an area function for the [e] vowel, and the SM2 set does not have an [ε]. Hence these latter sets represent only ten vowels each.

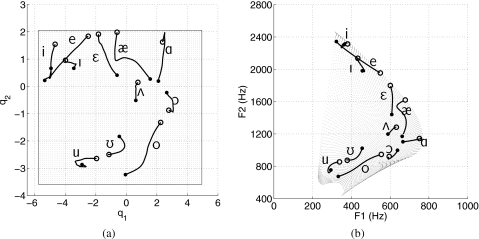
As an example, the coefficient-to-formant mapping calculated for speaker SM0-2 is shown in Fig. 1 where the coefficient mesh [Fig. 1a] is mapped to the [F1,F2] formant mesh [Fig. 1b]. The [F1,F2] trajectories superimposed on the formant mesh in Fig. 1b are those from the analysis described in Sec. 2A, except that they have been slightly rescaled so that they fit entirely within the mesh. Transforming these trajectories to the coefficient domain results in the (q₁,q₂) trajectories superimposed on the mesh in Fig. 1a. When used in Eq. 1, each coefficient trajectory will generate a time-varying area function whose F1 and F2 frequencies will emulate the original formant contours.

Figure 1.

Demonstration of the formant-to-coefficient mapping based on speaker SM0-2. (a) The mesh in the background, bounded by the thin line, represents the mode coefficient space generated from the PCA of SM0-2’s original 11 vowels, and the trajectories correspond to the formant trajectories in (b). (b) The deformed mesh in the background represents the [F1,F2] space generated from the coefficient mesh in (a), and the formant trajectories are those measured with formant analysis but slightly rescaled so that they fit entirely within the mesh. In both (a) and (b), the open and closed circles at the end points of each trajectory denote the onset and offset of the vowel, respectively.

For the other seven speakers, the [F1,F2] trajectories were rescaled so that they fit entirely within a given speaker’s formant mesh, similar to Fig. 1b for SM0-2, and then transformed to that speaker’s coefficient space so that a time-varying area function could be produced with Eq. 1. In total, 88 time-dependent area functions were generated across 8 speakers and 11 vowels. Note that even though 3 of the original area function sets (for SF0, SM0, and SM2) contained only 10 vowels, 11 vowels could be generated with the formant-to-coefficient mapping technique.

Synthetic vowel samples

A synthetic vowel sample was generated for each time-varying area function with a voice source model acoustically and aerodynamically coupled to a wave-reflection model of the trachea and vocal tract (Liljencrants, 1985; Story, 1995). The vocal tract shape, which extended from glottis to lips, was dictated at every time sample by the given area function A(x,t). The wave propagation algorithm included energy losses due to yielding walls, viscosity, heat conduction, and radiation at the lips (Story, 1995), and accommodated the different vocal tract lengths of each speaker.

The voice source model was based on a kinematic representation of the medial surface of the vocal folds (Titze, 1984, 2006). Control parameters for this study consisted of fundamental frequency, degree of posterior adduction, and respiratory pressure. The fundamental frequency (F0) for each male vowel sample was varied according to the contours extracted in the acoustic analysis described in Sec. 2A. For the female vowels, each measured F0 contour was multiplied by a factor of 2. For example, the peak F0 in the contour for the male [i] vowels was 112 Hz whereas for the female it was 224 Hz. The respiratory pressure for each sample, male or female, was ramped from 0 to 7840 dyn∕cm² in the initial 50 ms with a cosine function, and then maintained at a constant pressure for the remaining duration of the utterance. The posterior adduction of the vocal folds was varied slightly over the time course of each synthetic vowel according to the shape of the intensity contour measured in the acoustic analysis of the recorded vowels. That is, the adduction was greatest (vocal folds closest together) at the point where the intensity of a particular recorded vowel was highest. Because of the somewhat more breathy quality of female speakers (e.g., Klatt and Klatt, 1990), the posterior separation of the vocal folds was set to be 30% greater for the vowels generated from the female area functions. Other model parameters were set to constant values throughout the time course of each utterance.

The output of the vocal fold model is a glottal area signal. This was coupled to the propagating pressures and air flows in the trachea and vocal tract through aerodynamic and acoustic considerations as described by Titze (2002). The glottal flow was determined by the interaction of the glottal area with the time-varying pressures present just inferior and superior to the glottis. In addition, a noise component was added to the glottal flow signal if the calculated Reynolds number within the glottis exceeded 1200. The sound pressure signal radiated at the lip termination was converted to an audio file for later presentation in the listening experiment.

The durations of each synthetic vowel were based on the measurements reported for male and female speakers by Hillenbrand et al. (1995, p. 3103). However, because they were measured for vowels embedded within “hVd” words, the durations were increased by 50% so that the resulting isolated vowels would be similar to the length of an hVd word.

Listeners

Ten listeners (five males and five females) with a mean age of 28.1 years served as participants. Listeners were native speakers of American English, native to Arizona, and passed a hearing screening at 25 dB hearing level (HL) for frequencies of 0.5, 1, 2, and 4.0 kHz bilaterally.

Listening task

Vowel samples were presented via loudspeaker placed 1 m in front of individual listeners seated in a sound treated room. Sample presentation was controlled using the ALVIN interface (Hillenbrand and Gayvert, 2005). Prior to the experimental task, listeners completed a training task with naturally produced vowel samples from an adult male speaker to assure that listeners were able to identify all 11 English vowels and to familiarize them with the computer interface. Mean identification accuracy was 97.4% across listeners for this training task. For the experimental task, following presentation of the target vowel, listeners were asked to use the computer mouse to select one of the buttons displaying the 11 English vowels on the computer screen. Each button listed the phonetic symbol for the vowel and a corresponding hVd word. Listeners were allowed to replay each sample once. Each listener heard five repetitions of each vowel sample blocked by speaker sex in random order. Listening sessions lasted 30–40 min. A confusion matrix based on listener identification was calculated separately for each speaker and then compiled across speakers to form a composite confusion matrix.

Results

Percent correct identifications of each vowel based on each speaker are shown in Table 1. The mean identification accuracy across all vowels for individual speakers ranged from 79% to 87% (see bottom row of table). For individual vowels, the mean identification accuracy was greater than 70% with the exception of [ɑ], which was identified correctly 46% of the time.

Table 1.

Percentage of vowels identified correctly for each speaker across listeners. The bottom row indicates the mean identification accuracy across all vowels for each speaker, and the rightmost column indicates the mean identification accuracy across all speakers for each vowel.
Vowel	Speaker									Mean
	SM0	SM0-2	SM1	SM2	SM3	SF0	SF1	SF2	SF3
i	92	74	78	88	94	86	88	50	90	82
ɪ	42	68	88	78	80	80	84	82	80	76
e	100	98	100	100	98	98	94	94	98	98
ε	68	92	84	82	90	98	88	98	100	89
æ	94	62	84	92	92	92	58	92	74	82
ʌ	90	96	96	92	94	66	94	98	92	91
ɑ	52	40	48	68	52	22	52	32	50	46
ɔ	82	88	80	76	80	86	76	80	82	81
o	98	94	94	98	100	76	92	94	90	93
ʊ	64	80	92	76	90	88	86	88	76	82
u	82	86	86	92	86	70	66	68	78	79
Mean	79	80	85	86	87	78	80	80	83

A composite confusion matrix including the identification data based on all speakers (across listeners) is shown in the upper half of Table 2. Correct identification of target vowels can be seen along the diagonal in boldface cells. Vowel confusions were typically between adjacent vowel categories in the vowel space. For the vowel [i], confusions occurred with [ɪ] and [ε], and [ɪ] and [ε] were frequently confused with each other. Accuracy for the vowel [e] was the highest at 99% across speakers. For the male speakers, the identification accuracy for target vowel [ε] was 83% and was most frequently confused with [æ]. In contrast, the identification accuracy for [ε] was 96% across female speakers. For all speakers, the central vowel [Λ] was confused with both [æ] and [ɑ]. For the back vowels, accuracy for [ɑ] was the lowest of any vowel (46%), and was most frequently confused with [ɔ]. The vowels [u] and [ʊ] were confused by listeners for all speakers.

Table 2.

Composite confusion matrix of the vowels identified across speakers. The values in each cell are shown as percent. The upper half of the table shows data from the present study and the lower half shows identification databased on the static vowel experiment reported in Bunton and Story (2009).
		Listeners’ identification
		i	ɪ	e	ε	æ	ʌ	ɑ	ɔ	o	ʊ	u
Vowel intended by speaker (time-varying)	i	82	11	1	6	0	0	0	0	0	0	0
	ɪ	1	76	2	21	0	0	0	0	0	0	0
	e	0	0	98	0	1	0	0	0	0	0	0
	ε	0	0	0	89	9	1	2	0	0	0	0
	æ	0	0	2	10	82	2	3	1	0	0	0
	ʌ	0	0	0	3	2	91	4	1	0	0	0
	ɑ	0	0	0	0	16	1	46	37	0	0	0
	ɔ	0	0	0	0	0	1	17	81	0	0	0
	o	0	0	0	0	0	0	2	2	93	3	0
	ʊ	0	0	0	0	0	6	1	0	2	82	9
	u	0	0	0	0	0	1	0	0	2	18	79
Vowel intended by speaker (static)	i	93	6	0	1	0	0	0	0	0	0	0
	ɪ	2	25	39	22	1	9	0	0	0	0	0
	e	2	27	34	35	1	0	0	0	0	0	0
	ε	0	2	12	36	35	2	0	0	0	10	2
	æ	0	0	0	2	97	0	1	1	0	0	0
	ʌ	0	0	0	0	0	34	20	14	5	24	4
	ɑ	0	0	0	0	12	6	50	28	4	0	0
	ɔ	0	0	0	0	0	1	25	61	13	1	0
	o	0	0	0	0	0	9	7	7	39	28	11
	ʊ	0	0	0	0	0	2	7	8	12	40	32
	u	0	0	0	0	0	0	0	0	1	11	88

To compare the results for the time-varying vowels in the present study to those for static vowels, a composite confusion matrix was calculated from the individual speaker confusion matrices reported in Bunton and Story (2009). This is shown in the lower half of Table 2. Based on a two-way analysis of variance (ANOVA), the main effects of synthesis condition (time-varying vs static), F(1,176)=117.88, p<0.001, and vowel, F(10,176)=9.86, p<0.001, were statistically significant. The interaction was also significant, F(10,176)=13.88, p<0.001.

It can be seen in Table 2 that seven of the vowels ([ɪ,e,ε,Λ,ɔ,o,ʊ]) synthesized with a time-varying vocal tract shape were identified more accurately than the vowels based on static vocal tract shapes reported by Bunton and Story (2009). With the exception of [ɔ], the increase in accuracy over the static cases was 50% or more. For [ɔ] the increase was 20%. Identification accuracy of the [ɑ] vowel was similarly poor for the time-varying compared to the static case (46% vs 50%, respectively). In both studies the [ɑ] vowel was primarily confused with the [ɔ], which is likely because these two categories tend to be collapsed in the southwest United States (Labov et al., 2006). The other corner vowels [i, æ, u] were less accurately identified when the vocal tract shape varied in time than when it was static. The differences for these three vowels ranged from 9% to 16%.

Audio samples of the 11 vowels in the static and time-varying conditions for speaker SM0-2 are available for listening in Mm. 1 and Mm. 2. The order of presentation in each condition is identical to that listed in the first column of Table 2.

Mm. 1.

Download audio file ^{(791.6KB, wav)}

[SM0-2_static.wav (792 KB). This is a file of type “wav.”]

Mm. 2.

Download audio file ^{(1MB, wav)}

[SM0-2_timevary.wav (1 MB). This is a file of type “wav.”]

Discussion

The hypothesis of this study was that identification accuracy of synthetic vowels based on vocal tract area functions would be enhanced if the shape defined by the area function was allowed to change over the duration of each vowel, and duration was vowel dependent. Demonstrating improvement in identification of some vowels by incorporating additional time-varying cues is, of course, not unexpected. Time-varying formant transitions and vowel duration are well known to be important cues for improved identification accuracy (Nearey and Assmann, 1986; Nearey, 1989; Hillenbrand and Nearey, 1999; Hillenbrand et al., 2000; Nittrouer, 2007). The question remains, however, as to why the identification accuracy of the time-varying vowels is still well below those reported for similarly time-varying vowels generated with a formant synthesizer (e.g., Hillenbrand and Nearey, 1999). A major difference is that formant synthesis allows precise control of the formant frequencies and bandwidths over the time course of a vowel, whereas the method of synthesis used in the present study is based on generating movement of the vocal tract. Although formants extracted from natural speech were mapped into movement information (i.e., [q₁,q₂] coefficients) to drive the vocal tract model, this was based only on F1 and F2 (see Fig. 1). That is, when coupled to the voice source and trachea, the time-varying area functions produced sound samples that contained [F1,F2] formant trajectories based on the original recording, but there was no direct control of the formants higher than F2 even though higher formants existed in the signal due to the resonant structure of the vocal tract shape. Thus it is possible that for some of the vowels generated, the pattern of formants F3 and higher created information that conflicted with the target vowel. An example is the time-varying [i] based on SM-02’s vocal tract (the first sample in the accompanying Mm. 2). The [F1,F2] trajectory for this synthetic vowel is precisely that shown in the upper left corner of Fig. 1b, and indicates little movement of either F1 or F2. There is, however, a downward glide of F3 such that the distance between F2 and F3 decreased over the duration of the vowel, and perhaps contributed to its confusion with [ɪ]. Interestingly, the length of the corresponding [q₁,q₂] trajectory for this vowel in the coefficient space [Fig. 1a] indicates that there was a change occurring in vocal tract shape, but in this case the change primarily affected F3.

It is not surprising that time-varying changes in the area function intended to move F1 and F2 in some specific pattern might also have unintended effects on the upper formant frequencies. Acoustic modeling of the vocal tract shape has shown that even subtle changes in cross-sectional area may have large effects on some formants (e.g., Stevens, 1989; Story et al., 2001; Story, 2006), especially when such changes occur in a part of the vocal tract that is already fairly constricted. Thus, it can be predicted that the vowels [i,ɑ,u] would be particularly susceptible to these effects because, compared to other vowels, they typically are produced with the most constricted vocal tract shapes. Perhaps this is at least a partial explanation of why these vowels were not identified with greater accuracy than the static versions. It is not clear why the time-varying [æ] vowel was identified less accurately than its static counterpart. A next step in this process is to build in more control of the upper formant frequencies via the area function model.

From the results of the present study it is concluded that (1) time-varying area functions produce vowels that are more identifiable than those produced with static area functions (with the exceptions noted previously) and (2) a model of the vocal tract area function can serve as the basis for future studies to assess the perceptual relevance of various structural and kinematic variations of the vocal tract.