Abstract
Proteins interacting with membranes can result in substantial membrane deformations and curvatures. This effect is known in its broadest terms as membrane remodeling. This review article will survey current multiscale simulation methodologies that have been employed to examine protein-mediated membrane remodeling.
Keywords: Multiscale, simulation, membrane, remodeling, proteins, BAR, mesoscopic
1. Introduction
This review article will survey a number of multiscale simulation approaches that are capable of examining the process of protein-generated membrane curvature. Protein-generated, or mediated, membrane curvature will from this point be denoted “membrane remodeling”.
A number of proteins and protein modules have been targeted as potential membrane remodelers [1, 2], and play key roles in, for example, vesicular transport [3], where coat complexes containing clathrin and other coat proteins sculpt the membrane in preparation for the generation of a nascent transport vesicle. Accessory proteins such as amphiphysin, endophilin and epsin all contain structural elements (e.g., the BAR (Bin/amphiphysin/Rvs) and ENTH (epsin N-terminal homology) [1] domains) that can bind with the membrane surface, resulting in significant membrane bending. In particular, the BAR protein domain is a crescent-shaped homo dimer with several positively charged residues on its concave surface [4–14] that plays a key role in clathrin mediated endocytosis [1] and other membrane processes. Both the molecular structural details and electrostatic charge distribution of the dimer result in BAR domains preferentially binding to regions of specific membrane curvature, and as such, it has been proposed that at least in vivo BAR domains can act as a membrane curvature sensor and remodeler [5, 6]. In vitro, BAR domains containing an additional N-terminal amphipathic helix, denoted N-BARs, have been observed to tubulate liposomes [6–8, 15]. Theoretically it has been proposed that N-terminal amphipathic helices on their own can result in membrane bending [16]; however, experimentally this issue is still up for debate [17]. It should be noted that membranes without proteins are capable of similar remodeling via careful lipid mixing, and such problems have been studied in membrane biophysics [18], which are beyond the scope of this review.
Protein-mediated membrane remodeling involves the interaction of proteins with membranes over multiple time and length-scales. For example, it has been observed with all atom molecular dynamics (MD) simulation (as shown in image (a-1) of Fig. 1) that protein mediated local membrane bending can occur over timescales of less than one hundred nanoseconds [19–22]. Yet experimentally, membrane remodeling of liposomes into tubules or vesiculated structures can take seconds, even minutes, for a single liposome to remodel into a tubulated structure [23] (as shown in the electron microscopy (EM) image (d) of amphiphysin remodeling in Fig. 1, courtesy of V. Unger). The process of membrane remodeling also can involve proteins in the surrounding solvent and in fact remodeling of liposomes has been found to be dependent on the bulk concentration of N-BARs in the surrounding solvent [5], resulting in small buds at low N-BAR concentrations, tubules at intermediate concentrations, and then small vesicles at the highest concentrations [5]. Intuitively, this observation suggests that there is likely some sort of collective organization and perhaps even oligomerization of multiple N-BAR proteins over long length and timescales [10]. Tubulation of liposomes has also been observed with other BAR domains, for example F-BAR (FCH-BAR) domains, which [8–12] possess an oligomerized F-BAR coat and whose tubule diameters are almost three times that for amphiphysin and endophilin.
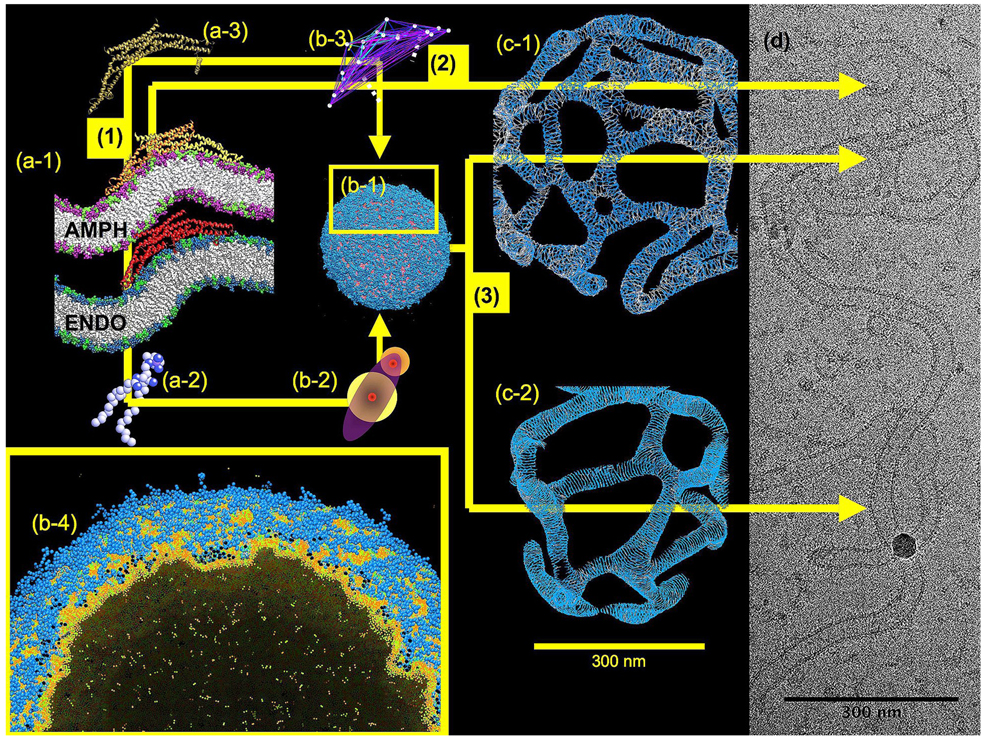
Figure 1.
A schematic of the multiscale characteristics of protein mediated membrane remodeling. Images (a-1) to (a-3), (b-1) to (b-4), and then (c-1) and (c-2) give simulation snapshots of N-BAR domain driven membrane remodeling at the atomic, CG, and mesoscopic scales, respectively. The colored arrows designate different multiscale paths where by the simulations can ultimately connect with EM imaging (EM image (d) of amphiphysin tubulation courtesy of V. Unger). Path (1) connects image (a-1), the atomic level, with (b-1) the CG scale. In this path, lipids (a-2) and proteins (a-3) are systematically coarse-grained into much simpler objects (b-2) and (b-3), but still retain residual atomic-level information. An entire 200 nm diameter liposome composed of around half a million CG lipids undergoing the early stages of remodeling is shown in image (b-1). Path (2) directly connects the atomic with the mesoscopic scale, and is a methodology sometimes employed. This path requires fairly extensive phenomenological information. However, as path (2) connects to image (c-1) and (c-2), the mesoscopic representation, liposome remodeling of 500 nm diameter liposomes can be described over effectively very long (macroscopic) timescales. It is at this end point that direct comparisons with EM imaging can be achieved (image d). The two different mesoscopic images, (c-1) and (c-2), give an indication of the polymorphism of structures that can be generated depending on relatively small variations in the N-BAR oligomerization energy, and when compared to the ensemble of real experimental images that can occur in image (d), further demonstrates how complex the protein-mediated membrane remodeling process can be. The multiscale path (3) connects the atomistic scale to the mesoscopic scale via an intermediate CG simulation scale. Here, long length-scale correlations of entire N-BAR domains (as in image (b-1)) systematically guide the development of mesoscopic models that then do not have to rely on phenomenological information. The lower inset, image (b-4) shows a close-up cut-away of image (b-1), the CG scale, where the membrane is becoming remodeled by CG N-BAR domains embedding amphipathic helices into the low density regions of the outer CG bilayer.
2. Multiscale Nature of Membrane Remodeling
The multiscale aspect of protein mediated membrane remodeling (e.g., as depicted in images (a-1) through (c-2) of Fig. 1) poses a number of computational and conceptual challenges, and thus has played a role in the rapid growth in the development of atomic, coarse-grained (CG) and other multiscale computational methods for biomolecular systems (see Ref. [24] for a general overview, along with a recent review [25]). A significant amount of effort has already been devoted to biological membranes (see, e.g., Ref. [26] for an example of an atomic-scale lipid force field and recent reviews [27, 28]), along with the development of atomic and CG models for proteins and peptides (see recent reviews in Refs. [29–31] for a more complete description). Theoretically, mesoscopic (or continuum) membrane models also have a long history beginning with the seminal work of Helfrich [32], along with newer models that can incorporate the spontaneous curvatures generated anisotropic protein inclusions [33–36]. Recent work by Brown and co-workers has made significant steps to present a unified elastic membrane model that can incorporate protein inclusions, Gaussian curvature effects, bending, and membrane thickness fluctuations [37, 38], and has been directly compared to CG membrane simulation [39]. Computationally, mesoscopic membrane approaches tie into the upper end of the multiscale simulation approach, as depicted in images (c-1) and (c-2) of Fig. 1, and again, a number of approaches could be employed [40–52].
Returning to Fig. 1, the multiscale decomposition for membranes can be roughly divided into the atomic (Å, ns), CG (µm, µs), and mesoscopic scales (mm, ms), as illustrated in images (a-1) to (a-3), (b-1) to (b-4), and (c-1), (c-2) of Fig. 1 for the specific example of N-BAR domain driven membrane remodeling using the multiscale approaches for N-BARs developed in our research group [19–21, 51–54]. Of course, this decomposition is completely general, and there are multiple complementary multiscale approaches that can be employed (e.g., the CG and mesoscopic methodologies mentioned previously and as given in Ref. [55]). Image (a-1) of Fig. 1 shows the “full resolution” atomic level MD simulation where the details of molecular-level interactions are explicitly included. Simulation snapshots of both amphiphysin (AMPH) and endophilin (ENDO) are shown, where in both cases it is clear how the single N-BAR domain has locally bent the membrane underneath the “arch” of the dimer. On this scale, single (or a few) N-BAR domains can bend a lipid bilayer over relatively short time scales (about 40 ns) [19–21]. Image (b-1) next shows a CG simulation snapshot of over 2000 CG N-BAR domains (where a single CG N-BAR is shown in image (b-3)) [56] interacting with an entire liposome composed of systematically derived CG lipids (with a single CG lipid shown in image (b-2)) [53, 54]. This particular CG simulation employs over half a million CG “sites” (equivalent to about 1011 atoms in total) and is orders of magnitude faster than an all-atom MD simulation of the same system. In this case, key interactions in the CG representation were systematically determined from the original atomic level interactions via the multiscale coarse-graining (MS-CG) methodology [57–61] for the membrane. The CG approach used for the membrane, denoted the Hybrid Analytic-Systematic (HAS) method [53, 54], further employs a more generic, analytic component to the CG interaction to model those configurations that were not well-sampled in the original MD simulation. (It should be noted that other CG models for BAR domains could also be employed [22, 62].) The BAR protein CG model employs a related fluctuation matching method [63] to define a heterogeneous elastic network model (HeteroENM [56]) for the N-BAR dimer. The interactions between the membrane and protein are resolved via an inverse Boltzmann technique [54].
Images (c-1) and (c-2) in Fig. 1 next depict the mesoscopic scale, where the system is described by new collective variables [48, 64, 65] which incorporate atomic information (via coarse-graining) from “the bottom up”. At this scale, various approaches originating from elastic continuum models for membranes could be employed [37–39, 42, 45–52]. This final mesoscopic component of the overall multiscale simulation methodology for membrane remodeling has the ability to access very long length and times scales and can make direct contact with experiment [52] (e.g., the EM image (d) in Fig. 1) as will be described in more detail later.
3. Multiscale Simulation of Membrane Remodeling
In this section, some of our recent multiscale simulation studies pertinent to the problem of protein mediated membrane remodeling will be discussed in more detail.
3.1 Atomic level molecular dynamics
Atomic MD simulation has proven to be a key starting point in analyzing protein mediated membrane remodeling. The first simulations by Blood et al. [19], unprecedented at the time, aimed to reproduce the experimental conditions in Ref. [5] by placing a single amphiphysin N-BAR domain on an all atom membrane composed of 70%/30% dioleoylphosphatidylcholine (DOPC)/dioleoylphosphatidylserine (DOPS), all modeled with the CHARMM 22 and 27 force fields [66, 67]. It was found that a single N-BAR domain (e.g., image (a-3) in Fig. 1) could bend a bilayer over atomic level timescales (i.e., about 40 ns), as shown in image AMPH (a-1) of Fig. 1, where the single amphiphysin N-BAR locally sculpts the membrane. Further studies [20] explored the role of amphipathic helix insertion, and similar studies by others [22] were able to reproduce this key atomic level result.
More studies of endophilin N-BAR domains have shown that endophilin’s additional helix (called the insert helix) under the main arch of the BAR can modulate and significantly affect the degree of membrane bending [21]. The additional insert helices allow endophilin to induce larger curvatures compared to an amphiphysin N-BAR via a somewhat different binding mechanism [68], and in vitro, the tubulated structures generated via endophilin N-BAR domains generally are smaller in diameter than those generated by amphiphysin N-BAR domains [23]. When the additional insert helix is parallel to the other two amphipathic helices and perpendicular to the main axis of the BAR in the MD simulations, the induced curvature is found the largest, and almost as large as the local curvature induced by amphiphysin; a simulation snapshot is shown in image ENDO (a-1) of Fig. 1. The fact that the local curvature generated by a single endophilin N-BAR is slightly less than with amphiphysin, while at the mesoscopic level the ENDO tubules have a greater curvature, points to the importance of a collective interaction and perhaps oligomerization associated with the N-BAR domains in actual tubulated structures. Interestingly, the smallest curvature was found when the insert helix was 45 degrees to the long axis, and was in fact less than that observed with a computational mutant where the insert helix was removed. This result, that the orientation of the amphipathic helix insertion can have such a large effect on the magnitude of the induced membrane curvature, again points to amphipathic helix insertion as a key driving mechanism for membrane remodeling by N-BAR domains. Further work at the CG and mesoscopic level is required, along with close collaboration with experiment (e.g., electron paramagnetic resonance (EPR) spectroscopy [69–71]).
3.2 Coarse-grained Simulation
Systematically connecting the atomic level with the CG scale (i.e., path (1) in Fig. 1) can be accomplished via the MS-CG methodology [24, 57–61, 72–77] which gives a framework whereby CG force fields can be formally constructed from underlying atomic level MD simulation. The variational aspect of the approach guarantees that MS-CG will give the optimum force field compared to the exact force field as predicted from the CG potential of mean force (PMF) [60, 61, 72, 73], for a particular choice of CG basis set, and the given MD data.
MS-CG has been applied to a wide variety of complex biomolecular systems including lipids and lipid mixtures [57, 58, 76], solvent free lipid bilayers [77], monosaccarides [78], peptides [79, 80], and mixed resolution all-atom proteins and CG lipids [81]. Most notably, the ability of MS-CG to formally remove the surrounding solvent to give a solvent-free model [82, 83] significantly extends the accessible time and length-scales of the simulation.
When combined with highly reduced analytic models for lipids (e.g., a single site ellipsoid of revolution using the Gay-Berne liquid crystal model [84, 85], or perhaps even the shape based approach proposed recently for lipids [22]), MS-CG can “decorate” the analytic model force field with atomically obtained information (the so called Hybrid Analytic-Systematic (HAS) approach as shown in image (b-2) of Fig. 1). HAS has been employed to simulate a 200 nm diameter liposome composed of over half a million CG sites [53] over timescales such that the fast wavelength undulations could be sampled. The overall CG simulation approach can further be extended via fluctuation matching [63] and Essential Dynamics Coarse-graining (ED-CG)[86] to provide a Heterogenous Elastic Network protein model (HeteroENM) [56] of the membrane proteins such as the N-BAR domain (denoted an ED-BAR, shown in image (b-3) of Fig. 1).
It should be noted that other recent CG simulations of N-BAR domain induced membrane remodeling [22, 62] have employed both high-resolution [87–89], and low-resolution shape-based CG schemes [90] (resolved at about 150 atoms per CG site). These CG simulations were able to examine different spatial arrangements N-BAR domains on rectangular membrane slabs. This particular CG approach is much more advanced than that employed in Ref. [40], but still operates well below typical liposome length-scales [5]. A challenge for any CG simulation is to connect critical CG interactions (e.g., the N-BAR to membrane interactions) to those as evaluated in the fully atomic system. The approach taken in Refs. [22, 62] assumed a dielectric constant of 1 in the interfacial region between the N-BAR and membrane, and as such the driving force for the membrane remodeling process at the CG scale was largely predetermined in the CG model to arise from electrostatic effects, rather than by amphipathic helix insertion [16]. Yet, a close analysis of the MD data [19] indicates that, indeed, there is a non-negligible amount of water in between the N-BAR and membrane, and therefore, the interaction between the positive residues of the N-BAR and the negatively charged headgroups should reflect this solvent screened environment. With the ED-BAR model [54], the N-BAR-membrane interaction strength was estimated from the PMF obtained from MD data between the charged lipid headgroups and N-BAR residues under the dimer arch. From this analysis, the interaction strength was found to be too weak for N-BARs to strongly bind to the membrane via screened electrostatics alone; rather, it was the amphipathic helices that “dig in” to the lower density regions of the outer membrane leaflet (as shown in image (b-4) of Fig. 1 which depicts a close-up view of the CG remodeling of the membrane with over 2000 ED-BARS [54]). In this case, the remodeling is primarily driven by the CG representations of the amphipathic helices of the ED-BAR, shown in image (b-3) of Fig. 1. These results overall reflect both the subtle aspects of the CG simulation as well as the challenges inherent in obtaining a physically accurate picture at the CG scale.
3.3 Mesoscopic and field-based approaches
Mesoscopic simulation utilizes collective variables to model essential properties of the system at length-scales beyond the resolution of the individual molecules or even the CG models. Our approach employs a discretized “quasiparticle” model [48–52] that is designed to give, under certain deformations, an approximate discrete solution to a corresponding continuum elastic membrane bending model [32–36]. This discrete mesoscopic quasiparticle approach, denoted the Elastic Membrane version 2 (EM2) model [49] can be extended to give a discrete representation of the anisotropic inclusion model [51, 52], and when additional composition fields [48] designed to model both lipid composition and N-BAR density are included [52], a unified mesoscopic model for large length-scale N-BAR induced membrane remodeling is achieved. The underlying equations are quite involved and the reader is pointed to Refs. [48–52] for a more complete description.
An important feature in this computational methodology was the incorporation of the anisotropy associated with N-BAR domain remodeling. N-BAR domains tend to bend membranes along certain directions due to their elongated shape [19, 20], and as noted in Sec. 2 a modified reference continuum elastic membrane model should be employed [33–36] as N-BAR domain binding can break the rotational symmetry implied by the original Helfrich model [32]. The anisotropic inclusion model proposed in Refs. [33–36] requires both a mean and deviatoric energetic contribution, where the deviatoric contribution is not a topological invariant as with the Gaussian modulus that appears in the Helfrich model [36].
The mesoscopic simulations have initially employed a 500 nm in diameter liposome, over twice the diameter of that used at the CG scale as in image (b-1) of Fig. 1. An anisotropic N-BAR density field was then allowed to anneal on the surface of the liposome, and the underlying EM2 membrane, augmented with a spatially varying lipid composition and N-BAR density, then was coupled with the resulting anisotropic N-BAR curvature fields. The final simulation results can be seen in images (c-1) and (c-2) in Fig. 1 and are compared to the EM image (d) (provided by V. Unger). A close inspection of the two simulation snapshots reveals small white regions (especially in image (c-1)), where the white regions correspond to regions with a depleted N-BAR density. The striations in the tubulated structures correspond to the anisotropic N-BAR oligomerization fields which give the average directionality of adsorbed N-BARs on the membrane surface. The tubulated structure in image (c-2) has an additional energy term included in the model which accounts for the explicit oligomerization of N-BARs as has been observed experimentally with F-BARS [10]. As a result, the striations and N-BAR density are more defined than in image (c-1). It should be noted that the resulting diameter of the tubulated structures quantitatively matches the experimental measurements. The experimental EM image (d) contains a wide variety of possible structures; this behavior is generated in the simulations by small variations in, for example, the oligomerization strength, whose magnitude could depend locally on details of the membrane composition and even the local coupling to the membrane.
As alluded to in Sec. 2, the end goal of the overall multiscale simulation effort is to modify path (2) in Fig. 1 to include path (1) and path (3). In this way, information obtained at the CG level can be used to define, for example, the oligomerization strength of the mesoscopic model, analogous in spirit to the MS-CG methodology used to derive the CG model from its corresponding atomic level representation. Work to complete this overall approach is currently underway.
Conclusions
This review has highlighted the role of multiscale simulation in understanding the process of protein mediated membrane remodeling. Multiscale approaches should be considered if protein mediated membrane bending is to be examined such that meaningful connections with experiment can be made. This review has focused on a “bottom-up” multiscale approach, where key properties at a higher scale can be systematically derived from the behavior at lower scales. Arguably, such a bottom-up approach might be framed as a key defining difference between multiscale “simulation” and “modeling”. The end goal of the former is to start with molecular scale interactions, systematically propagate them upward in scale to predict phenomena that were not known in advance. With the proper combination of all-atom MD, CG simulation, and mesoscopic approaches, it is conceivable that the entire endocytotic pathway may eventually be studied within a multiscale simulation framework.
Acknowledgements
This work was supported by National Institutes of Health (GM063796). Computational resources were provided by the National Science Foundation through TeraGrid computing resources of the Texas Advanced Computing Center, the Pittsburgh Supercomputing Center, the San Diego Supercomputing Center, and the National Institute for Computational Sciences.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Itoh T, De Camilli P. BAR, F-BAR (EFC) and ENTH/ANTH domains in the regulation of membrane-cytosol interfaces and membrane curvature. Biochim et Biophys Acta. 2006;1761:897–912. doi: 10.1016/j.bbalip.2006.06.015. [DOI] [PubMed] [Google Scholar]
- 2.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodeling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 3.Pucadyil TJ, Schmid SL. Conserved functions of membrane active GTPases in coated vesicle formation. Science. 2009;325:1217–1220. doi: 10.1126/science.1171004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Takei K, Slepnev VI, Haucke V, De Camilli P. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat Cell Biol. 1999;1:33–39. doi: 10.1038/9004. [DOI] [PubMed] [Google Scholar]
- 5.Peter BJ, Kent HM, Mills IG, Vallis Y, Butler PJG, Evans PR, McMahon HT. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science. 2004;303:495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- 6.Gallop JL, McMahon HT. BAR domains and membrane curvature: bringing your curves to the BAR. Biochem Soc Symp. 2005;72:223–231. doi: 10.1042/bss0720223. [DOI] [PubMed] [Google Scholar]
- 7.Gallop JL, Jao CC, Kent HM, Butler PJG, Evans PR, Langen R, McMahon HT. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Futterer K, Machesky LM. "Wunder" F-BAR domains: Going from pits to vesicles. Cell. 2007;129:655–657. doi: 10.1016/j.cell.2007.05.006. [DOI] [PubMed] [Google Scholar]
- 9.Shimada A, Niwa H, Tsujita K, Suetsugu S, Nitta K, Hanawa-Suetsugu K, Akasaka R, Nishino Y, Toyama M, Chen L, et al. Curved EFC/F-BAR-domain dimers are joined end to end into a filament for membrane invagination in endocytosis. Cell. 2007;129:761–772. doi: 10.1016/j.cell.2007.03.040. [DOI] [PubMed] [Google Scholar]
- 10.Frost A, Perera R, Roux A, Spasov K, Destaing O, Egelman EH, De Camilli P, Unger VM. Structural basis of membrane invagination by F-BAR domains. Cell. 2008;132:807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Itoh T, Erdmann KS, Roux A, Habermann B, Werner H, De Camilli P. Dynamin and the actin cytoskeletin cooperatively regulate plasma membrane invagination by BAR and F-BAR proteins. Cell. 2005;9:791–804. doi: 10.1016/j.devcel.2005.11.005. [DOI] [PubMed] [Google Scholar]
- 12.Henne WM, Kent HM, Ford MGJ, Hegde BG, Daumke O, Butler PJG, Mittal R, Langen R, Evans PR, McMahon HT. Structure and analysis of FCHo2 F-BAR Domain: A dimerizing and membrane recruitment module that effects membrane curvature. Structure. 2007;15:839–852. doi: 10.1016/j.str.2007.05.002. [DOI] [PubMed] [Google Scholar]
- 13.Mattila PK, Pykalainen A, Saarikangas J, Paavilainen VO, Vihinen H, Jokitalo E, Lappalainen P. Missing-in-metastasis and IRSp53 deform PI(4,5)P2-rich membranes by an inverse BAR domain-like mechanism. J Cell Biol. 2007;176:953–964. doi: 10.1083/jcb.200609176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Low C, Weininger U, Lee H, Schweimer K, Neundorf I, Beck-Sickinger AG, Pastor RW, Balbach J. Structure and dynamics of helix-0 of the N-BAR domain in lipid micelles and bilayers. Biophys J. 2008;95:4315–4323. doi: 10.1529/biophysj.108.134155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Takei K, Slepnev VI, Haucke V, De Camilli P. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat Cell Biol. 1999;1:33–39. doi: 10.1038/9004. [DOI] [PubMed] [Google Scholar]
- 16.Campelo F, McMahon HT, Kozlov MM. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys J. 2008;95:2325–2339. doi: 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fernandes F, Loura LMS, Chichon FJ, Carrascosa JL, Fedorov A, Prieto M. Role of helix 0 of the N-BAR domain in membrane curvature generation. Biophys J. 2008;94:3065–3073. doi: 10.1529/biophysj.107.113118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mui BL-S, Dobereiner H-G, Madden TD, Cullis PR. Influence of transbilayer area asymmetry on the morphology of large unilamellar vesicles. Biophys J. 1995;69:930–941. doi: 10.1016/S0006-3495(95)79967-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Blood PD, Voth GA. Direct observation of Bin/amphiphysin/Rvs (BAR) domain-induced membrane curvature by means of molecular dynamics simulations. Proc Nat Acad Sci. 2006;103:15068–15072. doi: 10.1073/pnas.0603917103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Blood PD, Swenson RD, Voth GA. Factors influencing local membrane curvature induction by N-BAR domains as revealed by molecular dynamics simulations. Biophys J. 2008;95:1866–1876. doi: 10.1529/biophysj.107.121160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cui H, Ayton GS, Voth GA. Membrane binding by the endophilin N-BAR domain. Biophys J. 2009 doi: 10.1016/j.bpj.2009.08.043. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arkhipov A, Yin Y, Schulten K. Four-scale description of membrane sculpting by BAR domains. Biophys J. 2008;95:2806–2821. doi: 10.1529/biophysj.108.132563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Masuda M, Takeda S, Sone M, Ohki T, Mori H, Kamioka Y, Mochizuki N. Endophilin BAR domain drives membrane curvature by two newly identified structure-based mechanisms. EMBO J. 2006;25:2889–2897. doi: 10.1038/sj.emboj.7601176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ayton GS, Noid WG, Voth GA. Multiscale modeling of biomolecular systems. In serial and in parallel. Curr Opin Struct Bio. 2007;17:192–198. doi: 10.1016/j.sbi.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 25.Sherwood P, Brooks BR, Sansom MSP. Multiscale methods for macromolecular simulations. Curr Opin Struct Biol. 2008;18:630–640. doi: 10.1016/j.sbi.2008.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Smondyrev AM, Berkowitz ML. United atom force field for phospholipid membranes: Constant pressure molecular dynamics simulation of dipalmitoylphosphatidylcholine/water system. J Comp Chem. 1999;20:531–545. [Google Scholar]
- 27.Feller SE. Molecular dynamics simulations of lipid bilayers. Curr Opin Colloid Interface Sci. 2000;5:217–223. [Google Scholar]
- 28.Anezo C, deVries AH, Holtje HD, Tieleman DP, Marrink SJ. Methodological issues in lipid bilayer simulation. J Phys Chem B. 2003;107:9424–9433. [Google Scholar]
- 29.Tozzini V. Coarse-grained models for proteins. Curr Opin Struc Bio. 2005;15:144–150. doi: 10.1016/j.sbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 30.Lindahl E, Sansom MSP. Membrane proteins: molecular dynamics simulations. Curr Opin Struct Biol. 2008;18:425–431. doi: 10.1016/j.sbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 31.Ayton GS, Voth GA. Systematic multiscale simulation of membrane protein systems. Current Opinion in Structural Biology. 2009;19:138–144. doi: 10.1016/j.sbi.2009.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Helfrich W. Elastic properties of lipid bilayers: Theory and possible experiments. Z Naturforsch (c) 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 33.Fischer TM. Bending stiffness of lipid bilayers. III. Gaussian curvature. J Phys II (France) 1992;2:337–343. [Google Scholar]
- 34.Kralj-Iglic V, Iglic A, Hagerstrand H, Peterlin P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys Rev E. 2000;61:4230–4234. doi: 10.1103/physreve.61.4230. [DOI] [PubMed] [Google Scholar]
- 35.Iglic A, Babnik B, Bohinc K, Fosnaric M, Hagerstrand H, Kralj-Iglic V. On the role of anisotropy of membrane constituents in formation of a membrane neck during budding of a multicomponent membrane. J Biomech. 2007;40:579–585. doi: 10.1016/j.jbiomech.2006.02.006. [DOI] [PubMed] [Google Scholar]
- 36.Fournier JB. Nontopological saddle-splay a curvature instabilities from anisotropic membrane inclusions. Phys Rev Lett. 1996;76:4436–4439. doi: 10.1103/PhysRevLett.76.4436. [DOI] [PubMed] [Google Scholar]
- 37.Brannigan G, Brown FL. Contributions of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys J. 2007;92:864–876. doi: 10.1529/biophysj.106.094953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Brannigan G, Brown FLH. A consistent model for thermal fluctuations and proteininduced deformations in lipid bilayers. Biophys J. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.West B, Brown FL, Schmid F. Membrane-protein interactions in a generic coarse-grained model for lipid bilayers. Biophys J. 2009;96:101–115. doi: 10.1529/biophysj.108.138677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Reynwar BJ, Illya G, Harmandaris VA, Muller MM, Kremer K, Deserno M. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature. 2007;447:461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 41.Ayton G, Voth GA. Bridging microscopic and mesoscopic simulations of lipid bilayers. Biophys J. 2002;83:3357–3370. doi: 10.1016/S0006-3495(02)75336-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Brown FLH. Regulation of protein mobility via thermal membrane undulations. Biophys J. 2003;84:842–853. doi: 10.1016/S0006-3495(03)74903-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ayton GS, Voth GA. The simulation of biomolecular systems at multiple length and timescales. Int J Mult Comp Eng. 2004;2:291–311. [Google Scholar]
- 44.Lin LCL, Brown FLH. Dynamics of pinned membranes with application to protein diffusion on the surface of red blood cells. Biophys J. 2004;86:764–780. doi: 10.1016/S0006-3495(04)74153-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lin LCL, Brown FLH. Dynamic simulations of membranes with cytoskeletal interactions. Phys Rev E. 2005;72:011910. doi: 10.1103/PhysRevE.72.011910. [DOI] [PubMed] [Google Scholar]
- 46.Lin LCL, Gov N, Brown FLH. Nonequilibrium membrane fluctuations driven by active proteins. J Chem Phys. 2006;124:074903. doi: 10.1063/1.2166383. [DOI] [PubMed] [Google Scholar]
- 47.Khelashvili G, Harries D, Weinstein H. Modeling membrane deformations and lipid demixing upon protein-membrane interaction: The BAR dimer adsorption. Biophys J. 2009;97:1626–1635. doi: 10.1016/j.bpj.2009.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ayton GS, McWhirter JL, McMurtry P, Voth GA. Coupling field theory with continuum mechanics: A simulation of domain formation in giant unilamellar vesicles. Biophys J. 2005;88:3855–3869. doi: 10.1529/biophysj.105.059436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ayton GS, McWhirter JL, Voth GA. A second generation mesoscopic lipid bilayer model: Connections to field-theory descriptions of membranes and nonlocal hydrodynamics. J Chem Phys. 2006;124:064906. doi: 10.1063/1.2165194. [DOI] [PubMed] [Google Scholar]
- 50.Ayton GS, Izvekov S, Noid WG, Voth GA. Multiscale simulation of membranes and membrane proteins: Connecting molecular interactions to mesoscopic behavior. Current Topics in Membranes. 2008;60:181–225. [Google Scholar]
- 51.Ayton GS, Blood PD, Voth GA. Membrane remodeling from N-BAR domain interactions: Insights from multiscale simulation. Biophys J. 2007;92:3595–3602. doi: 10.1529/biophysj.106.101709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ayton GS, Lyman E, Krishna V, Swenson R, Mim C, Unger V, Voth GA. New insights into BAR domain induced membrane remodeling. Biophys J. 2009;97:1616–1625. doi: 10.1016/j.bpj.2009.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ayton GS, Voth GA. A hybrid coarse-graining approach for lipid bilayers at large length and time scales. J Phys Chem B. 2009;113:4413–4424. doi: 10.1021/jp8087868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ayton GS, Lyman E, Voth GA. Hierarchical coarse-graining strategy for proteinmembrane systems to access mesoscopic scales. Faraday Discussions. 2010;144:347–357. doi: 10.1039/b901996k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Voth GA, editor. Coarse-graining of condensed phase and biomolecular systems. Boca Raton: CRC Press/Taylor and Francis Group; 2009. [Google Scholar]
- 56.Lyman E, Pfaendtner J, Voth GA. Systematic multiscale parameterization of heterogeneous elastic network models of proteins. Biophys J. 2008;95:4183–4192. doi: 10.1529/biophysj.108.139733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Izvekov S, Voth GA. A multiscale coarse-graining method for biomolecular systems. J Phys Chem B. 2005;109:2469–2473. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 58.Izvekov S, Voth GA. Multiscale coarse-graining of mixed phospholipid/cholesterol bilayers. J Chem Theor Comp. 2006;2:637–648. doi: 10.1021/ct050300c. [DOI] [PubMed] [Google Scholar]
- 59.Noid WG, Chu J-W, Ayton GS, Voth GA. Multiscale coarse-graining and structural correlations: Connections to liquid state theory. J Phys Chem B. 2007;111:4116–4127. doi: 10.1021/jp068549t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Noid WG, Chu JW, Ayton GS, Krishna V, Izvekov S, Voth GA, Das A, Anderson HC. The multiscale coarse-graining method I: A rigorous bridge between atomistic and coarse-grained models. J Chem Phys. 2008;128:244114. doi: 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Noid WG, Liu P, Wang Y, Chu J-W, Ayton GS, Izvekov S, Andersen HC, Voth GA. The Multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J Chem Phys. 2008;128:244115. doi: 10.1063/1.2938857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Yin Y, Arkhipov A, Schulten K. Simulation of membrane tubulation by lattices of amphiphysin N-BAR domains. Structure. 2009;17:882–892. doi: 10.1016/j.str.2009.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Chu J-W, Voth GA. Coarse-grained modeling of the actin filament derived from atomistic-scale simulations. Biophys J. 2006;90:1572–1582. doi: 10.1529/biophysj.105.073924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Chaikin PM, Lubensky TC. Principles of condensed matter physics. Cambridge: University Press; 1995. [Google Scholar]
- 65.McWhirter JL, Ayton GS, Voth GA. Coupling field theory with mesoscopic dynamical simulations of multi-component lipid bilayers. Biophys J. 2004;87:3242–3263. doi: 10.1529/biophysj.104.045716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Feller SE, MacKerell AD. An improved empirical potential energy function for molecular simulations of phospholipids. J Phys Chem B. 2000;104:7510–7515. [Google Scholar]
- 67.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 68.Farsad K, Ringstad N, Takei K, Floyd SR, Rose K, De Camilli P. Generation of high curvature membranes mediated by direct endophilin bilayer interactions. J Cell Biol. 2001;155:193–200. doi: 10.1083/jcb.200107075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hubbell WL, Cafiso DS, Altenbach C. Identifying conformational changes with site-directed spin labeling. Nat Struct Biol. 2000;7:735–739. doi: 10.1038/78956. [DOI] [PubMed] [Google Scholar]
- 70.Hubbell WL, Gross A, Langen R, Lietzow MA. Recent advances in site-directed spin labeling of proteins. Curr Opin Struct Biol. 1998;8:649–656. doi: 10.1016/s0959-440x(98)80158-9. [DOI] [PubMed] [Google Scholar]
- 71.Jao CC, Hegde BG, Chen J, Haworth IS, Langen R. Structure of membrane-bound alpha-synuclein from site-directed spin labeling and computational refinement. Proc Natl Acad Sci. 2008;105:19666–19671. doi: 10.1073/pnas.0807826105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Ayton GS, Noid WG, Voth GA. Systematic coarse graining of biomolecular and soft-matter systems. MRS Bulletin. 2007;32:929–934. [Google Scholar]
- 73.Noid WG, Ayton GS, Izvekov S, Voth GA. In: Coarse-Graining of Condensed Phase and Biomolecular Systems. Voth GA, editor. Boca Raton: CRC Press/Taylor and Francis Group; 2009. pp. 21–39. [Google Scholar]
- 74.Chu J-W, Ayton GS, Izvekov S, Voth GA. Emerging methods for multiscale simulation of biomolecular systems. Mol Phys. 2007;105:167–175. [Google Scholar]
- 75.Chu J-W, Izvekov S, Voth GA. The multiscale challenge for biomolecular systems: Coarse-grained modeling. Mol Sim. 2006;32:211–218. [Google Scholar]
- 76.Lu L, Voth GA. Systematic coarse-graining of a multi-component lipid bilayer. J Phys Chem B. 2009;113:1501–1510. doi: 10.1021/jp809604k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Izvekov S, Voth GA. A solvent free lipid bilayer model using multiscale coarse-graining. J Phys Chem B. 2008;113:4443–4455. doi: 10.1021/jp810440c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Liu P, Izvekov S, Voth GA. Multiscale coarse-graining of monosaccharides. J Phys Chem B. 2007;111:11566–11575. doi: 10.1021/jp0721494. [DOI] [PubMed] [Google Scholar]
- 79.Zhou J, Thorpe IF, Izvekov S, Voth GA. Coarse-grained peptide modeling using a systematic multiscale approach. Biophys J. 2007;92:4289–4303. doi: 10.1529/biophysj.106.094425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Thorpe I, Zhou J, Voth GA. Peptide folding using multiscale coarse-grained models. J Phys Chem B. 2008;112:13079–13090. doi: 10.1021/jp8015968. [DOI] [PubMed] [Google Scholar]
- 81.Shi Q, Izvekov S, Voth GA. Mixed atomistic and coarse-grained molecular dynamics: Simulation of a membrane bound ion channel. J Phys Chem B. 2006;110:15045–15048. doi: 10.1021/jp062700h. [DOI] [PubMed] [Google Scholar]
- 82.Brannigan G, Brown FLH. Solvent-free simulations of membrane bilayers. J Chem Phys. 2004;120:1059–1071. doi: 10.1063/1.1625913. [DOI] [PubMed] [Google Scholar]
- 83.Brannigan G, Lin LCL, Brown FLH. Implicit solvent simulation models for biomembranes. Eur Biophys J. 2006;35:104–124. doi: 10.1007/s00249-005-0013-y. [DOI] [PubMed] [Google Scholar]
- 84.Gay JG, Berne BJ. Modification of the overlap potential to mimic a linear site--site potential. J Chem Phys. 1981;74:3316–3319. [Google Scholar]
- 85.Brown JT, Allen MP. Effect of elongation on the phase behavior of the Gay-Berne fluid. Phys Rev E. 1998;57:6685–6699. [Google Scholar]
- 86.Zhang Z, Lu L, Noid WG, Krishna V, Pfaendtner J, Voth GA. A systematic methodology for defining coarse-grained sites in large biomolecules. Biophys J. 2008;95:5073–5083. doi: 10.1529/biophysj.108.139626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Marrink SJ, deVries AH, Mark AE. Coarse grained model for semiquantitative lipid simulations. J Phys Chem B. 2004;108:750–760. [Google Scholar]
- 88.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, deVries AH. The MARTINI force field: Coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 89.Shih AY, Arkhipov A, Freddolino PL, Schulten K. Coarse grained protein-lipid model with applications to lipoprotein particles. J Phys Chem B. 2006;110:3674–3684. doi: 10.1021/jp0550816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Arkhipov A, Freddolino PL, Schulten K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure. 2006;14:1767–1777. doi: 10.1016/j.str.2006.10.003. [DOI] [PubMed] [Google Scholar]