Intracranial Pressure Pulse Morphological Features Improved Detection of Decreased Cerebral Blood Flow

Abstract

We investigated whether intracranial pressure (ICP) pulse morphological metrics could be used to realize continuous detection of low cerebral blood flow. Sixty-three acutely brain injured patients with ICP monitoring, daily ¹³³Xenon CBF, and daily Transcranial Doppler (TCD) assessment were studied. Their ICP recordings were time-aligned with the CBF and TCD measurements so that an one-hour ICP segment near the CBF and TCD measurement was obtained. Each of these recordings was processed by Morphological Cluster and Analysis of Intracranial Pressure (MOCAIP) algorithm to extract pulse morphological metrics. Then the Differential Evolution algorithm was used to find the optimal combination of the metrics that provided, using the regularized linear discriminant analysis, the largest combined positive predictivity and sensitivity. At a CBF threshold of 20 ml/min/100g, a sensitivity of 81.8 ± 0.9% and specificity of 50.1 ± 0.2% were obtained using the optimal combination of conventional TCD and blood analysis metrics as input to a regularized linear classifier. However, using the optimal combination of the MOCAIP metrics alone was able to achieve a sensitivity of 92.5 ± 0.7% and specificity of 84.8 ± 0.8%. Searching the optimal combination of all available metrics achieved the best result that was marginally better than those from using MOCAIP alone. This study demonstrated that the potential role of ICP monitoring may be extended to provide an indicator of low global cerebral blood perfusion.

1. Introduction

Techniques of measuring cerebral blood flow (CBF) have a long-established role in neurocritical care practice. Yet, non-invasive monitors of cerebral blood flow provide intermittent measures alone, rather than continuous monitoring of CBF. Invasive monitors for CBF exist, but carry additional risk to patients, require additional equipment and cost, and provide only regional measures of CBF. The ultimate goal would be to create a continuous, bedside, and low cost technique which does not increase risk and is generalizable.

An alternative to attempts at directly measuring CBF is to use surrogate biomarkers of cerebral ischemia and metabolism. Existing work in this direction includes utilization of electroencephalography (EEG) (Bezerianos et al., 2003; Claassen et al., 2004; Geocadin et al., 2000; Sheorajpanday et al., 2009) and Microdialysis (MD) techniques (Sarrafzadeh et al., 2004; Nilsson et al., 1999; Valadka et al., 1998) to find biomarkers of cerebral ischemia. Both EEG and MD are bedside techniques and EEG can be continuously and invasively measured. These are desirable traits for practice in neurocritical care. However, specificity of biomarkers extracted from EEG has long been questioned as they are often confounded by other factors irrelevant to cerebral ischemia. For traumatic brain injury patients, MD abnormality, e.g., elevated cerebral lactate pyruvate ratio (LPR), may not reflect low cerebral perfusion as suggested in our recent study (Vespa et al., 2005). In addition, both techniques can only indicate reduction of blood flow after it has led to electrophysiological or metabolic disturbance. This may carry the risk of delaying treatment.

Intracranial pressure (ICP) remains a pivotal physiological signal for managing brain injury patients in neurocritical care units. ICP is intrinsically related with CBF, which dictates that ICP may actually contain information about CBF. However, this complex relationship has only been partially explored such that ICP is used in the simple equation: Cerebral Perfusion Pressure (CPP) = Systemic Arterial Blood Pressure (ABP) – ICP to derive the driving pressure of blood flow through the cerebral vasculature. To date, the influence from cerebral vascular changes, including vasoconstriction and vasodilatation, on both ICP and the cerebral blood flow have not been well studied in humans. Subtle changes in the morphology of ICP pulses can reflect cerebral vascular changes. To be more specific, the particular form of an ICP pulse is formulated by transforming an incidental arterial pressure pulse under the modulation influences from multiple intracranial compartments. Hence we hypothesize that the ICP waveform carries information about changes in cerebral vasculature and hence CBF.

Given that the cerebral vasculature is one major intracranial compartment that can shape ICP pulse, a novel technique of assessing cerebral perfusion status based on analyzing continuous ICP can be potentially achieved that is a bedside, continuous, and low cost technique. Our group has recently developed and validated an algorithm of analyzing continuous ICP (Hu et al., 2009b) that can be used to provide a comprehensive array of ICP morphological metrics. Due to the complexity involved in accurately describing, in mathematical terms, how these ICP morphological metrics reflect changes in the cerebral vasculature, a data-driven engineering approach toward quantifying and assessing this relationship is needed. The main objective of the present work is thus to test the hypothesis that reduction of cerebral blood flow can be differentiated from normal cerebral perfusion. This hypothesis is tested by conducting a classification experiment that leverages advanced data exploration tools including a regularized quadratic classifier, global search of optimal combinations of ICP pulse morphological metrics, and cross-validation techniques.

2. Methods and Subjects

2.1 Patient Data

We utilized an archived data set in the present study. This data set contains daily ¹³³Xenon CBF, Transcranial Doppler (TCD), blood gas analysis, and intracranial pressure (ICP) monitoring results from 63 brain injury patients. Subarachnoid hemorrhage from aneurysm rupture was the most prevalent diagnosis accounting for 31 patients. This was then followed by 26 traumatic brain injury (TBI) patients. Besides aneurysm rupture and TBI, a small number of patients had ICP monitoring and CBF assessment for arteriovenous malformation, brain tumor, and Intraparenchyma hemorrhage. Table 1 summarizes the mean and standard deviation of the ages of the patients grouped by their diagnosis. The anonymous use of this data set in the present work was waived patient consent by the local institutional review board. These 63 patients were selected because their data from all of the following measurements were available for this retrospective study.

Table 1.

Mean and standard deviation of age of patients grouped by the primary diagnosis

Diagnosis	SAH	Age	N
			F	M
TBI	Yes	46 ± 24.2	3	14
	No	47 ± 13.8	2	7
Aneurysm Rupture	Yes	54 ± 14.3	18	13
Other	No	58 ± 20.8	5	1

TBI: traumatic brain injury; SAH: subarachnoid hemorrhage; Other conditions include arteriovenous malformation, brain tumor, and intraparenchyma hemorrhage.

¹³³Xenon CBF measurement

Bedside CBF measurement was performed using the previously described intravenous ¹³³Xenon clearance technique (Obrist et al., 1979; Narayan et al., 1995). Patients were injected with 20 to 30 mCi of ¹³³Xenon dissolved in saline. A Ceretronix Cerebrograph Cortexplorer 16 (Randers, Denmark) measured gamma radiation from 133Xenon using eight detectors positioned over each cerebral hemisphere. End tidal ¹³³Xenon was measured simultaneously to estimate arterial ¹³³Xenon concentration. Study duration was 11 minutes. Data were collected by a laptop computer, and the mean global CBF₁₅ was used in this present work. During the CBF measurement, technicians also recorded the mean arterial pressure (MAP) displayed on the monitor together with CBF measurements.

Transcranial Doppler Ultrasonography

Vessels including the extracranial internal carotid artery (ICA) and the basilar artery (BA) were insonated bilaterally using the method described previously (Aaslid et al., 1984; Aaslid et al., 1982). Recordings were performed using a 2-MHz pulsed probe and a commercially available TCD unit (Neuroguard Cerebrovascular Diagnostic System by Nicolet Biomedical, Inc., Madison, WI. or DWL, Charlotte, NC). The TCD and CBF study were usually done in a sequential fashion on the same day.

Arterial blood gas analysis

Blood samples were taken immediately before or after CBF measurement with 1–2 ml arterial blood samples collected in heparinized syringes, capped, and immediately placed on ice and sent to the clinical laboratory.

ICP Monitoring

ICP monitoring was done using ventriculostomy per clinical needs. The waveform data from bedside monitors were archived using the commercial BedmasterEx^™ software at a sampling rate of 240 Hz. ICP and ECG were used in the present work.

For the subsequent analysis, we searched for an one-hour useable ICP recording that either preceded or followed the CBF measurement based on the approximate CBF measurement date time as recorded by the technicians. The inclusion criteria of the ICP recording were: 1) it was free from cerebrospinal fluid (CSF) drainage; 2) it was the one-hour recording closest to the CBF measurement. We chose one hour as the length of the recording because of the limitation of exporting function of the software. The TCD assessment results on the same day of CBF measurement were paired. The total number of such CBF-TCD-ICP pairs is 199 from the 63 patients who were treated between 2/1/2007 and 8/18/2009.

2.2 Selection of predictive clinical variables

Based on prior physiological knowledge, we selected several relevant clinical variables from Transcranial Doppler measurement, blood analysis, vital signs and the amount of the CSF drainage. The predictive power of these variables will be assessed together with ICP pulse morphological metrics. In total, we have the following eight such variables: 1) average mean flow velocities of the right and the left internal carotid artery (ICA); 2) average diastolic flow velocities of the right and the left ICA; 3) average pulsatility indices (PI) of the right and the left ICA; 4) partial carbon dioxide pressure (CO₂); 5) total amount of hemoglobin (Hgb); 6) fraction of the blood composed of red blood cells (Hct); 7) mean arterial blood pressure (MAP); 8) amount of CSF drainage in the hour of CBF measurement.

2.3 Morphological Clustering and Analysis of Intracranial Pressure (MOCAIP)

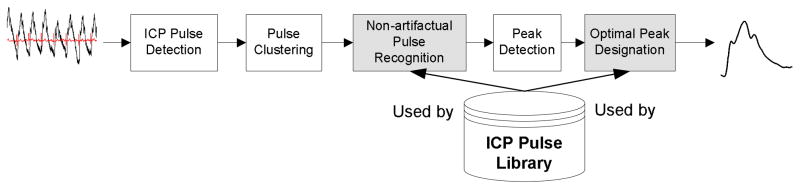
MOCAIP was proposed to provide an automatic analysis of ICP pulse morphological changes by designating the locations of three well established sub-peaks in an ICP pulse (Hu et al., 2008a; Hu et al., 2009b). Our extensive experience in ICP monitoring enabled us to design an integrated and modular framework for this algorithm that also takes into the consideration the practical problem of handling noises and artifacts that ubiquitously exist in signals collected in an active neurocritical care environment. The block diagram of the MOCAIP algorithm used in the present work is shown in Fig. 1. It essentially remains the same as what we presented in the original publication. The MOCAIP algorithm contains five major processing blocks including a beat-by-beat pulse detection component, pulse clustering, non-artifactual pulse recognition, peak detection component, and an optimal peak designation component. In addition, the algorithm makes use of a library that contains a collection of pulses and locations of their designated three sub-peaks. The detection of ICP pulse is conducted using an algorithm developed in our previous work (Hu et al., 2008b). Pulse clustering is applied to consecutive sub-sequences of the raw ICP pulses to generate a dominant pulse for each sequence. This process results in a series of dominant ICP pulses that is further analyzed by the pulse recognition component. Only the legitimate pulses are further processed to detect all candidate peaks in each of them. Finally, the peak designation process is executed to optimally designate the three well established ICP peaks in each legitimate dominant pulse.

Figure 1.

Block diagram of the Morphological Clustering and Analysis of Intracranial Pressure (MOCAIP) algorithm. The input to the algorithm is a segment of intracranial pressure and Electrocardiogram signals and the output of the algorithm is a dominant intracranial pressure pulse representative of the majority of the pulses of the segment and designation of the three sub-peaks on this dominant pulse. The two shaded blocks in the diagram were recently improved since the publication of the original MOCAIP.

The modular structure of the MOCAIP algorithm facilitates further improvement of each individual processing blocks as demonstrated in our recent efforts (Scalzo et al., 2009; Asgari et al., 2009). Particularly, a nonlinear regression based approach was proposed to improve the performance of optimal peak designation (Scalzo et al., 2009) and a singular value decomposition (SVD) based signal/noise space separation algorithm was proposed to improve the performance of recognizing legitimate pulses (Asgari et al., 2009). Due to the emphasis of this paper on the classification problem, these extended aspects of the MOCAIP algorithm will not be further discussed here.

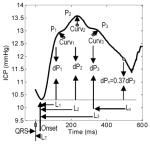
In summary, the MOCAIP algorithm provides a designation of the three sub-peaks of dominant ICP pulses so that a set of 24 metrics as illustrated in Table 2 can be readily calculated. It should be noted that not all pulses have three peaks. We adopted the following simple rules to calculate MOCAIP metrics in such situations: 1) If only P₁ is missing, we consider P₁ and P₂ are merged, i.e., they are located at the same place; 2) if only P₂ is missing, we consider P₁ and P₂ are merged; 3) if only P₃ is missing, we consider P₂ and P₃ are merged; 4) if only one peak is present, we consider that all three peaks are merged into one.

Table 2.

An illustration of the 24 MOCAIP metrics.

	MOCAIP Metric Group		Metrics
	Amplitude	Absolute	mICP, dP1, dP2, dP3, diasICP
		Ratio	dP12(dP2/dP1), dP13(dP3/dP1), dP23(dP3/dP2)
	Time Interval	Absolute	LT, L1, L2, L3
		Relative	L2 – L1, L3 – L1, L3 – L2
	Pulse Curvature	Absolute	Curv1, Curv2, Curv3
		Ratio	Curv2/Curv1, Curv3/Curv1, Curv3/Curv2
	Slope		(P1 − diasICP)/L1
	Decay time constant		Lx where dPx = 0.37 dP3

2.4 Classifier

We selected a simple linear classifier in the present work. This classifier was introduced by Friedman in 1989 (Friedman, 1989) as a regularized version of the classic linear Gaussian quadratic classifier (QDC). The regularization was applied to the calculation of the covariance matrices of each class such that the regularized covariance matrix of ith class ${\mathrm{\sum }}_i^{″}$ is calculated as

$${\mathrm{\sum }}_i^{″}=(1-w_2){\mathrm{\sum }}_i^{\prime }+w_2\text{Diag}\left(\text{Tr}({\mathrm{\sum }}_i^{\prime })/p,p\right)$$ 1)

where Dia (gx,n) is an operator to make an n×n diagonal matrix whose diagonal terms are the scalar x and Tr(M)is the trace of matrix M. Here we assume the dimension of the feature vector is p and Σ′ in the above equation is a weighted sum of the conventional sample within-class covariance matrix of the ith class Σ̂_i and pooled within-class covariance matrix $\widehat{\mathrm{\sum }}={\displaystyle \sum _{i=1}^c}\frac{N_i}{N}{\widehat{\mathrm{\sum }}}_i$ as

$${\mathrm{\sum }}_i^{\prime }=\frac{(1-w_1)N_i{\widehat{\mathrm{\sum }}}_i+w_{1}N\widehat{\mathrm{\sum }}}{(1-w_1)N_i+w_{1}N}$$ 2)

where N_i is the number of training samples of the ith class, N is the total number of training cases, and c is the total number of classes. w₁ and w₂ are two algorithm parameters within [0,1] that control the degree of regularization. In the extreme that w₁ = 0, ${\mathrm{\sum }}_i^{\prime }$ equals Σ̂_i so that the resultant classifier is close to a quadratic Gaussian classifier. On the other hand when w₁ = 1, ${\mathrm{\sum }}_i^{\prime }$ equals Σ̂ so that the resultant classifier is close to a linear Gaussian classifier. This regularized discriminant analysis has been proven effective in cases where the number of training samples is small as compared to the dimension of the feature vector. It will be introduced in next Section that the optimal selection of w₁ and w₂ can be incorporated into the optimization process of feature selection.

2.5 Selection of Optimal Feature Set for Classification

It is tempting to use all available metrics as input features to a classifier to separate different cerebral perfusion states. However, correlations exist among different available metrics leading to redundancies if they are all used as input features. In addition, it would be beneficial to use a minimal set of available metrics to avoid unnecessarily complicating the classification problem with a high-dimensional feature vector. The challenge is that no prior knowledge exists with regard to what are the relevant available metrics for characterizing cerebral perfusion states. Therefore, an automated way of choosing an optimal subset of available metrics as input feature vector needs to be found. This was achieved in the present work by searching for the optimal combination of available metrics. However, large number of possible combinations prevents a brute-force search due to computational cost.

Instead, we adopted much more efficient global optimization techniques that guarantee to find much better solutions given finite amount of time. In particular, we adopted the differential evolution (DE) algorithm (Price and Storn, 1997) as suggested in our previous experience that it is an efficient global search algorithm as compared to traditional methods including genetic algorithm and simulated annealing (Hu et al., 2007). The flowchart of this optimization process is presented in Fig. 2, which can accommodate different classifiers. In addition, it can be seen from the flowchart that searching optimal values of any tuning parameters of classifiers can also be handled by this process.

Figure 2.

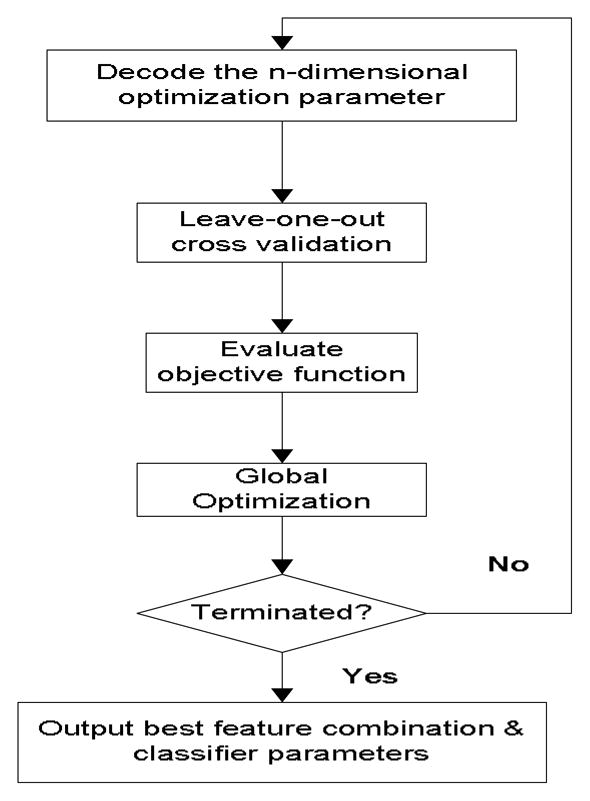
Flowchart of the optimization process to find the best feature combination and tuning parameters of a classifier. This process is followed in the present work to find the optimal combination of metrics for use as input feature vector to a regularized quadratic classifier that has two tuning parameters. The optimization was terminated mostly because the maximal number (200 adopted in the present work) of iterations was reached.

To proceed, an encoding schema is defined for the variables to be optimized. Whether or not to include a metric as a feature is thus denoted by a real number between 0 and 1 such that a value greater than 0.5 will indicate that the corresponding metric should be included. Furthermore, w₁ and w₂ in Equations 1 and 2 will be optimized by the same optimization process of selecting features. The objective function for the DE algorithm is the average of the sensitivity and the positive predictivity (PPV), by optimizing which a balance between these two competing performance measures can be achieved.

From the flowchart of the training process (Fig. 2), it can be seen that each evaluation of the objective function will involve a leave-one-out cross-validation procedure, which is part of the reason for the large computational load of this optimization process. Multiple training samples can be contributed by the same patient. Therefore, the leave-one-out strategy adopted in the present work actually removed all samples belonging to a patient.

2.6 Experiment Protocol

We designed a two-class classification experiment where a threshold value based on CBF was chosen to dichromate the perfusion state. A regularized quadratic classifier was trained using the above optimization process, which resulted in the determination of the optimal combination of the available metrics as well as the optimal w₁ and w₂. Under this optimal setup, a further cross-validation using a bootstrapping approach (Webb, 2002) was conducted to obtain various performance measures of the classification.

Details of this process were given as the follows:

• Each metric is first normalized to stay within [0, 1] using the minimal and maximal values pooled from all cases.

• The differential evolution algorithm was executed for certain number of iterations.

• Based on a chosen CBF threshold of 20 ml/min/100g, we denote any CBF measurements less than or equal to the threshold as an abnormal (oligemia) state while any CBF measurement above the threshold as a normal state. The chosen threshold is clinically significant that can potentially change the course of the patient care, e.g., a low CBF in the absence of anesthetic drugs.

• The bootstrapping process was based on 200 re-sampled copies of the original data set following the standard procedure described in Chapter 8 of the text book (Webb, 2002).

To assess the reproducibility, the above optimization and bootstrapping processes were independently repeated for three times in a random fashion so that we can check what constitutes the most frequently selected metrics and what the variability among the final classification performance measures is.

We designed four separate macro combinations of all 32 available metrics, within which an optimal subset was obtained using the classifier training algorithm described above. The first macro combination includes all 32 metrics. The second one only includes MOCAIP, CSF drainage and TCD metrics. The third one includes only MOCAIP and CSF drainage metrics and the last one includes only seven TCD and blood analysis metrics. It is of interest to analyze the performance of the third combination to establish the feasibility of using ICP alone for detecting low CBF state. The second combination is important because it offers clue with regard to whether TCD can add useful information for detecting low CBF. Assessing the fourth combination provides information about whether incorporating MOCAIP metrics will improve detection of low CBF.

3. Results

3.1 Data characteristics

The data set was highly imbalanced with a dominant number of negative cases. In particular, eight patients were found to have at least one low CBF measurement and a total of fifteen CBF measurements from these patients were ≤ 20 ml/min/100g. Despite ICP was continuously monitored, certain amount of timing difference exists between ICP and CBF measurement because we had to select ICP data free from CSF drainage. The average timing difference between the ICP segment used in this study and CBF measurements is −13.6 minutes and the standard deviation is 122.1 minutes. For aneurysmal patients, this timing difference was within 60 minutes for 66.7% and within 120 minutes for 84.8% of ICP-CBF pairs, respectively. On the other hand, the ratio is higher for TBI patients with 79.3% for 60-minute difference and 93.9% for 120-minute difference, respectively. Furthermore, one ICP-CBF pair with CBF was ≤ 20 ml/min/100g had a 65-minute timing difference while the rest of such ICP-CBF pairs had timing differences within 60 minutes. A negative timing difference indicates that the first sample of the ICP segment precedes the measurement time, as logged in the database, of the CBF.

3.2 A case report

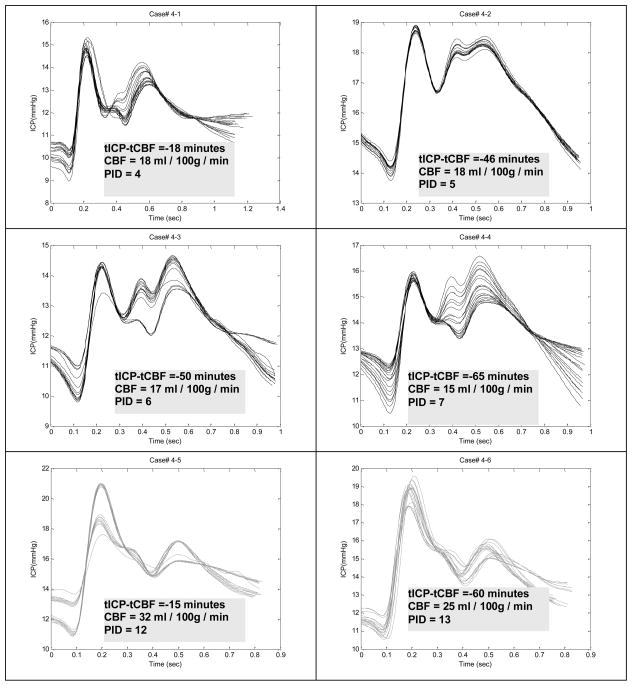
To visually assess how ICP pulse morphology is associated with different perfusion states, we present one typical case in Fig. 3 from a traumatic brain injury patient who had ICP recordings both in the normal and in the low CBF states. This patient had six CBF measurements on different days. In each plot, we overlap the dominant ICP pulses extracted from every 3 minutes of data. In addition, we display the CBF value associated with the ICP recording and the time difference between the approximate CBF measurement time and the start time of ICP segment. We observe that the elevation of the third peak of ICP pulse is clearly associated with low CBF value. This pattern of elevated third peak was observed in six out of the eight patients with positive cases.

Figure 3.

Comparing dominant ICP pulses from six recordings of subject #4 who had four recordings associated with CBF values below the threshold of 20 ml/min/100g. PID: post injury day when the measurement was taken. It can be observed that the elevation of the third peak is associated with low CBF. This pattern was observed in 6 out of 8 patients who had at least one low CBF measurement.

3.3 Classification performance

Table 3 lists the mean and standard deviation of sensitivity, specificity, and positive predictivity value of the three independent runs of the classification experiment. Results from both the leave-one-out (LOO) cross-validation and the bootstrapping (BS) cross-validation are listed to assess whether the optimal configuration found using the leave-one-out is generalizable as tested by a second cross-validation using the bootstrapping. It is expected that the combined sensitivity and positive predictivity value should be larger for the leave-one-out approach. This is indeed the case. However, the difference is small indicating that the process of optimizing the feature combination did not overfit the data.

Table 3.

List of three mean performance measures and their standard deviations calculated from three independent runs of the experiment. Results from both leave-one-out and bootstrapping cross-validation are listed.

Exp.	Val.	SE	SPE	PPV
MOCAIP+TCD+BA	LOO	0.933 ± 0.000	0.862 ± 0.003	0.356 ± 0.005
	BS	0.941 ± 0.014	0.852 ± 0.013	0.341 ± 0.024
MOCAIP + TCD	LOO	0.933 ± 0.000	0.853 ± 0.005	0.342 ± 0.008
	BS	0.920 ± 0.014	0.846 ± 0.011	0.316 ± 0.018
MOCAIP	LOO	0.933 ± 0.000	0.851 ± 0.003	0.339 ± 0.005
	BS	0.925 ± 0.007	0.848 ± 0.008	0.320 ± 0.020
BA	LOO	0.867 ± 0.000	0.516 ± 0.000	0.127 ± 0.000
	BS	0.818 ± 0.009	0.501 ± 0.002	0115 ± 0.001

Se: Sensitivity; Spe: Specificity; PPV: Positive predictivity value; LOO: Leave-One-Out; BS: Bootstrapping.

Based on the bootstrapping results, it is observed that combining metrics of MOCAIP, TCD, and blood analysis achieves the best performance. Despite the performance gain is small when compared to two other combinations that also have MOCAIP metrics as part of the search basis, the difference is actually significant (p <0.05) based on t-test. The biggest gain of the performance is clearly caused by the incorporation of the MOCAIP metrics.

Table 4 gives further details of the classification performance in terms of false positive and negative rates within each different patient group. These results were based on the leave-one-out cross-validation for the first run of the experiment. An interesting pattern is that performance is better for SAH patients as compared to non-SAH ones. Also, the performance is better for non-TBI patients as compared to TBI ones.

Table 4.

False positive and false negative rates within diagnosis group.

	False Positive				False Negative
	SAH	Non SAH	TBI	Non TBI	SAH	Non SAH	TBI	Non TBI
MOCAIP+TCD+BA	13.61%	19.23%	24.39%	8.55%	2.04%	1.92%	2.44%	1.71%
MOCAIP+TCD	17.01%	21.15%	25.61%	12.82%	1.36%	1.92%	1.22%	1.71%
MOCAIP	18.37%	21.15%	25.61%	14.53%	1.36%	1.925	1.22%	1.71%
TCD+BA	52.38%	55.77%	58.54%	49.57%	0.68%	0.00%	1.22%	0.00%

3.4 Difference between metrics of different CBF states

Table 5 gives more detailed information regarding each of the 32 metrics that includes the number of times they were selected as a classifier feature and their mean and standard deviation values within each group. Metrics with a significant difference by a unpaired t-test between the normal and the low CBF groups were marked with ‘*’. Among these metrics, dP₁₃,dP₃, diasP, mICP, L_t, L₃, and ICAEd were always selected in these three experiments. However, there are 10 more metrics, including ICAPI and Hct, were selected for majority of the runs (>1). Also, there are 10 metrics that were never selected as part of classifier features including PCO₂, Hgb, and ICAMean et al.

Table 5.

Detailed list of the mean, standard deviation, and number of times of selection of twenty-five variables including 24 MOCAIP metrics and hourly CSF drainage rate.

CBF Threshold = 20
	n	CBF >20 (m ± S.D.)	CBF ≤ 20 (m ± S.D.)
CSF (ml)	0	11.74 ± 12.39	7.20 ± 11.19
dp12	2	1.12 ± 0.58	1.12 ± 0.40
dp13	3	0.78 ± 0.40	0.97 ± 0.35
dp23	0*	0.70 ± 0.19	0.90 ± 0.32
dp1 (mmHg)	0*	5.49 ± 2.68	3.96 ± 1.26
dp2 (mmHg)	2	5.85 ± 3.54	4.33 ± 1.91
dp3 (mmHg)	3	4.09 ± 2.57	3.65 ± 1.42
diasP (mmHg)	3*	8.60 ± 5.85	11.78 ± 2.84
mICP (mmHg)	3	11.61 ± 6.04	14.04 ± 3.09
Lt (ms)	3*	125.37 ± 25.35	143.77 ± 16.72
L1 (ms)	2	91.48 ± 19.76	94.71 ± 19.25
L2 (ms)	2*	200.43 ± 35.44	238.41 ± 38.43
L3 (ms)	3*	336.26 ± 40.42	380.95 ± 50.55
L12 (ms)	0*	108.92 ± 31.36	143.75 ± 39.97
L13 (ms)	1*	244.83 ± 40.05	285.42 ± 56.67
L23 (ms)	0	135.97 ± 29.48	142.08 ± 37.63
Lx (ms)	2*	20.25 ± 8.93	29.83 ± 9.35
Slope (mmHg/s)	1*	62.25 ± 32.96	43.70 ± 14.46
Curv1(10−2)	2	2.10 ± 2.49	1.52 ± 1.20
Curv2(10−2)	1	1.33 ± 1.19	0.85 ± 0.48
Curv3(10−2)	0	0.76 ± 0.81	0.47 ± 0.36
Curv12	1	19.55 ± 140.27	8.01 ± 13.48
Curv13	0	2.19 ± 8.40	1.59 ± 3.39
Curv23	2	2.13 ± 5.74	0.76 ± 0.62
Curvm(10−2)	2*	0.80 ± 0.46	0.46 ± 0.15
pCO2 (mmHg)	0	35.98 ± 5.75	34.40 ± 5.73
Hgb	0	10.54 ± 2.03	9.83 ± 2.34
Hct	2	31.52 ± 4.16	32.04 ± 2.60
MAP (mmHg)	1	102.23 ± 18.71	105.60 ± 19.94
ICAMean (cm/s)	0	38.60 ± 10.74	36.20 ± 15.41
ICAPI	2	1.23 ± 0.46	1.40 ± 0.37
ICAEd (cm/s)	3*	23.30 ± 10.07	17.03 ± 7.32

n: number of runs (out of three independent runs) when the corresponding metric is selected as a classifier feature by the optimization process.

‘*’ is used to indicate cases that are statistically different (p < 0.05) by the unpaired t-test.

Additionally, Table 5 indicates that some of the metrics are significantly (p < 0.05) different between two groups based on an unpaired t-test. However, a metric that is significantly different between the two groups was not necessarily always selected as a classifier feature. Furthermore, metrics that were selected for majority of runs were not necessarily different between the two groups. Some examples of the former cases include dP₁₃ and dP₂₃ and examples of the later cases include dP₃.

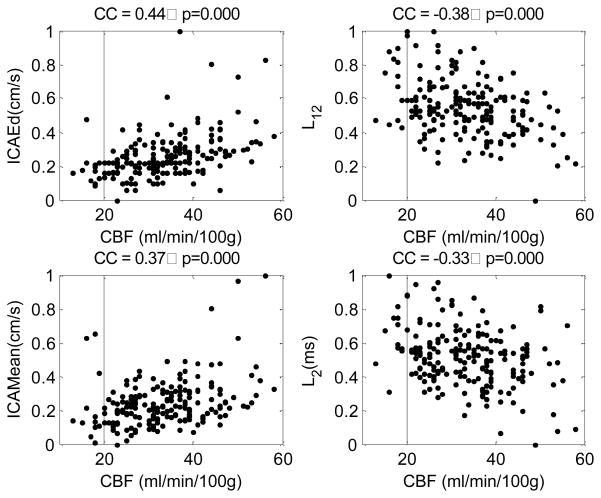
3.5 Correlation of metrics with CBF

Figure 4 displays scatter plots of four metrics against CBF. These metrics are ICAEd, ICAMean, L₁₂, and L₂. They are presented because they were the top four metrics, among the 32 metrics, having the greatest absolute correlation coefficients with CBF. Besides these four metrics, other metrics that had a significant (p<0.001) correlation with CBF included dP₂₃ (cc = −0.261), L₃(cc = −0.299), L₁₃(cc = −0.310), andICAPI(cc = −0.275). Although these individual metrics have significant correlation with CBF, it can be seen from the scatter plots that using a single metric will not be able to detect low CBF perfusion state.

Figure 4.

Scatter plots of four metrics against CBF. These four metrics include end-diastolic value of ICA, time interval between the first and the second ICP pulse peaks, the mean of the ICA, and the time interval from the onset to the second ICP pulse peak. They were selected as the top four metrics having the largest absolute correlation coefficient with CBF. The correlation coefficient and the p-value were displayed as the title of each plot.

4. Discussion

The present work tested the hypothesis that low global cerebral blood perfusion may be detected by using a set of ICP pulse morphological metrics through a trained pattern recognizer. Due to the lack of accurate prior knowledge regarding the pathophysiological implication of each of the MOCAIP metrics and their interactions, we utilized advanced data exploration tools that included global optimization, regularized quadratic classifier, and bootstrapping cross-validation techniques to design the experiment that requires minimal subjective choices of parameter values, e.g., which morphological metrics to use. It is therefore expected that the experiment thus designed will not only help test the original hypothesis but also may discover new ones in a data-driven fashion. We also included a comparative experiment to assess the classification performance in different combinations of MOCAIP and routinely acquired CBF-related clinical variables. Our main finding was that the incorporation of MOCAIP metrics was able to significantly improve the classification performance as compared to only using optimal combination of metrics from conventional TCD and blood analysis measurement.

In our following discussion, one should bear in mind the retrospective and data-driven nature of this study. It is not our goal to provide accurate explanations of interesting physiological findings that may result from this study. Instead, we believe that it should motivate further studies to investigate the implications and the underlying mechanism of the association between ICP pulse morphology and cerebral blood perfusion.

4.1 The optimal feature selection method

Feature selection in the present work was handled by an optimization process. The outcome of this selection process was assessed by three independent runs of the optimization and the bootstrapping cross-validation. There are some metrics that were always selected while others were never selected. The possible cause for not selecting a metric may be either because it does not contribute to the classification or it provides redundant information. However, it can be noticed that some metrics were selected at least once. Because the performance among the three different runs had a small variability as shown by results in Table 3, these metrics seemed to have negligible influence on the classification performance.

Feature selection by itself is an active area in machine learning (Saeys et al., 2007). Based on a recent review paper (Saeys et al., 2007), the approach adopted in the present work belongs to the category of wrapper method. This category of feature selection methods has the advantage of being able to exploit the interactions among input metrics and thus achieve better performance. Their disadvantage is the enormous computational time and the risk of overfitting the data. We employed a second cross-validation using bootstrapping to evaluate the final optimal configuration to test whether overfitting occurred. Results in Table 3 actually indicate that the optimization process did not overfit the data because only a small amount of difference existed between the two cross-validation approaches. It remains interesting to investigate whether other less time consuming feature selection approaches can achieve the same level of performance.

4.2 Implication and explanation of the findings

One of the findings from the classification experiment is that the elevation of the third peak of an ICP pulse may indicate low global cerebral perfusion. This is both visually confirmed in Fig. 3 and by the fact that P₃ related-metrics was often selected as contributing features. Further physiological studies are needed to investigate this new discovery and elucidate the association between P₃ elevation and low global cerebral perfusion. At present, we can only speculate some explanation for this observation. The origin of the P₃ has been largely attributed to the cerebral venous circulation (Adolph et al., 1967; Cardoso et al., 1983; Hamer et al., 1977). Therefore, an elevation of P₃ may indicate some pathological changes in the cerebral venous bed or elevated cerebral venous pressure, which consequently lead to the reduction of the cerebral perfusion pressure and reduce global cerebral perfusion. Some recent studies also indicate that cerebral venous hypertension may also be associated with idiopathic intracranial hypertension (Bateman et al., 2009; Stevens et al., 2008). However, the applicability of this interpretation may be questionable because intracranial hypertension was not the case for the patients studied here because of ICP is tightly controlled according to the established clinical protocol. However, this study raised some questions regarding whether controlling ICP can also lead to the control of cerebral venous pressure. This is important because the true perfusion pressure is actually determined by the difference between arterial and venous pressure. Even the mean ICP may be well within the prescribed limit, the true perfusion pressure may be still low in situation of cerebral venous hypertension. Despite this remains to be investigated, paying attention to ICP pulse morphology in addition to the mean ICP may potentially offer a practical monitoring practice for probing the functioning integrality of the cerebral vasculature including the cerebral venous bed.

Besides metrics that reflect P₃ elevation were selected as classifier features, the metrics including L_t, L₁, L₂, and L_x were also frequently selected. The engagement of L_t in the classification process can be probably explained by the fact that it measures the timing difference between ECG QRS peak and the onset of ICP pulse, which is significantly influenced by systemic arterial blood pressure as we discussed in a recent publication (Hu et al., 2009a). Therefore, L_t is a relevant measure as it contains information about the driving pressure of the cerebral blood flow. Under the most widely accepted explanation for the origins of P₁ and P₂ and the theory of pressure pulse wave propagation (Hu et al., 2009a), L₁ and L₂ might be related to the propagation of the arterial blood pressure pulse in different parts of the cerebral vasculature and therefore they are relevant to assessing cerebral perfusion. This explanation is at best speculative before the origins of these sub-peaks are completely established.

The finding that classification performance is better for SAH and non-TBI patients seems to be supportive of our hypothesis that MOCAIP metrics are useful indicators of cerebral perfusion because ICP pulse morphology is under the influence of cerebral vascular changes. On the other hand, a low CBF occurs for SAH and non-TBI patients mostly because of cerebral vascular changes including cerebral vasospasm. If our hypothesis is true, MOCAIP metrics are indeed more capable of capturing these vascular changes and thus achieved a better performance for SAH and non-TBI patients.

One important implication of this study is that the techniques of analyzing and extracting morphological features from continuous ICP may be used to facilitate near-real time pattern recognition of low global cerebral blood perfusion. This would be a very useful extension of the conventional ICP monitoring. Additionally, it can be used to facilitate a prospective study where one uses ICP pulse morphological changes, which can be conveniently tracked, to actively trigger more detailed cerebral vascular, neuro-electrical, brain imaging and metabolism studies so that more accurate explanations can be found.

4.3 Limitations of the study

Even though this study leveraged the latest development in ICP signal analysis and a rigorous classification experiment design, the results should still be considered preliminary due to the lack of low CBF cases when a CBF threshold was chosen to be 20 ml/min100g. A low number of low CBF cases may prevent us from making concrete assessment of the classification performance, e.g., the low positive predictivity value as reported in Table 3.

We only studied the performance of the proposed method under on CBF threshold. It can be expected that increasing CBF threshold for classifying a low CBF state may cause the deterioration of the method because the cerebral vascular changes may be less dramatic so that ICP pulse morphological changes will be more subtle. It also remains interesting to investigate whether a hyperemic state can be detected based on the proposed method however its clinical relevance is not as critical as detecting low CBF and potential cerebral ischemia.

In addition, limitations of clinical variables exist. That includes the laterality of the ICP measurement, which may need an extensive CT scan review to verify the catheter locations. One would argue that matching the laterality of ICP and CBF measurement may provide better results in cases where the intracranial space is compartmentalized so that the measured ICP pulse at one site does not represent the global CBF. There are limited numbers of studies on the spatial heterogeneity of ICP pulse morphology (Eide, 2008). One indeed would expect to see some degree of heterogeneity because the particular form of an ICP pulse is probably influenced by multiple cerebral vascular pulsation sources that originate from the forward propagation and backward reflection of systemic blood pressure pulse in the cerebral vasculature. Therefore, depending on the ICP measurement location, these constituent pulsation sources will assume different waveform shapes and so do the resultant ICP pulses. Nevertheless, ICP pulse morphology should still contain cerebral vascular information and are useful for inferring extreme CBF states.

We also did not investigate how many patients were in vasospasm and their medication and sedation states. It may be assumed that these factors will change CBF by their direct vascular influences and thus can be detected by the ICP pulse morphological changes.

Information about the systemic circulation is also missing in the present study. Despite the ICP latency (L_t) may indirectly provide information about the systemic arterial blood pressure, the lack of cardiac output may have profound confounding influence because one cannot expect ICP pulse morphological changes to be able to detect low CBF that is caused by low cardiac output. However, this weakness theoretically should be partially compensated by having the ICA flow velocity as part of the classifier feature. Our results did not demonstrate a significant benefit of having TCD metrics. This may be caused by not having TCD and CBF measurement simultaneously performed. We did not include the velocity and pulsatile index from vertebral arteries because not all patients with ICA measurements had also measurement from vertebral arteries. It may be expected that adding TCD metrics from additional intracranial arteries may help improve the performance.

Finally, the signal quality of our ICP recording was generally good enough for the detailed pulse morphological analysis as required by the present work. However, the number of eligible cases could have been larger and the time difference between ICP measurement and ¹³³Xenon CBF measurement could have been smaller if the cessation of ICP pulse recording due to the CSF drainage for subarachnoid hemorrhage patients could be minimized. Because we are using the steady sate CBF, the time difference between CBF and ICP measurement in the order of minutes might not be a primary concern.

Finally, concurrent CBF and CBFV measurements were not performed as part of standard care. Therefore, this retrospective study reflects this inherent limitation. Exact matching of ICP and CBF could not be achieved in the present study because of three reasons: 1) CBF study time as manually recorded by the technician is an approximation; 2) We are using the steady state CBF so that the exact time of CBF measurement cannot be defined accurately; 3) ICP measurement has to be taken from a period when ICP pulse waveform was available. While these timing issues will have to be addressed in future prospective studies, we believe that the results concerning the usefulness of the MOCAIP metrics in assessing cerebral hypo-perfusion are still valid because 1) Majority of the ICP-CBF pairs, 74.6% and 89.8%, had a timing difference within 60 and 120 minutes, respectively. 2) None of ICP-CBF pairs with CBF ≤ 20 ml/min/100g had extremely large timing difference (the maximum is 65 minutes). 3) Clinical interventions that would affect CBF were most likely introduced hours after the CBF was assessed because CBF results were essential elements for clinical decisions on treating these patients. 4) SAH group, despite having a larger portion of samples with greater timing difference, had a better classification results. This indicates that timing difference was unlikely a major factor affecting the major results of this study.

5. Conclusion

Capability of traditional intracranial pressure monitoring in neurocritical care can be potentially expanded in terms of supplying additional pulse waveform analysis modules to recognize precursors to clinically important events including low cerebral blood perfusion. The present work produced encouraging preliminary data in such a direction.