Spatial and Temporal Variations of a Screening Current Induced Magnetic Field in a Double-Pancake HTS Insert of an LTS/HTS NMR Magnet

Abstract

This paper presents experimental and simulation results of a screening current induced magnetic field (SCF) in a high temperature superconductor (HTS) insert that constitutes a low-/high-temperature superconductor (LTS/HTS) NMR magnet. In this experiment, the HTS insert, a stack of 50 double-pancake coils, each wound with Bi2223 tape, was operated at 77 K. A screening current was induced in the HTS insert by three magnetic field sources: 1) a self field from the HTS insert; 2) an external field from a 5-T background magnet; and 3) combinations of 1) and 2). For each field excitation, which induced an SCF, its axial field distribution and temporal variations were measured and compared with simulation results based on the critical state model. Agreement on field profile between experiment and simulation is satisfactory but more work is needed to make the simulation useful for designing shim coils that will cancel the SCF.

I. INTRODUCTION

The demand for a higher field and better resolution nuclear magnetic resonance (NMR) magnet has been growing continuously as its application expanded and becomes more sophisticated. Although a frequency of 950 MHz has recently been achieved by an all-LTS (low temperature superconductor) magnet [1], 1000 MHz (1 GHz) is considered a practical limit achievable with all-LTS NMR magnets. Therefore, we adopted a new configuration for a high-field NMR magnet in which a high-temperature superconducting (HTS) insert is placed in the cold bore of an LTS background magnet. A 3-phase program of which a final goal is to complete a 1 GHz or above LTS/HTS NMR magnet has continued at the MIT Francis Bitter Magnet Laboratory (FBML) since 2000 [2], [3]. In 2006, after the final test of a Phase 2 700 MHz LTS/HTS NMR magnet, we found a remanent magnetic field of 0.02 T or an equivalent NMR frequency of 0.85 MHz, even after both magnets were completely discharged at 4.2 K. Based on a simple assumption, accompanied by calculation, we concluded that the remanent field is generated by a screening-current-induced magnetic field (SCF) and furthermore an SCF could be a major source of field impurities in the two LTS/HTS NMR magnets completed to date in this 3-phase program, a 350 MHz magnet (Phase 1) and 700 MHz (Phase 2) [4]. A remanent field in an HTS magnet has been studied [5], [6], mainly focused on the magnitude of the self-field induced SCF at the HTS magnet center. For NMR magnets that require a highly homogeneous field distribution, the axial distribution and field gradients of an SCF, either external-field or self-field induced, and their effects on field homogeneity are critically important.

In this paper, we investigated the axial magnetic field profile of an SCF in an HTS insert, each induced by one of the following modes of magnetic field excitation: 1) a self field induction of the HTS insert itself; 2) an external field induction; and 3) combinations of both 1) and 2). In an LTS/HTS NMR magnet, not only the magnitude of SCF but also its harmonic gradients—spatial variation—need to be taken into consideration in the magnet design and operation. This paper also presents a numerical simulation based on the critical state model to compare results and measurements.

II. EXPERIMENTS

A. Experimental Setup

Table I shows specifications of the HTS insert wound with Bi2223/Ag tape and the LTS background magnet used for the SCF tests. For this series of measurements the HTS insert was operated in a bath of liquid nitrogen at 77 K, though it was operated at 4.2 K, contributing 50 MHz (at 49 A) in the Phase 1 350 MHz LTS/HTS NMR magnet, completed in 2003 [7]. The HTS insert is comprised of 50 double-pancake (DP) coils. As a background magnet to induce an SCF in the HTS insert, a 5-T/300-mm room temperature bore LTS magnet was used.

TABLE I.

Specifications of the HTS Magnet, Bi2223 Tape, and LTS Magnet

Component	Parameters	Value
HTS magnet	Inner diameter	78.2 mm
	Outer diameter	119–119 mm
	Length	327.6 mm
	Number of DPs	50
	Total number of tuns	7200
	Inductance	1.12 H
	Field constant	0.025 T/A
	Ic @ 77K, self field	19A
High-strength reinforced 3-ply	Width; thickness	3.1 mm; 0.25 mm
Bi2223/Ag tape	Ic @ 77K, self field	> 60 A
LTS magnet	Inner diameter	326.8 mm
	Outer diameter	414.8 mm
	Length	338 mm
	Number of tuns	24000
	Inductance	142.9 H
	Field constant	0.0595 T/A

The magnetic field was measured by a search coil wound with a 0.2-mm diameter of copper wire in a single layer of 1000 turns. The search coil was moved from the bottom to the top extent of the HTS magnet along its z-axis, driven by a variable speed DC motor. The search coil motion was monitored to confirm its constant speed. The search coil voltage was integrated to obtain the axial field profile. Since the SCF strongly depends on the charging and discharging history of an applied field, self, external or both, the HTS insert and LTS magnet were warmed up to room-temperature to eliminate hysteresis effects after each test sequence.

B. Measurement of the SCF by Self Field

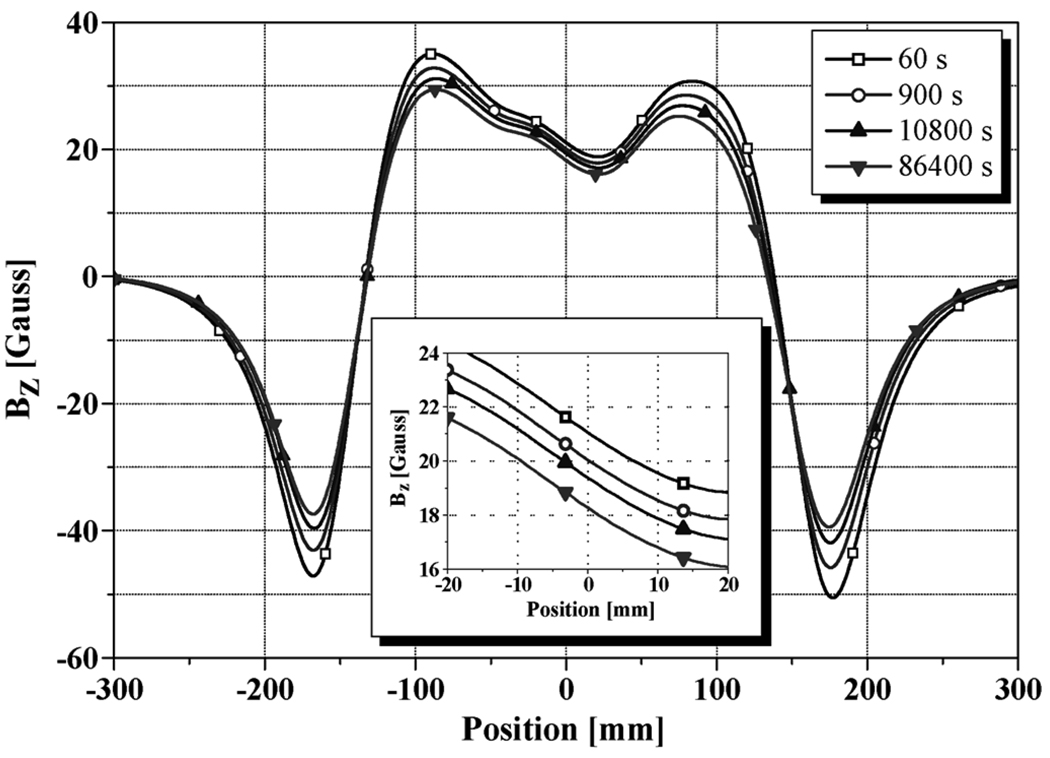
The test sequence to induce a typical SCF consists of the following steps: 1) immerse the HTS insert in liquid nitrogen; 2) energize the insert to 15 A; and 3) completely discharge the current. As observed by others [5], [6], the SCF is rate-independent, increasing or decreasing. Fig. 1 shows four measured axial field vs. axial (z) position traces of an SCF at four instances, with t = 0 defined at the instance when the HTS insert completed a 0 → 15 A → 0 excursion and z = 0 defined at the insert midplane. The axial locations of the two negative peaks, at z = ±167 mm, correspond to the top and bottom ends of the insert, respectively. Each measured SCF profile is asymmetric about the insert midplane, specifically: 1) the two positive peaks are unequal; 2) the field gradient at z = 0 is nonzero; and 3) the field minimum occurs at z = +25 mm. The inset presents a magnified view of the field traces at and near the midplane. If the insert’s 50 DP coils are identical in dimensions and in critical current density, the SCF is expected to be perfectly symmetric about the insert midplane. To elucidate the observed anomalies, we developed a simulation, discussed in Section III.

Fig. 1.

Measured axial field vs. axial location traces at four instances after a 0 → 15 A → 0 excursion of the HTS insert. Inset shows a magnified view at and near the insert midplane.

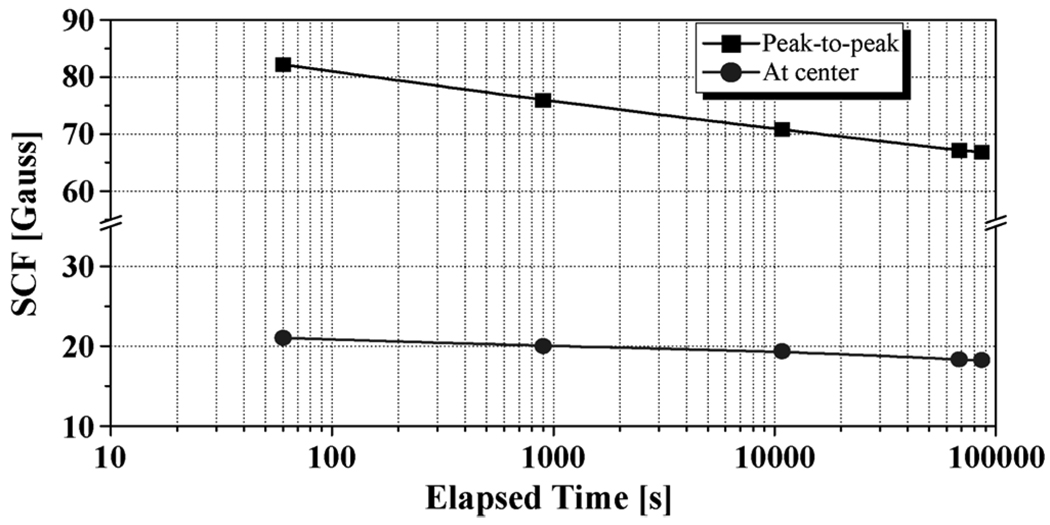
Fig. 2 shows two field vs. time plots, both decreasing with time, where the time scale is logarithmic: 1) left-hand side peak-to-peak (squares); and 2) midplane (circles). Since the SCF decreases considerably initially over a period of seconds after the conclusion of each field excursion, a field mapping is performed after the initial transient effects have subsided. This procedure applies also when field-shimming the insert. In our two LTS/HTS NMR magnets, one of the most dominant field errors was Z1, which showed a significant temporal decay during the test [3]. However, the measured Z1 gradients, shown in the inset of Fig. 1, do not appear to decrease significantly with time. The Z1 gradients at t = 60, 900, 10800, and 86400 s are 1.734, 1.719, 1.718, and 1.704 gauss/cm, respectively.

Fig. 2.

Field vs. time plots: left-hand side peak-to-peak (squares) and midplane (circles).

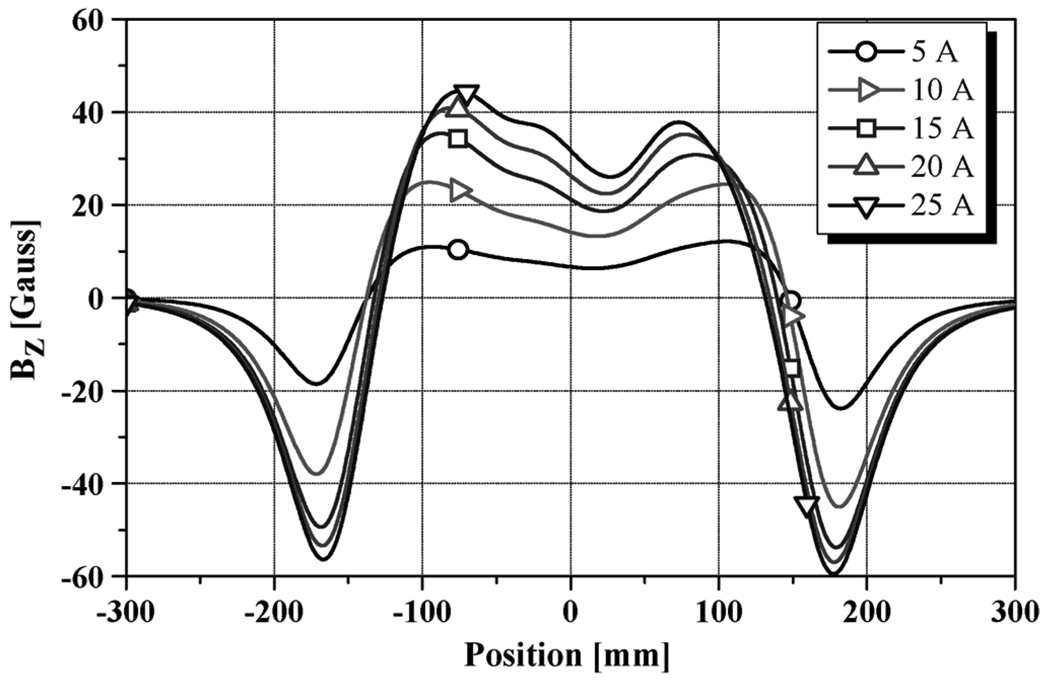
Fig. 3 shows SCF profiles for 5 self-field excursions, each identified with its peak current and measured at t = 60 a. It is obvious that the larger the exciting current the greater the positive and negative peaks. Although the critical current of the insert is 19 A at 77 K, the insert was charged up to 25 A to observe what may happen if the current exceeded its I_c. The result is minimal. The Z1 gradient at the midplane increases linearly with charging current.

Fig. 3.

SCF from various currents.

C. Measurement of the SCF by Applying a Background Field

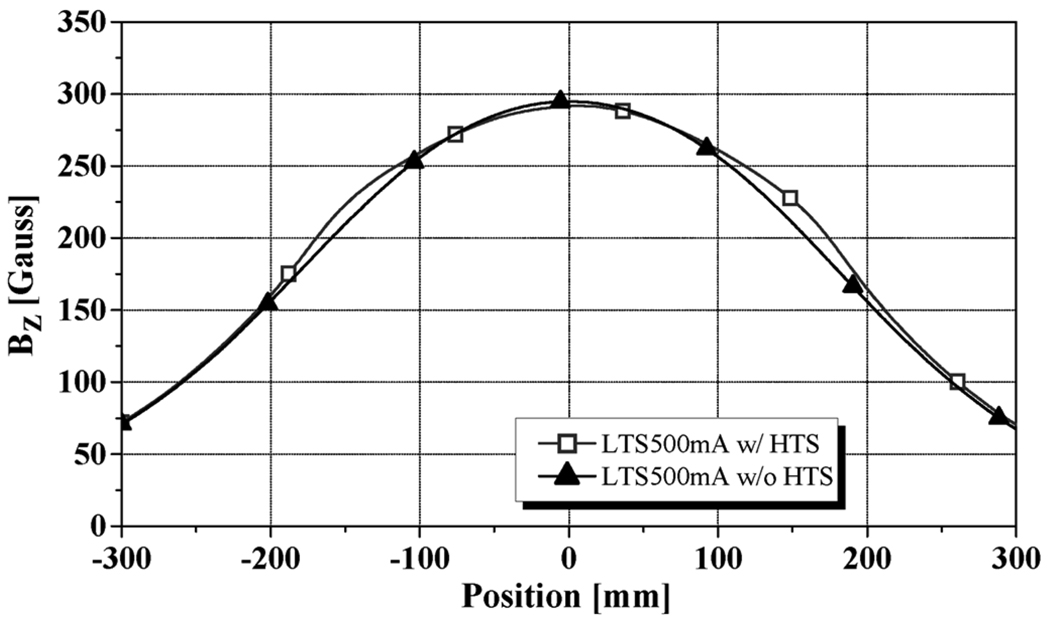
In an LTS/HTS NMR magnet, a field from the LTS magnet could also generate an SCF in the HTS insert. To observe the external field effect on the SCF in the HTS insert of the LTS magnet in an LTS/HTS magnet, we charged the 5-T LTS magnet to 500 mA (at which the center field is 298 gauss), either in the presence or absence of the un-energized HTS insert in the bore. Fig. 4 shows the measured axial field profiles for the two cases. As seen in Fig. 4, despite that there is no transport current in the HTS insert, its SCF clearly affects the axial profile.

Fig. 4.

Spatial axial field distributions, each with the LTS magnet energized at 500 mA, either in the presence (square) or absence (triangle) of the HTS insert.

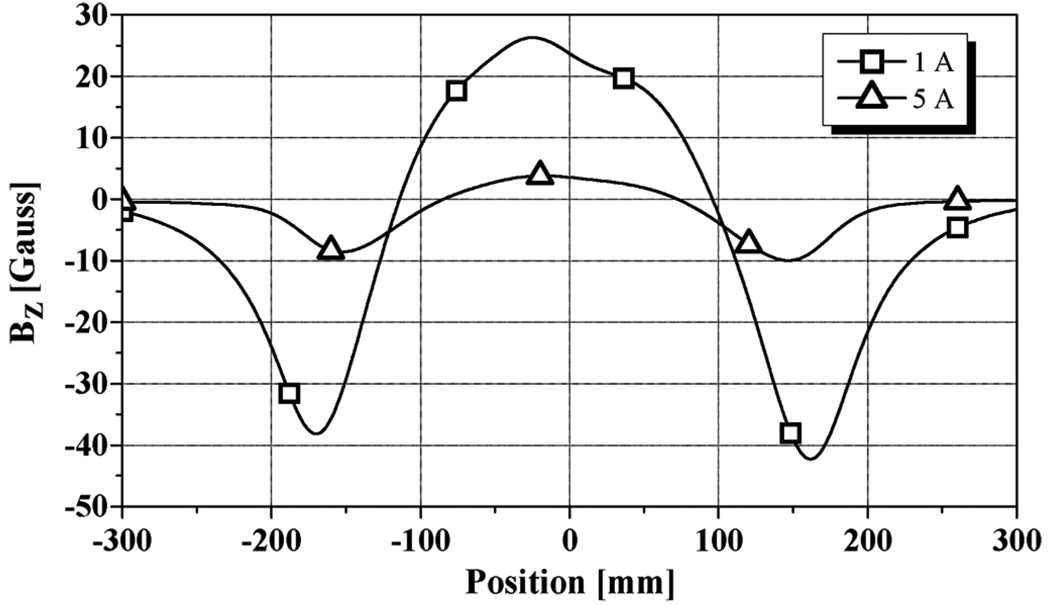
Fig. 5 illustrates two SCF profiles generated by the LTS magnet, one at its peak excursion current of 1 A and the other of 5 A. Compared with the self field profiles shown in Fig. 1, each profile has only one positive peak.

Fig. 5.

SCF profiles after the LTS magnet excursions, one with a peak current of 1 A (triangle) and the other of 5 A (square).

D. Combination of Two-Field-Source Excursion

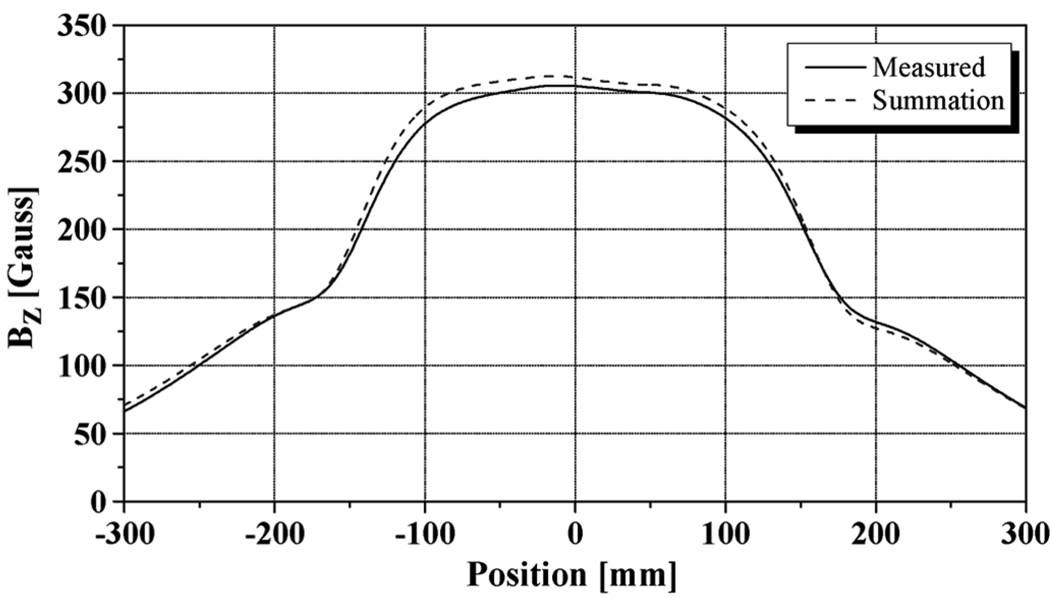
To study the SCF of the HTS insert generated by a combination of two field sources, self (HTS) and external (LTS), a 0 → 15 A → 0 current excursion was applied to the HTS insert first, followed by the LTS magnet energized to 500 mA. Fig. 6 shows a measured SCF profile (solid line) after this two-field-source excursion. There are two unmistakable changes in the field gradient, respectively, at z = ±170 mm. The dashed curve in Fig. 6 is the sum of the SCF profile (t = 86400 s) shown in Fig. 1 and that (squares) shown in Fig. 4.

Fig. 6.

B_z when charging the LTS magnet up to 500 mA in the presence of the SCF induced SCF at 15 A.

III. SIMULATION AND DISCUSSION

In our earlier simulation study, based on a simple application of the Bean critical state model, the computed SCF distributions were all symmetric about the midplane [4], while measured distributions, as presented above, are not. To correct this discrepancy, we have refined our model.

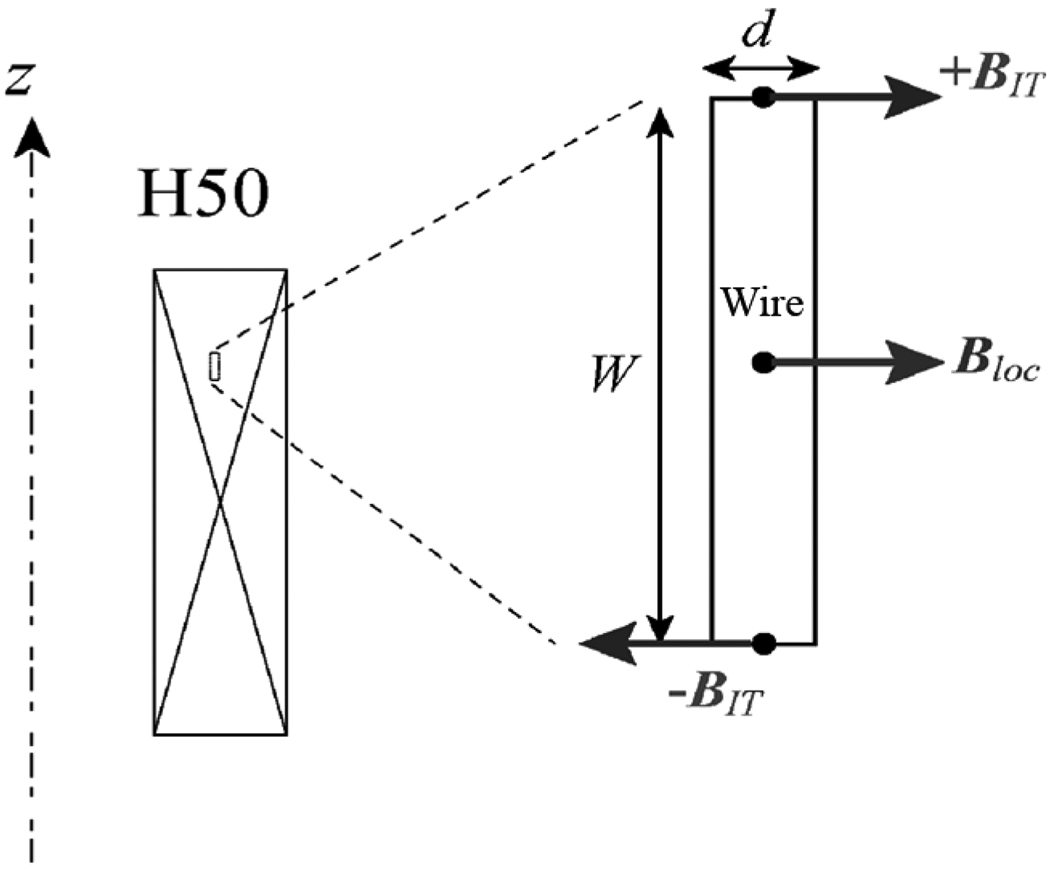
To simulate an SCF profile, we apply the Kim model to each unit length of the Bi2223 tape in the HTS insert. The schematic diagram of the unit tape length in the insert is shown in Fig. 7. The net magnetic field impinging on the unit length in a given location in the insert, though generated by transport current I_T, may be decomposed into two components: 1) B_loc, the “local” field produced by the entire insert assembly; and 2) B_IT, the “self” field produced by the transport current at both edges of the tape. Furthermore, we consider only each field’s component perpendicular to the broad surface of the tape, because the screening current induced by the parallel component is negligible.

Fig. 7.

Schematic diagram of applied field to HTS magnet.

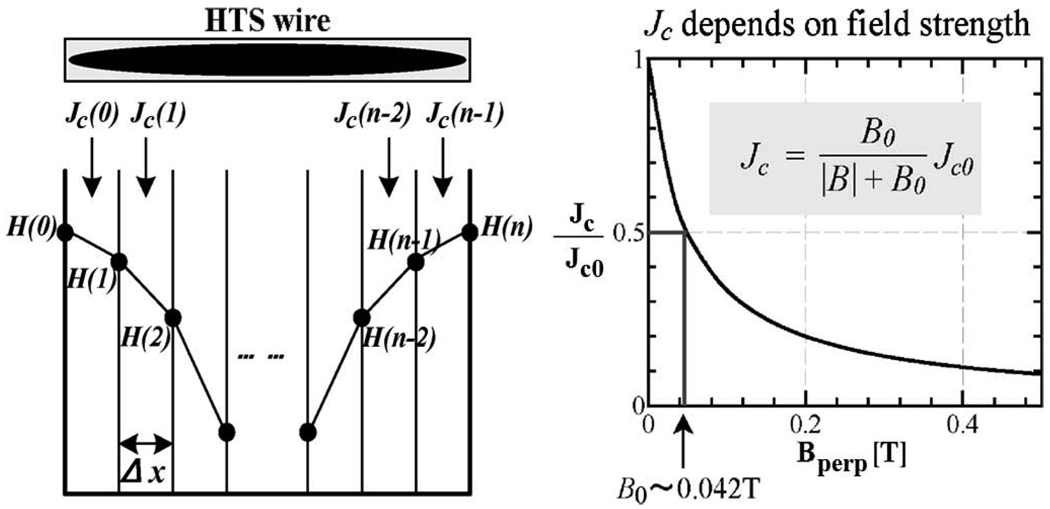
Fig. 8 shows a schematic drawing of a supercurrent distribution according to the Kim model, i.e., J_c is no longer field-independent as in the Bean model. The tape is divided into n parts over its width, and J_c (k), defined as the critical (or screening) current density in the k^th part of tape where its field strength is H (k) is given by:

$$H(k+1)=-J_c(k)\mathrm{\Delta }x+H(k):\text{from the left side}$$ (1)

$$H(k+1)=-J_c(k)\mathrm{\Delta }x+H(k):\text{from the right side}$$ (2)

$$J_c(k)=\frac{H_0}{|H(k)|+H_0}{J}_{c0}$$ (3)

where J_c0 is a primary critical current density without any field and H₀ is a field strength at which the current density becomes half of J_c0. The Δx in (1), (2) is one division width. Finally, we can get a series representation given by:

$$H(k)=\frac{{\displaystyle \sum _{i=0}^{k-1}\text{sign}(i)(H(i)+H_0)H_0}}{(H(k-1)+H_0)\cdots (H(0)+H_0)}{J}_{c0}\mathrm{\Delta }x+H(0)$$ (4)

where sign(i) represents either the plus or minus sign. After the field distribution is computed, a J_c (k) may be computed:

$$J_c(k)=\frac{H(k+1)-H(k)}{\mathrm{\Delta }x}$$ (5)

Fig. 8.

Explanation drawing of the Kim’s critical state model. The H₀ is a field strength at which the current density becomes half the value at zero field.

To calculate an SCF, we model screening currents as comprising concentric loop currents. The SCF at a given axial position is the sum of the field due to each current loop.

In fact, the surface field, B_surface, on an HTS tape is much larger than the original applied field, B_appl, which was reported as an “Edge Enhanced Effect” by E. Zeldo et al. [8]. The experimentally-obtained coefficient of this enhancement factor depends on the tape aspect ratio, w/2d, and thus:

$$B_{\mathit{\text{surface}}}=\sqrt{\frac{w}{2d}{B}_{\mathit{\text{applied}}}}$$ (6)

For accurate simulation of SCF, we consider the measured parameters (o.d. of individual pancake, wire thickness, I_c).

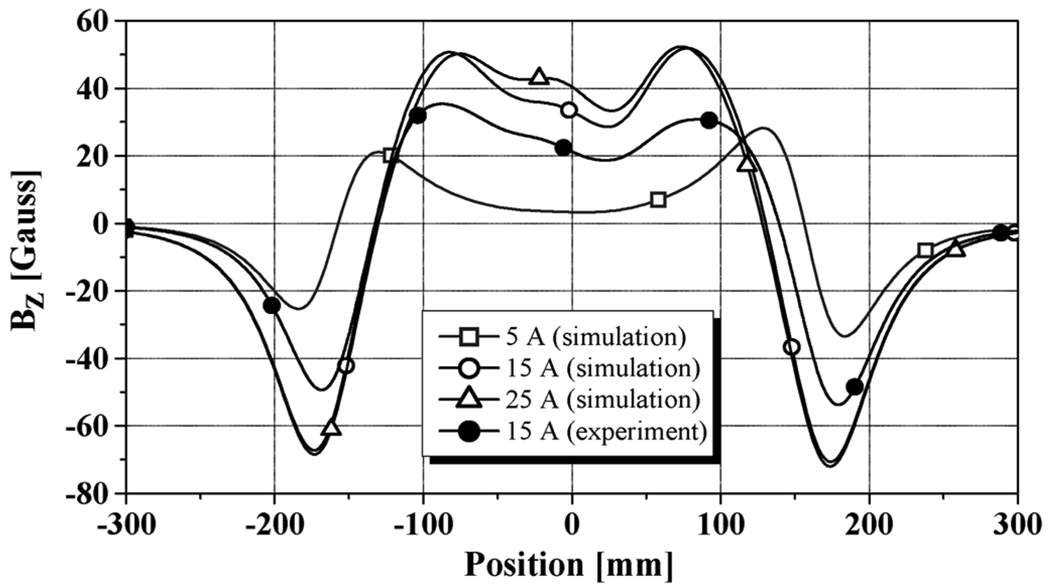
Fig. 9 shows simulation SCF profiles under the self-field excursions (5 A, 15 A, and 25 A) used in the experiment, results of which are shown in Fig. 3. Although the simulation results have large extreme values near both ends of the HTS insert, there are a few remarkable features at and near the mid-plane:

1. The anomaly is well simulated.

2. The negative peak at each end for each excursion is also well simulated, though not its amplitude.

We found that a large discrepancy in these parameters is chiefly responsible in creating an asymmetric B_r component near the inner diameter of the insert, which in turn creates an asymmetric axial distribution in SCF.

Fig. 9.

Simulation results of the SCF for various transport current cases. A experimental result, in case of 15 A, is also plotted for comparison.

IV. CONCLUSION

For a high-field NMR magnet consisting of an LTS background magnet and an HTS insert, the screening-current-induced magnetic filed (SCF) of the HTS insert is generated not only by a self field of the HTS insert but also by the field of the LTS magnet. It has been found, through measurement, that the magnitude of SCF decreases logarithmically with time, whereas its Z1 gradient at and near the mid-plane remains nearly constant with time.Our revised simulation code to compute an SCF profile incorporates the measured parameters of the HTS insert. The code quite satisfactorily simulates the profile anomaly observed around the mid-plane but disagreement between measurement and simulation still remains. Since the temporal field decay of an SCF is likely related to the phenomenon of flux creep, the field decay rate could depend on operating temperature and magnetic field. This dependence of the SCF decay rate on temperature and magnetic field is needed to estimate the elapse time for an SCF to “settle.” Note that in order to design a set of shim coils specifically targeted to minimize the harmonic errors generated by an SCF, its field distribution must first be measured.