Modelling trypanosome chronicity: VSG dynasties and parasite density

Abstract

A new mathematical model developed by Lythgoe et al. shows that the semi-predictable order of trypanosome antigenic variation can be generated by two parasite-intrinsic factors. The first is the different probabilities of antigen-gene activation that result from the different molecular mechanisms by which the genes become expressed. The second is the density-dependent differentiation of slender to stumpy cells. The study has important implications for understanding the dynamics of antigenic variation and for modelling the consequences of therapeutic strategies directed against trypanosomes.

Molecular mechanisms underlying antigenic variation

The African trypanosome is rightly famous for its ability to exchange surface antigens and thereby keep ahead of the mammalian immune system. Although systems of antigenic variation are seen in several pathogens, including viruses (e.g. Influenza), bacteria (Borrelia, Neisseria, Anaplasma) [1] and protozoan parasites (Plasmodium, Giardia, Babesia) [2–4], nowhere is the system developed so extensively as in the trypanosome. This is necessary because the host can remain infected with the parasites for months to years, during which time the parasite is exposed fully to the armamentarium of host immune defences. The surface on any one parasite is composed homogenously of a uniform type of antigen, the variant surface glycoprotein (VSG). For many years, it was thought that each VSG protein was encoded by a gene, formerly silent, which had become activated either: (i) by its relocation downstream of an active VSG expression-site promoter; or (ii) by activation of a new expression-site promoter in an expression site in which that gene happened to reside. However, completion of the genome sequence for Trypanosoma brucei revealed a more complex picture, with two classes of VSG gene being present [5–7]. The smaller proportion of genes, which are intact and awaiting expression, are housed at either silent telomeric VSG expression sites (approximately 20) or at one end of the 200 or so minichromosomes contained in the trypanosome nucleus. The remaining genes, numbering up to 2000, are largely interrupted by stop codons and frame-shifts, thereby forming pseudogenes that are unable to encode a functional protein. For these genes, expression can only occur if they become ‘repaired’ by the formation of mosaic genes through multiple gene-conversion events [8]. These two groups of VSG genes have different probabilities of activation [9] and this is dependent on different regions of DNA homology. For those intact genes in expression sites or on minichromosomes, activation is thought to be dependent on the sequences flanking the genes that direct their relocation into an active expression site by gene conversion. In particular, this comprises a common 70 bp repeated sequence found upstream of VSG genes in expression sites and, to a far lesser extent, subtelomeric genes. For pseudogenes in subtelomeric arrays, however, homology between coding sequences seems to drive gene conversion and requires sequence homology among the components of the assembly. This might require multiple conversions to produce a functional VSG, such that the successful assembly of an intact mosaic is far less probable than the activation of an intact telomeric gene. This difference in activation frequency among the genes in each of these groups, and among the genes within each group, forms the basis of a new mathematical model to describe the infection profile of African trypanosomes in their mammalian host [10].

Modelling antigenic variation

Lythgoe et al. use various parameters in their model based on data from previous experimental studies of infection. Crucially, as well as the VSG-specific immune response of the host, they also chose to include the impact of the density-dependent differentiation of slender cells to stumpy cells. This entails the transition of a proliferative cell type (slender forms) to a non-proliferative cell type (stumpy forms) with obvious (although difficult to measure quantitatively) consequences for the parasitaemia [11]. Explicitly excluded in the model was any direct host involvement in the switching mechanism, which is controlled entirely by the parasite itself. Further, because the dispersed anatomical location of the trypanosomes within the host seems to have little, if any, quantitative effect on infection, it was not included as a parameter. Although location might have an impact on stumpy formation if exposure to, or turnover of, the inducing signal [normally referred to as stumpy induction factor (SIF)] [12] varies in different compartments of the host, current experimental evidence is against this [13].Finally, any immunosuppression associated with the trypanosome infection was argued to have no impact on antigenic variation and was therefore excluded from the model.

The models evaluated different scenarios for antigenic switching and were used to simulate infections with one original infecting variant and a total of 30 variants available to the parasite. Although the trypanosome has a far larger repertoire, modelling a smaller number of variants does not affect the overall profile of antigen ordering in the predicted infection but its duration is shortened. To analyse the impact of the switching rates of the antigens, these rates were varied in the computational simulations. Initially, the model was used to demonstrate that, if all antigens had a uniform switching rate, then there would be no order to the expression of the antigens. In this simulation, all potential variants were expressed early in infection and the host immune response cleared the infection rapidly. However, simply by incorporating differential activation rates for each of the variants into the model, irrespective of the current antigen being expressed, a procession of expressed variants appeared, matched by a procession of VSG-specific immune responses by the host. By grouping antigen-switching rates into high, medium and low probabilities, they induced clustering of the antigens expressed, which mimicked the appearance of natural infections. This clustering into groups with differing probabilities of activation reflects the known activation mechanisms discussed earlier. Thus, those with relatively high activation frequency are likely to comprise genes using flanking-sequence homologies for gene conversion (i.e. independent non-directional switches), whereas those with low activation frequency would involve those requiring coding-sequence homologies to produce mosaic genes (i.e. dependent non-directional switches).

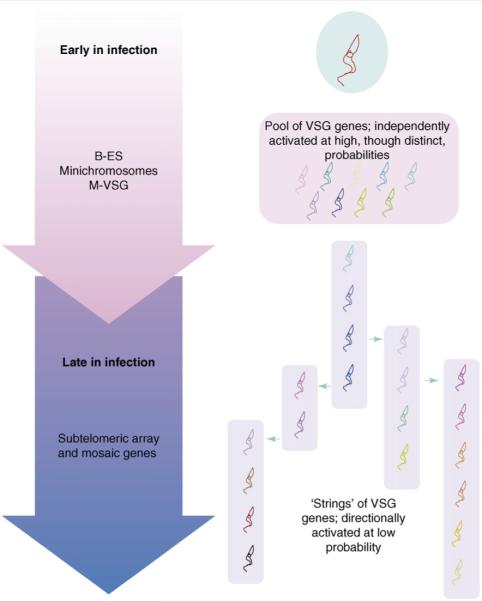
The important consequence of their model is that trypanosome infections in the field are likely to comprise two phases, the continuous spectrum of activation frequencies for different genes causing them to merge seamlessly (Figure 1). In the early phase, there would be frequent independent switching among genes with a high probability of activation producing a ‘cloud’ of antigen expressions and differing activation frequencies would produce some order within this. In this phase, the model introduces the interesting concept of competition among genes for expression [9]. However, once an immune response has been raised against all the products of these genes, there is selection for the expression of new variants generated by mosaic-gene conversion. Because the production of these depends on coding-sequence homology among genes, the result is the expression of VSG dynasties with dependency between one expressed antigen and the next. The authors refer to this phenomenon as the production of ‘strings’ of VSG expression [14]. They suggest that there is also a potential biological importance to this. In infections in the field, hosts – through exposure to many trypanosome populations – might develop effective immunity to VSG types expressed frequently. By the production of unique strings of VSG types, however, the trypanosome is able to introduce unique lineages of antigens to overcome this ‘herd immunity’ [14].

Figure 1.

Model for the expression of distinct antigenic variants during chronic infections with Trypanosoma brucei. Early in infection, genes with a high probability of activation are expressed, which comprise intact VSG genes located in expression sites or on mini-chromosomes. Later, subtelomeric-array VSG genes are expressed, although these require assembly from pseudogenes to form functional mosaics. Because these events are dependent on coding-sequence homology between currently expressed VSG genes and the newly assembled gene, unique lineages of VSG expression develop. Throughout, the periodic accumulation of stumpy induction factor, which generates non-proliferative, transmissible, stumpy forms, contributes to the chronicity of infection by limiting the increase in parasite numbers in any one wave of parasitaemia. By using differential gene-activation frequencies to generate hierarchical expression of VSG types, the model of Lythgoe et al. differs from previous models, which relied on interdependency among expressed VSG types [18], differential growth rates of antigenic variants [19] or an interplay with the immune system to generate ordered antigen expression [20].

Implications

The models generated illustrate elegantly the power of using mathematical modelling to explain important mechanisms in infection biology. Such models are limited inevitably by the key assumptions on which they are based but provide testable hypotheses for further analysis. For example, the authors argue compellingly that the efficacy of the immune response to antigenic variants is retained throughout the infection. This has experimental support because the serum from late infections retains lytic potential against early-expressed variants [9,15,16]. However, there is evidence for immunomodulation during trypanosome infection [17] and it might be that the capacity to respond to newly arising variants decreases somewhat late in infection or is impacted in the presence of coinfecting parasites or by earlier exposure to them. This would provide an interesting counterbalance to the decreasing frequency of productive switches that occurs during infection because an increasing proportion of parasites switch to antigen types used previously (against which there is already an immune response) or undergo non-productive switches. Also, the inherent superimposition onto the model of the transition between slender and stumpy forms is limited because our understanding of this differentiation event is poor. In particular, the inability to distinguish unambiguously slender and stumpy forms and intermediates between these extremes provides some barrier to quantitative modelling of the impact of this developmental step on an infection profile. More accurate quantification of this differentiation in the future awaits reliable markers for each developmental form. This is an important issue because the model of Lythgoe et al. demonstrates that the rate of stumpy formation has significant bearing on establishing the chronicity of an infection.

Lythgoe et al. illustrate how trypanosome antigenic ordering is determined by parasite-intrinsic factors (VSG activation rate and density-dependent differentiation), rather than those imposed by the host. These factors are presumably independent of one another, although it would be particularly elegant if recently switched trypanosomes were refractory to SIF, thereby selecting for the proliferation of new variants. As well as reaffirming the beauty of antigenic variation in trypanosomes, the model provides insight into its mechanistic control by assessing the relative importance of the different VSG gene-activation mechanisms during a chronic infection. Further, the model also has value for predicting the wider impact of strategies to control infection. For example, identification of the currently mysterious SIF might enable strategies to drive trypanosome populations prematurely into division arrest, thereby limiting their potential for antigen switching and promoting clearance. However, increasing the rate of stumpy formation also has the potential to enhance the transmissibility of the parasite population. Clearly, mathematical models, such as those developed by Lythgoe et al., enable the impact of changing the normal balance to be predicted and therapeutic strategies targeted or optimised appropriately.