Total Imprecision of Exposure Biomarkers: Implications for Calculating Exposure Limits

Introduction

Exposure assessment is a key aspect of environmental epidemiology. In standard statistical analysis, the exposure variable is treated as an independent variable without error. However, commonly occurring non-differential errors tend to bias the dose-response relationship toward null [Fuller, 1987]. A measure of individual exposure is often obtained from exposure biomarkers, i.e., contaminant concentrations in samples of human tissue or body fluids [Grandjean, 1995]. The validity of these parameters is usually expressed in terms of laboratory uncertainty, where the imprecision is given as the coefficient of variation for repeated analyses of the sample [ISO, 1993]. However, the total imprecision includes both analytical and preanalytical sources of variation. The latter encompasses all types of variation associated with the specimen sampling, storage, transportation, toxicokinetic variability, and related factors. Thus, improvement of laboratory performance does not automatically lead to a reduction of the total error [Bonini et al., 2002], and the total imprecision may be underestimated.

In laboratory quality assurance, an analysis may be validated by analyzing a reference material and comparing the result obtained with the certified value for the material. This approach is not appropriate for estimating the validity of a biomarker that may be affected by preanalytical variability. Correlations between related biomarkers have sometimes been used to estimate their validity, but interpretation such data is difficult in the absence of a gold standard or certified value, with which to compare the results. A supplementary approach is to assess the predictive validity of the biomarkers from their associations with known outcome variables [Grandjean et al, 1999].

Advanced statistical methods may be applied to estimate the total imprecision of biomarkers. In principle, the result for each exposure biomarker can be expressed as an intercept, an error function, and a loading factor multiplied by the “true” exposure, similar to a regression equation. Because three parameters are unknown, at least three sets of exposure indicators from a group of subjects is required to allow factor analysis that can provide estimates of the unknown parameters [Budtz-Jørgensen et al., 2003]. The error function obtained reflects the total imprecision of the biomarker. A more sophisticated approach is to apply a structural equation model, where the influence of confounders and effect variables may be included, thereby utilizing all available information from a study to assess the imprecision [Budtz-Jørgensen et al., 2002].

The impact of imprecision of exposure parameters has recently attracted attention regarding methylmercury toxicology. In a prospective epidemiological study of a Faroese birth cohort [Grandjean et al., 1997], we found that two commonly used exposure biomarkers showed a linear relationship with scatter as a reflection of a substantial degree of imprecision [Budtz-Jørgensen et al., 2004a]. We therefore use this study to demonstrate a statistical approach to assessing exposure biomarker imprecision and providing proper adjustment for its consequences.

Materials and Methods

Cohort formation and biomarker analyses

A birth cohort of 1022 subjects was formed from consecutive live births between 1 March, 1986 and the end of 1987 at the three Faroese hospitals [Grandjean et al., 1992]. In connection with each birth, we collected umbilical cord tissue, cord blood, and maternal hair. Cord blood and maternal hair were analyzed for mercury [Grandjean et al., 1992]. Because the full hair length corresponding to the complete pregnancy duration had originally been analyzed, we subsequently determined the mercury concentration in the proximal 2-cm segment as an indication of methylmercury exposure during the third trimester [Grandjean et al., 2003b]. For some cohort members, one or more specimens were not available, and some hair samples were sufficient only for the full-length analysis. For cord tissue, the dry weight of the sample was determined after freeze-drying for 48 hours, and analysis followed the procedure used for hair samples [Grandjean et al., 2005]. The quality assurance data for the mercury analyses suggested a highly acceptable imprecision with a coefficient of variation (CV) of approximately 5% [Grandjean et al., 2002; Budtz-Jørgensen et al., 2004a].

Clinical follow-up

Follow-up of this cohort included an extensive neurobehavioral examination at age 7 years, where five main outcome tests were selected to represent different brain functions [Grandjean et al., 1997]. Finger Tapping with the preferred hand (motor speed) was the main motor function test. Verbally-mediated function encompassed Continuous Performance Test reaction time (attention); Bender Visual Motor Gestalt Test (visuospatial); Boston Naming Test (language); and California Verbal learning test – Children short-term reproduction (verbal memory).

The study was carried out in accordance with the Helsinki convention and with the approval of the ethical review committee for the Faroe Islands and the institutional review board in the US.

Statistical analysis

Following descriptive analyses, logarithmic transformations were used for mercury concentrations with skewed distributions, and geometric means were calculated. This transformation aimed at reducing the impact of some very high mercury concentrations. In addition, this transformation is needed to obtain approximately linear relationships with homogenous scatter between the exposure biomarkers, as required by the subsequent analysis. Interrelationships between the transformed exposure biomarkers were determined by correlation coefficients.

Using the main outcomes at age 7 years, we carried out multiple regression analyses that included the same set of confounders that was originally selected [Grandjean et al., 1997; Budtz-Jørgensen et al., 2007b]. As methylmercury exposure biomarkers, we used the mercury concentrations in cord blood, maternal hair, and cord tissue [Grandjean et al., 1999; Budtz-Jørgensen et al., 2002; Grandjean et al., 2005]. The mercury effect is expressed in terms of the change in the response variable relative to the standard deviation of the response that was associated with a doubling in the mercury concentration [Grandjean et al., 1999].

To assess the degree of uncertainty in exposure biomarkers, a confirmatory factor analysis was first carried out [Budtz-Jørgensen et al., 2003]. In this approach, each marker of mercury exposure (M-Hg) can be assumed to be a manifestation of the true (unobserved) exposure (Hg):

$$\text{log}(M-Hg)={\alpha }_{\text{m}}+{\lambda }_{\text{m}}\text{log}(Hg)+{\epsilon }_{\text{m}}$$ (1)

Thus, the log-transformed marker will depend linearly on the true (log-transformed) mercury exposure and a measurement random error (ε_m). In a factor analysis, at least three markers with independent error terms are needed for the model to be identified [Bollen, 1989]. We therefore included the mercury concentrations in cord blood and maternal hair as well as the questionnaire response on the frequency of pilot whale consumption during pregnancy. The regression coefficient λ_m – also known as the factor loading – was fixed at 1 for the cord-blood concentration so that the true exposure is expressed on the scale of the mercury concentration in cord blood. Thus, a one-unit increase in log-Hg will on average lead to a one-unit increase in log cord blood Hg. Because a natural log transformation is used, error standard deviations are mathematical approximations to the error CVs of the untransformed concentrations. Using these results, the biomarkers can be compared both in terms of their imprecision and from their estimated correlations with the true exposure [Budtz-Jørgensen et al 2003]. Likelihood-based 95% confidence limits for the error standard deviation were determined to quantify estimation uncertainty.

Information from additional mercury biomarkers as well as outcome variables and covariates were then included in a structural equation model analysis [Budtz-Jørgensen et al., 2002]. In parallel to the factor analysis model, the observed variables are considered to be manifestations of one or more latent variables, which are not available for direct observation, but can be estimated from the observed variables. The structural equation models therefore allow estimation of causal relationships between the latent variables after possible adjustment for the effects of covariates. Thus, the structural equation model combines the (confirmatory) factor analysis and the path analysis [Bollen, 1989].

In regard to the exposure model, this analysis included the above exposure indicators, supplemented by the mercury concentrations in dry-weight cord tissue and proximal segment of the maternal hair. Similar to equation (1), all exposure biomarkers are considered as manifestations of an underlying latent variable (Hg). In this type of analysis, measurement errors (ε_m) in different markers are usually assumed to be independent. However, we anticipated dependence between error terms in the two hair measurements and between errors in the two cord-based measurements. Adjustment for such local dependence is possible in structural equation models, and we therefore allowed ε_m to be correlated for the two sets of maternal hair concentrations and for the two cord concentrations (tissue and blood), respectively.

Based on a priori neurobehavioral considerations, outcome variables were separated into verbal and motor outcomes so that test results belonging to the same group could be assumed to represent the same latent functional variable, i.e., in the same way as the exposure markers. Exposure and outcome variables were then related by assuming a linear effect of the true exposure on both latent response functions. Potential confounders in the dose-response relationship were included as covariates, which were allowed to be associated both to the exposure and the outcome functions (Figure 1). Children with incomplete information on the study variables were included in a missing data analysis based on the maximum likelihood principle [Little and Rubin, 2002]. Compared to standard complete case analysis, this approach is more powerful and less likely to yield biased results.

Figure 1.

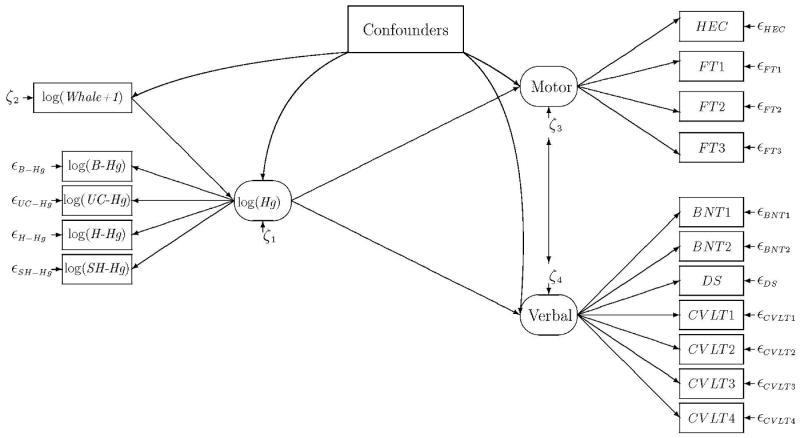
Path diagram for a structural equation model linking mercury exposure to adverse effects, while taking into regard confounders. The estimated true exposure (Hg) is modeled as a latent parameter based on mercury concentrations in cord blood (B), umbilical cord tissue (UC), maternal full-length hair (H), and maternal short-segment hair (SH). In addition, the maternal pilot whale meat intake during pregnancy (Whale) is taken into account. Two latent effect parameters (Motor and Verbal) are likewise based on clinical test outcomes analysis [Budtz-Jørgensen et al., 2002]. Motor and verbal function may be correlated (indicated by double-headed arrow) and potential confounders are allowed to be associated both with the latent exposure and to the latent effect variables.

The structural equation model induces a specific structure on the (expected) covariance matrix of the observed variables. Thus, apart from scale differences, the covariances between, say, a given motor score and a given verbal score will be the same for all pair of variables. The model parameters are estimated by examining all possible covariance matrices satisfying the model assumptions to identify the one closest to the covariance matrix of the observed data. An overall assessment of the model fit is then obtained by comparing the observed distance between covariance matrices to the expectation under the assumption that the model is correct. If this distance is statistically significant, then it is a sign that some model assumptions are violated.

When determining limits for acceptable exposures, regulatory agencies often use benchmark dose (BMD) calculations as a starting point. The BMD is the dose that increases the risk of an abnormal response by a benchmark response (BMR); if fixed at 5%, it represents a doubling of the background risk of 5%. The lower 95% confidence limit of the BMD is called the benchmark dose level (BMDL) [Crump, 1995; Budtz-Jørgensen et al., 2001]. For methylmercury, the BMDL has been applied for calculation of exposure limits by the U.S. National Research Council [2000] and the World Health Organization [JECFA, 2003]. However, both BMD and BMDL may be overestimated if account is not taken of the measurement error. We therefore included the estimated degree of imprecision to calculate adjusted BMDLs [Budtz-Jørgensen et al., 2004b] and then applied the revised data these for calculation of adjusted exposure limits.

Results

In this population with substantial differences in methylmercury exposures, all exposure biomarkers showed the anticipated wide ranges, where the highest concentration approached 1000-fold the lowest (Table I). The correlations between the biomarkers showed that mercury concentrations in cord tissue and cord blood were closely associated. The two hair parameters correlated well with one another, but somewhat less so with the cord blood concentration.

Table 1.

Geometric means, 25^th-75^th percentiles, and total ranges of mercury concentrations in specimens used as prenatal methylmercury exposure biomarkers in a Faroese birth cohort.

Exposure biomarker	N	Geometric mean	Interquartile range	Total range	Correlation with cord blood
Umbilical cord
Blood (μg/L)	996	22.4	13.1-40.4	0.90-351	(1)
Tissue (μg/g dry weight)	447	0.210	0.132-0.36	0.000-1.28	0.940
Maternal hair at parturition
Proximal segment (μg/g)	683	4.46	2.76-14.6	0.34-40.5	0.837
Full length (μg/g	1019	4.17	2.52- 7.7	0.17-39.1	0.784

The regression coefficients (Table II) showed similar results for cord tissue and cord blood concentrations as predictors of neurobehavioral deficits. Because the mercury concentrations were logarithmically transformed, regression coefficients are calculated to allow comparison between the effects of a doubling of the concentration level. However, cord tissue was available only for a small subgroup, and some calculations are therefore based on small numbers. Except in regard to motor speed, the cord-based biomarkers appeared to be better than maternal hair in predicting toxicity risks

Table 2.

Numerical change (beta, expressed as percent of the standard deviation) in five different response variables associated with a doubling of three different mercury exposure biomarkers after adjustment for confounders (Grandjean et al., 1999; Grandjean et al., 2005). The direction of all effects is toward increasing deficit at higher exposures (p-values are two-sided).

	Beta (p)
Response	Cord tissue	Maternal hair	Cord blood
Motor speed	3.00 (0.47)	5.99 (0.04)	5.37 (0.05)
Attention	29.6 (0.01)	8.99 (0.04)	15.9 (<0.0001)
Visuospatial	1.70 (0.66)	3.60 (0.21)	3.83 (0.15)
Language	11.3 (0.006)	7.47 (0.009)	10.5 (<0.0001)
Verbal memory	7.45 (0.08)	5.93 (0.05)	6.64 (0.019)

A factor analysis was carried out for the mercury concentrations in cord blood and maternal hair as well as the questionnaire information on the frequency of maternal pilot whale dinners during pregnancy. The results indicate that the cord blood concentration had a weaker error term (ε) than the maternal hair concentration (Table III). This difference in total imprecision was statistically significant with a p-value of 0.004 [Budtz-Jørgensen et al., 2003]. This finding is in agreement with – but independent of – the observation that the cord-blood concentration also showed stronger relations to the neurobehavioral outcome variables. Nonetheless, both biomarkers are associated with a total imprecision, which, is substantially in excess of documented laboratory imprecision levels of about 5%. Thus, even for the cord blood marker the estimated CV was as high as 30%, with a 95% confidence interval from 21% to 38%.

Table 3.

Factor loading (λ), standard deviation of the error term (ε) and estimated correlation to the true exposure calculated for two major biomarkers of prenatal methylmercury exposure in a factor analysis model.^*

Biomarker sample	Factor loading	Error standard deviation	Correlation to estimated truth
Cord blood	(1)	0.30	0.93
Maternal hair (full-length)	0.84	0.44	0.85

^*The frequency of maternal pilot whale dinners during pregnancy was used as the third independent exposure indicator. Because of the logarithmic transformation of exposure variables, the error standard deviation is considered the same as the coefficient of variation.

The advanced structural equation model showed a good fit to the data (p=0.067 in overall test of lack of fit) and thus confirmed the results of the simpler factor analysis (Table IV). Again the cord blood measurement was less imprecise than the other exposure biomarkers (p < 0.05), and the full-length hair concentration had the strongest error component. As anticipated, the two cord measures differed little, as did the two hair measurements. The advanced analysis was in close agreement with the factor analysis results for cord blood and maternal hair (Table III). Inclusion of additional exposure biomarkers, covariates, and neurobehavioral outcomes lead to small changes in estimated imprecision. In addition, the structural equation analysis confirmed the association between prenatal methylmercury effects and deficits in motor and verbal functions. Thus, a two-fold increase in mercury exposure decreased the verbal function level by 10.5 % (p=0.001) of the standard deviation while a similar exposure increase decreased the motor level by 10.8% (p=0.02) of the standard deviation in this outcome function.

Table 4.

Factor loading (λ), standard deviation of the error term (ε) and estimated correlation to the true (latent) exposure calculated for biomarkers of prenatal methylmercury exposure in a structural equation model.^*

Biomarker sample	Factor loading	Error standard deviation	Correlation to estimated truth
Cord blood	(1)	0.30	0.94
Cord tissue (dry weight)	0.89	0.33	0.91
Maternal hair (proximal)	0.89	0.36	0.89
Maternal hair (full-length)	0.85	0.45	0.84

^*The model included confounders and outcome variables. Because of the logarithmic transformation of exposure variables, the error standard deviation is considered the same as the coefficient of variation.

The U.S. National Research Council [2000] based its calculations on a BMDL of 58 μg/L cord blood, with the Boston Naming Test as the effect parameter. Using an uncertainty factor of 10, the resulting 5.8 μg/L blood was then considered an appropriate exposure limit, which would correspond to a mean daily methylmercury intake of 0.1 μg/kg body weight [National Research Council, 2000]. Subsequent calculations have shown that imprecision of exposure parameters will result in benchmark dose calculations being biased toward higher values [Budtz-Jørgensen et al., 2004b]. When adjusted for the imprecision, the cord-blood-based BMDLs benchmark dose level decreased to 43 μg/L (Table V).

Table 5.

Exposure limit calculation for methylmercury based on benchmark dose levels (BMDLs) before and after adjustment for statistical imprecision.

	NRC		JECFA
	Originala	Updated	Originalb	Updated
BMDL
Maternal hair (μg/g)	-	-	12	6
Cord blood (μg/L)	58	44c	-	-
Adult blood (μg/L)	-	29d	48	24c
Uncertainty factors
Hair-to-blood ratio	-	-	2	1.5
Individual vulnerability	-	-	3.2	6.4
Total	10	10	6.4	10
Exposure limit (μg/L)	5.8	2.9	7.5	2.4
Converted to intake (μg/g*d)	0.1	0.05	0.15	0.04

^aNational Research Council [2000];

^bJECFA [2003], based on Faroes data only;

^cBMDL from Budtz-Jørgensen et al. [2004];

^dAssuming a 50% excess in cord-blood concentrations

In addition, cord blood contains a higher methylmercury concentration than adult blood. An adjustment factor can be obtained by comparison of hair/blood ratios [Budtz-Jørgensen et al., 2004a]. The ratio for cord blood is about 190, as compared to about 250 for mature blood. This difference in hair/blood ratio suggests that cord blood may contain about 33% more mercury than does whole blood in general. Other studies have compared cord blood and maternal blood and reported an even higher ratio [Sakamoto et al., 2004; Stern and Smith, 2003]. Taking into account a decreased hematocrit during late pregnancy, we therefore assumed that the cord-blood mercury concentration is 50% higher than the one in adult blood. With these two adjustments, the exposure limit in terms of the blood concentration is then calculated to be 2.9 μg/L. This final result is a downward revision by 50% of the exposure limit calculated by the National Research Council [2000].

The similar JECFA [2003] calculations were based on BMDLs expressed in terms of the hair-mercury concentrations. Because of the greater imprecision of hair-based BMDLs, the adjustment causes a larger decrease of the BMDL (Table V) [Budtz-Jørgensen et al., 2004b]. This adjustment may take into account some of the uncertainty of the hair/blood mercury concentration ratio, and a smaller uncertainty factor will then be needed for this purpose. Because detailed data are available from the Faroes data only, the adjusted JECFA calculations were based only on this data set. The results of the two sets of revised calculations are similar.

Discussion

An imprecise exposure assessment will tend to underestimate the true effect of the exposure and may also complicate confounder adjustment [Carroll, 1998, Budtz-Jørgensen et al., 2003]. Assessment of total exposure biomarker imprecision therefore is a key to environmental epidemiology studies. However, even superb laboratory repeatability results cannot substantiate the validity of a biomarker in regard to a causative exposure and the associated disease risk. Unfortunately, the degree of imprecision of the exposure data is usually unknown in epidemiological studies.

The present study has employed different statistical strategies to explore this issue. The correlation coefficients between exposure biomarkers and outcomes provide only limited guidance to choosing the most precise indicator, because a disagreement between two correlated exposure parameters must rely on the result of a third, independent variable. When at least three variables are available, factor analysis can be carried out. The factor analysis results show that the mercury concentration in cord blood provides lesser imprecision than that of maternal hair. The more detailed calculations using structural equations, with inclusion of information on covariates and outcomes, showed virtually the same results. While each model is based on certain assumptions, the observed covariance in the structural equation model confirmed that the fit was adequate. Further, the results agree with independent regression analyses, where cord blood tended to be the best predictor of neurobehavioral deficits at age 7 years. The recently completed 14-year examinations also confirmed these findings [Debes et al., 2006].

The most frequently used sample for methylmercury exposure assessment today is scalp hair [Grandjean et al., 2002]. Sampling of hair is noninvasive and painless, and it is a feasible and efficient procedure under most field study conditions. Depending on the rate of hair growth, the mercury concentrations along the hair shaft can represent a calendar of past exposures. Yet, environmental mercury vapor may bind to the hair [Yamaguchi et al., 1975], and hair permanent treatments can remove some endogenous mercury from the hair [Yamamoto and Suzuki, 1978; Yasutake et al., 2003]. Also, hair color or structure may affect the incorporation of mercury into the hair [Grandjean et al., 2002]. These factors might well account for the greater overall imprecision of this biomarker.

The blood concentration of a contaminant is often considered the appropriate indicator of the absorbed dose and the amount systemically available, but this biomarker may also be subject to possible variation. Methylmercury binds to hemoglobin, and the high affinity to fetal hemoglobin results in a higher mercury concentration in cord blood than in maternal blood [Sakamoto et al., 2004]. Further, whole-blood mercury concentrations are affected by the hematocrit, and some researchers therefore prefer to measure the mercury concentration in erythrocytes [Sakamoto et al., 2004]. Routine analyses for total mercury concentrations include both methylmercury and inorganic mercury, but the cord blood mercury concentration likely reflects the methylated form, for which the placenta does not constitute a barrier [Kelman et al., 1982].

The umbilical cord offers is formed mainly during the second and third trimesters, and it reaches two thirds of its full length already by the end of the second trimester [Kaufmann and Scheffen, 1998]. Assuming a biological half-life of about 45 days for methylmercury [Smith and Farris, 1996], the cord-tissue mercury concentration is likely to represent a measure of the average mercury burden during the third trimester. The cord tissue mercury concentration will likely be less sensitive to short-term changes than will the cord-blood mercury concentration. When expressed in terms of dry weight, variations in the content of blood and Wharton's jelly will probably have only a minor impact on the precision [Grandjean et al., 2005].

Other authors have shown a scattered association between maternal hair-mercury concentrations and subsequent mercury concentrations in the child's brain obtained at autopsy [Huang et al., 2003]. These data are in accordance with the size of the measurement error for the hair-mercury parameter found in the present study. Our overall findings are therefore in agreement with the observation of cord blood as the best available indicator of prenatal methylmercury exposure.

Our results also suggest that even the best exposure biomarker may be much more imprecise than suggested by laboratory quality data. Thus, attention to laboratory quality must be coupled with vigilance in choosing specimens for analysis, as guided by physiological information and documentation on exposure variability. Because the total imprecision may vary from study to study, and because the impact on study findings will depend on the total range of exposures covered, each study should ideally include at least three exposure indicators, so that the imprecision can be determined by factor analysis. If this is not feasible, an assumed imprecision level of at least 25%, as indicated by Tables III and IV, should be used in sensitivity analyses.

Exposure imprecision and thus misclassification will generally be non-directional, thereby leading to an underestimation of dose-effect relationships [Grandjean et al., 2003a]. This problem may be exaggerated by potential confounders that are correlated with the exposure. In a regression inclusion of such variables may then further add to the bias toward the null hypothesis [Budtz-Jørgensen et al., 2003], even in cases where the potential confounder has no independent effect on the outcome.

The issue of biomarker imprecision is crucial in regard to dose-response relationships and calculation of exposure limits. Neither of the two major risk assessments carried out by the National Research Council [2000] and the World Health Organization [JECFA, 2003] considered this factor. In addition, the two reports differed in several other respects. For example, the NRC applied an uncertainty factor of 10 (individual differences, including kinetic variability, and incomplete data base), while JECFA used 3.2 (for differences in kinetics) and an additional factor of 2 for the blood-hair mercury concentration ratio. Overall, the JECFA limit is higher than the one calculated by NRC; EFSA [2004] refrained from choosing one above the other, while recommending that exposures should be minimized. The present study suggests that both are too high, and that an imprecision-adjusted limit would be 50% below the NRC limit.

Blind reliance on exposure indicators, without adjustment for imprecision, will bias the study findings and any conclusions derived from them. Imprecisions of 25%-50% are realistic and should be incorporated in sensitivity analyses. Total biomarker imprecision may be assessed if at least three independent exposure indicators are included. Adjustment can then take place using factor analysis or structural equation models.

We have shown elsewhere [Budtz-Jørgensen et al., 2007a] that fish intake, as a marker of beneficial nutrient supply, may affect the neurobehavioral outcomes associated with methylmercury exposure from seafood, and that confounder adjustment must also take into account the imprecision of the fish intake parameter to obtain an unbiased assessment of the mercury effect. Also in this case, failure to adjust for the imprecision results in an underestimation of the mercury effect.