Characterization of Gastric Electrical Activity Using Magnetic Field Measurements: A Simulation Study

Abstract

Gastric disorders are often associated with abnormal propagation of gastric electrical activity (GEA). The identification of clinically relevant parameters of GEA using noninvasive measures would therefore be highly beneficial for clinical diagnosis. While magnetogastrograms (MGG) are known to provide a noninvasive representation of GEA, standard methods for their analysis are limited. It has previously been shown in simplistic conditions that the surface current density (SCD) calculated from multichannel MGG measurements provides an estimate of the gastric source location and propagation velocity. We examine the accuracy of this technique using more realistic source models and an anatomically realistic volume conductor model. The results showed that the SCD method was able to resolve the GEA parameters more reliably when the dipole source was located within 100 mm of the sensor. Therefore, the theoretical accuracy of SCD method would be relatively diminished for patients with a larger body habitus, and particularly in those patients with significant truncal obesity. However, many patients with gastric motility disorders are relatively thin due to food intolerance, meaning that the majority of the population of gastric motility patients could benefit from the methods developed here. Large errors resulted when the source was located deep within the body due to the distorting effects of the secondary sources on the magnetic fields. Larger errors also resulted when the dipole was oriented normal to the sensor plane. This was believed to be due to the relatively small contribution of the dipole source when compared to the field produced by the volume conductor. The use of three orthogonal magnetic field components rather than just one component to calculate the SCD yielded marginally more accurate results when using a realistic dipole source. However, this slight increase in accuracy may not warrant the use of more complex vector channels in future superconducting quantum interference device designs. When multiple slow waves were present in the stomach, the SCD map contained only one maximum point corresponding to the more dominant source located in the distal stomach. Parameters corresponding to the slow wave in the proximal stomach were obtained once the dominant slow terminated at the antrum. Additional validation studies are warranted to address the utility of the SCD method to resolve parameters related to gastric slow waves in a clinical setting.

INTRODUCTION

Electrical waves in the stomach and small intestine control the peristaltic contractions that mix and propel food through the gastrointestinal (GI) tract. In the human stomach, an omnipresent electrical slow wave initiates at the upper/mid-corpus region of the human stomach and spreads down the antrum at a frequency of approximately 3 cycles per minutes (cpm).^14,19 Conditions such as gastroparesis are associated with ICC network disruption resulting in disorders in the underlying electrical activity.^17,34 In addition, conditions such as intestinal ischemia can result in arrhythmias and conduction blocks in the intestinal slow wave activity.^24,28 Therefore, the ability to efficiently, noninvasively characterize the electrical activity in the GI system would be highly beneficial as a preoperative screening tool.

Cutaneous electrogastrography (EGG) has previously been used to noninvasively record the information about gastric electrical activity (GEA) using multiple electrodes placed on the abdomen. It has been shown that cutaneous EGG could detect propagation of GEA^8,9 or gastric contraction,⁷ but the reliability and accuracy of detecting the true sources of the electrical current in the stomach from EGGs has been questioned in some studies.^3,26 A superconducting quantum interference device (SQUID) is a highly sensitive detector that is capable of recording the weak biomagnetic fields associated with GI electrical activity. Magnetogastrograms (MGG) are the magnetic measurements resulting from GEA and provide an alternative method of noninvasively sensing GEA.^3,21,33 The magnetic measurements have the advantage of being less attenuated by the multiple layers of electrical insulators of the torso when compared to electric measurements and they have been shown in limited studies to be capable of providing additional information about the characteristics of the underlying gastric activity.^1,5,11

The surface current density (SCD) method was first introduced by Cohen and Hosaka¹⁶ to assist with the interpretation of magnetic field recordings from the heart. The SCD method calculates current density from the recorded magnetic field values and with these maps it was possible to identify the location of the underlying sources more effectively than using magnetic field maps directly using simple simulations.¹⁶ The SCD described here is actually a pseudocurrent density as there exists no current density at the location of the measurement as the curl of the magnetic field at this location is also zero. Nevertheless, the nonzero values obtained by the H–C transformation can be related to the current running under the surface parallel to the sensor plane.¹⁸ In recent years, the SCD method has been applied widely in the studies of heart, nerve, or brain due to the development of computing and visualization tools.¹⁸ Recently, the SCD method has shown promise in being able to resolve GEA propagation velocity in both simple simulations and in experimental recordings.⁴

In the Bradshaw study,⁴ a single horizontal dipole with a fixed orientation was used with a half space representation of the volume conductor to test the accuracy of the SCD method. In addition, only the magnetic field component normal to the anterior surface of the torso was considered. In this study, we aim to examine the ability of the SCD method to accurately resolve GEA parameters using more realistic simulations than those used in Bradshaw et al.⁴ We include the use of multiple dipole sources with temporally and spatially varying centers and orientations, an anatomically realistic representation of the torso anatomy as well as not restricting our calculations to only one component of the magnetic field.^10,23

METHODS

The volume conductor model used in the simulations consisted of an anatomically realistic torso model constructed from visible human project data.^6,32 Magnetic fields were calculated at a plane of sensors located external to the torso using a number of different dipole source configurations. From these magnetic fields, SCD maps were derived. The position of the maximum SCD value is believed to provide an estimate of the location of the underlying dipole sources. By tracking this maximum point, the position and velocity of the underlying source was estimated in the plane of the sensors and directly compared to the parameters of the actual dipole sources. Here, we analysed the magnitude and orientation of velocity separately.

Dipole Sources

In this simulation study, each gastric slow wave was assumed to be represented by a single dipole source with a temporally moving center and orientation. The dipole source configurations used included single static dipoles, a single realistic dipole, and a sequence of overlapping realistic dipoles that represented multiple slow waves present in the stomach. The realistic dipoles were derived from biophysically based simulations of gastric slow wave activity.

Initially, a number of simple static dipole source configurations were used to improve our understanding of the relationships between the dipole position and orientation and their effects on the resultant magnetic field and the SCD maps. The static dipoles were positioned at five locations overlaying the corpus and the antrum of the stomach at two separate depths (75 mm and 150 mm from the sensor plane). The dipoles were also prescribed to be orientated in each of the three orthogonal planes, resulting in a total of 30 different dipole configurations.

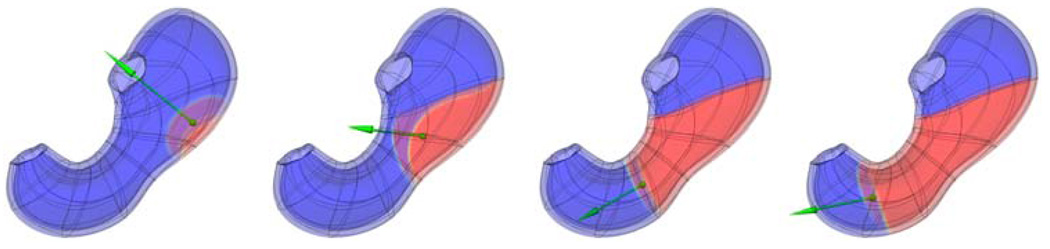
Next, a single temporally and spatially varying dipole source was derived from a previously described simulated gastric slow wave activity.^12,13,27 Figure 1 illustrates the simulated gastric slow wave originating at the mid-corpus area and propagating down the stomach to the antrum. The location, magnitude, and direction of the dipole source (shown the by the green arrow) has been derived from the gradient of the transmembrane potential.² Only the depolarization phase of the slow wave was assumed to contribute to the dipole source (the repolarization phase of the slow wave is commonly assumed to be negligible in numerical simulations).

FIGURE 1.

Simulation of normal GEA propagating down the length of the stomach and the corresponding equivalent dipole source (green arrow). Shown are the slow wave solution and the equivalent dipole source at four time instances. The gastric slow wave starts in the mid-corpus region and propagates distally toward the pylorus. The equivalent dipole source tracks the wave front (the transition between the blue and red zones) down the length of the stomach.

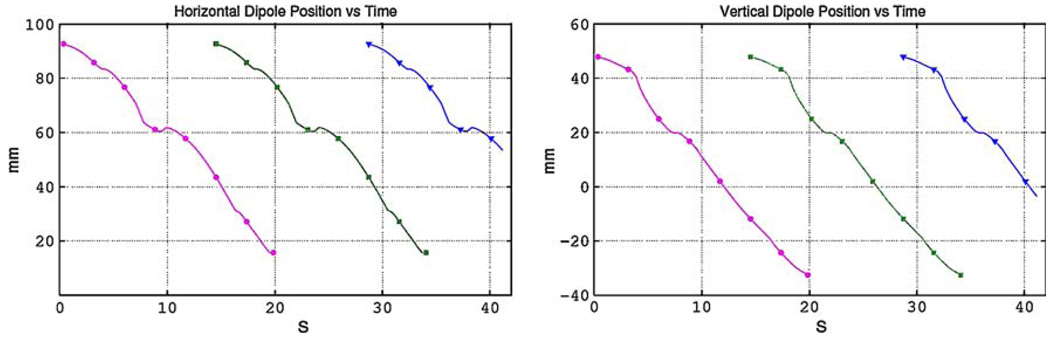
Recent studies using a large number of serosal and/or mucosal measurements have shown that multiple slow waves can be present in the stomach at one point in time.^15,25 The presence of multiple waves or sources can greatly affect the resultant far field magnetic and electric fields. For this reason, the final dipole configuration used in our simulation study was a sequence of dipole sources that was based on the previously described single realistic dipole source. In this sequence, a new source initiated in the mid-corpus area prior to the previous source terminating at the pylorus. (i.e., when a dipole was approximately 75% down the length of the stomach a subsequent source initiated in the mid-corpus region). The positions of these dipoles are illustrated in Fig. 2.

FIGURE 2.

Illustration of the spatial–temporal position of a sequence of dipoles. Shown are the (a) vertical and (b) horizontal positions of the sources over time for three slow waves. The second and third sources initiate at the mid-corpus region prior to the termination of the previous source at the antrum. Each dipole source overlaps the previous source by approximately 25%.

Magnetic Field Calculations

The magnetic field (B) resulting from a dipole source in a conducting medium comprised two components as shown in Eq. (1).

$$\mathbf{B}={\mathbf{B}}_{\mathrm{d}}+{\mathbf{B}}_{\mathrm{v}}$$ (1)

where B_d is the magnetic field due to the dipole itself and B_v is the magnetic field due to the volume current in the body. Often B_d is referred to as the primary source and B_v is referred to as the secondary source.

The calculation for the primary dipole source is relatively simple and is given by Eq. (2),

$${\mathbf{B}}_{\mathrm{d}}(r_f)={\mu }_0\frac{\mathit{\rho }\times \mathbf{r}}{4\pi r^3}$$ (2)

where μ₀ is the permittivity in free space, ρ is the dipole magnitude, r is the vector between the dipole center and the field point (r_f) and r is the absolute distance of r.

The calculations of B_v are more complex, especially when the volume conductor is not an idealized shape. With the use of simplified geometries (e.g., sphere, cylinder, or infinite half planes), the calculations for B_v can be reduced to certain algebraic relations.^4,30 In many studies, the volume conductor effects have been totally ignored.²⁹ In our study, we used a realistic torso model^10,23 and explicitly calculate the volume conductor effects via the use of Eq. (3).

$${\mathbf{B}}_{\mathrm{v}}(r_f)=-\frac{{\mu }_0}{4\pi }{\displaystyle \sum _{j=1}^n{\sigma }_j}{\displaystyle \underset{{\mathrm{\Omega }}_j}{\int }\mathrm{\nabla }\varphi (r_{\mathrm{d}})\times \frac{\mathbf{r}}{r^3}d{\mathrm{\Omega }}_j}$$ (3)

where B_v(r_f) is the magnetic field at field point r_f, n is the total number of surfaces surrounding regions of different conductivity, j identifies a surface of a region with assumed constant conductivity σ_j and boundary defined by Ω_j and φ(r_d) is the potential on the surface due to a dipole located at r_d.

Each of the dipole sources described previously was then embedded into the torso model and used to compute the magnetic fields on a hypothetical SQUID magnetometer as described in Bradshaw et al.⁴ This sensor comprised a regular array of 11 × 16 sensors with a separation of 20 mm between each sensor. The SQUID array was centered over the stomach just above the anterior surface of the torso as shown in Fig. 3.

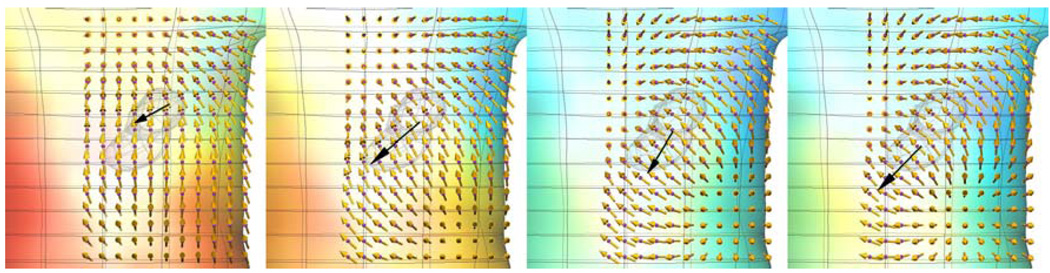
FIGURE 3.

Magnetic fields (gold arrows) at 176 sensor locations external to the torso model. The lengths of the arrows correspond to the magnitudes of the magnetic fields. Each of the maps corresponds to the GEA shown in Fig. 1. The larger dark arrow shows the dipole source position and orientation.

Figure 3 shows the magnetic field maps calculated from the corresponding single realistic dipole source shown in Fig. 1. The colored surface shows the magnitude of the potential fields on the torso (red positive potential and blue negative potential) and gold arrows show the magnetic field at the sensor locations. The directions of the arrows indicate the direction of the magnetic field and the lengths of the arrows correspond to the magnitude of the magnetic field. The larger black arrow shows the same dipole source as illustrated in Fig. 1.

SCD Method

The magnetic fields calculated by Eq. (1) were then used as input for the SCD method to estimate the location of the underlying source. The SCD method was initially proposed by Hosaka and Cohen²⁰ and Cohen and Hosaka¹⁶ and is computed essentially by taking the curl of the magnetic field as given in Eq. (4) where the vector J represents the surface current density.

$$\mathbf{J}=\frac{1}{{\mu }_0}\mathrm{\nabla }\times \mathbf{B}$$ (4)

In fact, there is no current density at the sensor location and as the curl of the magnetic field is zero. However, the nonzero current density values can be related to current running under the surface parallel to the sensor plane.¹⁸

The SCD values were calculated at each of the sensor locations using a finite difference approximation. The SCD maps were then visualized as vector maps representing the components of the SCD or the components combined to provide amplitude maps plotting the amplitude of the SCD values. The vector maps have been shown in simple simulations to approximate those currents under the surface which produced the field and the maps attempt to reveal characteristics about the underlying sources.¹⁶ The location of the maxima in the SCD maps has been shown (when not significantly “corrupted” by the volume current) to correspond to the location of a dipole source.^4,16 By tracking the maximum point in a sequence of maps it is believed that the location of the underlying source can be estimated as well as an estimate of a propagation velocity.

It should be noted that most SQUID magnetometers are only designed to record the magnetic fields in the orientation normal to the volume conductor. When used to analyze gastric signals, usually only the magnetic field in the direction radial to the anterior surface of the torso (denoted as B_z) is considered. In most cases, the B_x and B_y terms are therefore neglected in the estimation in the SCD calculations^18,22,31 and the calculations are reduced to only taking the spatial derivative of one magnetic field component as shown in Eq. (5).

$$\mathbf{J}=\left[\frac{1}{{\mu }_0}\left(\frac{\partial B_z}{\partial y}\right)\right]\cdot e_x-\left[\frac{1}{{\mu }_0}\left(\frac{\partial B_z}{\partial x}\right)\right]\cdot e_y$$ (5)

where e_x and e_y are unit vectors in x and y directions, respectively.

However, in our simulations, the magnetic field was not restricted to a setup determined by a SQUID magnetometer. Therefore, it was possible to evaluate all three components of the magnetic field in a high density grid and estimate the SCD using both Eqs. (4) and (5).

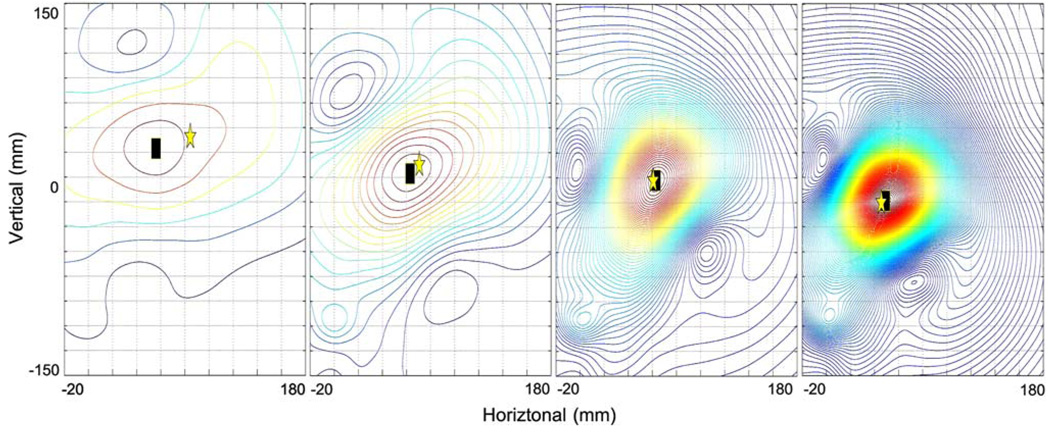
Figure 4 shows SCD maps derived using Eq. (4) from the magnetic fields shown in Fig. 3. The SCD values have been interpolated over the entire sensor plane using a cubic spline function. The contour lines show the pattern of the magnitude of the SCD maps. The maximum amplitude of the SCD map has been highlighted by the black square and provides an estimate of the projected location of underlying source in the plane of the sensors. This can be compared to the projected position of the actual dipole source position as indicated by the yellow star. By tracking the source positions over time, the velocity of the source in the plane of the sensors can also be estimated. It should be emphasized that the existing method is only able to resolve parameters in the same plane as the sensors (in our case the coronal plane) and thus only provides an estimate of position and velocity projected onto this coronal plane. This means that the estimated parameters will ignore any information regarding depth position (in the z direction).

FIGURE 4.

Contour plot of the surface current density (SCD) maps corresponding to the magnetic field maps presented in Fig. 3. The maximum point of the SCD map (black square) shows the estimated location of the underlying dipole source. The location of the actual dipole source is indicated by the gold star.

RESULTS

We investigated the accuracy of using the SCD method for resolving the source position and velocity (magnitude and orientation separately) using three main types of dipole configurations. The accuracy of the method when using the full magnetic field and the magnetic field component normal to the body (B_z) were also compared.

Simple Static Dipoles

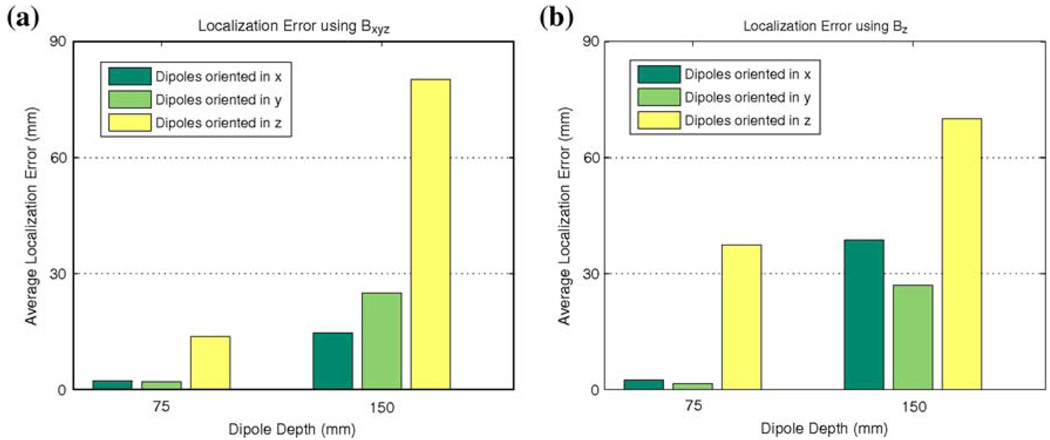
The dipole sources were prescribed to be located at five locations (in x–y plane) overlaying the corpus and antrum at fixed depths of 75 and 150 mm from the sensor plane. The dipoles were also prescribed to be oriented at three orthogonal positions aligned with the Cartesian axes. The results of the average localization error of the SCD estimates are illustrated in Fig. 5. The localization error was averaged over five locations at each depth and orientation. It can be clearly seen that larger errors result when with the source is located further from the sensor (and therefore located more centrally within the abdomen). In addition, significantly larger errors resulted when the dipole was oriented in the z direction (orthogonal to the sensor plane). In this orientation, the primary source contribution to the magnetic field will be zero, meaning the full magnetic field was due to the secondary source. In this situation, the SCD maps will have an indirect relationship to the location of the underlying dipole source. When all three magnetic field directions were used, more accurate results were generally obtained except when the dipole was oriented in the z direction and located at a depth of 150 mm. Therefore, the distance of the dipole sources from the sensors is not the only factor affecting the accuracy of the estimated location of dipole sources. The orientation of the dipole sources relative to the sensors also has a significant effect upon the accuracy of the SCD estimate.

FIGURE 5.

Average projected localization error for simplistic dipoles at different depths and orientations using (a) the full magnetic field B_xyz and (b) only the B_z component. Results show that when the dipole was closer to the sensor, the error was relatively low for all orientations. When the dipole was oriented orthogonal to the sensor plane (in the z direction) largest errors resulted at all depths as the full magnetic field was only due to the secondary source and SCD maps therefore have an indirect relationship to the location of underlying dipole source.

Single Realistic Dipole

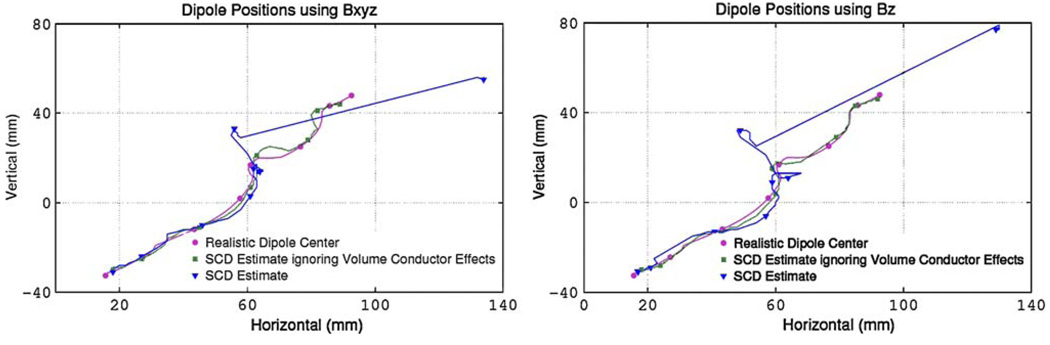
Localization results corresponding to the single realistic dipole source shown in Fig. 1 are presented in Fig. 6 and Table 1. The results shown in Fig. 6 compare the location of the realistic dipole center (circles and purple trace), the SCD estimate (triangle and blue trace), and the SCD estimate ignoring the volume conductor effects (square and green trace) in the coronal plane. In the plot, the dipole paths begin in the top right corner and end in the bottom left corner as the dipole propagated down the length of the stomach. The markers show the solutions at 3-s intervals. Note that the case where the volume conductor was ignored is only possible in a simulation as in actual SQUID experiments the volume conductor effects cannot be ignored. This result provides an indicator of the amount the volume conductor distorts the maximum position of the SCD values. When the volume conductor did not distort the magnetic fields, the source had an average localization error in the plane of the sensors of less than 4 mm and an average magnitude of velocity error of less than 1 mm/s in the plane of the sensors when using either the full magnetic field or B_z. Results showed that the volume conductor effects had a significant effect on the SCD estimates on the dipole source position for t = 1–10 s as denoted by the large differences in dipole position and velocity. During the second half of the slow wave cycle (10–20 s), dipole parameters were estimated relatively accurately. Similar results were obtained whether either all three magnetic field components were used to calculate the SCD (Eq. 2) or when only the B_z magnetic field component (Eq. 3) was used.

FIGURE 6.

Comparisons of realistic dipole center (purple circle) and estimated dipole location using an SCD estimate (blue triangle) and when ignoring the volume conductor effects (or assuming a free-space model) (green square). The dipole position initiates in the top right of the graph and progresses toward the bottom left corner over a period of 20 s (markers show the solutions at approximately 3-s intervals). The left plot shows the results when using the full magnetic field to estimate the SCD and the right plot when only the B_z was used. The values calculated using the free-space model do not include the volume conductor effects and cannot be measured in real life. The large errors using the torso model have resulted from the large distortions in the magnetic field due to the volume conductor effects.

TABLE 1.

Errors in estimating projected location, magnitude of velocity, and orientation of the dipole source using the full magnetic field and B_z when using the single realistic dipole.

Time (s)	Estimation error using Bxyz	Estimation error using Bz
Projected location (mm)
1–10	21 ± 15	26 ± 15
10–20	3 ± 2	6 ± 3
Projected magnitude of velocity (mm/s)
1–10	8 ± 41	11 ± 48
10–20	0 ± 3	0 ± 7
Projected orientation (°)
1–10	64 ± 45	57 ± 45
10–20	18 ± 33	25 ± 25

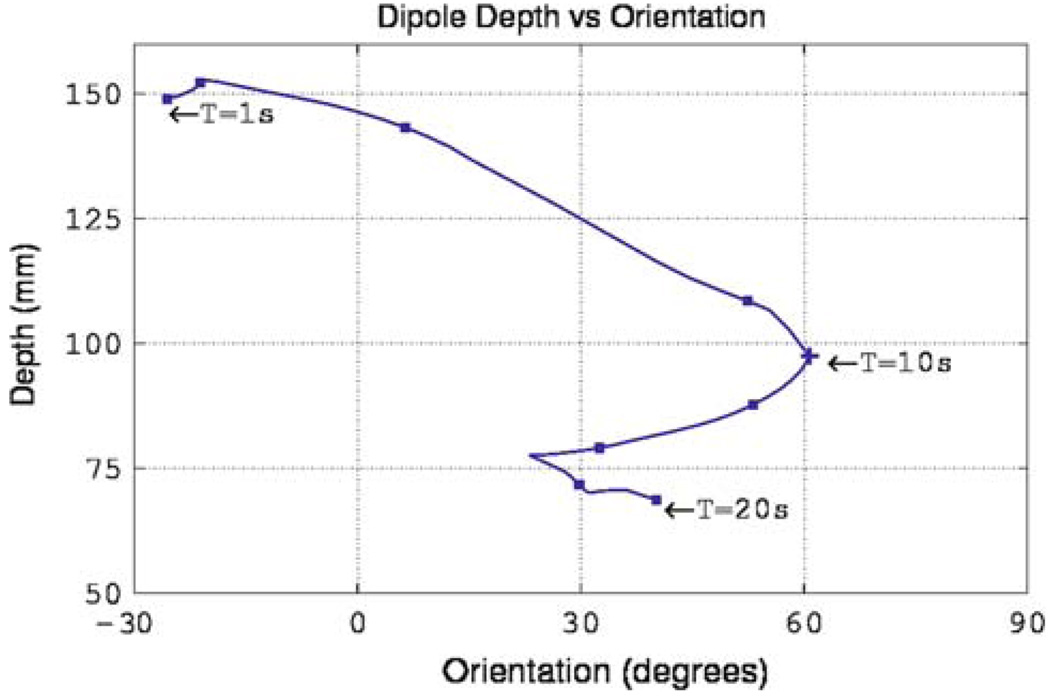
The results shown in Fig. 6 and Table 1 can be partially explained by analyzing the position of the dipole over time and its orientation relative to the coronal plane. Figure 7 depicts the angle of the dipole relative to the coronal plane at each point of the cycle. In first half of the simulation the dipole was always located at a distance greater than 100 mm from the sensors and as a result large inaccuracies occurred in the estimated dipole parameters. This is evident by examining the large errors (Table 1) corresponding to the first half of the cycle. Although the second half of the cycle contained dipole orientations of up to 60° relative to the sensor plane it was always located at distances less than 100 mm from the sensors and as such dipole position was estimated relatively accurately.

FIGURE 7.

Variation of depth and orientation of the single realistic dipole source (as presented in Fig. 1 and Fig. 6) over one slow wave cycle. The source initiates at the mid-corpus region of the stomach (located furthest from the sensor) and progresses toward the antrum (located closest to the sensor) while the dipole orientation oscillates between −30° and 60° through the cycle.

Multiple Realistic Dipoles

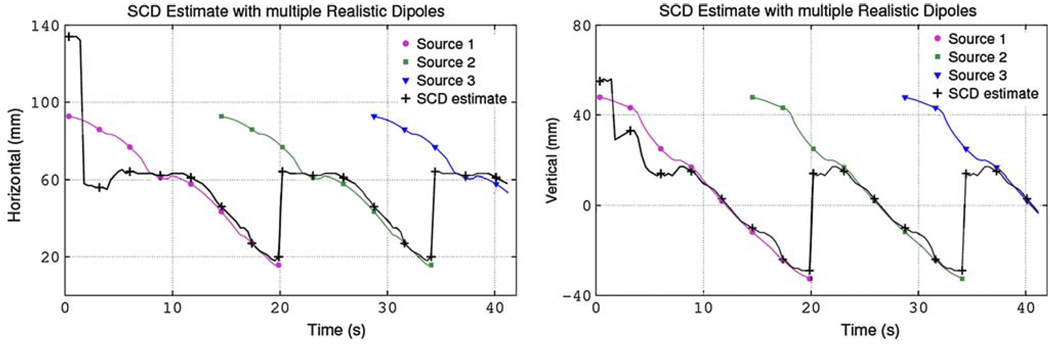
A sequence of repeating slow waves was used to provide a more realistic representation of normal gastric electrical activity. This repeated sequence was based upon the single realistic dipole previously described but a new dipole was introduced every 15 s prior to the previous dipole terminating in the pylorus. Table 2 shows a comparison between the estimated and actual source positions when multiple dipoles are present when using either the full magnetic field or only B_z. The same results when using the full magnetic field to calculate the SCD values are plotted in Fig. 8. Results showed that in the presence of multiple sources (between 15–20 s and 30–35 s) the SCD map had one maximum corresponding to the dominant distal source due to its proximity to the sensors. Once the dominant source terminated at the pylorus, parameters corresponding to the proximal source were then able to be estimated. When the full magnetic field was used the projected dipole position was located on average to within 5 mm. The average projected velocities were accurate to within 1 mm/s when either the full magnetic field or only B_z were used.

TABLE 2.

Errors in estimating the projected location, magnitude of velocity, and orientation of the dipole closest to the sensor when using the full magnetic field and B_z when using the train of dipoles.

	Estimated error using Bxyz	Estimated error using Bz
Projected location (mm)	4 ± 4	7 ± 4
Projected magnitude   of velocity (mm/s)	1 ± 3	1 ± 6
Projected orientation (°)	28 ± 36	32 ± 32

FIGURE 8.

Estimates of the dipole source position (black) when a sequence of overlapping dipole sources (purple circle, green square, blue triangle) was present. Shown are (a) the horizontal position and (b) the corresponding vertical position against time (markers indicate solutions at approximately 3-s intervals). The result for the first 15 s (when only one source is present) is identical to the single realistic dipole simulation. In the presence of multiple sources, the proximal source (located close to the sensors) dominated and this point corresponded to the maximum point in the SCD map. Once the proximal source terminated at the pylorus, the parameters corresponding to the distal source were estimated.

DISCUSSION

We have presented the application of the SCD method to simulated magnetic field data calculated using an anatomically realistic geometry, and a temporally and spatially varying dipole source derived from a biophysically based slow wave simulation. Using the simulated magnetic field data, estimates about the location, velocity, and orientation of the underlying sources were made.

Results have shown that the SCD method was able to resolve gastric slow wave parameters such as the projected location and velocity from external magnetic fields when the dipole was located within 100 mm of the sensor. In these cases, the dipole position was able to be resolved to within 4 mm and the magnitude of velocity was resolved to within 1 mm/s. Significantly larger errors resulted when the dipole was located further from the sensor and when the dipole orientation approached an angle normal to the sensor plane due to the relatively smaller contribute of the primary source compared to the source from the volume conductor. This suggests that the body habitus of the patient is likely to be an important factor in determining how accurately these parameters can be resolved. It is likely that only patients who have a normal or low body mass index could be positioned within 100 mm of the sensor, and therefore the theoretical accuracy of the SCD method would be relatively diminished for patients with a larger body habitus, and particularly in those patients with significant truncal obesity. Many patients with gastric motility disorders are relatively thin due to food intolerance, meaning that the majority of the population of gastric motility patients could benefit from the methods developed here. It has been shown that the method was unable to distinguish different sources when multiple sources were present in the stomach. When simultaneous sources were present in the proximal and distal stomach, the distal source (located significantly closer to the sensors) dominated and the parameters corresponding to this source were resolved. Once the distal source terminated at the pylorus, the parameters corresponding to the second proximal source could be obtained. In general, the estimated parameters were more accurate when all three magnetic field components (B_xyz) were used. However, it remains questionable, in this case, whether the use of more complex vector channels justifies the slight increase in accuracy.

The simulations have included a number of assumptions or simplifications to what can be measured in reality. However, the findings provide an indication of the possible utility of such methods to be able to characterize the slow wave activity using noninvasive measurements. We have assumed that each gastric slow wave can be represented as a single dipolar source. A distributed source model would possibly provide a better presentation of the underlying activity. However, this will add additional complexities to the models, especially if multiple slow waves must be represented in the stomach at any time. Although the magnetic fields have been calculated using a realistic shaped torso model, it was a homogeneous model and the conductivity effects of the muscle and fat layers will have some effect upon the resultant magnetic fields. However, it is anticipated that these effects will be much smaller than those observed by the electrical potential fields. In addition, we have used a hypothetical SQUID sensor with a much higher spatial resolution than is currently in existence. In the near future it is unlikely that there will be a SQUID for gastrointestinal studies with such a high spatial resolution and coverage. We have also assumed that there is no error in the positioning of the SQUID relative to the torso. This is a challenging task to achieve when taking real measurements with a SQUID. However, in most situations localization of the SQUID relative to the torso is unlikely to have errors larger than 10 mm and any positional errors will have a linear effect on any estimated parameters.

Another major limitation of the SCD method was its ability to able to only determine gastric parameters corresponding to the same plane as the sensors (in this case the coronal plane). This can particularly hinder the accuracy of results if the main axis of the stomach and corresponding slow wave activity happens to be primarily oriented in the anterior–posterior direction. Any movement in the direction normal to the sensor plane would largely be silent to this method. The inclusion of additional sensors in the different orientations such as the sagittal plane or in a semi-circle around the torso may help to alleviate this problem.

In conclusion, the SCD method provides a computationally efficient method for noninvasively estimating slow wave parameters. In situations where the distorting effects of the magnetic field from the volume conductor is known to be relatively small, then the slow wave position can be estimated in the plane of the senor to within 4 mm.