Mechano-Chemical Feedbacks Regulate Actin Mesh Growth in Lamellipodial Protrusions

Abstract

During cell motion on a substratum, eukaryotic cells project sheetlike lamellipodia which contain a dynamically remodeling three-dimensional actin mesh. A number of regulatory proteins and subtle mechano-chemical couplings determine the lamellipodial protrusion dynamics. To study these processes, we constructed a microscopic physico-chemical computational model, which incorporates a number of fundamental reaction and diffusion processes, treated in a fully stochastic manner. Our work sheds light on the way lamellipodial protrusion dynamics is affected by the concentrations of actin and actin-binding proteins. In particular, we found that protrusion speed saturates at very high actin concentrations, where filament nucleation does not keep up with protrusion. This results in sparse filamentous networks, and, consequently, high resistance forces on individual filaments. We also observed maxima in lamellipodial growth rates as a function of Arp2/3, a nucleating protein, and capping proteins. We provide detailed physical explanations behind these effects. In particular, our work supports the actin-funneling-hypothesis explanation of protrusion speed enhancement at low capping protein concentrations. Our computational results are in agreement with a number of related experiments. Overall, our work emphasizes that elongation and nucleation processes work highly cooperatively in determining the optimal protrusion speed for the actin mesh in lamellipodia.

Introduction

Cell migration plays an important role in such biological phenomena as embryonic development, wound healing, and immune response. The crawling motion of cells is a complex and dynamic process that involves the protrusion of the leading edge of a cell, adhesion to the substratum, generation of traction to move cell body, and the subsequent release of adhesions (1,2). Actin-based protrusion of the cell leading edge is the first step in cell locomotion, which relies on the force generated from polymerizing actin filaments to push the cell membrane forward. The sheetlike membrane protrusion structures along the leading edge of motile cells, such as fish epithelial keratocytes, are called lamellipodia. These cells are an excellent model system to study actin-based motility due to the simplicity of their geometry and persistent and fast motion (3–6). A lamellipodium is composed of dendritically branched actin filaments, which elongate through polymerization at their barbed ends and in which new filaments nucleate at ∼70° angles from the existing filaments (4,7). Hence, the dendritic nucleation/array treadmilling model (7,8) has been commonly used as the conceptual model of lamellipodial protrusion; however, force generation and regulation in lamellipodial protrusion is yet to be fully elucidated in microscopic detail.

Despite the complexity of actin-based motility, a reconstituted in vitro system with purified actin and just a few types of regulatory proteins could reproduce motility (9). Therefore, it should be feasible to construct simple, physically based computational models with a relatively small number of components to study actin-based motility. Hence, mathematical modeling and computer simulations have been essential in advancing the understanding of these processes (10–12). In particular, many computational models have been developed to study lamellipodial protrusion (13–22). Carlsson (15,16) developed a stochastic simulation method to study the growth of branched networks against rigid obstacles. Rubinstein et al. (17) performed multiscale, two-dimensional numerical modeling of the crawling cell using a finite element approach, in which their simulation could reproduce the canoelike shape of fish keratocytes. Schaus et al. (13) developed a two-dimensional computational model to study the dendritic nucleation/array treadmilling process, which incorporates elastic filaments and a flexible membrane as well as their interactions. Atilgan et al. (18) performed theoretical and computational study of the morphology of the lamellipodium, where their three-dimensional simulations showed that the spatial orientation of Arp2/3 is important for the formation of a filamentous network.

Despite significant progress made by the prior computational studies on lamellipodial protrusion, modeling was carried out on a coarse level of detail, where important microscopic interactions might have been overlooked. In our work, we study lamellipodial protrusion dynamics using a state-of-art stochastic simulation model, which treats actin filaments and various regulatory proteins at a microscopic level of detail in three-dimensional space. To the best of our knowledge, this model provides the most detailed treatment of fundamental physico-chemical interactions underlying lamellipodial dynamics. Our model integrates essential biochemical regulation processes as well as the mechanical aspect of actin polymerization, in which the interactions between the actin filaments and the flexible membrane are taken into account. In our simulations, the system is discretized into compartments in which monomeric species stochastically hop between the neighboring compartments. The spatially resolved reaction-diffusion stochastic simulations were implemented using the Gillespie algorithm (23–26).

The primary goal of our work was to understand how lamellipodial protrusion is affected by the various factors that regulate the actin filament elongation and nucleation processes. The interplay between the elongation and the nucleation of actin filaments is expected to subtly control actin-based motility; however, this effect is not fully understood. To address this interplay, we examined lamellipodial protrusion as actin concentration and Arp2/3 concentration were varied. Growth of the branched network is characterized by the protrusion speed of the model lamellipodia and the nucleation rate of filaments. We found that filament elongation and nucleation work cooperatively to control actin-based protrusion.

First, increasing actin concentration facilitates both the elongation and nucleation of filaments, but the rate of nucleation cannot keep up with the polymerization rate, and this leads to decreasing density of the filamentous network. The imbalance between polymerization rate and nucleation rate leads to inefficient motion as indicated by the diminishing growth of protrusion speed when actin concentration is increased.

Second, the protrusion speed varies with Arp2/3 concentration in a nonmonotonic way, which is of great interest. Our results indicate that the nucleation process is facilitated by Arp2/3, but maximal protrusion speed is achieved at some optimal Arp2/3 concentration. From our simulation results, we conclude that achieving a balance between polymerization and nucleation rates is central to producing maximal protrusion speeds.

Furthermore, capping protein is another key player in regulating actin-based motility. Capping proteins block the polymerization of filaments by competing with actins for the free barbed ends, thereby preventing the elongation of actin filaments. The role of capping proteins was unclear, as it had been found that they may actually promote actin-based motility; however, the mechanism behind this has been controversial (27–29). To address this question, we used stochastic simulations to investigate the dependence of the protrusion speed on capping proteins concentrations. Our simulations show that capping proteins indeed can promote actin-based motility. We investigated what physical processes are responsible for this effect, and found that, on average, there is an increase of the number of monomeric actin molecules as capping protein concentration increases. Higher G-actin concentration, in turn, favors both the polymerization and the nucleation processes, resulting in the promotion of protrusion rate. However, at excessive capping protein concentrations, the filament network density along the leading edge drops significantly, resulting in 1), higher resistance forces on individual filaments, and 2), smaller fraction of filaments with free barbed ends, where both of these effects lead to diminution of polymerization rates. The competition between increasing monomeric actin concentration and the latter two processes produces the maximum of protrusion speed as the capping protein concentration is upregulated.

Methods: A Stochastic Physico-Chemical Model of Lamellipodial Protrusion

Although deterministic reaction-diffusion description of the actin-based motility system offers important insights into the lamellipodial protrusion dynamics, a more fundamental description is based on stochastic chemical kinetics. A small copy number of molecules per elementary reaction volume produce discrete noise (30–38), which may be accounted by the master equation formalism. Thus, we have carried out stochastic simulations of lamellipodial protrusion using the spatially resolved version of the Gillespie algorithm (23–26). Fig. 1 a provides a schematic illustration of our model.

Figure 1.

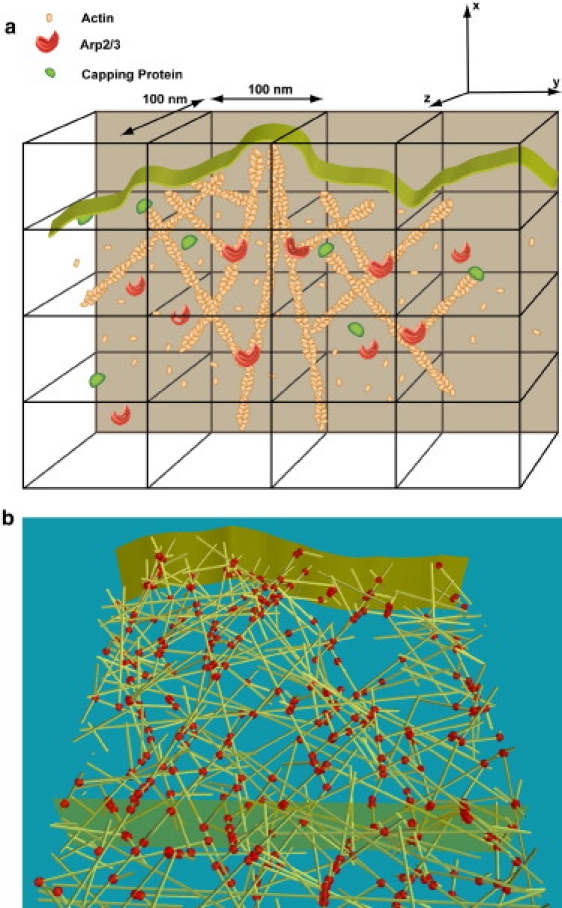
(a) Schematic drawing of our lamellipodial model is shown. (b) A snapshot from the simulation output showing the branched filamentous network. During simulation, both the front and the back of the membrane (shown as ribbons) move, and the region between them is the active reaction front. Filaments (shown as narrow tubes) are branched with branching points (shown as spheres; i.e., nucleated by Arp2/3 binding).

The simulation region where lamellipodia growth takes place is partitioned into compartments, whose size is determined from the so-called Kuramoto length (39), which is the typical length over which a molecule diffuses before reacting. We used a compartment size of 100 nm in our simulations, somewhat smaller than estimated Kuramoto length ≈450 nm (see Supporting Material for more details). Partitioning of the simulation region into compartments provides for computational efficiency, while the discreteness of the physical system is accurately taken into account. This technique has been successfully applied in the studies of stochastic dynamics of filopodial growth (25,26). In this model, molecules are tracked based on the compartment in which they are located. Molecules may randomly hop (diffuse) between neighboring compartments, while reactions may occur in individual compartments, with propensities determined by the number of reactants at any particular moment in time. Both diffusive and reaction events are stochastically chosen according to the Gillespie algorithm (23,24). In each Gillespie step, possible reactions that occur include (de)polymerization, (de)branching, and (un)capping. More details, including the rates of reactions and diffusion, are elaborated upon in the Supporting Material.

Growing filaments generate force to push the membrane, and depending on the assembly regulation factors, different membrane protrusion structures may be generated (40). According to the Brownian ratchet model (41), the rate of polymerization is dependent on actin concentration as well as the force acting on the filaments: $k_{\text{on}}\left[\text{A}\right]e^{-w/k_{\text{B}}T}$, where k_on is the polymerization rate constant, [A] is actin concentration, w is the mechanical work done in order for an actin monomer to be added to the filament, and k_BT is the thermal energy. In our simulations, filaments are typically no more than a few microns in length, much shorter than the persistence length (∼16 μm (42)) of actin filaments; therefore, we assume all filaments are straight. Given the orientational angles (θ, φ) of a filament, adding an actin monomer of size δ elongates the filament by δ sin(θ)cos(φ) along the motion direction x. The value δ is set to be 2.7 nm, which is half of the size of an actin monomer (5.4 nm) because actin filaments are double-stranded, and adding two monomers is equivalent to increasing the length of a filament by the size of one monomer. It should be noted that unlike the Brownian ratchet model, the mechanical work w for individual polymerizing filaments are unequal in our simulation.

Nucleation of new filaments is an integral part of the treadmilling process. We consider Arp2/3-mediated nucleation of new filaments from sides of preexisting filaments (43). Arp2/3 is one of the most important molecules in actin filaments assembly (43,44). We do not incorporate the upstream activation process of Arp2/3 explicitly in our model, but instead consider the activation zone, similar to prior works (13,15). In this model, nucleation events take place in a narrow band behind the plasma membrane, where N-WASP, which is an Arp2/3 activator, is localized (43). The width of the activation zone in our simulation is set to 10 nm, the size of a few actin monomers. The nucleation process generally involves an actin filament, G-actin(s), a nucleation promoter (for example, N-WASP), and Arp2/3 (10,44). Although N-WASP is not explicitly included in our model, its effect is included implicitly, assuming that N-WASP is uniformly distributed just below the membrane. Thus, Arp2/3 is activated only within a narrow zone near the membrane. There is no clear consensus in the literature to whether zero, one, or two G-actins are necessary for the Arp2/3-mediated nucleation of the filaments. Several prior computational works were based on two-G-actin activation (19,45,46). However, a recent experiment suggested that one G-actin is involved in branching nucleation (47). In this work, we assume that for Arp2/3 to nucleate a new filament, it needs to bind to both a G-actin and a filament. We have also considered the branching mechanism in which Arp2/3 binding to two actins is needed for a branching to occur, and found that, qualitatively, our results are not sensitive to the specifics of the number of actins involved in branching.

When a nucleation reaction occurs on a specific site of a preexisting filament, the orientation of the new filament is chosen in a random but biased way to mimic the experimentally observed pattern of filamentous network. Specifically, if the preexisting filament is defined by a unit vector ${\widehat{r}}_1$ (pointing from the pointed-end to the barbed-end of the filament), then the new filament unit vector ${\widehat{r}}_2$ satisfies ${\widehat{r}}_1\times {\widehat{r}}_2=\text{cos}\left(\alpha \right)$, where the branching angle is α = 70 ± 7°, in accordance with experimental data (7). In our simulations, the angle α was taken from the Gaussian distribution with the average 70° and the variance 7°; a random orientation around ${\widehat{r}}_1$ was chosen from the uniform distribution to make ${\widehat{r}}_2$ unique in three-dimensional space. Our simulations show that filamentous network generated in this way can be highly ordered with filaments predominantly pointing to the plasma membrane at the angles centered at ∼±35°, with respect to the leading edge; this is in agreement with experiments (7).

The actin filament network is enclosed by a plasma membrane. The interactions between the cytoskeleton and membrane have important consequences such as providing directionality to guide the actin polymerization process and determining cell shape (48). Mathematical modeling of membrane dynamics incorporating the interaction between the membrane components and actin polymerization showed that various protrusions could possibly form (49–51). Polymerizing actin filaments apply the needed force on membrane, pushing it forward. We model this mechanical process by introducing an effective steric repulsion between the membrane and the actin filaments. As elaborated in Supporting Material, the membrane Hamiltonian includes membrane-bending and surface-tension components. An additional external field acting on membrane is used to mimic attractive interactions between the filaments and the membrane due to possible tethering, as well as growth against an external obstacle and the effect of the plasma membrane tension. The physical confinement of the membrane by actin filaments is modeled by a repulsive potential. A harmonic potential is used to enforce periodic boundary conditions on the membrane. During a simulation, when the membrane is perturbed by the filaments due to polymerization, the equilibrium membrane configuration is obtained by minimizing the Hamiltonian.

We ran each simulation starting from some initial set of short filaments with random orientations and at a number of specific molecular concentrations for various species. To achieve a desired concentration for some particular species (actin, Arp2/3, and capping protein), the rear part of the lamellipodia is coupled to a bulk reservoir, whose concentrations are all kept fixed. The effect of this coupling in our stochastic simulations is analogous to imposing a boundary condition in deterministic reaction-diffusion equations (e.g., G-actin is consumed in front and is resupplied from the rear, establishing a concentration gradient; for an example of the concentration gradient, see Fig. S1 in Supporting Material). By adjusting the exchange rate between the bulk and diffusive part at the interface of these two parts, we can obtain different molecular concentrations as desired. When possible, we used physiologically relevant parameters in our simulations, but the goal of our numerical simulations was not necessarily to reproduce a specific experiment on lamellipodial protrusion; instead, it was to enable us to understand the trends controlling the protrusion behavior. We recorded the time trajectories of the position of the traveling front of the model lamellipodia and the number of filaments in the mesh, from which we calculated the steady-state protrusion speed and the rate of nucleation, the main kinetic quantities of interest. Data were typically averaged over 32 simulation runs, which also allows the computation of corresponding variances. A three-dimensional visualization of a single trajectory is available as Movie S1 in the Supporting Material.

Results and Discussion

Actin concentration dependence of the filamentous network growth

Actin is the building block of filaments, and its availability is key to the efficient assembly of filaments. However, actin's effect on growth is nontrivial because lamellipodial protrusion involves the growth of many individual filaments with different lengths and orientations. It is generally known that polymerization is faster at higher actin concentration, as illustrated in the Brownian ratchet mechanism. However, it would be interesting to see in what specific way varying actin concentration affects the three-dimensional lamellipodial filamentous network, including the growth dynamics, morphology, and distribution of regulatory proteins. To our knowledge, this has not been studied in depth before. To study this, we ran simulations at a range of monomeric actin concentrations and examined the protrusion speeds and nucleation rates. To help us understand the observed trend of protrusion speed saturation at high actin concentrations, we also carried out simple mean-field analysis, using quantities averaged over multiple simulation trajectories. It turned out that these rough estimates capture the main features of actin-mesh protrusion-speed dependence on actin concentration and shed light on cooperative processes controlling lamellipodial growth dynamics.

Our results show that both the protrusion speed and the nucleation rate grow with actin concentration, as expected. The extent of increase, however, is diminished at higher actin concentration (Fig. 2). To understand this, we need to examine both the elongation and nucleation processes of the filaments. In our model, the nucleation of a new branch requires a filament on which the daughter filament grows—an activated Arp2/3 and an actin monomer. Actin plays the role of facilitator for nucleation process, so the rate of nucleation increases with the actin concentration. When bulk actin concentration is increased, the rate of nucleation saturates, as can be seen from Fig. 2 b, and the nucleation process is now limited by the availability of Arp2/3, whose bulk concentration is kept constant. From the concentration gradient profiles, we derived the local concentrations of Arp2/3 and actin near the membrane, where nucleation occurs. It was found that with increasing bulk G-actin concentration, the concentration of G-actin near membrane increases correspondingly, but there is a steady decrease of local Arp2/3 concentration near the membrane (Fig. S2). The abundance of actins favors fast nucleation, which tends to deplete Arp2/3. Due to its low abundance, Arp2/3 concentration is affected to a greater extent than that of actin during filamentous network growth despite G-actins being consumed at higher rate by both the polymerization and nucleation processes. Thus, the nucleation is limited by the availability of Arp2/3. The filamentous network density becomes smaller at high actin concentration due to the saturation of nucleation. To illustrate this, in Fig. 3 a, we made a plot of the density of filaments along the leading-edge membrane. Clearly, there is a decreasing filament density along the leading edge with higher actin concentration: filament density along the leading edge decreases ∼30% when bulk actin concentration is increased from 5 μM to 50 μM. Because the membrane is supported by the filaments, filaments in a sparse network have to carry a greater load than those in a dense network. The actin concentration and the load on the polymerizing filaments are key quantities controlling polymerization rate. In particular, the polymerization rate is expected to increase with actin concentrations but decrease with the load. This tells us that despite the linear dependence of polymerization rate on actin (k_on[A]), the higher load experienced by filaments (the term $e^{-w/K_{\text{B}}T}$ decreases) diminishes the growth of protrusion speed. Thus, by varying actin concentration we have identified the correlations between protrusion dynamics and the network morphology. In Fig. 4, the dependence of average load and average local concentration of actin available for polymerization on actin concentration are shown, and a mean-field protrusion speed $\langle \left[\text{A}\right]\rangle e^{-\langle w\rangle /K_{\text{B}}T}$ is then calculated. The protrusion speed calculated from relevant averaged quantities in polymerization captures well the trend of protrusion speed obtained from simulations (see Fig. S3).

Figure 2.

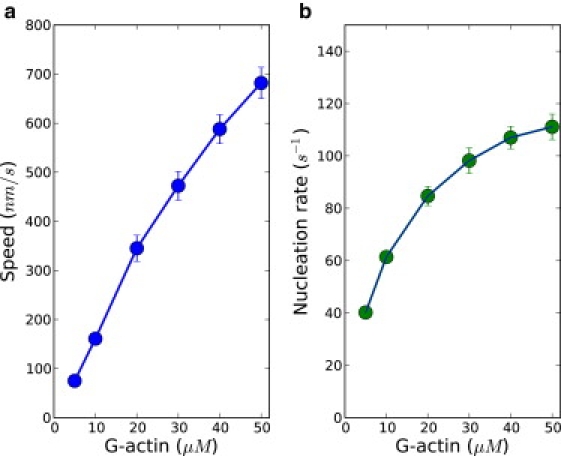
Actin concentration-dependence of (a) the protrusion speed and (b) the nucleation rate is shown. The concentrations of Arp2/3 and capping proteins were kept at 50 nM.

Figure 3.

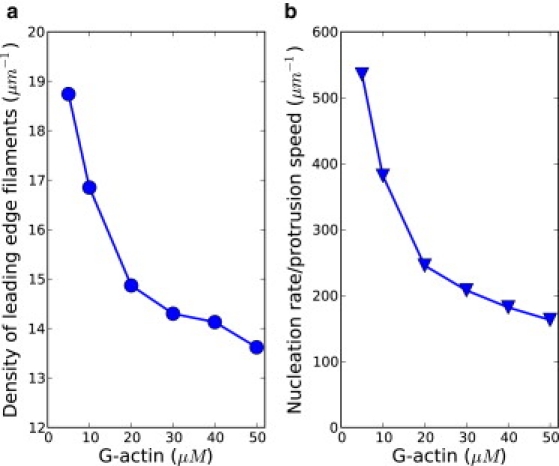
(a) Density of filaments along protrusion leading edge is shown as a function of G-actin concentration. Leading-edge filaments are defined as those close to the membrane (with distance no larger than 2.7 nm, the effective size of one monomeric actin). (b) The ratio of the nucleation rate to the protrusion speed (i.e., the density of new filaments) is shown. The curve indicates that new filament density decreases with actin concentration.

Figure 4.

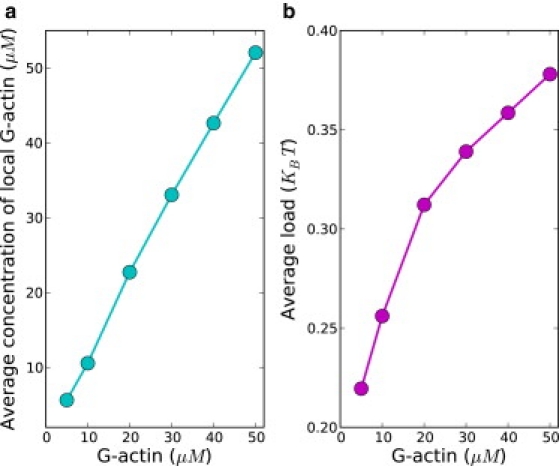
(a) Average local concentration [A] of monomeric G-actins available for polymerization near the membrane is shown as a function of G-actin concentration in the rear of the reaction front (i.e., bulk G-actin concentration). Local actins are these actins within the particular compartment in which a polymerization event occurs. (b) The average load 〈w〉 experienced by polymerizing filaments as a function of rear G-actin concentration. The load w diminishes the polymerization rate through the term $e^{-w/K_{\text{B}}T}$.

We have used both the protrusion speed and the rate of nucleation to characterize the growth of the filamentous network. The ratio of the nucleation rate versus the protrusion speed is in fact simply an indicator of the density of filamentous network. However, this density is related to the number of newly generated filaments per unit length, not the density of the total number of filaments. From Fig. 3 b, we can see that this ratio decreases with actin concentration. That is, the change of nucleation rate cannot keep up with the change of protrusion speed, so the filamentous network would become less dense at higher actin concentrations. Thus, we have shown microscopically how the dynamics of protrusion and the nucleation of filaments are affected by actin concentration at constant bulk Arp2/3 concentration.

It should be noted that at even higher G-actin concentrations of ∼10² μM, the protrusion speed would gradually saturate (data not shown). We do not explore this regime as such high concentrations may not be physiologically reasonable, and also because the system may be out of the quasi-steady-state region when the polymerization rate becomes much higher than the diffusion rate.

Arp2/3 dependence of the filamentous network growth

In the preceding section we studied the dependence of the protrusion speed on actin concentration, having shown that it monotonically increases, although it is saturating at high actin concentrations. We next investigate how the protrusion behavior depends on the nucleation. Our results indicate that for each actin concentration, there exists an optimal Arp2/3 concentration, at which the protrusion speed is maximal (Fig. 5).

Figure 5.

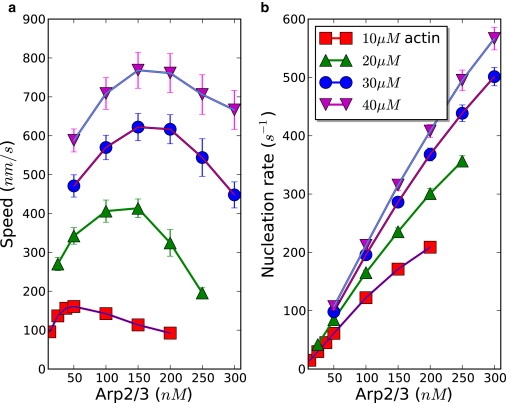
(a) Arp2/3 concentration dependence of the protrusion speed at different actin concentrations is shown. There exists an optimal Arp2/3 concentration at which the protrusion speed is maximal. (b) The nucleation rate grows with Arp2/3 concentration.

In absence of Arp2/3, there wouldn't be steady movement because of the lack of new filament generation, which is key to the successful treadmilling process. Suppose that Arp2/3 concentration is kept low such that the nucleation rate is low, and the filamentous network is sparse, then there would not be enough generated filaments to push the membrane and, consequently, slow motion is expected. On the other hand, if the concentration of Arp2/3 is so high that a large number of filaments are rapidly generated, the filamentous network would be dense and a large number of actin filaments would quickly deplete the monomeric G-actin pool. Thus, on average, the number of polymerization reactions per filament becomes small in this limit, resulting in slow protrusion.

Therefore, there should exist an optimal Arp2/3 concentration, at which the protrusion speed is maximal. The plot of the protrusion speed versus Arp2/3 concentration in Fig. 5 clearly confirms this. Following the analysis procedure performed in the preceding section, we illustrate the results with average local concentration of actin and average load. Protrusion speeds derived from these averaged quantities show the nonmonotonic dependence of protrusion speed on Arp2/3 concentration (see Fig. S4), indicating that protrusion dynamics could be estimated from simple mean-field analysis.

Our results, derived from microscopic simulations, are qualitatively consistent with the theoretical analysis of the optimal filament density presented by Mogilner and Edelstein-Keshet (52), in which they studied the relationship between the motion speed and the number of leading edge filaments using a set of deterministic reaction-diffusion partial differential equations. Their results indicated that tuning of parameters is important for effective motility (52). To have optimal motion, balanced elongation and nucleation of filaments is needed. Nonmonotonic dependence of motion speed on Arp2/3 concentration has also been observed in the experimental study of Listeria and Shigella movement in vitro (27). In addition, a nonmonotonic behavior was reported from the Brownian dynamics simulations of the movement of a flat disk in a solution of particles (53). However, our model of lamellipodia system is based on Brownian ratchet mechanism, whereas the work by Lee and Liu (53) studied the motility in the framework of self-diffusiophoresis, in which the forces driving cell motility are fundamentally different than assumed in our work and in the prior literature (13–16,18,52). In this light, the similarity of conclusions needs to be carefully evaluated for being either a robust feature of the physical system or a simple coincidence.

The dependence of the nucleation rate on both Arp2/3 and actin concentrations is shown in Fig. 5 b. When both concentrations of actin ([A]) and Arp2/3 ([R]) are sufficiently small, the rate of nucleation would be proportional to each concentration: k_nucl = $k_{\text{nucl}}^{\text{0}}$[R][A], where $k_{\text{nucl}}^{\text{0}}$ is the rate constant of nucleation. In our simulation, actins are abundant. At a given Arp2/3 concentration, the nucleation rate converges and tends to saturate when the actin concentration becomes higher. For the actin-saturated system, the nucleation rate is linearly dependent on Arp2/3 concentration, as can be seen from Fig. 5 b. The rate of nucleation can be approximately written as k_nucl = k_{nucl, eff}[R]. A simple linear fit of the curve (data corresponding to 40 μM actin in Fig. 5 b) gives the effective nucleation rate constant k_{nucl, eff} ≈ 2 nM⁻¹ s⁻¹. It should be noted that the linear regime of the Arp2/3 concentration-dependence of the nucleation rate is valid for relatively small Arp2/3 concentrations. At sufficiently high Arp2/3 concentrations, nucleation should saturate with Arp2/3 because of the limited number of branching sites within the activation zone, with protrusion speeds being relatively low in this regime.

The role of capping proteins

Lamellipodial protrusion is driven by the polymerizing free barbed ends of filaments. It is critical to keep a sufficient number of uncapped filaments to maintain the steady growth of the filamentous network. Hence, the protrusion behavior may be regulated by controlling the number of filaments with free barbed ends. Capping proteins compete with actins for free barbed ends, playing a central role in regulating cell motility.

The growth of filamentous network would be stalled when the concentration of capping protein is so high that nearly all the barbed ends are capped: such a regime is not particularly interesting. However, the regime in which capping protein concentration is modest might be of interest. Recently, in an experimental study with the reconstituted in vitro motility system containing polystyrene beads, it was found that capping protein increases the rate of actin-based motility (29). This surprising result was interpreted to be the consequence of capping protein promoting filament nucleation (29). Motivated by this experiment, we set out to investigate whether capping protein can promote nucleation of filaments in our computer simulations.

Our simulations indicate that capping proteins can indeed promote actin-based motility. In Fig. 6, a plot of the dependence of protrusion speed on capping protein concentration is given. The data shows that lamellipodial protrusion speed is increased when capping proteins are added relative to the case without capping proteins. Concurrently with the enhancement of protrusion speed, there is also an increase of the nucleation rate. Therefore, our simulations indicate that there is a correlation between capping protein promoting motility and facilitating nucleation.

Figure 6.

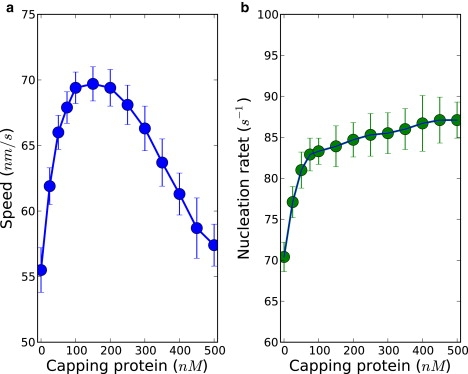
Capping proteins promote actin-based motility. There exists an optimal capping protein concentration at which the protrusion speed is maximal. The rate of nucleation grows with increasing capping protein concentration, being as it is correlated with the increase in protrusion speed. The concentrations of actin and Arp2/3 were kept at 5 μM and 100 nM, respectively.

To see why capping proteins promote the protrusion and the nucleation, we investigated various factors controlling the polymerization process. In particular, one might expect that the protrusion speed would depend on the average local concentration of G-actins available for polymerization, the fraction of uncapped filaments, and the average load on polymerizing filaments. Our simulations indicate that with higher capping protein concentration, on average, there is an increase of the number of monomeric actins available for polymerization. At the same time, the load on polymerizing filaments increases as well (see Fig. 7). The latter is caused by the decreasing density of filaments along the leading edge, due to the action of capping proteins (Fig. 8); this then causes the capped filaments to lag behind.

Figure 7.

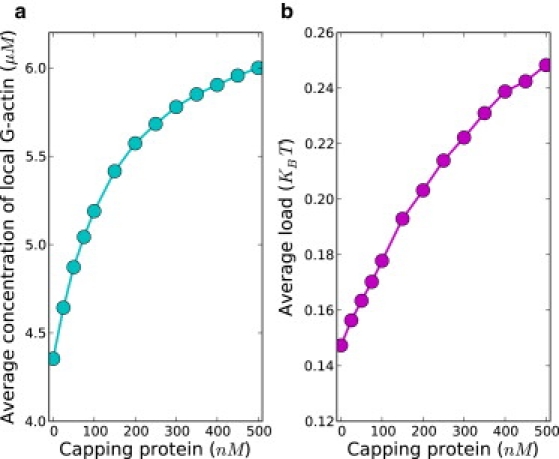
Average local concentration [A] of monomeric G-actins available for polymerization and average load on filaments along the leading edge is shown.

Figure 8.

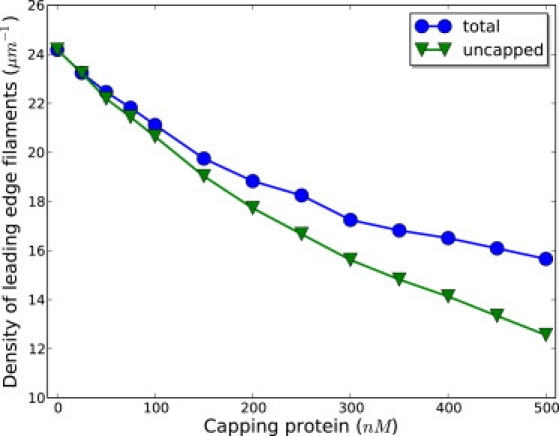
Density of filaments along the leading edge, some of which are uncapped, is shown. Both densities decrease with increasing capping protein concentration. The fraction of uncapped filaments also decreases with capping protein concentration (data not shown).

It turns out that the increase of the local concentration of monomeric actins and higher load on polymerizing filaments does not fully explain the nonmonotonic behavior of the protrusion speed as a function of capping protein concentration. These two terms are not sufficient to explain the role of capping proteins because they only account for the $k_{\text{on}}\left[\text{A}\right]e^{-w/k_{\text{B}}T}$ term, which is the polymerization rate for a single polymerizing filament when it is not capped. However, one needs to explicitly consider the difference between uncapped filaments and capped filaments in that the uncapped filaments not only provide mechanical support for the membrane, but also consume actins, although the capped filaments only provide mechanical support. Thus, to fully incorporate the effect of capping proteins, the probability p of a leading edge filament being uncapped needs to be taken into account, which is approximately the ratio of uncapped filaments to the total number of filaments along the leading edge. The ratio of uncapped filaments grows with higher capping protein concentration, as can be deduced from Fig. 8. Obviously, if all the filaments are capped, protrusion would be stalled. When capping proteins are introduced, both the load and the percentage of uncapped filaments terms are unfavorable to the protrusion, but the increasing actin concentration term is favorable. Hence, the promotion of protrusion at low capping protein concentrations is due to the increasing local concentration of monomeric actins available for polymerization. Protrusion speed calculated from the averaged quantity $p\langle \left[\text{A}\right]\rangle e^{-\langle w\rangle /K_{\text{B}}T}$ captures well the behavior of protrusion speed obtained from simulations (see Fig. S5).

Capping proteins enhancing actin-based motility is an interesting phenomenon. In this work we have applied detailed three-dimensional stochastic simulations to identify the main factor that causes the increase of the protrusion speed. We have shown that with capping proteins, there are more monomeric actins available for polymerization on average, leading to the faster protrusion at low capping protein concentrations. Although the nucleation rate is also enhanced, many filaments become capped and lag behind the leading edge, resulting in a diminution of the filament density near the leading edge. Our result is consistent with the actin-funneling hypothesis (28), and also provides an explanation for why capping proteins promote the nucleation processes (29). There are some interesting questions left unanswered. For example, it is still not clear what the maximal protrusion speed enhancement might be that could be achieved by introducing capping proteins. In addition to further studies examining the effect of capping proteins, it will also be useful to perform modeling that incorporates anticapping proteins such as Ena/VASP, which may play a key role in determining the morphology and dynamics of cell migration (5,54,55).

Conclusion

In this work we have investigated lamellipodial protrusion dynamics using a physically based computational model. Our three-dimensional stochastic simulation model is simple but powerful and allows us to study various factors that affect the protrusion behavior. We compared the protrusion speeds with the ones calculated from relevant averaged quantities in polymerization processes, and showed that such a mean-field analysis is useful for qualitatively interpreting the protrusion behavior.

We have examined how the growth of the filamentous network depends on actin, Arp2/3, and capping proteins. We found that protrusion speed grows with increasing actin concentration, but the growth rate diminishes at very high actin concentrations. This is explicated by the increased load on individual filaments due to the decrease in filament density at high growth rates, where nucleation does not keep up with protrusion. We also found that lamellipodial protrusion speed depends nonmonotonically on Arp2/3 and on capping protein concentrations. Our results indicate that optimal tuning of the polymerization and nucleation rates is essential for achieving highly efficient protrusion. We have shown that capping protein can promote actin-based motility. By studying the factors controlling the polymerization process, we found that the promotion of protrusion speed relative to the case of no capping proteins is mainly due to increase in the availability of the number of monomeric actins, providing support for the actin-funneling hypothesis.

Our computational model could be further enhanced by incorporating the flexibility of the filaments. A representation of the membrane configuration with a two-dimensional surface instead of the one-dimensional curve would also enhance model's realism. The interplay between actin filaments elongation and nucleation factors is essential in actin-based cell motility (44). In this work, we have included only the minimal number of regulatory proteins. Future work on models incorporating upstream regulators of nucleation activation as well as anticapping proteins should be carried out to further elucidate physical mechanisms behind actin-based lamellipodial protrusion. In addition, ADF/cofilin are key regulatory proteins that promote the disassembly of actin filaments behind the leading edge (8): it would be interesting to study, using a three-dimensional stochastic model, how the severing processes affect the lamellipodial protrusion dynamics and the actin network morphology.

Supporting Material

One table and five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)06151-7.