Folding Intermediate and Folding Nucleus for I→N and U→I→N Transitions in Apomyoglobin: Contributions by Conserved and Nonconserved Residues

Abstract

Kinetic investigation on the wild-type apomyoglobin and its 12 mutants with substitutions of hydrophobic residues by Ala was performed using stopped-flow fluorescence. Characteristics of the kinetic intermediate I and the folding nucleus were derived solely from kinetic data, namely, the slow-phase folding rate constants and the burst-phase amplitudes of Trp fluorescence intensity. This allowed us to pioneer the ϕ-analysis for apomyoglobin. As shown, these mutations drastically destabilized the native state N and produced minor (for conserved residues of G, H helices) or even negligible (for nonconserved residues of B, C, D, E helices) destabilizing effect on the state I. On the other hand, conserved residues of A, G, H helices made a smaller contribution to stability of the folding nucleus at the rate-limiting I→N transition than nonconserved residues of B, D, E helices. Thus, conserved side chains of the A-, G-, H-residues become involved in the folding nucleus before crossing the main barrier, whereas nonconserved side chains of the B-, D-, E-residues join the nucleus in the course of the I→N transition.

Introduction

The protein folding pathways include transition states and, in most cases, accumulation of intermediate states. The characterization of the folding mechanism requires our examining the structures and energetics of the stable intermediate (I) states and of unstable transition states (TS).

For the last decade and a half, structural studies of the transition states were mainly focused on small proteins with a two-state folding/unfolding mechanism, i.e., without accumulated intermediate states (1–13).

The transition states of proteins with a multistep folding/unfolding pathway are not very popular objects of study, because they require determination of the rates of all folding/unfolding steps over a wide range of denaturant concentrations. Besides, early intermediates are formed too rapidly to be measured directly; rather, their presence affects the visible rate constant of the native (N) state formation (14).

Currently, there is only one tool for experimental structural studies of the transition state (Φ-analysis by Fersht; see (1)), which uses Tanford's chevron plots (15) and point mutations for identification of residues whose replacement proves to be crucial for the protein folding rate and leaves its unfolding rate almost unaffected. Namely, these residues form the protein-folding nucleus, i.e., the structured part of the transition state (1,2). It should be emphasized that the Φ analysis has nothing to do with the transition state topology but only informs us about the strength of interactions between side chains of the residues in the transition state. In addition, it should be noted that the energy barrier may be counted from the I state (for the rate-limiting I→N transition) or from the unfolded (U) state (in the U→I→N transition). Depending on the transition type (I→N or U→I→N), Φ-values are different for a given amino acid in one and the same transition state, because for the I→N transition, the interactions, already fixed in the I state, do not contribute much to the residue's Φ-value. However, these interactions do contribute to Φ-values estimated for the U→I→N transition—an important peculiarity that arises in interpreting the folding nuclei of multistate proteins.

To overcome this difficulty, some modifications of the initial approach from Fersht (1,2) have been used. For example, some authors (16–21) analyzed the transition state structure, taking

$$\Phi =1-\Delta \Delta G_{\left(\text{TS}-\text{N}\right)}/\Delta \Delta G_{\left(\text{U}-\text{N}\right)},$$

whereas the initial form from Fersht (1,2) is

$$\Phi =\Delta \Delta G_{\left(\text{TS}-\text{U}\right)}/\Delta \Delta G_{\left(\text{N}-\text{U}\right)}\text{.}$$

Here, ΔΔG_(TS-N) is a change in TS free energy after mutation relative to N yielded by unfolding kinetics experiments (whereas ΔΔG_(TS-U) is obtained from folding kinetics), and

$$\Delta \Delta G_{\left(\text{U}-\text{N}\right)}\text{value}\left(\equiv -\Delta \Delta G_{\left(\text{N}-\text{U}\right)}\right)$$

is a change in stability of U relative to N after the introduced mutations, as derived from equilibrium unfolding experiments. However, this approach is applicable only when almost no accumulation of the intermediate state is observed in the mutant during equilibrium unfolding. If otherwise, the value of ΔΔG_(U-N), and hence the Φ value, is erroneous.

Importantly, the determination of ΔG from equilibrium experiments can contain rather large errors. These result from the presence of an equilibrium intermediate distorting the observed transition curve, which is responsible for inaccurate determination of the equilibrium ΔG.

Another approach was reported in our previous article (22). It allows estimating energetic parameters of the intermediate state and the main transition state for a protein with one rapidly forming intermediate from kinetics data, i.e., from the rate constants and amplitudes of the burst kinetic phase. When applied to mutant forms, it derives the Φ parameter solely from folding/unfolding kinetics data. This approach, unlike the traditional analysis, allows an independent determination of f_I, and consequently of k_IN values (see details in Materials and Methods).The only prerequisite to its applicability is a general condition of validity of the Φ-analysis (1,2): the absence of mutation-induced crucial changes in the folding pathway or folding nucleus or in the native state structure.

The stopped-flow analysis of apomyoglobin (apoMb) folding/unfolding kinetics is focused on the apoMb transition state that forms on the barrier between the native state and the intermediate state. Apomyoglobin is a single-domain protein with a molecular weight of 17 kDa. Its helical structure is formed by A–E, G, and H helices, whereas its F helix remains unfolded until the heme becomes bound. Properties of apoMb are well studied (23–27). ApoMb has a tertiary structure typical of holomyoglobin; it is capable of undergoing a heat-induced cooperative transition that is accompanied by significant changes in its enthalpy and heat capacity. The folding process of urea-unfolded apomyoglobin involves one kinetic intermediate state that is structurally close to an equilibrium intermediate I accumulating at pH 4.2, which includes A, G, H helices, as shown by nuclear magnetic resonance (NMR) (28). In addition, the I state may also include fragments of B, C, D, and E helices under certain conditions (29,30). The existence of such an obligatory on-pathway intermediate was reported previously (31,32).

This article describes folding/unfolding kinetics of apoMb and its 12 mutant forms over a wide range of urea concentrations, which allowed identifying residues responsible for protein stability and for the rate of its native structure formation. It shows a strong destabilization of the native (folded) state of the mutant proteins as compared with the wild-type form, and a relatively minor influence of the mutations on stability of the intermediate state relative to the unfolded one. It is shown that residues belonging to the A, G, H helical complex contribute to stability of the intermediate state and to that of the folding nucleus in the U→I→N transition, whereas in the I→N transition, the apoMb folding nucleus is formed after formation of the A, G, H helical complex mostly by residues pertaining to B, C, E helices.

In this article, we are the first to report an estimate of Φ values obtained for the same rate-limiting barrier that exists in both I→N and U→I→N transitions of apomyoglobin.

Materials and Methods

Apomyoglobin and its investigated point mutants

We used wild-type (WT) apoMb and its 12 mutants. Six of the substituted (by Ala) residues are conserved in the globin family, but not involved in heme binding: V10, W14 (A helix), I111, L115 (G helix), M131, and L135 (H helix). These have been pointed out by Shaknovitch et al. (33) and Ptitsyn and Ting (34) as being important for initiation of apoMb folding. The other six are nonconserved residues, but they play a key role in free energy landscape-based computer simulations of apoMb folding (35): I28, F33 (B helix), L40 (C helix), M55 (D helix), and L61, L76 (E helix). They have a large number of contacts in the native structure comparable with that of conserved residues (see Samatova et al. (36) and Fig. 4).

Figure 4.

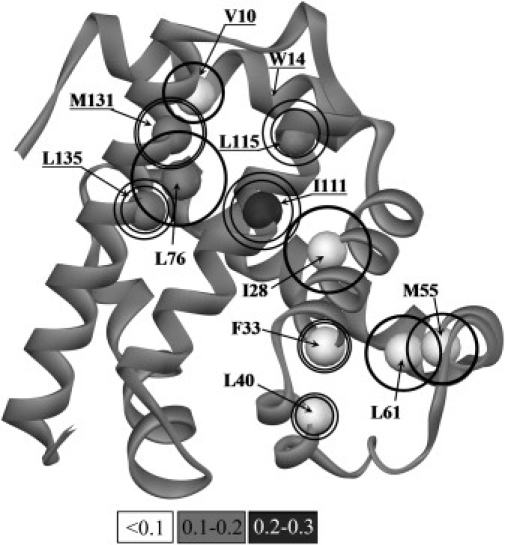
The sperm whale apomyoglobin fold (adapted from (48)). The studied residues are shown as spheres; their color intensity (see the scale below the figure) is proportional to the Φ_I value, i.e., to the extent of their side-chain involvement in the intermediate state I (according to both kinetic and equilibrium data). The outer circles are proportional to the Φ_TS(UN) value, the extent of involvement of side chains of these residues in the folding nucleus in the U→N transition; the inner circles are proportional to the Φ_TS(IN) value, the extent of involvement of side chains in the folding nucleus in the I→N transition. Labels of conserved nonfunctional residues of A, G, H helices are underlined.

Expression and isolation

Plasmids with mutant apoMb genes were constructed by polymerase chain reaction with the plasmid pET17 (a kind gift of P.E. Wright) containing the sperm whale apoMb gene, appropriate primers, and using a QuikChange (Stratagene, La Jolla, CA) kit (37). WT apoMb and its mutants were isolated and purified as described previously (22,37) after expression of appropriate plasmids in Escherichia coli BL21 (DE3) cells.

The protein purity was checked by SDS/PAGE electrophoresis. Protein concentration was determined spectrophotometrically from absorbance at 280 nm using the extinction coefficient $A_{280}^{0.1\%}$ = 0.80 for all samples (36,38), except for one Trp-lacking mutant with substitution W14A; for this one, the used extinction coefficient was determined from nitrogen-based measurements according to Jaenicke (39) and appeared $A_{280}^{0.1\%}$ = 0.56 (36).

Equilibrium studies of urea-induced denaturing transitions

All fluorescence and far ultraviolet (UV) circular dichroism (CD) measurements were carried out at 11°C; 0.01 M sodium acetate, pH 6.2, was used as a buffer system (40).

Equilibrium protein fluorescence measurements were taken on a model No. RF-5301 PC spectrofluorimeter (Shimadzu, Kyoto, Japan) using standard 1-cm path-length quartz cuvettes. The excitation wavelength was 293 nm. The emission spectra were recorded between 300 and 500 nm (with a special attention to the emission intensity at 335 nm (I₃₃₅)) at a protein concentration of 0.03 mg/mL.

A model No. J-600 spectropolarimeter (JASCO, Oklahoma City, OK) was used to perform CD experiments. Far UV CD spectra were measured between 200 and 250 nm using 0.1-mm path-length cells. The protein concentration was 1.0 mg/mL. Molar ellipticity [θ] was calculated as

$$\left[\theta \right]=\theta \times \text{MRW}/l\times c,$$

where θ is measured ellipticity (degree, 10⁻³); MRW is the average molecular weight of a residue calculated from the sequence; l is the path length (mm); and c is protein concentration (mg/mL).

Kinetic studies

Kinetic measurements were taken using a home-made spectrofluorimeter equipped with a stopped-flow attachment as described earlier (22). The excitation wavelength was 293 nm, and emission spectra were recorded using 320-nm cut-off glass optical filter. The dead time of the equipment was <<20 ms. All measurements were taken at 11°C, pH 6.2. The final protein concentration was 0.03 mg/mL. The initial urea concentration was 5.5 M for folding experiments, and 0.0 M for unfolding ones. The initial protein solution was mixed (1:6) with buffer of various urea content using the stopped-flow attachment. All obtained kinetic curves were well described (after the dead-time burst phase) by a single-exponential approximation. Kinetic data were repeated twice for two independently prepared solutions, and there were 3–4 sequential mixings for each point.

Determination of the population of the kinetic intermediate I

The kinetic intermediate population among the nonnative states, i.e., f_I(M) = [I]/([I] + [U]), where [I] and [U] are concentrations of the I and U states, was determined at various urea concentrations M from the burst phase fluorescence amplitude,

$$f_{\text{I}}\left(\text{M}\right)=\frac{A\left(\text{M}\right)-A_{\text{U}}\left(\text{M}\right)}{A_{\text{I}}\left(\text{M}\right)-A_{\text{U}}\left(\text{M}\right)},$$ (1)

where A_U(M) and A_I(M) are the integral fluorescence intensities for U and I states, and A(M) is the integral fluorescence intensity achieved as a result of the first, burst (U→I) phase in the (U→I) transition in protein folding at the given final urea concentration M.

Calculation of folding rates, free energies, and Φ-values for the transition and intermediate states

The rate constant k_IN of the second (slow as compared to the U→I) folding transition I→N across the major (rate-limiting) barrier between the native and intermediate states was calculated according to the literature (22,41,42), as follows:

$$k_{\text{IN}}\left(\text{M}\right)=\frac{k_{\text{obs}}\left(\text{M}\right)-k_{\text{NI}}\left(\text{M}\right)}{f_{\text{I}}\left(\text{M}\right)}\text{.}$$ (2)

Here f_I(M) is the kinetic intermediate population calculated from Eq. 1; k_obs is the observed rate constant for approaching equilibrium; and k_NI is the rate constant for the unfolding transition N→I.

To calculate free energies of the intermediate (G_I) and native (G_N) states relative to that of the unfolded (G_U) state from the folding/unfolding kinetics, the following equations were used (22):

$$\Delta G_{\text{IU}}\equiv G_{\text{I}}\left(\text{M}\right)-G_{\text{U}}\left(\text{M}\right)=-RT\times \text{ln}\frac{f_{\text{I}}\left(\text{M}\right)}{1-f_{\text{I}}\left(\text{M}\right)},$$ (3)

$$\Delta G_{\text{NI}}\equiv G_{\text{N}}\left(\text{M}\right)-G_{\text{I}}\left(\text{M}\right)=-RT\times \text{ln}\frac{k_{\text{IN}}\left(\text{M}\right)}{k_{\text{NI}}\left(\text{M}\right)}\text{.}$$ (4)

Here k_NI is the rate constant for the unfolding transition N→I dictated solely by the highest free energy barrier between N and I states (i.e., k_NI = k_NU) (22), k_IN is the rate constant for the folding transition I→N given by Eq. 2, and

$$\Delta G_{\text{NU}}\equiv G_{\text{N}}\left(\text{M}\right)-G_{\text{U}}\left(\text{M}\right)=\Delta G_{\text{NI}}+\Delta G_{\text{IU}}\text{.}$$ (5)

Involvement of a side chain of a given residue in the folding intermediate or folding nucleus was calculated using Φ-analysis (43). The value of

$${Ф}_{\text{I}}=\frac{\Delta (G_{\text{I}}-G_{\text{U}})}{\Delta (G_{\text{N}}-G_{\text{U}})}=\frac{\Delta (\Delta G_{\text{IU}})}{\Delta (\Delta G_{\text{NU}})}$$ (6)

(where Δ before parentheses means a difference between values in parentheses for WT apoMb and its mutant form) reflects involvement of the substituted residue in the folding intermediate I. The value of

$${\text{Ф}}_{\text{TS}\left(\text{IN}\right)}=\frac{\Delta (G_{\text{TS}}-G_{\text{I}})}{\Delta (G_{\text{N}}-G_{\text{I}})}=\frac{\Delta \left(\text{ln}\left(k_{\text{IN}}\right)\right)}{\Delta \left(\text{ln}(k_{\text{IN}}/k_{\text{NI}})\right)}$$ (7)

describes the increment of involvement of the substituted residue side chain in the folding nucleus corresponding to the I→N transition, and the value of

$${\text{Ф}}_{\text{TS}\left(\text{UN}\right)}=\frac{\Delta (G_{\text{TS}}-G_{\text{U}})}{\Delta (G_{\text{N}}-G_{\text{U}})}={\text{Ф}}_{\text{TS}\left(\text{IN}\right)}\times (1-{\text{Ф}}_{\text{I}})+{\text{Ф}}_{\text{I}}$$ (8)

shows total involvement of the side chain of this residue in the same folding nucleus corresponding to the whole the U→N transition.

We also used the well-known three-state expressions (see, e.g., the article by Parker et al. (44)) on chevron plot fitting.

Results and Discussion

Equilibrium urea-induced denaturing transitions of apomyoglobin and its mutants

Urea-induced equilibrium unfolding of the designed mutants was studied by far UV CD and by Trp fluorescence to learn the effect of these mutations on conformational stability of apomyoglobin and to find conditions favorable for formation of the native, unfolded, and intermediate states.

Fig. 1 shows changes in molar ellipticity at 222 nm (Fig. 1 a) and in Trp fluorescence at 335 nm (Fig. 1 b) for WT apoMb and for its representative mutants in dependence on urea concentration. The complete set of experimental data for all the mutants is presented in Fig. S1 in Supporting Material. As seen, the N→U transition of the WT form appears more cooperative than that of the mutants and occurs at a higher urea concentration.

Figure 1.

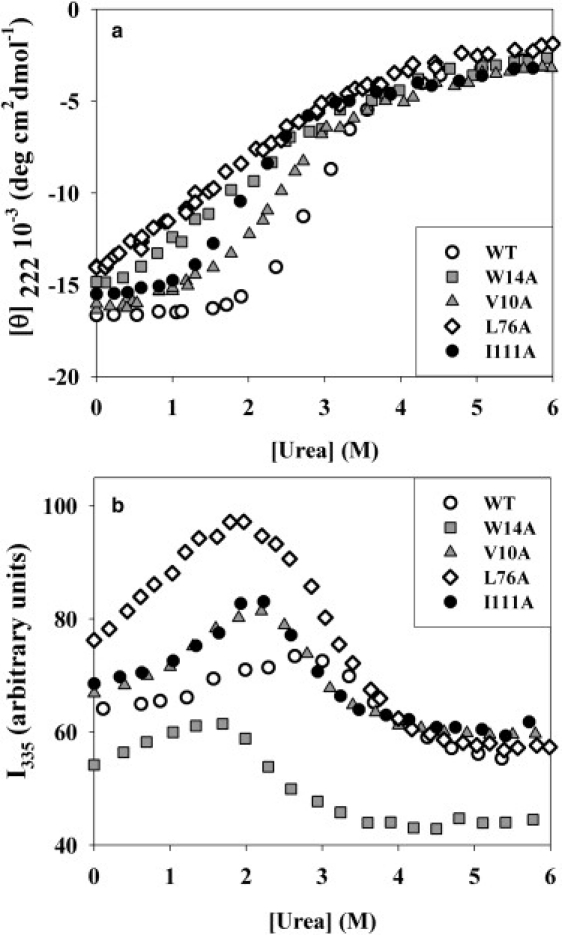
Equilibrium urea-induced unfolding of WT apomyoglobin and some of its representative mutant forms at pH 6.2: (a), as detected by molar ellipticity at 222 nm ([θ]₂₂₂); (b), as detected by changing intensity of tryptophan fluorescence at 335 nm (I₃₃₅). The complete set of data is given in Supporting Material.

A shift of the molar ellipticity midtransition toward lower urea concentrations demonstrates destabilization of the native (folded) structure of all the mutants, as compared to WT apoMb. The observed urea dependence of molar ellipticity [θ] at 222 nm does not provide a reliable quantitative estimate for the intermediate state in this process (22), thereby preventing us from using the equilibrium urea-induced denaturing transitions to measure a relative stability of the native and intermediate states of apoMb and its mutants. However, the CD-monitored decrease in cooperativity of transitions may suggest some accumulation of the intermediate state (45), which is more clearly demonstrated by the increase in Trp fluorescence at the intermediate urea concentrations.

Fig. 1 b shows the urea-induced equilibrium unfolding of the same mutants, as demonstrated by varying intensity of their Trp fluorescence at 335 nm. As we reported previously, at this wavelength, the presence of the intermediate state I and of the N→I and I→U transitions are most distinct (22). This is important for the analysis of equilibrium denaturing transitions. As follows from Fig. 1 b, for all the proteins studied, urea concentration dependence of fluorescence intensity shows a maximum, which demonstrates a certain accumulation of an intermediate state by displaying a more intensive fluorescence than both the native and unfolded states (22,46). On the curves for mutant proteins this maximum is more distinct and shifted toward lower urea concentrations, as compared to that of WT apoMb; the latter also indicates a drop in stability of structures of the mutant proteins. The increase in Trp fluorescence intensity at the intermediate urea concentrations can be explained by the increased intermediate state population (36).

Similar but even more pronounced results were obtained from equilibrium experiments on pH-induced denaturing transitions of apomyoglobin mutants (36).

Folding/unfolding kinetics of apomyoglobin and its mutants

As it follows from equilibrium measurements, Trp fluorescence intensity increased upon transition from the N to I state and decreased during transition from the I to U state (see Fig. 1 b). In kinetic studies, the previous finding was the existence of two consecutive fluorescence steps occurring in apoMb folding (renaturation): its increase during the stopped-flow dead time (<<20 ms) reflecting formation of an early kinetic intermediate (28) bearing a close structural similarity to the well-studied thermodynamically stable intermediate state (36,45) and subsequent decrease during transition from the intermediate to native state. The final step, a fluorescence intensity decrease, takes place in the measurable time interval (seconds) and denotes formation of the native state of apomyoglobin (28). A similar pattern is typical for folding kinetics of the apomyoglobin mutants.

Fig. 2 shows folding (a) and unfolding (b) kinetics of the mutant with L115A substitution, as a representative example. As seen, in the folding process, a low final concentration of urea induces increased burst-phase fluorescence depicting a burst appearance of the early intermediate state. Hence, two important parameters can be derived from the folding kinetics: the burst-phase amplitude A of fluorescent intensity, which is proportional to a fraction f_I of the intermediate state formed after the initial folding phase, and the observed rate constant k_obs for the last slow phase of folding. The folding/unfolding rate constants k_obs observed at various final urea concentrations M allow constructing the so-called chevron plots (1,2,15), i.e., plots of logarithm of the observed rate constant for the process of approaching equilibrium (lnk_obs) versus denaturant concentration M in solution. Knowing the rate constants k_obs(M), intermediate state fractions f_I(M), and rate constants k_NI(M) obtained from the unfolding branch (due to very fast U↔I transition, k_NI = k_NU), one can estimate the rate of the I→N folding k_IN(M) at a given final urea concentration (22) (see Materials and Methods). Thus, the three-state transition U↔I↔N can be divided into two two-state transitions, U↔I and I↔N. For all the mutant forms of apomyoglobin, the folding/unfolding process was studied over a wide range of final urea concentrations. In the folding process, the relationship between increasing population of the intermediate state (f_I) and decreasing final urea concentration can be derived from the urea dependence of the initial burst phase amplitude (of U→I transition) for all the mutant forms. Urea concentration dependences of the I→N and N→I transition constants (k_IN and k_NI, respectively) have been obtained as well. Fig. 3 gives as an example fitting of k_IN (M) and k_NI (M) for WT apomyoglobin (see also (22)) and for two of its representative mutant forms (L115A and I28A) showing different behavior of the chevron plots.

Figure 2.

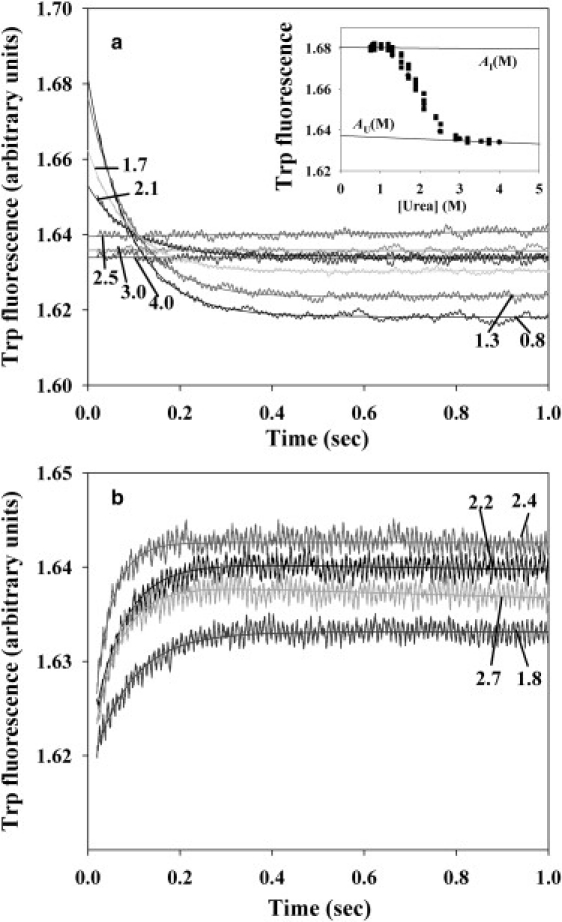
Kinetic curves for apomyoglobin mutant with Leu¹¹⁵ replaced by Ala in the process of its folding (a) and unfolding (b) at various final urea concentrations (indicated by numbers near the curves). The process was monitored at pH 6.2 by integral Trp fluorescence intensity. (Solid lines) Single-exponential approximations of the slow-phase folding and of unfolding kinetics. (Inset) Burst-phase amplitude A versus urea concentration M in the folding process and baselines A_U(M), A_I(M) for amplitudes of unfolded and intermediate states.

Figure 3.

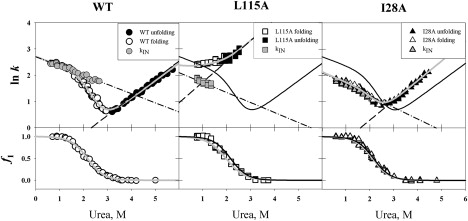
(Upper panels) Observed folding/unfolding rate constant (k_obs) versus the final urea concentration M for apomyoglobin mutants. All rate constants are measured in s⁻¹ and given in a logarithmic scale. The left part of each chevron corresponds to folding experiments (open symbols), the right part to unfolding experiments (solid symbols). (Shaded symbols) Folding rate constants k_IN(M) for the I→N transition; these are calculated from Eq. 2 using the corresponding k_obs(M), extrapolations of unfolding rates k_NI(M) = k_NU(M), and f_I(M) plots shown for each protein (lower panel). The k_NI(M) values were calculated from the folding data in the region where the f_I(M) > 0.1. (Dashed lines) Linear approximations of ln(k_NI(M)), and (dash-dot lines) linear approximations of ln(k_IN(M)). (Dark-shaded lines) Chevron plots calculated using an equation k_obs = k_NI + f_I × k_IN. (Solid lines, upper panels) Chevron plots for WT protein (see WT panel). (Shaded lines, lower panels) Two-state fitting of f_I versus urea concentration. (Solid lines, lower panels) The f_I plots for WT protein (see WT panel).

To fit the experimental chevron plots, the approach developed in our laboratory (22) was used. We also tried to fit the whole chevron plot by the well-known three-state expression (see, e.g., (44)), which does not use amplitudes A(M) and is based on k_obs(M) only, but it gives a reasonable description only for those chevron plots that show visible rollover at low urea concentrations. In other cases, this approach gives described k_IN(M) values with very large errors. The examples of such calculations are shown in Fig. S3. Thus, to obtain reliable kinetic parameters, we used, in addition to chevron plots of ln(k_obs(M)), the plots of f_I(M), independently obtained from the burst phase amplitudes, and applied Eq. 2 to compute k_NI(M). It should be emphasized that Eq. 2 is applicable in practice only within the denaturant content range where k_obs(M) is larger than k_NI(M) and f_I(M) reliably differs from zero. The folding rate constants k_IN calculated from Eq. 2 are marked by shaded symbols in Fig. 3. Based on the linear approximations of logarithms of the folding and unfolding rate constants and Eqs. 3–8, kinetic and thermodynamic parameters of folding/unfolding reactions were determined and presented in Table 1. The complete set of experimental data for kinetics of de- and renaturing transitions of apomyoglobin mutants is presented in Supporting Material. For each mutant, linear approximations of logarithms of the unfolding (k_NI) and folding (k_IN) branches of the chevron plots are also given.

Table 1.

Thermodynamic parameters on folding/unfolding kinetics in apomyoglobin and its mutant forms

Parameter	Substitutions in conserved nonfunctional positions							Substitutions in nonconserved positions
	WT	V10A	W14A	I111A	L115A	M131A	L135A	I28A	F33A	L40A	M55A	L61A	L76A
C1/2	2.2 ± 0.1	2.2 ± 0.2	2.0 ± 0.1	2.0 ± 0.1	2.0 ± 0.2	2.0 ± 0.1	2.0 ± 0.2	2.1 ± 0.1	2.1 ± 0.2	2.1 ± 0.1	2.1 ± 0.2	2.2 ± 0.1	2.0 ± 0.1
mIU	1.47 ± 0.05	1.43 ± 0.06	1.50 ± 0.06	1.5 ± 0.1	1.45 ± 0.05	1.46 ± 0.05	1.40 ± 0.07	1.49 ± 0.05	1.48 ± 0.06	1.49 ± 0.08	1.45 ± 0.09	1.5 ± 0.1	1.49 ± 0.05
ln kIN∗	2.70 ± 0.09	2.4 ± 0.1	?	2.3 ± 0.1	2.1 ± 0.2	1.4 ± 0.3	2.4 ± 0.1	2.1 ± 0.1	2.1 ± 0.2	2.5 ± 0.2	1.6 ± 0.2	1.4 ± 0.2	0.0 ± 0.2
mIN	−0.35 ± 0.02	−0.38 ± 0.04	?	−0.41 ± 0.03	−0.37 ± 0.07	−0.5 ± 0.2	−0.41 ± 0.06	−0.44 ± 0.03	−0.35 ± 0.02	−0.40 ± 0.04	−0.4 ± 0.1	−0.40 ± 0.08	−0.41 ± 0.06
ln kNI∗	−1.6 ± 0.4	−1.1 ± 0.3	0.2 ± 0.3	−0.7 ± 0.4	1.4 ± 0.6	0.8 ± 0.3	1.3 ± 0.4	−1.4 ± 0.4	1.1 ± 0.8	0.0 ± 0.2	0.1 ± 0.6	0.8 ± 0.8	−0.2 ± 0.3
mNI	0.68 ± 0.04	0.81 ± 0.04	1.67 ± 0.08	0.87 ± 0.04	0.6 ± 0.2	0.81 ± 0.06	0.71 ± 0.08	0.79 ± 0.04	0.7 ± 0.2	0.75 ± 0.03	0.9 ± 0.1	0.8 ± 0.1	0.75 ± 0.03

C_1/2 is the denaturant concentration in the middle of the f_I urea dependence in the U-I transition, in [M]; m_IU is the slope of the urea dependence of the intermediate state stability in relation to the unfolded state, in kcal mol⁻¹ [M]⁻¹.

^∗Extrapolated to the absence of denaturant; ln k_IN and ln k_NI are logarithms of the folding and unfolding rate constants linearly extrapolated to water; m_IN and m_NI are dependences of logarithms of the folding and unfolding rate constants with urea, respectively, in [M]⁻¹.

As it is seen from the Table 1, values of m_IN and m_NI (dependences of logarithms of folding and unfolding rate constants on urea concentration) are close to the value for WT protein within the experimental error. This means that used substitutions do not crucially change the folding pathway except for W14A, for which m_NI value is rather high, but in this case the largest aromatic residue is substituted by the smallest aliphatic one, and such a great difference makes the Φ-analysis for this mutant questionable.

All the mutant forms have been analyzed (see Fig. 3 and Materials and Methods) by the method developed for WT apomyoglobin using the three-state kinetics analysis (22). This method was applied to determine energetic parameters of folding and unfolding processes which are presented in Table 2, and was used to assess involvement of various residues in formation of the intermediate (see also (36)) and transition states.

Table 2.

Parameters derived from kinetic data on folding/unfolding of apomyoglobin and its mutant forms

Parameter∗	Substitutions in conserved nonfunctional positions							Substitutions in nonconserved positions
	WT	V10A	W14A	I111A	L115A	M131A	L135A	I28A	F33A	L40A	M55A	L61A	L76A
ΔGIU	−3.19 ± 0.03	−3.17 ± 0.07	−2.93 ± 0.06	−2.9 ± 0.2	−2.86 ± 0.09	−2.92 ± 0.06	−2.86 ± 0.09	−3.16 ± 0.05	−3.1 ± 0.1	−3.1 ± 0.1	−3.1 ± 0.1	−3.2 ± 0.2	−2.91 ± 0.05
ΔGNI	−2.50 ± 0.01	−1.80 ± 0.02	?	−1.54 ± 0.01	−0.64 ± 0.04	−0.22 ± 0.04	−0.74 ± 0.01	−1.86 ± 0.01	−0.61 ± 0.03	−1.47 ± 0.03	−0.69 ± 0.02	−0.46 ± 0.01	−0.20 ± 0.03
ΔGNU	−5.69 ± 0.03	−4.97 ± 0.07	?	−4.5 ± 0.2	−3.6 ± 0.1	−3.14 ± 0.07	−3.60 ± 0.09	−5.02 ± 0.05	−3.7 ± 0.1	−4.5 ± 0.1	−3.8 ± 0.2	−3.8 ± 0.2	−3.11 ± 0.05
ΦTS(IN)	—	0.3 ± 0.2	?	0.3 ± 0.2	0.16 ± 0.07	0.35 ± 0.07	0.10 ± 0.04	0.8 ± 0.5	0.17 ± 0.07	0.12 ± 0.09	0.3 ± 0.1	0.34 ± 0.09	0.67 ± 0.08
ΦI	—	0.0 ± 0.1	?	0.2 ± 0.1	0.16 ± 0.05	0.11 ± 0.02	0.15 ± 0.05	0.04 ± 0.09	0.05 ± 0.06	0.0 ± 0.1	0.04 ± 0.07	0.0 ± 0.1	0.10 ± 0.02
ΦTS(UN)	—	0.3 ± 0.2	?	0.5 ± 0.2	0.32 ± 0.08	0.42 ± 0.07	0.24 ± 0.06	0.8 ± 0.5	0.2 ± 0.1	0.1 ± 0.1	0.3 ± 0.1	0.3 ± 0.1	0.71 ± 0.08

^∗Extrapolated to the absence of denaturant. All ΔG are in kcal/mol; ΔG_NU = ΔG_IU + ΔG_NI (see Eq. 5); Φ_TS(UN) = Φ_I + Φ_TS(IN) × (1 − Φ_I) (see Eq. 8).

Identification of residues forming the I state and the I→N transition state

With the values of lnk_IN(M) and lnk_NI(M) known (and extrapolated to the absence of denaturant) for the mutants and for WT apomyoglobin, the Φ-analysis proposed by Fersht in Matouschek et al. (1,2) can be applied to assess involvement of the substituted residues in the structure of the transition state on the barrier between the I and N states. With Φ_TS(IN) close to zero, such a substitution disturbs stability of the transition state as much as that of the intermediate state, and hence, the substituted residue is involved in the folding nucleus only to the same extent as in the intermediate state. In contrast, with Φ_TS(IN) close to unity, the substitution equally disturbs stabilities of the transition state and the native state, and hence, the substituted residue participates in the folding nucleus of the I→N transition.

Table 2 shows that all these mutant forms with substituted conserved residues have a Φ_TS(IN) value of 0.2–0.3, which suggests that, in the transition state of the I→N transition, they participate in ≤30% of additional (relative to the I state) native interactions. However, one should note that most of these residues have Φ_I = 0.1–0.2, which means that they have already formed 10–20% of the native contacts in the state I. For the mutants with substitutions in the nonconserved residues of B, D, E helices (among these L76 has ∼10% of its native contacts in the state I, whereas the others have much less), Φ_TS(IN) varies from 0.1 to 0.8. It is as high as 0.8 for Ile²⁸ (located in the middle of B helix) and 0.7 for Leu⁷⁶ (in the C-terminus of E helix), which indicates their key role in the I→N transition. For Met⁵⁵ and Leu⁶¹, Φ_TS(IN) is ∼0.3, whereas Phe³³ and Leu⁴⁰ have low Φ_TS(IN) values. Thus, the majority but not all of the studied nonconserved residues play a more important role in the I→N transition than the conserved ones.

The difference between the two classes of mutants is striking as to their contribution to the intermediate state (Φ_I-values) and not so large when it comes to the transition state Φ_TS(IN), except for two positions, I28 and L76, whose contribution is large. Different behavior of L111 and L115, as well as M131 and L135, may be explained by nonnative contacts of L115 and L135 in the intermediate state, as shown by Nishimura et al. (30). It is quite plausible that these nonnative interactions become native only after the transition state is formed, with residues M55 and L61, and C, CD, D, and partly E helices involved in the hydrophobic cluster. Apparently, the residue F33 of B helix and L40 of C helix dock later because they have lower Φ-values.

The mutational analysis gives information on interactions of side chains rather than on the backbone behavior studied in detail by Nishimura et al. (30) using NMR. From this point of view, interactions of side chains in the molten globulelike intermediate are not so strong, but nevertheless, the conserved residues contribute markedly more than nonconserved ones, except for, possibly, L76. We can speculate that this residue may form some nonnative interactions in the intermediate state (because such interactions were reported in (30)). The same may be a reason for low Φ_TS(IN) values of L115A and L135A.

Another picture is seen if we consider Φ_TS(UN) values calculated for the three-state U→I→N transition. In this transition Φ_TS(UN) values for the conserved residues and for three mutants from nonconserved ones are in the same range, but side chains of the latter start to contribute to overall interactions only during the I→N transition, whereas side chains of the conserved residues participate in both I state and I→N transitions. F33, at the C-end of the B helix, and L40 of the C helix (showing fairly low Φ-values), probably dock after they have crossed the main rate-limiting barrier. I28A and L76A create the main contribution to side-chain interactions in the I→N transition state, as their docking to the already formed A, G, H helical complex makes the N-end of the B helix and the C-end of the E helix join this complex, which stabilizes it (i.e., these nonconserved residues and thereby the corresponding helices consolidate using the A, G, H complex as a nucleation point). However, the complete set of side-chain interactions can be expected only in the native state. It should be stressed that all of these side-chain interactions are observed when the backbone interactions have been, for practical purposes, fully realized (our far UV CD spectra clearly showed the presence of substantial secondary structure even at moderate denaturant concentrations, in the state I).

We see that the role of conserved residues is more significant than that of nonconserved residues specifically in the U→I transition, which supports Ptitsyn's supposition (47) that conserved residues are of special importance in forming the intermediate structure at the initial stage of apoMb folding.

Combining both sets of results gives a more accomplished picture of the intermediate and transition states. Residues from different helices are involved in the secondary structure at an early step of folding. However, as it follows from Φ-analysis, the fraction of interactions of side chains increases step by step, from 20% or less in the intermediate state to 30–70% in the I-N transition state, to reach its maximum in the apoMb native state.

A detailed investigation of apomyoglobin mutants by NMR was performed by Nishimura et al. (29,30) and Tsui et al. (32), who studied the folding pattern and mobility of the apomyoglobin backbone using the technique of amide H-D exchange in the I and N states. Here, we considered interactions of the apomyoglobin side chains and strength of their interactions in the I and TS states. Therefore, experimental results of the two teams are complementary and allow a more-detailed understanding of interactions occurring in apomyoglobin folding.

Conclusions

Fig. 4 shows the sperm whale apomyoglobin fold, where the studied residues are marked out and their role in the I state and in the I↔N and U↔I↔N transitions is outlined. As seen, the residues whose side chain form the kinetic intermediate state I are positioned mainly in G, H helices (in accordance with data on the equilibrium intermediate state (28,36)) whereas those limiting the apomyoglobin folding rate in the I↔N transition are in another part of the protein, namely, in B, D, E helices. The resulting folding nucleus for the three-state U↔I↔N transition is a sum of contributions of all these residues. Thus, the developed approach taking into account only kinetic experiments allowed us to estimate contribution of various residues at different steps of folding of a multistate protein. Additional studies using other ultrafast techniques are undoubtedly required to shed light upon the U↔I transition in apoMb.

Supporting Material

One table and three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00098-6.