Abstract
Using single-molecule force spectroscopy to probe ICAM-1 interactions with recombinant αLβ2 immobilized on microspheres and β2 integrin on neutrophils, we quantified an impressive hierarchy of long-lived, high-strength states of the integrin bond, which start from basal levels with integrin activation in solutions of divalent cations and shift dramatically upward to hyperactivated states with cell signaling in leukocytes. Taking advantage of very rare events, we used repeated measurements of bond lifetimes under steady ramps of force to achieve a direct assay for the off-rates of ICAM-1 from β2 integrin in each experiment. Of fundamental importance, the assay for off-rates does not depend on how the force is applied over time, and remains valid when the rates of dissociation change with different levels of force. In this first article, we present results from tests of a monovalent ICAM-1 probe against immobilized αLβ2 in environments of divalent cations (Ca2+, Mg2+, and Mn2+) and demonstrate in detail the method for assay of off-rates. When extrapolated to zero force, the force-free values for the off-rates are found to be consistent with published solution-based assays of soluble ICAM-1 dissociation from immobilized LFA-1, i.e., ∼10−2/s in Mg2+ or Mn2+ and ∼1/s in Ca2+. At the same time, as expected for adhesive function, we find that the β2 integrin bonds activated in Mn2+ or Mg2+ possess significant and persistent mechanical strength (e.g., >20 pN for >1 s) even when subjected to slow force ramps (<10 pN/s). As discussed in our companion article, using the same assay, we find that although the rates of dissociation for diICAM-1fc bonds to LFA-1 on neutrophils in Mn2+ are similar to those for mICAM-1 bonds to recombinant αLβ2 on microspheres, they appear to represent a dimeric attachment to a pair of tightly clustered integrin heterodimers. The mechanical strengths and lifetimes of the dimeric interactions increase dramatically when the neutrophils are stimulated by the chemokine IL-8 or are bound with an allosterically activating (anti-CD18) monoclonal antibody, demonstrating the major impact of cell signaling on LFA-1.
Abbreviations used: AFM, atomic force microscopy; BFP, biomembrane force probe; ICAM-1, intercellular adhesion molecule-1; LFA-1, lymphocyte function-associated antigen-1; mICAM-1, monomeric ICAM-1; PEG, polyethylene glycol; PMN, polymorphonuclear leukocyte or neutrophil; SD, standard deviation
Introduction
Circulating leukocytes selectively adhere to and migrate through the vascular endothelium proximal to sites of tissue injury or infection. This recruitment process is mediated by multiple sets of adhesion molecules (1) that are stimulated to appear or disappear, or become active or inactive, through specific signaling molecules that are either endogenous to the vascular cells (cytokines) or arise from other pathogenic sources (chemokines). Of these molecules, the cell-surface integrins are known to enable firm adhesion of leukocytes, cell spreading, and emigration into tissues (2). The family of integrins is itself made up of at least 24 heterodimers formed from 18 α-chains and eight β-chains (2,3). In the context of our study reported here, the particular subset of four β2 integrins and their interactions with super-Ig family ligands (ICAMs) are prominent because of their role in recruiting circulating leukocytes into inflamed or injured tissues. Electron microscopy has guided much of the current thinking about integrin interactions by providing striking images of large, multidomain structures. These structures range from a bent or collapsed shape correlated with imperceptible adhesion to extended or erect shapes correlated with different levels of adhesiveness (4–7). Phenomenological insight into β2 integrin adhesiveness has been gained by studies of rolling and tethering in flow chamber assays (8,9). By comparison, much less is known in detail about the mechanical performance of individual β2 integrin bonds; in particular, it remains to be determined how the different states of activation regulate the lifetime of an integrin bond under stress. Thus, our objective in this article is to show the persistence of single ICAM-1 attachments to αL β2 immobilized on microspheres over a wide range of tensile force values under basal activation by divalent cations (Mn2+, Mg2+, and Ca2+). Then, in our companion article (10), we demonstrate the major impact of cell signaling in leukocytes on the persistence of ICAM-1 attachments to the native β2 integrin under stress.
As with all integrins, ligand specificity to a β2 integrin is defined by the α-chain. The binding site for ICAM, which has been studied extensively for the β2 integrin, exists on the outer A domain of the α-chain (also labeled as the inserted I domain). Because of its proximity to a nearby site for binding divalent metal cations, the location for binding ICAM on the αA domain is called the metal ion-dependent adhesion site (MIDAS) (3). In addition to the requisite binding of divalent cation to the MIDAS, β2 integrin affinity for ICAM is also affected by binding divalent metal cations to sites on the outer A domain of the β-chain (an I-like domain that also possesses a MIDAS region that is important in ligand interactions). The other ion-binding sites include a ligand-induced metal ion-binding site and an adjacent-to-metal ion-dependent adhesion site. The latter is particularly notable because it mediates both the negative regulatory affects of high Ca2+ and the induction of a high-affinity state of the β2 integrin when Ca2+ is replaced by Mn2+ (3). While obviously positioning the outer αA domain for easier access to the binding site, the extended shapes of β2 integrins are also accompanied by important shifts in secondary and tertiary structure local to the MIDAS region of the αA domain. Coupled to the metal-ion coordination bond and other peptide interactions, these local changes in molecular conformation appear to play an important role in regulating ICAM affinity to the β2 integrin (3).
In this article, we describe the impact of force on the lifetimes of mICAM-1 interactions with a leucine-zipper construct of αL β2 (11) immobilized on microspheres in millimolar environments of the divalent cations Mn2+, Mg2+, and Ca2+. Forming rare point attachments with a high probability of single ligand interaction and applying controlled ramps of tensile forces with precision, we used an ultrasensitive BFP (12,13) covalently linked with a very low density of ligand to test the lifetimes of mICAM-1 interactions with the β2 integrin. Although diICAM-1 interactions with cell-surface LFA-1 have been probed with other force methods (e.g., AFM (14,15) and flow chamber experiments (16); see comments in the Supporting Material), the results have not provided a clear picture of the lifetimes for the LFA-1 bond at different levels of force and different states of activation. For this reason, we employed a novel method for analysis of bond lifetimes under force that provides a direct assay of off-rates throughout the course of each experiment. By establishing a baseline reference for pairwise interactions between monovalent ICAM-1 and αL β2, we show that extrapolation of the off-rate measurements to zero force yields force-free values consistent with solution-based assays, i.e., ∼10−2/s in Mn2+ or Mg2+ and ∼1/s in Ca2+. When probed in Mn2+ or Mg2+, mICAM-1 bonds to the β2 integrin are found to respond with significant mechanical strength under ramps of force in the range of ∼1–10,000 pN/s. Yet, throughout each ramp, the expected lifetimes of these bonds diminish rapidly, decreasing from their force-free persistence of ∼100 s to <1 ms at ∼70 pN of force.
Materials and Methods
Soluble, five-domain mICAM-1, a recombinant human protein, was purchased from R&D Systems (Minneapolis, MN) and used without further purification. Another recombinant, the soluble construct of αL β2 (LFA-1), was made available to us through an ongoing collaboration between Dr. Scott Simon and Dr. D. E. Staunton (ICOS Corp., Bothell, WA). This heterodimer was engineered by replacing the transmembrane and cytoplasmic domains of CD11a and CD18 with an acidic/basic leucine zipper cassette (11).
Linkage to glass microspheres
To immobilize ICAM-1 on BFP tips and αL β2 heterodimer on targets, glass spheres (2–3 μm; Duke Scientific, Palo Alto, CA) were cleaned and functionalized with a very low concentration of each protein as previously described (13). For BFP tips, a large amount of PEG-biotin was also added to enable strong binding to a PEG-streptavidinated red cell transducer. In the preparation procedure, microspheres were first bound with mercapto-silane groups. Then, mono-and bifunctional thiol reactive PEGs (Nektar Therapeutics, Huntsville, AL) were used to anchor PEG-biotin and the protein, respectively. Before experiments were conducted, the integrin microspheres were washed with 5 mM EDTA and 1.5 mM EGTA solution and then suspended in 0.1 M NaCl buffer containing 2 mM of MnCl2, MgCl2, or CaCl2. In control experiments, tests were performed in microscope chambers that contained either the HEPES buffer with 2 mM of a divalent salt (MnCl2 or MgCl2), or buffer with divalent cation plus the blocking anti CD18 monoclonal R15.7.
Red blood cells for BFP transducers
Fresh human blood samples were collected with a sterile syringe containing 10 U/mL heparin (Elkins-Sinn, Cherry Hill, NJ). Red cells were extracted from the sample by low-speed centrifugation and then linked with PEG-biotin, followed by streptavidin. To assemble the BFP transducer (12,13), a 2-μm-diameter biotinylated and protein-functionalized microsphere was attached to the avidinated red cell held by a micropipet (Fig. 1 A).
Figure 1.
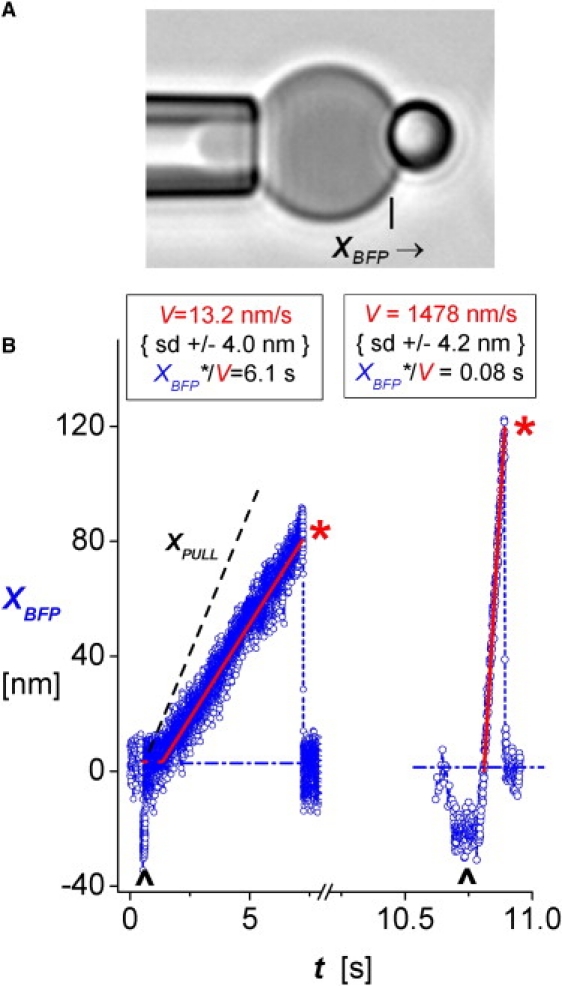
(A) BFP formed by bonding a 2 μm glass sphere to a micropipet-pressurized red blood cell. Along with very dilute monovalent ICAM-1, the microsphere tip is coated with concentrated PEG-biotin, enabling tight adhesion to the PEG-biotinylated and avidinated red blood cell. The BFP spring constant, kf, is set by micropipet suction control of the tension in the red cell membrane. (B) Traces of BFP tip deflections XBFP from tests of mICAM-1 bonds to αLβ2 on microspheres under slow retraction (left, Vpull = 20 nm/s) and fast retraction (right, Vpull = 2000 nm/s) with kf set to 0.5 pN/nm. A 10-fold break in the time axis serves to illustrate the major reduction in the lifetime of the integrin bond when the nominal loading rate (kf Vpull) is increased from slow to fast pulling speeds. Performed under feedback control, the up marks identify 0.1 s periods of soft impingement before piezo retractions of the integrin microspheres. The red traces are linear regressions to the deflections (open blue circles) used to determine the probe deflection speed V after a brief period of no deflection. The linear response to constant speed retraction reveals the time during which a bond experiences force, as determined by the ratio of maximum probe stretch XBFP∗ to deflection speed, i.e., t = XBFP∗/V. The dense fluctuations at intervals of 0.6 ms have a spread of ±4 nm SD; based on a spring constant kf = 0.5 pN/nm, the corresponding fluctuations in force are ± 2 pN SD.
Single-molecule force spectroscopy
When a tense BFP red cell is pressurized into a spherical shape, pulling or pushing on the microsphere tip with a small force results in an axial deflection that increases in proportion to the force (12). Within a reproducible geometric parameter factor of order unity, the effective spring constant, kf, of a BFP is set by tension in the red cell membrane, which is controlled by the applied micropipet suction ΔP and scaled by pipet radius Rp. In this way, the BFP spring constant can be accurately selected in a range from 0.25 < kf < 1.5 pN/nm (chosen as either 0.25 pN/nm or 0.5 pN/nm for the experiments reported here). The range of compressive to tensile forces accessible with a BFP is −30 pN to +300 pN, which are reported with ±1–2 pN precision. The precision in force is governed by the ±3–4 nm SD accuracy in tracking of the BFP tip displacement, which is performed with an online video-image analysis system at a sampling rate of ∼1400/s.
Mounted on a microscope stage and directed by computer, a second micropipet holding a receptor target is moved repeatedly by a linear-piezo translator to/from contact with the BFP tip following a programmed sequence of velocities over time. Attempts to form an attachment between the BFP and a receptor target are limited to a brief 0.1 s period of contact. To sense and control contact with the BFP tip, the target approach is programmed to stop when a preset value of negative (compressive) BFP deflection is detected (Fig. 1 B). The impingement force is typically chosen to be ∼−10 pN. Once detected, the target is then retracted at a fixed speed, Vpull, which results in either an increasing positive (tensile) deflection of the BFP if held by an attachment, or a return to baseline in the absence of an attachment. As shown by slow retraction of a target held by attachment at 20 nm/s in Fig. 1 B (left plot), the linear increase in probe deflection often commences a short time (Δto) after the zero crossing because of a small molecular-scale length contributed by the receptor and ligand structures. Although they are variable because of interface topography and imperceptible under fast pulling (Fig. 1 B, right), these time delays yield estimates of Vpull Δto ∼ 10–20 nm when integrin bonds form between the microspheres. This brief delay is most important at slow pulling speeds, and must be subtracted out when the lifetime ti of an attachment under tensile force is quantified. Thus, our approach is to determine the linear slope (velocity V) characterizing the tensile regime up to the displacement XBFP∗ at rupture and establish the time subjected to force from the ratio, ti = (XBFP∗/V)i as sketched in Fig. 1 B.
The linear regimes of BFP stretch XBFP reveal the actual force ramps, rf = κf V, applied to each attachment. Somewhat less than the programmed ramps, κf Vpull, the actual ramps show that the tip-target interface lowers the effective spring constant, κeff = rf /Vpull. As noted previously (13), the ratio of pulling speed to probe displacement velocity, Vpull /V, provides a direct assay for elasticity of the tip-target interface, κt∼t = κf /(Vpull /V − 1). For reacting molecules immobilized on glass microspheres using amino- or mercapto-silane and heterobifunctional polymer linkers, the ratios Vpull /V are typically between 1.2 and 1.3, with ∼10% SD for a particular preparation, showing that elastic constants for the interfaces lie in the range ∼1–5 pN/nm.
Statistics of rare-point attachments
The reacting molecules on a BFP tip and target surface possess limited lateral mobility (even for integrin on a PMN). When they are present at low densities, the likelihood of forming attachments to receptors upon touch depends primarily on the contact area and, to a much lesser extent, the contact time. By controlling the impingement force (approximately a few piconewtons) and duration of touch (≤0.1 s), one can establish uniform conditions for forming rare attachments at every touch to a target where the events can be characterized by Poisson statistics for a stationary-random process. Even when the contact conditions are controlled, procedures have to be established to deal with contaminating populations that arise from nonspecific and multiple-molecule attachments. Obviously, when molecular bonds are tested, force traces with multiple force drops are always rejected. Yet, simple inspection fails to identify nonspecific attachments. Moreover, a significant fraction of the multiple-molecule attachments seem to escape detection based on the predictions from Poisson statistics described below. To deal with the contaminating populations of nonspecific and undetected multiple-molecule attachments, we developed a conservative procedure to reliably extract putative single-molecule data from the raw statistics of rare attachments.
Procedure for treating nonspecific interactions
We performed control experiments under the same conditions of target impingement and retraction speed used in the functional tests to estimate the nonspecific events likely to occur at different levels of force. Because nonspecific interactions are mainly restricted to low forces (short times), the most reliable approach is to simply ignore the short-time statistics masked by significant numbers of nonspecifics. This approach merely sets a lower bound to the range of data analyzed and has no effect on the assay for off-rates at higher forces (longer times). For ligand and receptor molecules immobilized on glass microspheres at very dilute coverages, control experiments typically yield 10-fold fewer (or less) attachments in comparison to tests of specific interactions with the same spheres. Superposed on the histograms in this article and scaled to the same number of touches, we will show the small numbers of nonspecific attachments obtained from control tests in NaCl buffer plus 5 mM EDTA between a BFP microsphere linked covalently with mICAM-1 and microsphere targets with the recombinant αL β2 integrin held by a covalently linked activating monoclonal antibody, 240Q (11).
Procedure for treating multiple-specific interactions
The procedure for treating populations of undetected multiple-molecule attachments requires a more formal approach. To that end, we designed experiments to establish a stationary-random process for forming attachments by employing sensitive feedback to control initial contact and reducing the concentration of molecular reactants to achieve rare events. Thus, we use the frequency of attachments Aω to estimate the probability of zero molecular bonds, P0 = (1 − Aω), from which Poisson probabilities follow that predict the likelihoods for single-molecule attachment, P1 = (Aω − 1) ln(1 − Aω), and for all remaining multiple-molecule attachments, Pn≥2 = Aω + (1 − Aω) ln(1 − Aω). This Poisson treatment is supported by the lack of apparent correlations among outlier attachments appearing in the course of thousands of touches between a tip and target surface (see Fig. S1, A–C). Of most importance, multiple-molecule bonds are expected to share the applied force and survive much longer than single-molecule bonds. Even though partition of the force remains unknown, these attachments will most likely fail at times and forces beyond the range characterizing single-molecule attachments. Thus, we use the Poisson fraction for multiple bonds to estimate a set of outliers, Pn≥2 /Aω (≈ Aω /2 + Aω2 /6 + …), which is appropriate for exclusion at the longest times (largest forces). Although this represents small percentages (typically ∼10%) for the experiments described here, truncating the raw statistics by this number of outliers results in arrays of lifetimes N(ti) that have appropriate convergence for single-molecule statistics at long times.
Results and Analysis
In probing molecular interactions of ICAM-1 with αL β2, our objective was to measure the kinetic rates koff(t) at which single integrin attachments dissociate when pulled by force f. For each experiment under a given test condition, many thousands of contacts were tracked between a BFP tip and integrin targets with high precision, and of these a few hundred rare attachments were identified through the stretch and precipitous recoil of the probe (Fig. 1 B). For the raw data of each experiment, we measured the lifetimes ti of the attachments throughout the course of common force ramps (see Materials and Methods) and ordered them into an array expressing the number that survived to each failure event, i.e., from the total number at the shortest time down to one at the longest time. Then, as described in Materials and Methods, we truncated a small fraction of the longest times (≤∼10%) dictated by the observed frequency of attachment and the Poisson estimator for multiple bonds. This resulted in an array N(ti) that represents the putative single-bond population. As described in Appendix SI, the array N(ti), and its histogram ΔNk(tk) of failure events over fixed time increments Δt, provide experimental estimators for the probability of bond survival S(t) ≈ N(ti)/No, and the density distribution for unbinding transitions p(t) = −dS/dt ≈ ΔNk(tk)/(No Δt), respectively. Assuming that the evolution from bound to free states follows a random Markov process, the rate of dissociation at any time koff(t) is the ratio of probability density to probability p(t)/S(t). Thus, the ratios (ΔNk/Δt)/N(tk) establish a direct assay for the rates koff(tk) at the mean sampling times tk in the histogram for a particular experiment without fitting any function to the data.
The assay for off-rates is independent of how the force is applied over time. Given a deterministic history for the force rate rf(t), the forces corresponding to off-rate measurements are found simply from the integral of the force rate, f(tk) = ∫o→tk rf(t) dt. (As noted in Appendix SI, a related assay for off-rates can be expressed in terms of the forces measured in probe experiments; this assay was developed independently by Marshall et al. (17), Dudko et al. (18), and Evans et al. (19).) Of particular relevance in our experiments, we used a mode of force spectroscopy called a “steady force ramp” to stress the attachments. In this method, the target is pulled away at constant speed Vpull after contact is made with the probe. Although they are diminished somewhat by compliance at the tip-target interface (see Materials and Methods, Fig. 1 B), the ramps remain linear, so the measurements of probe deflection speed V and spring constant κf, i.e., rf = κf V, connect the force at failure fi to the lifetime under stress, fi = rf ti. (Note: When the target is pulled faster than a few thousand nanometers per second, a correction, ∼V × 0.00048 pN · s/nm, has to be added to the value rf ti to account for viscous damping (20).) Plotting the off-rates on a logarithmic scale versus the forces, we can use simple Arrhenius phenomenology, koff(fk) = ko exp[−ΔG(fk)/kBT], to derive the changes in activation energy, −ΔG(fk)/kBT, that accompany application of pulling force. Extrapolating each logarithmic plot to zero force provides the prefactor, ko = 1/to, characterizing force-free dissociation. (Note: Thermal energy kBT is taken as ∼4.08 × 10−21 J for our room-temperature (23°C) experiments.)
ICAM-1 interactions with immobilized αLβ2
To establish a baseline for allosteric activation of the integrin in environments of divalent cations, we focus on tests of a mICAM-1 probe against recombinant αL β2 linked to microspheres in separate solutions of Mn2+, Mg2+, or Ca2+ at 2 mM concentration. As demonstrations of the procedure to obtain experimental estimators for bound-state probabilities S(ti) ≈ N(ti)/No, we show in Fig. 2, A and B, examples of the raw data for survival statistics (black open circles) obtained in Mn2+ and Mg2+, respectively, at the same nominal force ramp (κf Vpull = 1000 pN/s). Also shown in Fig. 2, A and B, are the arrays N(ti) (open blue circles) of putative single-bond events that follow truncation of the raw data by a few Poisson multiples (5% and 8%, respectively) as dictated by the attachment frequency. The corresponding histograms plotted directly below on the same timescales (Fig. 2, C and D) show the unbinding transitions ΔNk cumulated over fixed time intervals Δt in each raw data set. The white-patterned bins mark the outliers truncated at long times, and gray bins at short times identify the nonspecific interactions predicted by controls. The yellow bins label unbinding transitions used as estimators for the probability density p(tk) defined by the rate of decrease in bound state probability, p(tk) = − [dS/dt]k ≈ (ΔNk/Δt)/N(0), at the bin centers tk. Finally, to provide the remaining ingredient needed to assay off-rates, koff(tk) ≈ (ΔNk/Δt)/N(tk), the solid-yellow circles superposed on the arrays in Fig. 3, A–C (for the three divalent cations at all pulling speeds) label the values found for unnormalized probability N(tk) by interpolation at the centers tk of yellow bins in the histograms. (Note: We ignored the occasional peripheral bin in distributions with too few statistics (∼0–5) to be analyzed reliably. This had no effect on the values of off-rates determined for the other bins.)
Figure 2.
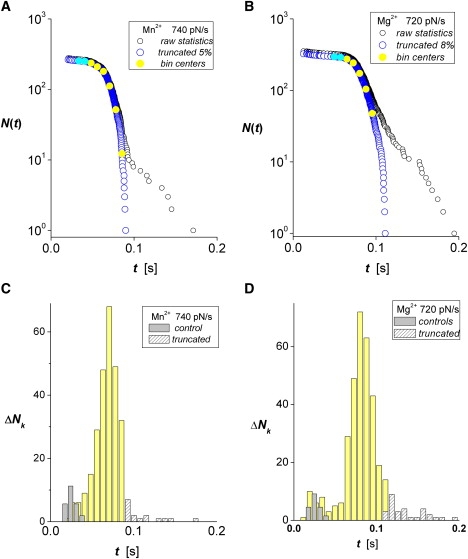
Lifetimes for mICAM-1 bonds to αLβ2 on microspheres subjected to a nominal force ramp of kf Vpull =1000 pN/s in 2 mM solutions of each divalent metal cation (measured ramps are marked on each panel). (A and B) Raw data (black open circles) for bond survival obtained in Mn2+ and Mg2+ are shown along with arrays N(ti) (open blue circles) characterizing the unnormalized probability for single-bond survival obtained after truncation of a small Poisson fraction of multiple bonds (0.05 and 0.08, respectively). (C and D) Histograms plotted directly below on the same timescales show the unbinding transitions ΔNk cumulated over fixed time intervals Δt in each raw data set. White-patterned bins identify the outliers truncated at long times, and gray bins at short times are nonspecific interactions obtained from control experiments rescaled to the same number of touches. Intervening yellow bins show the transitions used as estimators for the rates of decrease in bound state probabilities, p(tk) = − [dS1/dt]k ≈ (ΔNk/Δt)/N(0), at the bin centers tk.
Figure 3.
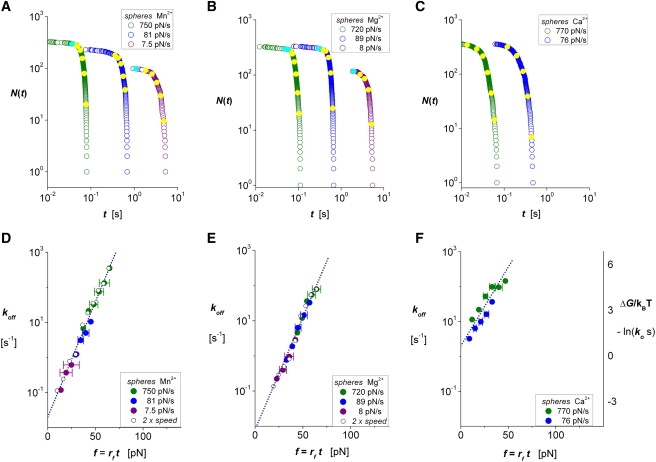
Statistics and off-rates for mICAM-1 bonds to αLβ2 on microspheres subjected to nominal force ramps kf Vpull from 10 to 1000 pN/s in 2 mM solutions of divalent metal cation (measured ramps are marked on each panel). The unnormalized probabilities N(ti) obtained with each force ramp (open colored circles) appear in A–C for Mn2+, Mg2+, and Ca2+, respectively; closed yellow circles identify the interpolation values found for bin centers tk in the corresponding histograms (not shown). Assayed by ratios of probability density/probability, (ΔNk/Δt)/N(tk), logarithms of the off-rates for integrin interactions are correlated in D–F to the forces, fk = rf tk, defined by ramp rates (± SD) at the bin centers. Also plotted in D and E for Mn2+ and Mg2+ are data from experiments performed at 2 × Vpull and 1/2 × κf, demonstrating that the off-rates depend only on instantaneous force. (Note: Because of fast dissociation, bonds to αLβ2 were not tested at 10 pN/s in Ca2+.) The linear regressions (dotted lines) superposed on each set of off-rate data demonstrate that mICAM-1 bonds to immobilized αLβ2 closely follow the exponential model introduced by Bell (21). The force scales fβ [ = 1/(ln10 × slope) ] and force-free off-rates ko found from intercepts of each regression appear in Table 1. The ordinate scale added at the right in panel F demonstrates that forces applied to the recombinant αLβ2 interactions over this range cause large reductions in activation energies relative to their stress-free state.
Extending the off-rates examined to much lower values, we show arrays of putative single-bond lifetimes in Fig. 3, A–C, that were obtained with slower nominal force ramps along with the interpolated values corresponding to bins in histograms of the data (not shown). Again determining the ratios (ΔNk/Δt)/N(tk) for all the data, we plot the off-rates in Fig. 3, D–F, on a log scale versus the forces, fk = rf tk, as defined by the ramp rates (± SD) multiplied by the times at bin centers. (Also plotted in Fig. 3, D and E (open circles), are results from experiments performed at 2 × Vpull and 1/2 × κf, demonstrating that the off-rates depend only on the instantaneous force, f = (κeff Vpull) t, rather than the pulling speed or BFP spring constant.) As shown by linear regressions (dotted lines) matched to each data set in Fig. 3, D–F, the logarithms of off-rates follow a linear dependence on the force level characterized by a force scale fβ [ = 1/(ln10 × slope) ] and a zero-force intercept ko. Together, the data and regressions in Fig. 3, D–F, exhibit the well-known exponential behavior proposed by George Bell (21) many years ago, i.e., koff ≈ ko exp[f xβ /kBT], in which the distance xβ represents the thermally averaged length gained in the direction of force when a bond is dissociated. In the context of the measurements, the length xβ corresponds to the force needed to lower the energy barrier governing off-rate by one thermal energy unit, i.e., fβ = kBT/xβ. Table 1 summarizes the parameters obtained from the linear regressions to the data for the three divalent cations over a range of force ramps between 10 and 1000 pN/s, which most likely encompass conditions experienced by β2 integrin bonds in vivo (22). As listed in Table 1, the stress-free rates ko characterizing spontaneous mICAM-1 dissociation from αL β2 on microspheres exhibit the well-known hierarchy of allosteric activation expected for solutions of the different metal cations (23), i.e., from 0.008/s in Mg2+ to 0.02/s in Mn2+ and ∼2/s in Ca2+.
Table 1.
Parameters characterizing the exponential dependences of koff on force in Fig. 3, D and E
| Metal cation[2 mM] | ko[s−1] | fβ[pN] | xβ = kBT/fβ[nm] |
|---|---|---|---|
| Mg2+ | 0.008(SD ± 0.001) | 6.8(SD ± 0.19) | 0.6 |
| Mn2+ | 0.02(SD ± 0.003) | 6.6(SD ± 0.18) | 0.62 |
| Ca2+ | ∼2(SD ± 0.7) | 9.6(SD ± 1.0) | 0.42 |
Ultrafast dissociation of ICAM-1 from immobilized αLβ2
As illustrated by sample data from tests of mICAM-1 against αL β2 spheres in Mg2+ and Ca2+ (Fig. 4, A and B,), numerous long-lived states in statistical arrays emerged at extremely fast ramps (κf Vpull ≥ 10000 pN/s) that could not be attributed to multiple bonds. As demonstrated by the histogram corresponding to Fig. 4 A, the white red-rimmed bins beyond the yellow bins in Fig. 4 C highlight the unexpected transitions that appear before the outliers predicted by Poisson multiples (white-patterned bins). Continuing with the same approach to analysis, the solid yellow circles and white rimmed circles superposed on the arrays in Fig. 4, A and B, identify the interpolation values corresponding to the centers of yellow and white-rimmed bins illustrated in Fig. 4 C. As shown in Fig. 4 D by solid red circles, the values (ΔNk/Δt)/N(tk) for off-rates at the centers of the yellow bins illustrated in Fig. 4 C extend the correlations to force appearing in Fig. 3, E and F (all of the off-rate data from the slower ramps appear as open clear or patterned circles in Fig. 4 D). Yet, when we analyze the numerous unexpected lifetimes and unbinding transitions that appear at ultrafast ramps, we find that the off-rates (open red circles in Fig. 4 D) deviate abruptly from the correlations shown in Fig. 3, E and F. Although for clarity it is not shown in Fig. 4 C, the same branching discontinuity was found for tests in Mn2+ at the fast nominal rate and at the same value of force as in Mg2+. And although they are only accessible over a limited range of force, the new branches for all three divalent metal cations appear to follow a similar weak exponential growth in off-rate with increase in force, albeit characterized by different preexponential factors. Crude fits to the new branches in off-rate indicate a major increase in force scale (fβ ∼68 pN) for exponentiation, ∼10-fold larger than the values found at slower ramps (e.g., fβ = 6.8 pN for Mg2+; Table 1). Likewise, the preexponential scales characterizing these off-rate regimes are large (∼180/s for Mn2+, ∼63/s for Mg2+, and ∼145/s for Ca2+). The ratios of these preexponential factors to the force-free off-rates of the initial linear regimes (ko2/ko in Table S2) yield apparent differences in activation energies correlating with the strengths of allosteric activation (∼9 kBT for Mn2+ or Mg2+, and ∼4 kBT for Ca2+).
Figure 4.
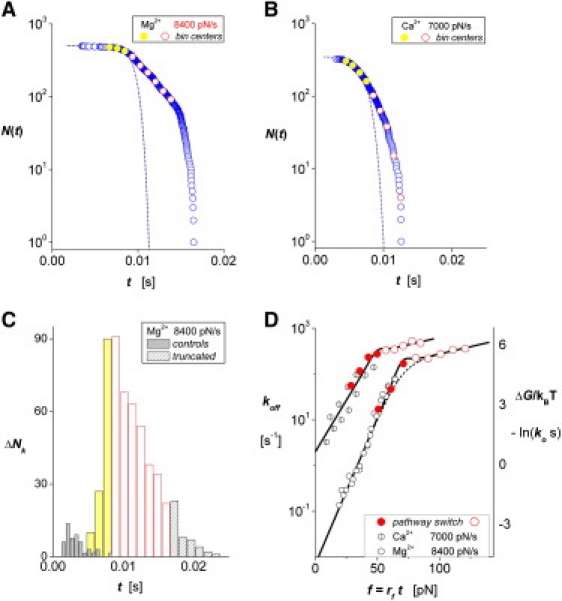
Tests of a mICAM-1 probe against αLβ2 spheres in Mg2+ and Ca2 at extremely fast nominal ramps κf Vpull ≥ 10,000 pN/s (measured ramps are marked on each panel). (A and B) Arrays for unnormalized probability after truncation of putative multiple-attachment outliers, and the corresponding histogram of raw data for Mg2+ directly below in C show that large numbers of long-lived events cannot be accounted for by multiple bonds. The white red-rimmed bins beyond the yellow bins show the unexpected transitions at long times corresponding to A. The solid yellow circles and white red-rimmed circles in A and B mark interpolation values used in the assay for off-rates, corresponding to centers of bins like those illustrated in C. Shown in D by solid red circles, the values (ΔNk/Δt)/N(tk) for off-rates at the centers of the yellow bins extend the data correlations appearing in Fig. 3, E and F (open clear and patterned circles for Mg2+ and Ca2+, respectively). The open red circles correspond to the unexpected transitions that deviate markedly in kinetic response at high forces. (Although for clarity it is not shown, the same branching discontinuity appeared in tests with Mn2+ under a ramp of 7510 pN/s.) As discussed in the text, the new branches of off-rates in D appear to be best described by a model (solid curves) based on a force-driven switch between different molecular configurations than by a model (dotted curves) based on a single pathway with two activation barriers.
The ordinate for activation energy added at the right in Fig. 4 D exposes two activation barriers: one dominating kinetics at low forces, and one dominating at high forces. Although they differ significantly from the results in Fig. 4 D, previous AFM measurements of leukocytic cell detachment from ICAM-1-coated surfaces also indicated a crossover between two kinetic regimes at ultrafast pulling speeds (discussed in the Supporting Material). The AFM results were interpreted in terms of a model (see Eq. SAII-4 in Appendix SII)) based on dissociation along a single reaction pathway traversing a sequence of energy barriers (dashed curve in Fig. 4 D). However, this model fails to match the sharp crossover between kinetic regimes shown in Fig. 4 D. By comparison, an alternative model (Eq. SAII-9 in Appendix SII) closely follows the abrupt sharp crossover between the two regimes of kinetics (solid curves in Fig. 4 D), which is based on a mechanical switch between two separate pathways characterizing different molecular configurations. The simplest switching behavior that matches the sharp crossovers in Fig. 4 D is provided by a unit step function at a specific force f⊗ (0→1 to open the new pathway and 1→0 to close the initial pathway). However, to gain insight into how thermodynamics might influence switching, we incorporated a thermal width f12 governed by a free-energy barrier separating the two configurations (24), which provides continuous switching, exp[−(f⊗ − f /f12)] /{1 + exp[−(f⊗ − f /f12)]}, with the limit of a step response as f12 → 0.
Conclusions
By probing mICAM-1 interactions with recombinant αL β2 on microspheres, we have demonstrated that the times for bond dissociation obtained under linear force ramps provide the basis for a model-independent assay of the off-rates at each level of force. Although off-rates can also be derived from analysis of the forces (17–19), the assay described in this work is based entirely on measurements of event times; correlations to force follow independently. By setting force ramps with different combinations of pulling speed × spring constant, we found that the values obtained for off-rates of mICAM-1 from the recombinant αL β2 depend only on the level of pulling force and the cation environment. To illustrate the lack of dependence on the mode of force application, we describe here sample data taken from a test of the same recombinant proteins in 2 mM Mg2+ performed some time ago (25) with a force clamp (fast step to constant force) of 64 pN. Fig. 5 A shows the raw data and the array N(ti) of putative single-molecule lifetimes that follow from truncation of a small fraction of outliers. Using the histogram of the raw data below in Fig. 5 C, and finding values for N(tk) at the bin centers tk by interpolation, we show in Fig. 5 B that the assay for the reciprocal off-rate, [N(tk) Δt/ΔNk], at each bin time (solid red circles) correlates well with the mean lifetime (dashed line at 0.019 s) derived from linear regression to ln[N(ti)]. Demonstrating a related approach to the assay, we also show the reciprocal off-rates obtained using a nine-point polynomial-regression algorithm to produce a smoothed function N(t) and its derivative [dN/dt]i (open blue circles in Fig. 5 B). In comparison with polynomial-regression and other local smoothing algorithms (e.g., cubic spline functions), the histogram approach provides better coarse-grained averaging of sampling fluctuations and closer agreement with the kinetics of exponential decay. Finally, the mean off-rates obtained with the three force clamps in the earlier work are shown in Fig. 5 D to agree well the data and linear correlation appearing in Fig. 3 E for the force ramp tests. However, because of the difficulty of accurately setting clamp forces, and the tedious process involved in acquiring large amounts of data, we believe that force ramps provide a more effective means of exploring large spans in lifetime and force, while also yielding many more statistics. Still, in probing ligand-receptor bonds, we cannot escape the necessity to identify a population of unbinding events that contain nearly all single-molecule interactions. Likewise, no criteria are perfect when hidden spurious statistics are excluded. Yet, when the contact process in force-ramp experiments is controlled and the frequency of attachments is aggressively reduced, the Poisson prediction for multiple events in a random process seems to provide minimal reduction of the raw data, significantly enriching the fraction of single-molecule statistics.
Figure 5.
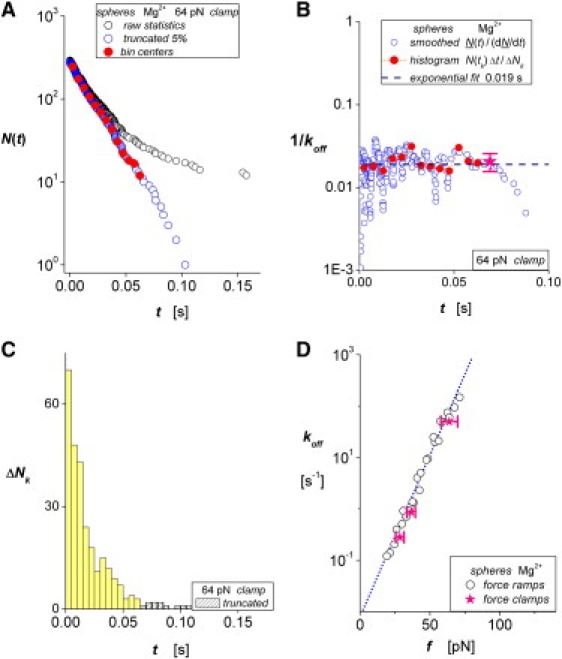
Lifetimes of mICAM-1 bonds to αLβ2 on microspheres in Mg2+ subjected to a force clamp of 64 pN (SD ± 7). (A) The raw data (black open circles) measured for ∼300 attachments and the unnormalized probability of single-bond survival N(ti) after truncation of a small Poisson fraction (0.05) of outliers (open blue circles). Plotted below on the same timescale in C, the histogram shows the unbinding transitions ΔNk in the raw data cumulated over fixed time intervals Δt. White-patterned bins identify the Poisson fraction of events truncated from the raw data, and yellow bins identify transitions in the unnormalized single-bond probability (open blue circles). Solid red circles label the interpolations in A at the bin center times tk and the assay [N(tk) Δt/ΔNk] for lifetimes in B. (A pink star and brackets show the mean ± SD of the assay.) The dashed line in B marks the mean lifetime (0.019 s) obtained from linear regression to the unnormalized probability in A. To illustrate a less effective approach, we show the assay N(t)/[dN(t)/dt] in B (open blue circles) computed from a moving nine-point polynomial-smoothing algorithm, which yields a local function N(t) and its derivative [dN/dt]. (D) Off-rates for mICAM-1 bonds to αLβ2 on microspheres in Mg2+ obtained with three force clamps (solid pink stars) are shown to match the force ramp data from Fig. 3E (open circles).
When we test mICAM-1 interactions with recombinant αL β2 at force ramps from ∼10 to 1000 pN/s, we find that the unbinding rates increase very rapidly, rising as exponential functions of the instantaneous force, reducing the survival of integrin bonds to ∼3 ms when forces reach ∼70 pN in Mg2+ or ∼64 pN in Mn2+, but much lower (∼50 pN) in Ca2+. When extrapolated to zero force, the values for lifetimes of the integrin bonds in the cation environments range from ∼1/2 s in Ca2+ to 2 min in Mg2+. Although it was two- to threefold faster than the force-free off-rates in Mg2+ or Mn2+ derived here from force-ramp tests (Table 1), the same hierarchy of off-rates (∼0.03/s in Mg2+, ∼0.05/s in Mn2+, and >1/s in Ca2+) was obtained many years ago from surface plasmon resonance tests of soluble ICAM-1 binding to detergent extracted LFA-1 immobilized on a hydrophobic surface (23). More recently, fluorescence flow cytometry experiments yielded comparable rates for the release of soluble ICAM-1 from the recombinant αL β2 construct in Mg2+ when anchored noncovalently to latex microspheres (26). However, at the other extreme of ultrafast detachment, we find that applying force ramps ≥7–8 × 103 pN/s leads to abrupt suppression of the force sensitivity in off-rates at very large forces depending on the divalent cation. Although the relevance to physiological adhesion is unclear, the sharp transition to force-insensitive off-rates suggests that large forces cause a major switch in molecular configuration of the complex between recombinant αL β2 and ICAM-1.
Also depending on the divalent cation, the force scales fβ governing off-rate exponentiation in Table 1 provide thermodynamic measures of the critical fluctuations in distance xβ that couple with the pulling force to lower the energy barrier regulating the kinetics. As such, the lengths xβ determined for biomolecular interactions usually increase and decrease qualitatively with the size of the binding region. For example, consistent with the binding region between domain 1 of ICAM-1 and the αL I domain indicated by crystal structure (27), the values of xβ in Table 1 for Mg2+ or Mn2+ are similar to values for xβ (∼0.5–0.6 nm; data not shown) we obtained from tests of interactions between anti-CD18 or anti-CD11a monoclonals and αL β2 immobilized on microspheres. In this context, the abrupt drop in length scale to <1 Å at high forces (≥70 pN) suggests that the putative change in molecular configuration results in the force being localized on the metal ion-coordination bond. At the same time, suppression of the nonpolar interactions surrounding the MIDAS (3) may account for the large reduction in apparent activation energy implied by the ratio of the preexponential scales for off-rates.
Supporting Material
One figure and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00084-6.
Supporting Material
Acknowledgments
This work was supported by National Institutes of Health grants HL65333 and HL31579 (to E.E.) and AI47294 (to S.S.).
References
- 1.McEver R.P. Adhesive interactions of leukocytes, platelets, and the vessel wall during hemostasis and inflammation. Thromb. Haemost. 2001;86:746–756. [PubMed] [Google Scholar]
- 2.Hynes R.O. Integrins: bi-directional, allosteric, signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 3.Luo B.H., Carman C.V., Springer T.A. Structural basis of integrin regulation and signaling. Annu. Rev. Immunol. 2007;25:619–647. doi: 10.1146/annurev.immunol.25.022106.141618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shimaoka M., Takagi J., Springer T.A. Conformational regulation of integrin structure and function. Annu. Rev. Biophys. Biomol. Struct. 2002;31:485–556. doi: 10.1146/annurev.biophys.31.101101.140922. [DOI] [PubMed] [Google Scholar]
- 5.Arnaout M.A., Mahalingam B., Xiong J.P. Integrin structure, allostery, and bidirectional signaling. Annu. Rev. Cell Dev. Biol. 2005;21:381–410. doi: 10.1146/annurev.cellbio.21.090704.151217. [DOI] [PubMed] [Google Scholar]
- 6.Luo B.H., Springer T.A. Integrin structures and conformational signaling. Curr. Opin. Cell Biol. 2006;18:579–586. doi: 10.1016/j.ceb.2006.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nishida N., Xie C., Springer T.A. Activation of leukocyte β2 integrins by conversion from bent to extended conformations. Immunity. 2006;25:583–594. doi: 10.1016/j.immuni.2006.07.016. [DOI] [PubMed] [Google Scholar]
- 8.Salas A., Shimaoka M., Springer T.A. Rolling adhesion through an extended conformation on integrin αL β2 and relation to α I and β I-like domain interaction. Immunity. 2004;20:393–406. doi: 10.1016/s1074-7613(04)00082-2. [DOI] [PubMed] [Google Scholar]
- 9.Shamri R., Grabovsky V., Alon R. Lymphocyte arrest requires instantaneous induction of an extended LFA-1 conformation mediated by endothelium-bound chemokines. Nat. Immunol. 2005;6:497–506. doi: 10.1038/ni1194. [DOI] [PubMed] [Google Scholar]
- 10.Kinoshita K., Leung A., Simon S.I., Evans E. Long-lived high-strength states of ICAM-1 bonds to αL β2 integrin: II. Lifetimes of LFA-1 bonds under force in leukocyte signaling. Biophys. J. 2009;98:1467–1475. doi: 10.1016/j.bpj.2009.12.4316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lupher M.L., Harris E.A., Staunton D.E. Cellular activation of leukocyte function-associated antigen-1 and its affinity are regulated at the I domain allosteric site. J. Immunol. 2001;167:1431–1439. doi: 10.4049/jimmunol.167.3.1431. [DOI] [PubMed] [Google Scholar]
- 12.Evans E., Ritchie K., Merkel R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 1995;68:2580–2587. doi: 10.1016/S0006-3495(95)80441-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Evans E., Heinrich V., Kinoshita K. Nano-to-micro scale dynamics of P-selectin detachment from leukocyte interfaces: I. membrane separation from the cytoskeleton. Biophys. J. 2005;88:2288–2298. doi: 10.1529/biophysj.104.051698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang X., Wojcikiewicz E.P., Moy V.T. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophys. J. 2002;83:2270–2279. doi: 10.1016/S0006-3495(02)73987-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wojcikiewicz E.P., Abdulreda M.H., Moy V.T. Force spectroscopy of LFA-1 and its ligands ICAM-1 and ICAM-2. Biomacromolecules. 2006;7:3188–3195. doi: 10.1021/bm060559c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vitte J., Pierres A., Bongrand P. Direct quantification of the modulation of interaction between cell- or surface-bound LFA-1 and ICAM-1. J. Leukoc. Biol. 2004;76:594–602. doi: 10.1189/jlb.0204077. [DOI] [PubMed] [Google Scholar]
- 17.Marshall B.T., Sarangapani K.K., Zhu C. Force history dependence of receptor-ligand dissociation. Biophys. J. 2005;88:1458–1466. doi: 10.1529/biophysj.104.050567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dudko O.K., Hummer G., Szabo A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA. 2008;105:15755–15760. doi: 10.1073/pnas.0806085105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Evans E., Halvorsen K., Wong W.P. A new approach to analysis of single molecule force experiments. In: Hinterdorfer P., van Oijen A.M., editors. Handbook of Single-Molecule Biophysics. Springer Science; New York: 2009. In press. [Google Scholar]
- 20.Evans E., Leung A., Simon S. Chemically-distinct transition states govern rapid detachment of single bonds to L-selectin under force. Proc. Natl. Acad. Sci. USA. 2001;98:3784–3789. doi: 10.1073/pnas.061324998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 22.Alon R., Dustin M.L. Force as a facilitator of integrin conformational changes during leukocyte arrest on blood vessels and antigen-presenting cells. Immunity. 2007;26:17–27. doi: 10.1016/j.immuni.2007.01.002. [DOI] [PubMed] [Google Scholar]
- 23.Labadia M.E., Jeanfavre D.D., Morelock M.M. Molecular regulation of the interaction between leukocyte function-associated antigen-1 and soluble ICAM-1 by divalent metal cations. J. Immunol. 1998;161:836–842. [PubMed] [Google Scholar]
- 24.Evans E., Leung A., Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 2004;101:11281–11286. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Evans E., Kinoshita K. Using force to probe single-molecule receptor-cytoskeletal anchoring beneath the surface of a living cell. Methods Cell Biol. 2007;83:373–396. doi: 10.1016/S0091-679X(07)83016-0. [DOI] [PubMed] [Google Scholar]
- 26.Sarantos M.R., Raychaudhure S., Simon S.I. Leukocyte function-associated antigen 1-mediated adhesion stability is dynamically regulated through affinity and valency during bond formation with intercellular adhesion molecule-1. J. Biol. Chem. 2005;280:28290–28298. doi: 10.1074/jbc.M501662200. [DOI] [PubMed] [Google Scholar]
- 27.Shimaoka M., Xiao T., Springer T.A. Structures of the αL I domain and its complex with ICAM-1 reveal a shape-shifting pathway for integrin regulation. Cell. 2003;112:99–111. doi: 10.1016/s0092-8674(02)01257-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


