Middle ear function and cochlear input impedance in chinchilla

Abstract

Simultaneous measurements of middle ear-conducted sound pressure in the cochlear vestibule P_V and stapes velocity V_S have been performed in only a few individuals from a few mammalian species. In this paper, simultaneous measurements of P_V and V_S in six chinchillas are reported, enabling computation of the middle ear pressure gain G_ME (ratio of P_V to the sound pressure in the ear canal P_TM), the stapes velocity transfer function SVTF (ratio of the product of V_S and area of the stapes footplate A_FP to P_TM), and, for the first time, the cochlear input impedance Z_C (ratio of P_V to the product of V_S and A_FP) in individuals. |G_ME| ranged from 25 to 35 dB over 125 Hz–8 kHz; the average group delay between 200 Hz and 10 kHz was about 52 μs. SVTF was comparable to that of previous studies. Z_C was resistive from the lowest frequencies up to at least 10 kHz, with a magnitude on the order of 10¹¹ acoustic ohms. P_V, V_S, and the acoustic power entering the cochlea were good predictors of the shape of the audiogram at frequencies between 125 Hz and 2 kHz.

INTRODUCTION

In terrestrial vertebrates, sound pressure waves are transmitted from the outside world to the fluid-filled inner ear primarily via the tympanic membrane (TM) and the ossicular chain of the middle ear. In mammals, the ossicular chain is made of three small bones: the malleus, the incus, and the stapes. Motion of the stapes footplate in the oval window produces pressure waves in the perilymph of the vestibule, the entrance to the cochlea. These waves propagate in the cochlea and are sensed by the organ of Corti, transduced into neural impulses, and sent to the central auditory system via the auditory nerve.

The middle ear acts as a transformer by increasing sound pressure and decreasing volume velocity (see, e.g., von Helmholtz, 1877; Wever and Lawrence, 1954; Dallos, 1973; Shera and Zweig, 1992; Rosowski, 1994). Middle ear function has been characterized in several species by measuring frequency-dependent transfer functions between the sound pressure in the ear canal (the input to the middle ear) and the input to the cochlea. One such function is the stapes volume-velocity transfer function (SVTF)1 defined as the ratio between stapes volume velocity U_S and ear canal sound pressure near the TM P_TM (SVTF=U_S∕P_TM). SVTF has been studied in many species, using a variety of techniques. Another transfer function of interest is the middle ear pressure gain (G_ME) defined as the ratio between the pressure in the vestibule (P_V) and P_TM (G_ME=P_V∕P_TM).

Because of the difficulties associated with intracochlear pressure measurements, G_ME has been reported in only a few individuals from a few species: in cat (Nedzelnitsky, 1980; Décory, 1989; Décory et al., 1990), guinea pig (Dancer and Franke, 1980; Décory, 1989; Décory et al., 1990; Magnan et al., 1997), chinchilla (Décory, 1989; Décory et al., 1990), gerbil (Olson, 1998, 2001; Dong and Olson, 2006; de La Rochefoucauld et al., 2008) and human temporal bone (Puria et al., 1997; Aibara et al., 2001; Puria, 2003; Nakajima et al., 2009). The difficulties in P_V measurements arise from the requirement of drilling a hole in the base of the cochlea to insert a pressure sensor. The hole needs to be small enough so that the middle and inner ear structures are not damaged, and the sensor needs to be small with a large impedance so as not to disturb the pressure waves being measured.

The cochlear input impedance Z_C, the frequency-dependent complex ratio of P_V to stapes volume velocity U_S (Z_C=P_V∕U_S), quantifies the acoustic load of the inner ear on the middle ear and is important for our understanding of middle ear function. Changing this load can induce changes in middle ear input admittance Y_ME (the ratio of the TM volume velocity to P_TM), stapes motion, and auditory sensitivity: For example, draining the cochlea introduced a resonance at 250 Hz in the middle ear input admittance of chinchillas and suppressed the non-linear dependence on level of Y_ME observed below 300 Hz (Rosowski et al., 2006). The same manipulation in cats resulted in the introduction of various resonances and anti-resonances in Y_ME between 1 and 30 kHz (Peake et al., 1992; Puria and Allen, 1998). In human temporal bones, complex rotary stapes motion, in addition to the piston component, was observed at high frequency when the cochlea was fluid-filled, but not after it was drained (Hato et al., 2003). A less dramatic change in Z_C can also have an effect: In chinchillas, introducing an opening in the bony superior semi-circular canal, which reduces Z_C in a frequency-dependent manner (Songer and Rosowski, 2007b), produced an increase in the magnitude of Y_ME between 100 Hz and 1 kHz and an increase in the magnitude of SVTF between 120 Hz and 5.8 kHz (Songer and Rosowski, 2006), as well as a broadband decrease in auditory sensitivity as measured by cochlear potentials (Songer and Rosowski, 2005).

Knowledge of Z_C is also important to the understanding of sound power flow through the middle and inner ears: The real part of Z_C can be used to compute the acoustic power entering the cochlea W_C (see Sec. 4G), where reasonable matches between auditory thresholds and the sound pressure necessary to produce a constant W_C in various species suggest middle ear power transfer is an important determinant to auditory sensitivity (Khanna and Tonndorf, 1969; Rosowski, 1991).

Z_C has been computed previously from simultaneous or non-simultaneous measurements of P_V and V_S in several mammalian species. By definition, U_S rather than V_S is needed to compute Z_C. Assuming piston-like motion of the stapes, U_S is deduced from V_S by multiplication of the stapes footplate area A_FP: U_S=A_FPV_S. Estimates of Z_C have been computed from the combination of non-simultaneous measurements of P_V and V_S in guinea pig (Dancer and Franke, 1980), chinchilla (Ruggero et al., 1990), human temporal bone (Puria et al., 1997), and gerbil (Overstreet and Ruggero, 2002; Decraemer et al., 2007). Simultaneous measurements of P_V and V_S were performed in only a few individuals from cats (Lynch et al., 1982) and gerbils (de La Rochefoucauld et al., 2008), as well as in human temporal bone (Aibara et al., 2001; Puria, 2003; Nakajima et al., 2009). In these studies, estimates of Z_C are different than in studies combining non-simultaneous measurements of P_V and V_S: In human temporal bone, estimates from simultaneous and non-simultaneous measurements showed differences in magnitude and phase (Puria et al., 1997; Aibara et al., 2001), but there were also important differences between the three studies using simultaneous measurements (Aibara et al., 2001; Puria, 2003; Nakajima et al., 2009). In gerbil, the magnitude of the non-simultaneous estimate (Overstreet and Ruggero, 2002) agreed with the simultaneous estimate (de La Rochefoucauld et al., 2008), but there were differences in the phase, especially above 6 kHz. Moreover, an estimate of Z_C from simultaneous measurements of P_V and V_S in one animal showed differences in its detailed structure from an estimate from non-simultaneous measurements in the same animal (de La Rochefoucauld et al., 2008). Based on these comparisons, it seems important to measure P_V and V_S simultaneously to characterize Z_C more precisely.

We measured P_V and V_S simultaneously in chinchillas, a species whose hearing range (20 Hz–30 kHz) is similar to that of humans, using miniature fiber-optic pressure sensors and laser Doppler vibrometry in response to acoustic stimulation. Based on these measurements, we present a new estimate of G_ME in this species, extending previous measurements to higher frequencies, and, to our knowledge, the first estimate of Z_C in chinchillas derived from simultaneous measurements. G_ME had a magnitude of the order of 30 dB and a phase close to 0 between 300 Hz and 4 kHz, similar to the predictions of a simple transformer ratio model. Our G_ME was similar to published data in the chinchilla (Décory, 1989; Décory et al., 1990) at stimulus frequencies of 500 Hz to 3 kHz and 12 to 20 kHz, but had a larger magnitude at other frequencies. Z_C had a flat magnitude and a phase close to 0, which are the characteristics of an acoustic resistance, over a broad frequency range. Our Z_C had a larger magnitude with a smaller slope below 1 kHz and a phase angle closer to 0 than a previous estimate from non-simultaneous measurements of P_V and V_S (Ruggero et al., 1990). We also compare measurements of auditory threshold in chinchilla (Miller, 1970) with estimates of the sound pressure required to produce a constant P_V across frequency, a constant V_S, and a constant power into the vestibule. Overall, these new findings extend our knowledge of the chinchilla middle ear, and, together with other measured middle and inner ear mechano-acoustic quantities in this species, help draw a more complete picture of middle ear function. Understanding sound transfer through the middle ear could eventually improve therapeutic approaches to diseases and malfunctions of the middle ear.

MATERIALS AND METHODS

Fiber-optic pressure sensors

Measurements of P_V are constrained by the limited space available for the pressure sensors (the volume of the chinchilla vestibule is on the order of 5 μl: see Plontke et al., 2002) and the fragility of the inner and middle ear structures. We chose to use fiber-optic pressure sensors (Olson, 1998) because they have good sensitivity, good high frequency response (up to about 100 kHz), and because they are very small. Their small size (about 145 μm in diameter) ensures the following:

• (a)minimal disruption of the pressure field in the inner ear at frequencies in the chinchilla’s hearing range, because of both the small size (145 μm is less than 1% of the wavelength in water at 30 kHz) and the relatively high impedance associated with such a small microphone, and
• (b)minimal damage to the middle and inner ear structures during insertion into the vestibule.

The fiber-optic pressure sensors were fabricated following the techniques of Olson (1998). They are composed of a glass capillary tube (145 μm outer diameter) with a gold-coated polymer diaphragm affixed to one end. A single optical fiber (100 μm outer diameter) is inserted into the other end. The optical fiber is spliced to a Y coupling. A light emitting diode (LED) attached to one coupler branch produces incoherent light, and a photodiode attached to the other branch measures the light reflected from the diaphragm. Sound pressure flexes the diaphragm and modulates the reflected light.

Similarly to Olson (1998), calibration of the sensors was performed in water, according to the method described by Schloss and Strasberg (1962): The sensor is immersed in a column of liquid that is shaken vertically by a known amount (Brüel & Kjær Vibration Calibration Exciter Type 4290 with built-in reference accelerometer; Brüel & Kjær Measuring Amplifier Type 2525); the pressure at the diaphragm depends on both the depth of immersion and on the acceleration of the column. Calibration functions were defined as the ratio between the sound pressure at the sensor diaphragm and the voltage at the output of the photodiode. For typical sensors, the calibration function magnitude was essentially flat up to 10 kHz, with a value of about 150 dB re 20 μPa∕V, and then decreased between 10 and 30 kHz by about 8 dB. The phase was roughly flat and close to 0 on the entire range of measurements. In earlier experiments, we also calibrated the sensors in air, against a reference microphone of known sensitivity. In our experience, the two calibration methods (in water or in air) led to very similar sensitivities in magnitude and phase. Therefore, we only performed water calibration in subsequent experiments.

The main issues with the fiber-optic pressure sensors are their fragility and their stability. We periodically recalibrated the sensor to test for variations in its sensitivity. We report data only from sensors whose calibration was stable throughout the measurement session: In three animals, there was less than a 2 dB variation over the entire tested frequency range between repeated calibrations throughout the experiment; in two other animals, calibration was repeatable within 2 dB in the mid- and high frequencies, and within 5–8 dB in the lows; in another animal, calibration was repeatable within 10 dB. The calibration function used to compute P_V was the closest in time to the measurement.

Stability of the pressure sensor was also continuously monitored via the direct current (DC) component of the sensor photodiode output. In many sensors, a large change in the DC value was correlated with a change in sensitivity. Therefore, we report P_V measurements for which the DC value of the sensor during the measurements was close to the DC value during calibration: In the 6 animals from which data are presented, the change in DC between calibration and measurement was less than 8% (8% in one animal, 4% in two animals, 3% in one animal, 2% in one animal, and <1% in one animal).

Laser Doppler vibrometry

To measure stapes velocity, we used a single-beam laser Doppler vibrometer (Polytec CLV 700) aimed at small reflective plastic beads (<50 μm diameter) placed on the posterior crus and the footplate. Sound-induced velocity of the stapes was measured using the Doppler shift of light reflected from the moving beads. The sensitivity of the laser was checked by comparing the velocity of a shaker as measured by the laser with its acceleration as measured by the reference accelerometer. The sensitivity was constant over the frequency range of measurement.

Our surgical exposure of the stapes allowed measurement of the piston-like component of stapes motion within an angle of about 30° relative to the piston-like direction. The volume velocity U_S was estimated assuming piston-like motion of the stapes. In this case, the volume velocity U_S is simply the product of measured linear velocity V_S and the average area of the chinchilla footplate (A_FP=2 mm², Vrettakos et al., 1988).

Animal preparation

The surgeries and experiments were performed in accordance with guidelines published by the U.S. Public Health Service and were approved by the Massachusetts Eye and Ear Infirmary (MEEI) Animal Care Committee.

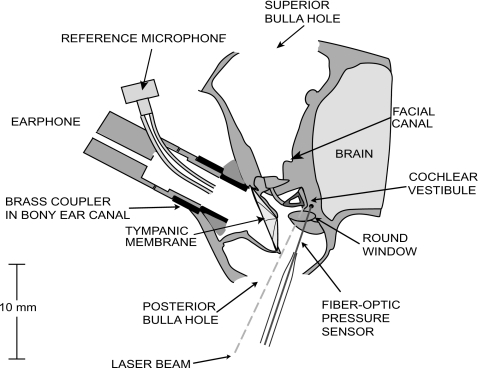
The animals were anesthetized with intraperitoneal injections of sodium pentobarbital (50 mg∕kg) and Ketamine (40 mg∕kg). After a tracheotomy to facilitate respiration, an opening was made in the superior bulla. The tensor tympani muscle and the tympanic branch of the facial nerve, which innervates the stapedius muscle, were cut to prevent random contractions of these muscles during the experiment (Rosowski et al., 2006). A second hole in the posterior bulla was made to view the stapes and round window. Part of a bony wall posterior to the round window, in which the facial nerve passes, was removed in order to see the wall of the vestibule posterior to the stapes. In doing so, extreme care was taken to avoid pulling or damaging the stapedius tendon. A hole for placement of the P_V fiber-optic pressure sensor, of approximate diameter 180–250 μm, was made in the vestibule 1–2 mm away from the oval window with a fine sharp pick (Fig. 1). On several occasions, we verified that this hole opened into the vestibule by breaking the annular ligament and pushing the stapes into the vestibule; the footplate was then seen through the P_V hole.

Figure 1.

Schematic of the animal preparation. The bulla was opened superiorly and posteriorly, and a hole approximately 200 μm in diameter was made in the vestibule for the fiber-optic pressure sensor. The cartilaginous ear canal was cut and a brass tube was glued in the bony ear canal to allow repeatable couplings of the earphone delivering the sound stimuli. A built-in reference microphone measured sound pressure in the ear canal. A laser Doppler vibrometer was aimed at reflective beads placed on the posterior crus and the footplate of the stapes.

The cartilaginous ear canal was cut and a brass tube was placed and glued in the bony ear canal to allow repeatable couplings of the earphone delivering the sound stimuli. The middle ear was open during the measurements.

Stimuli and responses

In early experiments we used an electrodynamic hearing-aid earphone (Knowles, Itasca, IL) coupled to a power amplifier as our sound source. In later experiments, an electrostatic earphone (Tucker-Davis Technologies Type EC1, driven by a Tucker-Davis Technologies ED1 earphone driver) was used. The selected speaker was sealed to the brass tube in the ear canal, and the input of the speaker driver was coupled to the output of a programmable attenuator (Tucker-Davis Technologies Type PA5). We used LABVIEW (National Instruments, Austin, TX) to construct stimuli, control the attenuator, and measure the voltage outputs of our different sensors. The stimuli consisted of stepped pure tones (six points∕octave) from 62.5 Hz to 28.5 kHz, with sound pressure levels (SPLs) ranging from 65 to 110 dB SPL at the entrance of the brass tube. The duration of each tone was 1–2 s; the responses were averaged and Fourier analysis was used to quantify the magnitude and phase of the fundamental and harmonic components of the response as well as the stimulus noise floor.

Correction of ear canal pressure measurements

Although the middle ear pressure gain G_ME is defined as the ratio between P_V and P_TM (the sound pressure at the TM near the umbo), during most of our measurements, we measured ear canal sound pressure (P_EC) using a reference microphone built into the entrance of the brass coupling tube, about 7 mm from the umbo (Fig. 1). At frequencies less than 5 kHz (where the wavelength of sound is about 70 mm), the sound pressure in the ear canal and the sound pressure near the TM are essentially equal (P_TM∼P_EC), but at higher frequencies significant differences occur between P_TM and P_EC. To account for these differences, we used an average correction computed from simultaneous measurements of P_TM and P_EC in nine ears used in other studies (included in Ravicz et al., 2009) to compute a correction factor P_TM∕P_EC that was used to correct our measurements of G_ME and SVTF (see Sec. 4). No correction was necessary for Z_C, whose computation from simultaneously measured P_V and V_S does not involve P_TM.

Frequency range and choice of earphone

We estimated the signal-to-noise ratios (SNRs) for all of our measured quantities (P_V, V_S, and P_EC) by comparing the magnitude of the response spectrum at the stimulus frequency to the magnitude at nearby frequencies that were not in the stimulus and not harmonics of the stimulus frequencies. The electrodynamic earphone used in earlier experiments had low outputs at frequencies above 15 kHz, which led to low signal levels and low SNRs in our measurements at higher frequencies. In later experiments, we used an electrostatic earphone and obtained a good SNR over most of the stimulus frequency range (out to 28.5 kHz).

We include only data for which the SNR was larger than 10 dB. Moreover, in all the plots presented in this paper, we marked with a circle all the mean data points for which the SNR of the measurements involved was less than 20 dB in at least one of the animals. We further tested the reliability of the measurements by testing their repeatability: In most cases, G_ME and SVTF were nearly exactly repeatable when the SNR was greater than 10 dB in all channels, but in some cases, we further restricted the frequency range to exclude data points that lacked repeatability.

Statistics

The mean and standard deviation of G_ME’s decibel magnitude was computed from the decibel magnitudes of each animal. For SVTF and Z_C, we used the mean and standard deviation of the logarithm of the magnitudes, and took their exponential to go back to the linear domain. For the phases of those three functions, we computed the means and standard deviations of the unwrapped individual phases. In all cases, we included only the data points that passed our SNR and repeatability criteria in the computation of the mean and standard deviation. Therefore, the number of animals included depended on frequency and was, in particular, lower at high frequencies.

In our plots, we usually show the mean and 95% confidence interval (CI). The 95% CI is defined by two standard errors of the mean above and below the mean. We computed the standard error by dividing the standard deviation by the square root of the frequency-dependent number of animals.

RESULTS

Thirteen animals were used in this study. Among these, four had their middle or inner ears damaged during surgery. In three other experiments the pressure sensor proved unstable. We therefore present G_ME, SVTF, and Z_C results in six animals. For each experiment, we restrict the results shown to the frequency range over which the measurements were repeatable and had a SNR larger than 10 dB (see Sec. 2).

Middle ear pressure gain G_ME

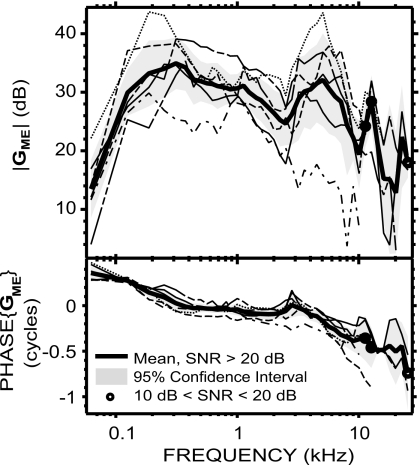
G_ME=P_V∕P_TM was computed from simultaneous measurements of P_V and P_EC, and corrected for the differences between P_TM and P_EC, as explained in Sec. 2. G_ME in each animal is plotted in Fig. 2. Both magnitude and phase angle were similar among the six animals. The 95% CI was between 2 and 8 dB for the magnitude over almost the entire frequency range of measurement, and less than 0.1 cycles for the phase below 8 kHz. One animal was an outlier with low gain magnitude and more negative phase angles at high frequencies. The mean |G_ME| across these six ears ranged from 13 to 35 dB over the measurement frequencies. Between 62 and 125 Hz, the mean |G_ME| rapidly increased from 14 dB to 30 dB, with a slope of 16 dB∕octave. It then continued to increase with a slower 4 dB∕octave slope to reach a maximum of 35 dB at 375 Hz. Between 375 Hz and 2.5 kHz, |G_ME| slowly decreased to 25 dB with an average slope of −3.7 dB∕octave. It then increased sharply to reach 32 dB at 5 kHz (10 dB∕octave slope), and decreased sharply to reach a 19 dB local minimum at 10 kHz (−13 dB∕octave slope). Above 10 kHz, the mean |G_ME| displays a 28 dB peak at 12.7 kHz, a 13 dB notch at 20.2 kHz, and a 22 dB peak at 22.6 kHz.

Figure 2.

G_ME in six animals (individual data: thin lines; mean: thick solid line; 95% CI: shaded areas). Data points with a SNR<10 dB were not included; frequencies for which SNR<20 dB in at least one of the individual data point were marked by a circle (see Sec. 2).

G_ME’s mean phase angle (which is the phase difference between P_V and P_TM) decreased from 0.4 to 0 cycles from 62 to 300 Hz, was near 0 between 0.3 and 3 kHz, and accumulated with frequency above that, reaching −0.4 cycles by 10 kHz and −0.7 cycles by 25 kHz. The ripple near 3 kHz associated with a dip in |G_ME| is likely due to a resonance between the bulla air space and the open holes in the bullar walls (Rosowski et al., 2006). The group delay2 was about 45 μs between 500 Hz and 2 kHz and about 61 μs between 3 and 9 kHz.

von Helmholtz (1877) proposed that the middle ear works as an acoustico-mechanical transformer composed of several levers in cascade, to increase sound pressure from the ear canal to the cochlea. It is interesting to note that our mean |G_ME| reached a maximum comparable to this “transformer ratio” of 38 dB computed from anatomical data (Vrettakos et al., 1988)3 at 300 Hz (see Fig. 2) and was within 10 dB of this value over a wide frequency range (roughly 125 Hz–8 kHz). Moreover, the phase was close to 0 (within 0.1 cycles) in a similar frequency range (roughly 250 Hz–4 kHz), which is also consistent with an ideal transformer at these frequencies. However, outside this frequency range, the magnitude and phase characteristics largely differed from that of an ideal transformer, confirming that the ideal transformer hypothesis does not accurately describe middle ear function at all frequencies (e.g., Funnell, 1996).

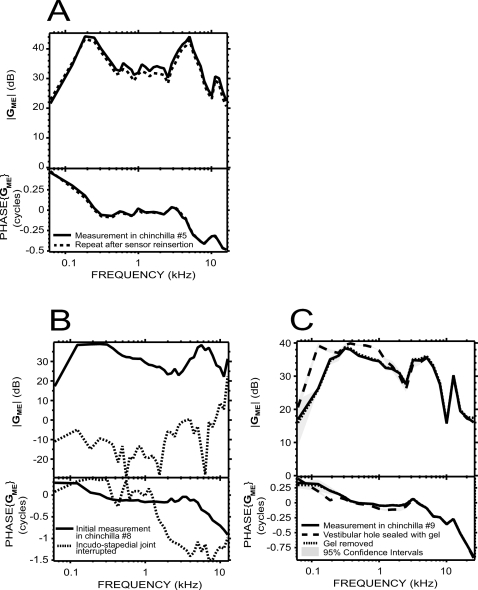
We tested the stability of the preparation and the pressure measurement sensor by taking the pressure sensor out of the inner ear, recalibrating, reinserting the sensor into the vestibule, and remeasuring P_V. Figure 3A compares the initial and repeated measurements in an experiment where the pressure sensor was very stable (recalibration sensitivity was within 2 dB of the original sensitivity estimate, and the photodiode DC output was constant). |G_ME| upon reinsertion was within 2 dB of the original measurement over the entire range of frequency. The phase angles were also almost identical, with variations of less than 0.01 cycles at most test frequencies. These results are consistent with a highly stable preparation.

Figure 3.

G_ME controls. (A) Stability: comparison of G_ME measured in chinchilla No. 5 before (solid line) and after (dotted line) taking the pressure sensor out of the vestibule and recalibrating it. Differences were less than 2 dB in magnitude and less than 0.01 cycles in phase. (B) Effect of interrupting the ossicular chain: G_ME in chinchilla No. 8 with an intact ossicular chain (solid line), and after interrupting the incudo-stapedial joint (dotted line). (C) Effect of plugging the vestibular hole on G_ME: in one animal (chinchilla No. 9), after sealing around the pressure sensor with a gel of high molecular weight (dashed line), there was a limited increase in |G_ME|. After removing the gel (dotted line), G_ME went back to baseline (solid line). The 95% CI (shaded areas) represent the variability of repeated measurements in the same condition.

In some experiments we also verified that the gain we measured was indeed due to the middle ear and not some other artifactual signal path (e.g., bone conduction) by measuring G_ME before and after interrupting the incudo-stapedial joint. Figure 3B shows an example from one experiment. Before the interruption, G_ME had the characteristic magnitude and phase described earlier. After interrupting the incudo-stapedial joint (and making sure that the lenticular process was not touching the stapes head), |G_ME| dropped dramatically at all frequencies, essentially reaching the noise floor of our sensor (about 50 dB below the pressure measured with an intact joint, except as shown). This control is a clear demonstration that we measured ossicular sound conduction.

To determine the influence of the vestibular hole with the inserted pressure sensor on G_ME, we tried to seal the pressure sensor in place with dental impression material (Jeltrate), dental cement, or a sodium hyaluronate viscoelastic gel of high molecular weight (Healon GV 14 mg∕ml). With a hole of approximate diameter 180–250 μm and a 145 μm diameter sensor, the area of the hole not occupied by the sensor was roughly 0.009–0.026 mm². In most preparations, it was not possible to seal around the sensor effectively because of the limited space available and because the outward flow of perilymph pushed the sealant material away. In one case, as shown in Fig. 3C, the viscoelastic gel appeared to cover most of the hole, resulting in an increase in P_V, and therefore in G_ME, especially at frequencies below 1 kHz: |G_ME| increased by as much as 15 dB at 125 Hz and the phase decreased by about 0.15 cycles at 200 Hz. After removing the gel, P_V went back to the lower level, and G_ME was very similar in amplitude and phase to the initial measurement. Several other attempts at sealing the hole produced smaller changes. Overall, the effect of sealing the hole on G_ME was small and limited to the lowest measured frequencies.

Stapes velocity transfer function SVTF

SVTF=U_S∕P_TM was computed in each animal from the measured stapes velocity V_S and a 2 mm² mean stapes footplate area as described in Sec. 2, normalized by the measured P_EC, and corrected by the P_TM∕P_EC transfer function. V_S was measured in two conditions:

• (1)with an intact vestibule, and
• (2)after the vestibular hole was drilled and the pressure sensor inserted in the vestibule.

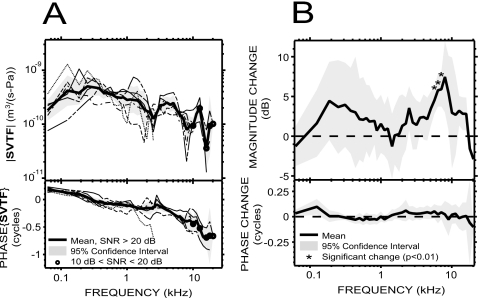
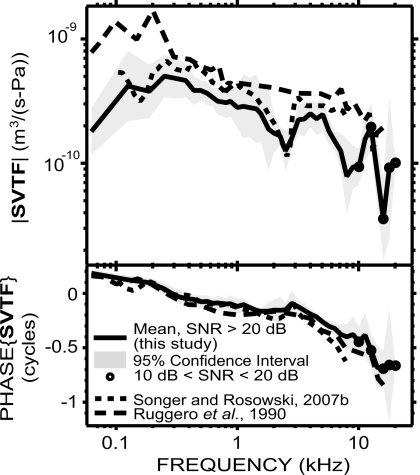
In the intact vestibule condition [Fig. 4A], SVTF was very similar among the six ears, except for one phase outlier (the outlier is terminated at 2.5 kHz due to SNR problems). The range of the 95% CI was within a factor of 2–3 for the magnitude, and less than 0.1 cycles for the phase angle (equal to the phase difference between V_S and P_TM), over most of the frequency range of measurement. |SVTF| increased by about a factor of 2.8 with frequency over the two-octave range of 62–250 Hz, and the phase decreased from +0.25 to 0 cycles over the same frequency range. The phase of the admittance (inverse of an impedance) of a combination of compliance and resistance is between 0 and +0.25 cycles. SVTF is an admittance as it is the ratio of a volume velocity (U_S) to a pressure (P_TM); therefore the phase over 62–250 Hz is consistent with a compliance-resistance combination. |SVTF| decreased by a factor of 3.4 over the three octaves between 0.3 and 2.4 kHz and the phase was between 0 and −0.25 cycles, consistent with a mass-resistance combination. |SVTF| increased by a factor of 1.7 between 2.5 and 5 kHz, and decreased by a factor of 3 between 5 and 8 kHz, while the phase decreased toward −0.4 cycles. The notch in |SVTF| associated with a ripple in the phase near 3 kHz is similar to what was observed in G_ME and is consistent with a resonance of the compliant air within the bulla and the acoustic mass associated with the holes in the bullar wall. Between 8 and 20 kHz, |SVTF| is characterized by a peak centered at 12.7 kHz and a notch centered at 16 kHz; the phase further decreased, reaching −0.7 cycles by 14 kHz, and then flattened. The group delay was about 51 μs between 500 Hz and 2 kHz and about 44 μs between 3 and 9 kHz.

Figure 4. SVTF.

in six animals. (A) SVTF before the vestibular hole was made (individual data: thin lines; mean: thick solid line; 95% CI: shaded areas). (B) Mean effect of introducing the vestibular hole on SVTF in six animals. We computed the change in magnitude and phase before the hole was made and afterward with the pressure sensor in place. Changes in magnitude were significant (p<0.01) only in a small region around 6 kHz (asterisks).

To assess the influence of the hole in the vestibule wall on SVTF, we compared measurements of SVTF before the hole was made and afterward with the pressure sensor in place. We found small (<7 dB) increases in |SVTF| in the condition with the vestibular hole [Fig. 4B], which is consistent with the hole decreasing cochlear input impedance and facilitating stapes motion. A paired t-test performed at each frequency showed that the changes were significant (p<0.01) only in a small region around 6 kHz.

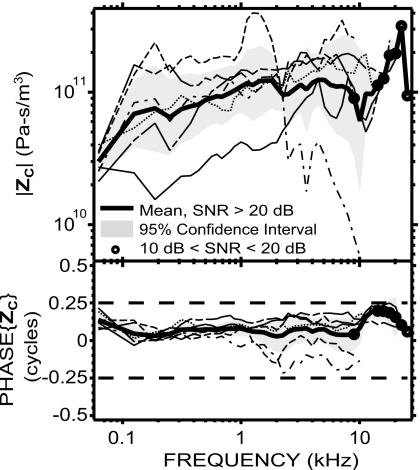
Cochlear input impedance Z_C

Z_C=P_V∕U_S was computed from simultaneous measurements of P_V and V_S. As mentioned earlier, the computation of Z_C does not use P_TM; therefore our results are not affected by the correction employed to convert P_EC to P_TM. Z_C was similar among six ears (Fig. 5), except for a low outlier for |Z_C| in one ear at low frequencies and a low outlier in a different ear at high frequencies (corresponding to the ear with a low |G_ME| at high frequencies).

Figure 5.

Z_C in six animals (individual data: thin lines; mean: thick solid line; 95% CI: shaded areas) from simultaneous measurements of P_V and V_S. Z_C was resistive (roughly flat magnitude, phase close to 0) up to at least 10 kHz.

The average |Z_C| was about 10¹¹ acoustic ohms. The factor of 3 range of the 95% CI is similar to the range of 95% CI in G_ME and SVTF. Between 62 and 125 Hz, |Z_C| increased and the phase (equal to the phase difference between P_V and U_S) decreased from close to 0.125 cycles to about 0; this is consistent with a mass-resistance combination (phase between 0 and +0.25 cycles) at the lowest frequency tested. |Z_C| was roughly constant with frequency between 125 Hz and 10 kHz, and the phase was near zero in this frequency range; this is consistent with a resistance. |Z_C| increased sharply from 10 to 22 kHz and fell sharply at 25 kHz. Consistent with the input impedance of a passive system, the phase had values between −0.25 and +0.25 cycles at all frequencies measured.

DISCUSSION

We simultaneously measured the sound pressure in the vestibule P_V and stapes velocity V_S in chinchilla preparations in response to acoustic stimulations. The middle ear gain G_ME, stapes velocity transfer function SVTF, and cochlear input impedance Z_C were computed from these measurements in six ears where the middle and inner ear structures were intact and the pressure sensors stable. In this section, we (a) discuss the role of the ear canal correction we applied to SVTF and G_ME; (b) address some other factors that may bias our high frequency responses; (c) assess the influence of the vestibular hole on our estimates in the context of (d) an acoustic model; (e) compare our results with other studies in chinchilla and (f) other mammals; and (g) test the hypothesis that auditory thresholds can be predicted by P_V, U_S, or the acoustic power delivered to the cochlea.

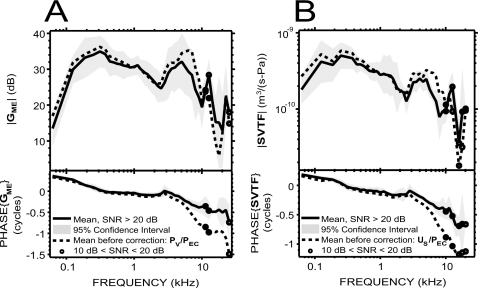
Effect of ear canal correction on G_ME and SVTF

The G_ME and SVTF data presented in Figs. 24A, respectively, have been corrected by the mean ratio of sound pressures measured near the umbo (P_TM) and about 7 mm from the umbo (P_EC) measured in nine other ears (a location that corresponded to the P_EC microphone in these experiments), as described in Sec. 2. The effects of this P_TM∕P_EC correction function on G_ME and SVTF are shown in Fig. 6. As expected, the effect was small below 3 kHz, because the wavelength of sound at these low frequencies is much longer than the dimensions of the ear canal and the sound pressure is approximately constant throughout the ear canal (e.g., Beranek, 1986). Above 3 kHz, the correction caused significant changes in both G_ME and SVTF and reduced the measured group delay of both G_ME and SVTF by about 45 μs.

Figure 6.

Effect of an ear canal correction (to account for the differences between P_EC and P_TM—see Sec. 2) on G_ME and SVTF. (A) Mean G_ME before (dotted line) and after (solid line, from Fig. 2) correction. (B) Mean SVTF in the intact vestibule condition before (dotted line) and after [solid line, from Fig. 4A] correction.

Above 3 kHz, the corrected and uncorrected mean |G_ME|s [Fig. 6A] are similar in shape, but the correction had the effect of (a) shifting the 7 kHz maximum to 5 kHz, while decreasing |G_ME| by 4 dB on average between 2 and 10 kHz, (b) shifting the 11.5 kHz maximum to 12.5 kHz, while increasing |G_ME| by 4 dB between 10 and 20 kHz, and (c) shifting the 18 kHz minimum to 20 kHz, while increasing |G_ME| by about 7 dB. The effects of the correction on |SVTF| [Fig. 6B] above 3 kHz were to enhance the maximum at 5 kHz and the minimum at 16 kHz. High frequency correction effects are discussed further below.

High frequency responses

The high frequency responses we obtained for G_ME and SVTF are characterized by an increased variance in magnitude and∕or phase relative to lower frequencies. For |G_ME|, the 95% CI was 7–12 dB above 16 kHz, and generally 3–6 dB at lower frequencies (Fig. 2). Similarly for the phase, the 95% CI was greater than 0.1 cycles above 10 kHz, smaller below. As for SVTF, the 95% CI of the magnitude was roughly similar across frequencies, but the 95% CI of the phase was usually higher above 9 kHz [Fig. 4A]. These increased confidence intervals at high frequencies may be due to several factors.

• (i)Differences between ear canal sound pressure at our measurement location P_EC and near the TM P_TM: The correction factor P_TM∕P_EC we used to account for these differences was averaged over measurements in nine ears that were different from the ears in which we made the P_V and V_S measurements reported here. The peaks and valleys observed in |P_TM∕P_EC|, in particular, above 10 kHz, are dependent on the anatomy of the ear canal, which varies among individuals. Consequently, we can expect the correction to be imperfect.
• (ii)Fewer animals were included: In earlier experiments, the earphone we used did not provide sufficient sound pressure stimulus at frequencies above 15 kHz, so there are fewer data at high frequencies with a SNR greater than 10 dB (our criteria: see Sec. 2). In particular, for G_ME, data from six animals were included up to 10 kHz, but only two animals met the SNR criterion above 22 kHz; for SVTF, six animals were included up to 9 kHz, two are included at 20 kHz, and only one above that. The breakdown in number of animals included in the estimates of Z_C is similar to that for SVTF.
• (iii)The signal-to-noise ratios in the included animals were lower: The data points for which the SNR is between 10 and 20 dB are all concentrated in the high frequencies (see the circles in Figs. 24A, 5). Even though a 10 dB SNR means that the signal was more than three times higher than the noise, noise may have contributed to the increased variance at high frequencies.
• (iv)For U_S, we assume piston-like motion of the stapes, and measure velocity in only one direction. During an experiment, the laser angle was set so as to have a clear view of reflectors on the stapes footplate or posterior crus. The actual measurement angle was therefore highly dependent on the animal’s specific anatomy and position of the reflectors, usually within 30±10°. If the motion is truly piston-like, our measurements are not very sensitive to the laser beam angle. For example, measuring with a 30° angle relative to the piston axis introduces an error corresponding to a factor of cos(30°) or −1.2 dB in measuring the piston component, and small variations about that angle only produce small changes in estimated piston-like velocity: A 40° angle leads to an error in the estimate of piston-like velocity of −2.3 dB, while a 20° angle results in a −0.5 dB error. Therefore, if stapes motion was truly piston-like, the uncertainty on the measurement angle would only result in less than a 3 dB error for these angle values.

  Piston-like motion of the stapes is probably a valid assumption at low frequencies; however, it is unlikely that this assumption is valid at high frequencies, and other modes that cause transverse and rotational motion of the stapes at the measurement points may make large contributions to the measured V_S (e.g., in human temporal bone: Heiland et al., 1999; Hato et al., 2003; Chien et al., 2006; in gerbil: Decraemer et al., 2007; Ravicz et al., 2008; and in cat and cat temporal bone: Guinan and Peake, 1967; Decraemer et al., 2003; Decraemer and Khanna, 2003). The existence and variability of such non-piston modes of motion at high frequency could explain the larger variance for U_S and SVTF in that frequency range.

The 12 kHz peak and the 16 kHz notch we found in |SVTF| [Fig. 4A], as well as the sharp peak in |Z_C| at high frequencies (Fig. 5), may also be explained by complex motion of the stapes at high frequency. A hypothesis is that the rocking component of stapes motion above 12 kHz is significant, and would result in a measured linear motion of greater or smaller amplitude than the actual V_S, depending on the relative phase between the translational and rocking movements. This hypothesis is credible in light of the aforementioned studies in human temporal bone, gerbil, and cat; however, a detailed description of non-piston modes for the chinchilla has not been done.

Influence of the vestibular hole

It was necessary to make a hole in the vestibule to introduce the pressure sensor and measure P_V. Overall, the effects of the vestibular hole on G_ME and SVTF were small and limited in frequency: Sealing the hole in one ear produced a small increase in |G_ME| below 1 kHz [Fig. 3C], and introducing the hole produced an average increase in |SVTF| of less than 7 dB in 6 ears [Fig. 4B], which was not statistically significant (p<0.01) at most measured frequencies.

The changes we observed for SVTF were consistent with a study by Songer and Rosowski (2006). In that study, they looked at the effect of semi-circular canal dehiscence on SVTF in chinchillas. They found an increase in |SVTF| above 100 Hz that was maximal at frequencies between 150 and 500 Hz (5–10 dB), decreased with frequency between 500 and 1000 Hz to a value of roughly 2 dB, and persisted at about 2 dB above the intact case from 1 to 7 kHz. It could not be determined if the increase in |SVTF| persisted to higher frequencies because measurements were noisy above 7 kHz. In our study, the increase in |SVTF| had a similar shape below 1 kHz, but had a lower value (the maximum of the mean was less than 5 dB at these frequencies) and this lower value was not statistically significant. We also found a small 0.1-cycle increase in phase angle between 100 and 200 Hz, smaller but consistent with Songer and Rosowski’s (2006) 0.4 cycle increase at similar frequencies. The significant changes we observed in |SVTF| around 6–7 kHz are not visible in Songer and Rosowski’s study, but this could be because of their noise issue at these high frequencies. There are also differences in the experimental setup: We introduced a small (180–250 μm diameter) hole, partially plugged (by a 145 μm diameter pressure sensor), in the wall of the vestibule, whereas they introduced a larger (500 μm diameter) open hole in the narrow superior semi-circular canal about 3–5 mm from the vestibule. The smaller changes we observed at low frequencies (5 dB on average in our case, and ∼10 dB in their study) are consistent with the introduction of a smaller hole, while the lack of change at higher frequencies in the Songer and Rosowski data may be explained by the 3–5 mm narrow tube that separated their semi-circular canal dehiscence from the vestibule.

Changes in G_ME can be due to changes in P_V, P_EC, or both; similarly, changes in SVTF can be due to changes in V_S, P_EC, or both. It was not possible to ascertain accurately whether part of the changes we measured in G_ME and SVTF was due to changes in P_EC: Comparison of the measured P_EC before the hole is made and afterward is not valid because we had to move the animal’s head to make the hole, which sometimes changed the quality of the seal of the ear-phone in the brass-tube coupler, and affected P_EC. Nevertheless, in three experiments, P_EC was nearly identical after the hole was introduced. It is highly unlikely that a change in the ear canal coupler seal would perfectly counteract an effect of the hole on P_EC. There is a greater likelihood that in those experiments, the coupler seal did not vary after the hole introduction, and the changes we observed in G_ME and SVTF were mostly due to actual changes in P_V and U_S.

Predictions of an acoustic model of a hole in the vestibule

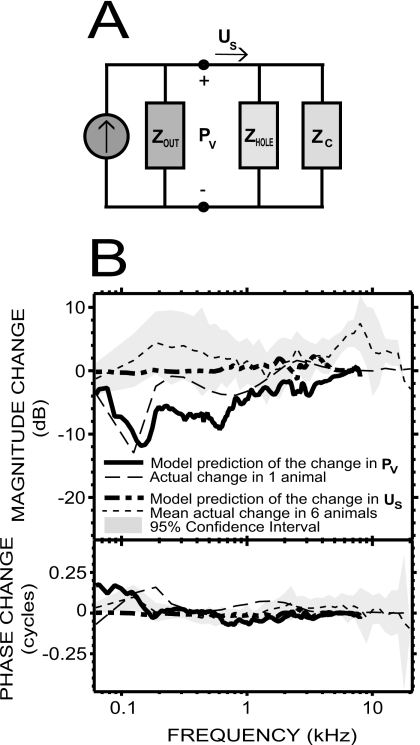
Direct measurement of the effect of the vestibular hole on G_ME, by plugging the hole around the pressure sensor, was difficult because of the proximity of the stapes, the flow of lymph out of the hole, and other anatomical and positional constraints. As we have controlled data for the effect of such plugging on G_ME in only one animal, we now describe a lumped-element acoustic model that provides further insight into the influence of the hole.

The model we use to investigate the effect of the open hole around our P_V sensor [Fig. 7A] represents the middle ear as a Norton equivalent circuit (made up of an equivalent volume-velocity source and a parallel impedance equal to the output impedance of the middle ear and sound source Z_out) that provides the stapes volume velocity U_S to the parallel combination of the inner ear load (Z_C) and the impedance of the hole (Z_hole). The pressure across each of the parallel branches of the circuit in Fig. 7A is P_V. The changes in P_V and U_S introduced by opening the hole can be inferred from this circuit by simple linear current divider equations. If we further assume the output of the source P_EC is not affected by the introduction of the hole, as suggested by some of our experiments (see Sec. 4C above), we can define

$$\frac{{\mathbf{P}}_{\mathbf{V},\text{hole}}}{{\mathbf{P}}_{\mathbf{V},\text{normal}}}=1-\frac{{\mathbf{Z}}_{\mathbf{C}}{\mathbf{Z}}_{\text{out}}}{{\mathbf{Z}}_{\mathbf{C}}{\mathbf{Z}}_{\text{out}}+{\mathbf{Z}}_{\mathbf{C}}{\mathbf{Z}}_{\text{hole}}+{\mathbf{Z}}_{\text{hole}}{\mathbf{Z}}_{\text{out}}},$$ (1a)

$$\frac{{\mathbf{U}}_{\mathbf{S},\text{hole}}}{{\mathbf{U}}_{\mathbf{S},\text{normal}}}=1+\frac{\mathbf{Z}_{\mathbf{C}}{}^{\mathbf{2}}}{{\mathbf{Z}}_{\mathbf{C}}{\mathbf{Z}}_{\text{out}}+{\mathbf{Z}}_{\mathbf{C}}{\mathbf{Z}}_{\text{hole}}+{\mathbf{Z}}_{\text{hole}}{\mathbf{Z}}_{\text{out}}},$$ (1b)

where these ratios represent the change in G_ME and SVTF.

Figure 7.

Model predictions of the effect of the vestibular hole. (A) Simple model of the middle ear as a Norton equivalent circuit, providing volume velocity U_S to the parallel combination of the inner ear load (Z_C) and the impedance of the hole (Z_hole). The Norton equivalent is composed of an ideal volume-velocity source and the output impedance of the middle ear (Z_out). (B) Predictions of our simple model with a 180 μm diameter hole partially plugged by a pressure sensor (equivalent radius=53 μm) were at least qualitatively similar to the experimental changes we found in P_V and U_S [see text and Figs. 3C, 4B]: The changes in P_V were limited to low frequencies (solid and dashed-dotted lines); the changes in U_S were small (dashed and dotted lines).

These ratios depend on three unknown impedances: Z_C, Z_out, and Z_hole. We used estimates of Z_C and Z_out by Songer and Rosowski (2007a), which they computed based on a transmission matrix model of the middle ear, fed by measurements of ear canal pressure and stapes velocity in chinchillas below 8 kHz.4 To compute Z_hole, we modeled the hole as a lossy transmission line.5 This model was originally developed by Egolf (1977), and used to model fluid-filled tube segments by Songer and Rosowski (2007b). In our case, Z_hole is computed as follows:

$${\mathbf{Z}}_{\text{hole}}=\frac{\mathbf{A}{\mathbf{z}}_0+\mathbf{B}}{\mathbf{C}{\mathbf{z}}_0+\mathbf{D}},$$ (2)

with z₀ the termination impedance of the hole, and A, B, C, and D parameters depending on various thermodynamic parameters of the medium, frequency, and the dimensions of the hole. A detailed description of these parameters can be found in Songer and Rosowski (2007b).

The original model is for a tube of radius a and length l. For our purpose, this description is not entirely satisfying because the hole is partially obstructed by the pressure sensor. In order to apply the model, we computed an “equivalent radius” corresponding to the radius of a hole of cross-section area equal to the area of the annulus delimited by the pressure sensor and the circular edge of the hole. Specifically,

$$a_{\text{equivalent}}=\sqrt{a_{\text{hole}}{}^2-a_{\text{sensor}}{}^2},$$ (3)

with a_sensor=145∕2=72.5 μm the radius of the pressure sensor.

During the experiments, making the hole usually resulted in perilymph leaking out from the cochlea at a slow rate. Therefore, the termination impedance z₀ that we used was the mass of the fluid terminating the tube.6

The results obtained with this model share similarities with the experimental data for both P_V and U_S [Fig. 7B]. Introducing a 180 μm diameter hole (corresponding to the smallest hole size we achieved experimentally, and leading to a_equivalent=53 μm) reduced |P_V| near 150 Hz by about 10–12 dB, which is consistent with the 10–15 dB increase in the experimental data upon introduction of the gel to seal the hole. The effect of the hole was smaller as frequency increased, with less than a 3 dB difference by 1 kHz in both the experimental and predicted data. Nonetheless, the detailed shape of the predicted change in |P_V| is different from the measured change, where much of the differences come from frequency-dependent variations in Z_C and Z_out that originate in the details of the data used in their calculation (Songer and Rosowski, 2007a). As for the phase, the ∼0.15 cycles increase predicted by the model at 150 Hz is consistent with the experimental data around this frequency, but the measured and predicted changes differ slightly at other frequencies.

The predicted changes in U_S are very small: The change in phase was close to 0 over the entire frequency range of the data (except the first data point at 62 Hz), and the change in magnitude was less than 1 dB below 1.5 kHz, and between 1 and 2 dB at frequencies 1.5–8 kHz (except for a small notch of −1 dB at 2.5 kHz). This is consistent with the experimental data over a wide range of frequencies: The average change in six animals was about 5 dB in magnitude below 6 kHz, but not statistically significant at these frequencies, and the phase was close to 0. Nonetheless, the slightly larger and significant experimental changes obtained around 6 kHz were not predicted.

To conclude, the predictions of this simple model are qualitatively similar to the experimental data in frequency dependence, and the predicted and measured changes in magnitude and phase angle are quantitatively similar: The model predicts that the small acoustic leak created by the vestibular hole would change P_V magnitude by no more than 12 dB at low frequencies, and phase angle by generally less than 0.15 cycles, and would cause only very small changes in U_S over 62 Hz–8 kHz.

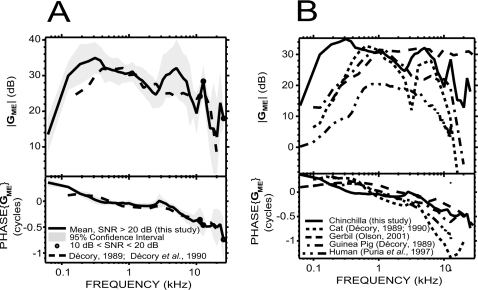
Comparison with other studies in chinchilla

Our G_ME results are very similar to a previous study in chinchilla by Décory (1989; Décory et al., 1990) between 500 Hz and 3 kHz, and between 8 kHz and 20 kHz, for both the magnitude and the phase [Fig. 8A]. Moreover, the slightly negative slope of |G_ME| between 500 Hz and 3 kHz, as well as the sharp decrease between 12 kHz and 20 kHz, was similar in both studies. Between 500 Hz and 3 kHz, the phase we measured was closer to 0 than Décory’s (1989; Décory et al., 1990), but the two did not differ by more than 0.1 cycles. Below 500 Hz, and between 3 and 8 kHz, we found a larger |G_ME|, by as much as 7 dB at 250 Hz and 8 dB at 5 kHz. The low frequency difference may be explained by a difference in the acoustic leak introduced by the vestibular hole (see Sec. 4D). The difference near 5 kHz may be due to the animal preparation in Décory’s (1989; Décory et al., 1990) study: In their study, the vestibular hole was drilled about 5.5 mm away from the base of the cochlea, at a location corresponding to the 5 kHz place along the tonotopic axis. Therefore, as they propose, their measurements around 5 kHz may have been biased by a component due to the peak of the basilar membrane traveling wave, whereas our measurements were performed through a hole closer to the oval window (within 1–2 mm), far from the peak of the traveling wave over most of the measurement range (Rhode and Recio, 2000).

Figure 8.

Comparison of our measurements of G_ME (solid lines) with other studies. (A) In chinchilla: comparison with a previous study by Décory (1989) and Décory et al. (1990): dashed line. The two data sets were very similar at stimulus frequencies of 500 Hz–3 kHz and 12–20 kHz, but different at other frequencies. (B) In other mammals: comparison with studies in cat, guinea pig (from Décory, 1989 and Décory et al., 1990: dotted and dashed-dotted lines), gerbil (from Olson, 2001: dashed line), and human temporal bone (from Puria et al., 1997: dashed-double dotted line). All these measurements were carried out with open holes in the bullar walls. The septum of the middle ear (Møller, 1965; Huang et al., 1997) was intact in the cat study.

Our measurements of SVTF are similar to those in a study by Songer and Rosowski (2007a) in magnitude as well as phase (Fig. 9). Our results are also roughly similar to those of Ruggero et al. (1990) at frequencies below 12 kHz. However, we generally obtained a smaller |SVTF|, especially below 300 Hz [(2–5)×10⁻¹⁰ m³∕(s Pa) in our study, and 6×10⁻¹⁰ to 2×10⁻⁹ in Ruggero et al., 1990] and near 3 and 8 kHz where we can see small notches in our study. These differences in magnitude may be due to the correction Ruggero et al. (1990) applied to take into account that the tensor tympani muscle was cut. Differences in the experimental setup may also explain some variations: We measured V_S with a laser Doppler vibrometer directed through the bulla, whereas Ruggero et al. (1990) used a Mössbauer source placed on the stapes footplate through a small slit in the TM. The bulla was widely open in both studies; however, the notch in our data at 2.5 kHz is likely the result of a bulla cavity-bullar-hole resonance (Rosowski et al., 2006). The notch we found between 14 and 18 kHz is in contradiction with another study by Ruggero et al. (2007), in which they measured ossicular vibrations in chinchillas up to 40 kHz and obtained a roughly flat SVTF magnitude at least up to 25 kHz. As we discussed earlier, our high frequency results are not as reliable as the lower frequency range of our data, which could explain the difference. Another potential reason for these differences at high frequency is that Ruggero et al. (2007) measured velocity of the lenticular process, and added gains measured across the incudo-stapedial joint, whereas we measured velocity from locations on the footplate and parts of the crura close to the footplate.

Figure 9.

Comparison of our measurements of SVTF (solid line) with previous studies in chinchilla by Songer and Rosowski (2007a): dotted line and Ruggero et al. (1990): dashed line. The differences in magnitude between ours and the Ruggero et al. (1990) study may be due to differences in the experimental setup (see text).

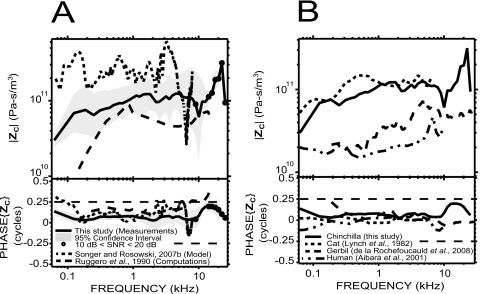
We compared our measured Z_C with previous estimates in chinchilla by Ruggero et al. (1990) and Songer and Rosowski (2007a). Our Z_C is a more direct estimate than either of these previous studies because we derived Z_C from simultaneous measurements of P_V and V_S whereas (1) Ruggero et al. (1990) combined their own V_S measurements (see Fig. 9) with Décory’s (1989; Décory et al., 1990)P_V measurements in other animals [see Fig. 8A], and (2) Songer and Rosowski (2007a) computed Z_C from a transmission matrix model of the middle ear fed by measurements of ear canal sound pressure and stapes velocity. The three data sets share many similarities [Fig. 10A]: In particular, the impedances are mostly resistive (phase angles close to 0 and approximately flat magnitude on a broad frequency range) with a magnitude of about 10¹¹ acoustic ohms; the phase angles of all three estimates are similar at frequencies between 0.3 and 4 kHz. There are also marked differences.

• (1)Ruggero et al.’s (1990) estimate has a lower magnitude than ours below 500 Hz and between 3 and 10 kHz, consistent with the larger |G_ME| we measured at these frequencies. Their phase angles are higher, and take values greater than +0.25 cycles above 7 kHz, whereas our estimate remains within ±0.25 cycles at all frequencies.
• (2)There is a consistent factor of 2–3 difference between the impedance computed by Songer and Rosowski (2007a) and our direct measurements. Their phase angle, although generally near 0, displays some irregularities near 3 kHz and near 7 kHz.

Figure 10.

Comparison of our measurements of Z_C (solid lines) with other studies. (A) In chinchilla: comparison with the prediction of a model by Songer and Rosowski (2007a): dotted line and computations by Ruggero et al. (1990): dashed line, who used their own U_S measurements and Décory’s (1989)P_V measurements in other animals [see Fig. 8A]. (B) In other mammals: comparison with studies in cat (from Lynch et al., 1982: dotted line), gerbil (from de La Rochefoucauld et al., 2008: dashed line), and human temporal bone (from Aibara et al., 2001: dashed-double dotted line).

Comparison with other mammals

G_ME is shown for chinchilla (our data) along with cat and guinea pig (from Décory, 1989; Décory et al., 1990), gerbil (from Olson, 2001), and human temporal bone (from Puria et al., 1997) in Fig. 8B. All these data were measured with the middle ear space open. The septum was intact in the cat study. |G_ME| is largest for the chinchilla, especially at low frequencies, but |G_ME| in all these species is similar (within 10 dB) for frequencies between 500 Hz and 3 kHz.

Except for human temporal bone, the overall shape of |G_ME| can be roughly described in these species by two more-or-less broad lobes. For chinchilla, the first lobe ranges from 62 Hz to 2.5 kHz and peaks at 35 dB, while the second one ranges from 2.5 to 9 kHz and peaks at a slightly lower value (32 dB); at higher frequencies, the gross tendency is a decrease in gain, but there is no evidence of a sharp roll-off. For cat and guinea pig, the first lobe has a larger maximum than the second one (about 32 dB for cat and 31 dB for guinea pig). The separation between the two lobes is more prominent in the cat data (the large notch centered at 3 kHz is related to a resonance between the tympanic middle ear cavity and the foramen in the septal wall of the bulla, e.g., Møller, 1965; Guinan and Peake, 1967; Huang et al., 1997). There are sharp high frequency roll-offs for cat and guinea pig. For the cat, the roll-off occurs at slightly lower frequencies (0 dB is reached by 15 kHz) than for guinea pig. For the gerbil data, the separation between the two lobes is at about 7 kHz, but the second lobe extends to at least 46 kHz [data not shown in Fig. 8B] and there is no evidence of a roll-off at these frequencies. The more-or-less pronounced notch separating the two lobes in the animal data described above is likely due to a resonance between the bulla and the open hole in the bullar wall (e.g., Møller, 1965; Ravicz et al., 1992; Rosowski et al., 2006).

The phases of G_ME in these species have similarities in shape, but the decrease with frequency varies across species (fastest for the cat and slowest for the gerbil). The average group delay between 0.2 and 10 kHz is about 52 μs in our study, 131 μs in cat, 51 μs in gerbil, 82 μs in guinea pig, and 92 μs in human. For cat and guinea pig, the phase increases slightly at high frequency after reaching a minimum. It is difficult to tell whether this increase is real or if it is an artifact of phase unwrapping.

We compared our Z_C results with other studies where P_V and V_S were simultaneously measured [Fig. 10B] in cat (from Lynch et al., 1982), gerbil (from de La Rochefoucauld et al., 2008), and human temporal bone (from Aibara et al., 2001). Z_C in chinchilla and cat are very similar up to 8 kHz for both magnitude and phase. For all these species, the magnitudes are approximately flat with frequency and the phase angles close to 0. The mostly resistive cochlear input impedance in all those mammalian species ensures that most of the energy transmitted through the middle ear is dissipated into the cochlear fluid, and may be important for cochlear traveling wave propagation (Décory, 1989; de La Rochefoucauld et al., 2008).

Acoustic power W_C, P_V, U_S, and the audiogram

We tested the hypothesis that the shape of the audiogram is set by a constant threshold value of some input quantity such as the average acoustic power delivered to the cochlea W_C (Khanna and Tonndorf, 1969; Rosowski, 1991), P_V, or U_S.

W_C can be computed from P_V and the cochlear input impedance Z_C as follows:

$$W_C=\frac{1}{2}\text{Re}\left\{{\mathbf{P}}_{\mathbf{V}}\mathbf{U}_{\mathbf{S}}{}^{*}\right\}=\frac{1}{2}{\left|{\mathbf{P}}_{\mathbf{V}}\right|}^2\text{Re}\left\{\frac{1}{{\mathbf{Z}}_{\mathbf{C}}}\right\},$$ (4)

where Re{X} indicates the real part of X. In terms of our measured quantities,

$$\frac{W_C}{{\left|{\mathbf{P}}_{\mathbf{\text{TM}}}\right|}^2}=\frac{1}{2}{\left|\frac{{\mathbf{P}}_{\mathbf{V}}}{{\mathbf{P}}_{\mathbf{\text{TM}}}}\right|}^2\text{Re}\left\{\frac{1}{{\mathbf{Z}}_{\mathbf{C}}}\right\}=\frac{1}{2}{\left|{\mathbf{G}}_{\mathbf{\text{ME}}}\right|}^2\text{Re}\left\{\frac{1}{{\mathbf{Z}}_{\mathbf{C}}}\right\},$$ (5)

and the sound pressure at the TM P_TM,0 required to produce a criterion value of acoustic power W_C,0 is

$$\left|{\mathbf{P}}_{\mathbf{\text{TM}},0}\right|=\sqrt{\frac{W_{C,0}}{\frac{1}{2}{\left|{\mathbf{G}}_{\mathbf{\text{ME}}}\right|}^2\text{Re}\left\{\frac{1}{{\mathbf{Z}}_{\mathbf{C}}}\right\}}}.$$ (6)

By definition of G_ME and SVTF, the sound pressure at the TM P_TM,0 required to produce a criterion value of vestibular pressure P_V,0 or of stapes volume velocity U_S,0 is given by

$${\mathbf{P}}_{\mathbf{T}\mathbf{M},0}=\frac{{\mathbf{P}}_{\mathbf{V},0}}{{\mathbf{G}}_{\mathbf{\text{ME}}}},$$ (7)

$${\mathbf{P}}_{\mathbf{\text{TM}},0}=\frac{{\mathbf{U}}_{\mathbf{S},0}}{\mathbf{\text{SVTF}}}$$ (8)

We compare free-field sound pressure at auditory threshold in chinchilla (Miller, 1970) with the sound pressure required to produce a constant level of W_C [by Eq. 6], P_V [by Eq. 7], and U_S [by Eq. 8]. A complication is that the chinchilla audiogram from Miller (1970) was measured in free field, whereas our experiments were done with the sound stimuli specified at the TM. To account for the differences between free-field pressure P_FF and ear canal pressure near the TM P_TM, we used an average head related transfer function (HRTF) measured in the chinchilla by von Bismark and Pfeiffer (1967). This HRTF quantifies the filtering effect of the head and pinnae on the incoming sound. Another complication is that all our measurements were done with the bulla open, whereas Miller’s (1970) audiogram was measured in behaving animals with an intact bulla. We used a correction factor from Ruggero et al. (1990) to account for the effect of opening the bulla on G_ME and SVTF: |G_ME| and |SVTF| in the open bulla condition were larger than in the closed bulla condition by as much as 16 dB in the low frequencies; the effect was less than 3 dB above 600 Hz.

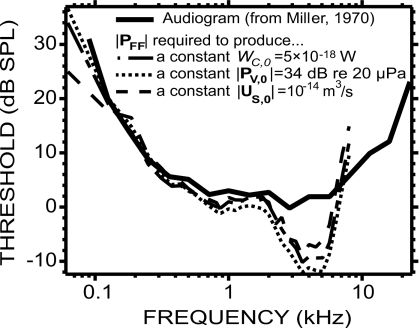
Figure 11 compares three free-field sound pressure estimates |P_FF| to Miller’s (1970) audiogram: the |P_FF| required to generate W_C,0=5×10⁻¹⁸ W of acoustic power in the vestibule, the |P_FF| required to generate |P_V,0|=34 dB re 20 μPa, and the |P_FF| required to generate |U_S,0|=10⁻¹⁴ m³∕s. These values were chosen by eye for a close fit to the audiogram over the frequency range 125 Hz–2 kHz. The HRTF was available only between 250 Hz and 8 kHz, which limited the range of P_FF. Nonetheless, given that the wavelength of sound at low frequencies (>1.4 m below 250 Hz in air) is large compared to the size of the head and pinnae, we can assume that the HRTF has a 0 dB gain below 250 Hz, and therefore P_TM well approximates P_FF below 250 Hz.

Figure 11.

An average chinchilla audiogram (thick solid line, from Miller, 1970) was compared to the free-field sound pressure |P_FF| required to produce a constant level of |P_V| (thin dotted line), |U_S| (thin dashed line), and W_C (thin dashed-dotted line).

The audiogram is well predicted by the three quantities tested between 125 Hz and 2 kHz. Below 125 Hz, both W_C and P_V produce similar slopes to the audiogram, whereas U_S produces a shallower slope and therefore is not a good predictor at those frequencies. Above 2 kHz, none of the three quantities are good predictors: The audiogram is almost flat with thresholds between 0 and 5 dB SPL, whereas P_FF in the three cases decreases to a minimum near 2 kHz before increasing again with frequency, crossing the audiogram at about 7 kHz.

In Rosowski (1991), W_C was estimated from a power flow model using various mechano-acoustic quantities in cat, chinchilla, and human temporal bone. The P_FF required to produce a constant W_C=5×10⁻¹⁸ W was plotted against Miller’s (1970) audiogram in the case of the chinchilla (see his Fig. 12, middle panel). The fit between P_FF and the audiogram was determined so as to minimize the mean square error over the full range of tested frequencies, whereas we minimized (by eye) the error below 2 kHz (which by chance led to the same value of 5×10⁻¹⁸ W). In both studies, W_C is a poor predictor of the audiogram above 2 kHz. Below 2 kHz, the shape of our P_FF more reliably predicts the shape of the audiogram.

CONCLUSIONS

We used the miniature fiber-optic pressure sensors described by Olson (1998) to measure the sound pressure within the vestibule P_V of the inner ears of chinchillas, and laser Doppler vibrometry to measure stapes velocity V_S, while presenting sound stimuli to the ear canal (Fig. 1). Our simultaneous measurements of P_V and V_S led to new estimates of the middle ear pressure gain G_ME and of the stapes velocity transfer function SVTF in chinchillas, and to the first direct measurement of cochlear input impedance Z_C in this species. Measurements of V_S before and after introducing the hole in the bony vestibular wall and placing the fiber-optic pressure sensor in the vestibule (Fig. 4), as well as measurements of P_V before and after sealing the pressure sensor in place (Fig. 3), suggest that the introduction of the vestibular hole and placement of the sensor had a small effect on middle ear sound transmission. We were able to qualitatively predict this effect using a simple acoustic model (Fig. 7).

The measured G_ME (Fig. 2) was band-pass in nature with a peak magnitude similar to the 38 dB middle ear gain predicted from the product of the TM∕footplate area ratio and the malleus∕incus lever ratio. The phase angle of G_ME varied by more than a cycle over the 62 Hz–30 kHz measurement range and was generally consistent with a group delay of 52 μs. When compared with cat, gerbil, guinea pig, and human temporal bone (Fig. 8), |G_ME| was largest for the chinchilla, especially at low frequencies. However, |G_ME| in all these species was similar (within 10 dB) over 500 Hz–3 kHz.

Our Z_C was resistive from 0.2 to at least 10 kHz, with a magnitude on the order of 10¹¹ acoustic ohms (Fig. 5). Together with previous direct measurements of Z_C in cat, gerbil, and human temporal bone (Fig. 10), this suggests that a resistive Z_C is characteristic of the mammalian ear. Over 125 Hz–2 kHz, estimates of the free-field sound pressures necessary to maintain a constant sound power into the inner ear, a constant P_V, or a constant V_S had a frequency dependence similar to that of auditory thresholds (Fig. 11); this similarity did not hold at higher sound frequencies. A better predictor of the shape of the audiogram may be the basilar membrane differential pressure (difference between P_V and the sound pressure in scala tympani), which will be the object of a future study in a similar chinchilla preparation.