Abstract
Most mathematical models of the mammalian cochlea neglect structural longitudinal coupling. However, recent experimental data suggest that viscoelastic longitudinal coupling, in the basilar membrane (BM) and the tectorial membrane (TM), is non-negligible. In this paper, mathematical models for BM and TM longitudinal coupling are presented to determine the influence of such a coupling on the tuning of the BM. The longitudinal coupling models are added to a macroscopic linear model of the guinea pig cochlea that includes the micromechanics of the organ of Corti and outer hair cell (OHC) somatic motility. The predictions of the BM response to acoustic stimulus show that the characteristic frequency is controlled by a TM radial resonance and that TM longitudinal coupling has a more significant effect than BM longitudinal coupling. TM viscoelasticity controls the sharpness of the BM frequency response and the duration of the impulse response. The results with realistic TM longitudinal coupling are more consistent with experiments. The model predicts that OHC somatic electromotility is able to supply power to the BM at frequencies well above the cutoff of the OHC basolateral membrane. Moreover, TM longitudinal coupling is predicted to stabilize the cochlea and enable a higher BM sensitivity to acoustic stimulation.
INTRODUCTION
The mammalian hearing system combines high sensitivity to low level acoustic pressure stimulus with a dynamic range that extends over six orders of magnitude. In addition, cochlear responses are highly tuned in the frequency domain yet the system as a whole still possesses excellent transient capture, able to discriminate timing differences of 6–10 μs.1 The solution to these seemingly conflicting characteristics involves both the unique transduction properties of the auditory periphery and the processing capabilities of the central nervous auditory system. In the periphery, where the acoustic signals are converted to neuronal input, an intricate micromechanical and microfluidic cochlear anatomy has evolved. In the healthy cochlea, outer hair cells (OHCs) present a nonlinear electrical and mechanical response to acoustic stimulation. The mechanical force from the OHC is thought to be the main factor leading to both the nonlinear input-output characteristic and the sharp frequency filtering seen in the cochlea. The focus of current research aimed at uncovering the workings of the cochlea has been on two mechanisms of OHC mediated force generation, basolateral (somatic) and hair bundle (HB) motility. Both hypotheses hinge on the conversion of some form of stored nonmechanical energy (e.g., the endocochlear electrical potential2) to mechanical energy. The HBs are comprised of numerous stereocilia-like projections from the apex of each OHC. The HBs are of central interest, as shear deflection of the HB gates the large potassium current necessary for somatic OHC force generation, and the same shear motion of the HB is thought to initiate a cascade of events resulting in HB force generation. The apical termination of the tallest row of stereocilia of each HB is in the tectorial membrane (TM) which, therefore, plays a critical role in active cochlear mechanics. The basilar membrane (BM) is a main structural component of the cochlea since it is directly coupled to the fluid of the cochlear ducts. The sensory hair cells are sandwiched between the TM and the BM. In this paper we use a mathematical model of the cochlea that explicitly includes the micromechanics of the organ of Corti (OoC) with independent degrees of freedom for the BM and TM vibrations. We introduce longitudinal coupling in the TM and∕or in the BM using material properties based on experimental data to predict the effect of such coupling on the BM response to acoustic input.
Some researchers have postulated a central role for the TM in cochlear mechanics, and some before the electromotility of the OHC had been presented in 1985.3 Zwislocki4, 5 hypothesized that the TM acts as a second resonator coupled to the BM through the OHC HB linkage. He used this to explain the sharp tuning and secondary peaks in tuning curve. Allen6 postulated that a two degree of freedom resonator system consisting of the TM mass and BM-OoC mass would be sufficient to explain the sharpness seen in cochlear tuning.
Gummer et al.7 presented experimental results on TM resonance in the apex of the postmortem cochlea. If these results can be extended to the basal region of the living cochlea, they indicate the presence of two TM modes having different resonant frequencies. Mammano and Nobili8 developed a model of TM interaction with HB giving rise to OHC somatic electromotility. Chadwick et al.9 also developed a model that highlighted the importance of the TM for predicting the frequency response of the cochlea. In the former models, certain assumptions are made regarding the amplitude and∕or phase of the OHC somatic forcing that limit their predictive capability, especially with regard to the TM mechanics and OHC electromotility.
The TM is a gelatinous structure with three different noncollageneous glycoproteins (α-tectorin, β-tectorin, and otogelin). β-tectorin is an essential structural component providing longitudinal coupling in the TM (as shown by Ghaffari10). A mouse with genetically modified β-tectorin exhibits an enhanced tuning and reduced sensitivity in the high frequency region,11 which suggests that the TM plays a key role in tuning and that TM longitudinal coupling is important for cochlear mechanics. The mechanical properties of the TM have been measured in gerbils12, 13 and in guinea pigs14, 15 as well as in mice.16, 17, 18 The measurements in Ref. 17 show that the TM has frequency dependent properties. Moreover, although direct comparison between different measurements is difficult because of the difference in the experimental methods, the data show that the TM of mice (that have a higher frequency range than guinea pigs) is much stiffer than the TM of the guinea pigs and gerbils (that have a lower frequency range than guinea pigs). Zwislocki and Cefaratti13 found that the TM is significantly less stiff than the HBs in the gerbil cochlea. However, some more recent measurements lead to contradictory conclusions about the relative stiffness of the TM (which in turn influences the kinematics). Some studies in the mouse cochlea have found that the TM is significantly stiffer than the HB.16, 17 If this is the case, then the TM would then move as rigid body from the limbal attachment provided that the TM region near the spiral limbus is more compliant than the main body of the TM (see Ref. 19). Recent measurements in the gerbil and guinea pig cochlea found that the TM has a stiffness within an order of magnitude of the HB.12, 15 In this case, the TM would then deform elastically from the limbal attachment (if the limbal attachment is stiffer than the TM, as suggested in Refs. 14, 18). Richter et al.12 showed that the TM stiffness varies longitudinally with a higher radial stiffness at basal locations than at more apical locations. Shoelson et al.15 did not observe the presence of a stiffness gradient in the TM of the guinea pig but observed a longitudinal and radial inhomogeneity. An estimate of the shear modulus and Young’s modulus was derived in Refs. 12, 15 based on an isotropic model of the TM. As noted in these papers some caution must be taken in interpreting these results because of the isotropic and homogeneous assumptions of the model. Because of its microstructure the TM is anisotropic, as shown by Gavara and Chadwick14 using atomic force microscopy measurements of the elastic moduli. Ghaffari et al.20 demonstrated that the TM isolated from the mouse cochlea is capable of supporting shear waves that propagate in the longitudinal direction of the cochlea (see Fig. 1). Such waves would not be possible without significant longitudinal stiffness in the TM. While the mechanical properties of the TM estimated from these experiments are somewhat different with those from Gavara and Chadwick,14 both group’s estimates of modulus are consistent with a slow shear wave whose phase velocity is comparable to that of the traveling wave in the cochlea near the frequency dependent peak response location.
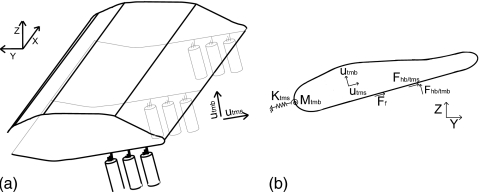
Figure 1.
(a) Illustration of the TM model. The x-coordinate corresponds to the longitudinal direction. (b) Cross-sectional view of the TM showing external forces (per unit length) acting on the TM. The HBs apply forces in the shear (Fhb∕tms) and bending (Fhb∕tmb) directions. Fluid forcing due to the viscous fluid interaction in the subtectorial space is given by a force in the shear direction proportional to the relative shear velocity between the TM and the RL, . The TM elasticity in the cross section is modeled by a linear spring (Ktms) applying a force in the shear direction and a rotational spring (Mtmb) applying a force in the bending direction. The plane sections (y-z) shear relative to one another. As in Ref. 20, internal viscous and elastic coupling is included.
In the BM stiffness measurements in dead animals from von Bekesy,21 longitudinal coupling appears to be significant. However, in the study from Voldrich22 in live guinea pigs, longitudinal coupling in the BM is negligible. More recent work in mongolian gerbil cochlea23 quantifies longitudinal coupling in the BM and organ of Corti and indicates that longitudinal coupling is significant and increases from the base to the apex of the cochlea. Liu and White24 used the published experimental data to compute the material properties of the BM described by an orthotropic plate model.
Recent experimental data indicate that viscoelastic coupling in the TM and elastic coupling in the BM is important. However, most cochlear models25, 19 are based on a locally reacting representation of the cochlear partition and neglect structural longitudinal coupling. Allen and Sondhi26 modeled the BM as an orthotropic plate but the TM is not included and the model is passive. The model of Wickersberg and Geisler27 includes elastic longitudinal coupling in the BM in a one dimensional model. In this model the effect of introducing longitudinal coupling in the BM governing equation for the low damping case is to broaden the BM frequency response and to reduce the magnitude of the peak. But the interpretation of this result is limited since the organ of Corti is reduced to one degree of freedom and the magnitude of longitudinal coupling is not based on any measurement. Steele and Taber28 included longitudinal coupling in the BM (treating it as a plate). The model of Mammano and Nobili8 introduces only viscous longitudinal coupling in the organ of Corti. If structural longitudinal coupling is important in the mechanics of the cochlea, what is the role of such coupling? We propose a role for the TM in electromotile processes and in shaping the frequency response of the BM to acoustic stimulus. We also predict the relative importance of the BM versus TM longitudinal coupling in influencing the sharpness of tuning of the BM.
METHODS
The fluid domain is idealized as uncoiled with two internal ducts separated by the basilar membrane. The macroscopic response of the fluid is modeled as inviscid and incompressible and is coupled to the mechanical response of the basilar membrane through the linearized Euler relation.19 A micromechanical model of the organ of Corti is coupled mechanically to the TM and the BM. Viscous fluid effects (e.g., shearing of the fluid in the subtectorial space) are also included in the micromechanical model. Electrical conduction through the scalae is modeled using a set of coupled cable equations. The electrical and mechanical domains are coupled through a piezoelectric model for the OHC somatic motility and a displacement dependent conductance of the HB. Details of the mechanical, electrical, and fluidic model are presented by Ramamoorthy et al.19 The main change to the model of Ramamoorthy et al. is the addition of longitudinal coupling in the TM and BM mechanics as is described next.
Tectorial membrane mathematical model
As shown in Fig. 1, each cross section of the TM is modeled as a two degree of freedom system with deformation in the radial or shear direction (utms) and in the normal or bending direction (utmb). The TM is characterized at each (y-z) plane by its effective stiffness and mass per unit length. The bending and shear motion varies in the longitudinal direction (x) and hence the cross sections move relative to one another. Longitudinal viscoelastic coupling of the shear motion of the TM is included (with a shear modulus Gxy and a shear viscosity ηxy) while TM bending rigidity is neglected. The governing equation for the shear motion of the TM is
| (1) |
where Fhb∕tms is the external force (per unit length) applied by the HB of the OHC in the shear direction,19 is the damping coefficient due to the viscosity of the fluid in the subtectorial space, us is the relative shear displacement between the TM and the reticular lamina (RL), and is an effective cross-sectional area of the TM. Because of its inhomogeneity,15 anisotropy,14 and of its frequency dependent properties,16, 17 it is difficult to estimate the values for the effective TM shear stiffness and mass. Here we chose the TM stiffness per unit length, Ktms, based on the values published by Richter et al. for the radial TM stiffness of the gerbil (as discussed in the Appendix0). Hence the TM stiffness is within one order of magnitude of the HB stiffness published in Ref. 29. For the TM shearing mass, we take into account the longitudinal variation observed in the TM cross section area in Ref. 12 and choose the value to fit the predictions of the BM response to acoustic stimulation with published experimental data. The values of the TM parameters are listed in Table 1.
Table 1.
Tectorial membrane properties (x is in m).
Basilar membrane mathematical model
To introduce elastic longitudinal coupling in the BM mechanics, we use an orthotropic plate model. The governing equation for the BM motion is
| (2) |
where Pbm is the pressure applied by the fluid and the OHC on the BM,19Cbm is the BM viscous damping per unit area, Mbm is the mass of the BM per unit area, b is the width of the BM, and ubm(x,y) is the BM displacement. Dxx, Dyy, Dxy, and Ds are the orthotropic plate bending stiffnesses of the BM. As in Ref. 19, we assume that the BM vibrates with the mode shape for −b∕2≤y≤b∕2. The values of the BM parameters are listed in Table 2.
Table 2.
Basilar membrane properties (x is in m).
| Properties | Value | Ref. |
|---|---|---|
| Dxx | 0 N m in LR and TM-LC models, 6.5×10−11 N m in BM-LC and TMBM-LC models | 24 |
| Dxy | 0 N m in LR and TM-LC models, 3.1×10−11 N m in BM-LC and TMBM-LC models | 24 |
| Ds | 0 N m in LR and TM-LC models, 4.3×10−11 N m in BM-LC and TMBM-LC models | 24 |
| Dyy | 30, 19 | |
| Mbm | ρbmhbm where ρbm=1000 kg∕m3 | 19 |
| Cbm | 0.85×10−1 N s∕m2 | |
| b | (80+54×10−2x)×10−6 m | |
| h | (7−2.86×10−2x)×10−6 m | 15, 20 |
Uncoupled structural longitudinal coupling space constants
In the macroscopic model of the cochlea, the motions of the TM and of the BM are coupled, especially in the active model. However, to evaluate the contributions of TM longitudinal coupling and of BM longitudinal coupling to cochlear mechanics, we determine here the equations used to compute the space constants for the shear motion of the TM and the transverse motion of the BM uncoupled from the other structures and the fluid. Analysis of these predictions will allow us to estimate the spatial extent of a single row of OHC forcing due to longitudinal mechanical coupling in the TM and BM.
The TM is attached to the reticular lamina by three rows of HBs (each with a stiffness per unit length Kst) and to the spiral limbus and has a stiffness per unit length, Ktms. The force applied by the HB on the TM in the shear direction is given by Fhb∕tms=−3Kstus. Therefore, according to Eq. 1, if the longitudinal variations in , Gxy, and ηxy are neglected locally, the complex wavenumber characteristic of TM longitudinal coupling (when the TM and HB are uncoupled from the other structures), ktms−hb, is given by
| (3) |
If we integrate out the radial dependence of the BM displacement and neglect locally the longitudinal variations in b and of the basilar membrane properties, the BM governing equation is reduced to
| (4) |
where Fbm is the force per unit length applied by the pressure and the OHC.19 The complex wave number characteristic of BM longitudinal coupling (for the BM uncoupled from the organ of Corti), kbm, is the solution of the following equation:
| (5) |
The space constants characteristic of structural longitudinal coupling are then given by
| (6) |
where Imag represents the imaginary part of the complex wave number.
Model activity: OHC somatic motility and HB conductance
The electrical and mechanical degrees of freedom of the model are coupled through the somatic electromotility of the OHCs and the conductance change in the HBs. HB motility is not included and the HBs are modeled as passive springs with stiffness (per unit length) Kst connecting the RL and the TM. Each OHC is modeled by linearized piezoelectric-like expressions relating the OHC deformation, , and fluctuating part of the transmembrane voltage, Δϕohcj, to the OHC force (per unit length), Fohcj, and current (per unit length), Iohcj:
| (7) |
| (8) |
where Kohc is the OHC stiffness (per unit length), ϵ3 is the electromechanical coupling coefficient (per unit length), Zm is the basolateral impedance of the OHC, and the subscript ohcj refers to each OHC where j corresponds to the row number, j=1,2,3.
The conversion of electrical power to mechanical power delivered by the OHC somatic force to the BM, , is then
| (9) |
where Re denotes the real part, vbm the BM velocity, and * the complex conjugate. The value of the electromechanical coupling coefficient ϵ3 determines the intensity of the active OHC force and we use a frequency independent value.31
The conductance of the HB (per unit length), Gaj, is considered to change linearly with the rotation of the HB relative to the RL:
| (10) |
where is the conductance (per unit length) at the resting state, ga represents the angular sensitivity of the mechanoelectrical transducer (MET) channel (per unit length) (note that , where Lhb is the length of the hair bundle and is the slope of the change in conductance with respect to the HB deflection, as defined in Ref. 19), and θhbj∕rlj is angle of the HB relative to the RL. The data from He et al.32 indicate that the transduction channel angular sensitivity is proportional to the maximum conductance and that the maximum conductance decreases from the base of the cochlea to the apex. The following spatial dependence for the MET angular sensitivity is used:
| (11) |
where α is the spatial decay rate of the maximum conductance. ga(0) is kept as a free parameter and is considered to be independent of frequency. The nonlinearity of the conductance-deflection relationship is approximately taken into account by using larger values for ga(0) for acoustic stimulations with low sound pressure level (SPL) stimulations and a value of zero for a passive model, as discussed by Ramamoorthy et al.19 The value needed to simulate (with the model, denoted as TM-LC model, that includes TM longitudinal coupling) the BM gain seen in experiment of Zheng et al.33 at 10 dB SPL is denoted as 100% activity. The values of the OHC and MET channel parameters are listed in Table 3.
Table 3.
OHC and HB properties (x is in m).
| Properties | Value | Ref. |
|---|---|---|
| ϵ3 for LR | −0.616(10−5+10−4x) N∕m mV | |
| ϵ3 for TM-LC | −1.04(10−5+10−4x) N∕m mV | |
| ϵ3 for BM-LC | −0.784(10−5+10−4x) N∕m mV | |
| ϵ3 for TMBM-LC | −1.12(10−5+10−4x) N∕m mV | 40 |
| α | 215 m−1 | 32 |
| ga(0) | 6.48 S∕rad m for 100% activity | |
| Kst | 5.8×104e−330x N∕m2 | (Kst)avg=7.3×104e−3.25x N∕m2 in Ref. 29 |
| Lhb | (1+270x)×10−6 m |
Finite element solution
A full three dimensional box model solution of the cochlear would be computationally expensive. To reduce the size of the problem, modal decomposition is first used in the radial direction (y) as in Ref. 19. Three symmetric mode shapes are used for the pressure in the fluid: ψn(y)=cos(nπ(y+w∕2)∕w) (n=1,3,5) for −w∕2≤y≤w∕2, where w is the width of the duct. One mode shape is used for the BM transverse displacement. With this modal decomposition the three dimensional model is reduced to a series of two dimensional models which can then be post-processed to synthesize the full result. A Bubnov–Galerkin finite element method34, 35 is then used. The weak form is first derived from the strong form of the equations. In this study, a discretization of 741 nodes in the longitudinal direction (x) and 41 nodes in the z-direction was used (this was determined to be sufficiently converged for our purposes). Linear shape functions are used for the TM shear and bending displacements and for the electrical degrees of freedom. Bilinear shape functions are used for the fluid. Hermite cubic shape functions are used for the BM displacement since the governing equation [Eq. 2] requires higher order continuity.
RESULTS
Longitudinal coupling (particularly in the TM) decreases the sharpness of the frequency response
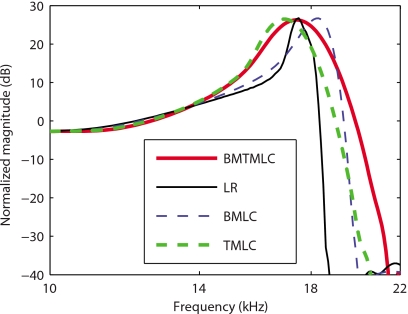
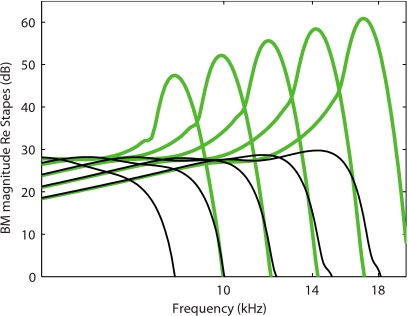
In Fig. 2, frequency domain model predictions of the gain in BM velocity relative to the stapes' velocity at a basal location (x=0.4 cm) with and without longitudinal coupling in the TM and∕or in the BM are compared. Four active models are used to predict the response of the BM to low level acoustic input. In the first (results shown with a thin solid line), a locally reacting model of the TM and of the BM (denoted as the LR model) is used. By this we mean that there is no longitudinal mechanical coupling in the TM or the BM (as in Ref. 19). In a model such as this, the dominant longitudinal coupling arises from two sources: fluid pressure and electrical conduction in the scalae of the cochlea. The fundamental components of the second model (denoted as the TM-LC model) are identical to the first, except that longitudinal coupling is now included in the representation of the TM according to Eq. 1 (results shown with a thick dashed line). In the third model (denoted as BM-LC model), longitudinal coupling is introduced in the BM according to Eq. 4 (results shown with a thin dashed line). In the fourth model (denoted as TMBM-LC model), longitudinal coupling is included in both the TM and the BM (results shown in thick solid line). In order to achieve the same BM gain at the characteristic frequency (CF) for the four models, the electromechanical coupling factors of the OHC [ϵ3 in Eq. 8] for the TM-LC, BM-LC, and TMBM-LC are, respectively, about 69%, 27%, and 79% higher than for the LR model (see Sec. 4). As shown in Fig. 2 and Table 4, the LR predicts a high mechanical quality factor (Q10 dB=15.2). In the BM-LC model the Q10 dB is reduced (Q10 dB=9.2). The TM-LC model predicts that the Q10 dB (Q10 dB=7.0) is much lower than in the LR model and lower than in the BM-LC model. The Q10 dB predicted by the TMBM-LC (Q10 dB=5.7) is slightly lower than that by the TM-LC model. Longitudinal coupling has a small effect on the CF for a given location. Longitudinal coupling in the TM slightly reduces CF (by about 4%) while longitudinal coupling in the BM slightly increases the CF (by about 5%), as shown in Fig. 2 and in Table 4. For reference, the magnitudes of the BM gain predicted by the four models with no activity [ga(0)=0] are shown in Fig. 3. The passive response predictions are almost indistinguishable. The passive LR model is slightly more sensitive than the other models (by less than 2 dB).
Figure 2.
Model predictions for the BM gain in the active case (80% activity). As in Ref. 19, the gain is normalized to the maximum passive model gain. Thin solid line: Active LR model response. Thick dashed line: Active TM-LC model response. Thin dashed line: Active BM-LC model response. Thick solid line: Active TMBM-LC model response. The values for ϵ3(x) for the different models are given in Table 3. The four models are capable of predicting realistic maximum gains but at these activity levels the Q10 dB for the LR and BM-LC models are always much higher than that predicted by the TM-LC and TMBM-LC models.
Table 4.
Mechanical quality factor (Q10 dB) and CF in the different models and in the experimental data.
| Model | Q10 dB | CF |
|---|---|---|
| LR | 15.2 | 16.7 Hz |
| TM-LC | 7.0 | 16.2 kHz |
| BM-LC | 9.2 | 17.5 kHz |
| TMBM-LC | 5.7 | 16.6 kHz |
| Experimental dataa | 6.5 | 16.5 kHz |
Reference 33.
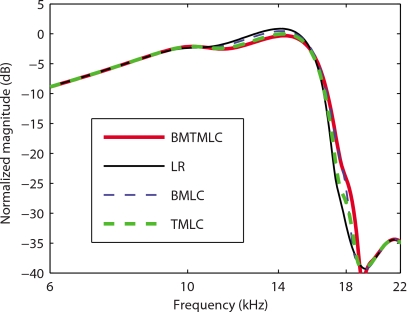
Figure 3.
Model predictions for the BM gain in the passive case (0% activity). As in Ref. 19, the gain is normalized to the maximum passive gain. Thin solid line: Passive LR model response. Thick dashed line: Passive TM-LC model response. Thin dashed line: Passive BM-LC model response. Thick solid line: Passive TMBM-LC model response. The effect of longitudinal coupling (in the BM or in the TM) is not significant on the passive BM frequency response.
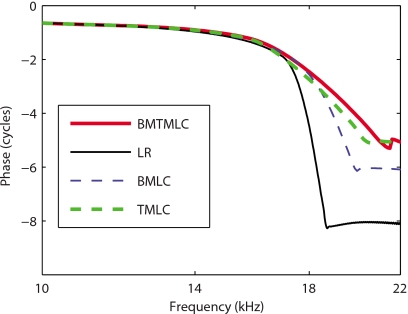
The prediction for the phase of the BM relative to the stapes in the active models is shown as a function of frequency in Fig. 4. In the LR model (shown with a thin solid line) the phase accumulation at high frequency is about 8 cycles while it is only about 5–6 cycles in the other three models. The absolute value of the slope of the phase in the LR model and of the BM-LC model (shown with a thin dashed line) is higher than in the TM-LC (shown with a thick dashed line) and TMBM-LC (shown with a thick solid line) models. Hence models with longitudinal coupling in the TM have a different behavior than those with no longitudinal coupling or coupling in the BM only.
Figure 4.
Model predictions for the BM phase relative to the stapes in the active case (80% activity). Thin solid line: Active LR model response. Thick dashed line: Active TM-LC model response. Thin dashed line: Active BM-LC model response. Thick solid line: Active TMBM-LC model response.
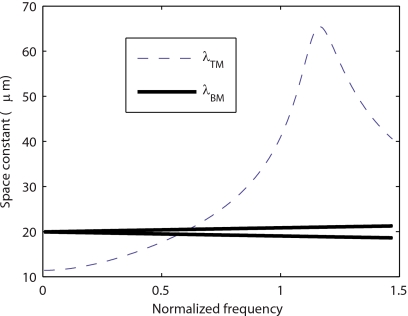
The predictions of the space constants for BM longitudinal coupling and TM longitudinal coupling [given by Eqs. 3, 5, 6] as a function of the frequency (normalized to CF) are shown in Fig. 5. These equations represent the effect of the two structures in isolation from the fluid and other structures. Even though the two constants are similar at low frequencies, the space constant characteristic of TM longitudinal coupling is more than three times higher close to CF. The TM resonance frequency is close to the CF, whereas the BM resonance frequency is much higher. Hence TM longitudinal coupling couples a higher number of OHC. Longitudinal coupling with a space constant λ can be considered significant over a distance of about 5λ.36 Hence, at CF the TM longitudinal coupling can couple about 30 rows of OHC and the BM longitudinal coupling can only couple about 10 rows of OHCs. Therefore, as seen in Fig. 2, the presence of TM longitudinal coupling has a more significant impact on the BM response than the presence of BM longitudinal coupling.
Figure 5.
Space constants characteristic of BM longitudinal coupling (λBM) and TM longitudinal coupling (λTM) as a function of the frequency (normalized to the CF). For BM longitudinal coupling there are two space constants because Eq. 5 is quadratic in kbm (Ref. 2). At low frequencies the space constants for the BM and the TM are similar (about 20 μm for the BM and 12 μm for the TM). But close to CF, the space constants characteristic of TM longitudinal coupling are more than three times as high as the space constant characteristic of BM longitudinal coupling.
Our results (Figs. 245) show that the dominant source of structural longitudinal coupling in the cochlea is the TM viscoelasticity. Our goal is to develop a mathematical model of the cochlea that is as simple as possible but can accurately predict the measurements of the BM response. Hence in the following results only the TM-LC model is used.
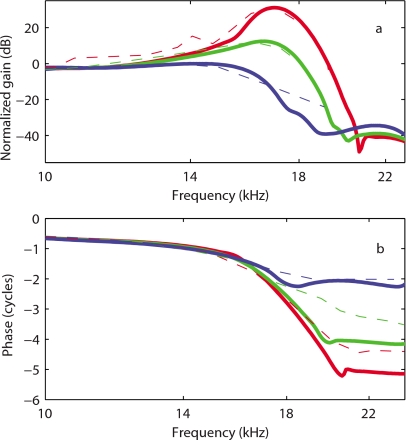
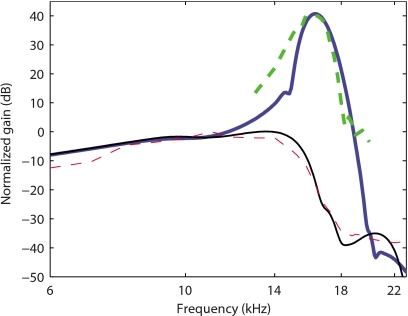
In Figs. 6a, 7, predictions of the BM gain by the TM-LC model are compared to experimental data for guinea pigs from de Boer and Nuttall37 and Zheng et al.33 Even though the protocols for these two experiments were different (in Ref. 37 bands of flat-spectrum pseudo-random noise stimulations were used while Zheng et al.33 used pure tone acoustic signals), the same model is able to replicate important characteristics for both experiments. The model is a linear model and the variation from the fully active model to the passive model is achieved by decreasing the MET sensitivity ga(0) (as discussed in Ref. 19 and in Sec. 2). The frequency responses of the basilar membrane track with the experimental data from de Boer and Nuttall at different SPLs [Fig. 6a] when the gain of the MET channels is reduced. The TM-LC model predicts around 35 dB gain for low level acoustic stimulation. As seen in experimental results, the shift in the peak frequency between the fully active and passive cases is about half an octave. The BM gain curve becomes sharper as the activity is raised. The mechanical quality factor predicted by the TM-LC model is more consistent with the experimental measurements than the results from the locally reacting model (see Fig. 2). The Q10 dB values predicted by the TM-LC model at the highest activity match approximately the experimental values for low SPL stimulation. For instance, Q10 dB is 7.7 in the fully active TM-LC model compared to 6.5 in Zheng et al.33 experiment (compare the heavy solid and dashed curves in Fig. 7). The TM-LC model prediction for the BM phase follows closely the data from de Boer and Nuttall [see Fig. 6b]. Note that the phase data are not available from Zheng et al.33 The phase accumulation at high frequency is about 5.0 cycles in the active TM-LC model compared to 4.5 cycles in the 20 dB SPL experiment. The phase accumulation at CF is about 2 cycles in both the model and the experiment. The model predictions for the phase slope at CF are slightly higher than in the experimental data.
Figure 6.
Comparison of the TM-LC model response (G0=7 kPa, η=0.05 Pa s) with experimental data from de Boer and Nuttall (Ref. 37). Solid lines: Model BM gain for 86% activity, 56% activity, and 0% activity. Dashed lines: Guinea pig data at 20, 80, and 100 dB. (a) Normalized (to the maximum passive response) BM magnitude in dB. (b) BM phase relative to the stapes in cycles.
Figure 7.
Comparison of the TM-LC model response for the gain (G0=7 kPa, η=0.07 Pa s) with experimental data from Zheng et al. (Ref. 33). Solid lines: Model BM responses for 100% activity (thick line) and 0% activity (thin line). Dashed lines: Experimental data at 10 dB (thick line) and 100 dB SPL (thin line).
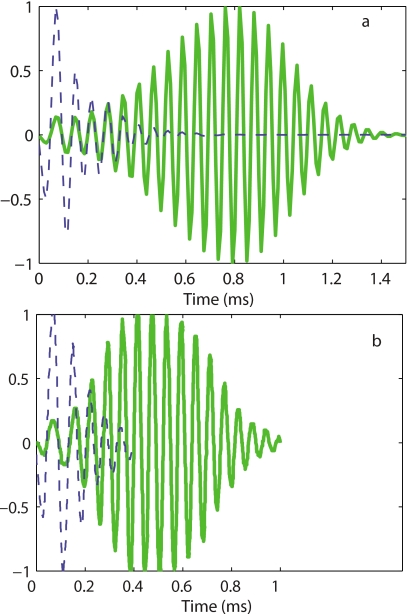
By taking the inverse Fourier transform of the frequency response, an impulse response can be derived from the experiments and simulations. Results from the TM-LC theory are compared to measurements from de Boer and Nuttall37 in Fig. 8. The oscillations of the response continue up to about 1 ms in experimental data [Fig. 8b] and 1.4 ms [Fig. 8a] for the model simulations in the active case. This is a considerable improvement over the TM-LR theory, which incorrectly predicted a much longer impulse response in the active case, with oscillations that continue up to 3 ms.19 In the passive case the oscillations are about 0.4–0.5 ms both in the experimental results and the model simulations. Note that for the passive case, the model is relatively insensitive to TM longitudinal coupling as both models match the experimental results quite well for the impulse response. The model also predicts the same zero crossings of the passive and active responses for the first few cycles, consistent with observations from de Boer and Nuttall.37
Figure 8.
Normalized theoretical and experimental impulse response functions. (a) TM-LC model impulse response. Dashed line: Passive response. Solid line: Active response (86% activity). (b) Normalized experimental BM impulse responses from de Boer and Nuttall (Ref. 37) at 10 dB SPL (solid line) and 100 dB SPL (dashed line).
The simulations of the gain at different longitudinal locations of the cochlea follow the expected trend, as shown in Fig. 9. The peak of the BM gain curves shifts to lower frequency as the location approaches the apex, accompanied by a lower gain and Q10 dB (see also Ramamoorthy et al.19).
Figure 9.
Prediction of the BM response relative to the stapes as a function of frequency in the TM-LC model at different longitudinal locations (x=0.4, 0.5, 0.6, 0.7, and 0.8 cm). The active (81% activity) model responses are shown with a thick solid line. The passive model responses are shown with a thin solid line. As the location approaches the apex, the peak of the BM gain curve shifts to a lower frequency, the magnitude of the BM gain is lower, and the tuning of the response is less sharp.
Parameter sensitivity
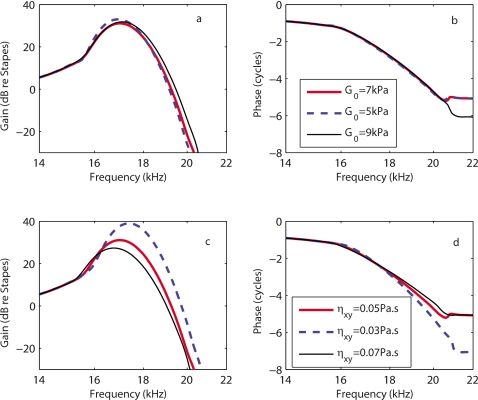
TM longitudinal coupling is characterized by the shear modulus (Gxy) and shear viscosity (ηxy) coefficients. Ghaffari et al.20 determined the longitudinal shear modulus (Gxy) and shear viscosity (ηxy) using a mathematical model of the TM similar to what we propose and their measurements of the shear traveling wave in a mouse TM at acoustic frequencies. The results show that the shear modulus is higher at the base than at the apex. Using the TM material property measurements, Gavara and Chadwick14 estimated the shear wave velocity at a basal and more apical location in the guinea pig. Based on their value for the shear wave velocity, the shear modulus is 0.67 kPa for a basal location and 0.44 kPa at a more apical location. We use for the shear modulus the same spatial variation as for the radial stiffness of the TM [Gxy(x)=G0 exp(αtmx)]. The values of the shear modulus are of same order of magnitude as the values in Ref. 14. In Ref. 20, the phase angle of the complex shear modulus at the CF of the basal location (about 80 kHz) is approximately 65°. For the guinea pig, at x=0.4 (CF=17 kHz), and if the phase angle at 17 kHz of the shear modulus is the same as in the mouse at 80 kHz, the shear viscosity should be about 0.04 Pa s.
In the theoretical results shown thus far, the shear modulus at the base is G0=7 kPa and a constant value of 0.05 Pa s is used for the shear viscosity. Varying these parameters affects the predictions of the BM magnitude in response to acoustic stimulations only for frequencies near the CF as the results in Fig. 10 show. Increasing the shear modulus G reduces the gain at the peak location (a few dB) and makes the response less sharp, as seen in Fig. 10a. Increasing the shear modulus is akin to increasing the longitudinal coupling of the TM; hence this result is consistent with differences seen in the TM-LC and LR models (see Fig. 2). Increasing the shear viscosity η reduces the gain, Q10 dB, of the BM response and the phase accumulation at frequencies higher than the CF, as shown in Figs. 10c, 10d. The TM shear viscosity plays an important role in modifying the slope of the phase at the CF; increasing the shear viscosity reduces the phase slope. For this range of parameters, the overall qualitative nature of the response predictions is not altered even though some of the quantitative details are affected.
Figure 10.
Model sensitivity to TM parameter variations. [(a) and (b)] Effect of changing the shear modulus G on the amplitude (a) and phase (b) of the BM gain relative to the stapes [legend in (b)]. [(c) and (d)] Effect of changing the shear viscosity η on the amplitude (c) and phase (d) of the BM gain relative to the stapes [legend in (d)]. For all simulations the activity is kept constant (86% activity).
DISCUSSION
TM longitudinal coupling is necessary to predict a BM gain curve and impulse response consistent with experimental data
As shown in Figs. 2467, only the TM-LC and the TMBM-LC models reproduce the Q10 dB seen in experimental data for a basal location. In the model, the shear resonance of the TM (i.e., the resonance of the TM mass attached to the spiral limbus and to the HBs) occurs at a frequency close to the CF. Hence one can loosely think of the radial resonance of the TM setting the CF for a given location (in the four models). Indeed changing the TM mass directly impacts the CF, but has little effect on the passive response.19 Somatic motility driven by the MET current is the only electromotile force in the model. For all four models it is possible to choose parameters to replicate the level of gain seen in the experimental results for low level sound [see Ramamoorthy et al.19 and Fig. 6a]. But, as seen in Fig. 2, only the TM-LC and BMTM-LC models replicate the Q10 dB as well as the duration of the impulse response of the experimental data. Figure 8 shows that the duration of the impulse for the model and experiments is roughly the same. However, there are differences as the predicted maximum amplitude is reached at 0.8 ms while experimentally the peak occurs at 0.5 ms. This may be due to the slight differences in the signal processing, but more likely it is due to some deficiencies in the model (notably the nonlinearity), as minor differences in phase-frequency relations between theory and experiments are also seen. The role of TM longitudinal viscoelastic coupling is partially corroborated by the experimental results of Russell et al.11 where they used a β-tectorin knockout mouse which possesses reduced longitudinal coupling (as measured by Ghaffari10) and showed sharper tuning, as we have predicted. Our model shows that the TM properties do not have a significant influence on the shape of the passive frequency response; such a finding is consistent with measurements of the BM response in mutant mice with a detached TM.38 The BM-LC model predicts a Q10 dB that is lower than in the LR model but still much higher than in the experimental data. Since the BM resonance is at a much higher frequency than CF, the effect of longitudinal coupling in the BM equation is not as dramatic on the tuning of the BM response as the effect of longitudinal coupling in the TM. Because of the mechanical connection to the HB and the fact that our model predicts that the shear resonance of the TM corresponds to the CF at the base of the cochlea, the TM appears to be the most important structure determining the broadness of the active frequency response (at a basal location).
Longitudinal coupling stabilizes the linearized cochlear model
Introducing longitudinal coupling, particularly in the TM, stabilizes the linear model. For the parameters chosen in this paper, the linearized LR model is at the limit of stability for a 25 dB BM gain, whereas the linearized TM-LC model is well under the stability limit for the BM gains seen experimentally (e.g., 35 dB). The stability limit is found by increasing the MET sensitivity until the impulse response is no longer finite and bounded (i.e., the system is unstable). Numerical experiments (results not shown) indicate that this change in the stability of the system is only due to the addition of longitudinal coupling and not to the modifications of the OHC parameters between the two models. A key finding of this work is that the cochlea is stabilized, in part, by the longitudinal coupling of the TM and that this stabilization allows for the cochlea to achieve higher stable levels of gain than would be possible without the longitudinal coupling. Since we predict that the system is not near a stability limit, this suggests that spontaneous otoacoustic emissions cannot be produced by a local spontaneous oscillation but may only be explained by a global phenomenon such as the coherent wave reflection theory.39
When we implement our TM-LC model with a significantly reduced shear modulus and shear viscosity while keeping other parameters constant, the BM gain is higher and the cochlear model is unstable at high activity. If such an instability were present when TM longitudinal coupling is reduced, then we should expect an increase in the gain and the presence of broad band otoacoustic emissions. However, in measurements by Russell et al.,11 the mutant mouse with reduced TM longitudinal coupling (as shown by Ghaffari10) has a reduced BM sensitivity compared to the wild-type mouse, and broad band otoacoustic emissions have not been reported. This apparent contradiction between model predictions and experimental results indicates that the mutant mouse cochlea might develop with a reduced MET sensitivity and∕or OHC somatic force compared to a wild-type mouse. In order to predict the same gain at the CF, a lower value of the electromechanical coupling coefficient of the OHC [ϵ3 in Eq. 8] is used in the LR model than in the TM-LC model. Note that both values of ϵ3 are realistic, within 50% of the experimental estimate from Iwasa and Adachi.40
Somatic motility of the OHC can operate at high frequencies and deliver power to the BM
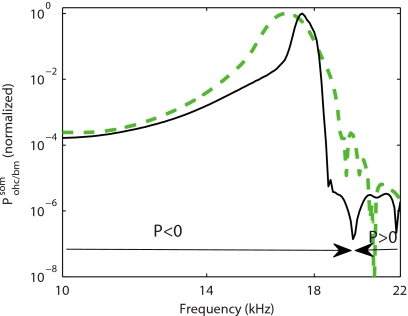
Further processing of the results for the LR and TM-LC models to determine the power delivered to the BM by the OHC (see Sec. 2) is shown in Fig. 11 (results shown with thin line and thick line, respectively) for a location near the 17 kHz best place. For both models, the OHCs are predicted to convert electrical to mechanical power and deliver power to the BM for frequencies lower than the CF. In the LR model, the OHCs deliver significant mechanical power to the BM in a narrower range of frequencies near the CF than in the TM-LC model (as normalized by the maximum mechanical power delivered to the system by the OHC). We attribute this to the coupling of multiple OHCs by the structural longitudinal coupling. The TM-LC and LR models predict that somatic motility of the OHC is able to deliver significant power to the BM even in the face of the RC-filtering of a 280 Hz corner frequency of the OHC at this location. The combination of a large electromechanical coupling coefficient, ϵ3, and HB transduction current (which arises from the shear resonance of the TM at the CF) overcomes the filtering. At 86% level of activity (see Fig. 6), the prediction of the transduction current sensitivity is 2.7 nA per nm of BM deflection. The magnitude of the HB current is 1.35 nA for a 0.5 nm BM displacement (a displacement which corresponds approximately to a 20 dB SPL acoustic stimulation41, 42). These values are lower than the maximal experimental estimates32 (see also Ramamoorthy et al.19 for further discussion).
Figure 11.
Absolute value of the power of the OHC active (somatic) force on the BM normalized to the value at the CF. Thick dashed line: in the TM-LC model. Thin solid line: in the LR model. For both models the parameters are the same as in Fig. 2. The sign of the power (P in the figure) is indicated in the figure to show the frequency region where the OHC somatic forces add power to the BM and the frequency region where it removes power from the BM . For both models the OHC somatic force adds power to the BM for frequencies less than the CF and up to about 20 kHz.
Conclusions
This model demonstrates that the TM has a significant influence on cochlear tuning as the tuning of the BM response arises from an electromechanical resonance mode of the OoC controlled mostly by the TM shear mode properties. BM longitudinal coupling has a more limited impact on the BM response. Rather than intrinsically tuned electromotility or mechanotransduction (as suggested by Müller and Gillespie43), our results show that the sharp BM frequency response is due to the dynamics of the combined electromechanical system (which does not require the electromotility itself to be tuned). The TM is a crucial structure for active cochlear mechanics because of its connectivity to the HBs. The TM motion relative to the reticular lamina deflects the HBs and opens the transduction channels, which increases the transmembrane potential. This drives OHC somatic motility by converting stored electrical energy from the endochlear potential to mechanical power delivered to the BM. Hence the presence of the TM and of OHC somatic motility is essential to assure a high BM sensitivity. Our model predictions for the BM frequency response and impulse response show that TM longitudinal coupling is critical for a well-functioning cochlea. The human ear needs to have both a high frequency selectivity and a short impulse response as well as a high sensitivity. This tradeoff between frequency discrimination and transient capture is controlled mostly by the longitudinal viscoelastic properties of the TM. The same longitudinal coupling is responsible for stabilizing the highly sensitive cochlea.
ACKNOWLEDGMENTS
The authors would like to thank Y. Li for her helpful discussions about the model and parameter choices. This research was supported by National Institutes of Health Grant No. NIH-NIDCD R01-04084.
APPENDIX: ESTIMATION OF THE TM STIFFNESS PER UNIT LENGTH, Ktms
Richter et al.12 measured the TM radial stiffness in the gerbil hemicochlea using a piezoelectric probe of diameter d=25 μm. For static measurements, the governing equation [Eq. 1] for the TM radial displacement of the TM is given by (neglecting the variations in and Gxy as a function of x)
| (A1) |
where fext is the force per unit length applied by the probe. The probe deforms the TM with the following mode shape:
| (A2) |
where x0 is the center of application of the probe force, U is the displacement of the TM at the probe tip, and . Therefore the stiffness measured by the probe is
| (A3) |
with the parameters used in our simulations, at x=0.4 cm (which corresponds to the 17 kHz BP in the guinea pig), Ktms=4.2 kPa, Gxy=2.1 kPa, so that λtm=40 μm, and K=4.2Ktmsd=0.44 N∕m. In the gerbil cochlea, at the 17 kHz BP, Richter et al. measured K=0.255 N∕m (when the TM is detached from the stereocilia).
References
- Dallos P., “Overview: Cochlear neurobiology,” in The Cochlea, edited by Dallos P., Popper A. N., and Fay R. R. (Springer, New York, 1996), pp. 1–43. [Google Scholar]
- Strelioff D., “Computer-simulation of generation and distribution of cochlear potentials,” J. Acoust. Soc. Am. 54, 620–629 (1973). 10.1121/1.1913642 [DOI] [PubMed] [Google Scholar]
- Brownell W. E., Bader C. R., Bertrand D., and De Ribaupierre Y., “Evoked mechanical responses of isolated cochlear hair cells,” Science 227, 194–196 (1985). 10.1126/science.3966153 [DOI] [PubMed] [Google Scholar]
- Zwislocki J. J., “Theory of cochlear mechanics,” Hear. Res. 2, 171–182 (1980). 10.1016/0378-5955(80)90055-6 [DOI] [PubMed] [Google Scholar]
- Zwislocki J. J., “Analysis of cochlear mechanics,” Hear. Res. 22, 155–169 (1986). 10.1016/0378-5955(86)90091-2 [DOI] [PubMed] [Google Scholar]
- Allen J. B., “Cochlear micromechanics—A physical model of transduction,” J. Acoust. Soc. Am. 68, 1660–1670 (1980). 10.1121/1.385198 [DOI] [PubMed] [Google Scholar]
- Gummer A. W., Hemmert W., and Zenner H. P., “Resonant tectorial membrane motion in the inner ear: Its crucial role in frequency tuning,” Proc. Natl. Acad. Sci. U.S.A. 93, 8727–8732 (1996). 10.1073/pnas.93.16.8727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mammano F. and Nobili R., “Biophysics of the cochlea: Linear approximation,” J. Acoust. Soc. Am. 93, 3320–3332 (1993). 10.1121/1.405716 [DOI] [PubMed] [Google Scholar]
- Chadwick R. S., Dimitriadis E. K., and Iwasa K. H., “Active control of waves in a cochlear model with subpartitions,” Proc. Natl. Acad. Sci. U.S.A. 93, 2564–2569 (1996). 10.1073/pnas.93.6.2564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaffari R., “The functional role of the tectorial membrane in the cochlear mechanics,” Ph.D. thesis, MIT, Cambridge, MA, 2008. [Google Scholar]
- Russell I. J., Legan P. K., Lukashkina V. A., Lukashkin A. N., Goodyear R. J., and Richardson G. P., “Sharpened cochlear tuning in a mouse with a genetically modified tectorial membrane,” Nat. Neurosci. 10, 215–223 (2007). 10.1038/nn1828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter C. P., Emadi G., Getnick G., Quesnel A., and Dallos P., “Tectorial membrane stiffness gradients,” Biophys. J. 93, 2265–2276 (2007). 10.1529/biophysj.106.094474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwislocki J. J. and Cefaratti L. K., “Tectorial membrane II: Stiffness measurement in vivo,” Hear. Res. 42, 211–227 (1989). 10.1016/0378-5955(89)90146-9 [DOI] [PubMed] [Google Scholar]
- Gavara N. and Chadwick R. S., “Collagen-based mechanical anisotropy of the tectorial membrane: Implications for inter-row coupling of outer hair cell bundles,” PLoS ONE 4, e4877 (2009). 10.1371/journal.pone.0004877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoelson B., Dimitriadis E. K., Cai H., Kachar B., and Chadwick R. S., “Evidence and implications of inhomogeneity in tectorial membrane elasticity,” Biophys. J. 87, 2768–2777 (2004). 10.1529/biophysj.104.040774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abnet C. C. and Freeman D. M., “Deformations of the isolated mouse tectorial membrane produced by oscillatory forces,” Hear. Res. 144, 29–46 (2000). 10.1016/S0378-5955(00)00041-1 [DOI] [PubMed] [Google Scholar]
- Gu J. W. W., Hemmert W., Freeman D. M., and Aranyosi A. J., “Frequency-dependent shear impedance of the tectorial membrane,” Biophys. J. 95, 2529–2538 (2008). 10.1529/biophysj.107.124727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gueta R., Barlam D., Shneck R. Z., and Rousso I., “Measurement of the mechanical properties of isolated tectorial membrane using atomic force microscopy,” Proc. Natl. Acad. Sci. U.S.A. 103, 14790–14795 (2006). 10.1073/pnas.0603429103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramamoorthy S., Deo N. V., and Grosh K., “A mechano-electro-acoustical model for the cochlea: Response to acoustic stimuli,” J. Acoust. Soc. Am. 121, 2758–2773 (2007). 10.1121/1.2713725 [DOI] [PubMed] [Google Scholar]
- Ghaffari R., Aranyosi A. J., and Freeman D. M., “Longitudinally propagating traveling waves of the mammalian tectorial membrane,” Proc. Natl. Acad. Sci. U.S.A. 104, 16510–16515 (2007). 10.1073/pnas.0703665104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bekesy G. V., Experiments in Hearing (McGraw-Hill, New York, 1960). [Google Scholar]
- Voldrich L., “Mechanical properties of the basilar membrane,” Acta Oto-Laryngol. 86, 331–335 (1978). [DOI] [PubMed] [Google Scholar]
- Naidu R. C. and Mountain D. C., “Longitudinal coupling in the basilar membrane,” J. Assoc. Res. Otolaryngol. 2, 257–267 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S. and White R. D., “Orthotropic material properties of the gerbil basilar membrane,” J. Acoust. Soc. Am. 123, 2160–2171 (2008). 10.1121/1.2871682 [DOI] [PubMed] [Google Scholar]
- Neely S. and Kim D., “A model for active elements in cochlear biomechanics,” J. Acoust. Soc. Am. 79, 1472–1480 (1986). 10.1121/1.393674 [DOI] [PubMed] [Google Scholar]
- Allen J. B. and Sondhi M. M., “Cochlear macromechanics: Time domain solutions,” J. Acoust. Soc. Am. 66, 123–132 (1979). 10.1121/1.383064 [DOI] [PubMed] [Google Scholar]
- Wickersberg C. D. and Geisler R. E., “Longitudinal stiffness coupling in a 1-dimensional model of the peripheral ear,” Peripheral Auditory Mechanisms (Springer-Verlag, Berlin, 1986), pp. 113–120. [Google Scholar]
- Steele C. R. and Taber L. A., “Comparison of WKB calculations and experimental results for three-dimensional cochlear models,” J. Acoust. Soc. Am. 65, 1007–1018 (1979). 10.1121/1.382570 [DOI] [PubMed] [Google Scholar]
- Strelioff D. and Flock A., “Stiffness of sensory-cell hair bundles in the isolated guinea-pig cochleas,” Hear. Res. 15, 19–28 (1984). 10.1016/0378-5955(84)90221-1 [DOI] [PubMed] [Google Scholar]
- Gummer A. W., Johnstone B. M., and Armstrong N. J., “Direct measurement of basilar membrane stiffness in guinea pig,” J. Acoust. Soc. Am. 70, 1298–1309 (1981). 10.1121/1.387144 [DOI] [Google Scholar]
- Frank G., Hemmert W., and Gummer A. W., “Limiting dynamics of high-frequency electromechanical transduction of outer hair cells,” Proc. Natl. Acad. Sci. U.S.A. 96, 4420–4425 (1999). 10.1073/pnas.96.8.4420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He D. Z. Z., Jia S. P., and Dallos P., “Mechanoelectrical transduction of adult outer hair cells studied in a gerbil hemicochlea,” Nature (London) 429, 766–770 (2004). 10.1038/nature02591 [DOI] [PubMed] [Google Scholar]
- Zheng J. F., Deo N., Zou Y., Grosh K., and Nuttall A. L., “Chlorpromazine alters cochlear mechanics and amplification: In vivo evidence for a role of stiffness modulation in the organ of corti,” J. Neurophysiol. 97, 994–1004 (2007). 10.1152/jn.00774.2006 [DOI] [PubMed] [Google Scholar]
- Hughes T. J. R., The Finite Element Method: Linear Static and Dynamic Finite Element Analysis (Dover, New York, 2000). [Google Scholar]
- Parthasarathi A. A., Grosh K., and Nuttall A. L., “Three-dimensional numerical modeling for global cochlear dynamics,” J. Acoust. Soc. Am. 107, 474–485 (2000). 10.1121/1.428352 [DOI] [PubMed] [Google Scholar]
- Naidu R. C. and Mountain D. C., “Basilar membrane tension calculations for the gerbil cochlea,” J. Acoust. Soc. Am. 121, 994–1002 (2007). 10.1121/1.2404916 [DOI] [PubMed] [Google Scholar]
- de Boer E. and Nuttall A. L., “The mechanical waveform of the basilar membrane. III. Intensity effects,” J. Acoust. Soc. Am. 107, 1497–1507 (2000). 10.1121/1.428436 [DOI] [PubMed] [Google Scholar]
- Legan P. K., Lukashkina V. A., Goodyear R. J., Kossl M., Russell I. J., and Richardson G. P., “A targeted deletion in alpha-tectorin reveals that the tectorial membrane is required for the gain and timing of cochlear feedback,” Neuron 28, 273–285 (2000). 10.1016/S0896-6273(00)00102-1 [DOI] [PubMed] [Google Scholar]
- Shera C. A., “Mammalian spontaneous otoacoustic emissions are amplitude-stabilized cochlear standing waves,” J. Acoust. Soc. Am. 114, 244–262 (2003). 10.1121/1.1575750 [DOI] [PubMed] [Google Scholar]
- Iwasa K. H. and Adachi M., “Force generation in the outer hair cell of the cochlea,” Biophys. J. 73, 546–555 (1997). 10.1016/S0006-3495(97)78092-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper N. P., “Harmonic distortion on the basilar membrane in the basal turn of the guinea-pig cochlea,” J. Physiol. (London) 509, 277–288 (1998). 10.1111/j.1469-7793.1998.277bo.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuttall A. L. and Dolan D., “Steady-state sinusoidal velocity responses of the basilar membrane in guinea pig,” J. Acoust. Soc. Am. 99, 1556–1565 (1996). 10.1121/1.414732 [DOI] [PubMed] [Google Scholar]
- Müller U. and Gillespie P., “Silencing the cochlear amplifier by immobilizing prestin,” Neuron 58, 299–301 (2008). 10.1016/j.neuron.2008.04.018 [DOI] [PMC free article] [PubMed] [Google Scholar]