Abstract
Background
Different mechanistic models have been used in the literature to describe the enzymatic hydrolysis of pretreated biomass. Although these different models have been applied to different substrates, most of these mechanistic models fit into two- and three-parameter mechanistic models. The purpose of this study is to compare the models and determine the activation energy and the enthalpy of adsorption of Trichoderma reesei enzymes on ammonia fibre explosion (AFEX)-treated wheat straw. Experimental enzymatic hydrolysis data from AFEX-treated wheat straw were modelled with two- and three-parameter mechanistic models from the literature. In order to discriminate between the models, initial rate data at 49°C were subjected to statistical analysis (analysis of variance and scatter plots).
Results
For three-parameter models, the HCH-1 model best fitted the experimental data; for two-parameter models Michaelis-Menten (M-M) best fitted the experimental data. All the three-parameter models fitted the data better than the two-parameter models. The best three models at 49°C (HCH-1, Huang and M-M) were compared using initial rate data at three temperatures (35°, 42° and 49°C). The HCH-1 model provided the best fit based on the F values, the scatter plot and the residual sum of squares. Also, its kinetic parameters were linear in Arrhenius/van't Hoff's plots, unlike the other models. The activation energy (Ea) is 47.6 kJ/mol and the enthalpy change of adsorption (ΔH) is -118 kJ/mol for T. reesei enzymes on AFEX-treated wheat straw.
Conclusion
Among the two-parameter models, Michaelis-Menten model provided the best fit compared to models proposed by Humphrey and Wald. For the three-parameter models, HCH-1 provided the best fit because the model includes a fractional coverage parameter (ϕ) which accounts for the number of reactive sites covered by the enzymes.
Background
Over the years, two kinds of cellulose hydrolysis models have been developed: empirical and mechanistic models. As empirical models lack a firm theoretical foundation, it is impossible to extend them beyond the range of data to which they were fit. Therefore, our attention was focused on mechanistic models that describe the reaction mechanism between lignocellulosic biomass and enzyme. In order to formulate an appropriate mechanistic model, we needed to know how enzymes hydrolyze lignocellulosic substrates.
The hydrolysis of lignocellulosic substrates depends on enzyme characteristics [1], including: (1) adsorption of enzyme onto lignocellulosic biomass prior to reaction; (2) end-product inhibition which is competitive [2] or noncompetitive [3]; (3) synergy of the various enzyme components; and (4) mass transfer limitations affecting the transport of the enzyme to the substrate [1]. Enzymatic hydrolysis also depends on substrate characteristics including: (1) lignin distribution; (2) the presence of other components such as hemicellulose, proteins and fats; (3) particle size; and (4) crystallinity [4].
Incorporating all these factors into a single model is cumbersome and highly complicated. We, therefore, divided these factors into short-term and long-term factors. For short-term hydrolysis (initial rate), Fan and Lee [5] have shown that: (1) product inhibition is not important; (2) hydrolysis is least affected by mass transfer effects; (3) chemical pretreatment is important; and (4) the pseudo-steady state assumption can be used [5]. For long-term hydrolysis, Fan and Lee [6] have indicated that: (1) rate is higher initially but changes later due to product inhibition; (2) pseudo-steady state assumptions do not apply; and (3) changes occur in the crystallinity index and surface area. Literature models consider the above factors and, in some cases, differential equations were used to model both the short-term and long-term hydrolysis process [7,8]. The simplest forms consider a single substrate and a single enzyme system.
Table 1 summarizes the cellulose hydrolysis models that have appeared in the literature. They can broadly be categorized as two- and three-parameter models [9]. The more complex mechanistic models consider multiple substrates (amorphous and crystalline cellulose) and the different enzyme components.
Table 1.
Summary of models.
| Model | Two-parameter models | References |
|---|---|---|
| 2A | 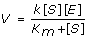 |
Ghose and Das [10], Dwivedi and Ghose [14], Howell and Stuck [11], Caminal et al. [15], Gan et al. [7] |
| 2B | 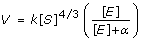 |
Humphrey et al. [16] Movagharnejad and Sohrabi [17] |
| 2C | 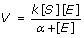 |
Wald et al. [18] |
| Three-parameter models | ||
| 3A | 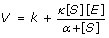 |
Fan and Lee [20] |
| 3B | 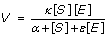 |
Huang [21] |
| 3C |
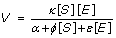 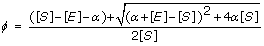
|
Holtzapple et al. [22] |
Model 2A
The Michaelis-Menten (M-M) model was used to describe the hydrolysis of Solka Floc and avicel [10-13]. The hydrolysis of alkali-treated bagasse by Trichoderma reesei cellulase was evaluated using M-M kinetics with competitive inhibition [14]. The M-M model was used by Caminal et al. [15], but the authors could not distinguish between competitive and noncompetitive inhibition by cellobiose. The M-M model works on the assumption that the substrate concentration is much higher than the enzyme concentration and this may not always be the case. A mechanistic model similar to M-M kinetics was proposed and differential equations were solved for the different substrate components [7].
Model 2B
The shrinking-site hydrolysis model with a Langmuir-type adsorption isotherm was used in order to get three different rate equations for cellulose, cellobiose and glucose [16]. Recently, the shrinking-site model was extended to rice pollards, sawdust, wood particles and used paper [17].
Model 2C
The model has a similar mathematical form to M-M, except that an enzyme term appears in the denominator rather than a substrate term [18,19].
Model 3A
A mechanistic model proposed by Fan and Lee that describes the hydrolysis of cellulose and cellobiose, but does not include an adsorption step [20].
Model 3B
This model was proposed by Huang when cellulose hydrolysis by T. viride cellulase was modelled using the M-M mechanism with competitive inhibition [21].
Model 3C
The HCH-1 model was proposed by Holtzapple et al. [22], which is essentially the M-M mechanism with noncompetitive inhibition and a parameter to account for the number of reactive sites covered by the enzymes. A pseudo-steady state approximation for the HCH-1 model was developed [23] and recently applied to lime pretreated corn stover [24].
Most of the mechanistic models used to describe cellulose hydrolysis in the literature fit into the six mathematical forms presented in Table 1[9]. In some cases, the constants are interpreted differently. In other cases, the models are applied multiple times to each enzyme and substrate component. It is worthwhile to compare these models in order to determine their relative merits. To simplify the system, an initial rate data was generated from ammonia fiber explosion (AFEX)-treated wheat straw that was hydrolyzed with T. reesei cellulase. The data were fitted to the various models so they could be compared on an equal basis.
Results and discussion
The enzyme loadings and substrate conditions at the specific temperatures are given in Tables 2, 3 and 4. The data (Tables 1, 2, 3, 4) were subjected to statistical analysis (analysis of variance and scatter plots). For each model, a plot of the predicted velocity versus the measured velocity (scatter) was made (Figures 1, 2, 3 and 4). The F values and model parameter estimates were obtained for each model (Tables 5, 6 and 7). The plots together with the F values were used to compare the models.
Table 2.
Initial velocity data for enzymatic hydrolysis of ammonia fibre explosion (AFEX)-treated wheat straw at 49°C.
| Experiment. No. | [S] (g/L) | [E] (g/L) | rs × 100 (g/L·min) |
|---|---|---|---|
| 1 | 15.60 | 0.738 | 0.629* |
| 2 | 3.85 | 1.145 | 0.648 |
| 3 | 1.93 | 0.736 | 0.194 |
| 4 | 3.85 | 0.364 | 0.220 |
| 5 | 7.90 | 0.365 | 0.197 |
| 6 | 7.90 | 0.735 | 0.580 |
| 7 | 47.77 | 0.739 | 0.792 |
| 8 | 3.91 | 1.138 | 0.485 |
| 9 | 7.86 | 1.138 | 0.739 |
| 10 | 15.52 | 1.138 | 1.257 |
| 11 | 15.49 | 0.365 | 0.297 |
| 12 | 31.01 | 0.365 | 0.310 |
| 13 | 15.47 | 0.187 | 0.215 |
| 14 | 15.47 | 0.094 | 0.098 |
| 15 | 15.50 | 0.364 | 0.323 |
| 16 | 7.76 | 0.364 | 0.216 |
| 17 | 15.43 | 1.712 | 1.460 |
| 18 | 3.87 | 1.712 | 0.770 |
| 19 | 15.41 | 1.141 | 1.044 |
| 20 | 31.01 | 1.141 | 1.319 |
| 21 | 7.76 | 0.730 | 0.616 |
| 22 | 15.43 | 2.287 | 2.229 |
| 23 | 3.89 | 2.287 | 0.979 |
| 24 | 48.73 | 1.138 | 1.579 |
| 25 | 3.97 | 4.559 | 1.358 |
| 26 | 15.72 | 4.561 | 3.549 |
| 27 | 48.34 | 4.561 | 6.241 |
| 28 | 7.74 | 4.561 | 2.218 |
| 29 | 3.93 | 3.412 | 1.237 |
| 30 | 3.89 | 6.825 | 1.738 |
| 31 | 15.50 | 6.825 | 5.014 |
* rs = 0.00629 g/(L·min)
Table 3.
Initial velocity data for enzymatic hydrolysis of ammonia fibre explosion (AFEX)-treated wheat straw at 42°C.
| Experiment No. | [S] (g/L) | [E] (g/L) | rs × 100 (g/L·min) |
|---|---|---|---|
| 1 | 48.34 | 3.412 | 3.479* |
| 2 | 15.50 | 1.142 | 1.063 |
| 3 | 31.01 | 1.153 | 1.171 |
| 4 | 3.93 | 1.153 | 0.483 |
| 5 | 15.39 | 3.420 | 2.598 |
| 6 | 48.15 | 4.562 | 4.795 |
| 7 | 8.49 | 4.562 | 1.956 |
| 8 | 7.74 | 1.152 | 0.666 |
| 9 | 11.92 | 4.563 | 2.653 |
| 10 | 11.90 | 2.548 | 1.927 |
* rs = 0.03479 g/(L·min)
Table 4.
Initial velocity data for enzymatic hydrolysis of ammonia fibre explosion (AFEX)-treated wheat straw at 35°C.
| Experiment No. | [S] (g/L) | [E] (g/L) | rs × 100 (g/L·min) |
|---|---|---|---|
| 1 | 48.34 | 3.412 | 2.516* |
| 2 | 15.50 | 1.144 | 0.668 |
| 3 | 30.82 | 1.153 | 0.804 |
| 4 | 3.89 | 1.153 | 0.357 |
| 5 | 15.49 | 3.420 | 1.232 |
| 6 | 48.15 | 4.562 | 2.998 |
| 7 | 7.74 | 1.152 | 0.515 |
| 8 | 25.42 | 4.563 | 2.117 |
| 9 | 16.10 | 2.092 | 1.209 |
* rs = 0.02516 g/(L·min)
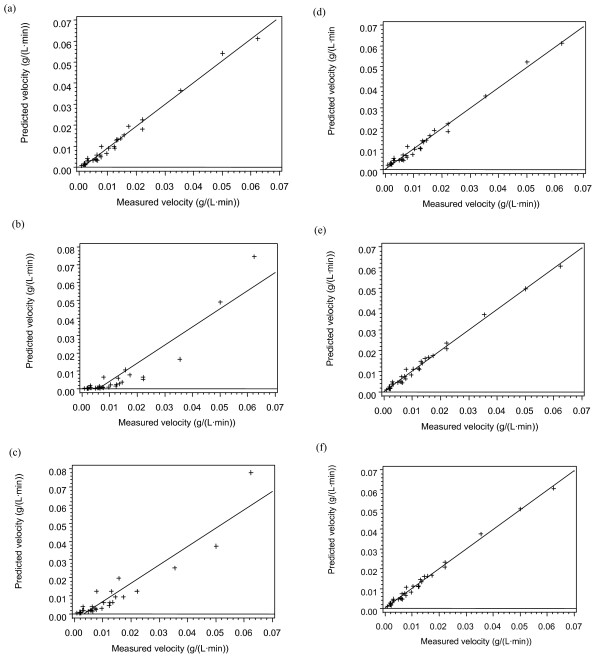
Figure 1.
Scatter plots at 49°C. (a) Model 2A (Michaelis-Menten); (b) Model 2B (Humphrey); (c) Model 2C (Wald); (d) Model 3A (Fan and Lee); (e) Model 3B (Huang); (f) Model 3C (HCH-1).
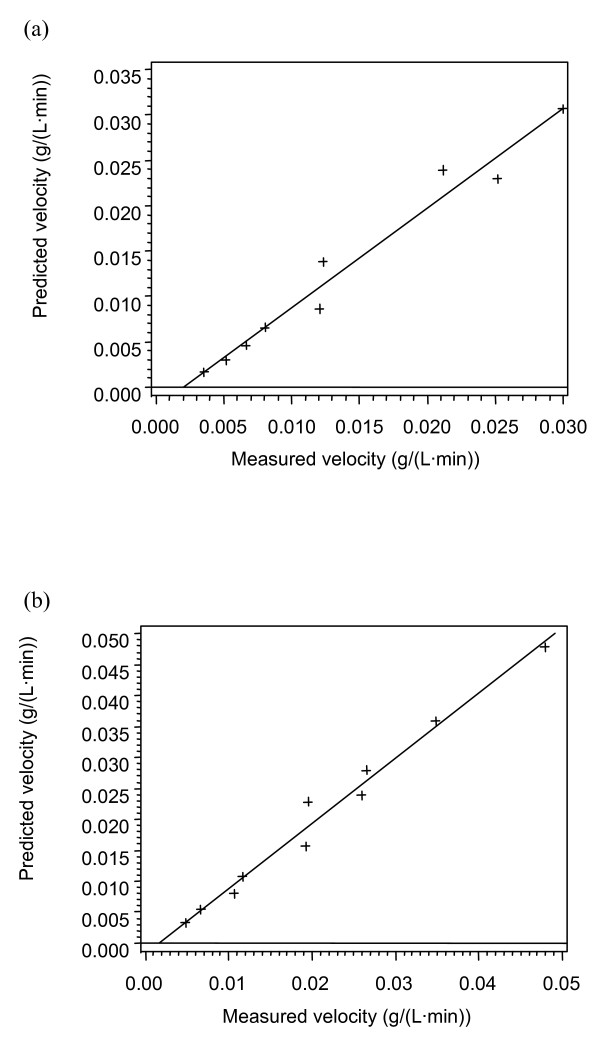
Figure 2.
Scatter plot for Model 2A (Michaelis-Menten). (a) 35°C; (b) 42°C.
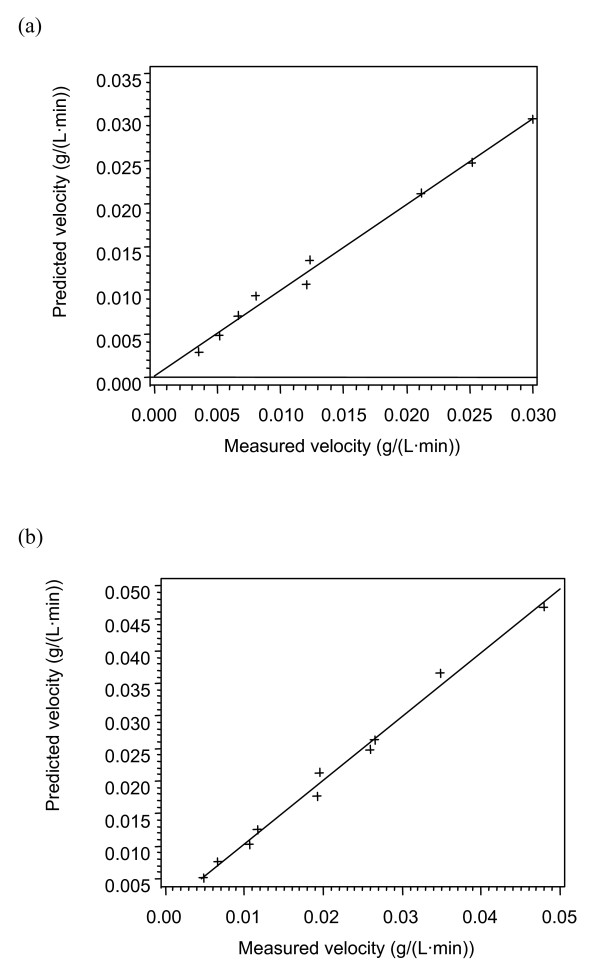
Figure 3.
Scatter plot for Model 3B (Huang). (a) 35°C (b) 42°C.
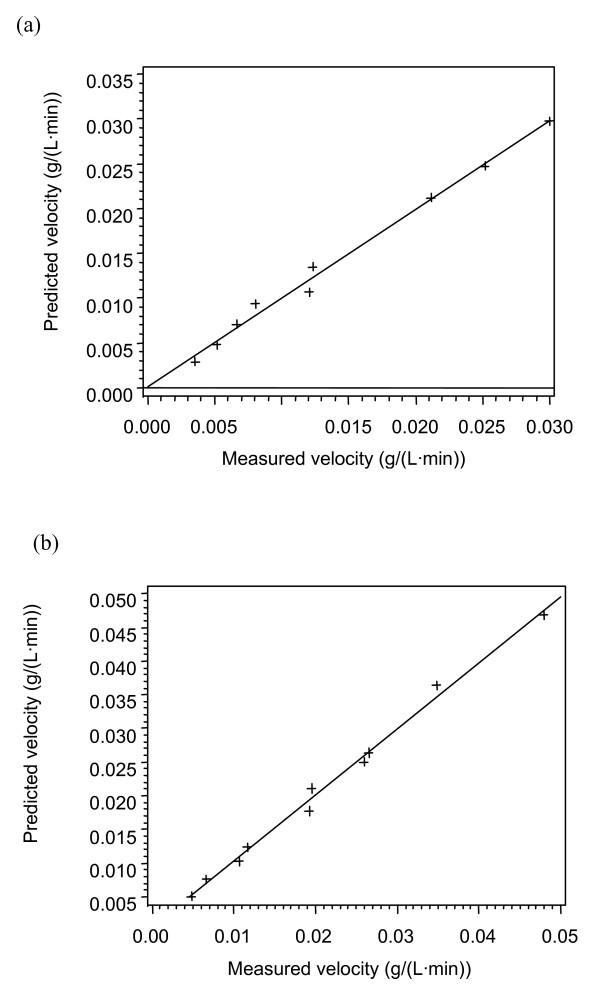
Figure 4.
Scatter plot for Model 3C (HCH-1). (a) 35°C; (b) 42°C.
Table 5.
Parameter estimates at 49°C.
| Models | Parameter 1 | Parameter 2 | Parameter 3 | F value | Residual sum of square |
|---|---|---|---|---|---|
| 2A |
k = 0.0200 (g/(g·min)) |
Km = 23.5237 (g/L) |
- | 1311.34 | 0.000117 |
| 2B |
K = -0.00042 (L/g)(1/3)·min-1 |
α = -9.1015 (g/L) |
- | 60.26 | 0.00208 |
| 2C |
k = 8489674 (g/L) |
α = 2.4E10 (g/(g·min)) |
- | 245.34 | 0.00117 |
| 3A |
k = 0.00156 (g/(L·min)) |
κ = 0.0204 (g/(g·min)) |
α = 27.1162 (g/L) |
1072.28 | 0.000076 |
| 3B | κ = 0.0190 (g/(g·min)) |
α = 12.7035 (g/L) |
ε = 1.7855 (g/g) |
2219.86 | 0.000045 |
| 3C | κ = 0.0168 (g/(g·min)) |
α = 10.2269 (g/L) |
ε = 2.4631 (g/g) |
2232.79 | 0.000045 |
Table 6.
Parameter estimates at 42°C.
| Models | Parameter 1 | Parameter 2 | Parameter 3 | F value | Residual sum of square |
|---|---|---|---|---|---|
| 2A |
k = 0.0137 (g/(g·min)) |
Km = 14.7743 (g/L) |
- | 548.33 | 0.000043 |
| 3B | κ = 0.0138 (g/(g·min)) |
α = 5.5471 (g/L) |
ε = 2.4092 (g/g) |
1044.74 | 0.000013 |
| 3C | κ = 0.0115 (g/(g·min)) |
α = 3.5973 (g/L) |
ε = 3.6250 (g/g) |
3428.53 | 0.000004 |
Table 7.
Parameter estimates at 35°C.
| Models | Parameter 1 | Parameter 2 | Parameter 3 | F value | Residual sum of squares |
|---|---|---|---|---|---|
| 2A |
k = 0.00978 (g/(g·min)) |
Km = 21.9288 g/L) |
- | 199.41 | 0.000042 |
| 3B | κ = 0.0119 (g/(g·min)) |
α = 5.7541 (g/L) |
ε = 7.4772 (g/g) |
805.81 | 0.000006 |
| 3C | κ = 0.00748 (g/(g·min)) |
α = 1.3730 (g/L) |
ε = 8.2915 (g/g) |
1196.19 | 0.000004 |
For the two-parameter models at 49°C, Model 2A (M-M) is clearly the best. The F values and the residual sum of squares (RSS) favour the M-M mechanism. Model 2B (Humphrey) produced negative parameters, so it is clearly inadequate. The fit from Model 2C (Wald) is very poor from the scatter plots. Of the three-parameter models, Model 3C (HCH-1) provided the best fit. The HCH-1 model has the highest F value of 2232 and provided a better fit from the scatter plot. Model 3B (Huang) has an F value of 2219 and the scatter plots were very similar to HCH-1. Therefore, Model 3B (Huang) is the closest competitor to the HCH-1 model.
As the F value, RSS or the correlation coefficient (R2) provide a comparison between models with the same number of parameters; they will be used to compare models with the same number of parameters [25-27]. Among the two-parameter models at 49°C, the F values and the RSS show that Model 2A is the best model. The two best models for the three-parameter models at 49°C are Model 3B and Model 3C based on the F values and the RSS. These three models (2A, 3B and 3C), were further tested at 35° and 42°C. Among the two three-parameter models tested at 35° and 42°C, the HCH-1 model (Model 3C) provided the best fit based on the F values and the RSS.
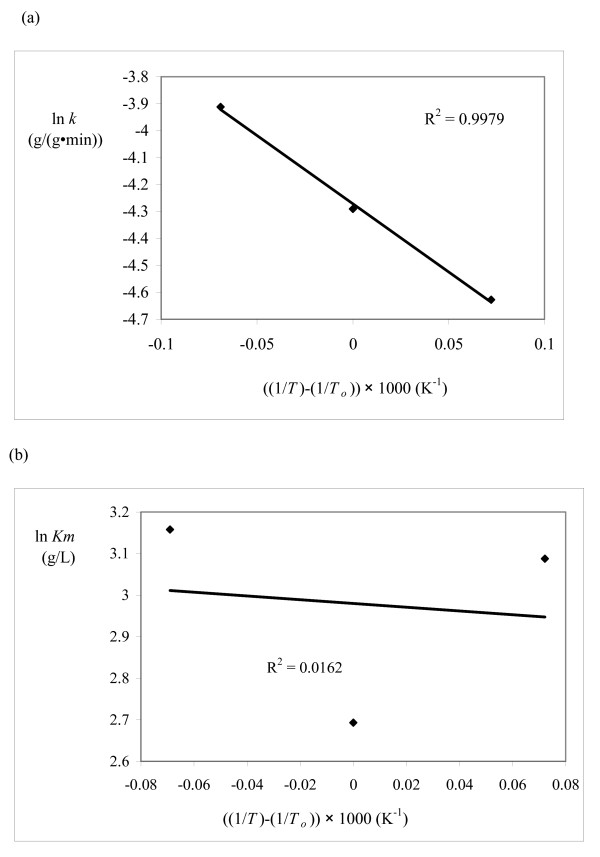
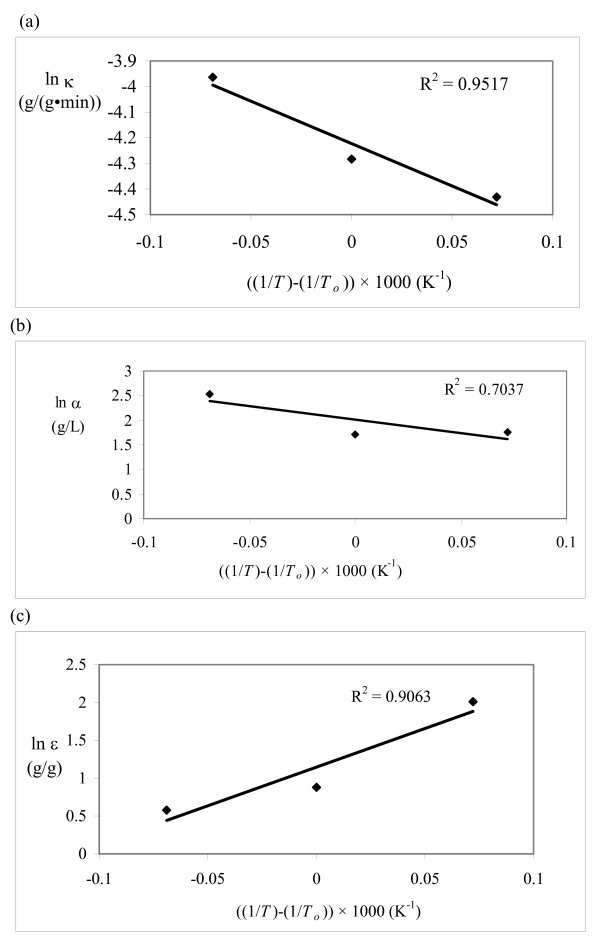
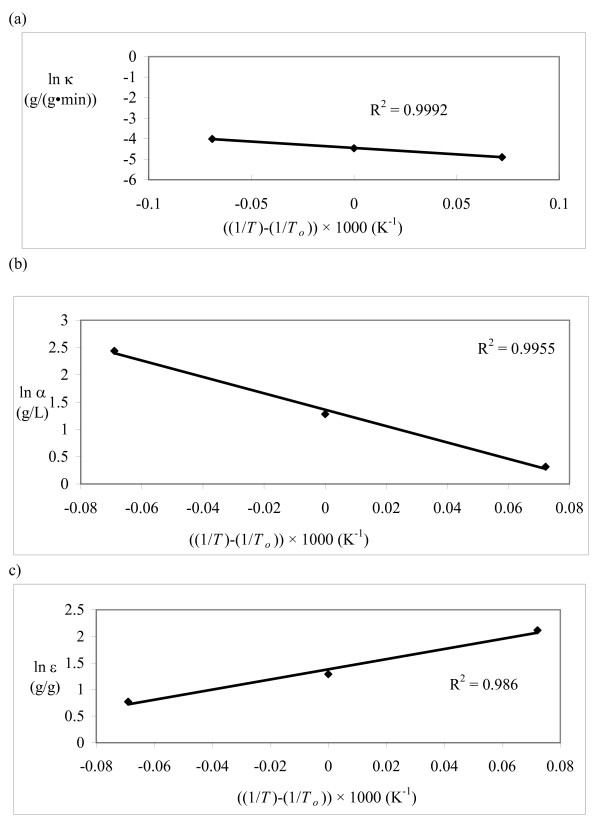
For a kinetic model to be valid, the rate constant should follow the Arrhenius equation and the adsorption/desorption parameters should follow the van't Hoff equation. The kinetic parameters from this study were plotted on Arrhenius/van't Hoff plots (Figures 5, 6 and 7) using 315°K as the reference temperature (To). The HCH-1 plot provided the best fit from the R2 values (Figure 7a - c), therefore the rate constants follow the Arrhenius equation. The kinetic parameters in the HCH-1 model for AFEX-treated wheat straw are temperature dependent and can, therefore, be predicted by the Arrhenius/van't Hoff relationships. The coverage parameter (ε) depends on the adsorption parameter, which explains the van't Hoff dependence on temperature. HCH-1 provided the best fit as it has a fractional coverage parameter (ϕ) that accounts for the number of reactive sites covered by the enzyme.
Figure 5.
Model 2A (Michaelis-Menten). Arrhenius/van't Hoff plots for (a) k and (b) Km.
Figure 6.
Model 3B (Huang). Arrhenius/van't Hoff plots for (a)κ, (b) α and (c) ε.
Figure 7.
Model 3C (HCH-1). Arrhenius/van't Hoff plots for (a) κ, (b) α and (c) ε.
The activation energy (Ea) is 47.6 kJ/mol and the enthalpy change of adsorption (ΔH) is -118 kJ/mol for AFEX-treated wheat straw. The activation energy compares very well with previous work on cotton fibres, pulp and cellobiose (Table 8) [28-30]. Table 9 summarizes results from the comparison of the models. The HCH-1 model (Model 3C) is the only model that meets all the criteria specified in Table 9.
Table 8.
Summary of cellulase activation energies and heats of adsorption.
| Enzyme Source | Substrate |
Ea (kJ/mol) |
ΔH (kJ/mol) | Reference |
|---|---|---|---|---|
| Trichoderma reesei | AFEX-treated wheat straw | 47.6 | -118 | This Work |
| T. viride (endo) | Cotton fibres | 54.6 | 16.5 | Beltrame et al. [28] |
| T. viride (endo) | Pulp | 55.1 | -48.9 | Beltrame et al. [28] |
| T. viride (exo) | Cotton fibres | 137.4 | 66.1 | Beltrame et al. [28] |
| T. viride (exo) | Pulp | 137.4 | 76.9 | Beltrame et al. [28] |
| T. viride | Cellobiose | 45.1 | 20.9 | Beltrame et al. [28] |
| Aspergillus niger | Cellobiose | 46.1 | - | Calsavara et al. [29] |
| T. reesei | Avicel | 29.8 | -148 | Drissen et al. [30] |
AFEX, ammonia fibre explosion
Table 9.
Summary of model comparison results.
| Model | F value | Parameter estimates* | Scatter plots | Arrhenius plots |
|---|---|---|---|---|
| 2A | √ | √ | √ | X |
| 2B | X | X | X | |
| 2C | X | √ | X | |
| 3A | X | √ | √ | |
| 3B | √ | √ | √ | X |
| 3C | √ | √ | √ | √ |
√ = Model success.
X = Model failure.
* Parameter estimates fail when estimates were negative.
Conclusions
Among the two-parameter models, Model 2A (M-M) is the best, although it does not include an adsorption step prior to hydrolysis. Model 2B (Humphrey) introduced an adsorption parameter, a lumped constant which might be responsible for the negative parameters that were generated. Model 2C (Wald) and Model 3A (Fan and Lee) are based on a complex reaction system that did not adequately describe the data. Model 3B (Huang) assumed fast adsorption and slow reaction. It was good at a given temperature. However, there was more scatter in the Arrhenius plot compared to HCH-1. Model 3C (HCH-1) includes the fractional coverage parameter (ϕ) which accounts for the number of reactive sites covered by the enzyme. The inclusion of the coverage parameter gives HCH-1 a better fit for the data. At a fixed temperature, Model 3C (HCH-1) was comparable to Model 3B (Huang). However, Model 3C had much less scatter in the Arrhenius plot.
Methods
Pretreatment
Using the AFEX process [31], moist wheat straw was contacted with liquid ammonia. After thorough mixing, ammonia (which disrupts hydrogen bonds in cellulose) was instantaneously released to the atmosphere. This sudden decrease in pressure caused the liquid ammonia trapped in the cellulose fibres to 'explode', which decreased the crystallinity of the cellulose and increased the surface area.
In order to pretreat the wheat straw used in this study, 1370 g of ground wheat straw (0.08 g water/g dry biomass) was mixed with 142 mL of water to bring the moisture content to 0.19 g water/g dry biomass. The wheat straw was placed in an airtight container in an incubator at 35°C for at least 15 min in order to distribute the moisture evenly throughout the straw. Batches of 150 - 250 g of moist wheat straw were treated with ammonia at a ratio of 1.2 g NH3/g dry wheat straw in an AFEX apparatus [32] at 220 psig (1.62 MPa) and 125°F (52°C) for 15 min.
After this first treatment, all of the batches were recombined and allowed to dry for 36 h. Prior to the next treatment, the wheat straw was mixed with water to bring the moisture content to 0.20 g water/g dry biomass and the AFEX process was repeated. This procedure was repeated again, so that the entire amount of wheat straw was AFEX-treated a total of three times.
After treatment, the final moisture content was 0.18 g water/g dry biomass. In order to prevent changes in cellulose structure during storage, the treated wheat straw was kept frozen until its use in the hydrolysis runs. Table 10 lists wheat straw composition as measured by the forage fibre analysis of Goering and Van Soest [33], particle size analysis [3] and other physical properties.
Table 10.
Physical properties of pretreated wheat straw.
| No. of treatments | 3 |
|---|---|
| Moisture content (g H2O/g dry matter) |
0.18 |
| Cellulose (%) | 36.9 |
| Hemicellulose (%) | 27.9 |
| Lignin (%) | 10.7 |
| Cell solubles (%) | 19.9 |
| Protein (%) | 2.3 |
| Ash (%) | 2.2 |
| Average length (mm) | 2.9 ± 0.9 |
| Average width (mm) | 0.8 ± 0.3 |
Hydrolysis apparatus
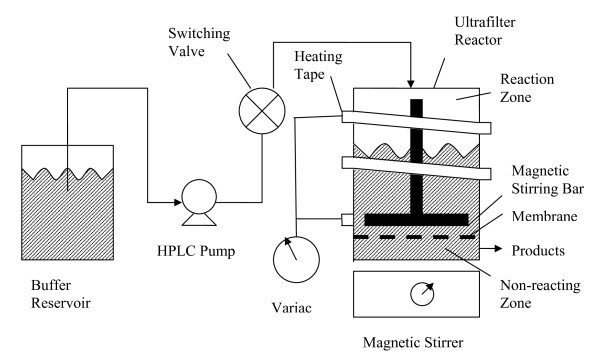
The enzymatic hydrolysis experiments were conducted in an apparatus employing an Amicon ultra-filter membrane (Figure 8). In order to perform the hydrolysis, the AFEX-treated wheat straw was placed in the Amicon stirred cell (10,000 MW-cutoff membrane filter) with 0.05 M, pH 4.8 citric acid buffer. The stirred cell was completely filled with solution. The apparatus was wrapped by a heating tape and the temperature was manually regulated using a Variac. When the desired temperature was achieved, insulation (polyurethane) was placed around the holder in order to maintain the temperature. The temperature could be maintained to within 0.1°C of the desired setting by adjusting the Variac setting or moving the insulation. In order to initiate the reaction, cellulase was injected into the Amicon filter holder using a six-port Rheodyne model 7125 high-performance liquid chromatograph (HPLC) switching valve with a 5-mL sample loop. The 10,000 MW-cutoff filter (Millipore PTGC 076 10) retained the AFEX-treated wheat straw and cellulase but allowed product (cellobiose and glucose) to pass.
Figure 8.
Amicon filter apparatus.
Enzymes
The enzymes used in this study were T. reesei cellulase (Genencor 300P) and β-glucosidase (Novozyme 188). The Novozyme 188, with a reported activity of 250 cellobiose units per gram, was purchased in liquid form and was kept refrigerated until use. As purchased, the Novozyme 188 contained about 40 g/L of glucose.
In order to remove the glucose in the Novozyme 188 by dialysis, an Amicon filter unit with a 10,000 MW cut-off filter was used. Two grams of the dialyzed Novozyme 188 was diluted with 0.05 M, 4.80 pH citrate buffer solution to bring the total volume to 1L. It was preserved with 0.03 wt% NaN3. This procedure reduced the glucose by 1000 times; the final diluted Novozyme 188 solution contained 0.04 g/L glucose. The β-glucosidase was added to each sample to convert cellobiose to glucose. The standard procedure was to add 100 μL of the diluted Novozyme 188 solution to the sample (0.5 - 1.0 mL) and incubate the sample at 50°C for 24 h. The concentrations of the glucose before and after β-glucosidase was added, were determined with YSI Model 27 glucose analyser. The glucose concentration before and after β-glucosidase addition was used to determine the cellobiose produced after hydrolysis.
Data analysis
The ultra-filter (UF) cell was partitioned into two parts. The first compartment had a volume of 440 mL, which is where the reaction occurred. The second compartment, with a volume of 2 mL, was the space below the membrane where the effluent collected and was directed into the tube exiting the reactor. The cell was modelled as two perfectly mixed vessels in series. The glucose produced 30 min after reaction initiation was assumed to be the initial rate. The sugars present (glucose and cellobiose) inhibit the reaction. Glucose and cellobiose inhibition parameters determined by Cognata [34] and Holtzapple et al. [35] were used to correct the initial rates. As the sugar concentrations were small, little correction was required.
Statistical analysis
The nonlinear regression procedure NLIN was used for the SAS programming. The Marquardt method was used for the iteration and the Hougaard option was used to determine the skewness. The analysis of variance tables provided information on the sum of squares, F values, model parameter estimates and skewness. Scatter plots indicated the goodness of fit. The best models for each temperature were determined and the kinetic parameters were fitted using Arrhenius/van't Hoff plots using the re-parameterized equations suggested by Kittrell [36]. For the experiments at 35° and 42°C, a sequential design of experiments was used to decrease the number of experiments required to determine the parameters [37].
Abbreviations
AFEX: ammonia fibre explosion; M-M: Michaels-Menten model; RSSH: residual sum-of-squares under the null hypothesis for the lack of fit F-test; RSS: residual sum of squares; UF: ultra-filter; [E]: cellulase concentration; g/L, k: rate constant; g/(g·min), Km: Michaelis-Menten constant; g/L, n: total number of observations; p: difference in the number of parameters; rs: the rate of appearance of sugars; [S]: substrate concentration; g/L, V: rate of reaction; g/(L·min), α: lumped parameter; g/L, ε: coverage parameter; g/g, κ: rate constant; g/(g·min); ϕ: ratio of free substrate to total substrate, dimensionless.
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
RFB carried out the experiments, performed data analysis and helped to draft the manuscript. FKA performed the data analysis and worked on writing the manuscript. MTH worked on the experimental design, coordination of the study and writing of the manuscript.
Contributor Information
Russell F Brown, Email: Russell.Brown@SolomonOnline.com.
Frank K Agbogbo, Email: fagbogbo@mascoma.com.
Mark T Holtzapple, Email: m-holtzapple@tamu.edu.
References
- Saddler JN, Mooney C, Mansfield SD. Substrate and enzyme characteristics that limit cellulose hydrolysis. Biotechnol Prog. 1999;15:804–816. doi: 10.1021/bp9900864. [DOI] [PubMed] [Google Scholar]
- Huang AA. Kinetic studies on insoluble cellulose-cellulase system. Biotechnol Bioeng. 1975;17:1421–1433. doi: 10.1002/bit.260171003. [DOI] [PubMed] [Google Scholar]
- Holtzapple MT, Cognata M, Shu Y, Hendrickson C. Inhibition of Trichoderma reesei by sugars and solvents. Biotechnol Bioeng. 1990;36:275–287. doi: 10.1002/bit.260360310. [DOI] [PubMed] [Google Scholar]
- Fan LT, Gharpuray MM, Lee YH. Cellulose Hydrolysis. Heidelberg: Springer; 1987. [Google Scholar]
- Fan LT, Lee YH. Kinetic studies of enzymatic hydrolysis of insoluble cellulose: analysis of the initial rates. Biotechnol Bioeng. 1982;24:2383–2406. doi: 10.1002/bit.260241107. [DOI] [PubMed] [Google Scholar]
- Fan LT, Lee YH. Kinetic studies of enzymatic hydrolysis of insoluble cellulose: II. Analysis of extended hydrolysis times. Biotechnol Bioeng. 1983;25:939–966. doi: 10.1002/bit.260251115. [DOI] [PubMed] [Google Scholar]
- Gan Q, Allen SJ, Taylor G. Kinetic dynamics in heterogeneous enzymatic hydrolysis of cellulose: an overview, an experimental study and mathematical modeling. Process Biochem. 2002;38:1003–1018. doi: 10.1016/S0032-9592(02)00220-0. [DOI] [Google Scholar]
- Shao X, Lynd L, Wyman C, Bakker A. Kinetic modelingof cellulosic biomass to ethanol via simultaneous saccharification and fermentation: Part 1. Accomodation of intermittent feeding and analysis of staged reactors. Biotech Bioeng. 2009;102(1):59–65. doi: 10.1002/bit.22048. [DOI] [PubMed] [Google Scholar]
- Peri S, Karra S, Lee YY, Karim MN. Modeling intrinsic kinetics of enzymatic cellulose hydrolysis. Biotechnol Prog. 2007;23:626–637. doi: 10.1021/bp060322s. [DOI] [PubMed] [Google Scholar]
- Ghose TK, Das K. In: Advances in Biochemical Engineering. No. 1. Ghose TK, Fiechter A, editor. New York: Springer Verlag; 1971. A simplified kinetics approach to cellulose-cellulase system. [Google Scholar]
- Howell JA, Stuck JD. Kinetics of Solka Floc cellulose hydrolysis. Biotechnol Bioeng. 1975;17:873–893. doi: 10.1002/bit.260170608. [DOI] [Google Scholar]
- Bezerra RMF, Dias AA. Discrimination among eight modified michaelis-menten kinetics models of cellulose hydrolysis with a large range of substrate/enzyme ratios. Appl Biochem Biotechnol. 2004;112:173–184. doi: 10.1385/ABAB:112:3:173. [DOI] [PubMed] [Google Scholar]
- Bezerra RMF, Dias AA, Fraga I, Pereira AN. Simultaneous ethanol and cellobiose inhibition of cellulose hydrolysis studied with integrated equations assuming constant or variable substrate concentration. Appl Biochem Biotechnol. 2006;134:27–38. doi: 10.1385/ABAB:134:1:27. [DOI] [PubMed] [Google Scholar]
- Dwivedi CP, Ghose TK. A model on hydrolysis of Bagasse cellulose by enzyme from Trichoderma reesei QM 9414. J Ferment Technol. 1979;57:15–24. [Google Scholar]
- Caminal G, Lopez-Santin J, Sola C. Kinetic modeling of the enzymatic hydrolysis of pretreated cellulose. Biotechnol Bioeng. 1985;27:1282–1290. doi: 10.1002/bit.260270903. [DOI] [PubMed] [Google Scholar]
- Humphrey AE. In: Hydrolysis of Cellulose: Mechanisms of Enzymatic and Acid Catalysis. Advances in Chemistry Series, No. 181. Brown RD, Jurasek L, editor. Washington DC: American Chemical Society; 1979. The hydrolysis of cellulosic materials to useful products. [Google Scholar]
- Movagharnejad K, Sohrabi M. A model for the rate of enzymatic hydrolysis of some cellulosic waste materials in heterogeneous solid-liquid systems. Biochem Eng J. 2003;14:1–8. doi: 10.1016/S1369-703X(02)00104-3. [DOI] [Google Scholar]
- Wald S, Wilke CR, Blanch HW. Kinetics of the enzymatic hydrolysis of cellulose. Biotechnol Bioeng. 1984;26:221–230. doi: 10.1002/bit.260260305. [DOI] [PubMed] [Google Scholar]
- Liao W, Liu Y, Wen Z, Frear C, Chen S. Kinetic modeling of enzymatic hydrolysis of cellulose in differently pretreated fibers from dairy manure. Biotechnol Bioeng. 2008;101(3):441–451. doi: 10.1002/bit.21921. [DOI] [PubMed] [Google Scholar]
- Fan LT, Lee YH. Kinetic studies of enzymatic hydrolysis of insoluble cellulose: Derivation of a mechanistic kinetic model. Biotechnol Bioeng. 1983;25(11):2707–2733. doi: 10.1002/bit.260251115. [DOI] [PubMed] [Google Scholar]
- Huang AA. Kinetic studies on insoluble cellulose-cellulase system. Biotechnol Bioeng. 1975;17:1421–1433. doi: 10.1002/bit.260171003. [DOI] [PubMed] [Google Scholar]
- Holtzapple MT, Caram HS, Humphrey AE. The HCH-1 model of enzymatic cellulose hydrolysis. Biotechnol Bioeng. 1984;26:775–780. doi: 10.1002/bit.260260723. [DOI] [PubMed] [Google Scholar]
- Brown RF, Holtzapple MT. A comparison of the Michaelis-Menten and HCH-1 models. Biotechnol Bioeng. 1990;36:1151–1154. doi: 10.1002/bit.260361110. [DOI] [PubMed] [Google Scholar]
- O'Dwyer JP, Zhu L, Granda CB, Holtzapple MT. Enzymatic hydrolysis of lime-pretreated corn stover and investigation of the HCH-1 model: inhibition pattern, degree of inhibition, validity of simplified HCH-1 model. Bioresource Technol. 2007;98:2969–2977. doi: 10.1016/j.biortech.2006.10.014. [DOI] [PubMed] [Google Scholar]
- Mannervik B. Regression analysis, experimental error, and statistical criteria in the design and analysis of experiments for discrimination between rival kinetic models. Methods Enzymol. 1982;87(Part C):370–391. doi: 10.1016/s0076-6879(82)87023-7. full_text. [DOI] [PubMed] [Google Scholar]
- Seber GAF. Linear Regression Analysis. New York: John Wiley & Sons; 1977. pp. 96–99. [Google Scholar]
- Montgomery DC, Runger GC. Applied Statistics and Probability for Eengineers. New York: John Wiley & Sons; 2003. p. 661. [Google Scholar]
- Beltrame PL, Carniti P, Focher B, Marzetti A, Sarto V. Enzymatic hydrolysis of cellulosic materials: a kinetic study. Biotechnol Bioeng. 1984;26:1233–1238. doi: 10.1002/bit.260261013. [DOI] [PubMed] [Google Scholar]
- Calsavara LPV, De Moraes FF, Zanin GM. Modeling cellobiose hydrolysis with integrated kinetic models. Applied Biochem Biotech. 1999;77-79:789–806. doi: 10.1385/ABAB:79:1-3:789. [DOI] [PubMed] [Google Scholar]
- Drissen RET, Maas RHW, Maarel JEC Van der, Kabel MA, Schols HA, Tramper J, Beeftink HH. A generic model for glucose production from various cellulose sources by a commercial cellulase complex. Biocatalysis Biotransform. 2007;25(6):419–429. doi: 10.1080/10242420701510668. [DOI] [Google Scholar]
- Dale BE, Moreira M. A freeze explosion technique for increasing cellulose hydrolysis. Biotechnol Bioeng. 1982;12:31–43. [Google Scholar]
- Brown RF. PhD thesis. Texas A&M University, Chemical Engineering Department; 1990. Kinetics of the enzymatic hydrolysis of AFEX-treated wheat straw. [Google Scholar]
- Goering HK, Van Soest PJ. Agricultural Handbook, No. 379, Jack No. 387-598. Washington, DC: US Department of Agriculture, Superintendent of Documents; 1970. Forage fiber analysis (Apparatus, Reagents, Procedures, and Some Applications) [Google Scholar]
- Cognata MB. MS thesis. Texas A&M University; 1988. Inhibition of Trichoderma reesei cellulase by cellobiose, glucose, ethanol and butanol. [Google Scholar]
- Holtzapple MT, Cognata M, Shu Y, Hendrickson C. Inhibition of Trichoderma reesei by sugars and solvents. Biotechnol Bioeng. 1990;36:275–287. doi: 10.1002/bit.260360310. [DOI] [PubMed] [Google Scholar]
- Kitrell JR, Hunter WG, Watson CC. Advances in Chemical Engineering. New York: Academic Press; 1970. Mathematical Modeling of Chemical Reactions. [Google Scholar]
- Box MJ, Draper NR. Factorial designs, the |X'X| criterion, and some related matters. Technometrics. 1971;13:731. doi: 10.2307/1266950. [DOI] [Google Scholar]