Reliability of league tables of in vitro fertilisation clinics: retrospective analysis of live birth rates

Abstract

Objective: To determine to what extent institutions carrying out in vitro fertilisation can reasonably be ranked according to their live birth rates.

Design: Retrospective analysis of prospectively collected data on live birth rate after in vitro fertilisation.

Setting: 52 clinics in the United Kingdom carrying out in vitro fertilisation over the period April 1994 to March 1995.

Main outcome measure: Estimated adjusted live birth rate for each clinic; their rank and its associated uncertainty.

Results: There were substantial and significant differences between the live birth rates of the clinics. There was great uncertainty, however, concerning the true ranks, particularly for the smaller clinics. Only one clinic could be confidently ranked in the bottom quarter according to this measure of performance. Many centres had substantial changes in rank between years, even though their live birth rate did not change significantly.

Conclusions: Even when there are substantial differences between institutions, ranks are extremely unreliable statistical summaries of performance and change in performance, particularly for smaller institutions. Any performance indicator should always be associated with a measure of sampling variability.

Introduction

There is increasing use of performance indicators in health care which may measure aspects of the process of care,¹ outcomes for health authorities and trusts,² and even the mortality for individual named surgeons.³ Interest is expressed by various audiences, including politicians, purchasers, providers, clinicians, and patients. Doubts have been expressed both about the use of such indicators as a basis of any assessment of the “quality” of an institution and about the statistical methods used to obtain performance estimates adjusted for case mix.^4–7 This paper focuses on one particular aspect of the reporting of such data—the comparison and explicit ranking of institutions. Although this is generally avoided by those responsible for the assessment exercise, the media almost inevitably publish “league tables” of performance, and anecdotal reports suggest individual institutions take considerable interest in their rank. This mirrors the response of public and media to publication of school examination results, a point emphasised in recent collaborations between educational and medical statisticians.⁸

We have illustrated these issues by using publicly available data on the success rates of clinics providing in vitro fertilisation. The clinics are easily ranked on the basis of their results, but from a statistical perspective the rank has sampling error in the same way as any other measured quantity based on the limited number of treatments given in each clinic. Recent developments in computer intensive statistical techniques can be used to place uncertainty intervals around the rank given to each institution. We then can judge to what extent any firm inferences regarding relative performance can be drawn from these ranks and to what extent change in rank is indicative of change in performance.

Methods

Data

The Human Fertilisation and Embryology Authority has a responsibility to monitor clinics in the United Kingdom licensed to carry out donor insemination and in vitro fertilisation.⁹ As part of their annual publication the authority gives for each clinic an adjusted live birth rate per treatment cycle started, where the adjustment is intended to take account of the mix of patients treated by the clinic by using factors such as age, cause of infertility, number of previous treatment cycles, and so on. The analysis is based on a logistic regression analysis of all in vitro fertilisation treatments given in the United Kingdom in the relevant year, which also provides a 95% confidence interval for each adjusted live birth rate. Adjusted live birth rates per egg collection and per embryo transfer are also provided but are not analysed here. Success rates per patient would also be of interest, although success rates per cycle are possibly more relevant for purchasing decisions.

Key messages

• Institutional ranks are extremely unreliable statistical summaries of performance

• Institutions with smaller numbers of cases may be unjustifiably penalised or credited in comparison exercises

• Additional statistical analysis may help to identify the few institutions worthy of review

• Any performance indicator should always have an associated statistical sampling variability

Statistical methods

We first compared graphically the most recent available data⁹ on the adjusted live birth rate for each clinic with the national average, plotting the clinics in rank order. The uncertainty associated with the ranks was then calculated by using the simulation procedure described in the Appendix. We also carried out a multilevel analysis in which each clinic’s live birth rate was treated as if drawn from some underlying population,⁸ but because of the substantial numbers of cases per clinic this analysis had little influence and is not shown here.

Changes in the adjusted live birth rates were calculated for 47 centres that appeared in both the 1995 report (covering cycles started in the period April 1993 to March 1994)¹⁰ and the 1996 report (covering cycles started in the period April 1994 to March 1995).⁹ Approximate 95% confidence intervals for these changes were calculated by taking the variance of the difference in two proportions to be the sum of the variances of the annual estimates and the results contrasted with the observed changes in rank between the two years.

Results

In July 1996 the Human Fertilisation and Embryology Authority reported on 25 730 in vitro fertilisation treatments carried out in 52 clinics over the period from April 1994 to March 1995, providing data on live births up to December 1995.⁹ An overall live birth rate of 14.5% was found. Figure 1 shows the estimated adjusted live birth rate for each of the 52 clinics, together with the associated 95% confidence interval as provided in the published report. The dotted vertical line represents the national average. A common procedure is to identify a particular institution for further review if the interval surrounding their estimate of performance does not include the national average.³ Under this rationale 18 clinics would be picked out: eight for having “significantly” low adjusted live birth (success) rates and 10 for having “significantly” high success rates.

Figure 1.

 Estimates and 95% confidence intervals for adjusted live birth rate in each clinic. Estimated adjusted live birth rate for each clinic given in brackets with number of treatment cycles started. Vertical dotted line represents national average of 14%

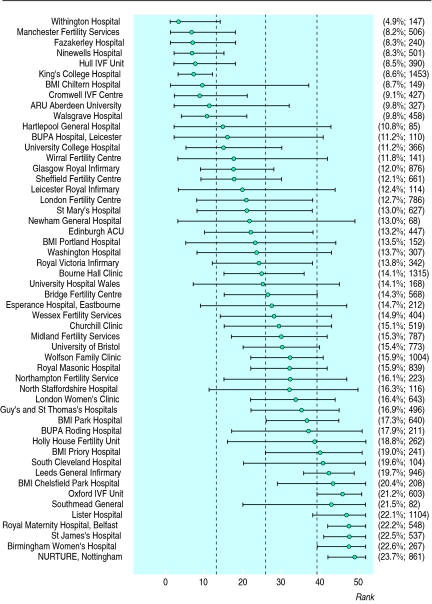
Figure 2 shows the point estimates and 95% confidence intervals for the ranks associated with these success rates (the higher the rank the better). The intervals are generally wide, illustrating the great uncertainty associated with the ranks. The 18 “significantly” outlying clinics can all be confidently placed in either the top or bottom half of the table, although we can conclude that only one clinic is in the lower quarter and five are in the upper quarter.

Figure 2.

 Median and 95% confidence intervals for rank of each clinic. Estimated adjusted live birth rate for each clinic given in brackets with number of treatment cycles started. Dashed vertical lines divide clinics into quarters according to rank

The influence of sample size is clear: King’s College Hospital (1453 treatments) is ranked fifth from the bottom and is the only clinic that can confidently be placed in the bottom quarter, whereas Southmead General Hospital, sixth from the top with a success rate of 21.5% on only 82 treatments, cannot even be confidently placed in the top half.

For clinics placed in the middle the rankings are particularly unreliable, even if the clinics have carried out a large number of treatments. Bourne Hall is ranked 25th from the bottom with 14.1% success rate from 1315 treatments, but the “true” rank has a 95% confidence interval ranging from 15th to 36th from the bottom.

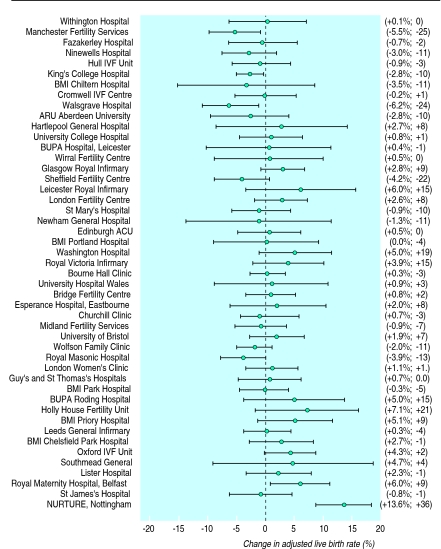
Figure 3 shows the change in adjusted live birth rate between two successive years, with its associated 95% confidence interval. A comparison of these intervals with the line of “no change” shows that three clinics have significantly declined and two have improved. Substantial changes in rank are not necessarily indicative of convincing change in performance: with only two exceptions, changes in rank of up to 23 places are not associated with a significant improvement or decline in adjusted live birth rate. For example, Sheffield Fertility Centre’s adjusted live birth rate had a non-significant fall of 4.2% but led to a drop of 22 places in the rankings. The three clinics that rose or fell by more than 23 places, however, could be confidently said to have changed performance.

Figure 3.

 Estimates and 95% confidence intervals for change in adjusted live birth rate for cycles started between April 1993 and March 1994 compared with those started between April 1994 and March 1995. Observed change in adjusted live birth rate from 1994 to 1995 and accompanying change in rank is shown in brackets

The rank correlation between the rankings in the two years was 0.65 (P<0.001), showing a reasonably strong consistency in the order.

Discussion

In their recent commentary on the Pennsylvania system for publishing mortalities for coronary artery bypass grafts specific to individual surgeons, Schneider and Epstein identified three major problems associated with such performance indicators: inadequate adjustment for pre-existing risk, manipulation of data, and the concentration on a single outcome measure such as mortality.⁷ All these are vital points. The Human Fertilisation and Embryology Authority system has been criticised by Professor Robert Winston for insufficient adjustment for risk,¹¹ although they are careful to emphasise that “live birth rates only give a general guide and you should discuss with the clinic the likelihood of success in your own particular circumstances” and that “it is important to remember that the other issues mentioned in this guide should also be fully considered before any decision is made about which clinic to attend.”⁹

Even if all these considerations were taken care of, however, the basic issue of statistical variability remains an essential and often underplayed aspect of the reporting and interpretation of performance indicators. An extreme example is BUPA Hospital in Norwich, which was identified in the BMJ as having the worst performance in 1993-4 with no live births, but this was based on only 22 treatments.¹¹ The Human Fertilisation and Embryology Authority follows the good example set by the New York State Department of Health³ and the Scottish Office² in attempting to adjust for risk factors and in providing confidence intervals for the main outcome measure. Nevertheless, it is clear that any attempt at using ranks either to compare clinics or summarise change over time may be seriously misleading even when, as in this example, there are substantial differences between institutions. This is only to be expected as most institutions have overlapping intervals and hence precision in ranking is rarely obtainable, particularly for smaller institutions. The strength of recent statistical developments is to quantify this lack of precision and hence emphasise the caution with which any “league tables” must be treated.

Our message is not intended to be entirely negative. Schneider and Epstein argue that simplistic reliance on performance indicators can lead to defensive medicine in which higher risk patients may suffer.⁷ Perhaps additional statistical analysis would help to avoid this unintended consequence of what should be an open and honest appraisal of outcomes.

Appendix

Simulation methods for obtaining intervals for ranks

We shall illustrate the principles of the simulation method through a simple example. Suppose we observe just three clinics, labelled A, B, and C, which, respectively, have success rates (with 95% confidence intervals) of 4% (3% to 5%), 5% (3% to 7%), and 6% (3% to 10%). The relative plausibility of the underlying true success rate for each clinic might be represented by an appropriate normal distribution as on the left of the figure—for example, the distribution for clinic A has a mean of 4% and an SD of 0.5%. These distributions could be given a Bayesian interpretation,¹² although no subjective judgment has gone into their calculation.

Figure.

Left: distributions showing relative probability of possible true values for success rate of three fictional clinics. Right: distributions showing relative probability of possible true ranks of three clinics—these distributions are obtained empirically by successively sampling from distributions on left and ranking results

For each clinic a random “true rate” can be successively drawn from that clinic’s distribution—for example, the chance of drawing a value of, say, 5.00 for clinic A is proportional to the height of the distribution for clinic A at rate=5.00. The first draws are shown in the table, in which values of 4.69, 6.36, and 7.85 were obtained for clinics A, B, and C, respectively. These random draws can then be ranked, as shown in the right hand side of the table. The process is known as an iteration and is then repeated; the next set of simulated success rates show that clinic C is ranked middle and clinic B is highest. Such reversals are to be expected given the clear overlap of the distributions. The simulation should be run sufficiently long to ensure adequate accuracy of the conclusions; in our case 10 000 iterations, with the final iteration producing values of 3.82, 3.84, and 5.46. For each clinic we then have 10 000 simulated ranks—for example, clinic A was ranked lowest on 7372 (74%) iterations, between B and C on 1727 (17%) iterations, and highest on 901 (9%). The distribution of these simulated ranks is shown on the right of the figure. The true rank of clinic B is even more uncertain than that of A as it ranked as the middle clinic on only 55% occasions. Thus we can conclude that there is a 9% chance that the top clinic is clinic A, a 21% chance it is clinic B, and a 70% chance it is clinic C.

Table.

Plausible success rates for three clinics, as simulated from distributions shown in figure. These simulated rates are then ranked and those ranks recorded. Empirical proportions based on 10 000 iterations are shown in figure as estimates of probabilities of “true rank” of each clinic

Iteration	Simulated success rate				Simulated rank
	Clinic A	Clinic B	Clinic C		Clinic A	Clinic B	Clinic C
1	4.69	6.36	7.85		1	2	3
2	4.01	5.71	5.00		1	3	2
....	..	..	..		..	..	..
....	..	..	..		..	..	..
10 000	3.82	3.84	5.46		1	2	3

When this procedure is carried out for larger numbers of clinics the resulting distributions of ranks have to be summarised in a simple way. In our case we carried out 10 000 iterations and then for each clinic ordered the 10 000 simulated ranks. We then identified the median rank (that is, position 5000) and a 95% confidence interval (the distance between those ranks in position 250 and 9750). These are reported in figure 2.

This computationally demanding simulation is known as a Monte Carlo procedure because of its explicit reliance on large numbers of random draws and is used in preference to approximation formulas¹³ as it easily handles varying numbers of cases per clinic. In more complex statistical models it is necessary to use a more sophisticated method known as the Markov chain Monte Carlo (MCMC); this could, for example, take account of the clinics sharing some common source of uncertainty, such as the true extent to which success rates should be adjusted for age. Modern computer power has meant that Markov chain Monte Carlo methods are now feasible for increasingly large problems and are starting to have a dramatic effect on the practice of statistics in difficult contexts.¹⁴ Recent published medical examples focus on challenging issues such as temporal models for changes in childhood immunity,¹⁵ allowing for measurement error in epidemiological studies,¹⁶ spatial variation in mosquitoes in malarial areas,¹⁷ and in meta-analysis of the effects of environmental tobacco smoke.¹⁸

The simulations were performed with the BUGS software,¹⁹ although similar analyses could be carried out with other statistical packages and possibly even with more advanced spreadsheet programs.