pH-dependent self-association of zinc-free Insulin characterized by concentration-gradient static light scattering

Abstract

Insulin self-association at pH 1.85, 1.95, 3.0, 7.2, 8.0 and 10 was studied via composition gradient light scattering (CG-SLS). At pH 1.95 in acetic acid, insulin was found to exist as a monomer, and in pH 1.85 HCl as a dimer. At pH values of 3.0 – 8.0, the dependence of scattering intensity upon total insulin concentration at concentrations of up to 1.5 mg/mL may be quantitatively accounted for by a simple isodesmic association equilibrium scheme requiring only a single association constant for addition of monomer to monomer or any oligomer. At pH 10, the association constant for addition of monomer to monomer was found to be smaller than the association constant for addition of monomer to all higher oligomers by a factor of approximately five. The isodesmic association scheme was also found to quantitatively account for the concentration dependence of the weight-average molecular weight derived from previously published sedimentation equilibrium measurements made at pH 7.0, and the best-fit value of the stepwise equilibrium constant obtained therefrom was in excellent agreement with that obtained from analysis of the light scattering data obtained at pH 7.2

Introduction

The monomeric insulin molecule, thought to be the functional form in solution [1], is known to exist in equilibrium with oligomeric forms in vitro, as determined using different methods: (a) Sedimentation equilibrium [2–6], (b) Static and Dynamic Light scattering [7–10] (c) Small angle neutron and X-ray scattering [11–13], (d) Osmotic pressure [14], (e) mass-spectrometry and NMR [15,16], and (f) Circular dichroism [17].

A number of equilibrium association models have been proposed to account for concentration-dependent properties of insulin solutions, including the following

1. Two insulin monomers form dimer (K₁₂), three dimers form hexamer (K₂₆), and subsequent self-association proceeds with the addition of hexamer only involving a single stepwise association constant K_6a [2].

2. Mark et al. [4] proposed the formation of two types of dimers termed α-α and β-β, involving two association constants K_α K_β. Subsequent growth proceeds with stepwise addition of monomer with alternation of the two association constants.

3. Indefinite isodesmic self association of dimers involving two association constants K₁₂ and K_2I [18].

4. A variant of model 1 has been proposed by Bocian et al. [16], according to which tetramer formation is permitted with an additional association constant K₂₄. Growth beyond hexamer may proceed via the stepwise addition of dimers with a single stepwise association constant.

At the present time the most widely-accepted model appears to be that of Pekar and Frank [2], which was shown to quantitatively account for the most extensive set of sedimentation equilibrium data obtained under a single set of conditions published so far.

The recently introduced technique termed composition gradient static light scattering (CG-SLS) has been shown to provide a rapid, high resolution quantitative characterization of macromolecular self- and hetero-association equilibria [19–22]. In the present study we apply this technique to the study of insulin self-association, with two objectives: (1) To check and verify previously reported observations made under a variety of experimental conditions, and (2) to provide additional high resolution data that may be used to test alternative models for equilibrium self-association. By using a single set of instrumentation and procedures described below, the present study avoids discrepancies in previously reported data arising from the influence of different contact materials upon insulin association [23, 24].

We investigated the self-association of insulin at different pH values ranging from 1.85 to 10, under conditions held uniform except as specifically noted. Data from these experiments were modeled using the Pekar-Frank model and simpler models described below in order to determine which model or models can account for the data with the fewest assumptions and variable parameters at each pH value. It was then shown that the same model and parameter values that accounts most parsimoniously for the CG-SLS data can also account for the most comprehensive sedimentation equilibrium data obtained under comparable conditions by Pekar and Frank [2].

Materials and Methods

In all experiments bovine pancreas insulin (batch: 058K10723) procured from Sigma Aldrich was used. Insulin solutions were prepared by dilution into the following buffers utilizing ultra-pure deionized UV treated water (KD Medical): (1) 20% Acetic acid, 0.1 M NaCl, pH 1.95; (2) 0.025 HCL, 0.1 M NaCl, pH 1.85; (3) 20mM Formate, 0.1 M NaCl, pH 3.0; (4) 4.3 mM Na Phosphate, 0.1 M NaCl, 1 mM EDTA, pH 7.2; (5) 4.3 mM Na Phosphate, 0.1 M NaCl, 5 mM EDTA, pH 8.0; and (6) 5.3 mM glycine, 3.2 mM NaOH, 0.095 M NaCl, pH 10.

Insulin solutions were stored at 4 °C in polypropylene tubes (Corning) for no more than 1 day prior to measurement. Immediately prior to light scattering measurement, solutions were filtered through Anotop 0.02 μm pore size syringe filters to ensure the removal of undisolved aggregates, and then were degassed by centrifugation at 3500 g for 15 minutes at 4 °C. Insulin concentrations were determined by using absorbance at 276 nm, using the value of 1.0 for absorbance in OD units/cm pathlength for 1 g/l solution [25]. All CG-SLS experiments were performed in duplicate at 25°C.

Concentration-gradient static light scattering measurements were performed as previously described [19–22] using a Calypso system (Wyatt Technology Corp, Santa Barbara) consisting of a software-controlled multiple syringe pump used to create the concentration gradient, a DAWN-EOS multi-angle light scattering photometer and an Optilab rEX differential refractometer configured to collect data in parallel from the incoming sample stream. The raw data acquired consist of the time-dependent scattering intensity at fourteen scattering angles and the time-dependent differential refractive index. These data are processed as previously described [20, 21] to yield the concentration-dependent Rayleigh ratio R normalized to units of an optical constant defined as

$$K_{\mathit{opt}}=\frac{4\pi n_0^2{(dn/dw)}^2}{N_A{\lambda }_0^4}$$ (1)

where n₀ denotes the refractive index of the solvent (1.335 for phosphate buffer saline), λ₀ the vacuum wavelength of incident light (690 nm), N_A, Avogadro’s number, and dn/dw the specific refractive increment of insulin, taken as 0.185 cm³/g [19, 26]. In the absence of detectable angular dependence of R/K_opt, the data obtained at all angles in a single experiment were combined for subsequent modeling using various models for equilibrium self-association.

Modeling of self-association

In dilute solution, the scaled Rayleigh ratio of solution containing a single scattering component (in the present case, insulin) is given by [27]

$$\frac{R}{K_{\mathit{opt}}}=\sum M_i{w}_i=M_W{w}_{\mathit{tot}}$$ (2)

where M_i and w_i respectively denote the molecular weight and weight/volume concentration of each oligomeric state of insulin, w_tot the total weight/volume concentration, and M_W the weight average molecular weight, given by

$$M_W=\frac{{\displaystyle \sum _i}{w}_i{M}_i}{{\displaystyle \sum _i}{w}_i}=\frac{{\displaystyle \sum _i}{c}_i{M}_i^2}{{\displaystyle \sum _i}{c}_i{M}_i}$$ (3)

where c_i denotes the molar concentration of the ith species. It is self-evident that any equilibrium model used to generate a calculated dependence of R/K_opt upon w_tot may be also used to generate a calculated dependence of $M_W=\frac{\left(R/K_{\mathit{opt}}\right)}{w_{\mathit{tot}}}$ upon w_tot, which is exactly the form of the results presented in the published studies of insulin self-association via sedimentation equilibrium. Thus with minor modification, the same association scheme may be used to model the composition dependent results of both light scattering and sedimentation equilibrium experiments.

We have used the following three equilibrium association schemes to model light scattering data obtained in the present study and published results of sedimentation equilibrium studies.

1. Monomer-dimer-hexamer-multihexamer (1-2-6-12-18-24)

This is the model used by Pekar and Frank (1972) to account for their sedimentation equilibrium results. The model is defined by three equilibrium constants.

$$K_{12}=c_2/c_1^2$$ (4)

$$K_{26}=c_6/c_2^3$$ (5)

$$K_{6a}=c_{12}/c_6^2=c_{18}/c_{12}{c}_6=c_{24}/c_{18}{c}_6$$ (6)

The conservation of mass is given by

$$c_{\mathit{tot}}=\frac{w_{\mathit{tot}}}{M_1}=c_1+2c_2+6c_6+12c_{12}+18c_{18}+24c_{24}$$ (7)

Given the values of w_tot, M₁, and the three association constants, equations (4–7) may be solved numerically for the equilibrium value of c₁, and then equations (4–6) used to calculate the equilibrium values of the five oligomeric species. Then equation (3) is used to calculate M_W and equation (2) to calculate R/K_opt.

2. Isodesmic indefinite self-association

In this model it is assumed that the oligomer size may increase indefinitely, and that the equilibrium constant for addition of a monomer to another monomer or oligomer of any size is independent of oligomer size, i.e.,

$$K_a=\frac{c_i}{c_{i-1}{c}_1}$$ (8)

is independent of the value of i. The conservation of mass is given by

$$c_{\mathit{tot}}=\frac{w_{\mathit{tot}}}{M_1}=\sum _{i=1}^{\infty }i{c}_i=\frac{c_1}{{\left(1-K_a{c}_1\right)}^2}$$ (9)

Given values of w_tot, M₁, and K_a, equation (9) may be solved analytically for the equilibrium value of c₁, and then equation (8) utilized iteratively to obtain the equilibrium concentrations of all oligomeric species. The normalized scattering intensity is then given by

$$\frac{R}{K_{\mathit{opt}}}=\sum _{i=1}^{\infty }{c}_i{M}_i^2=\frac{M_1^2}{K_a}\frac{(q+q^2)}{{(1-q)}^3}$$ (10)

where q ≡ K_ac₁, and M_w is obtained by dividing R/K_opt by w_tot (equation 2).

3. Enhanced isodesmic indefinite self-association

This model is identical to the isodesmic model, except that the equilibrium association constant for formation of dimer, K₂ differs from the equilibrium constant for all successive monomer additions, K_a, by a factor α. Conservation of mass is given by

$$c_{\mathit{tot}}=\frac{w_{\mathit{tot}}}{M_1}=\sum _{i=1}^{\infty }i{c}_i=\frac{1}{K_a}\left[\frac{q}{{(1-q)}^2}+2(\alpha -1)q^2\right]$$ (11)

Given values of w_tot, M₁, K_a and α, equation (10) may be solved numerically for the equilibrium value of q, or c₁, and then equation (8) utilized iteratively to obtain the equilibrium concentrations of all oligomeric species. The normalized scattering intensity is then given by

$$\frac{R}{K_{\mathit{opt}}}=\sum _{i=1}^{\infty }{c}_i{M}_i^2=\frac{M_1^2}{K_a}\left[\frac{(q+q^2)}{{(1-q)}^3}+4(\alpha -1)q^2\right]$$ (12)

Results

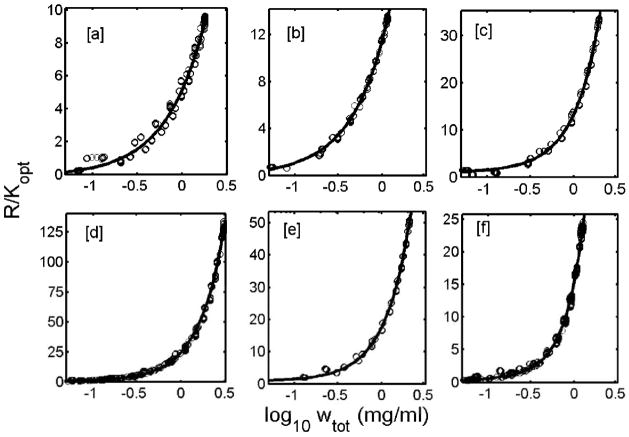
The dependence of R/K_opt upon insulin concentration, measured under each set of experimental conditions, is plotted in Figures 1a–f. Also plotted in each figure is the best fit of the isodesmic self-association model (panels a–e) or the enhanced isodesmic self-association model (panel f), calculated using the corresponding best-fit values of the parameters given in Table 1.

Figure 1.

Mean values (open circles) of R/K_opt obtained from 14 detectors, pooled from replicate runs, are plotted as a function of log₁₀ w_tot of insulin concentration (mg/ml). The plots in each panel represent the different pH at which the experiments were performed: [a] pH 1.95 acetic acid); [b] pH 1.85 (HCl); [c] pH 3.0; [d] pH 7.2; [e] pH 8.0; and [f] pH 10.0. Best fit obtained from isodesmic self-association model is shown in panels [a] to [e] as a solid line. The best fit line shown in panel [f] was obtained from enhanced isodesmic self association model.

Table 1.

Results of modeling CG-SLS experimental data at different solution pH, in context of different insulin equilibrium self-association schemes.

Self-association Model ⇨	1→2→6→12→18→24	Isodesmic	Enhanced-isodesmic
⇩ Insulin solution composition	Fitted Parameters: log10(K12), log10(K26), and log10 (K6a)	Fitted Parameter: log10(Ka)	Fitted Parameters: log10(Ka) and α = K2/Ka
20% Acetic acid, 0.1 M NaCl: pH 1.95 n (# data points) = 930	-----------	M1 = 5344±192 Ka= 0 RMSR= 0.36	-----------
0.025 M HCl, 0.1 M NaCl: pH 1.85 n = 735	-----------	M1 = 10990±990* log10(Ka) = 2.53±0.64 RMSR = 0.53	-----------
20 mM Formate, 0.1 M NaCl: pH 3.0 n = 2910	M1 = 5400c log10(K12) = 6c log10(K26) = 6.9 log10(K6a) = 3.24 RMSR = 0.68	M1 = 5400c log10(Ka) Ka = 3.7±0.03 RMSR = 0.69	-----------
20 mM Phophate, 0.1 M NaCl, 1mM EDTA: pH 7.2 n = 3012	M1 = 5400c log10(K12) = 5.6c log10(K26) = 8.33 log10(K6a) = 3.69 RMSR = 2.0	M1 = 5400c log10(Ka) =4.41±.06 RMSR = 2.07	-----------
20 mM Phosphate, 0.1 M NaCl, 5 mM EDTA: pH 8.0 n = 1232	M1 = 5400c log10(K12) = 8.0c log10(K26)=7.43 log10(K6a) = 3.47 RMSR = 0.82	M1 = 5400c log10(Ka) = 4.1±0.03 RMSR = 0.93	-----------
5.3 mM Glycine, 3.2 mM NaOH, 95 mM NaCl: pH 10.0 n = 1765	M1=5400c log10(K12) = 3.77c log10(K26) = 8.29 log10(K6a) = 3.99 RMSR = 0.47	-----------	M1=5400c log10(Ka) =3.82±0.2 α=0.18 ± 0.15 RMSR = 0.26

^cMolecular weight for insulin monomer was constrained to 5400 Dalton while fitting the data to get best fit estimates of association constants.

^*The fitted value for the molecular weight was 10990 Dalton, indicating that under these solution conditions insulin was predominantly present as dimer.

Root mean squared residual: $\text{RMSR}=\sqrt{\mathit{SSR}/n}$

The data plotted in Figures 1a–f may also be fit by the Pekar-Frank 1-2-6-12-18-24 model, but in no case is the best fit of this model better than that of the isodesmic model, as judged by comparison of the respective values of the mean squared residual given in Table 1. The dependence of R/K_opt upon protein concentration calculated using the 1-2-6-12-18-24 model with best-fit parameter values given in Table 1 is in each case indistinguishable from the corresponding best-fit curve calculated using the isodesmic model (panels a–e) or enhanced isodesmic model (panel f).

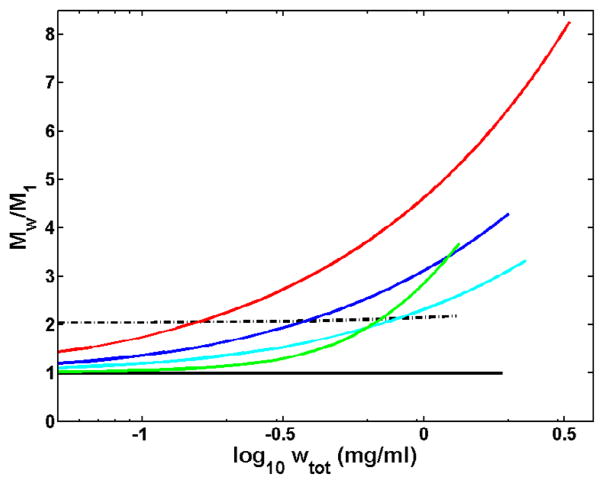
The dependence of weight-average molecular weight upon concentration, calculated for each set of conditions using the corresponding best-fit parameter values, is plotted in Figure 2. At pH 1.95 in acetic acid buffer, insulin appears to exist exclusively as a monomer, with no detectable tendency to self-associate at concentrations under 2 mg/mL. At pH 1.85 in HCl, insulin appears be irreversibly dimerized, and exhibits only an extremely weak and marginally detectable tendency to further self-associate at concentrations less than 1.5 mg/mL. Significant reversible self-association is observed to occur at all pH values above 1.95, with the greatest tendency to self-associate observed at pH 7.2.

Figure 2.

Normalized M_w distribution to the monomeric insulin molecular weight (5400 dalton) is plotted as a function of concentration (log₁₀ w_tot (mg/ml)). Each drawn curve ( red, pH 7.2; blue, pH 8.0; cyan pH 3.0; solid black, pH 1.95, 20% acetic acid; dotted black, pH 1.85, 0.025 M HCl; and green, pH 10) represent the M_W distribution as obtained from corresponding best fit parameters values for isodesmic self-association model (enhanced isodesmic for pH 10) calculated for each set of experimental conditions.

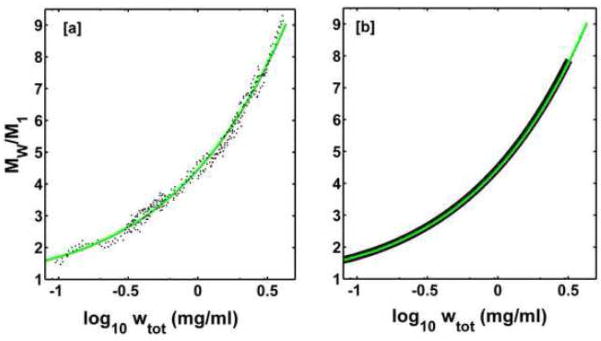
In order to compare results obtained in this study with earlier studies of insulin self-association, we examined the dependence of weight-average molecular weight upon total insulin concentration as determined from sedimentation equilibrium at pH 7.0 at 24.5°C in a buffer of ionic strength 0.1 by Pekar and Frank [2] These data and best-fit of the isodesmic model, calculated using the best-fit parameter value given in Table 2 are plotted in Figures 3a. The best fit of the isodesmic model to these data is as good or better than the best fit of the 1-2-6-12-18-24 model originally proposed by Pekar and Frank [2]. In Figure 3b we compare the dependence of the weight-average molecular weight upon total concentration, calculated using the isodesmic model with best-fit parameter values obtained from modeling the sedimentation equilibrium data of Pekar and Frank [2] and from modeling the concentration-dependent light scattering data obtained in the present study at pH 7.2 and the same temperature and ionic strength. The near-quantitative agreement between these two derived curves and the corresponding best-fit values of log K_a given in Tables 1 and 2 provides additional confidence in the reliability of the original data from which the curves were calculated.

Table 2.

Calculated best-fit parameters obtained from models fitted to sedimentation equilibrium data of Pekar and Frank [2].

1→2→6→12→18→24	Isodesmic
M1 = 5775c log10(K12) = 5.64 log10(K26) = 8.36 log10(K6a) = 3.69 RMSR= 1191	M1=5775c log10(Ka) = 4.43 RMSR = 1197

^cMolecular weight for insulin monomer used by Pekar and Frank [2] 5775.

Root mean squared residual: $\text{RMSR}=\sqrt{\mathit{SSR}/n}$

Figure 3.

[a] Dependence of weight-average molecular weight of insulin upon protein concentration at pH 7.0, obtained from sedimentation equilibrium experiments (data points) and calculated according to best-fit of the isodesmic model as described in text with the best-fit parameters given in Table 2 (curve). [b] Calculated dependence of the weight-average molecular weight of insulin upon protein concentration according to best-fit of the isodesmic model to data of Pekar and Frank (green) and calculated according to best-fit of the isodesmic model to CG-SLS data obtained in the present study at pH 7.2 (Figure 1, panel d.)

Discussion

Our finding that at pH 1.95 in acetic acid, insulin is monomeric at concentrations up to ca 1.9 mg/mL is in semi-quantitative agreement with results previously reported by Weiss et al. [28] and Uversky et al. [13]. Our finding that at pH 1.85 in HCl, insulin exists predominantly as a dimer at concentrations up to ca 1.9 mg/mL is in agreement with the interpretation by Nielsel et al. [12] of the results of their small angle x-ray scattering experiments, but is not in agreement with the results of Mark et al [4] indicating a concentration-dependent equilibrium between monomer, dimer, and at least one higher oligomer under these conditions.

We find that at pH 3, 7.2 and 8, the dependence of light scattering intensity upon concentration may be quantitatively accounted for by a simple isodesmic self-association scheme with a single equilibrium constant for monomer addition. At pH 10, a slight modification of this scheme is required, according to which the equilibrium constant for association to dimer is reduced by about a factor of 5 relative to that for subsequent monomer addition. While all of these data may also be quantitatively accounted for by the 1-2-6-12-18-24 model of Pekar and Frank [2], the latter scheme requires three association constants compared to one for the isodesmic scheme or two for the enhanced isodesmic scheme. The formulation of the Pekar-Frank [2] model seems to have been motivated by an extra-thermodynamic consideration of placing emphasis upon oligomers (dimer, hexamer) that have been observed in crystallographic studies [6]. It is generally agreed that the formation of hexameric insulin is driven by the binding of zinc [29], which is absent from the solutions studied here. In a companion study of insulin self-association in zinc-containing solutions (submitted), we have observed that the insulin hexamer is indeed an important state of association in such solutions. However, to the best of our knowledge there exists no independent experimental evidence for a special status of hexamer in zinc-free solutions. On the basis of Ockham’s razor, we suggest that the more parsimonious isodesmic (or, at pH 10, enhanced isodesmic) association model is to be preferred unless or until additional data of equal reliability invalidate this model.

For many years, sedimentation equilibrium has been considered the most reliable method for quantitative characterization of association equilibria in solution [30]. The near-quantitative agreement between results obtained from sedimentation equilibrium at pH 7.0 and composition gradient static light scattering at pH 7.2 shown in Figure 3b demonstrates once again that CG-SLS may be considered equally reliable for this purpose, while providing the advantages of rapidly conducted experiments (less than 1 hour total duration) and substantially lower cost of instrumentation and maintenance.

Abbreviations

CG-SLS

composition gradient-static light scattering

PBS

phosphate buffered saline