Abstract
The single-handedness of biological molecules has fascinated scientists and laymen alike since Pasteur's first painstaking separation of the enantiomorphic crystals of a tartrate salt more than 150 yr ago. More recently, a number of theoretical and experimental investigations have helped to delineate models for how one enantiomer might have come to dominate over the other from what presumably was a racemic prebiotic world. This article highlights mechanisms for enantioenrichment that include either chemical or physical processes, or a combination of both. The scientific driving force for this work arises from an interest in understanding the origin of life, because the homochirality of biological molecules is a signature of life.
Chemical and/or physical enrichment processes led a prebiotic racemic mixture of molecules to generate living systems in which all sugars and amino acids are right- and left-handed, respectively.
INTRODUCTION
Homochirality as a Signature of Life
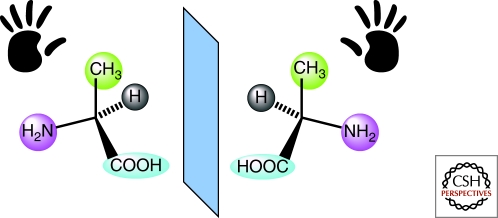
For centuries, symmetry concepts have fascinated scientists as well as artists, mathematicians and writers, laymen and children. The property of chirality—nonsuperimposable forms that are mirror images of one another, as are left and right hands—is manifest in both molecular and macroscopic objects As early as 1874, and a quarter century after Pasteur showed that salts of tartaric acid exist as mirror image crystals, van't Hoff and Le Bel independently postulated the existence of chiral molecules (Heilbronner and Dunitz 1993) (Fig. 1). Chirality held Alice's attention as she pondered the macroscopic world she glimpsed through the looking glass, and her musings over whether looking-glass milk would be good to drink presaged our quest to understand the molecular importance of chirality.
Figure 1.
The two mirror-image enantiomers of the amino acid alanine.
The two forms of a chiral molecule, called enantiomers, have identical physical and chemical properties, but they manner in which each interacts with other chiral molecules may be different, just as a left hand interacts differently with left- and right-hand gloves. Chiral molecules in living organisms in Nature exist almost exclusively as single enantiomers, a property that is critical for molecular recognition and replication processes and would thus seem to be a prerequisite for the origin of life. Yet left and right-handed molecules of a compound will form in equal amounts (a racemic mixture) when we synthesize them in the laboratory in the absence of some type of directing template.
The fact of the single chirality of biological molecules—exclusively left-handed amino acids and right-handed sugars—presents us with two questions: First, what served as the original template for biasing production of one enantiomer over the other in the chemically austere, and presumably racemic, environment of the prebiotic world? And second, how was this bias sustained and propagated to give us the biological world of single chirality that surrounds us?
Short of constructing a Time Machine, we have no way of elucidating precisely the chain of events that led to life on earth today. What we may do instead is highlight the modern experimental and theoretical work that has attempted to probe these questions. After a brief discussion of the first question, this review focuses primarily on the second of the two questions raised earlier: the discussion of plausible mechanisms for the evolution of molecular homochirality as exemplified by the d-sugars and l-amino acids found in living organisms today.
BACKGROUND
How It All Got Started: Chance versus Determinism
“Symmetry breaking” is the term used to describe the occurrence of an imbalance between left and right enantiomeric molecules. This imbalance is traditionally measured in terms of the enantiomeric excess, or ee, where ee = (R−S)/(R + S) and R and S are concentrations of the right and left hand molecules, respectively. Proposals for how an imbalance might have come about may be classified as either terrestrial or extraterrestrial, and then subdivided into either random or deterministic (sometimes called “de facto” and “de lege” respectively). Evidence of small enantiomeric excesses in amino acids found in chondritic meteor deposits (Pizzarello 2006) (see Zahnle et al. 2010) allows the hypothesis that the initial imbalance is not of our world (although it begs the question of where and how it did originate). Discussions of how an imbalance could have originated here on earth often debate the question of whether life was preordained to be based on d-sugars and l-amino acids or whether this happened by chance, implying that a life form based on the opposite chirality might have been just as likely at the outset. Here, physics enters the picture: the discovery of parity violation and the elaboration of one of its consequences, that the two enantiomers have a very small energy difference between them, led many to consider the implications for biological homochirality (Quack 2002). Quantitative estimates of this energy difference have been made and revised in the intervening years, but it is clear that it is very, very small; whereas experimental and theoretical work is ongoing, and the question is not yet settled, a relationship between biological homochirality and parity violation is not yet supported by experimental findings.
Proponents on the “chance” side of this question point out that absolute asymmetric synthesis—defined as the production of enantiomerically enriched products in the absence of a chemical or physical chiral directing force—could occur stochastically (Mislow 2003). A trivial example is that any collection of an odd number of enantiomeric molecules has, by definition, broken symmetry. Fluctuations in the physical and chemical environment could result in transient fluctuations in the relative numbers of left- and right-handed molecules. However, any small imbalance created in this way should average out as the racemic state unless some process intervenes to sustain and amplify it. Thus, whether or not the imbalance in enantiomers came about by chance, arising on earth or elsewhere, an amplification mechanism remains the key to increasing enantiomeric excess and ultimately to approaching the homochiral state. A description of mechanisms for how this imbalance might be amplified is the main subject of this review.
Amplifying the Imbalance
Theoretical models for how a small initial imbalance in enantiomer concentrations might ultimately be turned into the subsequent production of a single enantiomer have been discussed for more than half a century (Frank 1953; Calvin 1969), but only more recently have experimental studies begun to address this question directly. In the past two decades several distinct models with strikingly different features have emerged, leading to the comment that scientists are now “spoilt for choice” (Ball 2007) among possible explanations for how one enantiomer came to dominate over the other in biological molecules. These models draw on both the chemical and the physical behavior of chiral molecules, and they may be classified according to their relative emphasis on kinetics vs. thermodynamics of the processes involved. “Far-from-equilibrium” models involving autocatalytic chemical reactions or crystallization processes lie at one end of the spectrum. At the other end, a model based on equilibrium phase behavior proposes a physical explanation. And in between lies a model that invokes an interplay between thermodynamics and kinetics to explain how a combination of physical and chemical processes can drive a system of near-equal numbers of enantiomeric molecules to the left or to the right.
CHEMICAL MODELS
Homochirality via Autocatalysis
More than 60 yr ago, Frank developed a mathematical model for an autocatalytic reaction mechanism for the evolution of homochirality. The model is based on a simple idea: a substance that acts as a catalyst in its own self-production and at the same time acts to suppress synthesis of its enantiomer enables the evolution of enantiopure molecules from a near-racemic mixture. The experimental challenge to discover a reaction with these features was posed in the last sentence of this purely theoretical paper: “A laboratory demonstration may not be impossible” (Frank 1953; Wynberg 1989).
Mutual Antagonism
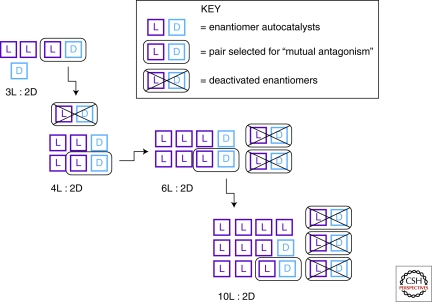
Frank's proposal serves to highlight the critical role played by an inhibition mechanism in autocatalytic models for the evolution of homochirality. Figure 2 illustrates this point using an example of a small group of l and d enantiomers that act as autocatalysts in an unlimited pool of substrate molecules. Each enantiomer is capable of reproducing itself in a reaction with a substrate molecule. In addition, there is “mutual antagonism” between l and d such that when they react together, both become deactivated and lose their capacity to self-replicate. The original pool shown in Figure 2 has an imbalance of one extra l molecule compared with the total number of d molecules, or 3:2 for this simple example. Let's say that one l and one d meet by chance and deactivate, whereas the remaining molecules feed on the pool of substrate and reproduce themselves. The active pool of enantiomers has now become 4:2. When these same processes repeat, the active pool becomes 6:2, then, then 10:2, and so on. One l and one d enantiomer are paired off in each mutual antagonism event, and hence the self-production of enantiomers will cause the ratio of l:d to grow as long as an initial imbalance was present at the beginning of the process. Together, autocatalysis and mutual antagonism propagate and amplify the imbalance in enantiomers. The only catch is that the smaller the initial imbalance, the greater the number of l and d molecules lost in the deactivation process before significant enantioenrichment can occur. If the substrate pool is large enough, however, productivity can remain high, and the selectivity of autocatalytic production of one enantiomer will eventually dominate.
Figure 2.
Schematic representation of the Frank model for the evolution of homochirality based on autocatalytic replication and mutual antagonism of enantiomers.
Proof of Concept
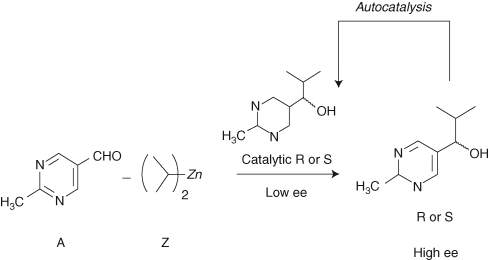
This model might be considered trivial, and no experimental system is known to follow the process in Figure 2. But Frank's understated exhortation to experimental chemists to discover an autocatalytic reaction with these key features captivated several generations of chemists. More than forty years later, the first experimental proof of this concept was found when Soai and coworkers reported the autocatalytic alkylation of pyrimidyl aldehydes with dialkylzincs (Soai et al. 1995) (Scheme 1), in which the reaction rate is accelerated by addition of catalytic amounts of its alcohol product. In addition, and most strikingly, this reaction was shown to yield the autocatalytic product in very high enantiomeric excess starting from a very low enantiomeric excess in the original catalyst.
Scheme 1.
The Soai autocatalytic reaction, in which the product catalyzes its own formation. The –CH3 group in the pyrimidyl aldehyde may be replaced with other groups such as alkynyl groups.
Since this initial discovery, Soai's group has gone on to present remarkable further observations of asymmetric amplification in the reaction that now bears his name. Enantiomeric excesses as high as 85% were reported for a reaction initiated with an initiator produced at 0.1% ee from exposure to circularly polarized light (Shibata et al. 1998). Asymmetric amplification has also been observed for the reaction initiated by inorganic chiral materials such as quartz (Soai et al. 1999). Most recently Soai has shown that the reaction may be selectively triggered solely by the minute mirror-image difference provided by 12C/13C carbon isotope chirality of an initiator molecule (Kawasaki et al. 2009), demonstrating that the reaction needs only an extremely small nudge to direct it consistently to the left or to the right.
Mechanistic Corroboration of the Frank Model
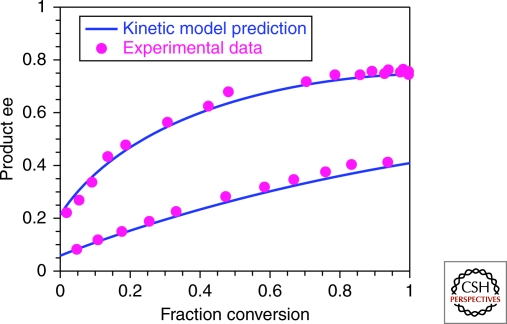
Soai's observations continued to amaze and confound the community for several years before the first mechanistic rationalization of the reaction was reported by Blackmond and Brown in 2001 (Blackmond et al. 2001). A kinetic model was developed based on highly accurate in-situ measurements of the reaction's progress. What's more, the kinetic model independently predicted both the temporal degree of asymmetric amplification, confirmed by compositional analysis, as well as the relative concentrations of the catalyst species, confirmed by NMR spectroscopy. Figure 3 shows how the kinetic model compares with experimental data for asymmetric amplification in the Soai reaction performed with two different initial catalyst ee values. This work showed that the Soai reaction couples autocatalysis with a form of “mutual antagonism,” thus evoking the main features of the Frank model, albeit in a more sophisticated chemical scenario.
Figure 3.
Product enantiomeric excess as a function of reaction progress in the Soai reaction of Scheme 1. Reactions catalyzed by 10 mol% of the reaction product with an initial ee of 6% and 22% (Buono and Blackond, 2003). Prediction of the Blackmond/Brown kinetic model (solid blue lines) and experimental values from HPLC analysis (filled magenta circles).
The Blackmond/Brown model rationalizes asymmetric amplification in the autocatalytic Soai reaction based on an extension of Kagan's model for nonlinear effects in catalytic reactions (Girard and Kagan 1998), that is, cases in which the reaction product ee does not scale linearly with the catalyst ee. Such behavior may ensue when the catalyst molecules aggregate to form higher order species. The ML2 model describes the formation of homochiral (RR and SS, Eqs. 1 and 2) and heterochiral (SR, Eq. 3) dimers from monomeric R and S molecules. The relative concentration of these dimers depends on an equilibrium constant, KD (Eq. 4).
| 1 |
| 2 |
| 3 |
| 4 |
Kagan's model proposes that the two homochiral dimers act as enantiomeric catalysts, giving opposite product ee values with identical rate constants, whereas the heterochiral dimer catalyst produces racemic product and may show a rate constant different from that of the homochiral dimer catalysts. Some degree of asymmetric amplification will result for any system in which the heterochiral dimer catalyst is less active than its homochiral counterparts. A value of KD = 4 indicates a stochastic or nonselective distribution of dimers, and larger values of KD skew the distribution toward a preference for the heterochiral species.
The upper limit attainable of ee amplification attainable in a catalytic reaction following this model occurs for when the heterochiral dimer is inactive and is dictated by the magnitude of KD: thus for a 1% ee catalyst showing a stochastic distribution of dimers, the maximum amplification in the product ee is only twofold, to ca. 2% ee. Stronger amplification of ee may be realized only by creating a specific stereochemical bias toward a stable, inactive heterochiral dimer, that is, for systems showing KD values that are significantly higher than that for a stochastic distribution. For example, a 1% ee catalyst would require a KD value a million-fold higher than the stochastic distribution to approach a perfectly enantioselective reaction.
Selection Without Bias
Although this model provides a means for asymmetric amplification, it presents a quandary for the prebiotic evolution of homochirality. Today we can construct a strong bias in modern asymmetric catalysts to provide a high KD value by drawing on the extensive natural chiral pool of molecules for complex building blocks, but this resource would not have been available to prebiotic molecules. The simple chiral molecules present in the prebiotic soup would not necessarily be expected to form dimers with highly unequal homo/heterochiral stabilities. How could asymmetric autocatalysts have achieved the strong stereochemical bias in dimer formation presumably needed to ensure strong asymmetric amplification?
The simple answer is that they didn't! The basic finding of Blackmond and Brown's studies is that the Soai reaction R and S products form a stochastic distribution of homochiral and heterochiral dimers, with essentially no stereochemical bias between the dimers (KD = 4), and that the heterochiral dimer is inactive as a catalyst. The key to how this allows an approach to homochirality is provided by consideration of basic differences among catalytic reactions, which accelerate the formation of a species that is not the same as the catalyst, and autocatalytic reactions, in which the catalyst accelerates its own formation. Because the catalyst produces more of itself in autocatalysis, and because mutual antagonism allows the minor enantiomer to be siphoned off as an inactive heterochiral dimer (serving the role of “mutual antagonism” in the Frank model), the relative concentrations of the two enantiomers is not fixed at its initial value, as it is in a static catalytic system. Instead, in an autocatalytic system following this dimer model, catalyst concentration increases, and relative concentration of the two homochiral dimers changes, with reaction turnover. The ultimate product enantiomeric excess that may be achieved in such an autocatalytic reaction is limited only by the size of the substrate pool, not by the magnitude of KD. Returning to our example of catalyst 1% ee with KD = 4, comparison with an autocatalyst with identical initial ee and KD shows that the autocatalytic system approaches homochirality after just 5000 cycles; strong robustness trumps mild intrinsic selectivity. Amplification of ee in autocatalysis requires not sophisticated stereoselection but only higher activity for the homochiral dimers, repeated over many autocatalytic cycles.
Homochirality: Chance Aided by Luck
Thus the dimer model provides an elegant and simple solution to one mystery of the evolution of homochirality (Blackmond 2006). If, as in the Soai reaction, the relative dimer reactivities happen to give the edge to the homochiral species, amplification, and ultimately homochirality, is ensured even for nonselective dimer formation. Statistics (stochastic dimer formation) and one stroke of luck (lower activity of the heterochiral dimer) are sufficient prerequisites to account for the evolution of our homochiral world today.
PHYSICAL MODELS
Kinetics versus Thermodynamics
The Soai autocatalytic reaction is essentially irreversible under the conditions used; the reaction proceeds faster as more product (catalyst!) is formed, as long as it continues to receive the nutrients it requires. In the time scale of the laboratory, the system never approaches the equilibrium state that would allow the reverse reactions to participate and ultimately erode selectivity. Analogous “far-from-equilibrium” processes showing amplified enantioselectivity as described earlier for the Soai reaction have been observed in physical processes such as the crystallization of molecules that form chiral solids. In these cases, kinetics must win out over thermodynamics in order for homochirality to evolve. The interconnection between kinetics and thermodynamics is addressed further in our consideration of two additional models for homochirality invoking the physical phase behavior of chiral solids in equilibrium with their solution phase molecules. An intrinsic feature of both of these models is the dominant role of the equilibrium condition, in contrast to the “far from equilibrium” cases invoking either chemical reactions and crystallization processes discussed earlier. These phase behavior models are underpinned by the fundamental concepts of the Gibbs Phase Rule as articulated by ternary phase diagrams of l + d + solvent.
Phase Behavior of Chiral Solids
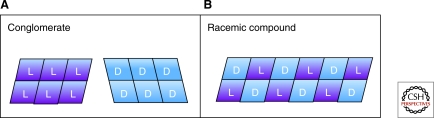
Before discussing these two models in detail, it is instructive to review the types of solution-solid behavior commonly found for enantiomeric molecules such as amino acids (Jacques et al. 1994). Chiral compounds crystallize most commonly in one of two forms: (a) as a racemic compound, in which crystals contain a 1:1 ratio of d:l molecules; or (b) as a conglomerate, in which each crystal is comprised of molecules of a single enantiomer, and the crystals themselves are mirror images (as were those Pasteur separated with his tweezers), and there is no direct molecular interaction between d and l molecules. These types of compounds are illustrated schematically in Figure 4. The type of crystal a chiral molecule forms in the solid phase is a fundamental property of that molecule at a given temperature and pressure. Racemic compounds are more prevalent than conglomerates by ca. 10:1 on planet Earth, including all but two of the 19 proteinogenic amino acids that are chiral (the twentieth, glycine, is an achiral molecule).
Figure 4.
Two types of crystalline solids formed by chiral compounds. Rectangles represent solid phase enantiomeric molecules. (A) conglomerates form separate crystals of each enantiomer; (B) racemic compounds form mixed crystals in a 1:1 ratio of the two enantiomers.
Eutectic Composition
When unequal numbers of molecules that form either type of crystal solid are partially dissolved in water, the Gibbs phase rule teaches us that the solution composition at equilibrium is fixed at what is called the “eutectic composition.” One interesting contrasting feature of the two types of compounds is that for conglomerates, this solution contains equal numbers of d and l molecules, giving a eutectic eeeut = 0, whereas racemic compounds will show a nonzero eeeut. This is easily rationalized by considering the solubility characteristics of each type of compound.
Conglomerates
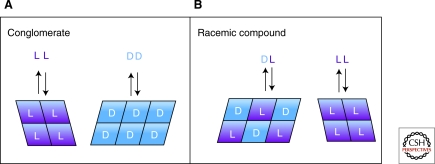
Because the separate d and l crystals of a conglomerate are enantiomeric, they have identical properties, including solubility. A saturated solution of d crystals thus has the same solution concentration as does a saturated solution of l crystals. If a mixture of d and l crystals is allowed to equilibrate together, each enantiomorphic solid shows its own (identical) solubility independently, and the solution phase at equilibrium will contain equal numbers of of d and l molecules, and twice as many in total as for either system separately (Meyerhoffer 1904) This remains true even if the system contains an unequal number of d and l molecules in total, as shown in Figure 5A.
Figure 5.
Depiction of equilibrium between chiral crystalline solids and their aqueous solution phases for nonracemic mixtures of enantiomers. Rectangles represent solid phase enantiomeric molecules; colored letters represent solution phase molecules in equilibrium with the solid phases. The solution phase composition is known as the eutectic. (A) conglomerates show eeeut= 0; (B) racemic compounds show nonzero eeeut.
Racemic Compounds
The equilibrium phase behavior for a species forming a racemic compound is more complex. For the case of an unequal total number of d and l molecules, mixed 1:1 d:l crystals form preferentially, pairing up with all of the minor enantiomer in the solid phase, and any molecules of the excess enantiomer remaining in the solid phase form homochiral crystals, as shown in Figure 5B. Thus at equilibrium this system will contain two separate solid phases, one enantiopure, and one racemic, along with the solution phase. The d:l mixed solid contributes equal numbers of d and l molecules to the solution according to its characteristic solubility, and the enantiopure solid does the same with its one enantiomer, according to its solubility. The solution composition at equilibrium will depend on the relative solubilities of the pure and mixed crystals, with the result that the solution will show a eutectic ee value somewhere between 0 and 100% (Fig. 5B). This value is a characteristic of the particular chiral compound and is not known a priori.
Enantiomer Partitioning
In both cases, as Figure 5 shows, conglomerates and racemic compounds present in a nonracemic composition in equilibrium with a solvent show a partitioning of enantiomers between the solution and solid phases that is dictated by the characteristics of the type of solid formed. Solution ee does not equal solid phase ee, and neither value will be the same as the overall ee. The models discussed later make use of this concept of phase partitioning in different ways to provide enantioenrichment in either the solid phase or the solution phase. Figure 5 suggests that solution phase enantioenrichment might be the goal when racemic compounds are considered, whereas a mechanism for solid phase enantioenrichment might make more sense for conglomerates. This is exactly what has been found, as the sections later describe.
PHASE BEHAVIOR I
“Eve Crystal” Model for Conglomerates
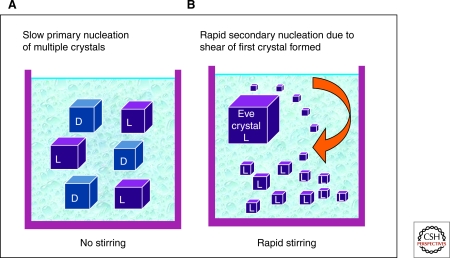
It has been known for more than one hundred years that certain achiral molecules such as NaClO3 crystallize as chiral solids. Work from the late 19th century noted that these crystallizations often resulted in a formation of two separate chiral solid phases (Kipping and Pope 1898). Most often, equal amounts of left and right-handed crystals are formed, but under some conditions the system breaks symmetry during the crystallization. The most striking example of this phenomenon was reported nearly two decades ago by Kondepudi (Kondepudi et al. 1990) who showed that when the crystallization process was accompanied by rapid stirring, crystals of single chirality could be formed, randomly left-handed or right-handed in repeated experiments. This was rationalized by considering the dynamics of crystallization: formation of the first crystals (primary nucleation) from a homogeneous supersaturated solution is slower than the process of crystal growth by adding molecules to crystals already formed (secondary nucleation). Under rapid stirring, the first crystal formed, or “Eve” crystal, may be broken by shear into thousands of smaller crystals of the same chiral form. These “daughter” crystals then grow rapidly by drawing on solution molecules, and the solution rapidly becomes depleted. If this occurs more rapidly than formation of any new primary crystals, a single chiral solid state may result (McBride and Carter 1991) (Fig. 6). This phenomenon bears resemblance to “far-from-equilibrium” autocatalytic reaction processes such as the Soai reaction discussed earlier in this article.
Figure 6.
Crystallization from supersaturated solution of achiral molecules that form mirror enantiomorphic solid crystals. (A) Without rapid stirring, equal quantities of left- and right-handed crystals are formed; (B) under rapid stirring conditions, all crystals are grown from the fragments of a single primary crystal (“Eve crystal”), resulting in formation of only one enantiomorph.
PHASE BEHAVIOR II
Near Equilibrium Systems
Most recently, this NaClO3 system that has fascinated scientists since van't Hoff's days was back in the news with a report by Viedma (2005) of a remarkable experimental finding. Viedma's experiment is not strictly a crystallization; it starts at what would be the end of a typical crystallization performed without the rapid stirring and shear described earlier, so that the system is equilibrated with an equal number of right- and left-hand crystals of NaClO3 in saturated aqueous solution, as in Figure 6A. Under these conditions, no new crystals nucleate; the only processes occurring in the flask are the continual dissolution and reaccretion of NaClO3 molecules to and from existing crystals, and these rates are balanced at equilibrium. No net change is expected, and that is exactly what has been found in such experiments for more than one hundred years. Viedma then added glass beads to the gently stirred vial, which enhanced the attrition of the crystals as they stirred. What he observed under these conditions is that the system evolved from equal quantities of left- and right-handed crystals to a single enantiomorphic solid. One chiral solid converted completely to the other over time, in a random fashion, sometimes to the left and sometimes to the right, with equal probability. The striking fact is that the system moved inexorably from an apparent equilibrium between two enantiomorphic solid states to a single chiral solid state, simply by virtue of the application of mechanical energy via the grinding of glass beads.
Viedma reasoned that the continual abrasion of the crystals by stirring with small glass beads enhanced both halves of the cycle of repetitive dissolution/crystallization that occurs at equilibrium. According to the Gibbs-Thomson rule, small crystals dissolve more readily than large crystals. Attrition by glass beads produces a greater number of smaller crystals, whose increased dissolution in turn causes a slight supersaturation of NaClO3 in solution. Not sufficiently supersaturated to support primary nucleation, the system strives to redress the balance between solid and solution by increasing the rate of reaccretion of solution phase NaClO3 onto existing crystals. A key point is that once a molecule of NaClO3 dissolves from a crystal, it no longer possesses chirality and it retains no memory of the chiral form it previously showed as part of a crystal. Solution-phase NaClO3 thus has no preference for re-accreting to a left- or right-handed crystal. What solution phase molecules do have, however, is a preference for adding to larger crystals over smaller ones, a phenomenon known as Ostwald ripening. If, by chance, the system contains a predominance of large crystals of one hand, solution phase NaClO3 will preferentially add to these crystals, and the quantity of this enantiomorphic solid will increase relative to its mirror image form.
Chiral AMnesia
The mechanical energy imparted to the system by the enhanced attrition thus triggers an overall process that is cyclical: The action of the glass beads truncates the Ostwald ripening process, continually breaking up crystals as they attempt to grow in size. The growth of the crystals occurs in response to an increased concentration driving force created by slight supersaturation in solution, which in turn is the result of dissolution of small crystals created by the glass beads breaking up larger crystals. Evolution of solid phase homochirality in this case requires only an initial imbalance in the crystal size of left-versus right-hand crystals.
This proposed rationalization implies that the system never departs very far from equilibrium conditions and that system strives continually to restore the balance between the physical processes of dissolution and reaccretion. The key to the evolution of one chiral solid state is the ability of an achiral solution phase molecule to choose to add to either hand of its solid phase crystals. The solution phase serves as the conduit through which the molecules that form one hand of the crystal forget their solid-state chiral history and are free to choose a new solid-state chiral destiny, a process that has been given the name “chiral amnesia” (Blackmond 2007; Viedma 2007).
Extension to Chiral Molecules
These results led many to consider a possible extension of this process from the achiral NaClO3 to intrinsically chiral molecules that form conglomerate solids, but this concept faces an important challenge. A chiral molecule in solution equilibrium with its two separate enantiomorphic solid phases would not have the ability to choose to add to either solid; a d-amino acid molecule may add only to a d-crystal, and an l-amino acid molecule to an l-crystal. Although this does not affect the Gibbs-Thomson and Ostwald ripening processes for dissolution and growth of crystals, conversion of crystals of one hand into the other would be frustrated without a process allowing the molecules to forget their chiral signature in solution. However, organic chemists engaged in asymmetric synthesis know well—and are often themselves frustrated by—solution reactions in which chiral molecules can be made to convert between their left and right forms, known as racemization. Long considered a bane in organic synthesis, solution-phase racemization provides the key to extending the Viedma model for homochirality to intrinsically chiral molecules, as shown schematically in Figure 7. This was successfully shown recently for an amino acid derivative (Noorduin at al. 2008), for the proteinogenic amino acid aspartic acid (Viedma et al. 2008) (Scheme 2), and for a Mannich reaction product (Tsogoeva et al. 2009).
Figure 7.
“Chiral amnesia” process for the evolution of solid-phase homochirality for chiral molecules that form conglomerate solids. In this example, an initial imbalance toward larger l crystals helps to drive the dissolution/re-accretion process from d crystals to l crystals. The process is aided by solution phase racemization, which converts the “excess” dissolved d molecules to l molecules, equalizing the solution composition and enabling molecules that were formerly part of a d crystal to add as l molecules to l crystals.
Scheme 2.
Transformation of aspartic acid crystals from one enantiomorphic solid to the other via solution phase racemization. Mechanical or thermal energy input drives the dissolution/re-accretion process.
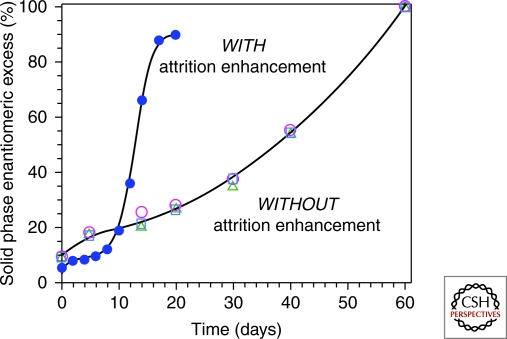
The studies of aspartic acid revealed that the inexorable move to one homochiral solid could be accomplished in the absence of glass beads, simply by application of thermal energy rather than mechanical energy as the means to nudge the system away from equilibrium. The crystal ee profiles lose the exponential shape they show under the grinding conditions (Fig. 8), suggesting that Ostwald ripening may allow more extensive crystal growth when the energy input is thermal rather than mechanical.
Figure 8.
Evolution of solid-phase homochirality for aspartic acid via solution phase racemization. Energy input from grinding the crystals in the presence of enhanced attrition because of glass beads leads to a sigmoidal profile (filled blue circles), whereas thermal energy input drives the process in a linear fashion (open symbols).
PHASE BEHAVIOR III
Thermodynamic Model for Enantioenrichment
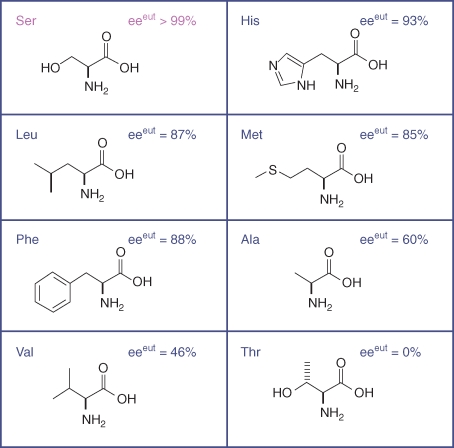
The phase properties of chiral compounds discussed earlier have been understood for more than one hundred years. More recently, a model for the origin of biological homochirality based on solution phase enantioenrichment of amino acids that form racemic compounds has been developed based on these concepts. It may be recognized from Figure 5B that in a heterogeneous mixture that contains unequal numbers of enantiopure and d and l molecules, the minor enantiomer is present in the solution phase only to the extent that it can dissolve from the d:l crystal. The lower the solubility of the d:l crystals, the more strongly “trapped” in the solid phase will be the minor enantiomer, and the higher the resulting solution phase partitioning of the major enantiomer, manifested as a high eeeut. Several of the proteinogenic amino acids form relatively insoluble d:l crystals and therefore show high eutectic ee values. For example, serine's eutectic occurs at >99% ee. This means that when a sample with nearly equal numbers of d and l serine molecules is partially dissolved, a virtually enantiopure solution results. Table 1 provides eutectic values for a number of amino acids (Klussmann et al. 2006).
Table 1.
Eutectic ee values for a number of proteinogenic amino acids, identified by their chemical structures and their three-letter names.
 |
Enantioenrichment in solution is thus dictated by thermodynamics for chiral compounds that happen to form relatively insoluble racemic compounds. This concept was first recognized by Morowitz (1969) 40 yr ago and was more recently elaborated by Blackmond's work probing eutectic composition for a variety of amino acids and other chiral compounds Klussmann et al. 2006), and by Breslow (Breslow and Levine 2006) who recently also reported high eutectic ee values for several nucelosides of prebiotic importance (Breslow and Cheng 2009). A recent theoretical treatment based on a two-dimensional lattice model successfully predicts the ternary phase behavior of amino acids based on the interactions that stabilize the racemic crystal, providing molecular level insight into the observed enantiomer partitioning (Lombardo et al. 2009). These studies suggest a general and facile route to homochirality that may have prebiotic relevance. Cycles of rain and evaporation establishing solid phase-solution phase equilibrium in pools containing a small initial imbalance of amino acid enantiomers could result in a solution of enantioenriched molecules that might then serve as efficient asymmetric catalysts or as building blocks themselves for construction of the complex molecules required for recognition, replication and ultimately for the chemical basis of life.
Sublime Partitioning
The phase partitioning of enantiomers that forms the basis of this model for solution phase enantioenrichment might be expected to predict other phase behavior of enantiomers (Blackmond and Klussmann 2007a). Indeed, eutectic ee values correlate with fusion temperature for a number of amino acids. In addition, reports of enantioenrichment of amino acids via sublimation of enantioimpure d/l mixtures are also well correlated with the eutectic ee values for amino acids: for example, the sublimate from serine is nearly enantiopure, whereas that from threonine, which forms a conglomerate, gives 0% ee (Perry et al. 2007). Sublimate ee values of 72%–89% were observed for leucine, in accordance with it measured eutectic value of 88% ee (Fletcher et al. 2007). Enantiomer partitioning via sublimation raises tantalizing speculation about amino acids in space and an extraterrestrial origin of enantioenrichment.
Crystal Engineering for Tuning Eutectics
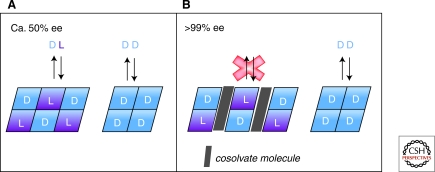
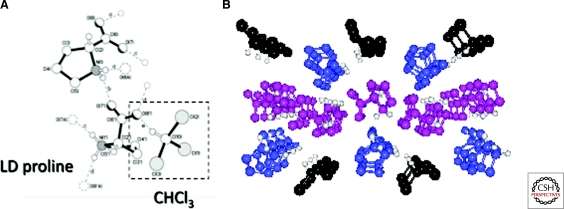
Because eutectic ee is a characteristic property of a compound, it would appear that enantioenrichment by this approach is limited to chiral compounds such as serine that happen to show high eutectic ee values. Thermodynamics suggests that other amino acids, such as valine with eeeut = 47%, may be stuck with the hand that Nature has dealt. However, further work revealed the exciting discovery of a route to solution phase enantioenrichment that may be achieved even for chiral compounds with low intrinsic eeeut values. Eutectic ee composition may be “tuned” in many cases by through incorporation of a variety of small, achiral molecules into the solid phase structure of amino acid crystals via hydrogen bonding (Klussmann et al. 2007). The existence of cocrystals known as solvates or polymorphs is well known, but effects on solubility and the accompanying implications for solution phase enantioenrichment were not recognized, until Blackmond and coworkers (Klussmann et al. 2007a) showed that enhanced eutectic ee values may be obtained in a number of such cases. If the incorporated molecule reduces the solubility of the racemic crystal relative to that of the enantiopure crystal, enhanced eutectic composition will result, as shown in Figure 9. For example, d:l proline incorporates CHCl3 into its structure with a concomitant rise in eeeut from 50% to >99% ee, and d:l valine and phenylalanine each form crystals incorporating fumaric acid; eeeut rose from 47% and 88%, respectively, to >99% in both cases. The structure of the d:l compound of proline with chloroform is shown in Figure 10. Manipulation of the eutectic composition by additives may be thought of as an analogy to clathrate compounds, although here it is the amino acid enantiomers themselves that are trapped in the solvate-racemate structure, causing them to dissolve much less readily.
Figure 9.
Manipulation of eutectic ee value by formation of a solvate that reduces the solubility of the racemic compound.
Figure 10.
Crystal structure of ld proline incorporating one molecule of chloroform. (A) five independent hydrogen bonds are shown; (B) long range structure with proline enantiomers in blue and magenta, chloroform in black (Klussmann et al. 2006).
The finding that the enantiomeric excess of an amino acid in solution may be significantly enhanced via solvate formation enables an approach to enantioenrichment for a wide range of chiral compounds. A particularly appealing feature of this model is that it is based on an equilibrium mechanism, in contrast to the far-from-equilibrium environment invoked in kinetically induced amplification via autocatalytic reactions discussed earlier. Prebiotic pools containing nearly racemic amino acids could exist over long periods of time awaiting an influx of appropriate hydrogen-bonding partner molecules to form solvates that help provide enantiopure amino acids in solutions where the chemical reactions leading to life might begin to occur (Klussmann and Blackmond 2007b).
CHALLENGES AND FUTURE DIRECTIONS
Homochirality First?
Amino acids and sugar molecules are produced as single enantiomers in biological processes on earth today, and these molecules provide the building blocks for homochiral polymers such as peptide chains, RNA and DNA. However, it is far from certain that homochirality on the molecular level was required before nascent biopolymers began to play a role in the growing chemical complexity that led to life. This leaves open the possibility that the prebiotic molecular pool need not have been enantioenriched. It has been suggested that in competition for growth, heterochiral chains containing both enantiomers would readily give way to homochiral polymers (Wald 1957; Kuhn 1972, 2007), and therefore selection of one hand of an amino acid over the other could have come with oligopeptides rather than at the molecular level (Zepk et al. 2002). However, such a scenario still needs to invoke a mechanism—either chance or deterministic—for symmetry breaking of the mirror image homochiral polymer chains that would evolve. A plausible proposal is that partial enantioenrichment could have taken place at the molecular level, but that prebiotic amino acids and sugars need not to have evolved completely to single chirality before the formation of the first biopolymer chains. The greater the pre-enrichment on the molecular level, the more efficient would be the construction of homochiral chains, but the burden of chiral selectivity might have been shared as complexity increased.
The Future for Autocatalysis
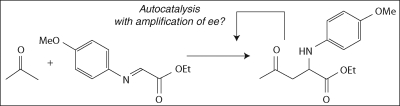
The experimental conditions of the Soai reaction preclude it from being of direct prebiotic importance, because it is unlikely that the dialkylzinc chemistry involved would thrive an aqueous, aerobic prebiotic environment. However, the reaction has been particularly instructive in helping understand how autocatalysis coupled with inhibition could lead to a homochiral state. A number of experimental aspects of the Soai autocatalytic reaction are still under study, and a number of other theoretical kinetic models have been proposed, but the Blackmond/Brown model remains the only proposal that provides an adequate rationalization of the experimental data for the Soai reaction (Blackmond 2004, 2006a). Most recently, reports by Tsogoeva (Mauksch et al. 2007) of a purely organic reaction showing similar properties of autocatalysis and amplification of ee (Scheme 3) have excited the community, because the chemistry involved is much closer to what could be prebiotically plausible. Further work to understand the mechanism of this reaction is currently underway in a number of laboratories.
Scheme 3.
Autocatalytic Mannich reaction reported by Tsogoeva.
Phase Behavior Models
Comparison of the chiral amnesia and crystal engineering phase behavior models for the origin of homochirality reveal that they are complementary in many ways: the former produces solid-phase homochirality whereas the latter provides enantioenrichment of the solution phase; the chiral amnesia model converts one enantiomer to the other, whereas the crystal engineering model simply partitions the existing molecules between phase. Chiral amnesia may be applied only to molecules that form conglomerates, which means that only about 10% of known chiral compounds are candidates for enantioenrichment by this model. On the other hand, about 85% of chiral compounds might be amenable to the selective partitioning provided by the crystal engineering model. Perhaps some combination of the two led to the initial enantioenrichment of biologically relevant molecules. Both models provide reasonable prebiotic scenarios, and further work to understand the mechanism of enantioenrichment in each case is underway.
Where Do We Go from Here?
The pathway to life may be seen as a saga of increasing chemical and physical complexity (see, for example, Hazen 2010). The modern field of “systems chemistry” (von Kiedrowski 2005) seeks to understand the chemical roots of biological organization by studying the emergence of system properties that may be different from those showed individually by the components in isolation. The implications of the single chirality of biological molecules may be viewed in this context of complexity. Whether or not we will ever know how this property developed in the living systems represented on Earth today, studies of how single chirality might have emerged will aid us in understanding the much larger question of how life might have, and might again, emerge as a complex system.
Footnotes
Editors: David Deamer and Jack W. Szostak
Additional Perspectives on The Origins of Life available at www.cshperspectives.org
REFERENCES
- Ball P 2007. Giving life a hand. Chem World 4:30–31 [Google Scholar]
- Blackmond DG 2004. Asymmetric autocatalysis and its implications for the origin of homochirality. PNAS 101:5732–5736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackmond DG 2006. Mechanistic study of the Soai autocatalytic reaction informed by kinetic analysis. Tetrahedron: Asymmetry 17:584–589 [Google Scholar]
- Blackmond DG 2009. The double solubility rule holds for racemizing enantiomers. Chem Eur J 15:3065–3068 [DOI] [PubMed] [Google Scholar]
- Blackmond DG, Klussmann M 2007a. Spoilt for choice: Assessing phase behavior models for the evolution of homochirality. Chem Commun 3990–3996 [DOI] [PubMed] [Google Scholar]
- Blackmond DG, Klussmann M 2007b. Investigating the evolution of biomolecutar homochirality, AICHE J 53:2–8 [Google Scholar]
- Blackmond DG, McMillan CR, Ramdeehul S, Schorm A, Brown JM 2001. Origins of asymmetric amplification in autocatalytic alkylzinc additions. J Am Chem Soc 123:10103–10104 [DOI] [PubMed] [Google Scholar]
- Breslow R, Cheng Z-L 2009. On the origin of terrestrial homochirality for nucleosides and amino acids. PNAS 106:9144–9146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow R, Levine M 2006. Amplification of enantiomeric concentrations under credible prebiotic conditions. PNAS 103:12979–12980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buono FG, Blackmond DG 2003. Kinetic evidence for a tetrameric transition state in the asymmetric autocatalytic alkylation of pyrimidyl aldehydes. J Am Chem Soc 125:8978. [DOI] [PubMed] [Google Scholar]
- Calvin 1969. Molecular evolution Oxford University Press, Oxford, UK [Google Scholar]
- Fletcher SP, Jagt RBC, Feringa BL 2007. An astrophysically relevant mechanism for amino acid enantiomer enrichment. Chem Commun 2578–2580 [DOI] [PubMed] [Google Scholar]
- Frank FC 1953. On spontaneous asymmetric synthesis. Biochim Biophys Acta 11:459–463 [DOI] [PubMed] [Google Scholar]
- Girard C, Kagan HB 1998. Nonlinear effects in asymmetric synthesis and stereoselective reactions: Ten years of investigation. Angew Chemie Int Ed 37:2923–2959 [DOI] [PubMed] [Google Scholar]
- Hazen RM 2010. Mineral surfaces, geochemical complexities, and the origins of life. Cold Spring Harb Perspect Biol 2:a002162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilbronner E, Dunitz JD 1993. Reflections on symmetry in chemistry … and elsewhere Verlag Helvetica Chimica Acta, Basel [Google Scholar]
- Jacques J, Collet A, Wilen SH 1994. Enantiomers, racemates and resolution, 2nd ed Krieger Publishing Company, FL [Google Scholar]
- Kawasaki T, Matsumura Y, Tsutsumi T, Suzuki K, Ito M, Soai K 2009. Asymmetric autocatalysis triggered by carbon isotope (13C/12C) chirality. Science 324:492–495 [DOI] [PubMed] [Google Scholar]
- Kipping WS, Pope WJ 1898. Enantiomorphism. J Chem Soc Trans 73:606–617 [Google Scholar]
- Klussmann M, Iwamura H, Mathew SP, Wells DH Jr, Pandya U, Armstrong A, Blackmond DG 2006. Thermodynamic control of asymmetric amplification in amino acid catalysis. Nature 441:621–623 [DOI] [PubMed] [Google Scholar]
- Klussmann M, Izumi T, White AJP, Armstrong A, Blackmond DG 2007. Emergence of solution-phase homochirality via crystal engineering of amino acids. J Am Chem Soc 123:7657–7660 [DOI] [PubMed] [Google Scholar]
- Klussmann K, White AJP, Armstrong A, Blackmond DG 2006. Rationalization and prediction of solution enantiomeric excess in ternary phase systems. Angew Chem Int Ed 47:7985–7989 [DOI] [PubMed] [Google Scholar]
- Kondepudi DK, Kaufman RJ, Singh N 1990. Chiral symmetry breaking in sodium chlorate crystallization. Science 250:975–976 [DOI] [PubMed] [Google Scholar]
- Kuhn H 1972. Self-organization of molecular systems and evolution of the genetic apparatus. Angew Chem Int Ed 11:798–820 [DOI] [PubMed] [Google Scholar]
- Kuhn H 2008. Origin of life—symmetry breaking in the universe: Emergence of homochirality. Current Opinion Colloid Interface Sci 13:3–11 [Google Scholar]
- Lombardo TG, Stillinger FH, Debenedetti PG 2009. Thermodynamic mechanism for solution phase chiral amplification. A lattice model. PNAS doi: 10.1073/pnas.0812867106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauksch M, Tsogoeva SB, Martynova IM, Wei S 2007. Evidence of asymmetric autocatalysis in organocatalytic reactions. Angew Chem Int Ed 46:393–396 [DOI] [PubMed] [Google Scholar]
- McBride JM, Carter RL 1991. Spontaneous resolution by stirred crystallization. Angew Chem Intl Ed 30:293–295 [Google Scholar]
- Morowitz M 1969. A mechanism for the amplification of fluctuations in racemic mixtures. J Theor Biol 25:491–494 [DOI] [PubMed] [Google Scholar]
- Meyerhoffer W 1904. Stereochemical notes, Pasteur's method of resolving by means of active compounds. Solubility of a tartrate compared with that of a racemate. Ber Dtsch Chem Ges 37:2604–2610 [Google Scholar]
- Mislow K 2003. Absolute asymmetric synthesis: A commentary. Collect Czech Chem Commun 68:849–864 [Google Scholar]
- Noorduin WL, Izumi T, Millemaggi A, Leeman M, Meekes H, Van Enckevort WJP, Kellogg RM, Kaptein B, Vlieg E, Blackmond DG 2008. Emergence of a single solid chiral state from a nearly racemic amino acid derivative. J Am Chem Soc 130:1158–1159 [DOI] [PubMed] [Google Scholar]
- Perry RH, Chunping W, Nefliu M, Cooks RG 2007. Serine sublimes with spontaneous chiral amplification. Chem Commun 1071–73 [DOI] [PubMed] [Google Scholar]
- Pizzarello S 2006. The chemistry of life's origin: A carbonaceous meteorite perspective. Acc Chem Res 39:231–237 [DOI] [PubMed] [Google Scholar]
- Quack M 2002. How important is parity violation for molecular and biomolecular chirality? Angew Chem Int Ed 41:4618–4630 [DOI] [PubMed] [Google Scholar]
- Shibata J, Yamamoto T, Matsumoto N, Yonekubo S, Osanai S, Soai K 1998. Amplification of a slight enantiomeric imbalance in molecules based on asymmetric autocatalysis. The first correlation between high enantiomeric enrichment ina chiral molecule and chircularly polarized light. J Am Chem Soc 120:12157–12158 [Google Scholar]
- Soai K, Osanai S, Kadowaki K, Yonekubo S, Shibata T, Sato I 1999. d- and l-Quartz-promoted Highly Enantioselective Synthesis of a Chiral Compound. J Am Chem Soc 121:11235–11236 [Google Scholar]
- Soai K, Shibata T, Morioka H, Choji K 1995. Asymmetric autocatalysis and amplification of enatiomeric excess of a chiral molecule. Nature 378:767–768 [Google Scholar]
- Tsogoeva SB, Wei S, Freund M, Mauksch M 2009. Generation of highly enantioenriched crystalline products in reversible asymmetric reactions with racemic or achiral catalysts. Angew Chemie Int Ed 48:598–602 [DOI] [PubMed] [Google Scholar]
- Viedma C 2005. Chiral symmetry breaking during crystallization: Complete chiral purity induced by nonlinear autocatalysis and recycling. Phys Rev Lett 94:065504. [DOI] [PubMed] [Google Scholar]
- Viedma C 2007. Chiral symmetry breaking and complete chiral purity by thermodynamic-kinetic feedback near equilibrium: Implications for the origin of biochirality. Astrobiol 7:312–319 [DOI] [PubMed] [Google Scholar]
- Viedma C, Ortiz JE, de Torres T, Izumi T, Blackmond DG 2008. Evolution of solid phase homochirality for a proteinogenic amino acid. J Am Chem Soc 130:15274–15275 [DOI] [PubMed] [Google Scholar]
- von Kiedrowski G. Ruhr-Universität Bochum, Germany; editor of a new open-access journal “Systems Chemistry.”.
- Wald G 1957. The origin of optical activity. Ann NY Acad Sci 69:352–368 [DOI] [PubMed] [Google Scholar]
- Wynberg H 1989. Asymmetric autocatalysis: Facts and fancy. J Macromol Sci Chem A26:1033–1041 [Google Scholar]
- Zahnle K, Schaefer L, Fegley B 2010. Earth's early atmospheres. Cold Spring Harb Perspect Biol 2:a004895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zepik H, Shavit E, Tang M, Jensen TR, Kjaer K, Bolbach G, Leiserowitz L, Weissbuch I, Lahav M 2002. Chiral amplification of oligopeptides in two-dimensional crystalline self-assemblies on water. Science 295:1266. [DOI] [PubMed] [Google Scholar]