Abstract
AMPA receptors are ligand-gated ion channels that show multiple conductance levels, indicating that gating of individual AMPA subunits is to some extent independent of the other subunits. To study AMPAR subunit interactions during activation gating, we recorded from single channels in the absence of channel block and desensitization and at negative and positive membrane potentials. In saturating glutamate, the relative occupancies of the various conductance levels are consistent with complete subunit independence. In contrast, the relative occupancies in subsaturating glutamate indicate that the channel switches between a low open probability mode and a high open probability mode in which the behavior of the channel is identical to that in saturating glutamate. These gating modes occur at both negative and positive potentials, with the high open probability mode becoming more prominent at positive potentials. The switch between gating modes and its modulation by voltage and other factors may constitute a novel mechanism regulating AMPAR-mediated synaptic activity.
Introduction
NMDA and AMPA receptors (NMDARs and AMPARs) are members of the glutamate receptor (GluR) family of ligand-gated ion channels. Both receptor subtypes are found on postsynaptic membranes, where they open in response to the presynaptic release of the neurotransmitter glutamate, and are key determinants of synaptic communication and plasticity and regulation of neuronal gene expression (Zucker and Regehr, 2002; Derkach et al., 2007; Citri and Malenka, 2008).
The most fundamental aspect of ligand-gated ion channel function is the relationship between ligand binding/unbinding and opening/closing of the ion channel. GluRs are tetramers, and each subunit has one ligand-binding site. In NMDARs, two binding sites are for glutamate, and two are for the coagonist glycine; in AMPARs, all four binding sites are for glutamate. Beyond this basic similarity of binding site stoichiometry, however, NMDARs and AMPARs differ strikingly in terms of the relationship between ligand binding/unbinding and ion channel opening/closing. NMDARs undergo concerted gating in which all four subunits must bind agonists for the channel to open, with the closed-to-open transition occurring essentially simultaneously in all subunits (Banke and Traynelis, 2003; Erreger et al., 2004; Kussius and Popescu, 2009). In contrast, the ion channel domains of AMPAR subunits that have bound glutamate can apparently transition between open and closed conformations independently of the ion channel domain conformation or ligand-binding site occupancy of the other subunits (Rosenmund et al., 1998; Smith and Howe, 2000), resulting in the multiple conductance levels that are a prominent feature of native and recombinant microscopic AMPAR currents (Howe et al., 1991; Wyllie et al., 1993; Swanson et al., 1997; Derkach et al., 1999; Banke et al., 2000; Smith et al., 2000; Jin et al., 2003; Tomita et al., 2005; Gebhardt and Cull-Candy, 2006; Zhang et al., 2008).
A logical first step in understanding the function of ligand-gated ion channels is to study their single-channel behavior in saturating agonist concentrations, and in the absence of additional gating processes such as channel block and desensitization, allowing the ion channel opening/closing process to be observed in isolation from ligand binding/unbinding and other gating processes. Here, we compare the behavior of non-desensitizing AMPARs in saturating and subsaturating glutamate, and at negative and positive membrane potentials, with an emphasis on the relative occupancy of the various conductance levels. In agreement with the prevailing model of independent subunit gating in AMPARs, we find that the relative occupancies of the conductance levels follow a binomial distribution in saturating glutamate. In subsaturating glutamate, however, the relative occupancies diverge dramatically from a binomial distribution, with the higher conductance levels occurring much more often than predicted. Surprisingly, channel activity in subsaturating glutamate was identical to that in saturating glutamate during periods lasting several milliseconds. We propose that the open probability of AMPARs is regulated by previously unknown subunit interactions, such that the apparent affinity of AMPAR subunits for glutamate is dependent on the number of occupied glutamate binding sites.
Materials and Methods
Molecular biology and heterologous expression
All experiments were performed with previously described expression constructs for the wild-type rat, “flip” splice-variant GluA1, GluA2(Q), or GluA4 subunits (Collingridge et al., 2009), where Q indicates the residue occupying the Q/R editing site (Sommer et al., 1991).
Channels were transiently expressed in human embryonic kidney 293 (HEK 293) cells. HEK 293 cells were transfected with GluR subunits using FuGene 6 (Roche). A vector for enhanced green fluorescent protein (pEGFP-C1, Clontech) was cotransfected at a ratio of 1:9 (pEGFP-C1:GluR subunit). Recordings were made 1–3 d after transfection.
Current recording
Currents in outside-out patches, isolated from HEK 293 cells, were recorded at room temperature (20–23°C). External solutions were applied using a piezo-driven double barrel application system made from theta glass. One barrel contained the external solution; the other contained the same solution with added glutamate (0.06–10 mm). For experiments involving desensitizing channels, we measured the solution exchange rate using the 10–90% rise time when switching between the standard external solution and a 10% dilution of that solution. Patches were not included in the analysis if the rise time was >300 μs. We did not use series resistance compensation, nor did we correct for junction potentials.
Macroscopic currents.
Macroscopic currents were recorded using an EPC-9 amplifier (HEKA Elektronik) with PULSE or PatchMaster software (HEKA Elektronik), low-pass filtered at 2.8 kHz (−3 dB) using an eight-pole low-pass Bessel filter and digitized at 50 or 100 kHz. Pipettes were pulled from thin-walled borosilicate glass and had resistances of 2–10 MΩ when filled with the pipette solution and measured in the external solution.
Microscopic currents.
Microscopic currents were recorded using an Axopatch 200B amplifier (Molecular Devices) with PatchMaster software and were initially filtered at 10 kHz using a four-pole low-pass Bessel filter and digitized at 50 kHz. Pipettes were pulled from thick-walled borosilicate glass and fire polished immediately before recording and had resistances of 10–40 MΩ when filled with the pipette solution and measured in the external solution. To reduce noise during microscopic recordings, currents were recorded with the headstage set to capacitive feedback mode, pipettes were coated three times with Sylgard (Dow Corning), the pipette holder was cleaned daily with 70% ethanol and stored in Drierite overnight, and care was taken to keep the level of the bath solution as low as possible. To eliminate noise resulting from oscillation of the piezo device at the start of the glutamate application, voltage steps to the piezo device were filtered at 200 Hz using an eight-pole Bessel filter.
Obtaining and identifying patches with only one channel.
To obtain patches with only one channel, it was necessary to continuously adjust the diameter of the pipette tips based on changes in the level of expression. We found that the level of expression in HEK cells varied widely depending on the passage number of the cells and the number of hours posttransfection. The approximate number of channels in each attempted patch was determined from the current amplitude in saturating glutamate, and based on the average expression level the pipette tip diameter was adjusted by changing the final line of the pipette pulling program or the amount of fire polishing. The pipette resistance was taken as an approximate indication of the tip diameter. We also observed that extensive suction when attempting to enter the whole-cell mode tended to increase the number of channels in the patch, and this was avoided. Even with these precautions, patches containing only one channel occurred rarely (∼5–10% of all attempts).
It was straightforward to identify patches containing only one channel. Non-desensitizing AMPARs have very high open probability in saturating glutamate, but occasionally show relatively long closed period (for an example, see Fig. 4A). If a patch contained a single channel, it could be clearly seen to jump from a mean open current level of ∼1.2–1.5 pA at −80 mV to the baseline current level during these long closed periods. In patches with a small number of channels, long closings resulted in a discrete change in the mean open current level.
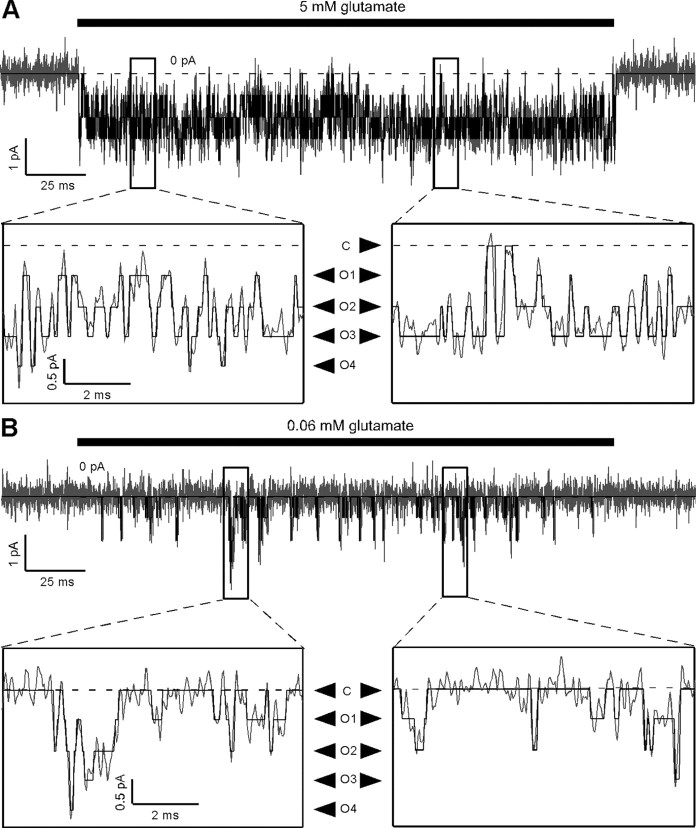
Figure 4.
AMPA receptor single-channel currents in the absence of polyamine block and desensitization, in saturating and subsaturating glutamate at +80 mV. A, Current in 5 mm glutamate from the outside-out patch containing a single GluA2(Q) channel shown in Figure 1, recorded at +80 mV, along with the idealization of the record generated by the SKM algorithm of QuB. The record is displayed as in Figure 1. The four open current levels at +80 mV in this patch were 0.90 (O1), 1.78 (O2), 2.51 (O3), and 3.20 (O4) pA, as seen more clearly in the expanded sections of the records. The dashed line indicates the baseline current level. B, Same as in A, but showing current from the same patch in 0.06 mm glutamate.
Solutions.
For macroscopic and microscopic recordings, the internal (pipette) solution contained the following (in mm): 110 NaCl, 20 Na2ATP [to chelate endogenous polyamines (Rozov et al., 1998)], 5 HEPES, and 1 BAPTA, pH 7.2 (NaOH). The external solution contained the following (in mm): 140 NaCl and 10 HEPES, pH 7.2 (NaOH). Unless otherwise indicated, cyclothiazide (CTZ, 30 μm) was included to prevent desensitization (Partin et al., 1993). For microscopic and in some instances macroscopic recordings, 1 mm CaCl2 was included.
Analysis and idealization of single-channel currents
Current records were exported from PatchMaster to Igor Pro (WaveMetrics) for initial processing (subtraction of the mean baseline current, resampling, and additional filtering) and characterization. Records with sufficiently low baseline noise (see below) were exported from Igor Pro to QuB (www.qub.buffalo.edu) for idealization, and idealized records were then exported back to Igor Pro, Mathematica (Wolfram Research), or ChannelLab (Synaptosoft) for additional analysis.
A typical single-channel experiment consisted of 200 ms applications of saturating (5 mm) or subsaturating (0.06 mm) glutamate at membrane potentials alternating between −80 and +80 mV. Although these recording times are much briefer than those of typical single-channel experiments, this was necessary to prevent the patches from becoming unstable as a result of prolonged depolarization to +80 mV. However, the open probability of AMPARs in the presence of CTZ is very high in saturating and relatively high in subsaturating glutamate, and the mean lifetimes of each of the four AMPAR conductance levels are on the order of 100–200 μs, so the idealized record for a single 200 ms glutamate application typically contained ∼1000 events for saturating glutamate and ∼100 events for subsaturating glutamate, and at least 1 s of channel activity was recorded for each experimental condition analyzed.
Patches with baseline root mean squared (rms) noise <500 fA after additional filtering at 5 kHz with a digital Gaussian filter (for a final filter frequency of ∼4.5 kHz), and with similar baseline noise at −80 mV and +80 mV, were used for initial analysis of the rectification and concentration response properties of microscopic currents (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Only patches with baseline rms noise ≤300 fA after filtering at 4 kHz (final frequency ∼3.7 kHz) were used for analysis of the variance of microscopic glutamate-activated currents (supplemental Fig. 2, available at www.jneurosci.org as supplemental material) and idealization in QuB (see Figs. 1, 4).
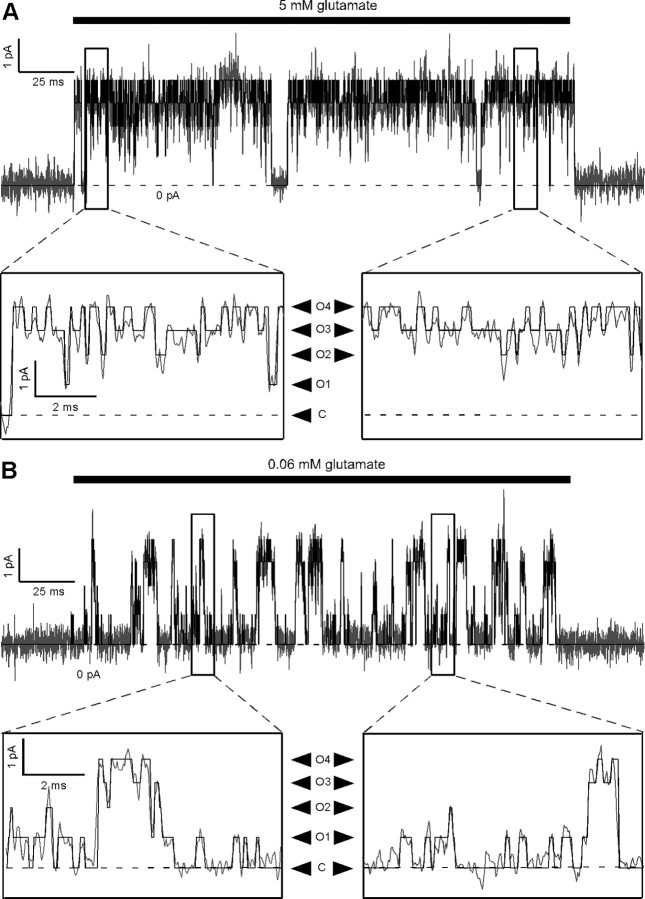
Figure 1.
AMPA receptor single-channel currents in the absence of polyamine block and desensitization, in saturating and subsaturating glutamate at −80 mV. A, Current from an outside-out patch containing a single GluA2(Q) channel in response to a 200 ms application of 5 mm glutamate, recorded at −80 mV, along with the idealization of the record generated by the SKM algorithm of QuB. The current was recorded in the presence of cyclothiazide (30 μm) to block desensitization and in the absence of polyamines. The record is shown sampled at 25 kHz and filtered at ∼3.7 kHz, the same sampling and filter frequencies used for idealization. The four open current levels at −80 mV in this patch were −0.60 (O1), −1.24 (O2), −1.84 (O3), and −2.45 (O4) pA, as seen more clearly in the expanded sections of the records. The dashed line indicates the baseline current level. B, Same as in A, but showing current from the same patch in 0.06 mm glutamate.
Idealization was performed after filtering at a final frequency of ∼3.7 kHz and resampling at 25 kHz. In QuB, the user determines the shortest event that can be resolved by setting a “dead time”. The resolution of the idealizations is equal to the dead time plus one sample interval. We idealized the data with a dead time of 40 or 80 μs. Both dead time values gave essentially identical results (supplemental Table 2, available at www.jneurosci.org as supplemental material), but results are reported and the idealizations illustrated are for 40 μs. Records were idealized using the segmental k-means algorithm (SKM) (Qin, 2004), which requires a kinetic model of the data as an initial input. The models we used for idealization had four open classes (O1–O4) that were all connected to one another and to a closed class. This closed class was connected to one additional closed class, or two additional closed classes in series; the additional closed classes were not connected to the open classes. In our preliminary attempts at idealization using SKM, we estimated the mean current levels and SDs of the open classes using the Grab Amplitudes feature of QuB and allowed the mean current levels and SDs to be reestimated during optimization of the model, but we found that this often resulted, illogically, in open classes with SDs less than the baseline rms noise. We therefore set the SD of all classes equal to the baseline rms noise and fixed the SDs during the idealization. In doing so, we assume that all of the variance of microscopic AMPAR currents is due to transitions between conductance levels, and that the conductance levels do not display significant open channel noise. For idealization of currents activated by saturating glutamate, we set the initial current amplitudes of the four open classes to ±0.6, 1.2, 1.8, and 2.9 pA and allowed the current levels to be reestimated during the idealization. The initial values were based on previously published values of the single channel conductance levels for recombinant homomeric GluA2(Q) channels (Zhang et al., 2008), assuming ohmic conductance. For idealization of currents recorded at −80 mV, the final current levels were only slightly different from the initial estimates; for currents recorded at +80 mV, the final current levels were generally larger than the initial estimates (see Fig. 5B).
Figure 5.
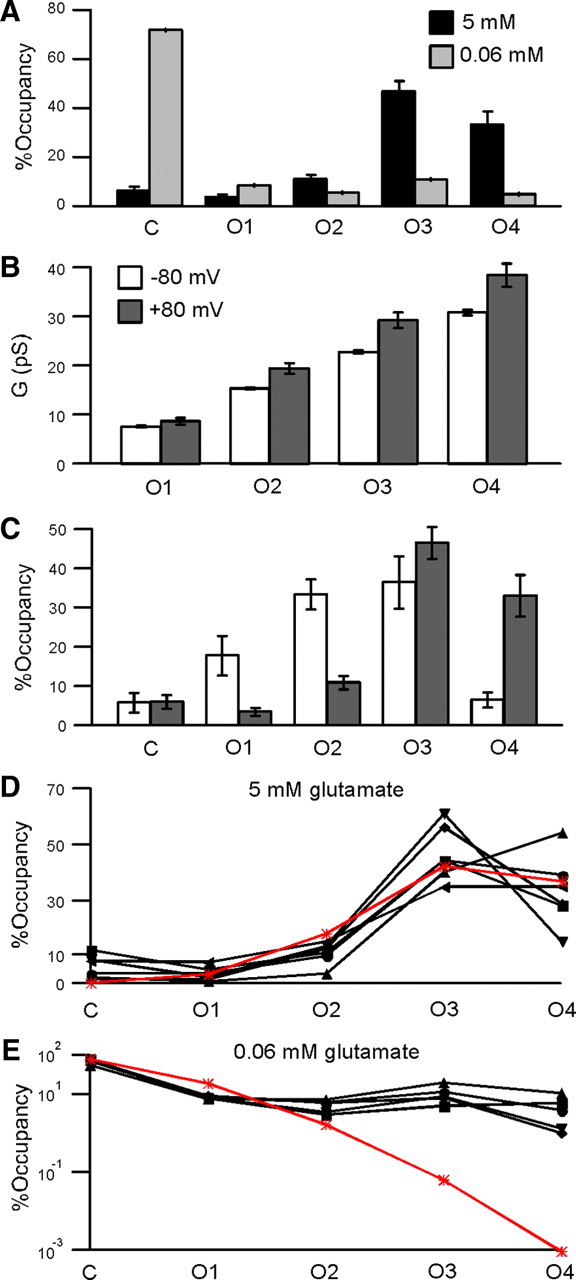
The relative occupancies of AMPA receptor conductance sublevels at +80 mV approximate a binomial distribution in saturating but not subsaturating glutamate. A, Mean time spent at each of the five conductance levels (C, O1–O4) at +80 mV, as a fraction of the total time that the channel was exposed to agonist (%Occupancy) for 5 mm (black, n = 6) and 0.06 mm (light gray, n = 5) glutamate. B, Comparison of the mean conductance for the four open levels (O1–O4) at −80 (open) and +80 (solid) mV (n = 6). C, Comparison of relative occupancies in saturating glutamate at −80 (open) and +80 (solid) mV. D, Relative occupancies of each of the five conductance levels (C, O1–O4) in 5 mm glutamate at +80 mV for each of the six patches used to determine the mean in A (solid symbols and lines), along with the relative occupancies predicted by the binomial distribution (*, red line). The subunit Po that gave the best fit for the binomial distribution (±SD) was 78% (±2%). E, As in D, but for currents in 0.06 mm glutamate and excluding one patch for which we did not obtain sufficient data in subsaturating glutamate, plotted on a logarithmic scale. The subunit Po that gave the best fit for the binomial distribution (±SD) was 6% (±1%).
For idealization of currents activated by subsaturating glutamate, the current levels were fixed to the levels obtained for saturating glutamate in the same patch and their SDs were fixed to the baseline rms noise. To control for false events (i.e., variations in baseline noise interpreted as openings to the lowest open conductance level) in the idealization of the relatively low open probability channel activity occurring in subsaturating glutamate, we idealized the adjacent baseline segments along with the glutamate-activated current. In all patches idealized, false openings to the lowest open conductance level constituted ≤1% of the total time for the idealized baseline records. Although the relative occupancies of O3 and O4 in subsaturating glutamate at −80 mV are similar to the proportion of false events, all of the false events were O1 events, so the occurrence of these conductance levels cannot be accounted for by false events. It is therefore unlikely that false events significantly bias our estimation of the relative occupancy of the current levels in subsaturating glutamate.
Statistical analysis and curve fitting
For statistical analysis, we used Microsoft Excel. A Student's t test was used to define statistical differences. Significance was assumed if p < 0.05. Results are shown graphically as mean ± SEM.
Functions (binomial distributions or weighted sums of binomial distributions) were fit to the data by minimizing the squared errors for the individual data points in all patches (least-squares fitting). For sums of binomial distributions, the weight of the first binomial component (w1) was a free parameter and the weight of the second component (w2) was set to 1 − w1. Curve fitting was performed in Igor Pro.
Results
To study activation gating in AMPARs, we recorded the activity of individual GluA2(Q) channels in outside-out patches under conditions designed to minimize channel block and desensitization. Specifically, ATP was included in the internal solution to eliminate polyamine block, and glutamate was applied in brief (200 ms) pulses with CTZ (30 μm) included in the external solution to minimize desensitization. These brief glutamate pulses also allowed us to monitor the baseline current level, which would otherwise have been difficult in saturating glutamate due to the high open probability.
AMPAR subunit interactions are apparent in subsaturating but not saturating glutamate
Figure 1 shows single-channel AMPAR currents in response to 200 ms applications of saturating (5 mm) (Fig. 1A) and subsaturating (0.06 mm) (Fig. 1B) glutamate at −80 mV. For macroscopic currents, 0.06 mm glutamate gave current amplitudes that were ∼10% of the maximal response at −80 mV. The current records are shown overlaid with the idealization of the current obtained using the SKM algorithm of QuB (Qin, 2004). The algorithm gave subjectively plausible idealizations, although there were inevitable ambiguities in the classification of events (see enlarged portions of the records in Fig. 1A,B). At −80 mV, the estimated conductances of the four open levels (O1–O4) were highly reproducible (mean ± SEM: O1, 7.6 ± 0.2 pS; O2, 15.4 ± 0.2, pS; O3, 22.8 ± 0.3 pS; O4, 30.8 ± 0.5 pS; n = 6) and were consistent with previously reported values (supplemental Table 1, available at www.jneurosci.org as supplemental material), although four open conductance levels have not been detected in all studies. In saturating glutamate, the channel occupied primarily intermediate conductance levels (Fig. 2), with openings to O2 and O3 accounting for the majority of the total occupancy (O2, 33 ± 4%; O3, 36 ± 7%). Closings (C, 6 ± 3%) and openings to the remaining levels were also detected (O, 18 ± 5%; O4, 7 ± 2%; n = 6). The relative occupancies in saturating glutamate at −80 mV thus resemble a binomial distribution for four independent trials, with the conductance level determined by the number of successes (i.e., the number of subunits with ion channel domains in the open conformation) (Fig. 2B). The probability of success that gave the best fit to the combined dataset was 58 ± 3%. To avoid confusion, we refer to the probability that an individual ion channel domain is in the open conformation as the “subunit Po,” and we use this abbreviated form only in the context of individual subunits. We reserve the unabbreviated forms “closed probability” and “open probability” (i.e., the probability that the channel is at any of the open conductance levels) for referring to the channel as a whole. Our results in saturating glutamate are consistent with the idea that AMPAR subunits gate independently (Rosenmund et al., 1998), and with the previously estimated subunit Po in saturating glutamate of 67% (Jin et al., 2003).
Figure 2.
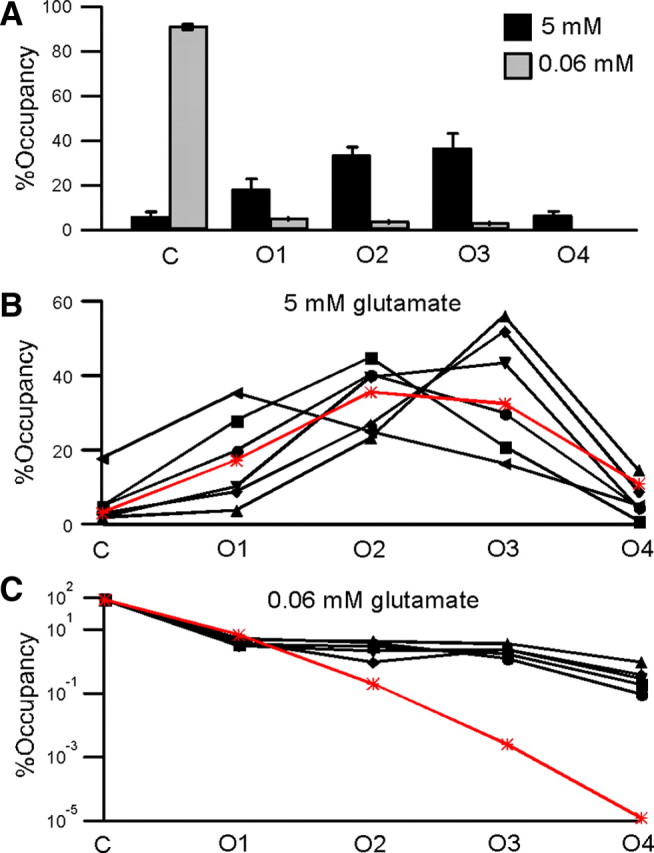
The relative occupancies of AMPA receptor conductance levels at −80 mV approximate a binomial distribution in saturating but not subsaturating glutamate. A, Mean time spent at each of the five conductance levels (C, O1–O4) at −80 mV, as a fraction of the total time that the channel was exposed to agonist (%Occupancy) for 5 mm (black, n = 6) and 0.06 mm (light gray, n = 5) glutamate. B, Relative occupancies of the five conductance levels in 5 mm glutamate at −80 mV for each of the six patches used to determine the mean in A (solid symbols and lines), along with the relative occupancies predicted by the binomial distribution (*, red line). The subunit Po that gave the best fit for the binomial distribution (±SD) was 58% (±3%). C, As in B, but for currents in 0.06 mm glutamate and excluding one patch for which we did not obtain sufficient data in subsaturating glutamate, plotted on a logarithmic scale. The subunit Po that gave the best fit for the binomial distribution (±SD) was 2% (±0.2%).
In subsaturating glutamate, the gating process is more complicated than in saturating glutamate, involving a glutamate binding/unbinding step followed by an ion channel opening/closing step. Still, the steady-state Po should be the same for all subunits and the relative occupancies should follow a binomial distribution if the subunits are independent—an important but possibly counterintuitive point. In subsaturating glutamate at −80 mV, the relative occupancy of the closed conductance level was 90 ± 1%, but all open conductance levels were represented during the open periods (O1, 4 ± 0.4%; O2, 3 ± 0.6%; O3, 2 ± 0.4%; O4, 0.4 ± 0.2%; n = 5) (Fig. 2). The occupancy of the closed conductance level obtained using the SKM idealization was similar to the closed probability obtained using a traditional threshold-crossing approach at a lower filter frequency (see supplemental Results and Discussion, available at www.jneurosci.org as supplemental material). In contrast to saturating glutamate, the binomial distribution fails to describe the relative occupancies in subsaturating glutamate (Fig. 2C). Here, the best fitting subunit Po, 2 ± 0.2%, predicts the relative occupancies of C and O1 reasonably accurately (C, 93% predicted vs 90% actual; and O1, 7% predicted vs 4% actual), but predicts that O3 and O4 essentially never occur (O3, 3 × 10−3% predicted vs 2% actual; and O4, 2 × 10−5% predicted vs 0.4% actual). The small amounts of O3 and O4 are unlikely to result from false events (see Materials and Methods), but nonetheless make it problematic to apply least-squares fitting of binomial distributions to the data, since orders of magnitude differences between small numbers will have little influence on the fit. Nonetheless, comparison of normalized χ2 values indicates that the fit was quantitatively better in saturating glutamate than in subsaturating glutamate (supplemental Table 3, available at www.jneurosci.org as supplemental material). This result suggests that, in subsaturating glutamate, AMPAR subunits interact in some manner that causes the relative occupancies to deviate from the predictions of absolute subunit independence.
How can AMPAR subunits interact in subsaturating glutamate, while apparently gating independently in saturating glutamate? One explanation is that the apparent independent subunit gating in saturating glutamate is actually the result of an interactive gating process that coincidentally produces binomially distributed occupancies. An alternative explanation that retains the binomial distribution as a physically meaningful description of the data in saturating glutamate is that the gating of individual AMPAR subunits is independent of the ion channel opening/closing process in the other subunits, but is influenced by the occupancy of other subunits by glutamate. Thus, when all four glutamate binding sites are occupied the subunits appear to gate independently. With this idea in mind, we noted that, in subsaturating glutamate, open periods containing O4 events were much longer than open periods containing only lower conductance events (supplemental Table 2, available at www.jneurosci.org as supplemental material). Assuming that occupancy of a subunit by glutamate is an absolute requirement for opening of its ion channel domain, this result suggests that long open periods result from subunit interactions that only occur when the receptor is occupied by multiple glutamate molecules. Because of the rarity of open periods containing O4, however, we were unable to explore this idea further using our data in subsaturating glutamate at −80 mV.
Voltage-dependent gating enhances subunit interactions in subsaturating glutamate
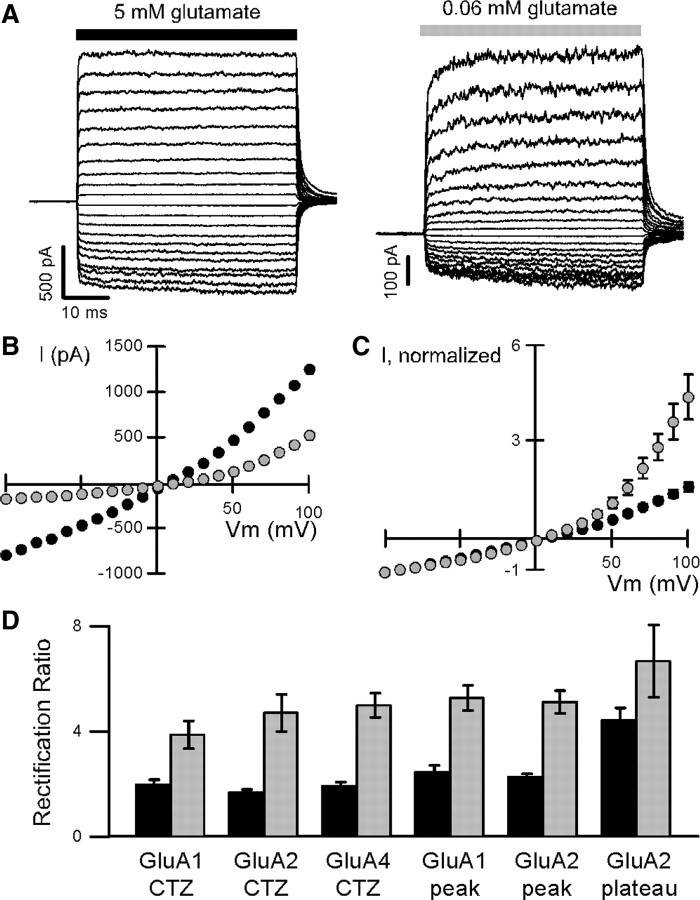
In the absence of block by intracellular polyamines, macroscopic current–voltage (I–V) relations for AMPARs are outwardly rectifying with the degree of outward rectification greater in subsaturating than in saturating agonist concentrations (Fig. 3A–C) (Raman and Trussell, 1995). The effect of glutamate concentration on outward rectification is similar for GluA1, GluA2(Q), and GluA4 channels, and also occurs for peak currents when desensitization is intact (Fig. 3D), suggesting that concentration-dependent outward rectification is a general property of AMPARs and not an artifact of conformational restrictions due to the binding of CTZ (Jin et al., 2005), and that it is relevant to the behavior of synaptic AMPA receptors.
Figure 3.
Outward rectification of macroscopic AMPA receptor currents in saturating and subsaturating glutamate. A, Example glutamate-activated currents in response to 100 ms applications of saturating (5 mm, left) or subsaturating (0.06 mm, right) glutamate (bars). Currents were recorded in outside-out patches obtained from HEK 293 cells expressing GluA2(Q) receptors, in CTZ and in the absence of polyamines, at membrane potentials from −100 to +100 mV (in 10 mV increments). B, Steady-state current–voltage relations for the patch shown in A in saturating (black) or subsaturating (light gray) glutamate. C, Mean current–voltage relations, normalized to the current amplitude at −100 mV, for GluA2(Q) receptors in saturating and subsaturating glutamate (n = 9). D, Mean ratios of current amplitudes at +100 mV to those at −100 mV (rectification ratios) for steady-state currents in CTZ or for peak currents (peak) and steady-state currents (plateau) in response to fast agonist application without CTZ, for various homomeric AMPARs. Currents were measured either in saturating (5–10 mm) or subsaturating (0.06–0.2 mm) glutamate. Mean values (±SEM) in saturating and subsaturating glutamate were 1.97 ± 0.19 and 3.86 ± 0.53 (GluA1, CTZ, n = 3), 1.66 ± 0.13 and 4.70 ± 0.71 (GluA2(Q), CTZ, n = 9), 1.92 ± 0.15 and 4.99 ± 0.46 (GluA4, CTZ, n = 5), 2.44 ± 0.26 and 5.25 ± 0.47 (GluA1, peak, n = 7), 2.27 ± 0.13 and 5.11 ± 0.43 [GluA2(Q), peak, n = 11], and 4.40 ± 0.49 and 6.66 ± 1.37 [GluA2(Q), plateau, n = 6]. The differences in outward rectification in saturating and subsaturating glutamate were statistically significant for all conditions (one-tailed paired t test, p < 0.05).
Previously, it was concluded based on macroscopic current variance analysis that in saturating agonist concentrations outward rectification primarily resulted from an increase in single-channel conductance, and that in subsaturating agonist concentrations it also included a voltage-dependent gating component (Raman and Trussell, 1995). However, this study was done before AMPARs were known to have multiple conductance levels, so it is difficult to tell whether the apparent increase in single-channel conductance reflects an actual increase in the conductance of any of the open levels, a change in the relative occupancy of the conductance levels due to voltage-dependent gating of individual subunits, or some combination thereof. We hypothesized that the increased outward rectification in subsaturating glutamate might reflect a voltage-dependent enhancement of the subunit interactions that we saw at −80 mV but were unable to analyze in detail. We therefore compared single-channel currents in saturating and subsaturating glutamate at +80 mV.
Figure 4 shows single-channel AMPAR currents in response to 200 ms applications of saturating (Fig. 4A) and subsaturating (Fig. 4B) glutamate at +80 mV, from the same patch shown in Figure 1 at −80 mV, along with the SKM idealizations. The amount of outward rectification in macroscopic and microscopic recordings was similar for both saturating and subsaturating glutamate concentrations (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). The open conductance levels at +80 mV were higher than those at −80 mV and more variable (O1, 8.7 ± 0.7 pS; O2, 19.5 ± 1.1 pS; O3, 29.3 ± 1.6 pS; O4, 38.5 ± 2.4 pS; n = 6) (Fig. 5B). However, the amount of outward rectification was independent of the conductance level with the mean ratio of the conductance at +80 mV to that at −80 mV being ∼1.2 for all open levels (1.14 ± 0.09, O1; 1.27 ± 0.07, O2; 1.28 ± 0.06, O3; 1.24 ± 0.06, O4). In saturating glutamate, and in contrast to the results at −80 mV, openings to higher open conductance levels predominated at +80 mV, with O3 and O4 accounting for most of the occupancy (47 ± 4%, O3; and 33 ± 5%, O4), and closings and openings to lower open conductance levels occurring rarely (C, 6 ± 2%; O1, 4 ± 1%; O2, 11 ± 2%; n = 6) (Fig. 5A). The distribution of open conductance levels was wider at −80 mV than that at +80 mV, consistent with the greater normalized variance seen in microscopic currents at −80 mV (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). These results indicate that outward rectification in saturating glutamate involves both rectification of the single-channel conductance (Fig. 5B) and voltage-dependent gating (Fig. 5C).
The relative occupancies of the conductance levels in saturating glutamate at +80 mV also resemble a binomial distribution (Fig. 5D). The best fitting subunit Po was 78 ± 2% (compared with 58% at −80 mV). This value predicts a substantially smaller occupancy of the baseline conductance level than actually obtained (C, 0.2% predicted vs 6% actual). Indeed, records in saturating glutamate occasionally contained relatively long shut periods that seemed mechanistically unrelated to the predominant mode of fast, subunit-independent gating (for example, Fig. 4A and supplemental Fig. 1A, top, available at www.jneurosci.org as supplemental material), though we do not know their functional basis, and they did not occur frequently enough for us to investigate in detail. Nonetheless, the increase in the subunit Po at +80 mV relative to that at −80 mV suggests a small amount of charge associated with each subunit moves through the membrane electric field during the opening/closing process.
In subsaturating glutamate, the relative occupancy of the closed conductance level at +80 mV (C, 71 ± 5%) decreased relative to that at −80 mV (C, 90 ± 1%), consistent with the macroscopic outward rectification in subsaturating glutamate, and the occupancy of the higher open conductance levels was surprisingly large (O1, 8 ± 0.2%,; O2, 5 ± 0.8%; O3, 11 ± 3%; O4, 5 ± 2%; n = 5) (Fig. 5A). At +80 mV, the binomial distribution again fails to describe the relative occupancies in subsaturating glutamate (Fig. 5E), with a subunit Po of 6 ± 1% giving the best fit. Quantitatively, the normalized χ2 value increased from 334 in saturating glutamate to 11,828 in subsaturating glutamate (supplemental Table 3, available at www.jneurosci.org as supplemental material). As at −80 mV, the most dramatic deviation occurred for higher conductance levels (O3, 0.06% predicted vs 11% actual; O4, 1 × 10−3% predicted vs 5% actual). The relatively long, high-conductance open periods that we observed in subsaturating glutamate at −80 mV were much more prominent at +80 mV (Fig. 4B), consistent with our prediction that the apparent subunit interactions at −80 mV would be enhanced by voltage-dependent gating. The duration of open periods depended on the highest open conductance level included in the open period (Fig. 6A,B), with open periods including O4 (mean duration 3.35 ± 0.28 ms) lasting on average ∼15 times as long as open periods including only O1 (i.e., O1 events preceded and followed by closed events) (0.212 ± 0.004 ms). (It should be noted, however, that the duration of the open periods is dependent on the resolution of the idealization, since failure to detect brief closed events will increase the apparent duration of open periods.)
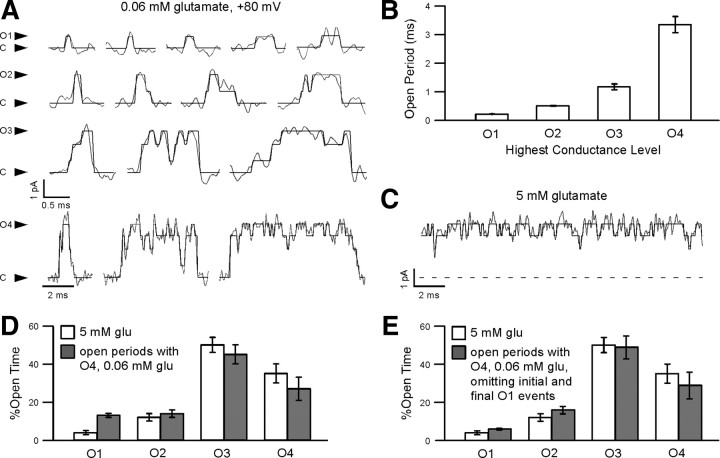
Figure 6.
AMPA receptors are apparently fully liganded during long open periods in subsaturating glutamate. A, Examples of open periods with each of the four open conductance levels (O1–O4) as the highest conductance level reached, with SKM idealization. The highest conductance level and the closed conductance level (C) are indicated (arrows). Note the different time scale for open periods reaching O4. The four open current levels in this patch were 0.66 (O1), 1.69 (O2), 2.55 (O3), and 3.19 (O4) pA; and the mean lifetimes of open periods as a function of the highest conductance level reached were 0.206 (O1), 0.522 (O2), 1.23 (O3), and 4.43 (O4) ms. B, Mean values of the mean lifetimes of open periods in 0.06 mm glutamate at +80 mV, as a function of the highest conductance level (Open Period). The mean (±SEM) values were 0.212 ± 0.004 (O1), 0.506 ± 0.017 (O2), 1.17 ± 0.10 (O3), and 3.35 ± 0.28 (O4) ms (n = 5). C, An example of the activity of the patch in (A) in 5 mm glutamate at +80 mV, with SKM idealization. The dashed line indicates the baseline conductance level. D, Comparison of the amount of time spent at each open conductance level at +80 mV, as a fraction of the total open time (%Open Time) for steady-state currents in 5 mm glutamate (open bars), and for open periods reaching O4 in 0.06 mm glutamate (solid bars). The difference in %Open Time was statistically significant for O1 (unpaired two-tailed t test, p < 0.05), but not for higher conductance levels. E, As in D, but omitting initial and final O1 events for open periods in 0.06 mm glutamate. The mean values (±SEM) were 4 ± 1% (O1), 12 ± 2% (O2), 50 ± 4% (O3), and 35 ± 5% (O4) in saturating glutamate (n = 6); and 6 ± 0.4% (O1), 16 ± 2% (O2), 49 ± 6% (O3), and 29 ± 7% (O4) in subsaturating glutamate (n = 5). There were no statistically significant differences in %Open Time (unpaired two-tailed t test).
AMPARs switch between low and high open probability gating modes in subsaturating glutamate
To understand the apparent deviations from independent subunit gating in subsaturating glutamate at +80 mV, we focused on open periods containing O4 events. Subjectively, the current records during these open periods seemed similar to those in saturating glutamate (Fig. 6, compare A, bottom, and C). This resemblance led us to hypothesize that, as in saturating glutamate, the four glutamate binding sites might be fully occupied throughout these high-conductance open periods. To test this hypothesis, we compared the amount of time spent at each open conductance level as a fraction of the total open time (%Open Time) for O4-containing open periods in subsaturating glutamate and for entire current records in saturating glutamate. The values of %Open Time were similar (Fig. 6D), but, contrary to our expectations, there was a statistically significant excess of O1 for the long open periods relative to saturating glutamate. However, O4-containing open periods frequently began and ended with O1 events (e.g., Figs. 4B, 6A). This observation, combined with the differences in %Open Time of O1 for the two conditions, suggested that AMPARs enter and exit a high open probability mode, represented by the long, high-conductance open periods, from a low open probability mode in which O1 is the predominant open conductance level. When these initial and final O1 events were omitted from the calculation of %Open Time, the values were essentially identical to those in saturating glutamate (Fig. 6E). Thus in subsaturating glutamate, the receptor appears to be fully occupied by glutamate for significant periods of time, despite the low glutamate concentration.
Based on these observations, we developed a kinetic model that qualitatively accounts for our results (Fig. 7A). In this model, the apparent affinity of AMPAR subunits for glutamate is dependent on the number of occupied glutamate binding sites, with unoccupied or singly occupied subunits having relatively low, and doubly, triply, or fully occupied subunits having relatively high apparent affinity. Since glutamate cannot dissociate from subunits with ion channel domains in the open conformation, the increase in apparent affinity could result from changes in the forward or backward reaction rates of either the glutamate binding/unbinding step or the ion channel opening/closing step. According to this model, AMPARs alternate between two gating modes in subsaturating glutamate: a low open probability mode characterized by short open periods in which zero or one glutamate molecules are bound; and a high-affinity mode characterized by long open periods in which the channel is fully occupied by glutamate. Consistent with our model, the distribution of open period durations could be fit with two exponential components (supplemental Fig. 3, available at www.jneurosci.org as supplemental material), and the time constant for the fast component (0.151 ± 0.005 ms) was similar to the mean lifetime of open periods with O1 as the highest conductance level (0.212 ± 0.004 ms).
Figure 7.
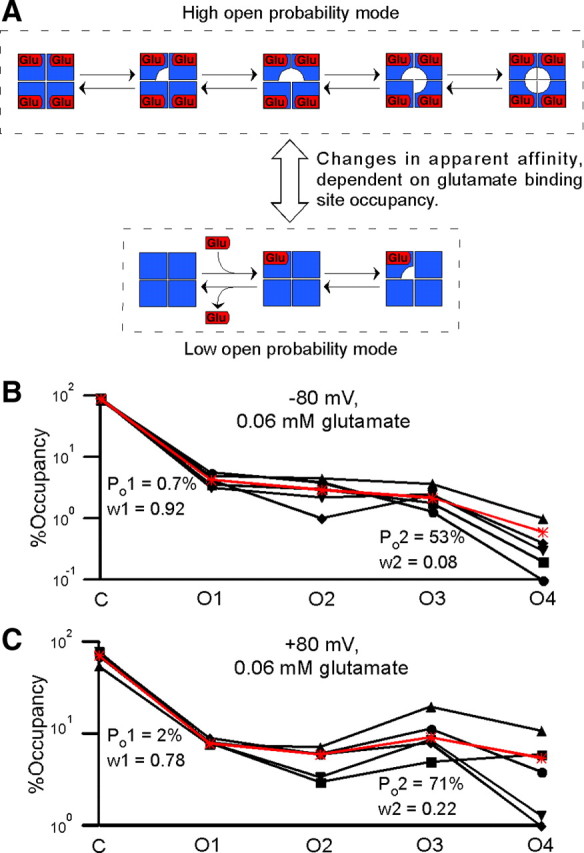
AMPA receptors switch between low and high open probability gating modes in subsaturating glutamate. A, Kinetic model illustrating the switch between low and high open probability gating modes in subsaturating glutamate. The apparent affinity of the receptor for glutamate is dependent on the number of occupied glutamate binding sites, with singly occupied channels having much lower apparent affinity than channels with two or more occupied binding sites. As a result, channels with one or zero occupied binding sites operate in a low open probability mode, but channels rapidly become fully occupied and enter a high open probability mode after binding a second glutamate molecule. B, Fit of the relative occupancies in 0.06 mm glutamate at −80 mV from Figure 2C (solid symbols and lines) by a weighted sum of two binomial distributions (*, red line). The parameters giving the best fit (±SD) were 0.7 ± 0.3 and 53 ± 8% for the low and high subunit Po values, with weights (w1 and w2) of 0.92 and 0.08 (±1), respectively. C, Fit of the relative occupancies in 0.06 mm glutamate at +80 mV from Figure 6F (solid symbols and lines) by a weighted sum of two binomial distributions (*, red line). The parameters giving the best fit (±SD) were 2 ± 1 and 71 ± 6% for the low and high subunit Po values, with weights of 0.78 and 0.22 (±3), respectively.
We do not distinguish between a “progressive” model, in which each glutamate-binding step leads to an increase in apparent affinity (in which case there would be intermediate modes between the low and high open probability modes), and a “threshold” model, in which the binding of two glutamate molecules is sufficient to increase apparent affinity to its maximum level. The increase in apparent affinity upon binding of a second glutamate molecule is sufficiently large that the transition between low open probability and (fully occupied) high open probability modes is in effect discrete. In theory, different mechanisms for the switch between gating modes could be distinguished based on differences in the area or time constant of exponential components of the closed time distribution associated with different nonconducting conformations of the channel at −80 mV relative to +80 mV. However, a model of AMPAR gating in subsaturating glutamate would require at least five different nonconducting states corresponding to nonconducting channels with from zero to four subunits occupied by glutamate, and would require 15 nonconducting states if the clamshell closing/opening step was explicitly included in the model. In any case, the expected number of closed states is larger than the number of exponential components we are able to detect in our closed time distributions (supplemental Fig. 4, available at www.jneurosci.org as supplemental material), so it is difficult to associate any of these components with a specific conformation of the channel. Although the model is intended only as a qualitative explanation of certain features of our data, it could serve as the basis of a more quantitative treatment of subunit interactions. However, detailed kinetic models of AMPARs have many open states with identical conductance (e.g., Robert and Howe, 2003), making a rigorous quantitative treatment extremely challenging, especially if subunit interactions are included.
This model of AMPAR gating suggested that the relative occupancies in subsaturating glutamate could be fit by a weighted sum of two binomial distributions with low and high subunit Po values, corresponding to the low and high open probability modes. Indeed this combination of binomial distributions provided an excellent fit to the relative occupancies at both −80 mV and +80 mV (Fig. 7B,C; supplemental Table 3, available at www.jneurosci.org as supplemental material). The low open probability mode had a subunit Po of 0.7 ± 0.3% at −80 mV and 2 ± 1% at +80 mV, and its weight decreased from 0.92 ± 0.01 at −80 mV to 0.78 ± 0.03 at +80 mV. In our model, this voltage-dependent decrease in the amount of time spent in the low open probability mode is a consequence of voltage-dependent subunit gating. Because glutamate cannot dissociate from subunits with ion channel domains in the open conformation, and because the subunit Po is greater at +80 mV than at −80 mV, there is a longer “window of opportunity” at +80 mV in which a second glutamate molecule can bind to a singly occupied channel, sending it into the high open probability mode. Notably, the subunit Po for the high open probability mode was similar to that in saturating glutamate at +80 mV (71 ± 6%, high open probability mode vs 78 ± 2%, saturating glutamate), as expected based on the comparison of %Open Time in Figure 6E, and also at −80 mV (53 ± 8%, high open probability mode vs 58 ± 3%, saturating glutamate), suggesting that the receptor becomes fully occupied by glutamate for significant periods of time in subsaturating glutamate at −80 as well as +80 mV. Thus our analysis of AMPAR subunit interactions at +80 mV leads to conclusions that are also applicable at more physiological membrane potentials.
Discussion
Our results indicate that AMPARs switch between low and high open probability modes at both negative and positive membrane potentials. This gating mode shift has not been described previously, perhaps because it is most prominent at positive membrane potentials that are not typically used in single-channel recordings of AMPARs. Our experiments were performed on unedited GluA2 channels with desensitization blocked by CTZ; however, the gating mode shift is a general property of all AMPAR subtypes and occurs when desensitization is intact, as indicated by the increased outward rectification in subsaturating glutamate (Fig. 3D)—a manifestation of the gating mode shift.
Previous studies of voltage-dependent gating in AMPARs, notably performed on native channels, are consistent with our results. For non-NMDAR channels, Wyllie et al. (1993) found a voltage-dependent increase in both single-channel conductance and open period length in rat granule cells, while Raman and Trussell (1995) found an increase in outward rectification in subsaturating agonist concentrations in chick neurons. The latter study also reported that the time course of deactivation of macroscopic glutamate-activated currents had fast and slow components, with the weight of the components voltage-dependent. The weights of the slow component at negative and positive potentials were practically identical to the weights of the proposed high open probability mode at −80 and +80 mV (Fig. 7B). Thus, while our results were obtained using recombinant homomeric channels, similar results obtained in two different preparations suggest that our conclusions are generally applicable to native AMPARs that are typically heteromers associated with auxiliary subunits. These studies of native channels were also performed without CTZ.
Only three other studies of microscopic AMPAR currents have been performed in saturating agonist concentrations with desensitization blocked. Two of these (Smith and Howe, 2000; Smith et al., 2000) were performed on native channels, and did not find binomially distributed relative occupancies. However, native channels are heteromers, and the subunit Po may not be the same for all subunits. The other study used recombinant homomeric channels, but focused on defining GluR stoichiometry, and did not examine in detail changes in conductance for fully liganded channels (Rosenmund et al., 1998).
Experimental considerations
Although we think that the switch between low and high open probability modes is the best explanation for our results, we considered several alternatives. One possibility is that the low open probability mode is due to receptors desensitizing for long periods of time in subsaturating glutamate. However, this hypothesis leads to several conclusions that are in conflict with well established results regarding AMPAR desensitization (supplemental Fig. 4, Table 4, Results, and Discussion, available at www.jneurosci.org as supplemental material). Another alternative, as mentioned previously, is that the resemblance between the relative occupancies in saturating glutamate and a binomial distribution is coincidental and not physically meaningful. Although this explanation is not parsimonious, it is plausible based solely on the results at −80 mV. However, that this coincidence would occur once at −80 mV and again +80 mV appears extremely unlikely.
Another consideration is that the current idealizations may not accurately represent the actual transitions between conductance levels, due to an excessively low signal-to-noise ratio, the effects of filtering and sampling, or other issues. However, the fundamental observation on which our model is based—that, during open periods lasting for several milliseconds, AMPARs in subsaturating glutamate behave like fully occupied channels (Fig. 6)—is ultimately independent of the accuracy of the SKM algorithm or the appropriateness of the binomial distributions. The combination of relatively brief, low-conductance and relatively long, high-conductance open periods in subsaturating glutamate at +80 mV is apparent upon examination of the raw records (e.g., Fig. 4B). The SKM idealizations are the output of an algorithm that is highly sensitive to the statistical properties of current records, and these statistical properties are evidently very similar in saturating glutamate and during long open periods in subsaturating glutamate (Fig. 6E). Nonetheless, the relative occupancies of AMPAR conductance levels in saturating glutamate at negative potentials were previously determined to follow a binomial distribution with a subunit open probability (67%) similar to what we obtain here (Jin et al., 2003), based on idealizations using time course fitting (Colquhoun and Sigworth, 1995), so we suspect that our idealizations are reasonably accurate. Finally, the conclusion that the relative occupancies in subsaturating glutamate do not follow a binomial distribution is independent of the detailed accuracy of the idealizations (see supplemental Results and Discussion, available at www.jneurosci.org as supplemental material).
Potential physiological significance of gating modes
The equilibrium between gating modes is shifted toward the high open probability mode at positive potentials, due to the increased subunit Po. This voltage-dependent enhancement of the high open probability mode may be a physiologically important mechanism whereby local synaptic activity regulates the excitability of glutamatergic synapses. Additionally, we expect that other mechanisms that influence AMPAR open probability, such as phosphorylation (Benke et al., 1998; Banke et al., 2000) and interaction with the auxiliary subunits stargazin (Priel et al., 2005; Tomita et al., 2005) and cornichon (Schwenk et al., 2009), will influence the equilibrium between gating modes in a manner analogous to membrane voltage. Interestingly, coexpression of AMPARs with stargazin increased the amount of O4 as a fraction of the total open time by approximately sevenfold (Tomita et al., 2005), but the mechanistic basis of this effect is unknown. Since the high open probability mode can be maintained for several milliseconds at a time, it could significantly influence the shape of synaptic responses. For example, desensitization can occur with only one occupied glutamate binding site (Robert and Howe, 2003), while entry into the high open probability mode requires two occupied binding sites. Thus the opposing influences of these two processes on the spatial extent of AMPAR activity may translate graded changes in local agonist concentration into sharply delineated boundaries between inactive and highly active receptors (for example, between perisynaptic and synaptic receptors).
Structural and mechanistic basis of gating modes and voltage-dependent gating
We propose that the apparent affinity of AMPARs for glutamate is dependent on the number of occupied binding sites. What is the mechanistic and structural basis for this relationship? We developed our model in the context of a basic two-step subunit gating process, involving glutamate binding/unbinding followed by ion channel opening/closing, but there is also an intermediate gating step consisting of closing/opening of the clamshell-like glutamate binding site (Armstrong et al., 1998; Abele et al., 2000; Armstrong and Gouaux, 2000; Mayer, 2006; Weston et al., 2006). Clamshell opening/closing appears tightly coupled to the ion channel domain opening/closing (Zhang et al., 2008). This intermediate step is not dependent on glutamate concentration, and is therefore relevant to gating in both saturating and subsaturating glutamate. Thus, in our model the clamshell closing/opening step is incorporated into the ion channel opening/closing step. Since the ligand-binding domains of GluRs form dimers (Armstrong et al., 1998), occupancy of the glutamate binding site of one subunit of a dimer pair may affect the gating of the other subunit through structural changes at the dimer interface. However, the discrete transitions between gating modes suggest that occupancy of the glutamate binding site of each subunit affects the gating of all other subunits. The GluA2(Q) structure shows that different pairs of subunits form dimers at the level of the ligand-binding domain and the level of the N terminus, and reveals several points of contact between dimers that may be functionally important (Sobolevsky et al., 2009). The switch between gating modes may therefore involve a complex network of interdimer and intradimer interactions.
The structural basis of voltage-dependent gating in AMPARs is also unknown. Voltage-dependent gating in two transmembrane domain KcsA channels is determined by a glutamate residue in the pore loop (Cordero-Morales et al., 2006a,b). The homologous position in AMPARs is occupied by a negatively charged aspartate, but this residue does not underlie voltage-dependent gating (M. L. Prieto and L. P. Wollmuth, unpublished data). NMDARs also show voltage-dependent gating (Nowak and Wright, 1992), which influences the rate of Mg2+ unblock (Clarke and Johnson, 2008). Similar structural mechanisms may underlie voltage-dependent gating in both GluR subtypes, and voltage-dependent gating in AMPARs may influence the rate of polyamine unblock, with important physiological consequences (e.g., Rozov and Burnashev, 1999).
Concluding remarks
During the high open probability mode, AMPARs appear to be saturated by 0.06 mm glutamate, and thus temporarily have an apparent affinity for glutamate comparable to that of NMDARs. Because of their uncoordinated subunit activity, however, AMPARs only maintain this high-affinity mode for limited periods of time. Interestingly, an invertebrate GluR that has relatively high conductance and low maximal open probability comparable to mammalian NMDARs does not show multiple open conductance levels but is activated by the AMPAR agonist quisqualate (Tour et al., 1998). Finally, cyclic nucleotide-gated channels, which have multiple open conductance levels like AMPARs, also switch between a low open probability mode with one occupied agonist binding site, and a high open probability mode with two or more occupied agonist binding sites (Biskup et al., 2007). Binding site occupancy thresholds for switching between low and high open probability modes may be a common regulatory mechanism for ligand-gated ion channels.
Footnotes
This work was supported by an R01 Grant MH066892 (L.P.W.) and a Minority Supplement (M.L.P.) from the National Institute of Mental Health. We thank Drs. James Dilger and James Howe for generous guidance and advice. We also thank Dr. David Talmage, Iehab Talukder, and Catherine Salussolia for critically reading the manuscript and Janet Allopenna for technical assistance with cell culture.
References
- Abele R, Keinanen K, Madden DR. Agonist-induced isomerization in a glutamate receptor ligand-binding domain. A kinetic and mutagenetic analysis. J Biol Chem. 2000;275:21355–21363. doi: 10.1074/jbc.M909883199. [DOI] [PubMed] [Google Scholar]
- Armstrong N, Gouaux E. Mechanisms for activation and antagonism of an AMPA-sensitive glutamate receptor: crystal structures of the GluR2 ligand binding core. Neuron. 2000;28:165–181. doi: 10.1016/s0896-6273(00)00094-5. [DOI] [PubMed] [Google Scholar]
- Armstrong N, Sun Y, Chen GQ, Gouaux E. Structure of a glutamate-receptor ligand-binding core in complex with kainate. Nature. 1998;395:913–917. doi: 10.1038/27692. [DOI] [PubMed] [Google Scholar]
- Banke TG, Traynelis SF. Activation of NR1/NR2B NMDA receptors. Nat Neurosci. 2003;6:144–152. doi: 10.1038/nn1000. [DOI] [PubMed] [Google Scholar]
- Banke TG, Bowie D, Lee H, Huganir RL, Schousboe A, Traynelis SF. Control of GluR1 AMPA receptor function by cAMP-dependent protein kinase. J Neurosci. 2000;20:89–102. doi: 10.1523/JNEUROSCI.20-01-00089.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benke TA, Lüthi A, Isaac JT, Collingridge GL. Modulation of AMPA receptor unitary conductance by synaptic activity. Nature. 1998;393:793–797. doi: 10.1038/31709. [DOI] [PubMed] [Google Scholar]
- Biskup C, Kusch J, Schulz E, Nache V, Schwede F, Lehmann F, Hagen V, Benndorf K. Relating ligand binding to activation gating in CNGA2 channels. Nature. 2007;446:440–443. doi: 10.1038/nature05596. [DOI] [PubMed] [Google Scholar]
- Citri A, Malenka RC. Synaptic plasticity: multiple forms, functions, and mechanisms. Neuropsychopharmacology. 2008;33:18–41. doi: 10.1038/sj.npp.1301559. [DOI] [PubMed] [Google Scholar]
- Clarke RJ, Johnson JW. Voltage-dependent gating of NR1/2B NMDA receptors. J Physiol. 2008;586:5727–5741. doi: 10.1113/jphysiol.2008.160622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collingridge GL, Olsen RW, Peters J, Spedding M. A nomenclature for ligand-gated ion channels. Neuropharmacology. 2009;56:2–5. doi: 10.1016/j.neuropharm.2008.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D, Sigworth FJ. Fitting and statistical analysis of single-channel records. In: Sakmann B, Neher E, editors. Single-channel recording. New York: Plenum; 1995. pp. 483–587. [Google Scholar]
- Cordero-Morales JF, Cuello LG, Perozo E. Voltage-dependent gating at the KcsA selectivity filter. Nat Struct Mol Biol. 2006a;13:319–322. doi: 10.1038/nsmb1070. [DOI] [PubMed] [Google Scholar]
- Cordero-Morales JF, Cuello LG, Zhao Y, Jogini V, Cortes DM, Roux B, Perozo E. Molecular determinants of gating at the potassium-channel selectivity filter. Nat Struct Mol Biol. 2006b;13:311–318. doi: 10.1038/nsmb1069. [DOI] [PubMed] [Google Scholar]
- Derkach VA, Oh MC, Guire ES, Soderling TR. Regulatory mechanisms of AMPA receptors in synaptic plasticity. Nat Rev Neurosci. 2007;8:101–113. doi: 10.1038/nrn2055. [DOI] [PubMed] [Google Scholar]
- Derkach V, Barria A, Soderling TR. Ca2+/calmodulin-kinase II enhances channel conductance of alpha-amino-3-hydroxy-5-methyl-4-isoxazolepropionate type glutamate receptors. Proc Natl Acad Sci U S A. 1999;96:3269–3274. doi: 10.1073/pnas.96.6.3269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erreger K, Chen PE, Wyllie DJ, Traynelis SF. Glutamate receptor gating. Crit Rev Neurobiol. 2004;16:187–224. doi: 10.1615/critrevneurobiol.v16.i3.10. [DOI] [PubMed] [Google Scholar]
- Gebhardt C, Cull-Candy SG. Influence of agonist concentration on AMPA and kainate channels in CA1 pyramidal cells in rat hippocampal slices. J Physiol. 2006;573:371–394. doi: 10.1113/jphysiol.2005.102723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howe JR, Cull-Candy SG, Colquhoun D. Currents through single glutamate receptor channels in outside-out patches from rat cerebellar granule cells. J Physiol. 1991;432:143–202. doi: 10.1113/jphysiol.1991.sp018381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin R, Banke TG, Mayer ML, Traynelis SF, Gouaux E. Structural basis for partial agonist action at ionotropic glutamate receptors. Nat Neurosci. 2003;6:803–810. doi: 10.1038/nn1091. [DOI] [PubMed] [Google Scholar]
- Jin R, Clark S, Weeks AM, Dudman JT, Gouaux E, Partin KM. Mechanism of positive allosteric modulators acting on AMPA receptors. J Neurosci. 2005;25:9027–9036. doi: 10.1523/JNEUROSCI.2567-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kussius CL, Popescu GK. Kinetic basis of partial agonism at NMDA receptors. Nat Neurosci. 2009;12:1114–1120. doi: 10.1038/nn.2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer ML. Glutamate receptors at atomic resolution. Nature. 2006;440:456–462. doi: 10.1038/nature04709. [DOI] [PubMed] [Google Scholar]
- Nowak LM, Wright JM. Slow voltage-dependent changes in channel open-state probability underlie hysteresis of NMDA responses in Mg(2+)-free solutions. Neuron. 1992;8:181–187. doi: 10.1016/0896-6273(92)90119-x. [DOI] [PubMed] [Google Scholar]
- Partin KM, Patneau DK, Winters CA, Mayer ML, Buonanno A. Selective modulation of desensitization at AMPA versus kainate receptors by cyclothiazide and concanavalin A. Neuron. 1993;11:1069–1082. doi: 10.1016/0896-6273(93)90220-l. [DOI] [PubMed] [Google Scholar]
- Priel A, Kolleker A, Ayalon G, Gillor M, Osten P, Stern-Bach Y. Stargazin reduces desensitization and slows deactivation of the AMPA-type glutamate receptors. J Neurosci. 2005;25:2682–2686. doi: 10.1523/JNEUROSCI.4834-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F. Restoration of single-channel currents using the segmental k-means method based on hidden Markov modeling. Biophys J. 2004;86:1488–1501. doi: 10.1016/S0006-3495(04)74217-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Trussell LO. Concentration-jump analysis of voltage-dependent conductances activated by glutamate and kainate in neurons of the avian cochlear nucleus. Biophys J. 1995;69:1868–1879. doi: 10.1016/S0006-3495(95)80057-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert A, Howe JR. How AMPA receptor desensitization depends on receptor occupancy. J Neurosci. 2003;23:847–858. doi: 10.1523/JNEUROSCI.23-03-00847.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenmund C, Stern-Bach Y, Stevens CF. The tetrameric structure of a glutamate receptor channel. Science. 1998;280:1596–1599. doi: 10.1126/science.280.5369.1596. [DOI] [PubMed] [Google Scholar]
- Rozov A, Burnashev N. Polyamine-dependent facilitation of postsynaptic AMPA receptors counteracts paired-pulse depression. Nature. 1999;401:594–598. doi: 10.1038/44151. [DOI] [PubMed] [Google Scholar]
- Rozov A, Zilberter Y, Wollmuth LP, Burnashev N. Facilitation of currents through rat Ca2+-permeable AMPA receptor channels by activity-dependent relief from polyamine block. J Physiol. 1998;511:361–377. doi: 10.1111/j.1469-7793.1998.361bh.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwenk J, Harmel N, Zolles G, Bildl W, Kulik A, Heimrich B, Chisaka O, Jonas P, Schulte U, Fakler B, Klöcker N. Functional proteomics identify cornichon proteins as auxiliary subunits of AMPA receptors. Science. 2009;323:1313–1319. doi: 10.1126/science.1167852. [DOI] [PubMed] [Google Scholar]
- Smith TC, Howe JR. Concentration-dependent substate behavior of native AMPA receptors. Nat Neurosci. 2000;3:992–997. doi: 10.1038/79931. [DOI] [PubMed] [Google Scholar]
- Smith TC, Wang LY, Howe JR. Heterogeneous conductance levels of native AMPA receptors. J Neurosci. 2000;20:2073–2085. doi: 10.1523/JNEUROSCI.20-06-02073.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobolevsky AI, Rosconi MP, Gouaux E. X-ray structure, symmetry and mechanism of an AMPA-subtype glutamate receptor. Nature. 2009;462:745–756. doi: 10.1038/nature08624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sommer B, Köhler M, Sprengel R, Seeburg PH. RNA editing in brain controls a determinant of ion flow in glutamate-gated channels. Cell. 1991;67:11–19. doi: 10.1016/0092-8674(91)90568-j. [DOI] [PubMed] [Google Scholar]
- Swanson GT, Gereau RW, 4th, Green T, Heinemann SF. Identification of amino acid residues that control functional behavior in GluR5 and GluR6 kainate receptors. Neuron. 1997;19:913–926. doi: 10.1016/s0896-6273(00)80972-1. [DOI] [PubMed] [Google Scholar]
- Tomita S, Adesnik H, Sekiguchi M, Zhang W, Wada K, Howe JR, Nicoll RA, Bredt DS. Stargazin modulates AMPA receptor gating and trafficking by distinct domains. Nature. 2005;435:1052–1058. doi: 10.1038/nature03624. [DOI] [PubMed] [Google Scholar]
- Tour O, Parnas H, Parnas I. Depolarization increases the single-channel conductance and the open probability of crayfish glutamate channels. Biophys J. 1998;74:1767–1778. doi: 10.1016/S0006-3495(98)77887-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weston MC, Schuck P, Ghosal A, Rosenmund C, Mayer ML. Conformational restriction blocks glutamate receptor desensitization. Nat Struct Mol Biol. 2006;13:1120–1127. doi: 10.1038/nsmb1178. [DOI] [PubMed] [Google Scholar]
- Wyllie DJ, Traynelis SF, Cull-Candy SG. Evidence for more than one type of non-NMDA receptor in outside-out patches from cerebellar granule cells of the rat. J Physiol. 1993;463:193–226. doi: 10.1113/jphysiol.1993.sp019591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Cho Y, Lolis E, Howe JR. Structural and single-channel results indicate that the rates of ligand binding domain closing and opening directly impact AMPA receptor gating. J Neurosci. 2008;28:932–943. doi: 10.1523/JNEUROSCI.3309-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]