The Contribution of Population Health and Demographic Change to Economic Growth in China and India

Abstract

We find that a cross-country model of economic growth successfully tracks the growth takeoffs in China and India. The major drivers of the predicted takeoffs are improved health, increased openness to trade, and a rising labor force-to-population ratio due to fertility decline. We also explore the effect of the reallocation of labor from low-productivity agriculture to the higher-productivity industry and service sectors. Including the money value of longevity improvements in a measure of full income reduces the gap between the magnitude of China's takeoff relative to India's due to the relative stagnation in life expectancy in China since 1980.

1. Introduction

Comparing China and India is a decades-old activity. Long known to the West as the world's two population superpowers, China and India have been until fairly recently only small players on the international economic scene. The emergence of China as a major economic power was followed by a slower, but still important, economic transformation in India.

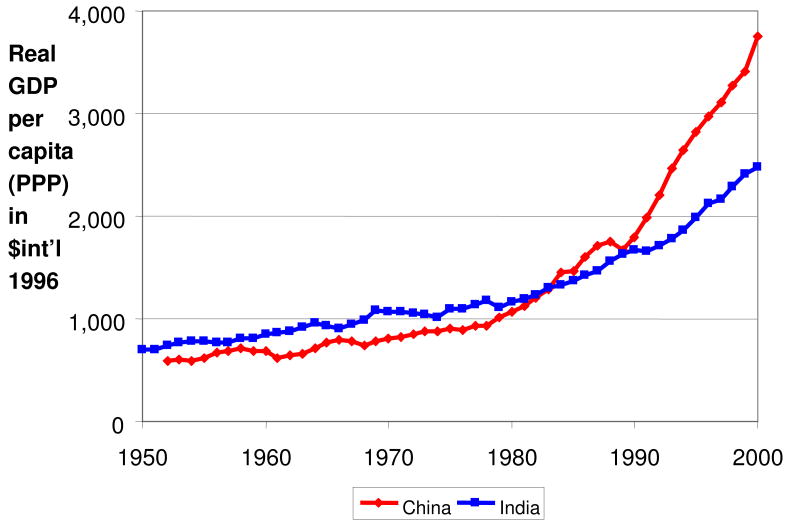
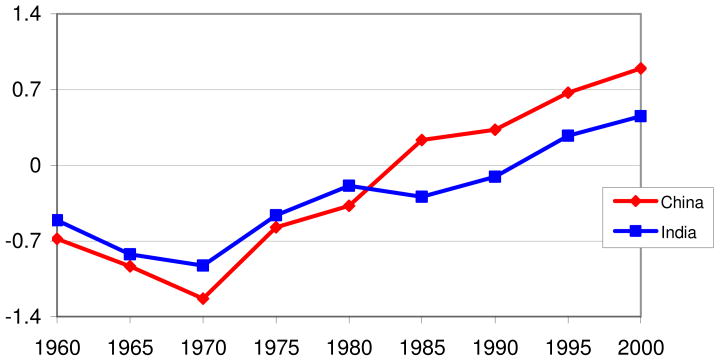
Before 1980, economic growth in both China and India, as measured by the growth rate of income per capita (in purchasing power parity terms), was relatively slow. After 1980, growth in both countries accelerated, dramatically in China and more modestly in India (see figure 1). China rapidly overtook India, and now has substantially higher income per capita. Hausmann, Pritchett, and Rodrik (2005) date these growth accelerations as starting in 1978 in China and 1982 in India. This growth has changed the nature of the West's interest in China and India. Both countries, by virtue of their population size, have the potential to be dominant forces in the international economy.

Figure 1. Real Income per Capita.

This paper analyzes and compares the acceleration of economic growth in China and India. We start with a simple shift-share analysis in which we decompose the growth of income per worker into a portion attributable to the reallocation of labor from low- to high-productivity sectors and a portion attributable to the growth of labor productivity within sectors. We then use cross-country panel data to estimate the parameters of an empirical growth model, which allows us to estimate the contribution of different variables to the recent growth trajectories of China and India. This approach lends itself naturally to an examination of the influence on growth of variables such as openness to trade and institutional quality, a feature that distinguishes it from other common approaches to the study of economic growth such as calibrating a production function using parameters estimated from micro data (see Young 1994, 1995).

The ability of models such as ours to explain takeoffs in economic growth is by no means assured. Easterly, Kremer, Pritchett, and Summers (1993) emphasize that national rates of growth of income per capita are essentially uncorrelated across successive five-year periods. They point out that it is difficult to explain these essentially random fluctuations using the fairly slow-moving variables used to explain variations in economic growth in cross-country panels. Our explanation emphasizes demographic changes, which can occur relatively quickly and have the potential to explain takeoffs into rapid economic growth. The two demographic factors we emphasize are rapid increases in life expectancy and declines in fertility. These have occurred in both China and India, though for each factor the magnitude of the effects has been greater in China.

An increase in life expectancy, which we regard as a proxy for population health, has a number of potential economic effects. To the extent that health affects labor quality and productivity, one would expect improved health in China, and therefore the rising standard of labor inputs, to have an effect on GDP per worker. Fogel (1994) emphasizes the role played by better health and nutrition in the Industrial Revolution, and Fogel (2004) argues that these same changes led to a substantial improvement in productivity in China. Bloom, Canning, and Sevilla (2004) estimate the effect of health as a form of human capital in a cross-country study of economic growth rates.² In addition to this effect of health on worker productivity, increases in health and prospective longevity can also drive increased savings for retirement (Bloom, Canning, and Graham (2003); Bloom, Canning, Mansfield, and Moore (2006)), higher rates of foreign direct investment (Alsan, Bloom, and Canning (2006)), and higher rates of domestic investment, savings, and school enrollment (Lorentzen, McMillan, and Wacziarg (2005)).

In the 1970s, declines in mortality in China and India, which included large declines in infant and child mortality, led to large cohorts of young people. Subsequent declines in fertility produced “bulge” generations in each country, although the bulges occurred earlier and are more pronounced in China than in India. In general, when relatively large generations reach the prime ages for working and saving, a country will experience a demographically induced economic boost, provided this demographic cohort is productively employed. Bloom and Williamson (1998), Bloom, Canning, and Malaney (2000), and Mason (2001) have investigated the role of this “demographic dividend” in the successful East Asian “Tiger” economies. Cai (2004) provides a similar study for China, and Bloom and Canning (2003) likewise examine through a demographic lens the recent economic boom in Ireland.

East Asia's macroeconomic performance is tracked very closely by its demographic transition and the resulting changes in age structure. Estimates indicate that the “demographic dividend” accounts for as much as one-third of the East Asian “economic miracle” (Bloom and Williamson (1998), Bloom, Canning, and Malaney (2000)). By contrast, the absence of demographic change also accounts for a large portion of Africa's economic debacle (Bloom, Canning, and Sevilla (2003); Bloom and Sachs (1998)). The results of these analyses have reduced the need to claim that factors exceptional to East Asia or Africa account for their different economic trajectories. Once age structure dynamics are introduced into the economic growth model, these regions appear to more closely obey common principles of economic growth (Bloom, Canning, and Malaney (2000)).

In 1975, the ratio of working-age (15-64) to non-working-age (0-14 and 65+) people in both China and India was around 1.3. This means that the number of working-age people was only modestly larger than the number of people who, by virtue of their age, were most likely dependents. In the 1970s, China launched the “later, longer, fewer” campaign (later marriage and age at first birth, longer inter-birth intervals, and fewer births (i.e., 2 in the cities and 3 in the countryside)). This evolved into the one-child policy adopted in 1980, which encouraged and very often required couples to limit their families to only one child.³ The campaign and policy propelled a sharp decline in fertility that began in the 1970s. This decline triggered a subsequent sharp rise in the ratio of working-age to non-working-age people, a rise that is expected to peak at 2.5 in 2010. India's demographics are changing similarly but more slowly, with an expected peak ratio of 2.1 in 2035, a level that China reached in 1995. In India, therefore, the greater portion of the potential demographic dividend lies ahead. China, by contrast, anticipates a very rapidly rising elderly population in the not-too-distant future, with over 400 million Chinese – 30% of the population – projected to be age 60 and over by 2050.

It is clear, both theoretically and empirically, that there is nothing automatic about the effects of demographic change on economic growth (Bloom, Canning, and Sevilla (2003), Bloom and Canning (2003)). Age distribution changes create supply-side potential for economic growth. Whether this potential is captured depends on the policy environment, as reflected by the quality of governmental institutions, labor legislation, macroeconomic management, openness to trade, and education policy, among other factors. Additional factors have contributed to China's and India's remarkable economic growth. Both countries undertook economic reforms characterized by deregulation and liberalization, which increased the role of markets, opened up their economies to international trade, and attracted foreign investment. China reformed earlier and much more aggressively than India. Reform of communal farming in China began in the late 1960s though it could be argued that it was only with the agricultural reforms of 1978, followed by industrial sector reforms in the early 1980s, that substantial productivity gains were realized. By contrast, India's market-oriented economic policy reforms began in the early 1990s in response to fiscal and balance-of-payments crises. Rodrik and Subramanian (2004), however, argue that pro-business reforms in India in the 1980s, which aided incumbent firms rather than increasing market competition, had beneficial growth effects.

In both countries, the reforms led to increased volumes of international trade and large inflows of foreign direct investment (FDI). The relationships among economic reform, the opening up of trade, and economic growth are discussed for the case of China by Demurger et al. (2002), Shen and Geng (2001), Chen and Feng (2000), and Cai and Du (1998). For India, they are discussed by Chopra et al. (1995) and Sachs et al. (1999). We try to capture these effects in our empirical analysis with a measure of institutional quality and a measure of openness to trade though these are admittedly imperfect proxies for the policy reforms that took place.

China and India have also made improvements in education. Cai and Du (1998), Wang and Yao (2001), and Chopra et al. (1995) examine the contribution of human capital, proxied by education level, to economic growth. We include a measure of education in our analysis.

Labor reallocation from agriculture to other sectors has also been singled out for attention as a source of economic growth in China and India. Prior to reform these two countries, like many others,⁴ had surplus labor in agriculture with a large differential in labor productivity between agriculture and industry. As a consequence, the inter-sectoral shift of labor (away from agriculture) increased overall productivity and therefore aggregate output. The effect in China of labor reallocation has been investigated by Sachs and Woo (1994), Woo (1997), and Cai and Wang (1999). We report a new analysis of this effect for China and India, and also include a measure of sectoral change in our cross-country panel data analysis of economic growth.⁵

Lucas (1993) emphasizes productivity growth as a source of economic “miracles.” We put more emphasis on demographic factors that increase labor supply per capita, and on improvements in the health and productivity of labor. However, our measures of openness to trade, institutional quality, and sectoral reallocation can also be interpreted as proxies for productivity growth effects rather than effects associated with changes in the quantity or quality of factor inputs.

The rationale for this paper is not to give a detailed explanation of economic growth in India and China, which has depended on many factors we do not model. Rather we investigate if a simple cross-country growth model, including demographic factors, can explain the take off in growth that these two countries experienced. The key idea is to compare their experience of growth with the experience of rest of the world. We argue it is interesting that much of the growth that was experienced in India and China would be predicted by a model that fits the rest of the world.

Our paper rests on two related premises. The first premise is that influences on economic growth can be divided into fundamental long-run factors (such as demographic change) and short-term cyclical or idiosyncratic factors (such as changes in fiscal policy). We capture the fundamental factors directly in an empirical growth model, while the short-term factors are reflected in an error term. The second premise is that the fundamental determinants of economic growth are common across countries, implying that inferences about the fundamental determinants can be made from the analysis of cross-country panel data. Within this framework, the experience of countries other than India and China is relevant to understanding the contribution to economic growth in China and India of fundamental factors like demographic change and population health.

In using a common model to explain different countries' growth experiences, we weight countries equally, taking each as an equally important observation of economic growth. Weighting large countries in such a regression more heavily is only appropriate if large countries contain more “information” in the form of lower variance in growth rates. However the volatility of growth rates declines only very slightly with country size (Canning, Amaral et al. 1998), meaning that the economic circumstances of individuals within countries tend to move together, rather than representing independent outcomes that are smoothed when we average over larger numbers. In addition, this issue is, in principle, addressed by the reporting of heteroskedasticity-consistent standard errors, which assign more weight to observations with lower variance.

Because we emphasize economic growth, we treat health as an input whose value is purely instrumental. A broader notion of “full income” would measure health as well as consumption. We follow the methodology used in Becker, Philipson, and Soares (2005) to monetize the value of gains in life expectancy and compare these gains to those due to rising consumption. Continued health improvements in India mean that full income has been rising faster than consumption. This is not the case in China, where population health has improved rather sluggishly since 1980. As a result, the comparative deficit in India's progress in development in relation to that of China is smaller when measured in full-income terms than when measured in terms of economic growth.

This paper complements earlier work that focused on explaining rapid economic growth in East Asia over the whole period 1970-2000 (Bloom, Canning, and Malaney, 2000). We provide a more detailed analysis of the contribution of health and demography to growth in India and China, in particular investigating if the timing of the health and demographic effects matched the timing of the takeoff in growth in India and China. Bloom and Canning (2003) undertake a similar study of the role of demography in the takeoff in the Irish economy after 1985. We also provide estimates of the direct welfare benefits of health improvements experienced in India and China, as well as their effect on welfare through generating economic growth.

2. Sources of Economic Growth

Most empirical models of economic growth focus on the growth of income per capita, which is a convenient summary indicator of the standard of living. However, economic theories typically address the level of output per worker. In addition, growth models often do not consider the sectoral composition of the economy. We therefore begin by considering the possible role that changes in the number of workers per capita and in sectoral composition play in explaining economic growth in China and India.

We start with an accounting identity that links income per capita (Y/N) to income per worker (Y/L)

$$\frac{Y}{N}=\frac{Y}{L}\frac{L}{\mathit{\text{WA}}}\frac{\mathit{\text{WA}}}{N}$$ (1)

In this identity, WA represents the population of working age. The identity merely states that the level of income per capita equals the level of income per worker times the labor participation rate (L/WA) times the ratio of working-age to total population (WA/N). Defining

$$y=\text{log}\frac{Y}{N},z=\text{log}\frac{Y}{L},\rho =\text{log}\frac{L}{\mathit{\text{WA}}},w=\text{log}\frac{\mathit{\text{WA}}}{N}$$ (2)

and totally differentiating the identity, we see that the growth rate of income per capita equals the growth of income per worker plus the growth of labor participation plus the growth of the ratio of working-age to total population. That is:

$$\dot{y}=\dot{z}+\dot{\rho }+\dot{w}$$ (3)

Table 1 performs this decomposition of growth in China and India for the period 1980 to 2000 with a corresponding decomposition for the period 1970 to 1980 reported for comparison. The figures suggest that faster growth in output per worker accounts for most of the speed up in growth in China and India, with modest contributions from rising participation rates and increases in the working-age share of the total population.

Table 1. Sources of Growth in China and India Annual Average Growth Rate (Percent).

Variable	India		China
	1970-80	1980-2000	1970-80	1980-2000
Growth Rate of Real GDP Per Capita	1.4	3.6	3.2	8.1
Decomposition of Growth Rate of GDP Per Capita:
Growth Rate of Real GDP Per Worker	1.2	3.9	3.0	6.7
Growth of Participation Rate	-0.1	-0.7	-0.4	0.7
Growth Rate of Ratio of Population Aged 15-64 to Total Population	0.3	0.3	0.7	0.6

Growth in income per worker can result from increases in worker productivity in each sector, or from the reallocation of workers from low-productivity to high-productivity sectors. Table 2 reports the shares of employment in agriculture, industry, and services, and Table 3 reports labor productivity in each sector for China and India since 1970.⁶ Both China and India have seen a movement of workers out of agriculture and into industry and services. This effect has been more pronounced in China, contributing to its higher growth rate. Table 3 shows that agricultural productivity is about a quarter of the level of worker productivity found in industry and services. The most striking feature shown in Table 3 is the rapid growth of output per worker in industry in China since 1980.

Table 2. Share of Employment by Sector.

Variable	India			China
	1970	1980	2000	1970	1980	2000
Share in Total Employment (%)
Agriculture	74	70	60	81	69	50
Industry	11	13	16	10	18	23
Services	15	17	23	9	13	27

Table 3. Output per Worker by Sector (1995 US$).

Variable	India			China
	1970	1980	2000	1970	1980	2000
Average GDP per worker	453	500	1072	296	396	1454
By Sector:
Agriculture	264	287	429	188	219	478
Industry	924	893	1806	738	801	3405
Services	1042	1062	2216	760	760	1630

We can decompose the effect of changing sectoral shares on economic growth more formally by writing

$$z=z_a{\beta }_a+z_i{\beta }_i$$ (4)

according to which GDP per worker is a weighted average of the output per worker in the agriculture and industry (which we take to include services), given by z_a and z_i, with the weights being the respective shares of each sector in total employment, given by β_a and β_i.

Totally differentiating and dividing by z, we can write

$$\frac{\mathit{\text{dz}}}{z}=\left(\frac{z_a}{z}{\beta }_a\right)\left(\frac{{\mathit{\text{dz}}}_a}{z_a}+\frac{d{\beta }_a}{{\beta }_a}\right)+\left(\frac{z_i}{z}{\beta }_i\right)\left(\frac{{\mathit{\text{dz}}}_i}{z_i}+\frac{d{\beta }_i}{{\beta }_i}\right)$$ (5)

so that the growth in output per worker depends on (1) the growth of worker productivity in each sector and (2) the growth of each sector's share of total employment. We can separate out these two effects. Growth in output per worker due to productivity growth within each sector is

$${\frac{\mathit{\text{dz}}}{z}|}_{\mathit{\text{productivity}}}=\left(\frac{Y_a}{Y}\right)\left(\frac{{\mathit{\text{dz}}}_a}{z_a}\right)+\left(\frac{Y_i}{Y}\right)\left(\frac{{\mathit{\text{dz}}}_i}{z_i}\right)$$ (6)

where each sector's productivity growth rate is weighted by the share of that sector in total GDP (e.g., Y_a/Y is the share of agricultural output in total output). The increase in output per worker due to changes in sectoral composition is given by

$${\frac{\mathit{\text{dz}}}{z}|}_{\mathit{\text{sectoral}}}=\left(\frac{z_a}{z}-\frac{z_i}{z}\right)d{\beta }_a$$ (7)

where we have used the fact that dβ_a = −dβ_i due to the adding up constraint that the share of the two sectors must sum to one. Table 4 gives the results of this decomposition (expanded to include services). The effect of growth in sectoral productivity is calculated by weighting each sector according to its share in GDP at the beginning of the period. The effect of changing sectoral employment shares is weighted using productivity levels at the beginning of the period. Using beginning-of-period weights, rather than continuously updating the weights as they change over time, means that our decomposition is an approximation and not an identity.⁷

Table 4. Productivity Growth: Shift-Share Analysis.

	India		China
	1970-80	1980-2000	1970-80	1980-2000
Growth Rate of Real GDP Per Worker (%), Annual Average	1.2	3.9	3.0	6.7
Decomposition:
Due to growth of productivity within sectors (with base year sector shares)	0.4	3.0	1.0	5.3
Due to change in sector shares (with base year productivity)	0.7	0.7	2.3	1.3

Our calculations suggest that over the period 1980 to 2000, most of the growth of GDP per capita in China and India was due to increased productivity within sectors (5.3 of the 8.1 percentage points in China, and 3.0 of the 3.6 percentage points in India). The results in Tables 1 and 4 also imply that increases in labor force participation, a rising share of working-age people in the total population, and movement from agriculture to industry and services accounts for 2.6 percentage points of growth in China (roughly one third of the observed growth rate), and a paltry 0.3 percentage points of growth in India.

This analysis is mechanical and the interpretation, which attributes the results to separate productivity and labor force effects, assumes that changing sectoral employment shares do not change productivity per worker (that is, we assume the marginal product of workers equals the average product). This is unlikely to be true. We also need to explain the growth in worker productivity itself.

We let z₀ be the initial level of income per worker and write the growth rate of income per worker ż as

$$\dot{z}=\lambda (z\ast -z_0)$$ (8)

where z* is the steady-state level of income per worker and λ is the speed of convergence (see Barro and Sala-I-Martin (1995) for a discussion of growth models of this type). The steady-state level of income per worker depends on many factors (such as capital stock and education levels per worker, and total factor productivity levels) that may affect labor productivity. We treat the inputs in z * that determine the steady-state level of income per worker in equation (8) as predetermined. They are fixed at the start of the period and affect subsequent growth in income per worker. This gives us their effect on income. It would be appealing to build a structural dynamic model where these factor inputs responded to lagged income, allowing us to study the process of cumulative causality; however, that is beyond the scope of this paper. Even in our framework we have the issue of identifying the direction of causality, from factor inputs to income, rather than vice versa. We discuss this issue in detail below when we come to estimation.

We now incorporate this into our model of growth in income per capita. Since y₀ = z₀ +ρ₀ + w₀ we have

$$\dot{y}=\lambda (z\ast +{\rho }_0+w_0-y_0)+\dot{\rho }+\dot{w}$$ (9)

In practice, we include in our empirical work only the effect of the ratio of working-age to total population and not the effect of the participation rate. Bloom and Canning (2003) investigate the effect of labor force participation on economic growth and find the estimated effect to be negative, in contrast to the unit positive accounting effect predicted by our growth equation. This appears to be attributable to the poor quality of the participation rate data as an indicator of labor supply. In rural areas, the household is often the production unit as well as the consumption unit and it is customary to count all adults as workers. This means that measured participation rates fall dramatically during urbanization because those who work at household tasks in urban areas (usually women) are not part of the official labor force. This measured fall in labor force participation does not reflect an actual fall in labor inputs and is not associated with a decline in output. We therefore exclude the labor participation rate from the empirical growth equation.

We include the effect of sectoral change in our model, simplifying by taking just two sectors, agriculture and non-agriculture (i.e., an amalgam of industry and services). The effect of sectoral change depends on the size of the flow and the differential productivity between the two sectors. We assume that the rate of sectoral change is an increasing function of the productivity differences between sectors (on which there is only scattered reporting in our data). We therefore proxy the size of the productivity gap by the size of the flow between sectors. That is we assume

$$\frac{d{\beta }_a}{{\beta }_a}=\left(\frac{z_a}{z}-\frac{z_i}{z}\right)$$ (10)

This means that the probability of a worker leaving the agriculture sector in a given time period depends on the gap in worker productivity between the agricultural sector and the industrial sector, which we assume is reflected by a gap in wages.

Given this assumption on migration between sectors, the contribution of sectoral change to economic growth, from equation (7), is:

$${\frac{\mathit{\text{dz}}}{z}|}_{\mathit{\text{sectoral}}}=\left(\frac{z_a}{z}-\frac{z_i}{z}\right)d{\beta }_a=\frac{d{\beta }_a}{{\beta }_a}d{\beta }_a$$ (11)

where dβ_a is the change in the share of workers in agriculture and dβ_a/β_a is the percentage change in the share (i.e., our proxy for the productivity gap between sectors). This means that very rapid sectoral change should be associated with large increases in productivity; we are moving workers from low-productivity sectors to high-productivity sectors, and the rapid movement implies that the productivity gap, and incentive to move between sectors, is large.⁸ This sectoral change effect can be seen as part of the catch-up towards steady state in which the (quality-adjusted) labor productivity in each sector will be equal. Taking the rest of the steady-state level of income per worker to be determined by a set of variables X yields

$$\dot{y}=\lambda (\beta X\ast +w_0-y_0)+\gamma s+\dot{w}$$ (12)

This final equation is similar in form to a standard empirical growth regression. It relates growth in output per capita to a range of variables, X, that influence the steady-state level of output per worker and the initial level of income per capita, y₀. However, several other terms appear. The log of the initial ratio of working-age to total population affects the steady-state level of income per capita, while the growth rate of the ratio of workers to total population affects the growth of income per capita directly. As a result of the identity used to derive this regression, the coefficients on these two terms are fixed; they represent what will happen if the extra labor supply per capita due to these age structure effects is fully employed and leads to no diminution in the level of inputs per worker given by X. Rather than impose coefficients on these demographic variables we prefer to estimate all the parameters of the above equation. This allows for the possibility that some of the enlarged labor force may not be gainfully employed, and that labor force growth may dilute non-labor inputs per worker. We also include our variable, s, which captures the effect of sectoral change on economic growth.

3. Data

We construct a panel of countries observed every five years from 1960 to 2000. Data on GDP per capita and the ratio of investment to GDP are obtained from Penn World Table Version 6.1 (updated by Heston, Summers, and Aten in 2002).⁹ Figure 1 shows how real income per capita grew in China and India between the early 1950s and 2000. Both countries experienced a take-off in growth beginning around 1980, with the rise in income being much more marked in China than in India. Income per capita in China was six times higher in 2000 than in 1955, while in India it was 3.2 times higher. Both cases show the remarkable effects that compound growth can have on the standard of living.

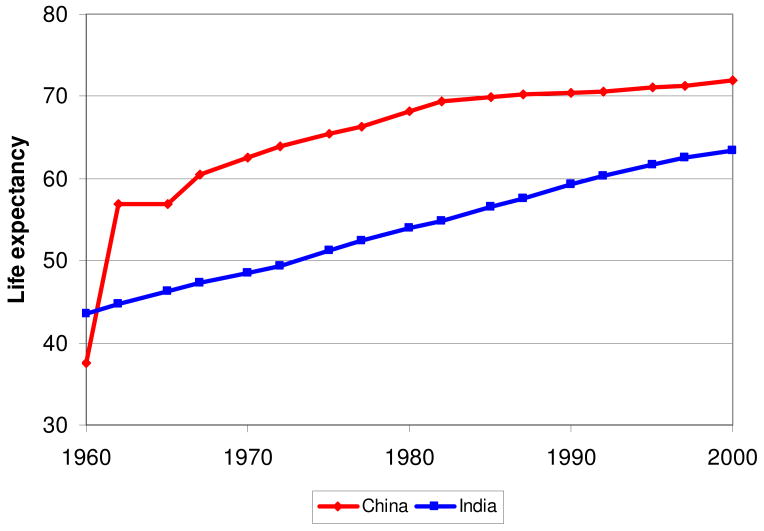
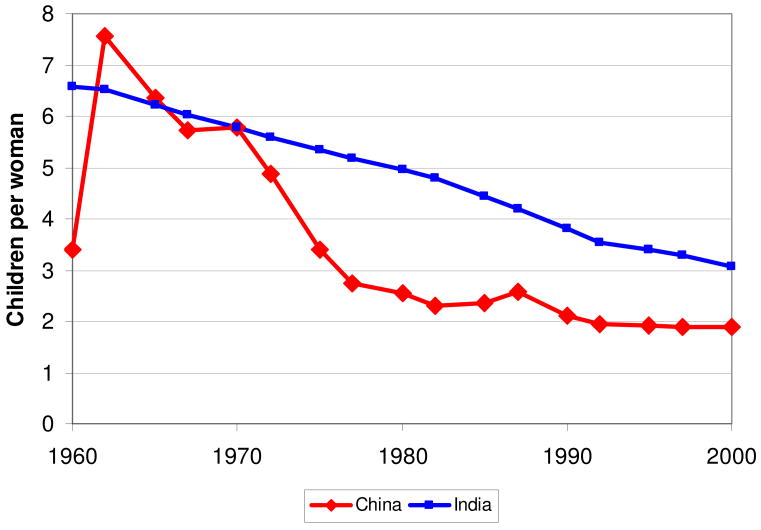
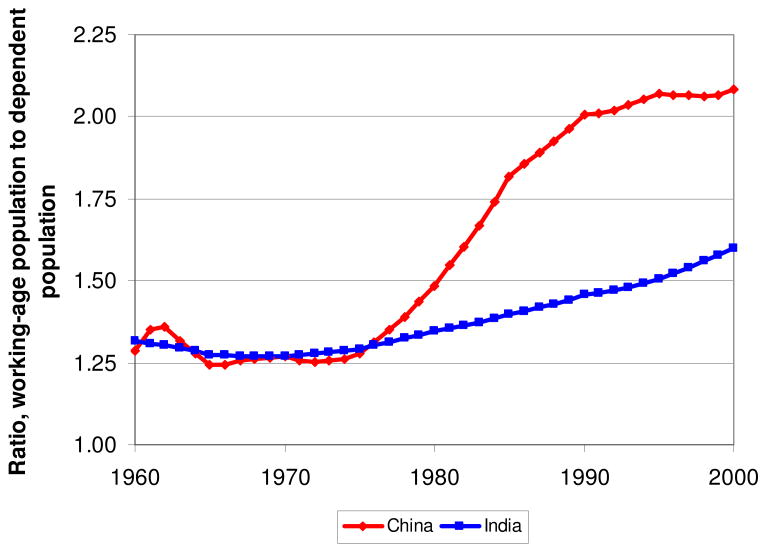
The data on working-age population (aged 15 to 64), total population, and life expectancy used in our regressions come from World Bank (2005). Figures 2, 3, and 4 show data on mortality, fertility, and age structure in China and India.

Figure 2. Life Expectancy.

Figure 3. Total Fertility Rate.

Figure 4. Ratio of Workers to Dependents.

Figure 2 shows the increasing life expectancy in China and India. Although there have been remarkable gains in both countries, the rapid improvement in population health in China between 1950 and 1975, which resulted largely from the government's focus on disease prevention and public health, is particularly striking. Figure 3 shows the total fertility rate in China and India. Both had total fertility rates of around 6 children per woman in the 1950s, and the fertility rate has fallen dramatically since then. The rate declined first in China, from over 6 children per woman in 1965 to around 2.5 children per woman in 1980.¹⁰

Figure 4 shows the effect of the gains in life expectancy and declines in fertility on the ratio of the working-age to the non-working-age populations. The rapid demographic transition in China resulted in a sharp rise in the ratio of workers to dependents, from under 1.5 in 1975 to around 2.5 today. However, this shift is temporary, and the ratio is projected to decline rapidly as the population ages. The growth in the ratio of workers to dependents in China will be of shorter duration and greater amplitude than it will be in India.

Education is measured by the average total years of schooling of the population aged 15 and over, taken from Barro and Lee (2000). The Barro and Lee (2000) data do not include data for China before 1975. We construct these data based on Lee (2001), which has data for average schooling between 1949 and 2000. The years of schooling in Lee (2001) are somewhat higher than those in Barro and Lee (2000) and we deflate the Lee (2001) data prior to 1975 by a fixed ratio so as to make the figures for 1975 agree.

Data on the share of labor in agriculture are from Food and Agriculture Organization (2005). In addition to these variables, we include geographic and institutional factors that may affect productivity. Data on the percentage of land area in the tropics come from Gallup, Sachs, and Mellinger (1999). Knack and Keefer (1995) report five indicators measuring institutional quality, corruption, rule of law, bureaucratic quality, expropriation risk, and repudiation of contracts by government. We use an updated version of this data set that contains data from 1982 through 1997¹¹. These variables are very slow moving, and we take the value in 1982 as fixed back to 1960. Not having pre-1982 data on institutional quality is an unfortunate limitation of our analysis, which may be particularly problematic for China, where reforms occurred from 1978 onwards. To some extent our “trade policy” variable (below), which shows improvement from 1975 onwards, may pick up these early institutional changes.

Through experimentation with different measures (including using an average of the five indicators) we found that bureaucratic quality, which measures the independence of the bureaucracy from political pressure and its ability to function continuously, seemed to be the most important in our growth regressions. The bureaucratic quality index, measured on a scale of 1 to 6, rose from 3 to 4 in India in the mid-1980s and has remained steady since, while in China it rose from 2.9 to 3 in the mid-1980s and to 3.7 in the mid-1990s (though it decreased after 1995). Although we rely on the bureaucratic quality measure, we consider this a proxy for the general institutional environment.

Reforms that have promoted trade have clearly contributed to the economic success of China and India. One measure of trade policy is the Sachs and Warner (1995) measure of openness, a dichotomous variable that takes the value 1 for open and 0 otherwise. Wacziarg and Welch (2003) update this measure to an annual series. The measure is problematic for the analysis of China and India. Both countries have openness measures of zero throughout the period we analyze, suggesting that this standard indicator is too crude to measure the marked changes in trade policy in these two countries.

We therefore construct our own measure of openness or trade policy. The ratio of imports and exports to GDP is often used as a measure of a country's openness. However, where rich economies tend to participate more in international trade, countries with large populations are more self-supporting and require less international trade. Both India and China are large countries that have large internal trade flows between regions and provinces that to some extent can act as a substitute for international trade. Since international trade clearly depends on the size of the country we propose the following model:

$$\text{Log trade}={\theta }_1\text{log population}+{\theta }_2\text{log GDP per capita}+{\theta }_3\text{trade policy}$$

Unfortunately we do not observe trade policy. We run a regression of log trade (“imports and exports divided by GDP” from Penn World Table 6.1) on log population and log GDP per capita using data for 1960 to 2000 (without time or country fixed effects).

$$\begin{array}{llll}\text{log trade}=& 5.869-0.200\text{log population}& +& 0.160\text{log GDP per capita}\\ & \left(0.170\right)\left(0.008\right)& & \left(0.014\right)\end{array}$$ (14)

R²= 0.417, N=1108, standard errors in parentheses.

We take the residual from this regression as a proxy for trade policy, the missing variable in the relationship. This new variable varies significantly over time for China and India, as shown in Figure 5 (each increase in the trade variable by 0.7 indicates a doubling of trade from its expected value given the regression above). We can regard our “trade policy” variable as a proxy for underlying economic policies that affect international trade. By construction, it is an imperfect measure; however, the use of such a proxy variable may help overcome what would otherwise be omitted variable bias and may improve the estimates on the other variables of interest (Krasker, Kuh, and Welsch 1983).

Figure 5. Trade (Residual from Expected Trade).

Trade policy may refer to more than simply tariffs and quotas. Rodrik (2006) argues that China's international trade has been driven more by industrial policy than market forces and as a result its export goods are more sophisticated, and more successful, than we would expect for a country at its level of development. Our “openness” or trade policy variable may reflect a range of policies both in internal markets and in relation to trade itself and is included in the specification as a proxy for a related range of country- and time-specific policy reforms.

4. Regression Results

We explain growth in per capita GDP in each five-year period for a panel of countries over the period 1960 to 2000. Causality is a serious issue in studies of economic growth. Because all of our explanatory variables are determined to some extent by income level, there is the potential for a strong feedback from growth to our right-hand side variables.

The key idea in our method of determining the direction of causality is that variables from before each five-year growth period can be treated as predetermined and exogenous. We treat as exogenous the variables measured at the start of, or before, the growth period being explained. For example, we assume that health in 1970 affects economic growth over the period 1970 to 1975. Although income does affect health in this assumption, it is income in 1970 and earlier that has an effect, and not future income growth. When we do have variables that are measured during the growth period (for example, the growth of the working-age share of the population) we instrument them with lagged values. This approach will be undermined if expectations of future growth affect current variables, or if there is a complex lag structure in the data so that growth shocks are correlated over time (in this case, our beginning-of-period variables may be picking up the effect of lagged economic growth on future growth). Easterly, Kremer, Pritchett, and Summers (1993) show that national growth rates are uncorrelated over time, which undermines the case for a complex lag structure. This still leaves the issue of expectations. This is a problem if lagged variables become correlated with the residual from our growth model via expectations. This requires that the agents in the model can forecast not only economic growth, but the residual in our model; that is, they have better forecasts than our model provides. While this may seem implausible, our results are conditional on the assumption that past factors determine future growth rather than vice versa.

Acemoglu and Johnson (2007) have argued that changes in life expectancy are not associated with contemporaneous changes in income. This is borne out in our data where the large increases in life expectancy in China took place between 1950 and 1980, with relatively small increases thereafter, while economic growth only took off after 1980. We do not argue that changes in life expectancy have a contemporaneous effect on economic growth. There is mounting evidence that childhood health has long-run effects on physical and cognitive development and on adult worker productivity (Bloom and Canning 2008). Life expectancy is, by construction, very sensitive to infant mortality rates, since a child death costs a great many future life-years, while an adult death costs relatively few. We use a lag structure where output per capita converges slowly to an equilibrium level that depends on the level of life expectancy. We expect changes in life expectancy, such as the rise seen in China up to 1980, to be associated with improvement in child health that slowly affect adult productivity as these children grow up and enter the labor force.

Acemoglu and Johnson (2007) use an instrument for changes in life expectancy in their growth model to control for possible endogenous health changes. Their instrument includes disease prevalence before the growth period occurs, which they argue is exogenous to future growth. We use a similar argument and take health status at the beginning of the growth interval to be exogenous.

The results are reported in Table 5. We first run a regression with all the independent variables being beginning-of-period values. The results of this ordinary least squares regression, reported in column 1, indicate that economies that have higher than expected levels of trade, a high investment rate, a high level of bureaucratic quality, high life expectancy, a high ratio of working-age to total population, and that are not located in the tropics and are initially poorer, tend to have higher rates of economic growth. The only surprising result in column 1 is that our schooling variable lacks significance; indeed, its estimate is of the wrong sign, given our strong prior evidence from microeconomic studies that schooling adds to worker productivity and wages. We experimented with a range of different schooling variables but found none that were robustly significant in our regressions. This lack of significance of schooling in growth regressions is quite common and may be due to measurement error in the schooling variables, as discussed by Krueger and Lindahl (2001) or may reflect a real lack of impact, due to schooling being low quality, rapidly rising education levels coupled with diminishing returns, or market failures in productively employing educated workers as suggested by Pritchett (2001).

Table 5. Estimates of the Determination of the Growth Rate of Income Per Capita.

	1 OLS	2 OLS	3 2SLS	4 2SLS
Constant	9.935** (2.503)	12.74** (2.54)	13.97** (2.80)	13.21** (2.84)
Log initial GDP per capita	-1.734** (0.307)	-1.689** (0.308)	-1.958** (0.364)	-1.900** (0.363)
Ratio of investment to GDP	0.054** (0.016)	0.045** (0.016)	0.035* (0.018)	0.029 (0.018)
Trade residual	0.932** (0.254)	0.718** (0.249)	0.817** (0.281)	0.777** (0.282)
Average years of schooling	-0.138 (0.074)	-0.047 (0.078)	-0.023 (0.092)	-0.025 (0.096)
Bureaucratic quality	0.211** (0.103)	0.206** (0.103)	0.252** (0.112)	0.053 (0.155)
Tropical area	-0.995** (0.335)	-0.925** (0.322)	-1.006** (0.338)	-0.983** (0.345)
Sectoral change		0.290** (0.074)	0.421** (0.121)	0.452** (0.130)
Life expectancy	0.125** (0.021)	0.078** (0.022)	0.092** (0.027)	0.106** (0.030)
Log share of working-age population	4.820** (1.935)	6.605** (1.961)	6.727** (2.145)	6.325** (2.214)
Growth of share of working-age population		0.869** (0.270)	0.563 (0.400)	-1.866 (1.444)
Growth of share of working age population times bureaucratic quality				0.694** (0.342)
Time dummies	Yes	Yes	Yes	Yes
N	661	647	571	571
R squared	0.271	0.608	0.282	0.258

Based on observations from five-year panel of countries, over the period 1960-2000. Time dummies included but not reported. Heteroskedasticity-consistent standard errors are reported in parentheses. Sectoral change, growth of share of working-age population, and the growth of share of working-age population times bureaucratic quality interactive term instrumented in the 2SLS regressions.

^**p < .01

^*p < .05

In column 2 we add the growth rate of the working-age share of the total population and our sectoral change variable. The coefficients on the other variables do not appear to change very much from those in column 1, and we find that both new regressors are highly significant. As expected, sectoral change has a positive effect on growth, as does the growth of the ratio of working-age to total population. However, these new variables are measured over the period in which the growth occurs, raising the possibility that growth may affect these variables. In order to control for the potential endogeneity of these two variables, we repeat the regression using instruments. For the growth in the share of the population that is working age, we use as instruments the lagged growth rates of total and working-age population and the beginning-of-period fertility rate. For the sectoral change variable we use as instruments the lagged sectoral change variable, the initial share of the workforce in agriculture, and the lagged growth rate of this “agriculture share.”

The result of using these instruments is shown in column 3. As before, rapid sectoral change seems to promote economic growth. However, the growth of the working-age share of the population is no longer significant once instrumented, though the initial ratio of working-age to total population still affects economic growth.

The rise in the working-age share, due to a fertility decline, will lead to a boom in income per capita simply due to the accounting effect of a smaller population with the same number of working-age people. This will increase income per capita mechanically, with no need to absorb or employ additional workers. However we find that when fertility declines and the working-age share rises, female labor market participation rates also tend to rise (e.g. Bloom and Canning, 2003, Bloom, Canning Fink and Finlay 2007b) This means that the economic boom will potentially be larger than that stemming from the pure accounting effect of fewer children and that there is a need for policies that allow the potential additional female workers to find employment.

A higher working-age population share therefore appears to represent a supply-side opportunity for a potential output boom. Whether this potential is realized depends on how the extra workers are employed. In column 4 of Table 5 we report estimates of the parameters of a regression model that is specified to include an interaction effect between the growth rate of the working-age population share and beginning-of-period bureaucratic quality. This tests whether the effect of an increasing working-age share depends on the institutional environment. This interactive term involves a contemporaneous growth rate and is instrumented with its lagged value.

We find that the interaction term has a significant and positive coefficient, while the coefficient on the growth of the working-age population share is negative, though not statistically significant. This indicates that the better its bureaucratic quality, the more a country will gain from growth of the working-age share of its population. There is a strong argument that with good governance, many inputs into the growth process, and not just age structure, become more effective (For example, Rajkumar and Swaroop, 2008, show that public sector spending is more effective with good governance). We focus on the age structure – governance interaction, although we note that others interactions are potentially important as well.

Our results suggest that a country with poor bureaucratic quality (a value of zero) will have no immediate gain from an increase in the share of working-age people in the population. In China and India, whose bureaucratic quality varies between 2.9 and 4 over the period, the estimated overall effect of growth in the working-age share (combining its direct effect with the interactive effect) is always positive. The effect on the rate of economic growth near the end of the period, when bureaucratic quality is highest, is close to one-for-one. In all countries the ratio of workers to total population has an effect on economic growth, indicating that the interaction with bureaucratic quality only influences the short-run response.¹²

It is possible to use specification 4 in Table 5 to generate fitted values for economic growth to compare with the actual growth experiences of China and India. However, this produces fitted values that do not track the actual outcomes at all well. We tried to determine why the fitted values were so poor using a number of different methods. Adding dummy variables for China and India did not improve the fit and the dummies were statistically insignificant; this indicated that the problem was not in fitting the average level of growth for these two countries. We ran regressions in which the period dummies (each five-year growth period has a dummy in the regressions in Table 5) applied to all countries except China and India, thereby treating these countries as if they were immune from worldwide growth shocks. The fitted values from this regression specification (from column 1 of Table 6, and also column 2) track the actual growth experiences of China and India better than the specification that treats China and India as being sensitive to global growth shocks.

Table 6. Estimates of the Determination of the Growth Rate of Income Per Capita.

	1 2SLS	2 2SLS	3 2SLS
Constant	14.26** (2.88)	13.13** (2.93)	13.28** (2.96)
Log initial GDP per capita	-1.931** (0.402)	-1.832** (0.401)	-1.714** (0.409)
Ratio of investment to GDP	0.034* (0.018)	0.027 (0.018)	0.024 (0.018)
Trade residual	0.822** (0.279)	0.804** (0.282)	0.808** (0.284)
Average years of schooling	-0.018 (0.092)	-0.019 (0.096)	0.171 [calibrated]
Bureaucratic quality	0.247** (0.112)	0.036 (0.156)	-0.012 (0.150)
Tropical area	-0.983** (0.346)	-0.922** (0.353)	-0.830** (0.360)
Sectoral change	0.418** (0.119)	0.468** (0.131)	0.543** (0.117)
Life expectancy	0.093** (0.027)	0.108** (0.030)	0.073** (0.028)
Log share of working-age population	6.575** (2.195)	5.789** (2.287)	4.868** (2.373)
Growth of share of working-age population	0.538 (0.376)	-2.149 (1.449)	-2.180 (1.455)
Growth of share of working age population times bureaucratic quality		0.735** (0.344)	0.763** (0.342)
Time dummies for countries other than China and India	Yes	Yes	Yes
N	571	571	571
R squared	0.287	0.258	0.247

Based on five-year panel of growth rates, over the period 1960-2000. Time dummies for countries other than China and India included but not reported. Heteroskedasticity-consistent standard errors are reported in parentheses. Sectoral change, growth of share of working-age population, and the growth of share of working age population times bureaucratic quality interactive term instrumented in the 2SLS regressions.

^**p < .01;

^*p < .05

The world time dummies predict high growth in the period 1960-1970 and then a slowdown after the oil shock in 1973 and again with the rise in oil prices and world interest rates after 1980. This is completely opposite of the pattern seen in India and China, whose economies stagnated at low levels before 1970 and then took off, especially after 1980. We leave open the question of why China and India do not seem to respond to worldwide shocks. It may be that India and China's large size makes them less affected by world shocks. Alternatively, we may have omitted variable bias in the form of growth-enhancing policy reforms after 1980 that spurred growth and counteracted negative world shocks.

The fitted values from these regressions seem plausible, but the negative coefficient on years of schooling, though not statistically significant, is puzzling. Although the model is not primarily designed to consider education, the likely failure to estimate this coefficient accurately may bias estimates of other coefficients in the regressions.

In addition, for decompositions, our negative schooling coefficient implies that the rising levels of education in China and India will have small negative effects on economic growth, which seems unreasonable. We address this issue by constraining the schooling coefficient based on independent literature-based estimates of its magnitude. We let β_s be the coefficient on years of schooling in the growth regression. Assuming that each year of schooling raises wages and income per capita by 10% in the steady state (which is roughly the average effect of schooling on wages found in a review of studies in many countries by Psacharopoulos and Patrinos (2004)), we have β_s = −0.1β_y where β_y is the coefficient on log initial income per capita in the growth equation. This equation implies that a one-year increase in schooling, coupled with a 10% rise in income per capita, leaves the growth rate unchanged. Estimating the regression while imposing this constraint on the coefficient on schooling gives the results found in column 3 of Table 6. The results are quite similar to those found in the preceding regressions, though the coefficient on life expectancy does fall slightly. This drop may be due to a causal link from higher prospective longevity and increased return to education at higher schooling levels and may point to a need for a structural model of growth in which the growth of factor inputs is itself modeled.

5. Explaining the Takeoff in Economic Growth in China and India

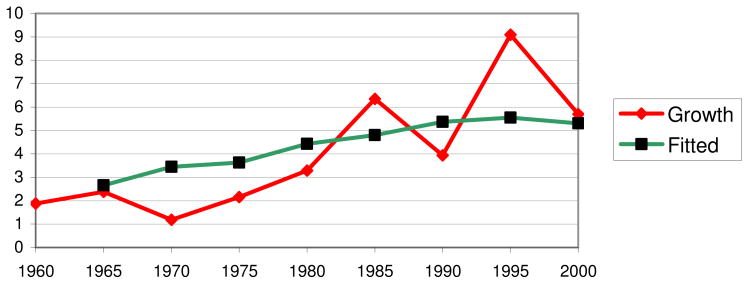
We now use the regression results shown in column 3 of Table 6 to see how well the model fits the experiences of China and India. Bloom, Canning, Fink, and Finlay (2007a) find that models of this type perform well with respect to the quality of out-of-sample forecasts. The fitted values assume that the trajectories for China and India depend on their country-specific values for the different factors posited to determine economic growth, using the worldwide regression weights (except for the period effects). Figure 6 shows the actual and fitted values for economic growth (in GDP per capita) in China from 1960 to 2000. Each observation gives the average annual growth rate over the previous five years (for example, the figure for 2000 is the average annual growth rate between 1995 and 2000).

Figure 6. China - Actual and Fitted Economic Growth.

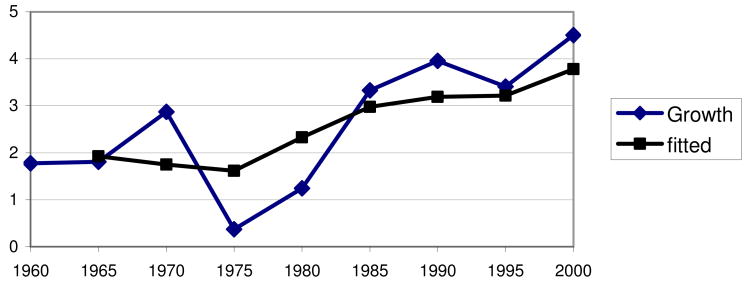
The fitted growth rates track the actual rates quite well. The fitted curve shows a steady rise in predicted economic growth between the periods 1960 to 1965 and 1985 to 1990, from around 2.5% a year to around 5.5% a year, with a leveling off thereafter. The fitted values do not capture the volatility in economic growth in China. They do capture the “takeoff”; however, it appears that they underestimate its pace somewhat. Figure 7 shows a similar graph for India. Note the difference in scale in the axis measuring economic growth; the “takeoff” in India has been much more modest. The fitted values predict growth being just under 2% a year in the 1960s and early 1970s and then rising steadily to over 3.5 % a year by the period 1995 to 2000. The fitted values for India also fit the actual behavior quite well, though they do not match the observed volatility in the actual growth rate and, as with the values for China, they underestimate the pace of the takeoff.

Figure 7. India - Actual and Fitted Economic Growth.

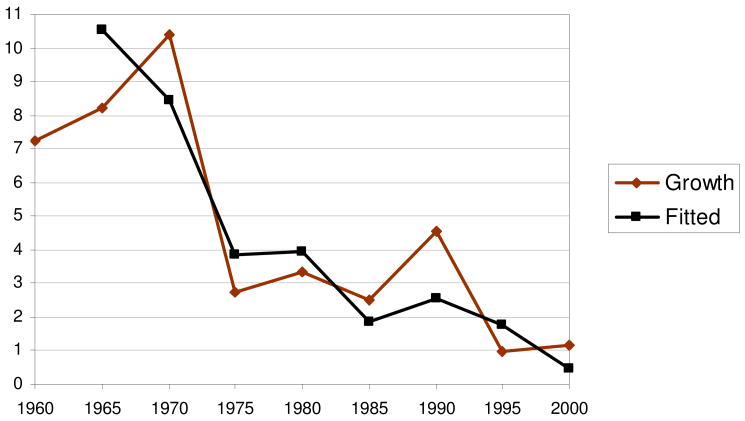
In principle, we can compare the fitted values with the actual growth outcomes in any country for which we have data. In most cases we have examined the fitted and actual values and find they are in reasonably close conformance. For example, the period since 1960 has seen a rapid decline in the growth rate in Japan. As shown in Figure 8, the fitted values of our model capture this decline quite well. Nevertheless, the fitted values are not precise. The R-squared of our regression is low and the 95% confidence interval for our fitted values is ± 5.3 percentage points, a very wide range, which indicates that there will likely be large deviations from the expected values.

Figure 8. Japan - Actual and Fitted Economic Growth.

We now address the issue of why the predicted growth rates in China and India rose so much over the period. We take the change in the predicted growth rate between the period 1965 to 1970 and the period 1995 to 2000 and decompose the sources of this change. The predicted growth rate for the period 1965-70 is based on coefficients from Table 6 column 3. We multiply each variable (usually measured in 1965) by its coefficient to get the fitted value for growth over 1965-70. We do the same for growth over the period 1995-2000. We then decompose the change in the predicted growth rate into the change in each of the explanatory variables times that coefficient on that variable. For interactive terms we apply the change times the coefficient, holding the other variable in the interaction constant. The contribution from each variable to growth is its own effect plus any interaction effects. The number reported for each variable is therefore how much predicted growth would have changed, given the change in the variable, holding all other variables constant.

We exclude the growth period 1960-1965 from the simulations because of the extremely low values of fertility and life expectancy we have for China in 1960 associated with the famine during 1959-61 at the time of the “Great Leap Forward”.¹³ These low values are not representative of the fertility rates and life expectancy from 1962 onwards, as can be seen in Figures 2 and 3.

The results are reported in Table 7. Predicted growth in China rose by 2.7 percentage points over the period, and predicted growth in India rose by 1.9 percentage points. In both cases a major source of this rise in predicted growth rates is the large rise in life expectancy. The second principal source of the increase in the growth rate has been the increased openness of both economies, as measured by our trade variable. We regard this as a proxy for the widespread reforms in China and India that increased the role of markets and incentives. Although, this may be an imperfect proxy, the timing of the growth spurts, shown in figure 6 and figure 7, does seem to coincide with our knowledge of specific reforms, particularly in China.

Table 7. Sources of the Increase in Predicted Growth Rates in China and India.

	China	India
Increase in Predicted Annual Average Percentage Growth in GDP per Capita between 1965-70 and 1995-2000	1.9	2.0
Effect of higher life expectancy	1.0	1.1
Effect of trade policy	1.3	0.9
Effect of increase in working-age share	1.0	0.7
Effect of higher levels of schooling	0.5	0.5
Effect of improved bureaucratic quality	0.2	0.2
Effect of industrialization	0.0	0.1
Effect of investment rate	0.3	0.0
Effect of higher level of income per capita	-2.2	-1.3

The next major contributing factor has been the rise in the level and growth rate of the working-age share of the population. One issue we encountered concerns the attribution of the change in growth to a rise in the value of the interaction term between bureaucratic quality and growth in the working-age share. We address this by calculating the effect of changes in each variable separately, while holding the level of the other at its 1995 value. The rise in bureaucratic quality is estimated to have a small positive effect on growth rates.

Sectoral change in the form of industrialization appears to have had surprisingly little effect on the change in economic growth in either country. Although there has been a movement out of agriculture and into industry, the pace of this movement has been relatively modest in China and India as compared to the pace in Japan or South Korea during their growth spurts. Similarly, the investment rate seems to have had little effect in either country. Investment rates for both countries were almost exactly the same in 1960 and 1995 (which in our model affects growth in the periods from 1960 to 1965 and from 1995 to 2000) making this an improbable source of change in growth rates.

The one factor mitigating China and India's rates of economic growth has been the effect of rising income levels. The model has the self-limiting property that anything that causes economic growth in one period tends to raise the initial income in the following period, leading to a moderation of future growth rates. The rapid increases in income levels between 1960 and 1995, particularly in China, are estimated to have had a large dampening effect on the growth rate. An extreme version of this is seen in Figure 8, where growth in Japan slowed dramatically over the period due mainly to the end of a phase of rapid industrialization and demographic change, and to the effect of rising income levels.

6. The Value of Health Gains

Our analysis of economic growth treats health as an input into the production process that raises income levels. This instrumentalist approach does not include the direct welfare gains that come from improved health. The large gains in life expectancy shown in Figure 2 suggest a large direct benefit of increased longevity to people in China and India. How important has the gain in health been for welfare? Becker, Philipson, and Soares (2005) argue that the welfare gains from improved health in developing countries have been large, and in some cases have outstripped the gains from rising incomes. We apply their methodology to an analysis of China and India.

Consider a country in which both income and health improve over time. We can measure the value of health gains over the period by the amount of extra income that would be required to produce the same welfare level at the end of the period if health were to be held constant at its initial level. Becker, Philipson, and Soares (2005) make a number of simplifying assumptions related to income and consumption over the life cycle; they also assume that utility in each period depends on consumption if an individual is alive and is zero if dead. A key issue in this formulation is the value of life, which is addressed by calibrating the parameters of the utility function from value of life studies. Lifetime welfare is the sum of the flow of utility in each period, where future utility is discounted at 3% per year due to time preference and is weighted by the probability of surviving to that age. The discounting implies that increasing survival probabilities at young ages tends to be more valuable than increasing survival probabilities at older ages.

When health improves, survival probabilities rise and welfare goes up. We can ask how much additional increase in annual income, with health held constant, would have given the same level of welfare at the end of the period as the observed rise in income and health. We take an ex ante perspective, and ask the question: which society would you rather be born into, assuming you undergo the current age-specific mortality rates and receive current average annual income throughout your life? We also assume that the instantaneous utility function is constant over time, and we discount future utility. Allowing for utility functions to vary with age and for social spillover effects on the welfare of family members might change our calculations dramatically.

We use the Becker, Philipson, and Soares (2005) methodology and their calibrated parameter values to ascribe monetary values to the health improvements in China and India over the last 40 years. To do this, we need life tables that show the probability of survival to each age at the beginning and at the end of the period. For China these survival probabilities are calculated from the mortality tables given in Banister and Hill (2004); for India, we use abridged life tables from the Registrar General of India.

The results of our calculations are shown in Table 8. Most of the gains in life expectancy in China came in the 1950s and 1960s; unfortunately, we do not have life tables before 1973. Although the period since 1973, particularly after 1980, has shown rapid economic growth, health improvements over this period have been modest. We calculate that although real income per capita rose by $2540 in China between 1980 and 2000, the value of the gain in health over the same period was only $202 (that is, an extra income of $202 per annum would give the same welfare increase in 2000 as the gain in health between 1980 and 2000).

Table 8. Value of Increases in GDP per Capita, Life Expectancy, and Full Income.

	GDP per Capita	Life Expectancy	Full Income Gain
China
1973	$870	61.4 years
1982	$1210	68.8 years
2000	$3750	71.1 years
Value of increase 1973-2000	$2880	$704	$3584
Value of increase 1982-2000	$2540	$202	$2742
India
1965	$927	46.8 years
1980	$1160	54.7 years
2000	$2480	61.8 years
Value of increase 1965-2000	$1553	$1224	$2777
Value of increase 1980-2000	$1320	$574	$1894

The value of life expectancy increase is the increase in annual income that would have given an equivalent welfare gain with a fixed level of life expectancy (the equivalent variation).

In contrast, there have been remarkable continuous health improvements in India over the period 1965 to 2000. The results of Table 8 suggest that over this period the value of the health gains in India, at $1224, rivaled the value of the income gains, at $1553. The final column in Table 8 gives the increase in full income, adding the value of the health gains to the usual income gains. This is the increase in annual monetary income that would have given the same increase in welfare as observed, if health had not improved over the period.

India lags China in terms of both income per capita and life expectancy. Over the period 1980 to 2000, income in China increased about twice as much as it did in India. However, the relative stagnation of health in China since 1980 and the rapid improvements in life expectancy in India mean that the increase in full income, valuing health as well as consumption, has been more similar in the two countries. Thus, the takeoffs in social welfare are less divergent between China and India than are their corresponding takeoffs in income growth.

7. Conclusion

A model explaining economic growth in a panel of countries over the period 1960 to 2000 tracks some key features of the economic growth spurts in China and India since 1980. The reasons behind the growth spurts as shown in the model are primarily a rise in life expectancy, a rise in trade or openness of the economy, and an increasing share of working-age members among the total population.

Our estimates yield two curious findings. First, we find the model provides a better fit of the growth experience of China and India if we exclude the effect of worldwide shocks; purely domestic factors explain their growth rates much better. Second, we fail to find a positive effect of education on economic growth. Because this failure is likely due to measurement error in our education variable, we impose a calibrated coefficient on education to contain the diffusion of bias among other coefficients.

The economic growth seen in China and India can be considered as rapid adjustment to new, higher, steady-state income levels. Our model predicts slower economic growth in China after 2010, based on projections of modest further increases in life expectancy and a rising dependency rate as the population ages. By contrast, we expect to see somewhat higher growth rates in India over the next 30 years as the effects of the fertility decline and of the “bulge” population cohort create a rise in the working-age share of the total population. Predictions based on these demographic changes seem reasonably secure. There appears to be further potential for a rise in growth through improvements in institutions and policies, but this is more uncertain. Full-income accounting suggests that the picture of stagnation until 1980 followed by takeoff in development may be misleading. India saw steady improvements in health earlier than 1980 and China saw rapid health gains from 1950 to 1970. The full-income approach suggests that welfare was rising even before 1980 and that, particularly in China, 1980 marked a shift in the composition of full-income growth – from health improvements to rising consumption levels – rather than a simple takeoff following a period of stagnation. While we examine improvements in average income levels and life expectancy we do not examine the issue of increasing levels of inequality both across regions and households in India and China, nor do we consider the widening of the urban-rural divide, both of which may reduce welfare benefits of the growth we observe.