Signal Amplification in a Microchannel from Redox Cycling with Varied Electroactive Configurations of an Individually-Addressable Microband Electrode Array

Abstract

Amperometric detection at microelectrodes in lab-on-a-chip (LOAC) devices lose advantages in signal-to-background ratio, reduced ohmic iR drop, and steady-state signal when volumes are so small that diffusion fields reach the walls before flux becomes fully radial. Redox-cycling of electroactive species between multiple, closely-spaced microelectrodes offsets that limitation and provides amplification capabilities. A device that integrates a microchannel with an individually-addressable microband electrode array has been used to study effects of signal amplification due to redox cycling in a confined, static solution with different configurations and numbers of active generators and collectors. The microfabricated device consists of a 22-μm high, 600-μm wide microchannel containing an array of 50-μm wide, 600-μm long gold microbands, separated by 25-μm gaps, interspersed with an 800-μm-wide counter electrode and 400-μm wide passive conductor, with a distant but on-chip 400-μm wide pseudoreference electrode. Investigations involve solutions of potassium chloride electrolyte containing potassium ferrocyanide. Amplification factors were as high as 7.60, even with these microelectrodes of fairly large dimensions (which are generally less expensive, easier, and more reproducible to fabricate), because of the significant role that passive and active (instrumentally induced) redox-cycling plays in confined volumes of enclosed microchannels. The studies are useful in optimizing designs for LOAC-devices.

INTRODUCTION

Increasing interest in miniaturized analysis systems (i.e. lab-on-a-chip, LOAC) involving small-volume samples drives development of methods with signal amplification suitable for detection of low concentrations or low absolute quantities of analyte. Electrochemical detection at microelectrodes in LOACs can address the need. Advantages of individual microelectrodes include high signal (faradaic)-to-background (charging) ratio, steady-state current on a short time scale, and low ohmic iR drop (due to low current). However, the limited accessible volume (such as in a microchannel with a dimension less than the smallest dimension of the electrodes) can offset those benefits because electroactive analytes deplete before radial diffusion and steady state current occur. If faster transient analysis or larger electrode areas are employed to achieve higher signals, electrochemical behavior reaches the macroelectrode regime, also eliminating benefits of microelectrode behavior. Redox cycling of reversible electroactive species between closely spaced electrodes overcomes the confinement problem and leads to amplification. Here, a device of individually-addressable microelectrodes in an array within a microchannel has allowed us to explore the important, but little addressed, relationships of generation and collection involved in redox cycling in a restricted volume.

A device employing microelectrochemical detection and microfluidics was designed. The goal was to develop LOAC heterogeneous assays (e.g. immunoassays, DNA-hybridization assays, and competitive binding assays). The first step is to evaluate electrochemical response as a function of electrode configuration. A general array design was fabricated to explore different electrode configurations on one chip. This design has multiple, microband electrodes, and larger electrodes that can serve as on-chip pseudoreference or counter electrodes, each being individually addressable. Thus, selected electrodes can be activated by setting a specific potential relative to a pseudoreference electrode, or left “passive” at open circuit (at truly floating potentials without being shorted to other electrodes). This design is evaluated in static solution within the closed microchannel. It is also evaluated open, in bulk solution having relevance to traditional well-based assays.

A possible final device involves the microelectrode array on the floor of the microchannel and a removable lid. This may serve as a modular site for immobilizing the assay components. By keeping the height of the channel shallow, two things happen. First, the volume of solution between the lid and the microelectrode array is small. Thus, reporter molecules released/generated at the lid can stay concentrated, and therefore provide a high electrochemical signal. Second, the close proximity of the electrode array to the assay surface allows detection on a relatively fast timescale.¹ In this configuration, reporter molecules do not have far to diffuse nor time to dilute. When microelectrodes in the array undergo redox cycling, signal amplification is possible. A benefit of confined volume is that narrow gaps between microelectrodes are not necessary for redox cycling. Thus, costs for fabricating electrodes with larger feature sizes can be significantly lowered, and the reproducibility and yield improved. Adaptors at the end of the microchannel allow interfacing with a syringe for convenient exchange of reagent and wash solutions. In the future, they will connect to a microfluidic pump control system that stops flow for incubation and detection steps during the assay.

In redox cycling, or generation-collection, a reversible electroactive species undergoes oxidation or reduction at a generator electrode, diffuses to a neighboring collector electrode where it undergoes the reverse reaction, and diffuses back to the generator, repeating the cycle. This technique has been used with rotating ring disk electrodes as well as with paired and interdigitated electrode arrays (IDAs).^2–7 It has recently been applied to detection of biomolecules at band electrodes in micro- and nanofluidic channels and of catechols at a ring-shaped array in capillary electrophoresis (CE-EC).^8–12 Other work has shown the utility of redox cycling for signal enhancement of electrochemical detection of DNA assays and immunoassays performed in microfluidic devices.^13–16

Only recently have the effects of incorporating microelectrodes into microchannels been examined. Girault and coworkers established with numerical simulations and experiments that electrochemical behavior of microband electrodes incorporated into a microchannel depends on scan rate (when voltammetry is used) as well as channel dimensions and geometry.¹⁷ As experimental timescale increases (i.e decreasing scan rate), the diffusion layer undergoes a transition. At early times, when the diffusion layer is small in comparison to the electrode width, the diffusion field is planar and semi-infinite. At longer times it becomes hemicylindrical, centered at the electrode, reaching a pseudo-steady state. However, if the channel height is shorter than the width of the band electrode, a full hemicylindrical diffusion field is not achieved before redox species above the electrode are exhausted when the front reaches the microchannel’s lid. Thin-layer behavior is never observed, however, because a semi-infinite diffusion front proceeds laterally on either side of the band along the length of the microchannel and perpendicular to the electrode face.

Amatore and coworkers expanded on the work of Girault and coworkers and used redox cycling between Nafion^®-modified dual microelectrodes to estimate changes in film thickness, as would occur with swelling of a polymer film.^18–20 However, redox cycling is more commonly used for signal enhancement at closely spaced microelectrodes.^{5–7, 9–11, 13, 21} Digital simulations²² have shown that, without redox cycling, closely spaced electrodes exhibit a decrease in current at timescales when their diffusion layers overlap, defined as the shielding factor, S_F. Redox cycling between closely spaced electrodes not only causes signal amplification but also decreases or eliminates S_F.

Lateral diffusion in thin films and confined microchannel solutions makes effects of S_F even more pronounced, where redox cycling may be especially advantageous. The pioneering work of Niwa et al. used redox cycling at a comb-type IDA to enhance dopamine signal in high performance liquid chromatography (HPLC-EC) and shows that signal amplification increases with decreasing flow rate and is most effective in stationary solution.^{23, 24} However, much of the subsequent research—fundamental and applied—on redox cycling at electrode arrays in small-volume systems has been performed with a flowing solution.^{4, 10, 11, 25–28}

There exists, then, a fundamental understanding of the effects of redox cycling in closed, small-volume systems⁸, as well as the effects of gap and collector electrode width, electrode geometry³, and solution flow^{10, 11, 23–26} on signal enhancement. However, much of the fundamental work used a single generator and only one or two flanking collector electrodes, or comb-type IDAs which preclude studies on the effects of different numbers of generators and collectors. Additionally, these studies were performed using external reference electrodes, and often, external counter electrodes, and are unlike many small-volume microfluidic applications in which internal (self-contained) counter electrodes may make a significant contribution to signal amplification by redox cycling.²³ Fundamental and theoretical studies with flowing solution are informative for redox cycling in applications such as HPLC-EC and CE-EC. However, flow can be disadvantageous for detection of immunoassays as well as catch-and-release assays and other systems in which electroactive reporters are produced in situ, as quiescent solution permits concentration of the analyte within a localized solution volume while flow causes dilution.

Thus, the work described here employs the individually addressable and fully self-contained microelectrode array to study redox cycling in stationary solution, and compares the electrochemical responses in the closed microchannel to those when the microchannel is open to bulk solution. The microelectrodes were shorted together in different combinations to study effects of different numbers and configurations of generator and collector electrodes on signal amplification. Ferrocyanide was used as a model analyte for these studies because of its well-behaved, reversible, one-electron electrochemistry.

EXPERIMENTAL

Chemicals and materials

All chemicals and materials were reagent grade and used as received, unless otherwise indicated. Oxidized silicon wafers (5″ diameter, 1-0-0 orientation, 600–650 μm thick with 2-μm thermal oxide) were purchased from Silicon Quest International (Santa Clara, CA). Chromium-plated tungsten rods from Kurt Lesker (Clairton, PA) and gold cut from Canadian Gold Maple Leaf coin (99.999%) were used for thermal evaporation. Potassium chloride, triethyl amine, ethyl acetate, and acetone were purchased from EMD Biosciences (Gibbstown, NJ). Potassium ferrocyanide was obtained from J.T. Baker (Phillipsburg, NJ). Tween-20 for molecular biology use was purchased from Sigma-Aldrich (St. Louis, MO). Silver wire (99.9%) for reference electrodes and platinum wire (99.95%) for counter electrodes were obtained from Alfa Aesar (Ward Hill, MA). DuPont Electronic Technologies (Circleville, OH) supplied the Kapton^™ 120FN616 film. Aqueous solutions were prepared in doubly deionized 18-MΩ resistivity water (Ricca Chemical Company, Arlington, TX).

Microelectrode array/microchannel device design

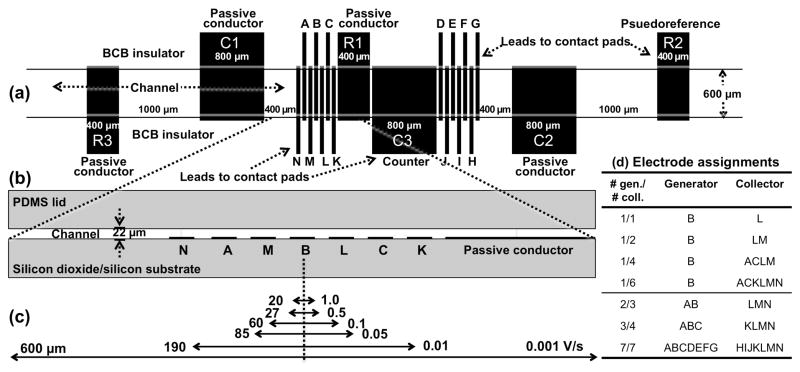
Figure 1 shows the relative placement and dimensions of the microchannel, the 20 gold electrodes and gaps between them, and the electrode-labeling scheme. A photograph of the entire 4.0 cm × 2.5 cm microelectrode array/microchannel chip (Figure S-1) and microfabrication details are provided in Supporting Information. The device consists of gold electrodes (each ~108 nm high, consisting of a 100. nm-thick gold layer, coated over a 7.5 nm chromium adhesion layer) on a silicon dioxide/silicon substrate. Fourteen of them are 50-μm wide microbands, separated by 25-μm gaps. Three are 800-μm-wide (labeled C1, C2, and C3) and another three are 400-μm wide (labeled R1, R2, and R3, the distant one, R2, serves as a pseudoreference electrode). Gaps between R1, C3 and the neighboring microbands are all 25 μm. The gaps between the two outermost larger conductors on each end (C1 and R3, and C2 and R2) are 1000-μm. The gaps between C1 and its closest microband as well as that between C2 and its closest microband are 400 μm. Each electrode is individually-addressable through contact pads on the edges of the device. Two sets of microband array electrodes are separated by a 800-μm counter electrode (C3, with an area that exceeds the combined areas of the 14 microbands) and a 400-μm passive conductor (R1).

Figure 1.

Design, dimensions, and labeling schemes of elements on the microelectrode array/channel chip. (a) Top-down schematic shows electrode-containing region of the chip. Active electrode lengths and channel width are defined by the 600-μm wide opening in the overlying BCB insulator layer and indicated by the two, thin horizontal lines. Microband array electrodes, A through N, are each 50-μm wide. All unlabeled gaps are 25-μm wide. (b) Lengthwise, cross-section schematic shows an expanded side-view region of the array with a 22-μm high microchannel when the PDMS lid is on. (c) Estimated diffusion lengths, δ (μm), measured specifically here from the “B” electrode for different timescales (represented by different scan rates, V/s). (d) Table lists generator and collector electrodes used during redox cycling experiments. All features within each image are drawn to-scale with the exception of the electrode heights in part (b) (100. nm gold plus a 7.5 nm chromium adhesion layer), which would otherwise be too thin to see in the diagram, and the thickness of the substrate and PDMS lid in part (b).

The electrode lengths are defined by the width (~600 μm) of the microchannel patterned in an overlying, insulating layer of bis-benzocyclobutene (BCB). BCB isolates the leads from solution, but is removed over contact pads so they are accessible with an edge connector. The 19-mm long rectangular microchannel ends in 2-mm diameter circles. The 22-μm microchannel height is determined by the thickness of the BCB and a poly(dimethylsiloxane) (PDMS) free-standing film is used as a lid. (The circles interface to holes punched in the PDMS through which solution is introduced and removed.)

Physical characterization of microchannel and microelectrodes

Microchannel dimensions were measured by contact profilometry using a Dektak 3030 (Veeco Instruments, Inc., Plainview, NY) at multiple points along its length. The microchannel’s width is 589.7±7.5 μm (N = 3), depth is 22.02±3.7 μm (N = 3), and volume is calculated to be 0.32±0.1 μL. Using microscopy on a single device, the microband electrodes were found to have a width of 47.6±1.4 μm (N = 14) and be separated by gaps of 25.1±1.9 μm (N = 12). The three large electrodes are 797±2.8 μm wide (N = 3) and the three intermediate electrodes are 394.5±5.6 μm wide (N = 3).

Preparation of PDMS lids

PDMS films were prepared by mixing Sylgard 184 elastomer and curing agent (Dow Corning, Midland, MI) in a 10:1 ratio by mass according to the manufacturer’s instructions. The mixture was degassed in a vacuum desiccator for 30–45 min until no bubbles remained, spin-coated onto a silicon wafer for 80 s at 500 rpm, and cured for 2 h at 85 °C. Cured PDMS was cut into pieces ~1.5 by ~2.5 cm. Unreacted oligomer was extracted by washing PDMS pieces for 2 h in triethyl amine, ethyl acetate, and acetone as described by Vickers et al.²⁹.

A hydrophilic region of the PDMS “lid” was created so that aqueous solution in the microchannel would wet its surface. Solvent-extracted PDMS was placed between two layers of Kapton^™ film. The top layer was cut with a razor blade to form a 15 mm-long × 0.5 mm-wide strip and a 2 mm-diameter hole was punched through both the Kapton^™ and PDMS at the ends of the strip. The bottom Kapton^™ layer supported the PDMS. The three-layer assembly was exposed to an oxygen plasma at 110 mtorr for 60 s (6.8 W applied to RF coil) using a Harrick PD-32G Plasma Cleaner (Harrick Plasma, Ithaca, NY) to generate a hydrophilic surface on the exposed strip of PDMS. After removing the Kapton^™ layers, the punched circles in the PDMS (hydrophilic strip facing the electrode chip) were aligned with the circular counterparts in the BCB pattern, followed by pressing the PDMS onto the electrode device, forming the lid (Figure S-2 in Supporting Information).

Filling the microchannel device

The hydrophilic strip in the PDMS lid allowed the 22-μm high microchannel to be filled by capillary action alone or pulled through using a vacuum on one end (a disposable glass pipette connected by tubing to a vacuum pump). This was possible despite the presence of hydrophobic BCB walls and without the need for a surfactant which increases occurrence of leaks at the PDMS/BCB interface. (Filling of a 7-μm high microchannel that had been fabricated was unsuccessful.)

Electrochemical characterization and redox cycling

Electrochemical experiments were performed using a CHI 760B bipotentiostat equipped with picoamp booster and Faraday cage (CH Instruments, Austin, TX). Two edge connectors (Digikey) were slipped over the sides of the microelectrode array chip, one for each set of contact pads, allowing connections to individual electrodes. “Open-channel” experiments, in which the electrode array chip was used without a PDMS lid (Figure 2a), were performed either in an “external” set-up with Ag/AgCl (saturated KCl) reference and Pt wire counter electrodes for characterization of the microband electrodes, or in an “internal” set-up using as the pseudoreference electrode the 400-μm wide on-chip conductor (R2) most distant from the microband electrodes (to maximize its stability) and the internal counter electrode (C3) nearest to the microband electrodes (to minimize voltage drops from uncompensated resistance, which is a problem with solutions having narrow cross sections⁴). “Closed-channel” experiments, in which a PDMS lid was used to confine solution to the microchannel (Figure 2(b)), were always performed using an internal electrode set-up.

Figure 2.

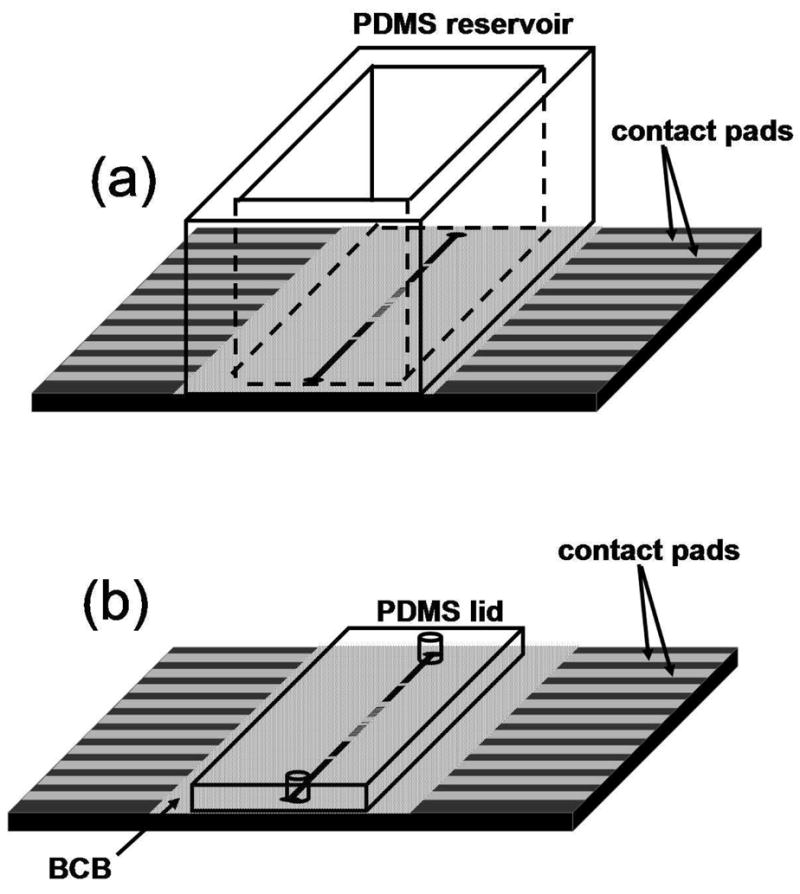
Schematic showing (a) open and (b) closed microchannel set-ups. In the open microchannel set-up, a PDMS reservoir is used to contain solution. In the closed microchannel set-up, a PDMS lid confines solution to the BCB microchannel. Holes through the PDMS lid facilitate filling and emptying the microchannel.

Initial characterization of electrodes was performed in an open microchannel by cyclic voltammetry (CV) at 0.050 V/s in a solution of 0.40 mM potassium ferrocyanide and 0.1 M KCl and showed high reproducibility from electrode to electrode within the device. For a given electrode width, the reproducibility of the background-subtracted, forward peak current was: microband electrodes 3.3% RSD (N = 14), ~800-μm wide electrodes 1.9% RSD (N = 3), ~400-μm wide electrodes 3.0% RSD (N = 3).

Redox cycling experiments used an internal electrode set-up with the microchannel both closed and open. In CV studies, the generator electrode was swept from −0.1 V to +0.3 V vs internal gold pseudoreference (R2), while the collector electrode was held at −0.1 V vs R2. Redox cycling experiments were performed at least in triplicate on the same device, using fresh solution each time so that compositional changes from electrochemistry in the confined volume did not carry over from one experiment to another.

For quantification of cyclic voltammetric data, when the system exhibited steady-state behavior (sigmoidally-shaped voltammograms), the plateau faradaic current in the forward sweep was measured at +0.200 V vs. E_1/2. In all other cases, the forward faradaic peak current was used. Faradaic peak current is defined here as the measured difference between the observed peak current and the background current measured at ~−0.1 V vs. the reference electrode. Charging current was essentially flat and was experimentally determined (N = 3) to comprise, at most, 4.8% of faradaic current for a single band electrode in the closed microchannel at 1 V/s and, on average, < 1.6% of faradaic current for any number of generator electrodes in the closed or open microchannel at all scan rates. Because we have subtracted charging current from the generator CV response in our analyses, the amplification factors that we report only reflect enhancements in faradaic current. Chronoamperometry (CA) data were quantified by averaging pseudo-steady state current from 9.0 s to 30.0 s.

Collection efficiency, C_e, is the ratio of the faradaic current at the collector electrode(s) to that at the generator electrode(s) obtained in a redox cycling experiment. The amplification factor, A_f, is the ratio of the faradaic current at the generator electrode(s) obtained when the collectors are on (during redox cycling) to that when the collectors are off (no redox cycling). Smaller generator currents and larger collection efficiencies lead to larger A_f values (as is observed for closed-channel studies). However, a large A_f value does not necessarily mean that the generator signal is large. Thus, absolute current values are provided in Supporting Information.

For clarity, the phrase “larger current magnitude” refers to a larger absolute value, as all anodic current values reported here are negative, in the standard sign convention. Diffusion length, δ, was estimated using the Einstein equation, δ = (2Dt)^1/2, where D is the diffusion coefficient and t is the time (defined in CV as the time it takes to scan from E_1/2 to the switching potential).

RESULTS AND DISCUSSION

Comparison of generator current in the open and closed microchannel in the absence of active redox cycling at microband electrodes

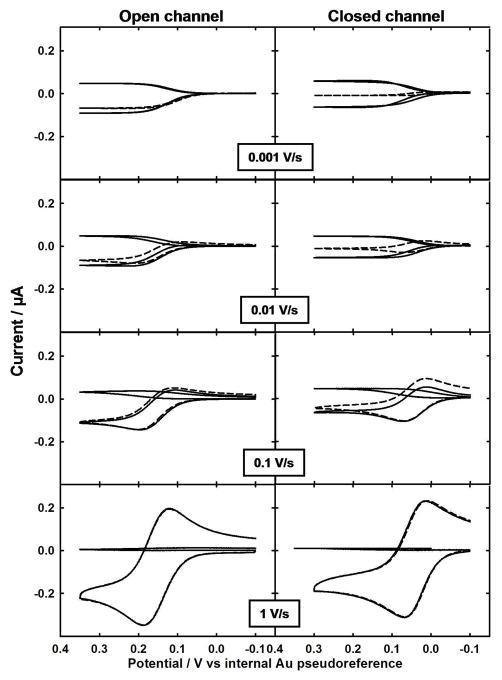
Confinement of solution to a thin layer over microelectrodes can lead to a change in diffusion profile and a corresponding change in current, compared to open, semi-infinite conditions. To investigate this phenomenon, studies were performed in closed and open microchannel configurations and at a range of scan rates for one (1g), two (2g), three (3g), and seven (7g) generator electrodes shorted together (without active redox cycling, 0 c). Figure 3 shows representative CV responses for the 7g/0c case. Figure 4 plots the absolute generator current measured from CV responses as a function of square root of scan rate for all four cases and Figure S-3 in Supporting Information provides an alternative overlay of the data in comparison to hemicylindrical diffusion theory.

Figure 3.

Representative cyclic voltammograms as a function of scan rate obtained with active redox cycling (solid curves for negative current at the generator and positive current at the collector electrodes) and without active redox cycling (dashed curves for generator only; collectors off) in the open (left panels) and closed (right panels) microchannel, using the internal electrode set-up. Seven generator electrodes were shorted together; seven collectors were shorted together and either left at open circuit (no active redox cycling) or held at −0.1 V (active redox cycling). The solution consisted of 0.4 mM K₄Fe(CN)₆ in 0.1 M KCl.

Figure 4.

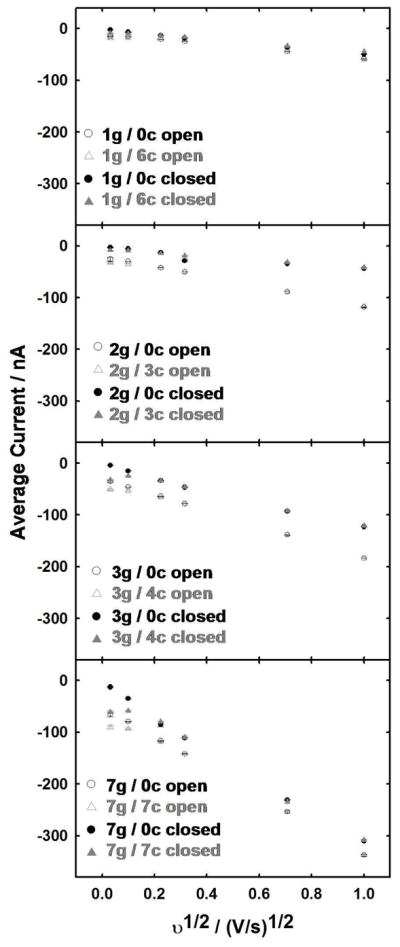
Comparison of electrochemical responses for different generator/collector electrode configurations, with (triangles) and without (circles) active redox cycling for the open (open markers) and closed (filled markers) microchannel. Observed current at the generator electrode(s) (either peak current or plateau current from the CV response, whichever is higher) is plotted as a function of square root of scan rate where initial potential was −0.10 V and switching potential was either +0.35 or +0.30 V for the open and closed microchannel, respectively. Collector electrodes were held at −0.1 V. Data points are averages from three experiments. Error bars represent ±1 standard deviation (N = 3) and are included, although they fall within the size of the markers. The solution consisted of 0.4 mM K₄Fe(CN)₆ in 0.1 M KCl.

When the channel is closed (Figure 2(b)), net diffusion of redox species proceeds primarily laterally along the microchannel length at the time scales investigated, resulting in a decrease in current magnitude as compared to that in the open microchannel (Figure 2(a)). This observation is explained by quick exhaustion of the mass transfer contribution from directly above the generator electrodes.¹⁷ This behavior is especially noticeable by comparing magnitudes and shapes (peak vs. sigmoid) of dashed CV curves in Figure 3 at 0.001 and 0.01 V/s for the closed with those for the open microchannel. Although CV responses in Figure 3 are for seven electrodes shorted together (A to G), the trend is also true when any of the other numbers of generator electrodes listed Figure 1(d) are activated (Figure 4 and Figure S-3). Even the fastest scan rate investigated (1 V/s) is begins to exhaust redox species directly above the electrode because the diffusion length (δ=~19 μm, although underestimated as described below) is similar to the microchannel depth.

When the microchannel is open, Figure 3 shows that the CV responses change from a sigmoid to a peak shape with increasing scan rate. This would be expected for microband electrodes in open, semi-infinite conditions when the contributions to flux switch over from planar to hemicylindrical diffusion.

Such planar diffusion-limited current is proportional to the square root of scan rate, v, as defined by equation 1 (at 25 °C):

$$i_p=2.69\times {10}^5{n}^{3/2}A{D}^{1/2}{C}^{\ast }{v}^{1/2}$$ (1)

where n corresponds to the number of electrons transferred per mole of redox species (n=1 for ferrocyanide), A is the electroactive area of the electrode, D is 6.5 × 10⁻⁶ cm²/s for ferrocyanide in aqueous 0.1 M KCl,³⁰ and C^* is the concentration of redox species in bulk solution.³¹ Equation 1 holds for “short time scales”, defined as t≪w²/(2D) for microband electrodes in open semi-infinite systems.

Although we did not perform an extensive analysis at fast scan rates, the slopes of current vs. v^1/2 using data obtained under conditions most valid for equation 1 (1 and 0.5 V/s), are ~−6.8 × 10⁻⁸ A/(V/s)^1/2 for both the open and closed microchannel. This is 90% of the value predicted from equation 1 (−7.59 × 10⁻⁸ A/(V/s)^1/2). Slight discrepancies are attributed to non-ideal conditions and errors in knowing actual values of variables.

At long time scales, t≫(w²/2D) in the open microchannel, the observed current with single or multiple generator electrodes is similar to that predicted using equation 2 (see overlay in Figure S-3), suggesting that hemicylindrical diffusion dominates mass transfer,

$$i(t)=2{\mathit{nFDlC}}^{\ast }\pi /ln(4Dt/r_o^2)$$ (2)

where F is the Faraday constant, l corresponds to length of the band electrode, t is time, and r_o represents the effective hemicylindrical electrode radius. The r_o term may be substituted with w/4,^{32, 33} for a band electrode of length l and width w at long timescales (Dt/r²>10) when l≫w and semi-infinite conditions apply.³² In this study, l>12w, the open microchannel qualifies for semi-infinite conditions, and multiple band electrodes are treated as distant electrodes rather than as a single band of increased width. The dashed, sigmoidally-shaped CV responses in Figure 3 for 0.001 and 0.01 V/s for the open microchannel are consistent with use of equation 2.

Equilibration of redox species at the neighboring, interdigitated electrodes at open circuit (passive) will further contribute to the overall flux. But because the current follows the hemicylindrical-diffusion theory so closely, contributions toward it from the equilibration phenomenon appears to be insignificant in the open microchannel. (A very small contribution is confirmed, however, based on shielding factor measurements, described below.)

In the closed microchannel, dependence of current on v^1/2 appears to be linear at the slower scan rates (Figure S-3). We do not compare electrochemical responses in the closed microchannel with equation 2, because a full hemicylindrical diffusion field cannot be attained before the front runs into the lid and begins to evolve laterally. It is the lateral, semi-infinite condition that is likely to explain this v^1/2 dependence.

One way to determine the influence of neighboring electrodes in the array on the electrochemical signal is to investigate the decrease in current from depletion of redox species by overlapping diffusion layers and described by the shielding factor, S_F.²²

$$S_F=1-[i_x/(i_{1}x)]$$ (3)

where i_x is current measured for x-electrodes shorted together and i₁ is current at a single electrode that behaves as a distant electrode. Table 1 lists the S_F values.

Table 1.

Shielding factors observed without (collectors off, 0c) and with (collectors on) redox cycling in the open and closed microchannel. For the calculation of S_f, the current at a single generator electrode (collectors off) was set to i₁, and the current at x-shorted-generator electrodes with collectors on was set to i_x.

		Scan Rate/V/s
	# gen./# coll.	0.001	0.010	0.050	0.100	0.500	1.000
Open	2g/0c	0.12	0.03	−0.01	0.00	−0.01	−0.01
	3g/0c	0.20	0.01	−0.03	−0.04	−0.05	−0.04
	7g/0c	0.37	0.27	0.20	0.19	0.18	0.18
	2g/3c	−0.10	−0.11	−0.02	0.00	0.00	0.00
	3g/4c	−0.15	−0.15	−0.06	−0.05	−0.04	−0.04
	7g/7c	0.13	0.14	0.19	0.19	0.18	0.18
Closed	2g/0c	0.28	0.58	0.53	0.23	0.54	0.56
	3g/0c	0.33	0.29	0.18	0.17	0.16	0.18
	7g/0c	0.15	0.28	0.11	0.15	0.11	0.11
	2g/3c	−0.99	0.38	0.47	0.48	0.57	0.59
	3g/4c	−4.06	−0.19	0.17	0.18	0.17	0.19
	7g/7c	−3.13	−0.20	0.17	0.16	0.08	0.12

Negative values at intermediate and high scan rates, where diffusion layers have minimal overlap, indicate that the signal of the single electrode is less than the average signal of x electrodes, but are within error of the electrode-to-electrode signal reproducibility. Negative values at low scan rates (0.001 and 0.010 V/s) result from large i_x values that reflect the amplified signal due to redox cycling.

In the open microchannel, S_F has no observable effect for 2g and 3g configurations (Figure 1(d)) at scan rates ≥ 0.010 V/s. For 7g, however, positive S_F values are obtained at all scan rates. This trend of increasing S_F values with increasing numbers of shorted generator electrodes is expected. Interestingly, a small amount of shielding can be observed even at the fastest scan rate for 7g, indicating that the diffusion length must still reach the distance across the gap between active and adjacent open-circuit electrodes. (The δ=~19 μm at 1 V/s is underestimated, because electrolysis actually occurs beyond the time used for this calculation.) This result shows the influence of non-shorted interdigitated electrodes at open-circuit (undergoing “passive redox cycling”) to “extend” the diffusion field and thereby affect electrode signal,^{23, 24} even for open, semi-infinite conditions.

In the closed microchannel, positive S_F values occur at all scan rates investigated, because redox species deplete not only laterally from neighboring active electrodes but also vertically due to the restricted volume. Peak-shaped CV responses at all scan rates result (Figure 3). When the configuration changes from 2g to 7g, the S_F values decrease, an opposite trend from that observed in the open microchannel. We attribute this result to a generator signal that is larger than expected from enhanced contribution from passive redox cycling at the interdigitated electrodes at open circuit, offsetting the decrease in current from shielding.

A significant difference between the 2g and 7g configurations is that the lateral diffusion field in the latter more quickly reaches large conductors (R1 and C3, spanning 1200 μm) in the middle of the array (Figure 1(c)), one of which is the counter electrode (a source of active redox cycling, only 25 μm away from D, and accessible even at 1 V/s) and the other is at open circuit (a source of passive redox cycling, 2, 25-μm gaps away from C and D, and accessible at 0.1 V/s).

The 3g configuration exhibits S_F values much lower than those for 2g. This is because the edge of the outermost active electrode is much closer (by 2, 25-μm gaps and 2, 50-μm passive conductors) to the large passive conductor R1 than the 2g configuration. Thus, it benefits from redox cycling and higher concentration gradients. The 3g configuration exhibits just slightly higher S_F values than those of 7g at all scan rates, and doubled at the slowest scan rate 0.001 V/s. Unlike 7g, the array involved in the 3g configuration is not immediately adjacent to the counter electrode, and so depletion of redox species wins out more, relative to the extent of redox cycling. At very long time scales, however, even the “refreshed” diffusion field growing outward from the passive conductors will eventually be depleted as it reaches the lid of the microchannel, leading to diminishing signals (e.g. 0.001 V/s).

Effect of active redox cycling involving one generator and different numbers of microband collector electrodes in the open and closed microchannel

Confinement of redox species to the microchannel and lateral diffusion along its length produce a substantial increase in collection efficiency, compared to when the channel is open. This leads to signal amplification, compensating greatly (but not completely) for the attenuated generator signal in the absence of redox cycling in the closed channel.

Electrochemical responses for the closed and open microchannel were compared, using a single band electrode as the generator and from one, up to six flanking bands as collector electrodes. Figure 1(d-top) lists the identity of the generator and collector electrodes used in these experiments and Table 2 summarizes the data in terms of amplification factors and collection efficiencies. (Raw generator current used to calculate values in Table 2 is plotted vs. v^1/2 in Figure S-4 in Supporting Information).

Table 2.

Amplification factors (A_f) and collection efficiencies (C_e) obtained by redox cycling between generator and collector electrodes (Ng/Nc) at various scan rates in the open (top) and closed (bottom) microchannel.

Open microchannel
# gen./# coll.	0.001 V/s		0.010 V/s		0.050 V/s		0.100 V/s		0.500 V/s		1.000 V/s
	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%
1g/1c	1.13	21.1	1.05	33.7	1.00	20.3	0.99	13.2	1.01	---	1.00	---
1g/2c	1.19	54.1	1.10	54.8	1.00	36.4	0.96	24.9	1.00	---	1.00	---
1g/4c	1.20	61.7	1.17	56.7	1.02	37.0	1.00	24.8	1.01	---	1.01	---
1g/6c	1.24	64.1	1.14	58.1	1.03	35.8	1.01	23.3	1.02	---	1.02	---
2g/3c	1.25	64.3	1.14	56.5	1.01	37.0	0.99	25.7	0.99	---	0.99	---
3g/4c	1.43	64.2	1.17	56.6	1.03	36.7	1.01	25.2	0.99	---	1.00	---
7g/7c	1.38	53.6	1.17	50.2	1.01	32.3	1.01	21.7	1.00	---	1.00	---

Closed microchannel
# gen/# coll.	0.001 V/s		0.010 V/s		0.050 V/s		0.100 V/s		0.500 V/s		1.000 V/s
	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%	Af	Ce/%
1g/1c	3.50	76.9	1.18	60.8	1.00	22.0	1.00	12.9	1.01	---	1.02	---
1g/2c	4.51	91.4	1.45	81.1	1.01	56.7	1.04	38.2	1.02	---	1.04	---
1g/4c	3.33	96.2	0.97	87.6	0.73	59.4	0.77	45.2	0.80	---	1.02	---
1g/6c	4.20	113.2	1.50	94.7	0.97	74.5	0.89	41.9	0.91	---	0.89	---
2g/3c	2.76	95.5	1.48	86.4	1.12	73.2	0.67	67.0	0.92	67.0	0.94	---
3g/4c	7.60	109.3	1.68	91.1	1.00	65.7	0.99	45.7	0.99	---	0.99	---
7g/7c	4.83	84.8	1.66	75.8	0.93	55.4	0.98	38.7	1.01	---	0.99	---

At the shorter timescales, 0.500 and 1.000 V/s, whether or not the microchannel is open or closed, redox cycling has no significant effect on signal at the generator electrode and collector electrode current is zero. The timescale is too short for redox species to diffuse to the nearest flanking collectors and return to the generator (Figure 1(c)).

At moderate timescales, 0.050 and 0.100 V/s, the advantage of the closed microchannel becomes apparent with increased collection efficiencies, even though the amplification factor remains ~1.0. (The experimental timescale remains too short for recycled species to significantly affect the concentration gradient at the generator.) When the microchannel is closed, collection efficiency for one generator with two flanking collector electrodes is more than twice that with one collector, whereas the improvement in collection efficiency is not quite two-fold in the open microchannel. Additional collectors in the open microchannel do not improve collection efficiency because redox species are lost by diffusion into bulk solution. However, in the closed microchannel, collection efficiency continues to increase (from ~60% to ~75%) with increasing number of collectors (from two to four at 0.100 V/s and from four to six at 0.050 V/s), even though the distance from the generator to the nearest edge of the second set of collector electrodes (100 μm) exceeds the diffusion length (85 μm at 0.050 V/s). Perhaps this continued improvement in collection efficiency is due to additional redox cycling from the counter electrode C3, which is adjacent to a large passive conductor R1 at the edge of the array.

At longer timescales, 0.005 and 0.010 V/s, the advantages of the closed over the open microchannel and increased number of collector electrodes are most pronounced. In the open microchannel, the collection efficiency reaches a maximum of ~60% with four flanking collectors and the amplification factor reaches a maximum of ~1.2 with two collectors. Additional collector electrodes in the open microchannel did not lead to improvements in collection efficiency or signal amplification.

In contrast, a single collector electrode in the closed microchannel achieves a collection efficiency of 77% and amplification factor of 3.5 (0.001 V/s). Increasing the number of flanking collector electrodes results in amplification factors as great as 4.5 and collection efficiencies approaching 100%. When six collector electrodes are used, collection efficiency is greater than 100%. This may be due to redox cycling from counter electrode C3, where redox species equilibrate quickly across the passive conductor R1 and affect solution concentration at the outermost set of collector electrodes.

Effect of active redox cycling with multiple generator and collector microband electrodes in the open and closed microchannel

Because the electrodes in the array are individually addressable, unlike previously published microchannel studies,^{2, 10–13, 21, 23, 25, 26} they may be employed to investigate the effect of various combinations of active generators and collectors on signal amplification. Additionally, conditions may be identified under which it is possible to counteract signal attenuation from S_F with active redox cycling. The multi-generator/collector configurations studied are 2g/3c, 3g/4c, and 7g/7c (assignments in Figure 1(d-bottom)). Table 2 lists collection efficiencies and amplification factors. Table 1 presents shielding factors. Figure 4 compares absolute current values at the generator electrodes obtained for different configurations vs. v^1/2 and were used to calculate values in Tables 1 and 2.

Results with all generator/collector pair configurations at the faster time scales for both the open and closed microchannel were the same as those observed for a single generator and multiple collectors. The collection efficiency was 0% and there was no signal amplification.

At moderate timescales, amplification factors in both the open and closed microchannel are ~1.0 because the timescales for 0.050 and 0.100 V/s are too brief for a significant amount of recycled species to diffuse back to the generator electrodes. Collection efficiencies in the open channel exhibit no improvement for different generator/collector pair configurations when compared to those for a single generator and more than one collector. However, in the closed microchannel, collection efficiency improves more than two-fold in some cases.

An unexpected trend is that collection efficiency in the closed microchannel at moderate time scales decreases with increasing generator/collector pairs. (A slight decrease is also observed in the open microchannel with the 7g/7c configuration compared to 3g/4c.) The explanation is tied to the same reason as for the shielding trends–overlap of diffusion fields with the nearby counter electrode C3 and passive conductor R1 produces additional redox cycling effects. Essentially, the generator current is higher and measured collector current at the microbands is lower with increasing pairs in this device design and therefore the calculated collection efficiencies are lower. Table 1 shows support for this explanation because S_F exhibits the same trends regardless of whether redox cycling at microband electrodes is on or off. Also, unlike the current at the microbands that serve as collector electrodes, current resulting from regeneration of species at the counter electrode is unaccounted for.

At longer time scales redox cycling overcomes or significantly diminishes the detrimental effect of S_F on generator current in both the closed and open microchannel. In the open microchannel, collection efficiency reaches a maximum of 64%, equal to that obtained with a single generator and six collectors at the same scan rate, 0.001 V/s. Amplification factors are modest (≥ 1.14) but are ~20% greater with multiple generators than with a single generator electrode and six collectors. In the closed microchannel, dramatic signal amplification was observed. It was at least two-fold and as much as five-fold greater than in the open microchannel. Collection efficiencies do not improve dramatically with use of multiple generator/collector pairs as compared to one generator with two or more collectors. But at 0.001 V/s, amplification factors as high as 7.6 are observed. Amplification factors and collection efficiencies decrease in going from the 3g/4c to 7g/7c configuration at 0.001 V/s and 0.010 V/s in a closed microchannel, because of the proximity of the counter electrode and large passive conductor as described above (i.e. the generator current is relatively bigger and not all of the collector current is accounted for). Nevertheless, the generator current for 7g/7c is the largest of all configurations here (Figure 4). Important to note for development of small-volume microchannel devices is that redox cycling offsets the depletion effect from confinement sufficiently to produce a current equal to that from hemicylindrical diffusion to a microelectrode in bulk solution.

Calibration curves using active redox cycling at microband electrodes in the closed microchannel

Calibration curves were obtained for CV and CA with the 7g/7c configuration and active redox cycling in the closed microchannel in order to evaluate sensitivity and limits of detection (Figure S-5). CV was performed in order to monitor shifts in the potential window due to the shift of the pseudoreference electrode R2 with different ferrocyanide concentrations. A scan rate of 0.010 V/s was used as a compromise between signal amplification and performing multiple analyses in a tolerable time frame. CA (generator stepped from −0.1 V to +0.3 V and collector held at −0.3 V) was used to eliminate charging current, expedite experiments, and facilitate signal averaging.

CA and CV gave similar diffusion-limited current responses, as expected. The least squares best fit line through the CV data yielded the following equation: y = (−9.94 × 10⁻⁵ A/M) x −8.04 × 10⁻¹⁰ A, R² = 0.999. That for CA data was: y = (−1.11 × 10⁻⁴A/M) x −1.74 × 10⁻⁹ A, R² = 0.999. The observed limit of quantification for both techniques was 10.94 ± 0.17 μM, corresponding to 3.501 ± 1.095 pmol in the closed microchannel. The calculated limits of detection based on 3σ of the noise: 5.95 μM for CA and 0.627 μM for CV, corresponding to 1.9 pmol and 0.2 pmol, respectively, in the closed microchannel. Although a Faraday cage was used to minimize noise, the primary channel (connected to the generator electrodes) on the bipotentiosat has a picoamp booster, but the second channel (connected to the collector electrodes) does not, introducing noise to the system. More effective elimination of noise through filtering would reduce electronic noise and decrease detection limits.

CONCLUSIONS

Choosing whether to use an electrochemical method involving a single-electrode or multiple-electrodes with redox-cycling in a confined system depends on a number of factors. Transient electrochemical methods “amplify” amperometric responses by recording current at short times (t≪w²/(2D)) and employing larger electrodes (e.g. i∝Av^1/2 for CV in equation 1) as long as channel height exceeds diffusion length (h>δ). They produced the highest signals here without the need for redox cycling (Figure 4). However, charging current increases with v, but subtracting it out is not always reproducible and drowns faradaic signal at very short times and low concentrations. Ohmic iR drop becomes an increasing problem as current increases and cell cross-section decreases. When radial diffusion dominates mass transfer, advantages of higher signal-to-background ratio and steady-state signal (for averaging and taking measurements beyond the RC time constant) are achieved, but the height of the cell must be large compared to the smallest dimension of the electrode (e.g. h ≫ w) to allow a full radial diffusion field to develop. It is between these two extremes where redox cycling offers benefits in confined volumes (h < w). The redox-cycling steady-state current allows better detection limits than transient approaches and cost-effective dimensions, where signal would otherwise be compromised by rapid depletion of electroactive species.

A self-contained device consisting of a microchannel and individually-addressable microband array electrodes with additional larger electrodes that can serve as on-chip counter and pseudoreference electrodes was constructed. It was used to evaluate the impact of redox cycling from different arrangements of active and passive electrodes in a confined volume and contrasted to bulk solution. A useful outcome from these studies is that even relatively large microelectrodes (≥50 μm) and gaps between them (≥25 μm) can exhibit substantial amplification from redox cycling when confined to the small volume of a microchannel and in the presence of large passive and active conductive elements. Larger feature sizes are easier, faster, and less expensive to fabricate, and tolerate defects better. Also important is the contribution of large “passive” conductors toward the signal due to the equilibration effect, which is especially effective in confined volumes. This phenomenon is well-known in the scanning electrochemical microscopy community,³⁴ and is called positive “feedback”. However, it is overlooked in the context of microelectrode array systems. Passive conductors enhance the signal at neighboring active electrodes without requiring additional wires or connections to an instrument, adding simplicity and, if the passive conductors span a large enough area, could eliminate the need for a bipotentiostat instrument altogether for a redox cycling experiment.

The confined volume of solution over the electrode array prevents escape of redox species and lateral diffusion results in collection efficiencies very near 100% and amplification factors as high as 7.6. We predict that amplification factors as high as 76 could be obtained with arrays having feature sizes like those used here, but with decreased generator/collector gap widths^{2, 22, 35} of 2.5 μm (rather than 25 μm), which are still straight-forward to fabricate. Amplification factors in this range have been reported only for IDAs with submicrometer-scale electrodes and gaps. ^{2, 36–38}

It is important to note that selection of an appropriate time scale has great impact on signal amplification in addition to the generator/collector configuration and design. Future work with computer simulations is needed to further elucidate the interactions of active generators and collectors, passive conductors, and counter electrodes with confined volumes and to predict geometries, dimensions, orientations, and placement that not only optimize signals but consider the simplest structures to minimize fabrication cost.