Transverse flow imaging based on photoacoustic Doppler bandwidth broadening

Abstract

We propose a new method to measure transverse flow velocity based on photoacoustic Doppler bandwidth broadening, which is determined by the geometry of the probe-beam and the velocity of the transverse flow. By exploiting pulsed laser excitation and raster motor scanning, three-dimensional structure and flow velocity can be imaged simultaneously. In addition, the flow direction can be determined with bidirectional scanning. In a flowing suspension of red-dyed microspheres (diameter: 6 μm), transverse flow speeds ranging from 0 to 2.5 mm∕s as well as flow direction were measured. A cross-sectional flow image was also obtained with the tube laid in a zigzag pattern.

Introduction

Combining the spatial resolution of ultrasound (US) imaging with the contrast of optical absorption in deep biological tissues, photoacoustic (PA) imaging has been widely used in high-sensitivity structural and functional imaging with micrometer-scale spatial resolution.^{1, 2, 3, 4} It has also shown the potential for measuring blood flow.^{5, 6, 7} Previously, PA Doppler (PAD) shift was observed from flowing particles illuminated by an intensity-modulated continuous-wave (CW) laser beam.^{5, 6} This physical phenomenon provides a basis for PAD flowmetry in optically scattering media.⁵ The PAD frequency shift is composed of two parts. The first part is the frequency shift of the photon density wave, which describes the propagation of light intensity in scattering media, “seen” by the particle as a moving receiver; the second part is the frequency shift of the resultant PA wave seen by the ultrasonic transducer, where the particle works as a moving source. Usually only the second part is detectable because the wavelength of the photon density wave is much longer than that of the PA wave.⁵ For a Gaussian laser pulse with full width of half maximum of ∼7 ns, the wavelength of the photon density wave is ∼60 cm in biological tissue,⁸ while the wavelength of the PA wave detected by a ultrasonic transducer with central frequency of 75 MHz is only ∼30 μm. Compared to other scattering-based Doppler flowmetries, such as optical Doppler tomography⁹ and US Doppler,¹⁰ PAD-based flowmetry benefits from less background noise.^{5, 6} Moreover, PAD is independent of the illumination angle⁵ and free of speckles.¹¹ In the previous works,^{5, 6} Doppler frequency shift was computed using the fast Fourier transformation (FFT). However, the sensitivity of this method depends mainly on the FFT time window, which limited the three-dimensional imaging speed.¹² Furthermore, because a CW excitation source was used without frequency chirping, depth could not be resolved. Like the other flowmetries based on the Doppler frequency shift,^{12, 13, 14, 15} PAD flowmetry was sensitive to the Doppler flow angle. In PA imaging of microvascular networks, the imaging depth is shallow and the transverse component of the flow is sometimes dominant.² When the Doppler angle approaches 90 deg, the PAD frequency shift almost vanishes. Previous works in the fields of optical coherence tomography and US imaging have demonstrated the feasibility of using the Doppler bandwidth broadening to provide quantitative information on transverse flow.^{9, 10, 16} However, in those works the flow direction could not be determined due to the symmetry of the optical objective or ultrasonic transducer. In the current work, we propose a method to measure both the transverse flow speed based on PAD bandwidth broadening and the flow direction based on bidirectional scanning.

Method and Material

Experimental Setup

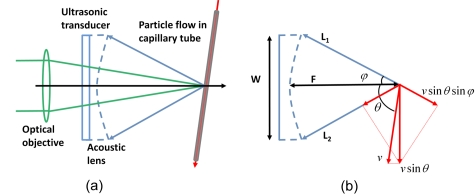
The optical-resolution photoacoustic microscopy (OR-PAM) system used in this work has been described in detail previously [Fig. 1a].² Briefly, a dye laser (CBR-D, Sirah) pumped by a Nd:YLF laser (INNOSAB, Edgewave, 523 nm) was used as the irradiation source with a repetition rate of 1724 Hz. The laser energy delivered to the sample surface was ∼100 nJ. Ultrasonic detection was achieved through a spherically focused ultrasonic transducer (V2012-BC, Panametrics-NDT, focal spot size: 27 μm) with a center frequency of 75 MHz and a round-trip 6-dB bandwidth of 80%, placed confocally with the optical objective. A volumetric image was generated by recording the time-resolved PA signal (A-line) at each horizontal location of the two-dimensional raster scan driven by a high-resolution motor at a speed of 1.1 mm∕s.

Figure 1.

(a) Schematic of the OR-PAM setup and (b) probe-beam geometry for the transverse flow measurement.

Method

Sources of broadening include geometry, transit time, Brownian motion, velocity gradient, and turbulence.^{5, 9} The contribution of Brownian motion to the overall broadening has been shown to be small and consequently neglected.¹⁷ The contributions of the velocity gradient and turbulence can be minimized if the spatial resolution is high enough. The contributions of transit time and geometry are equivalent within the focal region^{18, 19} and can be derived either from diffraction theory or beam-to-flow ray theory.¹⁰ In most PA imaging systems, the acoustic focus is much smaller than the optical focus. Because the bandwidth broadening caused by illumination is negligible, the Doppler bandwidth is determined by the two extreme PA rays emanating from a particle moving through the focal point and received by the edges of the transducer, as shown in Fig. 1b.

The Doppler bandwidth, B_d, is given by⁹

$$B_{\mathrm{d}}=f_{{\mathrm{L}}_2}-f_{{\mathrm{L}}_1}=2f_0\frac{v}{c}\sin \theta \sin \phi \approx f_0\frac{v}{c}\frac{W}{F}\sin \theta ,$$ (1)

where v is the flow velocity, c is the speed of sound, θ is the Doppler angle, φ is the aperture angle of the acoustic lens, and f₀, W, and F are the center frequency, the diameter, and the focus length of the ultrasonic transducer, respectively. The Doppler bandwidth is proportional to the transverse flow and is maximized when the Doppler angle is 90 deg. The derivation of Eq. 1 is illustrated in Fig. 1b. The projections of the transverse flow velocity on lines L₁ and L₂ contribute to the Doppler shift in opposite signs, which results in bandwidth broadening.

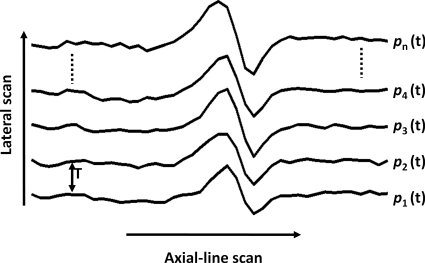
Because the resultant PA wave induced by pulse-laser excitation was wideband, we used the standard deviation of the sequential A-line scans to estimate the Doppler bandwidth broadening (Fig. 2).^{20, 21} The digitized PA signal p(t) was first passed through a digital bandpass filter (center frequency: 75 MHz; 3-dB bandwidth: 1 MHz) to increase the signal-to-noise ratio (SNR). The complex function $\tilde{p}\left(t\right)$ was determined by the Hilbert transformation from p(t). The Doppler bandwidth broadening is given by²²

$$B_{\mathrm{d}}=\frac{k}{T}{(1-\frac{\left|\sum _{j=1}^n{\tilde{p}}_j{\tilde{p}}_{j+1}^{*}\right|}{\sum _{j=1}^n{\tilde{p}}_j{\tilde{p}}_j^{*}})}^{1∕2},$$ (2)

where T is the time interval between sequential A-scans, n is the number of sequential scans used to compute the standard deviation, and k is an experimentally determined constant scale factor associated with the special confocal configuration of the OR-PAM system, where the optical focus is smaller than the acoustic focus.^{20, 21} Four A-scans were used in our study. The structural information was provided by the envelope amplitude of each A-scan, and the flow information was provided by the Doppler bandwidth broadening computed from sequential A-scans.

Figure 2.

Sequential A-scans used to calculate the Doppler bandwidth broadening.

In the current imaging system, the sample was translated by the scanning motor. Hence, the Doppler bandwidth broadening was actually determined by the combination of the flow velocity and the motor scanning velocity (Fig. 3). Therefore, a bidirectional scanning was used to determine the flow direction. The motor first scanned with velocity ${\vec{v}}_{m+}$, and then switched to velocity ${\vec{v}}_{m-}\cdot {\vec{v}}_{m-}$ has the same value as ${\vec{v}}_{m+}$ but in the opposite direction. The measured flow speeds under the two scanning directions are given by the combination speeds of the flow and the motor as follows:

$$v_{\mathrm{f}\text{\_}m+}={(v_f^2+v_m^2+2v_f{v}_m\cos \varphi )}^{1∕2}$$$$v_{\mathrm{f}\text{\_}m-}={(v_f^2+v_m^2-2v_f{v}_m\cos \varphi )}^{1∕2},$$ (3)

where v_{f_m+} and v_{f_m−} are the measured speeds with motor-scanning velocities ${\vec{v}}_{m+}$ and ${\vec{v}}_{m-}$, respectively; v_m is the motor scanning speed; ϕ is the angle between ${\vec{v}}_{m+}$ and the flow velocity ${\vec{v}}_f$, and |cos ϕ| can be provided by structural PA imaging. Solving for the flow speed gives

$$v_{\mathrm{f}}=\frac{\sqrt{2}}{2}{(v_{\mathrm{f}\text{\_}m+}^2+v_{\mathrm{f}\text{\_}m-}^2-2v_m^2)}^{1∕2}.$$ (4)

If v_{f_m+}>v_{f_m−}, we get ϕ<90 deg and vice versa. Therefore, the flow direction can be determined. In case that v_{f_m+}=v_{f_m−}, which means that the flow is perpendicular to the motor-scanning direction, the flow direction can be determined at other positions, because the flow path is usually nonlinear.

Figure 3.

Bidirectional scanning to determine the flow direction.

A straight capillary tube (inner diameter: 260 μm; Dow corning, Midland, Michigan) and a 0.1% solution of red-dyed particles (mean diameter: 6.0 μm; diameter standard deviation: 0.6 μm; peak absorption wavelength: 512 nm; Polysciences, Warrington, Pennsylvania) were used to study the dependence of the Doppler bandwidth on the flow velocity. The flow with speeds for 0–2.5 mm∕s was controlled by a 1-mL syringe driven by a syringe pump and illuminated at 570 nm. The relatively low speeds used here are limited by the laser repetition rate. Although the scan angle can be generalized, in this instance, the bidirectional scanning was along the tube (ϕ=0 deg). The flow direction was the same as ${\vec{v}}_{m+}$. The red-dyed particle is chosen here because its absorption spectrum can be covered by the current laser system. For real biomedical applications, contrast agents that have peak absorption within the near-infrared range should be used to decrease the background signal from blood.

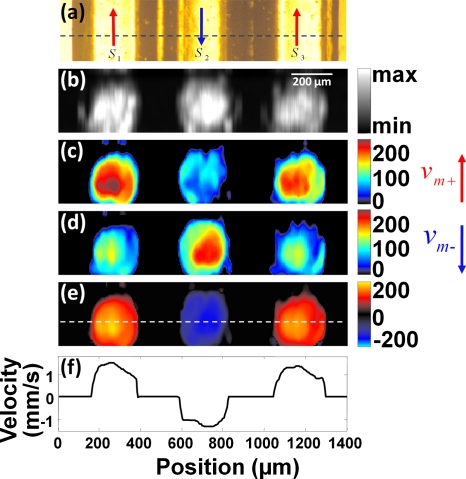
A tube laid in a zigzag pattern was used to get the structural and flow information, simultaneously. The flow speed was set to be 1.3 mm∕s, and the flow direction varied from segment to segment. Three adjacent segments of the tube, denoted as S₁, S₂, and S₃ in Fig. 4a, were imaged. The bidirectional scanning was along the longitudinal axis of these segments. The flow directions in S₁ and S₃ were the same as ${\vec{v}}_{m+}$ while the flow direction in S₂ was the same as ${\vec{v}}_{m-}$.

Figure 4.

(a) Doppler bandwidth as a function of flow velocity with a bidirectional motor scanning speed of 1.1 mm∕s and Doppler angle of 90 deg. The motor scanning direction was either the same as the flow direction (${\vec{v}}_{m+}$, square) or opposite to the flow direction (${\vec{v}}_{m-}$, triangle). Solid curves, theoretical predictions fitted with Eq. 2. Error bar, standard error. (b) Doppler bandwidth flow profiles at flow velocities of 2.3 mm∕s (circle) and 1.6 mm∕s (square), after subtraction of the contribution of the motor scanning. Solid curves, fitted parabolic flow profiles.

Results

In the first experiment, we extracted the data from the center of the capillary (Fig. 5a, θ≈90 deg). When the flow velocity was zero, the bandwidth broadening was caused only by the motor scanning, no matter the scanning direction. When the scanning was in the same direction as the flow (${\vec{v}}_{m+}$, square), the bandwidth increased as the flow speed increased. When the scanning was opposite to the flow (${\vec{v}}_{m-}$, triangle), the bandwidth first decreased as the flow speed increased. However, when the flow speed exceeded the scanning speed, the bandwidth began to increase. The turning point indicated the motor-scanning speed v_m. After subtraction of the contribution of the motor scanning, the bandwidth profiles at the speeds of 2.3 mm∕s (circle) and 1.6 mm∕s (square) are shown in Fig. 5b. A parabolic flow model was used to fit the experimental results (solid curves). Data points on the bottom half of the capillary tube (right side of the plot) were fewer than on the upper half, because light penetration was limited.

Figure 5.

(a) A transmission optical microscopy image of three adjacent segments of a tube laid in a zigzag pattern. The flow directions in S₁ and S₃ were the same as ${\vec{v}}_{m+}$, and the flow direction in S₂ was the same as ${\vec{v}}_{m-}$. (b) A cross section of the structural image. The approximate position of the cross section is indicated by the dashed line in (a). The scale bar for (b)–(e) is shown in (b). (c) The Doppler bandwidth image when the motor scanned in ${\vec{v}}_{m+}$. (d) The Doppler bandwidth image when the motor scanned in ${\vec{v}}_{m-}$. (e) The Doppler bandwidth image after subtraction of the contribution of the motor scanning. The positive flow (with the same direction as ${\vec{v}}_{m+}$) is shown in red, and the negative flow (with the same direction as ${\vec{v}}_{m-}$) is shown in blue. (f) The speed profile indicated by the dashed line in (e). (Color online only.)

For the flow imaging experiment, one cross section of the PA structural image is shown in Fig. 4b, and the approximate position of the cross section is indicated by the dashed line in Fig. 4a. The measured Doppler bandwidths when the motor scanned in ${\vec{v}}_{m+}$ and ${\vec{v}}_{m-}$ were quantified, as shown in Figs. 4c, 4d, respectively. Because the flow directions in S₁ and S₃ were the same as ${\vec{v}}_{m+}$, and the flow direction in S₂ was opposite to ${\vec{v}}_{m+}$, the measured Doppler bandwidth in S₁ and S₃ was greater than that in S₂ when the motor scanned in ${\vec{v}}_{m+}$ [Fig. 4c]. For the same reason, the measured Doppler bandwidth in S₁ and S₃ was smaller than that in S₂ when the motor scanned in ${\vec{v}}_{m-}$ [Fig. 4d]. After subtraction of the contribution of the motor scanning, the Doppler bandwidth in all three segments became similar [Fig. 4e], which means that the flow speed within the tube was consistent. The positive flow (with the same direction as ${\vec{v}}_{m+}$) is shown in red, and the negative flow (with the same direction as ${\vec{v}}_{m-}$) is shown in blue. The negative bandwidth is only used to indicate the flow direction. The calculated flow profile indicated by the dashed line in Fig. 4e is shown in Fig. 4f. At the boundary of the tube, the particle density and the flow speed were relatively low, which resulted in instability in the calculation (see the corresponding volumetric rendering in Video 1). The signal from the tube wall also contributed to the calculation error.

Video 1.

Download video file ^{(8.5MB, qt)}

A volumetric visualization of the Doppler bandwidth image of the tube. (QuickTime 8.54 MB)..

Discussion

Transverse flow velocity measured by the Doppler bandwidth method is related to the M-mode method, because both methods deal with the transit time of particles.⁷ One difference is that the M-mode method has to “see” the entire trace of the particle movement, but the bandwidth method does not. Another difference is that the M-mode method is sensitive to the particle size, but the Doppler bandwidth method is not. This is because the M-mode method is based on the amplitude modulation when the particle passes through the light focus. The Doppler bandwidth method in this paper is based on the signal phase shift caused by the particle movement. The particle size will not affect the phase information. In any case, the bandwidth method does not have to resolve single particles, because the fluctuation caused by the particles’ movement is of relevance.

In OR-PAM, the focal zone of the optical objective is smaller than that of the acoustic lens. When the moving particles pass through the optical focal zone, the excitation profile provides an amplitude modulation to the resultant PA wave, which also contributes to the ultimate bandwidth broadening. However, this contribution can be covered by the constant factor k in Eq. 2, because it is also proportional to the transverse flow.

Our technology is applicable to a given range of velocity. On the one hand, the minimum measureable velocity, which represents the velocity sensitivity of the system, is limited by the SNR. Increasing the number of sequential A-line scans used for the calculation can improve the SNR. On the other hand, the maximum measurable velocity is determined by the aliasing phenomenon described by B_d<f_s for a given A-line scanning frequency f_s. Under the current experimental configuration, the minimum and maximum are ∼100 μm∕s and ∼12 mm∕s, respectively. In real biomedical applications, the accuracy of the flow measurement is expected to be compromised caused by the lower SNR in tissue and the turbulence of flow, which can be improved by calibration of phantom study.

Blood flow is closely related to tumor growth,²³ angiogenesis,²⁴ and neuron-vascular-coupling.²⁵ Compared to other PA flow measurement methods,^{26, 27, 28, 29} the method proposed here has the potential to retain the methods for measuring volumetric structure and oxygen saturation in the same system, which will provide a promising tool to measure the oxygen metabolism rate.³⁰

In summary, Doppler bandwidth can be used to measure flow velocity that is transverse to the probing beam. The linear dependence of the Doppler bandwidth on the flow velocity permits accurate flow measurement. Structural and flow information can be obtained simultaneously, and the flow direction can be determined by bidirectional scanning.