Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 May 7.
Published in final edited form as: J Biomech. 2010 Feb 19;43(7):1316–1321. doi: 10.1016/j.jbiomech.2010.01.020

The Region-Dependent Biphasic Viscoelastic Properties of Human Temporomandibular Joint Discs under Confined Compression

Jonathan Kuo 1, Lixia Zhang 2, Thierry Bacro 3, Hai Yao 1,2
PMCID: PMC2857513  NIHMSID: NIHMS182484  PMID: 20171639

Abstract

The objective of this study was to determine the biphasic viscoelastic properties of human temporomandibular joint (TMJ) discs, correlate these properties with disc biochemical composition, and examine the relationship between these properties and disc dynamic behavior in confined compression. The equilibrium aggregate modulus (HA), hydraulic permeability (k), and dynamic modulus were examined between five disc regions. Biochemical assays were conducted to quantify the amount of water, collagen, and glycosaminoglycan (GAG) content in each region. The creep tests showed that the average equilibrium moduli of the intermediate, lateral, and medial regions were significantly higher than for the anterior and posterior regions (69.75±11.47 kPa compared to 22.0±5.15 kPa). Permeability showed the inverse trend with the largest values in the anterior and posterior regions (8.51±1.36×10−15 m4/N compared with 3.75±0.72×10−15 m4/N). Discs were 74.5% water by wet weight, 62% collagen, and 3.2% GAG by dry weight. Regional variations were only observed for water content which likely results in the regional variation in biphasic mechanical properties. The dynamic modulus of samples during confined compression is related to the aggregate modulus and hydraulic permeability of the tissue. The anterior and posterior regions displayed lower complex moduli over all frequencies (0.01–3 Hz) with average moduli of 171.8–609.3 kPa compared with 454.6–1613.0 kPa for the 3 central regions. The region of the TMJ disc with higher aggregate modulus and lower permeability had higher dynamic modulus. Our results suggested that fluid pressurization plays a significant role in the load support of the TMJ disc under dynamic loading conditions.

Keywords: Temporomandibular joint, Cartilaginous tissue, Hydraulic permeability, Dynamic compression, Soft tissue mechanics

INTRODUCTION

The temporomandibular joint (TMJ) is a load bearing joint with unique articular structure and function (Werner et al., 1991). The TMJ disc, a fibrocartilaginous tissue, is a major component of jaw function by providing stress distribution and lubrication in the joint (Nickel and McLachlan, 1994a; Nickel and McLachlan, 1994b). The TMJ disc pathophysiology, such as disc derangement, is central to many TMJ disorders (Stegenga et al., 1989), which affects more than 10 million Americans. It is generally believed that pathological mechanical loading, such as sustained mechanical loading during jaw clenching, is the leading cause of TMJ disc derangement (Milam, 2005). Although the exact mechanism has not been established, the understanding of the biomechanical behavior of the TMJ disc is the first step to elucidate the pathophysiology of TMJ disorders.

The TMJ disc has a unique matrix composition and cell phenotype when compared to hyaline cartilage and other fibrocartilaginous tissues (e.g., the intervertebral disc (IVD) or knee meniscus). The human TMJ disc is comprised mostly of water with a significant amount of collagen (mainly type I) and a very small amount of proteoglycans (Berkovitz and Robertshaw, 1993; Nakano and Scott, 1989). Differences in biochemical composition and structure distinguish the disc into three regions: the anterior band, intermediate zone, and posterior band (Rees, 1954). Most recently, finite element models based on the well-known biphasic (poroelastic) theory (Mow et al., 1980) have been developed to examine the viscoelastic mechanical behavior and loading support mechanism of the human TMJ disc (Beek et al., 2003; Donzelli et al., 2004). In these biphasic models, the TMJ disc tissue was considered as a mixture of water phase and solid phase. However, the major limitation of these models is the lack of realistic biphasic mechanical properties for the human TMJ disc. Very few studies have been done to characterize the viscoelastic properties of the human TMJ disc (Beek et al., 2001; Tanaka et al., 2000), most likely due to the limited access to human specimens. In all published studies, the TMJ disc was treated as a single phase viscoelastic solid. To our knowledge, only one study on the porcine TMJ disc has used a biphasic model to fit the indentation data (Kim et al., 2003). The biphasic mechanical properties, such as aggregate modulus and hydraulic permeability, have not been measured for human TMJ disc tissues.

When hydrated soft tissues are subjected to dynamic compression of loading frequencies higher than the characteristic frequency of the tissue, the interstitial fluid pressure will increase significantly and the tissue becomes stiffer due to the fluid pressurization effect (Soltz and Ateshian, 1998). Theoretical and experimental studies in articular cartilage and IVD have shown that the fluid pressurization effect is related to the biphasic mechanical properties of the tissue, such as hydraulic permeability and equilibrium compressive modulus. This effect contributes significantly to the measured dynamic stiffness of the tissue (Soltz and Ateshian, 2000; Yao et al., 2002).

It has been hypothesized that the compressive mechanical load on the human TMJ disc is mainly supported by fluid through the fluid pressurization effect (Tanaka and van Eijden, 2003). A biphasic finite element model of the porcine TMJ disc showed that more than 90% of the load during plowing experiments was supported by the fluid phase (Spilker et al., 2009). However, it is not clear how the biphasic mechanical properties affect the dynamic behavior of human TMJ disc tissue during compression. Therefore, the objective of this study was to determine the regional biphasic viscoelastic properties, as well as dynamic properties, of human TMJ discs in confined compression. Confined compression allows for well controlled 1-D strain state experiments, and compared to indentation and unconfined compression, fewer parameters are needed to be determined by the curve fit in order to obtain more reliable results (Mow et al., 1980). The biochemical composition of the disc was also determined to correlate with the biphasic mechanical properties. The effect of the aggregate modulus and permeability on the dynamic properties was examined to further delineate the load supporting mechanisms in the TMJ disc under compression.

MATERIALS AND METHODS

Specimen preparation

Human TMJ discs from the left joint of fresh cadavers were extracted in conjunction with the MUSC Gross Anatomy Laboratory under institutional approval. The discs were immediately photographed, morphologically examined, and wrapped in gauze soaked in a normal saline solution with protease inhibitors and stored at −80°C until mechanical testing. It has been reported that mechanical properties of porcine discs were retained over five freeze-thaw cycles (Allen and Athanasiou, 2005). Discs exhibiting physical signs of trauma, such as fissures or bruises, were discarded. In total, twelve morphologically healthy TMJ discs from twelve male human heads (mean age = 78 years) were sectioned and used for mechanical testing. To limit the heterogeneity of the experiment, only samples from male cadavers were used.

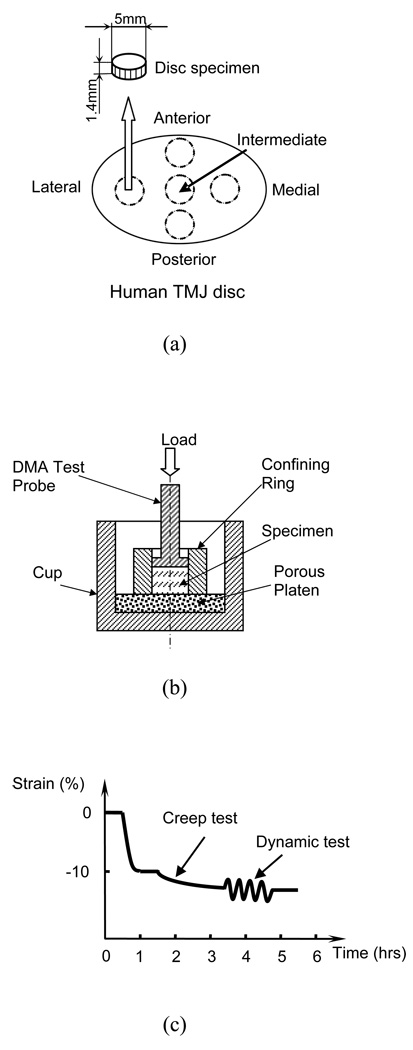
Cylindrical tissue plugs were obtained from the intermediate, posterior, anterior, lateral, and medial regions of the TMJ disc (Figure 1a), using a 5mm corneal trephine. The plugs were microtomed to remove the natural concave shape of the tissue with a sledge microtome (Leica SM2400) and allow for a flat surface for the confined compression test. Thin layers from both superior and inferior surfaces were removed to prepare disk shaped samples with an average height of 1.4mm and a diameter of 5mm.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic of specimen preparation. The region and size of test specimens are shown. (b) Schematic of a uniaxial and confined compression test chamber. (c) Schematic of the mechanical testing protocol.

Mechanical testing

All mechanical tests were performed in PBS (pH 7.4) on a Perkin-Elmer 7e Dynamic Mechanical Analyzer (DMA). The testing chamber with the sample was maintained at 37±0.5°C by a furnace with circulated cooling water. The precision of the DMA for force was 0.5mN while the precision for displacement measurements was 0.5µm. A uniaxial, confined compression test chamber was used for testing (Figure 1b). The specimen was confined laterally by a ring and compressed axially between a porous platen (20µm average pore size) on the bottom and the test probe (5mm nominal diameter) on top (Soltz and Ateshian, 2000; Yao et al., 2002). Figure 1c shows schematically the mechanical testing protocol which will be described in further detail. Prior to testing, measurements for the wet weight and weight in PBS were taken to be used in calculating the water volume fraction of the specimen.

The testing protocol of confined compression was similar to our previous studies on IVD tissues and hydrogels (Yao et al., 2002; Gu et al., 2003). First, the specimen was subjected to a minute compressive tare load (5mN) to measure specimen height prior to the addition of PBS and this height served as the initial height for all mechanical tests. The specimen was then compressed to the height corresponding to 10% compressive strain (relative to the initial height). This offset strain was to ensure interdigitation between the porous platen and the specimen and to fully confine the specimen at its periphery. The specimen was allowed to reach equilibrium (~60 minutes) and the stress was then recorded. Second, a 2-hour creep test was performed by applying a stress equal to 1.2 times the equilibrium stress at 10% strain. Steady state was achieved after 2 hours of compression and the resultant creep strain at the end of the creep test was on average 2–3% of the initial specimen height. This small creep strain was chosen to satisfy the linear biphasic theory. Finally, the specimen was subjected to a dynamic frequency scan test (0.01 to 3 Hz). The amplitude of the sinusoidal dynamic stress was equal to 50% of the static offset stress (i.e. creep stress). The criterion for choosing the amplitude of the dynamic loading was based on the dynamic displacement amplitude of the specimen at 3 Hz (≥5 microns). Using this requirement, our pilot study showed that the maximum dynamic strain, occurring at the lowest testing frequency (0.01 Hz), was less than 2.0%. Thus, the dynamic response of the specimen could be considered within the linear range (Lee et al., 1981).

The equilibrium compressive aggregate modulus ( HA ) and hydraulic permeability coefficient ( k ) were determined by curve-fitting the creep data to the biphasic theory developed by Mow et al (Mow et al., 1980). The dynamic complex modulus and phase angle were automatically recorded by the DMA over the frequency range of 0.01 to 3 Hz (Menard, 1999). After mechanical testing, each specimen was lyophilized for water, GAG and collagen content measurements.

Volume fraction of water

The volume fraction of water for each specimen was determined in PBS (pH 7.4) using a density determination kit (Sartorius YDK01, Germany) and an analytical balance. According to the Archimedes’ principle and biphasic assumption, the volume fraction of water was determined by (Gu et al., 1996)

ϕw=Wwet−WdryWwet−WPBSρPBSρw (1)

where W wet is specimen wet weight, W PBS is the weight of specimen measured in PBS, W dry is the dry weight, ρPBS is the mass density of PBS (1.005 g/ml), and ρw is the mass density of water. The volume fraction of solid (ϕs) is related to the volume fraction of water by ϕs = 1 − ϕw.

Collagen and GAG content

Biochemical analysis was performed on the lyophilized specimens. The total collagen content was determined with a modified chloramine-T hydroxyproline assay (Bergman and Loxley, 1970). Instead of using hydroxyproline standards, collagen standards (Accurate Chemical and Scientific Corporation, Westbury, NY) were chosen for a more direct comparison. The total glycosaminoglycans (GAG) content was quantified using the Blyscan Glycosaminoglycan Assay kit (Biocolor, Newtonabbey, Northern Ireland), based on 1,9-dimethylmethylene blue binding, with standards provided by the manufacturer.

Statistical analysis

The biphasic viscoelastic properties and biochemical quantities were examined for significant differences among the five TMJ disc regions using SPSS statistic software. One-way ANOVA and Tukey’s post hoc tests were performed to determine if significant differences existed between regions. Linear regression was performed to correlate biphasic properties with tissue composition. Statistical differences were reported at p-values < 0.05.

RESULTS

Creep compression behavior

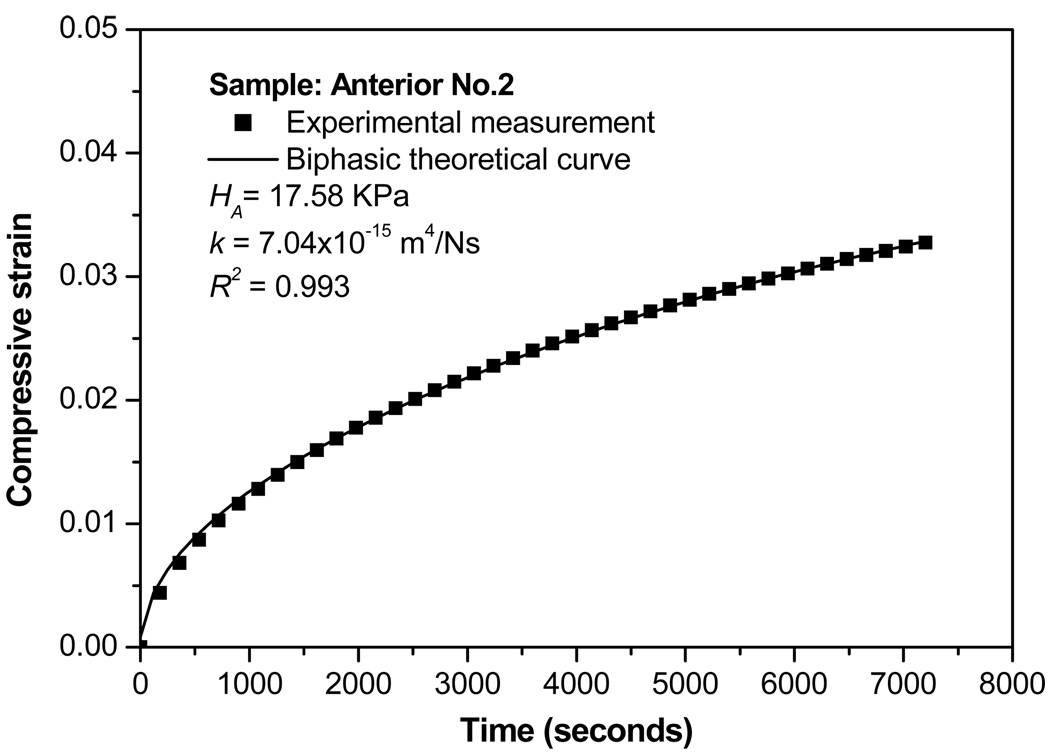
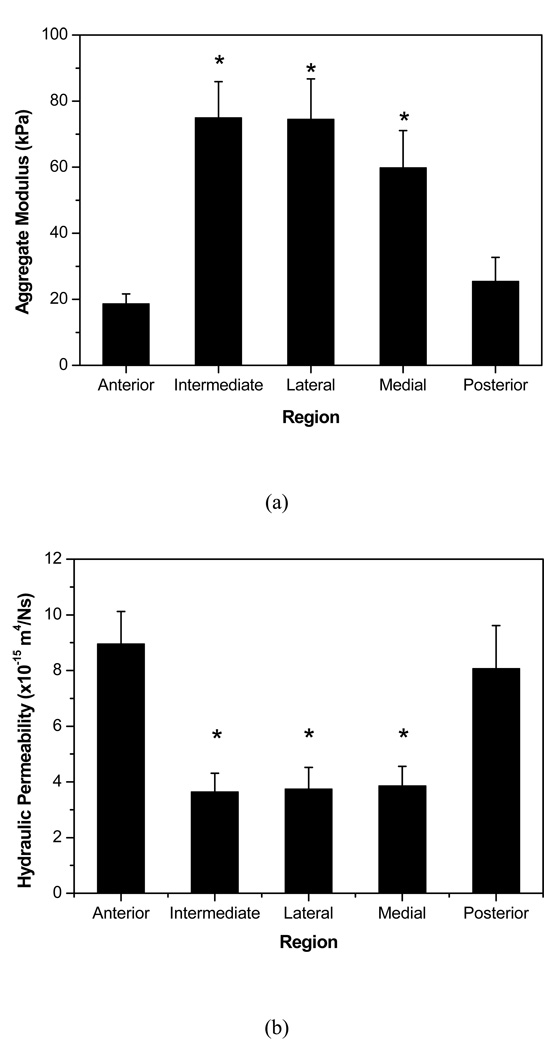
The creep data were well fitted to the biphasic theory to determine the equilibrium compressive aggregate modulus ( H A ) and hydraulic permeability ( k ) (Figure 2). The aggregate moduli of the peripheral bands of the disc (anterior: 18.61±3.02 kPa and posterior: 25.44±7.27 kPa) were approximately 1/3 that of the regions running mediolaterally (medial: 59.81±11.2 kPa, intermediate: 74.93±10.99 kPa, and lateral: 74.51±12.23 kPa) (Figure 3a). Significant differences were also observed for hydraulic permeability (Figure 3b). The anterior and posterior regions (anterior: 8.95±1.17×10−15 m4/N and posterior: 8.07±1.55×10−15 m4/N) were ~40% more permeable than the central regions of the disc (intermediate: 3.64±0.67×10−15 m4/N, lateral: 3.74±0.78×10−15 m4/N, and medial: 3.86±0.70×10−15 m4/N). Therefore, a strong inverse relationship between aggregate modulus and permeability was found with significant regional variation.

Figure 2.

Figure 2

Open in a new tab

Typical biphasic creep behavior of a human TMJ disc specimen. A good agreement is shown between the theoretical prediction and the experimental result.

Figure 3.

Figure 3

Open in a new tab

(a) Mean and standard deviation values for aggregate modulus of the five regions of interest. Significant regional variations were detected. *P<0.05 compared to anterior and posterior regions. (b) Mean and standard deviations for permeability of the five regions of interest. Significant regional variations were detected. *P<0.05 compared to anterior and posterior regions.

Dynamic compression behavior

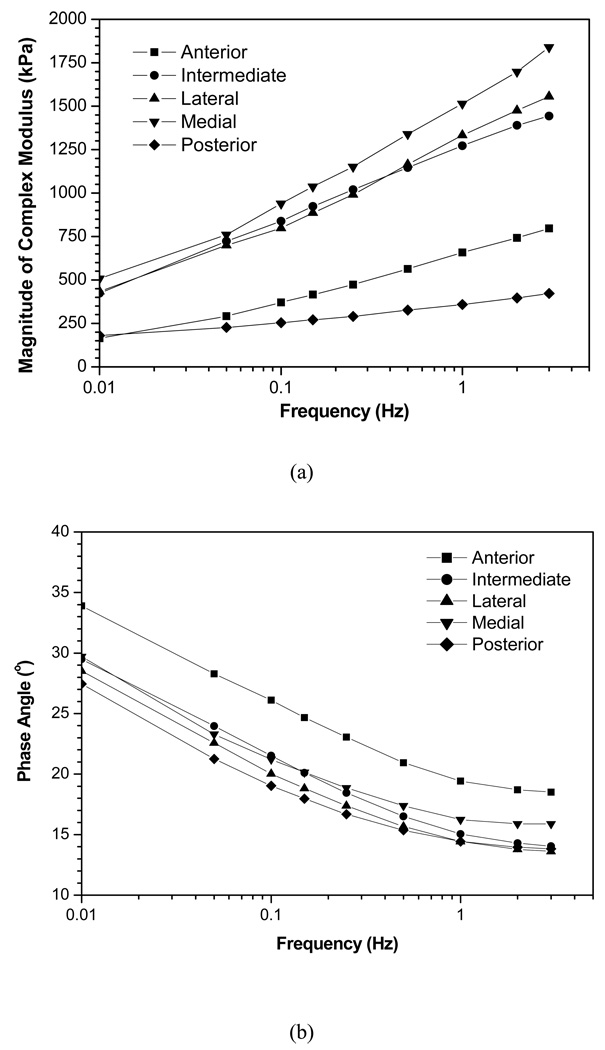
The dynamic compression behavior of the human TMJ disc was highly frequency-dependent. The complex modulus, a ratio of dynamic stress to dynamic strain, increased with increasing frequency (0.01Hz to 3.0Hz) in all five disc regions (Figures 4a). The anterior and posterior regions displayed lower complex moduli over all frequencies (average complex moduli over 0.01–3Hz for peripheral regions: 171.8–609.3 kPa and central regions: 454.6–1613.0 kPa). The three central regions had complex moduli approximately 2.5–3 times greater in magnitude over all frequencies tested. The phase angle shift, a measure of energy lost in one cycle of oscillation in a viscous deformation, decreased with increasing frequency in all five disc regions (Figure 4b). The anterior region demonstrated a greater phase angle over all tested frequencies indicating a greater viscous response during dynamic compression.

Figure 4.

Figure 4

Open in a new tab

(a) Mean complex modulus of each region over the frequency range of 0.01–3Hz. The differences in magnitude between the regions indicate that the dynamic material properties vary significantly across the disc surface. (b) Mean phase angle over five regions of interest. The values remain constant for each region over high frequencies, but below ~1 Hz the phase angle increases significantly. This increase in phase angle indicates a greater viscous response during low frequencies.

Biochemical composition

Mean and standard deviation values of the water content (% wet weight), volume fraction of water, total collagen content (% dry weight), and total GAG content (% dry weight) of human TMJ discs were listed in Table 1 for each disc region. The average tissue water volume fraction across the human TMJ disc was 80%. Significant differences were found between the central 3 regions and the posterior region which contained ~3% more water by total weight. Although it was not significantly different, anterior region samples on average contained slightly more water. The average total collagen and GAG content were 62% and 3.2% by dry weight, respectively. There were no significant differences of total collagen and GAG in disc regions for human TMJ discs.

Table 1.

Results (mean ± SD) of biochemical assays measuring water, total collagen, and total GAG content for each region of human TMJ discs. Significant differences were only found for water content, showing the posterior region contained a greater percentage of water than all other regions.

Water Content
(% Wet Wt.)		 Water volume
faction (%)		 Collagen Content
(% Dry Wt.)		 GAG Content
(% Dry Wt.)
Anterior 74.7 ± 5.6 80.9 ± 4.8 1.9 ± 10.2 3.2 ± 2.1
Intermediate 73.5 ± 2.7 79.0 ± 3.0 60.2 ± 13.0 3.1 ± 1.0
Lateral 73.0 ± 2.5 78.7 ± 2.5 61.6 ± 12.0 3.2 ± 1.2
Medial 73.5 ± 3.1 79.4 ± 1.8 63.1 ± 8.9 3.2 ± 1.4
Posterior 78.5 ± 5.2 82.8 ± 4.5 62.5 ± 14.7 3.3 ± 1.5
Total 74.5 ± 4.2 80.0 ± 3.6 62.0 ± 11.4 3.2 ± 1.4
Open in a new tab

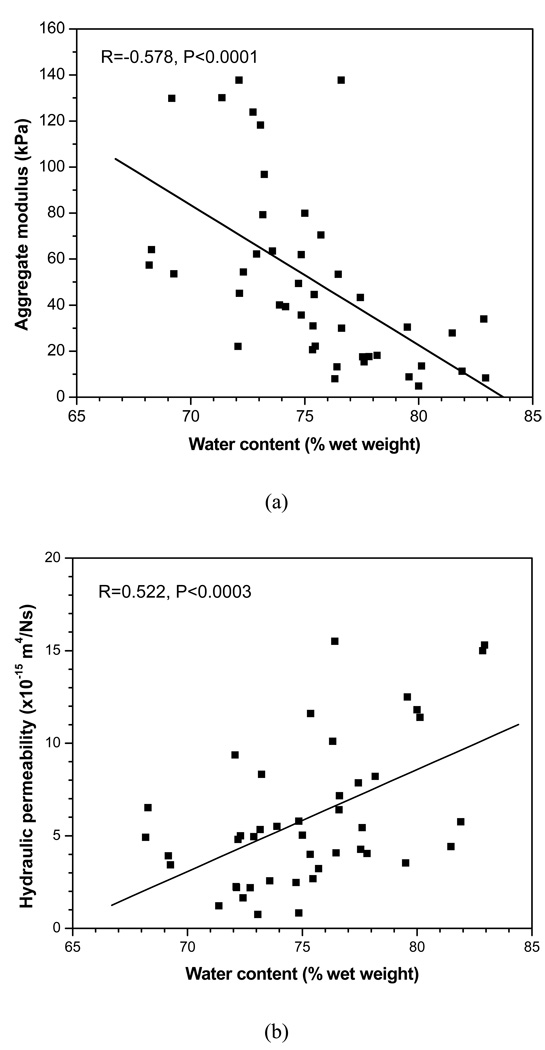
Correlation between biphasic properties and tissue composition

The correlation between the aggregate modulus and water content, as well as the correlation between the permeability and water content, was found statistically significant, as shown in Figure 5. The aggregate modulus was negatively correlated with the water content (R= −0.587, P<0.0001), while the hydraulic permeability positively correlated with the water content (R= 0.522, P<0.0003).

Figure 5.

Figure 5

Open in a new tab

(a) Correlation between the aggregate modulus and the water content. Significant negative correlation was detected (R= −0.578, P<0.0001). (b) Correlation between the hydraulic permeability and the water content. Significant positive correlation was detected (R= 0.522, P<0.0003).

DISCUSSION

The confined creep data of human TMJ disc in this study were well fitted to the biphasic model with an average R2 value of 0.987. This result indicates that confined compression is a reliable testing method to characterize biphasic properties of TMJ disc tissues. The biphasic mechanical properties of the human TMJ disc in this study are substantially different from the properties observed in cartilage from other human diarthrodial joints. In this study, the average aggregate modulus of the human TMJ disc was 50.66 kPa which is 1/25 of human hip joint cartilage and 1/12 of human knee joint cartilage (Athanasiou et al., 1994). The average permeability of the human TMJ disc was 5.652×10−15 m4/N which is 6 and 4 times higher than in human hip and knee cartilages, respectively (Athanasiou et al., 1994). These results indicate that the human TMJ disc is much softer and permeable than human hip and knee cartilage which is likely due to the difference of the tissue composition and structure.

The equilibrium aggregate modulus and permeability of cartilaginous tissues are highly correlated with the water and proteoglycan content. It has been shown that the equilibrium aggregate modulus for human cartilage correlates in an inverse manner with the water content and in a direct trend with the proteoglycan content (Armstrong and Mow, 1982). The hydraulic permeability is proportional to the water content (Yao and Gu, 2003), but varies inversely with proteoglycan content (Maroudas, 1975). In this study, we confirmed that the aggregate modulus of human TMJ disc negatively correlates with the water content, while the hydraulic permeability positively correlates with the water content (Figure 5). The correlation between the GAG content and biphasic properties, however, was not statistically significant due to extremely low GAG content in human TMJ disc tissues. The average water volume fraction of the human TMJ disc was 80% which is higher than the typical value for adult human articular cartilage (75%) (Mow and Ratcliffe, 1997). Moreover, the human TMJ disc has 3.2% (dry weight) total GAG content which is significantly lower than that of human articular cartilage (15–25%) (Mow and Ratcliffe, 1997). The pig TMJ disc has similar biochemical compositions to the human TMJ disc (Detamore et al., 2005). A study by Kim et al using indentation tests reported that the porcine TMJ disc was much softer and permeable compared to the human articular cartilage with the average aggregate modulus of the porcine TMJ disc as 21 kPa and an average permeability of 24.1×10−15 m4/N (Kim et al., 2003).

Regional variations were detected for both aggregate modulus and permeability for human samples with the anterior and posterior regions being significantly softer and more permeable than the other regions of the disc. These regional differences are likely due to the higher water content in the anterior and posterior regions compared to the central regions. Beek et al. examined seven human discs under indentation compression on the anterior band, intermediate zone, and posterior band (Beek et al., 2001). They reported a similar observation that the modulus of the intermediate zone was approximately 2 and 3 times the modulus of the anterior and posterior bands, respectively.

The dynamic modulus of the TMJ disc is much greater than the equilibrium modulus even at a low frequency of 0.01Hz (Figure 3a and Figure 4a). This is due to the interstitial fluid pressurization effect occurring within the tissue under dynamic loading conditions (Soltz and Ateshian, 1998). Based on the biphasic theory, the value of the dynamic modulus of hydrated soft tissue in the confined compression is proportional to HAα (for α > >1, which is true for this study). α is an amplification factor, reflecting the effect of fluid pressurization on dynamic modulus, and is given by: α=2πfh2HA/k (where h is the thickness of the sample) (Lee et al., 1981; Soltz and Ateshian, 2000). This relationship indicates that the sample with higher aggregate modulus and lower permeability correlates to a higher dynamic modulus. Using the biphasic mechanical properties obtained through creep experiments in this study, the ratio of the value of HA/k for the central regions to that of the anterior and posterior regions was approximately 2.68, which agrees well with the averaged modulus ratio (2.75) of the central regions to the anterior and posterior regions over all loading frequencies (Figure 4a).

In our sample preparation, the superficial layers from the top and bottom surface were removed by a sledge microtome to create flat surfaces for the confined compression test. For the porcine TMJ disc, it has been reported that there is significant surface variation between mechanical properties (Allen and Athanasiou, 2005). Therefore, it is necessary in the future to examine the surface differences of the biphasic mechanical properties in human discs.

In summary, regional biomechanical and biochemical characterization of the human TMJ disc was conducted to address the lack of data on human TMJ disc tissue currently available in the literature. Due to higher water content and lower GAG content, the human TMJ disc is much softer and permeable when compared to the human articular cartilage. The central regions of the disc have higher aggregate modulus and lower permeability when compared to the anterior and posterior regions, which correlated to the region-dependent water content. The dynamic modulus of the specimens in confined compression is related to the aggregate modulus and the hydraulic permeability of the tissue as a result of the biphasic nature of the tissue. The region of the TMJ disc with higher aggregate modulus and lower permeability had a higher dynamic modulus. The fluid pressurization plays a significant role in the load support of the TMJ disc under dynamic loading conditions.

ACKNOWLEDGEMENTS

This project was supported by NIH grants DE018741, RR017696, and AR055775. The first author was supported by a NIH T32 training grant DE017551.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

REFERENCES

  1. Allen KD, Athanasiou KA. A surface-regional and freeze-thaw characterization of the porcine temporomandibular joint disc. Ann.Biomed.Eng. 2005;33:951–962. doi: 10.1007/s10439-005-3872-6. [DOI] [PubMed] [Google Scholar]
  2. Armstrong CG, Mow VC. Variations in the intrinsic mechanical properties of human articular cartilage with age, degeneration, and water content. J Bone Joint Surg. 1982;64A:88–94. [PubMed] [Google Scholar]
  3. Athanasiou KA, Agarwal A, Dzida FJ. Comparative study of the intrinsic mechanical properties of the human acetabular and femoral head cartilage. J Orthop Res. 1994;12:340–349. doi: 10.1002/jor.1100120306. [DOI] [PubMed] [Google Scholar]
  4. Beek M, Aarnts MP, Koolstra JH, Feilzer AJ, van Eijden TM. Dynamic properties of the human temporomandibular joint disc. J.Dent.Res. 2001;80:876–880. doi: 10.1177/00220345010800030601. [DOI] [PubMed] [Google Scholar]
  5. Beek M, Koolstra JH, van Eijden TM. Human temporomandibular joint disc cartilage as a poroelastic material. Clin.Biomech.(Bristol., Avon.) 2003;18:69–76. doi: 10.1016/s0268-0033(02)00135-3. [DOI] [PubMed] [Google Scholar]
  6. Bergman I, Loxley R. New spectrophotometric method for the determination of praline in tissue hydrolyzates. Anal.Chem. 1970;42:702–706. doi: 10.1021/ac60289a036. [DOI] [PubMed] [Google Scholar]
  7. Berkovitz BK, Robertshaw H. Ultrastructural quantification of collagen in the articular disc of the temporomandibular joint of the rabbit. Arch.Oral Biol. 1993;38:91–95. doi: 10.1016/0003-9969(93)90161-e. [DOI] [PubMed] [Google Scholar]
  8. Detamore MS, Orfanos JG, Almarza AJ, French MM, Wong ME, Athanasiou KA. Quantitative analysis and comparative regional investigation of the extracellular matrix of the porcine temporomandibular joint disc. Matrix Biol. 2005;24:45–57. doi: 10.1016/j.matbio.2004.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Donzelli PS, Gallo LM, Spilker RL, Palla S. Biphasic finite element simulation of the TMJ disc from in vivo kinematic and geometric measurements. J.Biomech. 2004;37:1787–1791. doi: 10.1016/j.jbiomech.2004.01.029. [DOI] [PubMed] [Google Scholar]
  10. Gu WY, Lewis B, Lai WM, Ratcliffe A, Mow VC. A technique for measuring volume and true density of the solid matrix of cartilaginous tissues. Advances in Bioengineering, ASME BED. 1996;33:89–90. [Google Scholar]
  11. Gu WY, Yao H. The effects of porosity and fixed charge density on hydraulic permeability of cartilage. Annals of Biomed Eng. 2003;31:1162–1170. doi: 10.1114/1.1615576. [DOI] [PubMed] [Google Scholar]
  12. Gu WY, Yao H, Huang C-Y, Cheung HS. New insight into deformationdependent hydraulic permeability of gels and cartilage, and dynamic behavior of agarose gels in confined compression. J Biomech. 2003;36:593–598. doi: 10.1016/s0021-9290(02)00437-2. [DOI] [PubMed] [Google Scholar]
  13. Kim KW, Wong ME, Helfrick JF, Thomas JB, Athanasiou KA. Biomechanical tissue characterization of the superior joint space of the porcine temporomandibular joint. Ann.Biomed.Eng. 2003;31:924–930. doi: 10.1114/1.1591190. [DOI] [PubMed] [Google Scholar]
  14. Lee RC, Frank EH, Grodzinsky AJ, Roylance DK. Oscillatory compressional behavior of articular cartilage and its associated electro-mechanical properties. J.Biomech Eng. 1981;103:280–292. doi: 10.1115/1.3138294. [DOI] [PubMed] [Google Scholar]
  15. Maroudas A. Biophysical chemistry of cartilaginous tissues with special reference to solute and fluid transport. Biorheology. 1975;12:233–248. doi: 10.3233/bir-1975-123-416. [DOI] [PubMed] [Google Scholar]
  16. Menard KP. Dynamic Mechanical Analysis: A Practical Introduction. Boca Raton: CRC Press; 1999. [Google Scholar]
  17. Milam SB. Pathogenesis of degenerative temporomandibular joint arthritides. Odontology. 2005;93:7–15. doi: 10.1007/s10266-005-0056-7. [DOI] [PubMed] [Google Scholar]
  18. Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
  19. Mow VC, Ratcliffe A. Structure and function of articular cartilage and meniscus. In: Mow VC, Hayes WC, editors. Basic Orthopaedic Biomechanics. New York: Lippincott-Raven; 1997. pp. 113–177. [Google Scholar]
  20. Nakano T, Scott PG. A quantitative chemical study of glycosaminoglycans in the articular disc of the bovine temporomandibular joint. Arch.Oral Biol. 1989;34:749–757. doi: 10.1016/0003-9969(89)90082-4. [DOI] [PubMed] [Google Scholar]
  21. Nickel JC, McLachlan KR. In vitro measurement of the frictional properties of the temporomandibular joint disc. Arch.Oral Biol. 1994a;39:323–331. doi: 10.1016/0003-9969(94)90124-4. [DOI] [PubMed] [Google Scholar]
  22. Nickel JC, McLachlan KR. In vitro measurement of the stress-distribution properties of the pig temporomandibular joint disc. Arch.Oral Biol. 1994b;39:439–448. doi: 10.1016/0003-9969(94)90175-9. [DOI] [PubMed] [Google Scholar]
  23. Rees LA. The structure and function of the mandibular joint. Br.Dent.J. 1954;96:125–133. [Google Scholar]
  24. Soltz MA, Ateshian GA. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J Biomech. 1998;31:927–934. doi: 10.1016/s0021-9290(98)00105-5. [DOI] [PubMed] [Google Scholar]
  25. Soltz MA, Ateshian GA. Interstitial fluid pressurization during confined compression cyclical loading of articular cartilage. Ann.Biomed.Eng. 2000;28:150–159. doi: 10.1114/1.239. [DOI] [PubMed] [Google Scholar]
  26. Spilker RL, Nickel JC, Iwasaki LR. A biphasic finite element model of in vitro plowing tests of the temporomandibular joint disc. Ann.Biomed.Eng. 2009;37:1152–1164. doi: 10.1007/s10439-009-9685-2. [DOI] [PubMed] [Google Scholar]
  27. Stegenga B, de Bont LG, Boering G. Osteoarthrosis as the cause of craniomandibular pain and dysfunction: a unifying concept. J.Oral Maxillofac.Surg. 1989;47:249–256. doi: 10.1016/0278-2391(89)90227-9. [DOI] [PubMed] [Google Scholar]
  28. Tanaka E, Shibaguchi T, Tanaka M, Tanne K. Viscoelastic properties of the human temporomandibular joint disc in patients with internal derangement. J.Oral Maxillofac.Surg. 2000;58:997–1002. doi: 10.1053/joms.2000.8743. [DOI] [PubMed] [Google Scholar]
  29. Tanaka E, van Eijden T. Biomechanical behavior of the temporomandibular joint disc. Crit Rev.Oral Biol.Med. 2003;14:138–150. doi: 10.1177/154411130301400207. [DOI] [PubMed] [Google Scholar]
  30. Werner JA, Tillmann B, Schleicher A. Functional anatomy of the temporomandibular joint. A morphologic study on human autopsy material. Anat.Embryol.(Berl) 1991;183:89–95. doi: 10.1007/BF00185839. [DOI] [PubMed] [Google Scholar]
  31. Yao H, Justiz MA, Flagler D, Gu WY. Effects of swelling pressure and hydraulic permeability on dynamic compressive behavior of lumbar annulus fibrosus. Annals of Biomed Eng. 2002;30:1234–1241. doi: 10.1114/1.1523920. [DOI] [PubMed] [Google Scholar]

RESOURCES