THE DISTRIBUTION AND HYPOTHESIS TESTING OF EIGENVALUES FROM THE CANONICAL ANALYSIS OF THE GAMMA MATRIX OF QUADRATIC AND CORRELATIONAL SELECTION GRADIENTS

Abstract

Canonical analysis measures nonlinear selection on latent axes from a rotation of the gamma matrix (γ) of quadratic and correlation selection gradients. Here we document that the conventional method of testing eigenvalues (double regression) under the null hypothesis of no nonlinear selection is incorrect. Through simulation we demonstrate that under the null the expectation of some eigenvalues from canonical analysis will be nonzero, which leads to unacceptably high type 1 error rates. Using a two trait example, we prove that the expectations for both eigenvalues depend on the sampling variability of the estimates in γ. An appropriate test is to slightly modify the double regression method by calculating permutation p-values for the ordered eigenvalues, which maintains correct type 1 error rates. Using simulated data of nonlinear selection on male guppy ornamentation, we show that the statistical power to detect curvature with canonical analysis is higher compared to relying on the estimates from γ alone. We provide a simple R script for permutation testing of the eigenvalues in order to distinguish curvature in the selection surface induced by nonlinear selection from curvature induced by random processes.

Empirical estimation of nonlinear selection (i.e., stabilizing, disruptive, or correlational) on phenotypes, or curvature in the selection surface, bears on such important topics as the topography of the adaptive landscape (Lande and Arnold 1983, Phillips and Arnold 1989, Arnold et al. 2008), and the genetic architecture of complex traits (Blows and Hoffmann 2005, Hunt et al. 2007). Kingsolver et al.’s (2001) review of estimates of nonlinear selection from the literature revealed that disruptive selection and stabilizing selection were generally weak (16% were declared statistically significant), of similar magnitudes, and that correlational selection was rarely estimated at all. It is possible that lack of natural phenotypic variation in traits has limited the power to detect nonlinear selection, such that clear demonstration of stabilizing selection may require experimentally manipulated phenotypes (Creswell 2000; Conner et al. 2003). Although a simple analytical error in not doubling the quadratic selection gradients of the selection model may be partially to blame (Stinchcombe et al. 2008), it is curious that a more pervasive signal of stabilizing selection has not been found in natural populations using phenotypic selection approaches.

Although nonlinear selection estimates appear to be weak, the observed magnitude of stabilizing selection gradients on traits measured in natural populations are too strong to explain the observed level of genetic variation for those traits (Johnson and Barton 2005). Ample additive genetic variation is found for almost all traits measured in nature (Lynch and Walsh 1998), but the observed magnitudes of stabilizing selection indicate that traits should have limited additive genetic variation. A potential explanation for this apparent paradox is that nonlinear selection may be acting on trait combinations in the form of correlational selection (Lande and Arnold 1983, Phillips and Arnold 1989, Blows and Brooks 2003, Hunt et al. 2007, Reynolds et al. in press). Trait combinations may have low additive genetic variance if multivariate stabilizing selection is strong in the direction of those trait combinations (Hunt et al. 2007). Because adaptations can be complex and multidimensional, e.g., the many coordinated and interacting parts of flowers, or the chemical milieu of scents used to attract mates, natural selection would seem to favor certain combinations of traits over others (Blows et al. 2003, Blows 2007, Reynolds et al. in press). Although it seems reasonable that correlational selection should be a common form of nonlinear selection its precise estimation is complicated when multiple traits and their interactions are hypothesized to be under selection.

Statistical and analytical methods exist that can accommodate the increased complexity of the multidimensional selection problem. If the number of traits is p then there are p quadratic terms and p(p-1)/2correlational selection terms to estimate in the selection model. Phillips and Arnold (1989) demonstrated for p = 2 that given the same quadratic selection gradients the selection surface can change depending on the sign and magnitude of correlational selection. Thus with many traits it is difficult to interpret the nonlinear component of selection. Phillips and Arnold (1989) proposed using canonical analysis, a matrix diagonalization technique from the response surface methodology literature (Box and Hunter 1987), to reduce the dimensionality of the nonlinear component of the selection model. Using the canonical transformation loads all the information on nonlinear selection into p dimensions with the canonical coefficients (eigenvalues) now describing curvature along latent axes of the selection surface (eigenvectors).

Canonical analysis can be a powerful tool for observing nonlinear selection when the nonlinear selection gradients individually say little about curvature in the selection surface. Blows et al. (2003), in a reanalysis of Brooks and Endler’s (2001) study on sexual selection for multiple male guppy coloration traits, used canonical analysis to demonstrate that statistically significant positive nonlinear selection was detected on two axes and negative nonlinear selection on a third latent axis. The original analysis (Blows et al. 2003) found little evidence of nonlinear selection using the conventional second order model. Blows and Brooks (2003) suggested that in addition to the usefulness of canonical analysis for estimating nonlinear selection, the power of detecting nonlinear selection is higher using canonical analysis. Using published estimates of nonlinear selection gradients from 19 studies the magnitude of the largest eigenvalue was always higher than the magnitude of the maximum quadratic selection gradient. Intuitively this makes sense as the information contained in the original nonlinear selection estimates is condensed to a smaller number of predictors. The work by Blows and Brooks (2003) suggests that nonlinear selection may be strongest along latent axes of the selection surface rather than on the traits actually measured.

A testimony to the advantage of canonical analysis in detecting nonlinear phenotypic selection is its current use in the evolution literature (e.g., Blows et al. 2004, Brooks et al. 2005, Hall et al. 2008, Reynolds et al. in press). The greatest concern to date has been interpreting the biological meaning of the eigenvectors describing latent dimensions of nonlinear selection (e.g., Conner 2007). Here we investigate an arguably more fundamental aspect of canonical analysis, hypothesis testing of the eigenvalues. To test the eigenvalues for significance the original trait data are transformed into the space of the eigenvectors and the full second-order polynomial regression model is fit to the transformed data (Phillips and Arnold 1989; Simms 1990). This double regression approach tests the null hypothesis that the canonical coefficients (eigenvalues) are each zero, and it has been shown that the standard errors of the eigenvalues are asymptotically equivalent to a delta method approximation (Bisgaard and Ankemann 1996).

Here we demonstrate using simulations that the distribution of the ordered eigenvalues under the null hypothesis of no nonlinear trait effects on fitness may have nonzero expectation for finite sample sizes and will lead to unacceptably high false positive rates. Under a two trait scenario, we prove that the expectation of each eigenvalue under the null is only zero if the parameters corresponding to nonlinear selection are estimated without error, i.e. with an infinite sample size. We also show via simulations that a standard permutation procedure can provide appropriate error rate control at the desired nominal level. We apply the permutation procedure to a real dataset on pollinator-mediated phenotypic selection on Silene virginica floral traits. Finally we provide evidence via simulations that the power of detecting curvature in the selection surface is higher using canonical analysis compared to individually testing each one of the non-linear selection coefficients.

Methods

Regression Models for Nonlinear Selection

Let W_i denote the fitness measure (which we assume has been converted to relative fitness) observed on i = 1, 2,…, N individuals. Assume Z_i = [Z_i1, Z_i2,…,Z_ip] then represents p traits measured on each individual, which have been standardized to have mean 0 and standard deviation 1. We use boldface throughout to differentiate vector/matrix structures from scalar quantities. Nonlinear selection is estimated through a second order polynomial regression model of the form (Lande and Arnold 1983),

$$W_i={\beta }_0+\mathbf{\beta }\mathbf{Z}{}_i+\frac{1}{2}{\mathbf{Z}}_i\text{'}\mathbf{\gamma }{\mathbf{Z}}_i+{\epsilon }_i,{\epsilon }_i~N\left(0,{\sigma }^2\right)$$ 1.1

where β denotes a 1 × p vector of directional selection coefficients, γ denotes a p × p matrix of nonlinear selection coefficients, and ‘ denotes matrix transposition.

The mathematical interpretation of the quadratic selection gradients is complicated by the presence of the correlation gradients (γ_ij,i ≠ j). Phillips and Arnold (1989) suggest applying a canonical analysis by diagonalizing γ as (Box and Draper 1987),

$$\mathbf{M}\mathbf{\gamma }\mathbf{M}\mathbf{\text{'}}=\mathbf{\Lambda }$$ 1.2

where M contains the orthonormal eigenvectors and Λ is a matrix with the eigenvalues (λ_i,i = 1,2,…, p) along the diagonal and 0’s elsewhere. To test for statistically significant nonlinear selection, standard errors of the eigenvalues may be estimated using a double regression approach (Bisgaard and Ankemann 1996). The observed trait values are transformed onto the space of M by Y = ZM'. One then fits a second regression model of the form

$$\mathbf{W}=\mathbf{\alpha }+\mathbf{Y}\mathbf{\theta }+\mathbf{Y}\mathbf{\text{'}}\mathbf{\Lambda }\mathbf{Y}$$ 1.3

Each one of the quadratic coefficients in (1.3) corresponds to an eigenvalue, and so hypothesis tests for those coefficients provide a valid test of whether each of the eigenvalues is non-zero.

Simulation – Type I Error

We first evaluated whether the double regression approach provides appropriate control of the type I error rate in testing the null hypothesis of no curvature in the selection surface. To do this, we simulated datasets consisting of p=2, 5, or 10 traits observed on 150, 250, 500, and 1000 samples. For each simulated dataset, fitness was simulated as a normal random variable with mean 30 and standard deviation 5, and then transformed to relative fitness. Under the null, each trait is uncorrelated with fitness, and so the trait values were independently generated according to a p-dimensional multivariate normal distribution, Z ~ MVN (0, I). Tests of significant nonlinear selection were then computed using the double regression approach as well as using a permutation procedure which is described below.

Permutation tests of the eigenvalues were also calculated by randomly permuting the fitness variable 1000 times for each simulated dataset. The permutation p-value for a particular simulated dataset was calculated as the number of times the observed F statistic (from the double regression method) exceeded the F statistics from the permuted datasets. The permutation approach is testing whether the test statistic for a particular eigenvalue is larger than one would expect assuming a purely random fitness measure, and not necessarily whether an eigenvalue is statistically different from zero. As we will illustrate later, this reflects the correct null hypothesis given that the expectations of the eigenvalues under the null can be non-zero.

The type 1 error rate of testing the eigenvalues against zero using the double regression approach was calculated by the number of times out of the 1000 simulated null data sets that the p-value for each eigenvalue was less than the nominal values of 0.05, 0.025, 0.01, and 0.005, the latter three corresponding to a Bonferroni corrected α level for the 2, 5 and 10 trait scenarios. To calculate the type 1 error rate for the permutation test approach, a permutation p-value for each of the 1000 simulated datasets was generated and then compared to the nominal values indicated above over the 1000 simulated datasets.

All simulations were performed using the R Language (R Development Core Team, 2008). In the supplementary materials, we provide an R implementation of the permutation procedure. The script requires almost no knowledge of R to run, and can accommodate models with additional covariates.

Simulation - Power

Intuitively, the power to detect curvature in the selection surface using canonical analysis, because it is a dimension reduction technique, should be higher than individually testing the elements of γ because fewer tests on coefficients are being made. All the information in γ is being loaded onto the diagonal, with nothing left on the off diagonal. To make an explicit measure of the gain in statistical power from performing the canonical analysis of γ, we simulated data modeled after the published results of Brooks and Endler (2001) and Blows et al. (2003) for four traits describing male guppy coloration (Black, Fuzzy, Iridescent, and Orange). 250 observations for four traits were simulated as MVN (0, P) with the phenotypic variance-covariance matrix set as:

$$\mathbf{P}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill -0.123\hfill & \hfill -0.187\hfill & \hfill -0.062\hfill \\ \hfill -0.123\hfill & \hfill 1\hfill & \hfill -0.068\hfill & \hfill 0.036\hfill \\ \hfill -0.187\hfill & \hfill -0.068\hfill & \hfill 1\hfill & \hfill -0.097\hfill \\ \hfill -0.062\hfill & \hfill 0.036\hfill & \hfill -0.097\hfill & \hfill 1\hfill \end{array}\right]$$

In order to simulate a fitness measurement, the (250 × 14) matrix containing the trait values, cross-products, and squared terms was multiplied by the vector of selection coefficients (14 × 1) obtained from the estimates reported in Brooks and Endler (2001) and Blows et al. (2003). Random error was then introduced by adding an error term distributed as a standard normal random variable. Under the assumption that ε ~ N(0,1), it can be shown that the collective variance explained by the four traits is roughly 6.5% of the total fitness variance.

Since the canonical analysis evaluates curvature along the orthogonal eigenvectors, we chose to compare the power of finding curvature along at least one eigenvector to the power of finding at least one statistically significant nonlinear selection gradient in γ. The power of finding significant eigenvalues was assessed using the permutation procedure described previously and compared to the power of finding at least one nonzero nonlinear selection gradient. With four eigenvalues to test, the statistical power was estimated as the proportion of times out of the 1000 datasets that the F statistic of the double regression yielded a permutation p-value for at least one eigenvalue below the α = 0.05/4 level. Power for the collective terms in γ was calculated as the proportion of times the p-value for the F statistic for at least one nonlinear selection gradient was less than α =0.05/10.

Real Data Example

We also provide an illustration of the permutation procedure on data from a study of hummingbird - mediated phenotypic selection on Silene virginica floral traits (Reynolds et al. et al. in press). We compared permutation test p-values with the p-values from the double regression test of non-zero eigenvalues. Note that the p-values reported in Reynolds et al. (in press) were calculated using the permutation test. The method of collection, rationale and study location is described in detail in Reynolds et al. et al. (in press). Briefly, it consisted of total seed production, the number of flowers per plant (included as a covariate) and six floral traits averaged across the flowers of each plant (corolla tube length = TL, petal length = PL, petal width = PW, corolla tube diameter = TD, stigma exsertion = SE, and floral display height = DHT) recorded for 212 plants in 2005. This represents only a single dataset out of the 20 to which canonical analysis was applied in Reynolds et al. (in press).

Results

Type 1 error

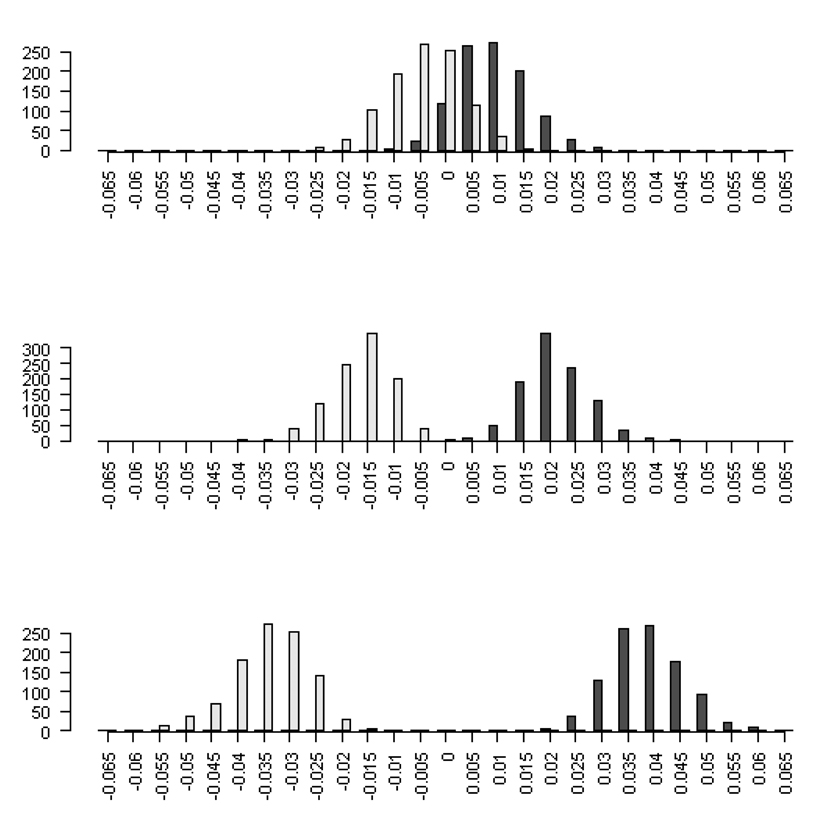
Analyzing data using canonical analysis and the double regression method with independent traits and no effect on fitness produced statistically significant non-zero eigenvalues. The distribution of the maximum and minimum eigenvalues from the null 2, 5, and 10 trait scenarios were shifted away from zero (Fig 1) and the magnitude of the shift increased with the number of traits in the analysis. For example, the magnitude of the mean maximum (minimum) eigenvalues across the 1000 simulated datasets for the two trait and ten trait analysis of 250 observations increased nearly five-fold from 0.00702 (0.00698) to 0.0367 (0.0368), respectively. The magnitude of the mean maximum and minimum eigenvalues and their respective standard deviations decreased as sample size increased.

Figure 1.

The distribution of the maximum (dark grey) and minimum (light grey) eigenvalues from canonical analysis of γ in which there were no linear or nonlinear trait effects on fitness for two, five and ten traits and N = 250 observations.

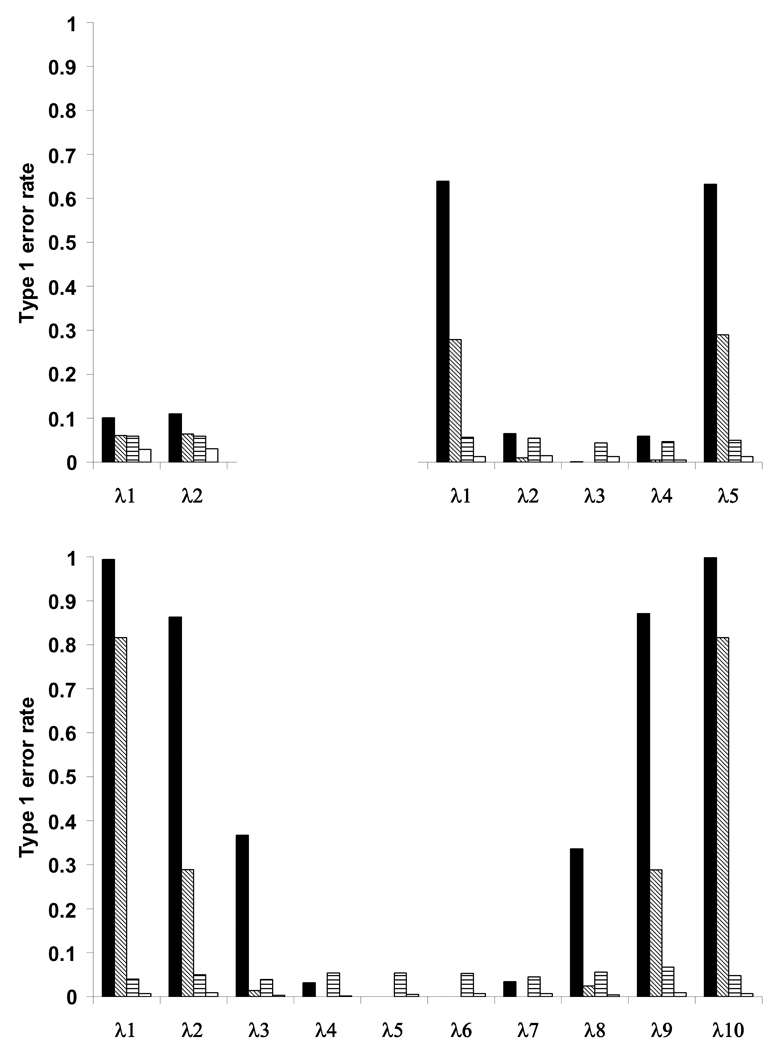
The non-zero expectation of the eigenvalues caused inflated type 1 error rates (Figure 2 and Digital Supplementary Material). With p=2, the type 1 error rate hovered around 10% across all sample sizes. However, these error rates displayed a distinctive U-shaped form as more traits were considered. See Figure 2 for the case of N = 250. For the maximum and minimum eigenvalues, the type 1 error rate approached one as the number of traits in the analysis increased from two to ten (Figure 2 and Digital Supplementary Material). With p=10, under the null, one is virtually assured of finding significant curvature. By contrast, the permutation procedure maintained the correct type I error rates for all sample sizes and number of traits considered. If one were to directly test the nonlinear parameters from the second order regression model without performing a canonical analysis, standard linear model theory applies and so this procedure will maintain correct type I error rates [Ravishanker and Dey, 2002]. The observed type I error inflation is introduced solely through performing a canonical analysis and comparing the eigenvalues to an incorrect null hypothesis.

Figure 2.

Type 1 error rates for testing the eigenvalues from a canonical analysis under the null hypothesis of no linear or non-linear effects on fitness for p = two, five and ten traits. Solid black and diagonal bars refer to the Type I error rates using the double regression approach corresponding to an α level of 0.05 and nominally adjusted α of 0.05/ p, respectively. Horizontal and open bars refer to tests of the eigenvalues using the permutation procedure at the unadjusted α level of 0.05 and nominally adjusted α of 0.05/ p, respectively.

We derived an analytical solution that explained the behavior of the eigenvalues under the null hypothesis (Appendix). Consider a simple two-trait (p=2) example, with γ generically defined as

$$\mathbf{\gamma }=\left[\begin{array}{cc}\hfill {\gamma }_1\hfill & \hfill {\gamma }_3\hfill \\ \hfill {\gamma }_3\hfill & \hfill {\gamma }_2\hfill \end{array}\right]$$

Under the null hypothesis, [γ₁,γ₂,γ₃] follows a multivariate normal distribution with mean [0,0,0] and some variance-covariance matrix Σ,

$$\mathbf{\Sigma }=\left[\begin{array}{ccc}\hfill {\sigma }_{11}^2\hfill & \hfill {\sigma }_{12}\hfill & \hfill {\sigma }_{13}\hfill \\ \hfill {\sigma }_{12}\hfill & \hfill {\sigma }_{22}^2\hfill & \hfill {\sigma }_{23}\hfill \\ \hfill {\sigma }_{13}\hfill & \hfill {\sigma }_{23}\hfill & \hfill {\sigma }_{33}^2\hfill \end{array}\right]$$

Let λ⁺ and λ⁻ denote the two resulting eigenvalues from the diagonalization of γ. Under these assumptions it can be shown that

$$\frac{\sqrt{2\pi }}{\pi }({\sigma }_U^{}+{\sigma }_{33})\ge |E[{\lambda }^{+}]|=|E[{\lambda }^{-}]|\ge \frac{\sqrt{2\pi }}{\pi }\text{max}({\sigma }_U,{\sigma }_{33})$$ (0.1)

where ${\sigma }_U=\frac{1}{2}\sqrt{{\sigma }_{11}^2+{\sigma }_{22}^2-2{\sigma }_{12}}$ (See appendix for proof). Because σ_U and σ₃₃ both represent standard errors associated with estimation of regression coefficients, both will be non-negative, implying that the expectation of the eigenvalues will only approach zero as N → ∞.

Power

Using the simulated male guppy ornamentation data, the statistical power of finding curvature in the selection surface was higher using canonical analysis (0.529) than the power indicated by the combined quadratic and correlational selection gradients of γ (0.390). For comparison’s sake, with recognition that the test does not properly control type 1 error, the power to detect curvature along at least one of the latent axes using the standard double regression approach was 0.883. Clearly this increase in power comes at the expense of an unacceptably high number false positives.

Real Data Example

Without using the permutation procedure there was statistical support for negative curvature along two latent axes of the selection surface describing fitness and trait covariation in S. virginica. Only one of the dimensions retained statistical support after applying the permutation procedure (Table 2). Therefore, we could not reject the hypothesis that the minimum eigenvalue had significantly larger magnitude than the expectation of the minimum eigenvalue from a random permutation. However the eigenvalue corresponding to the M2 eigenvector was statistically significant using the permutation test.

Table 2.

Eigenvalue estimates of non-linear selection from the canonical analysis of γ on six floral traits though seed production from R. Reynolds, M. Dudash, and C. Fenster, in Press.

	λ6	λ5	λ4	λ3	λ2	λ1
Estimate	0.121	0.0595	0.0346	−0.0225	−0.196	−0.268
Double regression P-value	0.06588	0.2723	0.4668	0.7166	0.005815	0.01078
Permutation P- value	0.778	0.569	0.242	0.709	0.004	0.163

Discussion

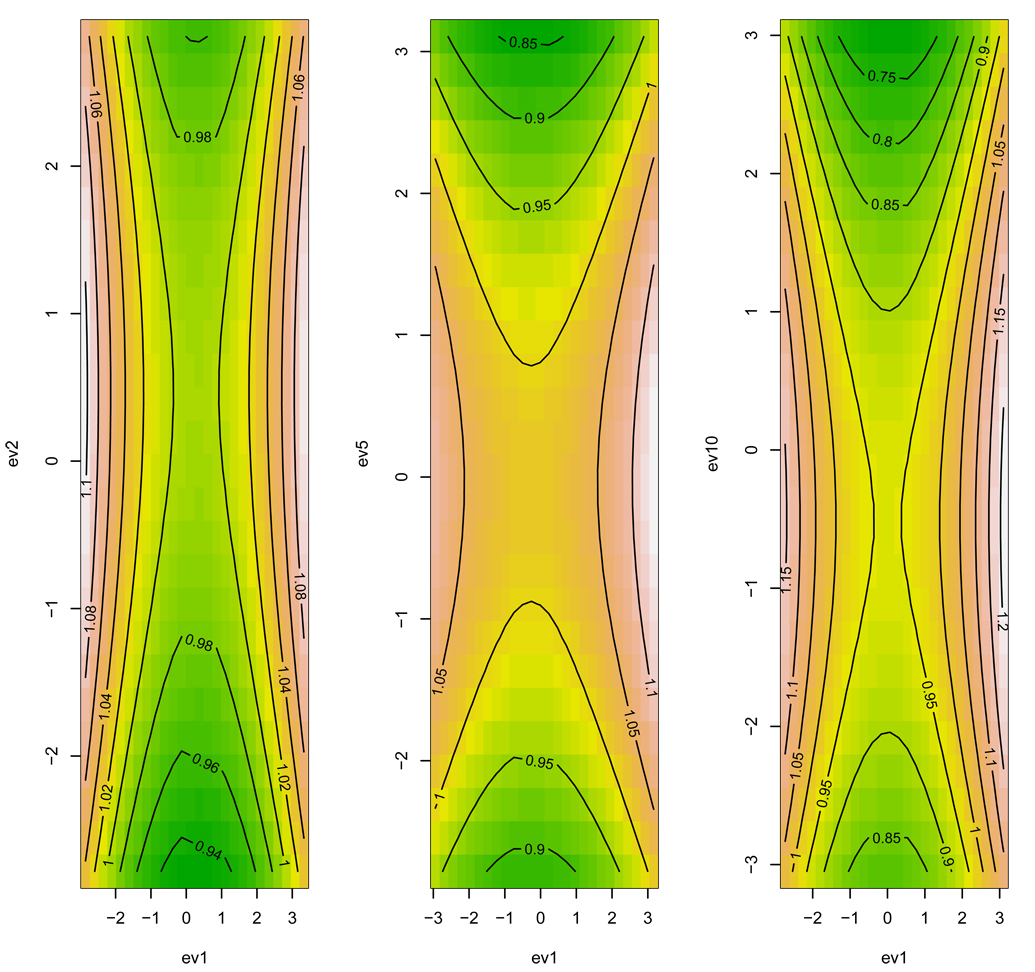
Canonical analysis is a powerful tool for finding curvature in the selection surface. However the currently accepted method in the literature for testing the significance of the eigenvalues, and hence statistical support for curvature in the selection surface, is incorrect. By all indications, the double regression method estimates of eigenvalue standard errors may be analytically correct, but we warn against using the method to test whether the eigenvalues are different from zero. The central advance of this work is linking the distributional properties of the estimates in γ with the distribution of the eigenvalues. What has perhaps gone unnoticed is how the variance of the estimates, i.e. the precision of the nonlinear selection gradients, is translated into eigenvalues via the spectral decomposition of γ. It is also interesting to note (based on our derivation with p=2), that the two eigenvalues in this case imply a saddle-shaped selection surface under the null hypothesis (Figure 3). As expected, when the dimensionality of γ increases the saddle-shaped surface is more pronounced (Figure 3). Therefore canonical analysis will reveal curvature in the selective surface even if the eigenstructure in γ actually reflects only random error. The surface describing covariance between fitness and the canonical axes can have a complex topography (e.g. Blows et al. 2003). What we now understand is that in part some of the topography is random. In order to get a sense of the true structure in the selection surface that is due to nonlinear selection, the permutation test we developed here can be used to correctly account for the random component.

Figure 3.

Contour plots of the selection surface under the null hypothesis for p = 2, 5, and 10 traits (left to right).

The derivation also helps to explain the curious pattern of the magnitudes of the mean maximum and minimium eigenvalues with different sample sizes under the null hypothesis. As the sample size increased the standard error of the estimates decreased, with the magnitudes of the eigenvalues moving closer to zero. Larger sample sizes lead to more precise estimates of the nonlinear coefficients, implying smaller sampling variability. However the gain in precision due to the larger sample sizes was not sufficient to overcome the random eigenstructure in γ for the range of sample sizes considered here. This simple derivation illustrates the problem with testing for non-zero eigenvalues. The expectations of the eigenvalues depend on the sampling variability of the nonlinear coefficients, implying that one should expect to see non-zero canonical coefficients even in the absence of nonlinear selection. Only if the variance of the selection gradients is zero, which happens in the limit as sample size approaches infinity, will the expectation of the individual eigenvalues equal zero.

Although the permutation procedure used here maintains correct error rates, it would be desirable to have a closed form expression for the full probability distribution of the ordered eigenvalues from a canonical analysis of γ for any p in order to construct test statistics that do not require permutation. Subject to certain assumptions concerning the structure of a random symmetric matrix (e.g. γ), the distributional properties of the eigenvalues is not an intractable problem [Edwards and Jones 1976, Füredi and Komlós 1981]. However, we are not aware of research that has considered the specific situation inherent to the selection problem, e.g. with potentially correlated entries in a random symmetric matrix. Furthermore, a general closed form expression for the expectation and variance of the eigenvalues would make it possible to explicitly consider the issue of bias in the estimates. Unfortunately, we are unable to address this important issue, but the permutation test is still valid for testing whether there is curvature along latent axes of the selection surface. Until results are developed for this specific situation, canonical analyses should rely upon nonparametric approaches such as permutation to obtain valid tests of significance.

With an acceptable framework in hand to perform canonical analysis we can turn to the perhaps more controversial topic of relevance. Evolutionary theory predicts that stabilizing selection should be a common if not preeminent form of selection on phenotypes as adaptive character states should be at or near their optimums. Proponents of canonical analysis have encouraged its use as a tool to detect nonlinear selection. Adaptations can be complex integrated phenotypes, and thus nonlinear selection rather than by targeting single traits, may instead act on trait combinations (correlational selection) (Blows and Hoffman 2005, Blows 2007, Arnold et al. 2008). Blows and Brooks (2003) claimed that canonical analysis had greater power to detect nonlinear selection as it can detect those axes of nonlinear selection that are not oriented in the direction of the single traits. Since the canonical rotation reduces the dimensionality of the nonlinear selection problem it is reasonable to expect higher power to detect nonlinear selection since fewer tests are being performed. Using the simulated guppy data, we explicitly considered and verified that canonical analysis indeed has higher statistical power to detect curvature than relying on the estimates in γ alone. This rigorous approach to the question of power makes it clear that if one is interested in detecting nonlinear selection, canonical analysis is the preferred method.

Based on our reanalysis of the real data on nonlinear selection on Silene virginica floral traits, it is possible that many of the published estimates of nonlinear selection using canonical analysis may not have as strong of statistical support as previously thought. Note that Reynolds et al. in press utilized the permutation procedure outlined here, and thus their reported p-values reflect the appropriate test for the eigenvalues’ significance. Using the permutation test only solid statistical support was found along the M2 canonical analysis while the conventional double regression analysis indicated curvature along the M1 and M2 axis. Of course, this result does not necessarily mean that no curvature exists along M1; we could simply have had insufficient power to detect curvature along that axis. Hersch and Phillips (2004) explicitly modeled the power to detect selection gradients, but their analysis focused strictly on the linear component. How factors such as the strength of nonlinear selection, dimensionality of γ and sample size interact to determine the power to detect curvature using canonical analysis remains to be seen. Nevertheless the power analysis attempted here suggests that the statistical power to detect curvature is higher using canonical analysis than from the estimates of γ alone.

Table 1.

The means and standard deviations (SD) of the maximum (λ_max) and minimum (λ_min) eigenvalues from the canonical analysis of γ based on 1000 simulated datasets under a null scenario of no non-linear selection. P indicates the number of traits in the analysis.

		N = 150			N = 250			N = 500			N = 1000
		λmin	λmax		λmin	λmax		λmin	λmax		λmin	λmax
p=2	Mean	−0.00904	0.00958		−0.00698	0.00702		−0.00483	0.00474		−0.00317	0.00332
	SD	0.00900	0.00877		0.00693	0.00677		0.00454	0.00467		0.00330	0.00315
p=5	Mean	−0.0263	0.0262		−0.0192	0.0191		−0.0129	0.0127		−0.00878	0.00874
	SD	0.00924	0.00910		0.00601	0.00611		0.00418	0.00422		0.00272	0.00271
p=10	Mean	−0.0587	0.0584		−0.0368	0.0367		−0.0224	0.0228		−0.0149	0.0149
	SD	0.0130	0.0131		0.00722	0.00707		0.00396	0.00407		0.00252	0.00273

Appendix

Let X, Y, and Z be random variables that define the matrix

$${[A]}_{2\times 2}=\left(\begin{array}{cc}\hfill X\hfill & \hfill Z\hfill \\ \hfill Z\hfill & \hfill Y\hfill \end{array}\right).$$

In what follows, let N (μ, σ²) define a univariate Normal distribution with expectation μ and variance σ². Similarly, let N_p (μ, Σ) denote a p-dimensional Multivariate Normal distribution with mean vector μ and variance-covariance matrix Σ.

Theorem 0.1

If (X, Y) ~ N₂ (μ, Σ) with μ = [μ_X, μ_Y] and

$$\mathrm{\Sigma }=\left(\begin{array}{cc}\hfill {\sigma }_X^2\hfill & \hfill {\sigma }_{\mathit{\text{XY}}}\hfill \\ \hfill {\sigma }_{\mathit{\text{XY}}}\hfill & \hfill {\sigma }_Y^2\hfill \end{array}\right),$$

then the eigenvalues of [A]_2×2 are the random variables

$${\mathrm{\lambda }}^{+}=G+\sqrt{U^2+Z^2}\mathit{\text{\hspace{1em} and \hspace{1em}}}{\lambda }_{-}=G-\sqrt{U^2+Z^2},$$

such that $G~N(\frac{{\mu }_X+{\mu }_Y}{2},\frac{{\sigma }_X^2+{\sigma }_Y^2+2{\sigma }_{\mathit{\text{XY}}}}{4})\mathit{\text{and}}U~N(\frac{{\mu }_X-{\mu }_Y}{2},\frac{{\sigma }_X^2+{\sigma }_Y^2-2{\sigma }_{\mathit{\text{XY}}}}{4})$.

Proof. By the definition of eigenvalue and the non-singular properties of a matrix, λ is an eigenvalue of the matrix A if, and only if, det(A − λI) = 0, where I is the identity matrix. Since det(A − λ I) = λ² − (X + Y)λ + XY − Z², the eigenvalues of A can be solved by using the quadratic formula. Hence

$$\mathrm{\lambda }=\frac{X+Y^{\pm }\sqrt{{(X-Y)}^2+4Z^2}}{2}.$$

Notice that since (X − Y)² + 4Z² ≥ 0, the two eigenvalues are well-defined real numbers. Let us denote these eigenvalues by

$$\begin{array}{cc}{\lambda }^{+}=G+W\hfill & \text{and \hspace{1em}}{\lambda }_{-}=G-W\hfill \\ \hfill & -\text{with}G=\frac{X+Y}{2}\text{and}W=\frac{\sqrt{{(X-Y)}^2+4Z^2}}{2}.\hfill \end{array}$$

Notice that W can be simplified to $W=\sqrt{{(\frac{X-Y}{2})}^2+Z^2}$. If we let $U=\frac{X-Y}{2}$, then the distributions of G and U directly follow from the properties of Normal random variables.

Theorem 0.2

Let ${[\gamma ]}_{2\times 2}=\left(\begin{array}{cc}\hfill {\gamma }_1\hfill & \hfill {\gamma }_3\hfill \\ \hfill {\gamma }_3\hfill & \hfill {\gamma }_2\hfill \end{array}\right)$ be a matrix with random entries (γ₁, γ₂, γ₃) ~₃ (0, Σ) such that

$$\mathrm{\Sigma }=\left(\begin{array}{ccc}\hfill {\sigma }_{11}^2\hfill & \hfill {\sigma }_{12}\hfill & \hfill {\sigma }_{13}\hfill \\ \hfill {\sigma }_{12}\hfill & \hfill {\sigma }_{22}^2\hfill & \hfill {\sigma }_{23}\hfill \\ \hfill {\sigma }_{13}\hfill & \hfill {\sigma }_{23}\hfill & \hfill {\sigma }_{33}^2\hfill \end{array}\right).$$

Let λ⁺, λ₋ represent the random variables defined by the eigenvalues of γ. Then we have that

$$\frac{\sqrt{2\pi }}{\pi }(\sigma U+{\sigma }_{33})\ge |\mathrm{E}({\mathrm{\lambda }}^{+})|=|\mathrm{E}({\mathrm{\lambda }}_{-})|\ge \frac{\sqrt{2\pi }}{\pi }\text{max}\{{\sigma }_U,{\sigma }_{33}\}),$$

where ${\sigma }_U=\frac{\sqrt{{\sigma }_{11}^2+{\sigma }_{22}^2-2{\sigma }_{12}}}{2}$.

Proof. First, the eigenvalues result from Theorem 0.1. Then note that since the means of γ₁ and γ₂ are zero under the null hypothesis, it follows by the properties of expectation that

$$|\mathrm{E}({\mathrm{\lambda }}^{+})|=|\mathrm{E}({\mathrm{\lambda }}_{-})|=\mathrm{E}(\sqrt{U^2+{\gamma }_3^2}).$$

Next, we will show that $\mathrm{E}(\sqrt{U^2+{\gamma }_3^2})\ge \frac{\sqrt{2\pi }}{\pi }\text{max}\{{\sigma }_U,{\sigma }_{33}\})$, where σ_U is defined as above. To see this, note that since $\sqrt{U^2+{\gamma }_3^2}\ge \text{max}\{|U|,|{\gamma }_3|\}$, the properties of expectation imply that $\mathrm{E}(\sqrt{U^2+{\gamma }_3^2})\ge \text{max}\{E|U|,\mathrm{E}|{\gamma }_3|\}$. Also note that $U~N(0,\frac{{\sigma }_{11}^2+{\sigma }_{22}^2-2{\sigma }_{12}}{4})$ by Theorem 0.1 and ${\gamma }_3~N(0,{\sigma }_{33}^2)$ by assumption under the null. This implies that $\mathrm{E}(|U|)=\frac{\sqrt{2\pi ({\sigma }_{11}^2+{\sigma }_{22}^2-2{\sigma }_{12}})}{2\pi }\text{and}\mathrm{E}(|{\gamma }_3|)={\sigma }_{33}\frac{\sqrt{2\pi }}{\pi }$. Now to see that $\frac{\sqrt{2\pi }}{\pi }({\sigma }_U+{\sigma }_{33})\ge \mathrm{E}(\sqrt{U^2+{\gamma }_3^2})$, observe that by the triangle inequality we have that $|U|+|{\gamma }_3|\ge \sqrt{U^2+{\gamma }_3^2}$. Then, again using the properties of expectation, this implies that $\mathrm{E}(|U|)+\mathrm{E}(|{\gamma }_3|)\ge \mathrm{E}(\sqrt{U^2+{\gamma }_3^2})$, with the expectations of |U| and |γ₃| derived above.