Analyzing Family Data: A GEE Approach for Substance Use Researchers

Abstract

Introduction

Analyzing data that arises from correlated observations such as husband-wife pairs, siblings, or repeated assessments of the same individuals over time requires more specialized analytic tools. Additionally, outcomes that are not normally distributed, count data, such as number of symptoms or number of problems endorsed, also require specialized analytic tools. Generalized Estimating Equations (GEE) are a very flexible tool for dealing with correlated data (such as data derived from related individuals such as families). The objective of this report was to compare traditional Ordinary Least Squares Regression (OLS) to a GEE approach for analyzing family data.

Methods

Using data from an ongoing five-wave longitudinal study of newlywed couples, we examined a subset of 173 families with children between the ages of 4 and 11 at two data collection points. The relation between parental risk factors (e.g., heavy drinking, aggression, marital quality) and child internalizing symptoms was examined within the context of two regression-based models: traditional OLS regression and a GEE approach.

Results

Overall, the GEE approach allowed a more complete use of the available data, provided more robust findings, and produced more reliable parameter estimates.

Conclusion

GEE models are a flexible regression-based approach for dealing with related data that arises from correlated data such as family data. Further, given the availability of the models in common statistical programs, family researchers should consider these models for their work.

1.0 Introduction

Although the choice of an appropriate statistical technique is often straightforward, there are a number of circumstances in which this decision presents a challenge for many researchers. This problem can be particularly difficult for researchers whose work does not focus on individual participants. For example, researchers who study family processes and have assessments on multiple family members such as husbands and wives or siblings, have an extra level of data analytic complexity—these related family members cannot be considered ‘independent.’ This lack of independence means that many traditional approaches to analyzing data (e.g., ordinary least squares (OLS) regression) cannot be used to analyze data as one of the key assumptions for OLS regression is that all observations are independent of one another (Kleinbaum, Kupper, Muller, & Nizam, 1998). With family analysis on spouses or siblings, this assumption is clearly violated.

In order to alleviate this problem, some researchers have opted to not study all siblings in a family, but rather focus on a targeted child. For example, some researchers have selected the first born child, selected the youngest child within an age range, or randomly selected one sibling out of the family to be the study participant. This method clearly avoids the issue of independence; however, it fails to capture the richness of the family unit and it reduces the overall sample size by assessing only one child of a multi-child family.

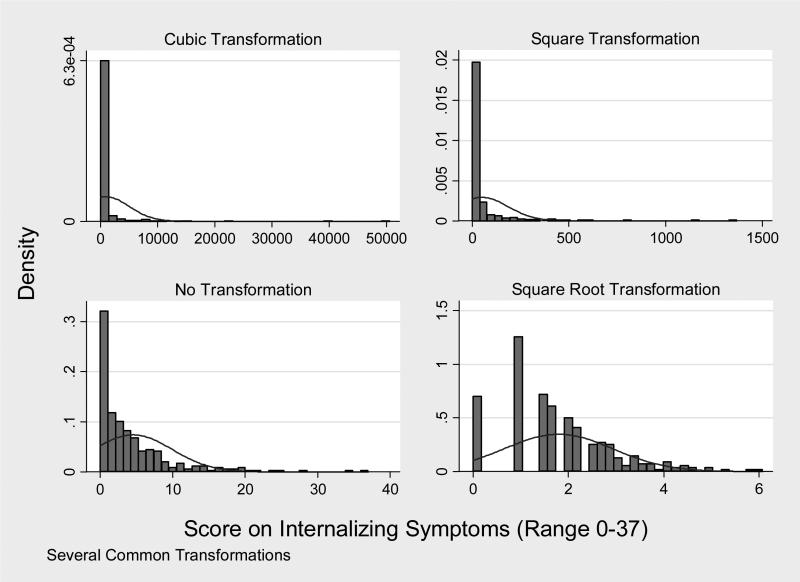
Another analytic problem that challenges some traditional data analytic techniques is the correct characterization of the outcome variable. Many researchers believe that the main regression models are limited to two choices, binary logistic regression models for a categorical outcomes, or linear regression models for continuous outcomes. Therefore, when researchers have an outcome variable that is score from a questionnaire (for example, number of symptoms in the past week), they often feel forced to choose between those two general models and will select linear regression models (Byers, Allore, Gill, & Peduzzi, 2003). Scores from many questionnaires, however, are not normally distributed, continuous variables. Rather, they often take on a limited range of values and tend to be right skewed and clustered around zero (see Figure 1) and do not fit the assumptions of OLS regression models (Gardner, Mulvey, & Shaw, 1995). Oftentimes researchers will employ a variety of transformations in attempt to make the data appear more normally distributed. However, in highly skewed data that has a preponderance of zeros, these transformations are often not sufficient. As shown in Figure 2, the bottom left panel is the raw data and the other panels present three common transformations. As shown in the Figure, the transformations do little to make the data normalized. Additionally, transformations also present other problems that complicate their use (Fisher & Van Belle, 1993).

Figure 1.

Distribution of observed scores from a questionnaire with normal probability plot fitted to the current data.

Figure 2.

Other regression-based models are available to handle correlated data structures as well as a variety of outcome variable distributions. One such model, Generalized Estimating Equations (GEE), is a very flexible approach to handling correlated data structures (Liang & Zeger, 1993). GEE models can handle a variety of correlated measure models that arise from family research (e.g., mother-child, husband-wife, brother-sister, etc.) or correlated data that arise from repeated measures of the same individuals over time (Diggle, Liang, & Zeger, 1994; Homish & Leonard, 2007; Homish, Leonard, & Cornelius, 2007; Liang & Zeger, 1993; Zeger & Liang, 1992). Additionally, these models can handle a variety of outcome data types (e.g., continuous, count, binary) as well as time-varying and time-invariant predictors and GEE models are more flexible for missing data compared to other models (Zeger, Liang, & Albert, 1988). These models are easily implemented on common, general statistical software packages such as SPSS (http://www.spss.com/advanced_models/), SAS (http://www.sas.com/technologies/analytics/statistics/stat/features.html), and Stata (http://www.stata.com/capabilities/panel.html) (For a review, see: Horton & Lipsitz, 1999).

The objective of this work was to present an easily accessible application of GEE methods to analyze data from multiple siblings. Specifically, it examined how several maternal, paternal, and relationship factors (e.g., heavy drinking, aggression, marital satisfaction) were related to the presence of internalizing symptoms among their children. Importantly, all siblings for each family are included in the analyses and the outcome is modeled as a count outcome, given its limited distribution with a clustering on zero indicating no internalizing symptoms. The GEE approach is contrasted to an Ordinary Least Squares Regression model. This paper is designed to present an overview of the application of GEE to real world data. It is not intended to provide information on the statistical theory behind GEE models and, given space limitations and the extreme flexibility of the GEE models, this article is not intended to be a step-by-step user manual. Readers interested in statistical development of the GEE approach are referred to the work of Zeger and colleagues (Liang & Zeger, 1993; Zeger & Liang, 1992; Zeger et al., 1988) and for more detailed information on the step-by-step procedures, readers are referred to Hardin and Hilbe (2003) or Twisk (2003).

2.0 Methods

2.1 Participants

Participants for this report were involved in a longitudinal study of marriage and alcohol involvement. All participants were at least 18 years old, spoke English, and were literate. Couples were ineligible for the study if they had been previously married. The main study consisted of 634 couples. The current report focused on only couples with at least one child between the ages of 4 and 11. This subsample consists of 173 families and 259 children between the ages of four and eleven. The majority of families had one or two children in our targeted age range (91 families had only one child, 73 families had two children in our target age range). Seven families had 3 children in our targeted age range and one family had 5 children in the targeted age range. At the initial assessment, the average age of the full sample of fathers was 28.7 (SD=6.3) years and the average of the mothers was 26.8 (SD=5.8) years. The majority of the fathers and mothers in the sample were European American (fathers: 59%; mothers: 62%). About one-third of the sample was African American (fathers: 33%; mothers: 31%). The sample also included small percentages (less than 5%) of Hispanic, Asian, and Native American participants. A large proportion of fathers and mothers had at least some college education (fathers: 64%; mothers: 69%) and most were employed at least part-time (fathers: 89%; mothers 75%). Consistent with other studies of newly married couples (Chadiha, Veroff, & Leber, 1998; Crohan & Veroff, 1989; Orbuch & Veroff, 2002), many of the couples were parents at the time of marriage (38% of the fathers and 43% of the mothers) and were living together prior to marriage (70%). The Institutional Review Board of the State University of New York at Buffalo approved the research protocol.

2.2 Procedures

After applying for a marriage license, couples were recruited for a 5-10 minute paid ($10) interview. The interview assessed demographic factors (e.g. race, education, age), family and relationship factors (e.g. number of children, length of engagement), and substance use questions (e.g. tobacco use, average alcohol consumption, frequency of intoxication in the past year). Recruitment occurred over a 3-year period from 1996-1999. For interested individuals who did not have time to complete this interview, a telephone interview was conducted later that day or the next day (N = 62). Less than 8% of individuals approached declined to participate in the brief recruitment interview. We interviewed 970 eligible couples.

Complete details of the recruitment process can be found elsewhere (Homish & Leonard, 2007; Leonard & Mudar, 2003), but briefly, couples who agreed to participate in the longitudinal study were given identical questionnaires to complete at home and asked to return them in separate postage paid envelopes (Wave 1 Assessment). Participants were asked not to discuss their responses with their partners. Each spouse received $40 for his or her participation. Only 7% of eligible couples refused to participate in the longitudinal study. Those who agreed to participate, compared to those who did not, were more likely to have lower incomes (p < .01) and the women were more likely to have children (p < .01). No other differences were identified. Of the 887 eligible couples who agreed to participate (13 of the original 900 did not marry), data were collected from both spouses for 634 couples (71.4%). Couples who returned the questionnaires were more likely to be living together compared to couples who did not return the questionnaires (70% vs. 62%; p < .05) and more likely to be European American. No other sociodemographic differences existed between the couples who responded compared to those who did not. Average past year alcohol consumption did not differ between couples that returned the questionnaires and those who did not. Fathers in non-respondent couples consumed 6 or more drinks or were intoxicated in the past year more often than fathers who completed the questionnaire; however, these differences were small.

At the couples’ first, second, fourth and seventh wedding anniversaries (Waves 2, 3, 4, and 5), they were mailed questionnaires similar to those they received at the first assessments. As with the first assessment, they were asked to complete the questionnaires and return them in the postage paid envelopes. Each spouse received $40 for his or her participation for assessments 2 and 3 and $50 for the fourth and fifth assessment. At the fifth assessment, 79.7% (N= 505) of women completed the questionnaire. Mothers who did not complete the fifth assessment did not differ from others mothers in terms of Wave 1 frequency of heavy drinking, alcohol expectancies, or marital satisfaction. At the fifth assessment, 68.1% (N= 432) of the original sample of fathers completed the questionnaires. Fathers who did not participate in the fifth assessment did not differ from other fathers on the basis of Wave 1 frequency of heavy drinking, alcohol expectancies or marital satisfaction. Following the completion of Wave 5, mothers with children under the age of 18 were sent questionnaire booklets. Families were paid $25 for each child booklet. Of the 356 packets that were mailed, 283 were returned (79.5%). The basis for this report is the 173 families with children between the ages of 4 and 11.

2.3 Measures: Outcome Variable

2.3.1 Child Internalizing Symptoms

Internalizing behavior problems were assessed with the 4-18 year old version of the Child Behavior Checklist (CBCL; Achenbach, 1994), which was completed by mothers at Wave 6. The CBCL is a widely used measure of children's behavioral/ emotional problems with well-established psychometric properties (Achenbach, 1994). Higher scores indicate higher levels of anxious, withdrawn, and depressed child behavior. The coefficient alpha of the internalizing subscale was .87.

Measures: Predictor Variables

2.3.2 Heavy Drinking

Heavy drinking was assessed with two items. Frequency of past year intoxication was assessed on a 9-point scale that ranged from “didn't get drunk last year” (coded 0) to “everyday” (coded 8). The frequency of drinking 6 or more drinks on an occasion in the past year was also assessed using the same 9-point scale. Following our earlier work (Homish & Leonard, 2007) heavy drinking was defined as the maximum of these two responses. Heavy drinking at Wave 5 was used in the models to predict Wave 6 child outcomes.

2.3.3 Depression

Depressive symptomatology was assessed at each interview using the Center for Epidemiologic Studies-Depression Scale (CES-D, Radloff, 1977). The CES-D is a 20-item self-report questionnaire. Each item is scored 0 to 3 with a possible total score ranging from 0 to 60. A higher score indicates a greater level of depressive symptomatology. This instrument does not provide a diagnosis of depression, however, in this report the term depression will also be used to indicate depressive symptomatology. The average coefficient alphas were 0.88 for fathers and 0.90 for mothers. Depression scores at Wave 5 were standardized to predict Wave 6 child outcomes.

2.3.4 Antisocial Behavior

Antisocial behavior was assessed at Wave 1 using 28 items from the Antisocial Behavior Inventory (Zucker & Noll, 1980). The Inventory assesses frequency of childhood (e.g., suspended from school) and adult (e.g., defaulted on a debt) antisocial behaviors using a 4-point scale (1 = never, 4 = often). Coefficient alphas were high for both the fathers (.90) and mothers (.86). Antisocial behavior scores were standardized to predict Wave 6 child outcomes.

2.3.5 Relationship Quality

Overall marital quality was assessed with the 15-item Marital Adjustment Test (MAT) (Locke & Wallace, 1959). Higher scores indicated greater relationship quality (range: 2-158). The MAT had an adequate reliability for the study (alpha= .81 for fathers; .80 for mothers). The MAT score at Wave 5 was standardized for the regression models and was used to predict Wave 6 child outcomes.

2.3.6 Physical Aggression

The physical assault subscale of the Conflict Tactics Scale – Revised (CTS-2; Straus, Hamby, Boney-McCoy, & Sugarman, 1996) was used to assess partner physical aggression. Respondents were asked the number of times in the past year that they and their partners engaged in a number of physically aggressive behaviors during a disagreement. To control for the under reporting of violence, a combined score representing the maximum of self-report and partner report of aggression served as the measure of physical aggression for both fathers and mothers. Reliability estimates (Cronbach's alpha) for the CTS-2 ranged from .86 to .94 across father and mother reports of their own and their partner's aggression. Wave 5 husband-to-wife aggression and wife-to-husband aggression were used to predict Wave 6 child outcomes.

2.3.7 Demographic Factors

Each spouses’ age, race/ethnicity, highest level of education obtained was included in the models as covariates. Child gender and child age were also included in the models as covariates.

2.4 Analysis

Two analyses were conducted to examine the relation between parental factors at one assessment and child outcomes at the next interview. The first approach, ordinary least squares (OLS) regression, requires that the observations are independent. Therefore, to meet this assumption, it was necessary to select only one child per family. For the OLS model, we selected the oldest child within the 4 to 11 year old age range. Additionally, OLS regression is designed for normally distributed, continuous outcome data. Based on Figure 1, this validity of this assumption is clearly questionable given the excess zero scores and the apparent skew. Further, the full range of our outcome variable is limited between the values of 0 and 37 and common transformations do little to improve the distribution (Figure 2).

The second approach utilized Generalized Estimating Equations (GEE) (Zeger & Liang, 1986; Zeger, Liang, & Albert, 1988). GEE models are used to analyze correlated data with binary, discrete, or continuous outcomes (Zeger et al., 1988). In the case of the current report, all children in the targeted age range were included in the model. In order to use a GEE model, several decisions must be made. First, the distribution of the outcome variable needs to be assessed. Based on Figure 1, the distribution of the outcome variable (count variables with a limited range, excess zero, large skew) suggests that a Poisson or Negative Binomial Family should be specified. Both of these distributions are appropriate for our count outcomes; however, the restrictive assumptions of Poisson model make the negative binomial model a more appropriate choice (Byers, Allore, Gill, & Peduzzi, 2003; Gardner, Mulvey, & Shaw, 1995). In addition to selecting the Family of the distribution, the correct link function must be specified. Although the statistical underpinnings of the link function are beyond the scope of this article, it is important to select an appropriate link function. For the current report, a log link is appropriate for either family. In the event that our outcome was continuous, a Gaussian (i.e., Normal) distribution would be selected for the family with an identity link. For binary outcomes, a binomial family with a logit link is one appropriate combination.

The next step in executing a GEE model is selecting an appropriate correlation structure. Because of the flexibility of the GEE models, there are variety of correlations that can be specified. For example, in a repeated measures design, an autoregressive correlation could be specified whereas for clustering at, for example, a family level, an exchangeable correlation structure is often more appropriate (Ballinger, 2004). Regardless of the specification of the correlation, GEE models are robust to the misspecification of the correlations structure (Zeger & Liang, 1986). Additionally, selecting robust standard errors (Huber/White Sandwich Estimators; as opposed to conventional standard errors) will allow the estimates to be valid even in the event of misspecification of the correlation structure (StataCorp, 2003). The results for the current GEE models are presented as Risk Ratios (RR). It is important to note, however, that parameter estimates can be provided as regression coefficients (for continuous outcome models) or Odds Ratios (for binary outcome models). RR's have a lot of appeal to many researchers because the interpretation can be a more intuitive measure of risk. RR's that are greater than 1 are interpreted as increasing the likelihood of an outcome (i.e., increasing risk) whereas ratios less than 1 are interpreted as decreasing the likelihood of an outcome (i.e., protective). RR's that are equal to 1 are not significantly associated with either increased or decreased risk. For example, in Table 1, the risk ratio for child age is 1.10. Thus, the interpretation means that for each year increase in age, there is a 10% increased risk for a one unit increase on the internalizing symptoms scale. It is important to note that the standard errors do not change on the basis of reporting of regression coefficients or risk ratios (or odds ratios), as risk ratios (as well as odds ratios) are simply calculated by exponentiating the coefficient.

Table 1.

Comparing OLS and GEE approaches

	OLS Regression				GEE Regression
	Regression Coefficient	Standard Error	95% Confidence Interval		Risk Ratio	Standard Error	95% Confidence Interval
H Heavy drinking	0.39	0.43	−0.46	1.25	0.96	0.04	0.89	1.04
W Heavy drinking	0.13	0.28	−0.43	0.69	1.16**	0.06	1.04	1.29
H Depression	0.77	0.55	−0.31	1.85	1.17*	0.09	1.01	1.37
W Depression	1.24*	0.59	0.08	2.40	1.27**	0.10	1.09	1.48
H Antisociality	1.57	1.59	−1.58	4.71	0.91	0.21	0.57	1.43
W Antisociality	2.12	2.52	−2.87	7.10	1.44	0.53	0.69	2.98
H Marital Satisfaction	−0.17	0.46	−1.08	0.75	1.03	0.07	0.90	1.19
W Marital satisfaction	−0.28	0.54	−1.34	0.78	0.98	0.08	0.84	1.15
H->W aggression	−0.15	0.09	−0.33	0.03	0.99	0.01	0.96	1.01
W->H aggression	0.07	0.07	−0.06	0.20	1.00	0.01	0.98	1.02
Child Gender	0.25	0.82	−1.37	1.87	1.13	0.14	0.88	1.17
Child Age	0.15	0.27	−0.38	0.68	1.10***	0.03	1.04	1.17
H Age	0.01	0.13	−0.24	0.26	0.98	0.02	0.94	1.02
W Age	−0.13	0.13	−0.39	0.14	0.99	0.02	0.96	1.03
H Race/Ethnicity	1.57	1.70	−1.78	4.93	1.38	0.44	0.75	2.57
W Race/Ethnicity	−0.66	1.72	−4.06	2.73	0.71	0.23	0.38	1.33
H Education	0.84	1.05	−1.25	2.92	0.97	0.19	0.67	1.41
W Education	−0.20	1.07	−2.31	1.91	1.05	0.17	0.76	1.44

Note. H: Husband; W: Wife

OLS: Ordinary least squares regression N= 173; GEE: Generalized Estimating Equations N= 259

^*p<.05

^**p<.01

^***p<.001

3.0 Results

Two models were used to study the relation between parental factors and child internalizing symptoms at a subsequent assessment. Both models contained the same mother and father substantive predictors (e.g., heavy drinking and depression) and covariates (e.g., age, education) as well as controlling for child factors such as age and gender. When contrasting the methodologies, there are three main findings of interest. The first main difference between the two models was the significant difference in overall sample size between the two models. As described above, the traditional OLS regression required that each family could only provide data from one child per family so that the assumption of independence of observations is not violated. This resulted in a sample reduction of 86 children (259 for GEE vs. 173 for OLS).

The second main difference is between the substantive content findings. In the OLS model, only one variable was significant. Mothers with greater levels of depression at Wave 5 were more likely to have children with more internalizing symptoms at the next assessment (Table 1, left columns). Consistent with the OLS findings, the GEE model found that mothers’ depression was significantly associated with child's internalizing symptoms at the next wave. Unlike the OLS model, several other factors also emerged as significant predictors of child internalizing symptoms. For example, fathers’ depression and mothers’ heavy drinking were also significantly related to child's internalizing symptoms at the subsequent interview. In addition, because the OLS was limited to only one child per family, there was less variability in the age of the children; thus, the significant positive association between increasing child age and internalizing symptoms was not found in the OLS model but was found in the GEE model.

Finally, the precision of the estimates differed greatly. Precision of the parameter estimates is assessed with the sampling variation; the most common measure of which is the standard error (Singer & Willett, 2003). When comparing the OLS and GEE approaches, it is clear that there is a consistent trend for the OLS approach to have larger standard errors compared to the GEE approach. In terms of specific comparisons, it is most appropriate to consider the differences in standard error only for parameters that reached our a priori significance of 0.05. Thus, we examined the standard errors for mothers’ depression, and found that the OLS approach yielded a standard error of 0.59 compared to 0.10 for the GEE approach.

4.0 Discussion

Real world data, by violating key assumptions to traditional statistical approaches, can present many challenges to selecting an appropriate analytic approach. The current report focused on modeling correlated data that arises from observations that fail the assumption of independence, such as those arising from family data or repeated assessments of the same individuals. The current report presented a brief introduction of the GEE approach for handling such data. Although the current report focused on data within families, the methodology can easily be adapted for repeated assessments of the same individuals (e.g., Homish et al., 2007).

There are many benefits of the GEE approach. For example, there is considerable flexibility in the GEE approach; these models can appropriately handle a variety of outcome distributions such as continuous outcomes, binary outcomes, and count outcomes. Additionally, they can appropriately handle time varying and time-invariant predictors and can display risk ratios or odds ratios for count and binary outcomes, respectively. In terms of longitudinal designs, GEE models are also more flexible with missing data compared to traditional repeated measures ANOVA's that require listwise deletion to handle missing values. Finally, these models are easily accessible with common general purpose statistical packages.

The current reported demonstrated three major findings when comparing the two approaches. First, there was a significant reduction in sample size when meeting the rigid assumption of OLS independence of observations. That is, with the OLS approach, multiple children in each family were not able to be included in the models because of the correlation within the families. Therefore, only one child per family was used in the OLS approach. By utilizing GEE, the sample analyzed was increased by 86 children and a richer analysis of the family unit was obtained. Second and perhaps most notably, the OLS approach failed to capture several key predictor variables that related to increased risk of child internalizing symptom outcomes. In fact, only one variable was significant the OLS model. Using GEE, other significant predictors were identified and the development of child internalizing behavior more clearly understood. Finally, the precision of the estimates, as assessed by the standard errors, was much greater in the GEE approach. Findings demonstrate the considerable strengths of GEE for analyzing family data and its potential utility as a tool for family researchers.

In conclusion, this report was meant to highlight the accessibility of other regression-based approaches available to researchers. As shown, GEE provides a powerful framework for analyzing the correlated data so common to family research as well as longitudinal research. The vast flexibility of the GEE methodology, although a benefit, prevents a detailed exposition of all available options and procedures in the current report. The interested reader is encouraged to refer to the literature cited in the introduction for a more detailed description of the methodology.