Covariate adjustment in randomized trials with binary outcomes: Targeted maximum likelihood estimation

SUMMARY

Covariate adjustment using linear models for continuous outcomes in randomized trials has been shown to increase efficiency and power over the unadjusted method in estimating the marginal effect of treatment. However, for binary outcomes, investigators generally rely on the unadjusted estimate as the literature indicates that covariate-adjusted estimates based on the logistic regression models are less efficient. The crucial step that has been missing when adjusting for covariates is that one must integrate/average the adjusted estimate over those covariates in order to obtain the marginal effect. We apply the method of targeted maximum likelihood estimation (tMLE) to obtain estimators for the marginal effect using covariate adjustment for binary outcomes. We show that the covariate adjustment in randomized trials using the logistic regression models can be mapped, by averaging over the covariate(s), to obtain a fully robust and efficient estimator of the marginal effect, which equals a targeted maximum likelihood estimator. This tMLE is obtained by simply adding a clever covariate to a fixed initial regression. We present simulation studies that demonstrate that this tMLE increases efficiency and power over the unadjusted method, particularly for smaller sample sizes, even when the regression model is mis-specified.

1. INTRODUCTION

Suppose we observe n independent and identically distributed observations of the random vector O = (W, A, Y) ~ p₀, where W is a vector of baseline covariates, A is the treatment of interest and Y = {0,1} is the binary outcome of interest, and p₀ denotes the density of O. Causal effects are based on a hypothetical full data structure X = ((Y_a : a ∈ 𝒜), W) containing the entire collection of counterfactual or potential outcomes Y_a for a ranging over the set of all possible treatments 𝒜.

The observed data structure O only contains a single counterfactual outcome Y = Y_A corresponding to the treatment that the subject received. The observed data O = (W, A, Y ≡ Y_A) is thus a missing data structure on X with missingness variable A. We denote the conditional probability distribution of treatment A by g₀(a|X) ≡ P (A = a|X). The randomization assumption or coarsening at random assumption states that A is conditionally independent of the full data X given W, g₀(A|X) = g₀(A|W). In a randomized trial in which treatment is assigned completely at random, we have g₀(A|X)=g₀(A). For the sake of presentation, we assume that the treatment A is binary and that A is completely randomized as in a typical randomized trial, but our methods are presented so that it is clear how our estimators generalize to observational studies or randomized trials in which g₀(A|W) is known. In the binary A case, g₀(1) = p(A = 1) = δ₀ and g₀(0) = p(A = 0) = 1 − δ₀ and n₁ the number of subjects in treatment group 1 and n₀ the number of subjects in treatment group 0, and n = n₁ + n₀. The quantity of interest is the causal effect of treatment A on Y, for example the risk difference (RD) ψ = E(Y₁) − E(Y₀), where Y₁ and Y₀ are the counterfactual outcomes under treatments 1 and 0, respectively. We note that as an alternative to the counterfactual presentation, we can write the parameter of interest as ψ = E_W[E(Y|A = 1, W) − E(Y|A = 0, W)]. This quantity is typically estimated in randomized trials with the unadjusted estimate

$${\widehat{\psi }}_1={\widehat{\mu }}_1-{\widehat{\mu }}_0$$

where ${\widehat{\mu }}_1=1/n_1{\displaystyle {\sum }_{i=1}^{n}I(A_i=1)Y_i}\text{and }{\widehat{\mu }}_0=1/n_0{\displaystyle {\sum }_{i=1}^{n}I(A_i=1)Y_i}$. An adjusted effect is also sometimes obtained;

$${\widehat{\psi }}_W=\widehat{P}(Y=1|A=1,W)-\widehat{P}(Y=1|A=0,W)$$

Adjusting for baseline covariates and the issues involved has been discussed in [1]. Although it has been recognized, at least for linear models, i.e. continuous outcomes, that adjusting for covariates increases the precision of the estimate of the marginal causal effect of treatment, investigators are still resistant to adjusting in logistic models and often rely on the unadjusted estimate. This generally appears to be due to confusion as to how to select the covariates and how to adjust for them [1]. In addition, there is a concern that if data-adaptive procedures are used to select the model for P(Y = 1|A, W) then investigators will be tempted to select the model that provides the most favorable results. However, we recommend that as long as the procedure is determined a priori we can avoid this latter issue. Thus, a black box-type data-adaptive procedure, e.g. forward selection, can still be applied as long as the algorithm and candidate covariates are specified a priori.

Adjusting for covariates with main terms in linear models, referred to as analysis of covariance in the randomized trial literature, for the purpose of estimation of the marginal causal effect has been limited to no interaction terms with treatment. When there is such an interaction term, it is often not clear in the literature on the analysis of randomized trial data how one uses this conditional model to obtain a marginal effect. However, even in the absence of the interaction term, the increase in precision has not been observed for nonlinear models such as the logistic model. In fact, it has actually been reported that the estimates are not more precise for logistic models [2, 3]. The crucial step that has been missing when the parameter of interest is the marginal causal effect of A on Y, is that when adjusting for covariates W, one must integrate/average the adjusted estimate over those W in order to obtain a marginal effect estimate that is comparable to the unadjusted effect estimate ψ̂₁. This method of averaging over W has been referred to as the G-computation formula and is often applied in observational studies when the treatment or exposure has not been assigned randomly [4, 5]. We show that with this additional step of averaging over W, even when the outcome is binary, and even if the regression model is mis-specified, we obtain a more efficient estimate in the randomized trial setting. Such an approach allows for interactions between A and W in the model for P(Y = 1|A, W) while still obtaining a marginal effect. We note that the conditional effect may be the parameter of interest in some studies, for example the effect of a drug conditional on age, and thus the investigator does not want to average over age.

In this paper we focus only on the marginal effect and using the covariates W to obtain the most efficient (precise) estimate of this marginal causal effect in a non-parametric model under the framework of targeted maximum likelihood estimation (tMLE). This estimation procedure is a new approach to statistical learning introduced in [6]. This general tMLE methodology applies to any estimation problem; however, here it is applied to the estimation of the RD, relative risk (RR) and odds ratio (OR), in the context of a randomized trial with and without censoring. This framework provides a new approach to covariate adjustment in randomized trials. In a few special cases the targeted maximum likelihood estimator is equivalent to the double robust inverse probability of treatment weighted (DR-IPTW) based on plug-in maximum likelihood estimates of the nuisance parameters. The DR-IPTW estimator is defined as the solution to the efficient influence curve estimating equation [7–10]. In [11], the DR-IPTW estimator was applied to the estimation of the average difference in outcomes between treatment in randomized trials with no censoring. This is an example where the efficient influence curve and targeted maximum likelihood estimators coincide. However, this is not generally true as demonstrated in examples provided in this paper.

In summary, the goals of this paper are threefold. First, we apply tMLE as a method of covariate adjustment to the estimation of marginal effects of treatment in randomized trials with binary outcomes. The second is to demonstrate the improved performance of this locally efficient estimator relative to the unadjusted method. The third goal is to compare different strategies of covariate adjustment, e.g. data-adaptive model selection algorithms, using simulation studies. This paper is structured as follows. In Section 2 we provide a brief overview of methods for covariate adjustment that have been proposed in the literature. In Section 4 we present the targeted maximum likelihood estimators for three marginal variable importance parameters: the RD, RR and OR. We address missing data on the outcome and covariates, and estimation of the treatment mechanism. In Section 6 we provide a formal relation between R² and efficiency gain. Section 5 provides testing and inference for the tMLE. In Section 7 we present simulation studies that demonstrate the performance of the tMLE. Finally, we conclude with a discussion in Section 8.

2. TARGETED MAXIMUM LIKELIHOOD ESTIMATION

Traditional MLE aims for a trade-off between bias and variance for the whole density of the observed data. Investigators however are typically not interested in the whole density of the data O, but rather a specific parameter of it. tMLE was purposefully named in that it carries out a bias reduction specifically tailored for the parameter of interest. For technical details about this general estimation approach we refer the reader to its seminal article [6].

Consider a model ℳ which is a collection of possible probability distributions of the data, where the true distribution of the data is p₀. Consider an initial estimator p̂. We are interested in a particular feature of the data, ψ₀ = ψ(p₀). The goals of tMLE are twofold. First, it aims to find a density p̂^* ∈ ℳ that solves the efficient influence curve for estimating equation for the parameter of interest resulting in a bias reduction as compared with the maximum likelihood estimate ψ(p̂). Second, the algorithm requires that p̂^* also achieves a small increase in the log-likelihood relative to p̂. The algorithm achieves these goals by identifying a ‘stretching’ of the initial p̂ so that it yields a maximal change in ψ. This is done by constructing a path denoted by p̂(ε) through p̂ where ε is a free parameter. The score of this path at ε = 0 equals the efficient influence curve. The optimal amount of ‘stretch’ is obtained by maximizing the likelihood of the data over ε. Applying this optimal stretch to p̂ yields p̂¹, which is the first step of the targeted maximum likelihood algorithm. This process is iterated until the ‘stretch’ is essentially zero. The final step of the algorithm gives the targeted maximum likelihood estimate p̂^*, which solves the efficient influence curve estimating equation thereby achieving the desired bias reduction with a small increase in the likelihood. The resulting substitution estimator ψ(p̂^*) is a familiar type of likelihood-based estimator and due to the fact that it solves the efficient influence curve estimating equation it thereby inherits its properties including asymptotic linearity, and local efficiency [7]. Thus, targeted maximum likelihood estimation provides a fusion between likelihood- and estimating function-based methodologies.

However, tMLE has various important advantages relative to the estimating equation methodology. First, by just solving the efficient influence curve equation in p itself, it does not rely on the assumption that the efficient influence curve can be represented as an estimating function and/or the particular representation of this estimating function. Second, estimating equations provide no criterion to select among multiple solutions in the parameter of interest for a given estimate of the nuisance parameters in the estimating equation, while targeted maximum likelihood can simply use the likelihood criterion to select among various tMLE indexed by different initial density estimators. Third, in the estimating equation methodology the parameter estimator is typically not compatible with the nuisance parameter estimates, while in the tMLE procedure the estimator of the parameter of interest and the nuisance parameters in the efficient influence curve are all compatible with a single density estimator.

The targeted maximum likelihood estimators of the parameters studied in this paper are double robust (DR) under uninformative censoring (missing at random) in the sense that they rely on either a consistent estimator of the treatment mechanism g or a consistent estimator of Q(A, W) = E(Y|A, W). When the treatment is assigned completely at random, the treatment mechanism, P(A|W) = P(A), is always known and thus the targeted maximum likelihood estimator is always consistent whatever the estimator for Q on which it relies. That is, even when the estimator Q̂(A, W) of Q(A, W) is inconsistent (e.g. if it relies on a mis-specified model), the tMLE remains consistent and one should hence not be concerned with estimation bias with this method in randomized trials. More specifically, if Q̂(A, W) converges to Q^*(A, W) ≠ Q(A, W) then targeted maximum likelihood estimators remain asymptotically linear and consistent in randomized trials. In practice, this means that the investigator is protected even when the a priori specified model selection algorithm selects a mis-specified model for Q(A, W). Note that if Q̂(A, W) is a consistent estimator of Q(A, W), then the targeted maximum likelihood estimator is consistent but also efficient. In the special case that we use, the true P(A|W) = P(A) or a marginal estimate δ̂ in the targeting step of the targeted maximum likelihood estimator, the tMLE is achieved in zero steps. Thus, in this case the tMLE coincides with the standard G-computation ML estimator thereby demonstrating that this latter estimator is already locally efficient. In the appendix, in one of our settings, we provide a relation between the DR, tMLE and G-computation estimator and the circumstances in which they coincide.

When censoring depends on baseline covariates, consistency of the targeted maximum likelihood estimator relies on consistent estimation of the censoring mechanism or Q(A, W). Even in this setting, for many causal parameters such as the causal RD the targeted maximum likelihood algorithm converges in a single step.

The targeted maximum likelihood estimator is a practically very attractive procedure since it can be achieved by simply adding a covariate to an initial estimate of the regression Q(A, W). The corresponding coefficient ε for this new covariate can be estimated with standard software and thus has a straightforward implementation.

It was shown in [12, pp. 1140–1141] that to obtain a DR estimate of the difference in two mean outcomes, one can extend a parametric model for Q(A, W) by adding the 2-dimensional covariate (I(A = 1)/g(1|W), I(A = 0)/g(0|W)) where in the randomized trial setting, g(1|W) = δ and g(0|W) = 1−δ, and estimate the combined parameter by solving the maximum likelihood estimating equation. In Section 4.1 we show that for this same additive effect the tMLE targeting both parameters (P(Y₀ = 1), P(Y₁ = 1)) also adds these two covariates, the first for P(Y₁ = 1) and one for P(Y₀ = 1) so that any function of these two parameters is estimated in a targeted manner. This tMLE still differs from the proposal in [12] by fixing the initial regression, which can thus also represent a data-adaptive machine learning fit and simply estimating the coefficients for the additional covariates. The proposed estimator of Scharfstein et al. [12] does not fix the initial regression but fits all coefficients for the parametric regression and the additional covariate simultaneously. This distinction in fixing the initial regression is important in that it allows one to apply data-adaptive algorithms for the initial estimate and simply update the estimate with the tMLE step. This is in contrast with the procedure proposed in [12, 13], which appears to rely on a parametric estimate for the regression. In [13] it is stated that when the initial model for Q(A, W) is correct, one can obtain a more efficient DR estimate by adding the 1-dimensional (rather than 2-dimensional) covariate I(A = 1)/g(1|W) − I(A = 0)/g(0|W). The covariate is equivalent to the tMLE covariate I (A = 1)/g(1|W) − I(A = 0)/g(0|W) targeting the RD effect P(Y₁ = 1)−P(Y₀ = 1). This covariate satisfies the condition of the tMLE fluctuation that the score of the initial density p̂⁰ at ε = 0 must include the efficient influence curve at p̂⁰. Again, the tMLE procedure fixes the initial regression and then estimates the coefficient for the additional covariate as opposed to the proposal in [13] where all coefficients for the parametric regression and the additional covariate are fit simultaneously. We note that the covariate that is added in the tMLE is specific to the parameter one is estimating and thus differs when the parameter of interest is the RR or OR as shown in Section 4.

3. CURRENT METHODS FOR OBTAINING COVARIATE-ADJUSTED ESTIMATES

Suppose we observe O = (W, A, Y) as above except that the outcome Y is now continuous. Let the parameter of interest be the marginal effect of A on Y, ψ = E(Y₁) − E(Y₀). For a continuous outcome Y, Q(A, W) = E(Y|A, W) is typically obtained using a linear regression model such as,

$$\widehat{Q}(A,W)={\widehat{\beta }}_0+{\widehat{\beta }}_{1}A+{\widehat{\beta }}_{2}W$$

In this setting, β̂₁ coincides with and has been shown to be at least as precise as the unadjusted estimate ψ̂₁. In particular, the increase in precision occurs when the correlation between the covariate(s) and outcome is strong [14]. However, when Q(A, W) is estimated as

$$\widehat{Q}(A,W)={\widehat{\beta }}_0+{\widehat{\beta }}_{1}A+{\widehat{\beta }}_{2}W+{\widehat{\beta }}_{2}AW$$

then β̂₁ no longer coincides with ψ̂₁. In this case, to obtain the marginal effect, one must integrate out or average over the covariate(s) W. The G-computation estimator introduced in [4, 5] is an estimator that does indeed average over W and thus gives a marginal effect,

$${\widehat{\psi }}_{\text{Gcomp}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n[\widehat{Q}(1,W_i)-\widehat{Q}(0,W_i)]}$$

When Q̂(A, W) is estimated with a linear model, and it does not contain any interaction terms, then ψ̂_Gcomp = β̂₁. The G-computation estimator is not limited to a linear model for Q(A, W) when estimating the treatment effect; for example, when the outcome is binary, one could use a logistic regression model to estimate Q(A, W) and use the G-computation formula to obtain the estimated RD. However, even in the absence of interaction terms, ψ̂_Gcomp is not necessarily equivalent to the estimate obtained from the logistic regression model.

In [11], the DR estimator is applied to estimate the marginal effect where the authors recommend estimating two regression models separately: Q₁(1, W) = E(Y|A = 1, W) is obtained using only the subpopulation of individuals for whom A = 1 and Q₂(0, W) = E(Y|A = 0, W) is obtained using only the subpopulation of individuals for whom A = 0. This was proposed so that two different analysts could independently select these models to prevent the analysts from selecting the model providing the most favorable results. Another possibility is to select one model Q(A, W) = E(Y|A, W) using the whole sample pooled together. When the procedure for selecting Q(A, W) is specified a priori this additional step of estimating Q₁(1, W) and Q₂(0, W) is not necessary.

The method for estimating the marginal difference E(Y₀) − E(Y₁) is provided in [11]. However, when the outcome is binary, investigators are often also interested in not only the RD E(Y₀) − E(Y₁) = P(Y₁ = 1) − P(Y₀ = 1), but the RR and ORs as well. In [15] the approach in [11] is expanded upon by applying the estimating function approach to the estimation of general parameters in randomized trials. The corresponding covariate-adjusted estimators are shown to provide an increase in precision over the unadjusted method. This general approach for constructing locally efficient double robust estimators that are guaranteed to improve on the unadjusted estimator can be found in [7]. The approach provided in this paper does not deviate from the line of research in [11, 15], but instead applies the relatively new targeted maximum likelihood methodology to randomized clinical trials. A particular advantage of tMLE over the estimating function approach is that for various effect parameters the efficient influence curve cannot even be represented as an estimating function in a parameter of interest and nuisance parameters, while the tMLE does not require such a representation. This is illustrated with the causal RR in a non-parametric model in Section 4.

Covariate adjustment in logistic regression models for binary outcomes in randomized trials has been studied in the literature. These models provide conditional effect estimates and have been shown to actually reduce the precision as compared with unadjusted methods. In [3] it was observed that adjusting for covariates in the logistic regression models leads to an increase in power due to the fact that estimates of the treatment effect in the conditional logistic models are further away from the null even though standard errors were larger for the adjusted effects. In [2] this fact was also demonstrated using simulation studies and it was observed that the increase in power was related to the correlation between the covariate and the outcome. The simulations included only a single covariate and no interactions between the covariate and treatment. Similar results were indicated in [14] in the logistic regression models in that ORs were generally further away from the null but the standard errors were larger than the unadjusted estimates. It appears that in general, when adjusting for covariates in a logistic regression model, the standard error provided by the software, i.e. standard maximum likelihood procedures, is the standard error used by the investigator though it is often not explicitly stated [16–19]. When adjusting for covariates in randomized trials using logistic regression, often the investigator is interested in a conditional effect identified by continuous covariates in which case this may be an appropriate approach. We focus on the tMLE method for covariate adjustment, which provides inference for the marginal (unconditional) effect. However, note that this method can be applied to different subgroups defined by categorical or discrete-valued covariates by simple stratification.

4. TARGETED MAXIMUM LIKELIHOOD ESTIMATION OF THE RISK DIFFERENCE, RELATIVE RISK AND ODDS RATIO

In this section we present the tMLE method for adjusting for covariates in estimating the marginal effect of a binary treatment on a binary outcome with the following three parameters: RD, RR and OR. We provide an overview of the derivation of the covariate that is added to an initial regression estimate. The covariate is derived in such a way that the update of the regression targets the specific parameter one is estimating and thus differs for each of the three we focus on in this paper. For technical details we refer the reader to the Appendix.

Let O = (W, A, Y) ~ p₀ and ℳ be the class of all densities of O with respect to an appropriate dominating measure: hence ℳ is non-parametric up to possible smoothness conditions. Let the parameter of interest be represented by Ψ(p₀). The first step of the algorithm involves finding an initial density estimator p̂⁰ of the density p₀ of O, identified by Q̂⁰(A, W), marginal distribution of A identified by $\widehat{\delta }=1/n{\displaystyle {\sum }_{i=1}^n{A}_i}$, the marginal distribution of W being the empirical probability distribution of W₁,…, W_n and A being independent of W.

An initial fit Q̂⁰(A, W) may be obtained in a number of ways. For example, we may fit a data-adaptive logistic regression model for the outcome Y fixing treatment A in the model and including covariates W as candidates. Since Y is binary, the density is given by,

$${\widehat{p}}^0(Y|A,W)={[{\widehat{Q}}^0(A,W)]}^Y{[1-{\widehat{Q}}^0(A,W)]}^{1-Y}$$

We could choose a logistic regression model for Q̂⁰(A, W),

$${\widehat{Q}}^0(A,W)=\frac{1}{1+\text{exp}-{\widehat{m}}^0(A,W)}$$

for some function m̂⁰.

The tMLE procedure updates the initial density by creating a parametric submodel through p̂⁰ indexed by parameter ε,

$${\widehat{p}}^0(\epsilon )(Y|A,W)={[{\widehat{Q}}^0(\epsilon )(A,W)]}^Y{[1-{\widehat{Q}}^0(\epsilon )(A,W)]}^{1-Y}$$

In the case that the initial choice Q̂⁰(A, W) is given by a logistic regression fit, then Q̂⁰(ε)(A, W) is given by the logistic regression model,

$${\widehat{Q}}^0(\epsilon )(A,W)=\frac{1}{1+\text{exp}-[{\widehat{m}}^0(A,W)+\epsilon h(A,W)]}$$

The targeted maximum likelihood algorithm finds this covariate h(A, W) by requiring that the score of p̂⁰ at ε = 0 is equal to the efficient influence curve at p̂⁰. In [6] it was shown that the efficient influence curve D(p₀) can be decomposed into three components corresponding with scores for p(Y|A, W), g₀(A|W) and the marginal probability distribution p(W) of W, which we refer to as D₁(p₀), D₂(p₀) and D₃(p₀), respectively (see Appendix). Since the score for p̂⁰ at ε = 0 corresponds with a zero score for ĝ⁰ and the empirical distribution of W is a non-parametric maximum likelihood estimator, we only need to choose h(A, W) so that the score of p̂⁰(Y|A, W) at ε = 0 includes the efficient influence curve component for p(Y|A, W), i.e. D₁(p₀). The next step of the algorithm involves estimating ε with maximum likelihood. The initial Q̂⁰(A, W) is thus updated to obtain Q̂¹(A, W) and the algorithm is iterated by replacing Q̂⁰(A, W) with Q̂¹(A, W).

It is a fortunate result that in randomized trials the covariate h(A, W) is none other than a linear combination of A and an intercept only. It follows that if m̂⁰(A, W) includes the main term A and the intercept, then ε̂ = 0, and the tMLE for Q₀(A, W) is given by Q̂⁰(A, W) itself. Specifically, consider the following RD, RR and OR parameters,

$$P_0\to {\mathrm{\Psi }}_{\text{RD}}(p_0)=E_{p_0}[E(Y|A=1,W)-E(Y|A=0,W)]$$ (1)

$$P_0\to {\mathrm{\Psi }}_{\text{RR}}(p_0)=\frac{E_{p_0}[E(Y|A=1,W)]}{E_{p_0}[E(Y|A=0,W)]}=\frac{{\mu }_1}{{\mu }_0}$$ (2)

and

$$P_0\to \mathrm{\Psi }(p_0)=\frac{E_{p_0}[E(Y|A=1,W)]/[1-E_{p_0}\{E(Y|A=1,W)\}]}{E_{p_0}[E(Y|A=0,W)]/[1-E_{p_0}\{E(Y|A=0,W)\}]}=\frac{{\mu }_1/(1-{\mu }_1)}{{\mu }_0/(1-{\mu }_0)}$$ (3)

Now consider the initial logistic regression fit Q̂⁰(A, W). It is straightforward to demonstrate (see Appendix) that the corresponding covariates that update the initial fit for each of the above parameters are given by,

$$\begin{array}{l}{h}_{\text{RD}}(A,W)=\frac{I(A=1)}{\widehat{\delta }}-\frac{I(A=0)}{(1-\widehat{\delta })}\hfill \\ h_{\text{RR}}(A,W)=\frac{1}{{\mu }_1}\frac{I(A=1)}{\widehat{\delta }}-\frac{1}{{\mu }_0}\frac{I(A=0)}{(1-\widehat{\delta })}\hfill \end{array}$$

and

$$h_{\text{OR}}(A,W)=\left(\frac{1}{{\mu }_1}+\frac{1}{1-{\mu }_1}\right)\frac{I(A=1)}{\widehat{\delta }}-\left(\frac{1}{{\mu }_0}+\frac{1}{1-{\mu }_0}\right)\frac{I(A=0)}{(1-\widehat{\delta })}$$

Each of these covariates is simply a linear combination of A and an intercept. Thus, if m̂⁰(A, W) includes the main term A and the intercept, then ε̂ = 0, and the tMLE for Q₀(A, W) is given by Q̂⁰(A, W) itself. In other words, the tMLE for ψ_RD, ψ_RR and ψ_OR is given by the standard maximum likelihood estimators,

$$\begin{array}{l}{\widehat{\psi }}_{\text{RD-tMLE}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n[{\widehat{Q}}^0(1,W_i)-{\widehat{Q}}^0(0,W_i)]}\hfill \\ {\widehat{\psi }}_{\text{RR-tMLE}}=\frac{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(1,W_i)}}{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(0,W_i)}}\hfill \end{array}$$

and

$${\widehat{\psi }}_{\text{OR-tMLE}}=\frac{\left[\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(1,W_i)}\right]/\left[1-\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(1,W_i)}\right]}{\left[\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(0,W_i)}\right]/\left[1-\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{Q}}^0(0,W_i)}\right]}$$

It is interesting to note that in estimating the RD, in addition to the equivalence between the tMLE and G-computation (MLE), the tMLE solves the efficient influence curve estimating equation by definition and thus the DR, MLE and tMLE all reduce to the same estimator in this general setting; for details see the Appendix.

As an alternative to using a logistic fit for the initial Q⁰(A, W), we can instead choose a relative risk regression fit,

$$\text{log}({\widehat{Q}}^0)(\epsilon )(A,W)={\widehat{m}}^0(A,W)+\epsilon h(A,W)$$

In estimation of the RR parameter, the corresponding covariate added to the initial regression model to obtain the tMLE is given by,

$$h(A,W)=\left\{\frac{1}{{\mu }_1}\frac{I(A=1)}{\widehat{\delta }}-\frac{1}{{\mu }_0}\frac{I(A=0)}{1-\widehat{\delta }}\right\}[1-{\widehat{Q}}^0(A,W)]$$

The maximum likelihood estimate,

$$\widehat{\epsilon }=\underset{\epsilon }{\text{arg max}}{\displaystyle \sum _{i=1}^n\text{log}{\widehat{Q}}^0(\epsilon )(A_i,W_i)}$$

can be estimated in practice by fitting a RR regression in m̂⁰(A, W) and h(A, W), fixing the coefficient in front of m̂⁰(A, W) to 1 and the intercept to 0. The resulting coefficient for h(A, W) is ε̂. In this case, the covariate is no longer simply a function of A and thus ε̂ does not necessarily equal 0 and the tMLE is no longer achieved in one step but rather iteratively. Now Q̂^k(A, W) is updated as,

$$\text{log}[{\widehat{Q}}^{k+1}(A,W)]={\widehat{m}}^k(A,W)+\widehat{\epsilon }{h}^k(A,W)$$

setting k = k + 1 and one iterates this updating step. One may also derive the updating covariate for targeting estimation of the RD or OR as well using this initial regression in addition to the logistic initial choice.

4.1. tMLE for the two treatment-specific means, and thereby for all parameters

Consider the OR, as an example. An alternative for targeting the OR is to simultaneously target both μ₁ and μ₀ and simply evaluate the OR from the tMLEs of μ₁ and μ₀. This is a straightforward approach where two covariate extensions are added to the logistic fit Q̂⁰,

$$h_1(A,W)={\epsilon }_1\frac{I(A=1)}{\widehat{\delta }}$$

and,

$$h_2(A,W)={\epsilon }_2\frac{I(A=0)}{(1-\widehat{\delta })}$$

Again, if the initial logistic regression fit already includes an intercept and main term A, then ε̂ = (ε̂₁, ε̂₂) = (0,0) so that this tMLE Q̂ = Q̂⁰(ε̂) = Q̂⁰ is not updated. This tMLE can now be used to map into a locally efficient estimator of any parameter of μ₀ and μ₁ such as the RD μ₁ − μ₀, the RR μ₁/μ₀ and the OR μ₁(1 − μ₀)/[(1 − μ₁)μ₀].

4.2. Estimating the treatment mechanism as well

Even when the treatment mechanism (the way treatment was assigned) is known as it is in a randomized trial, it has been shown that efficiency is increased when estimating it from the data if Q(A, W) is not correctly specified [7]. Estimating the treatment mechanism does not add any benefit to the G-computation estimator since it does not use this information. The tMLE can however leverage this information to obtain a more precise estimate of the treatment effect. This can be particularly beneficial when the model for Q(A, W) is mis-specified. The tMLE is still consistent when Q(A, W) is mis-specified; however, we can gain efficiency when estimating the treatment mechanism in such a case. The treatment mechanism can be estimated from the data using a logistic regression model; for example, g⁰(1|W) = 1/1+exp[−(α₁W₁+α₂W₂)], but one can also augment an initial fit ĝ⁰ with a targeted direction aiming for a maximal gain in efficiency [6]. We present the tMLE for the RD; however, this can be immediately extended to the RR and OR as well.

The covariate that is added to the logistic regression Q̂⁰(A, W) is given by,

$$h(A,W)=\frac{I(A=1)}{{\widehat{g}}^0(1|W)}-\frac{I(A=0)}{{\widehat{g}}^0(0|W)}$$

where $\widehat{\epsilon }={\text{arg max}}_{\epsilon }{\displaystyle {\sum }_{i=1}^n\text{log}{\widehat{Q}}^0(\epsilon )(A_i,W_i)}$ can be estimated in practice by fitting a logistic regression in m̂⁰(A, W) and h(A, W), fixing the coefficient in front of m̂⁰(A, W) to 1 and the intercept to 0. The resulting coefficient ε̂ for h(A, W) is no longer necessarily (and not typically) equal to 0. Let the tMLE for Q₀(A, W) be given by Q̂^*(A, W) = Q̂⁰(ε̂)(A, W). The tMLE for ψ₀ is then,

$${\widehat{\psi }}_{\text{RD-tMLE}2}=\frac{1}{n}{\displaystyle \sum _{i=1}^n[{\widehat{Q}}^{*}(1,W_i)-{\widehat{Q}}^{*}(0,W_i)]}$$

Note that Q̂⁰(A, W) is now updated, contrary to the case when we were not estimating the treatment mechanism as in previous subsections.

4.3. Missing data

Here we provide the tMLE for the case that the outcome Y is subject to missingness that can be informed by the baseline covariates W. In such a case the missingness cannot be ignored as it can lead to biased estimates since treatment groups are no longer balanced with respect to the covariates. Let C represent the indicator whether or not the outcome was observed. The observed data can be represented as O = (W, A, C, CY) ~ p₀ and the full data is given by X = ((Y_a:a ∈ 𝒜), W). We assume that the conditional distribution of the joint censoring variable (A, C) given X satisfies coarsening at random (CAR), i.e. g₀(A, C|X) = g₀(A, C|W). Let

$$P_0\to \mathrm{\Psi }(p_0)=E_{p_0}[E(Y|A=1,W)-E(Y|A=0,W)]$$

be the parameter of interest. We wish to estimate the RD with the tMLE. In choosing an initial logistic regression fit Q̂⁰(A, W), it can be shown (see Appendix) that the updating covariate is given by

$$h(A,C=1,W)=\frac{I(A=1)}{\widehat{g}(1,1|W)}-\frac{I(A=0)}{\widehat{g}(0,1|W)}$$

The estimate of ε given by $\widehat{\epsilon }={\text{arg max}}_{\epsilon }{\displaystyle {\sum }_{i=1}^{n}I(C_i=1)\text{log}{\widehat{Q}}^0(\epsilon )(A_i,W_i)}$. Now the logistic regression fit Q̂⁰(Y |A, C = 1, W) can be updated by adding as covariate h(A, C = 1, W) to obtain the tMLE Q̂^*(Y|A, C = 1, W) for Q₀(A, C = 1, W) based on all observations with C_i = 1. The estimate for P(C = 1|A = 0, W) as required to calculate the extra covariate h(A, W) can be obtained by using a logistic regression model selected either data adaptively or using a fixed pre-specified model for C conditional on W, A = 0. The tMLE for ψ₀ is given by

$${\widehat{\psi }}_{\text{RD-tMLE}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n[{\widehat{Q}}^{*}(1,1,W_i)-{\widehat{Q}}^{*}(0,1,W_i)]}$$

We note that the tMLE for missing covariate values is derived in exactly the same manner.

5. TESTING AND INFERENCE

Let p̂^* represent the tMLE of p₀. One can construct a Wald-type 0.95-confidence interval based on the estimate of the efficient influence curve, $\widehat{\mathit{\text{IC}}}(O)=D({\widehat{p}}^{*})$. The influence curves for the estimators presented in this paper are provided in the Appendix. An estimate of the asymptotic variance of $\sqrt{n}(\widehat{\psi }-{\psi }_0)$ can be estimated with

$${\widehat{\sigma }}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{\mathit{\text{IC}}}}^2(O_i)}$$

The corresponding asymptotically conservative Wald-type 0.95-confidence interval is defined as $\widehat{\psi }\pm 1.96\widehat{\sigma }/\sqrt{n}$. The null hypothesis H₀: ψ₀ = 0 can be tested with the test statistic

$$T_n=\frac{\widehat{\psi }}{\frac{\widehat{\sigma }}{n}}$$

whose asymptotic distribution is N(0,1) under the null hypothesis. To establish the asymptotics of the tMLE estimator, we apply Theorem 2.4 as provided in [7] and also noted in [6]. If Q̂⁰(A, W) converges to a mis-specified Q̂^*(A, W), then the tMLE estimate ψ̂ is asymptotically linear and consistent. Furthermore, if Q̂⁰(A, W) is consistent, then tMLE estimate ψ̂ is asymptotically linear, consistent and efficient. For further details, see [6].

We note that if the true treatment mechanism is used, inference based on the corresponding influence curve is not conservative whereas with an estimated treatment mechanism the corresponding influence curve is conservative. One can improve the variance estimator by either applying the bootstrap procedure or by deriving the true analytical form of the influence curve. The latter can be achieved by projecting the influence curve (based on the estimated treatment mechanism) on the tangent space of the model for the treatment mechanism.

First-order efficiency improves by using a larger model for the regression Q(A, W), which can be achieved by applying machine learning algorithms (e.g. deletion/substitution/addition (DSA)). However, the asymptotic results on which the IC-based inference relies can break down in that the second-order terms generated by data-adaptive approaches can be an issue. Fortunately in the case that the treatment mechanism is known we have found that neither the estimator nor the inference are affected by the second-order terms suggesting that fairly data-adaptive regression approaches can be used. Based on our experience model selection algorithms based on cross validation (e.g. DSA) generally result in similar estimates of the standard error using the influence curve or bootstrap procedure, which does take into account model selection. Thus, if such a methodology is used in the model selection algorithm or if the model for Q(A, W) is specified a priori then one can rely on the IC-based standard error estimates.

6. RELATION BETWEEN R² AND EFFICIENCY GAIN WITH TMLE

An analytical relationship exists between the relative efficiency (RE) of the TMLE and the unadjusted estimator and the predictive power of the baseline covariates W as expressed in the following formula:

$$\text{RE}=\frac{{\sigma }^2(\text{TMLE}(Q(A)))}{{\sigma }^2(\text{TMLE}(Q(A,W)))}=1-\frac{{\sigma }^2(\text{TMLE}(Q(A)))}{{\sigma }^2(\text{TMLE}(Q(A)))-4[E{(Y-\mathit{\text{EY}})}^2-E{(Y-Q(W))}^2]}$$

where Q(A)=E(Y | A), Q(W)=E(Y |W), σ²(TMLE(Q(A, W))) is the variance of the TMLE influence curve at Q(A, W) and σ²(TMLE(Q(A))) is the variance of the influence curve at Q(A) (i.e. the variance associated with the unadjusted estimator). The RE can also be expressed with respect to $R_{Q(W)}^2=1-E{(Y-Q(W))}^2/E{(Y-E(Y))}^2$ as

$$\text{RE}=1-\frac{{\sigma }^2(\text{TMLE}(Q(A)))}{{\sigma }^2(\text{TMLE}(Q(A)))-4E{(Y-E(Y))}^2{R}_{\overline{Q}(W)}^2}$$ (4)

Thus, as the $R_{Q(W)}^2$ increases, so does the gain in efficiency, i.e. the ratio of the variances of the influence curves increases. This formula clearly shows that whenever $R_{Q(W)}^2>0$, i.e. when outcome prediction with W through the model Q(W) outperforms outcome prediction through the simple intercept model (E(Y)) then one achieves a gain efficiency by adjusting for the covariates W with the TMLE relative to the unadjusted estimation approach. Note that this result is in agreement with published work that demonstrated an increase in estimation precision with the MLE when the correlation between the covariate(s) and the outcome (e.g. as measured by $R_{Q(W)}^2$) is strong [1, 14].

7. SIMULATION STUDIES

7.1. Simulation 1

In this simulation, the treatment A and outcome Y are binary and W is a two-dimensional covariate, W = (W₁, W₂). The simulated data were generated according to the following laws:

1. W₁ ~ N(2,2);

2. W₂ ~ U(3,8);

3. P(A = 1) = δ₀ = 0.5;

4. $Q_0(A,W)=P(Y=1|A,W)=1/1+\text{exp}[-(kA-5W_1^2+2W_2)].$.

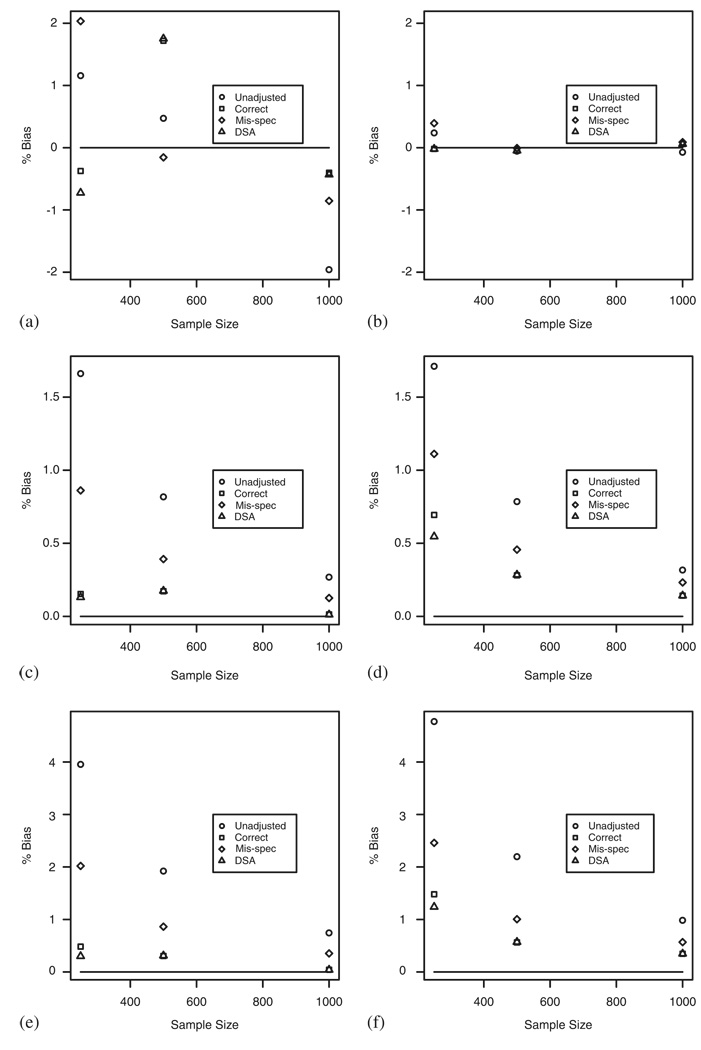
We simulated the data for two scenarios based on the value for k in P(Y = 1|A, W). In the first scenario, k = 1.2 and there is a small treatment effect and in the second k = 20, and there is a larger treatment effect. The RD, RR and OR were estimated. The true values were given by P(Y₁=1) = 0.372, P(Y₀=1) = 0.352 and (RD, RR, OR) = (0.019, 1.055, 1.087) for k = 1.2, P(Y₁ = 1) = 0.583, P(Y₀ = 1) = 0.352 and (RD, RR, OR) = (0.231, 1.654, 2.570) for k = 20. The parameters were estimated using four methods. The first method ‘Unadjusted’ is the unadjusted method of regressing Y on A using a logistic regression model. The second method ‘Correct’ is the targeted maximum likelihood method, which is equivalent to the standard G-computation (maximum likelihood) estimator with $\widehat{Q}(A,W)=1/\{1+\text{exp}[-({\widehat{\alpha }}_0+{\widehat{\alpha }}_{1}A+{\widehat{\alpha }}_2{W}_1^2+{\widehat{\alpha }}_3{W}_2)]\}$. The third method ‘Mis-spec’ used a mis-specified fit given by Q̂(A, W) = 1/{1+exp[−(α̂₀+α̂₁A+α̂₂W₁)]}. For the fourth method, ‘DSA’, the estimate Q̂(A, W) was obtained using deletion/substitution/addition (DSA). The DSA algorithm is a data-adaptive model selection procedure based on cross validation that relies on deletion, substitution and addition and moves to search through a large space of possible functional forms, and is publicly available at http://www.stat.berkeley.edu/~laan/Software/ [20]. The variable A was forced into the model and the DSA then selected from the remaining covariates. The maximum power set in the DSA algorithm for any term in the model was set to 2, meaning square terms and two-way interactions were allowed. Standard errors for the tMLE were estimated using the estimated influence curve. For the OR simulations, the estimator obtained by extracting the coefficient for A and the corresponding standard error from the logistic regression model fit is labelled ‘Adjusted’. The simulation was run 5000 times for each sample size: n = 250, 500, 1000. For k = 1.2, W strongly predicts Y and thus the tMLE, which adjusts for W results in a large increase in efficiency over the unadjusted method as observed by the REs provided in Table I. The largest gain in efficiency occurs as expected when Q̂(A, W) is correctly specified followed closely by the DSA method, which in general shows a slightly higher variability than the correctly specified model due to possible overfitting of Q̂(A, W). In the scenario where k = 20, A is more strongly predictive of Y as compared with W and thus, the increase in efficiency is not as marked as when k = 1.2. The largest increase in efficiency for both values of k occurs for the estimates of the OR. When Q̂(A, W) is mis-specified, there is still a noticeable increase in efficiency showing that it is advised to always adjust for covariates. This is a result of the double robustness of the estimator as discussed in Section 4 and the Appendix. A significant result is the increase in power of the tMLE as evidenced by the proportion of rejected tests. In particular, when k = 1.2, that is when the effect of A is weaker and more difficult to detect, the increase in power is quite significant. When k = 20, the performance of the unadjusted estimator is similar to the tMLE estimator with respect to power. In the strong treatment effect case, the conditional logistic regression method for estimating the OR (see ‘Adjusted’ in Table II) demonstrates the issue that the point estimates are further from the null value, which is consistent with the findings in the literature as discussed in Section 3. This is reflected in the coverage probabilities for the 95 per cent confidence intervals, ranging from 0 to 22 per cent. Another notable result is that the tMLE circumvents the issue of singularity, i.e. Y is perfectly predicted by A and W, that occurs when using the adjusted estimate. In this situation the adjusted estimate is drastically inflated and for this reason, the adjusted results were not included in the consistency plots. However, this is not an issue for the tMLE. The efficiency gain of the tMLE increases as the covariate becomes more predictive. This becomes even more drastic when the covariate is perfectly predictive, whereas the adjusted estimate completely breaks down. For example, in a single run of the simulation for the OR with k = 1.2, with n = 250, the coefficient for the treatment term in the conditional logistic fit was 25.4 and thus, an estimate OR of approximately 10¹¹. The corresponding tMLE using this same model gives an estimate of 1.083, noting that the true value is 1.087. This is of particular importance for small sample sizes but still occurs even for large sample sizes as shown in the RE estimates for the ‘Adjusted’ estimate in Tables I and II. We also note that the consistency plots provided in Figure 1 show a small positive bias for all methods for the OR and RR for smaller sample sizes. The tMLE methods, however, are less biased than the unadjusted method for all sample sizes.

Table I.

Simulation 1: k = 1.2: ‘MSE’ is mean squared error for unadjusted estimate, RE (relative efficiency) is the ratio of unadjusted MSE to MSE of remaining estimators’ and ‘Rej’ is the proportion of rejected tests at 0.05 level with the coverage probability of a 95 per cent confidence interval in parenthesis. Three methods for selecting Q(A, W), ‘Correct’ is correctly specified, ‘Mis-spec’ is mis-specified, ‘DSA’ is data-adaptive selection based on DSA algorithm. ‘Adjusted’ method for the OR results based on the conditional logistic regression model.

	n = 250	n = 500	n = 1000
Risk difference
Unadjusted MSE	3.8e−03	1.9e−03	9.5e−04
Correct RE	10.46	13.70	13.67
Mis-spec RE	2.14	2.19	2.18
DSA RE	11.72	13.31	13.49
Unadjusted Rej	0.07 (0.94)	0.08 (0.95)	0.10 (0.95)
Correct Rej	0.26 (0.90)	0.42 (0.94)	0.67 (0.95)
Mis-spec Rej	0.08 (0.94)	0.10 (0.95)	0.16 (0.95)
DSA Rej	0.26 (0.90)	0.43 (0.93)	0.67 (0.94)
Relative risk
Unadjusted MSE	3.6e−02	1.7e−02	8.2e−03
Correct RE	9.70	13.97	13.70
Mis-spec RE	2.22	2.27	2.25
DSA RE	12.50	13.59	13.53
Unadjusted Rej	0.05 (0.95)	0.07 (0.95)	0.10 (0.95)
Correct Rej	0.25 (0.90)	0.41 (0.94)	0.67 (0.95)
Mis-spec Rej	0.03 (0.95)	0.05 (0.96)	0.10 (0.96)
DSA Rej	0.19 (0.91)	0.37 (0.94)	0.64 (0.96)
Odds ratio
Unadjusted MSE	1.0e−01	4.6e−02	2.2e−02
Adjusted RE	0.46	0.51	0.48
Correct RE	2.83	14.60	14.04
Mis-spec RE	2.24	2.28	2.21
DSA RE	13.46	14.19	13.86
Unadjusted Rej	0.06 (0.95)	0.08 (0.95)	0.10 (0.95)
Adjusted Rej	0.05 (0.97)	0.07 (0.96)	0.11 (0.96)
Correct Rej	0.26 (0.90)	0.42 (0.94)	0.67 (0.95)
Mis-spec Rej	0.08 (0.94)	0.10 (0.95)	0.15 (0.95)
DSA Rej	0.26 (0.90)	0.43 (0.93)	0.67 (0.95)

Table II.

Simulation 1: k = 20.

	n = 250	n = 500	n = 1000
Risk difference
Unadjusted MSE	3.9e−03	2.0e−03	9.5e−04
Correct RE	3.58	4.70	4.60
Mis-spec RE	2.51	2.55	2.51
DSA RE	4.40	4.65	4.59
Unadjusted Rej	0.96 (0.94)	1.00 (0.94)	1.00 (0.95)
Correct Rej	1.00 (0.94)	1.00 (0.94)	1.00 (0.95)
Mis-spec Rej	1.00 (0.95)	1.00 (0.94)	1.00 (0.95)
DSA Rej	1.00 (0.94)	1.00 (0.94)	1.00 (0.94)
Relative risk
Unadjusted MSE	6.5e−02	3.1e−02	1.4e−02
Correct RE	2.14	4.13	3.97
Mis-spec RE	2.23	2.30	2.28
DSA RE	4.01	4.06	3.96
Unadjusted Rej	0.95 (0.95)	1.00 (0.95)	1.00 (0.95)
Correct Rej	1.00 (0.94)	1.00 (0.94)	1.00 (0.95)
Mis-spec Rej	1.00 (0.99)	1.00 (0.99)	1.00 (1.00)
DSA Rej	1.00 (0.99)	1.00 (0.99)	1.00 (1.00)
Odds ratio
Unadjusted MSE	5.7e−01	2.6e−01	1.2e−01
Adjusted RE	0.00	0.01	0.00
Correct RE	2.89	5.05	4.67
Mis-spec RE	2.63	2.65	2.52
DSA RE	5.01	4.97	4.67
Unadjusted Rej	0.96 (0.95)	1.00 (0.94)	1.00 (0.95)
Adjusted Rej	1.00 (0.22)	1.00 (0.03)	1.00 (0.00)
Correct Rej	1.00 (0.94)	1.00 (0.94)	1.00 (0.95)
Mis-spec Rej	1.00 (0.95)	1.00 (0.95)	1.00 (0.95)
DSA Rej	1.00 (0.94)	1.00 (0.94)	1.00 (0.95)

Figure 1.

Simulation 1: Consistency graphs: (a) risk difference, k = 1.2; (b) risk difference, k = 20; (c) relative risk, k = 1.2; (d) relative risk, k = 20; (e) odds ratio, k = 1.2; and (f) odds ratio, k = 20.

The RR regression initial model Q⁰(A, W) was also applied. The G-computation estimate based on Q⁰(A, W) was computed in addition to the tMLE for which the update covariate was required as discussed in Section 4. The G-computation estimate based on this RR regression model resulted in a small gain in efficiency of approximately 3 per cent with an additional 1 per cent gain achieved with the tMLE with the appropriate update.

7.2. Simulation 2: OR with interaction term

In this simulation, the treatment A and outcome Y are binary and W is a two-dimensional covariate, W = (W₁, W₂). The simulated data were generated according to the following laws:

1. W₁ ~ N(2,2);

2. W₂ ~ U(3,8);

3. P(A = 1) = δ₀ = 0.5;

4. $Q_0(A,W)=P(Y=1|A,W)=1/1+\text{exp}[-(1.2A-5W_1^2+2W_2-5A{W}_1)]$.

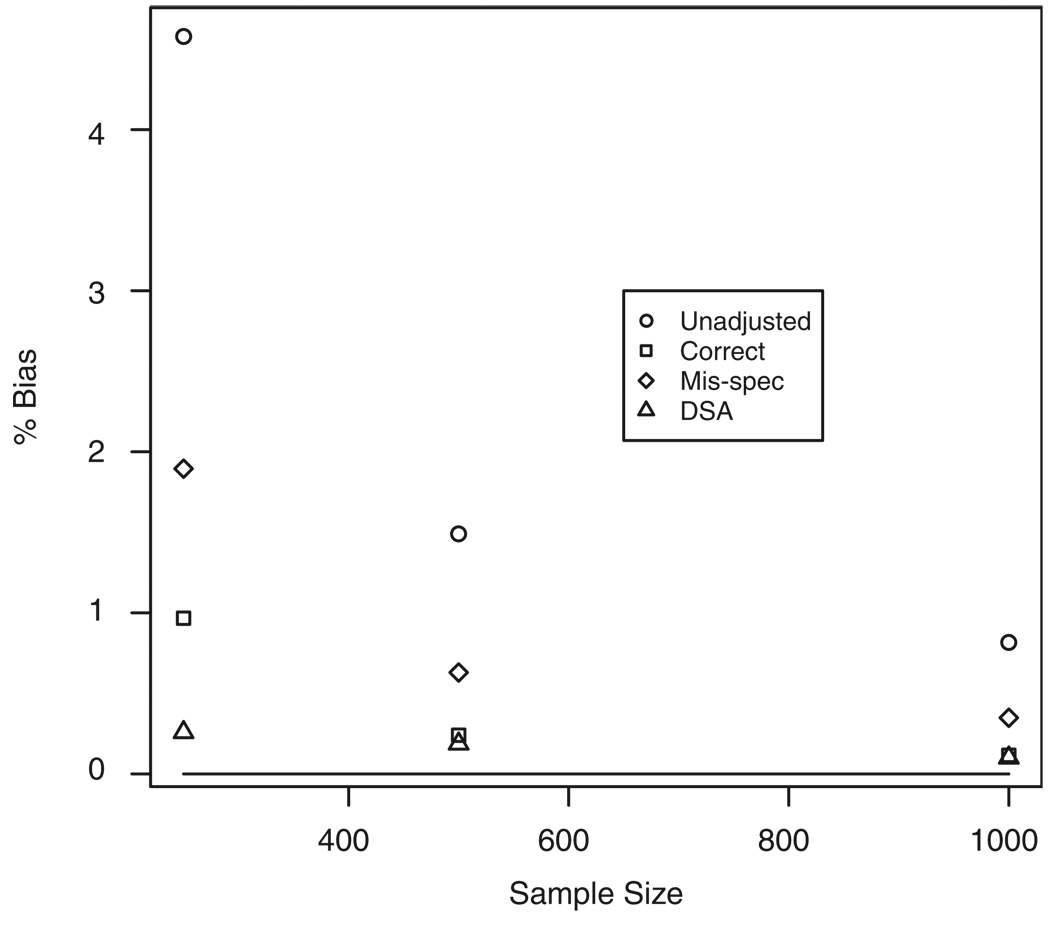
The true values were given by P(Y₁ = 1) = 0.312, P(Y₀ = 1) = 0.352 and OR = 0.833. The same methods used in simulation 1 were used here to estimate the OR. The simulation was run 5000 times for each sample size: n = 250, 500, 1000. For the ‘Mis-spec’ tMLE, the mis-specified fit was given by Q̂(A, W) = 1/{1+exp[−(α̂₀ + α̂₁A + α̂₂W₁)]}. Figure 2 provides the consistency plot for each of the estimators. The results are similar to OR for simulation 1 in that there is a small positive bias for all methods. The tMLE methods are again less biased than the unadjusted method for all sample sizes. Even when Q̂(A, W) is mis-specified the MSE is reduced as compared with the unadjusted estimate (Table III). The DSA, which allows for interactions, shows a significant improvement in terms of the MSE. A notable increase in power is again observed for the tMLE over the unadjusted method.

Figure 2.

Odds ratio with interaction: consistency graph.

Table III.

Odds ratio, with interaction.

	n = 250	n = 500	n = 1000
Unadjusted MSE	6.1e−02	2.7e−02	1.3e−02
Adjusted RE	0.68	0.55	0.39
Correct RE	6.59	6.12	5.89
Mis-spec RE	2.58	2.52	2.46
DSA RE	7.47	7.87	7.40
Unadjusted Rej	0.10 (0.95)	0.16 (0.95)	0.27 (0.96)
Adjusted Rej	0.13 (0.94)	0.26 (0.92)	0.48 (0.87)
Correct Rej	0.40 (0.94)	0.66 (0.94)	0.91 (0.95)
Mis-spec Rej	0.20 (0.95)	0.34 (0.95)	0.57 (0.95)
DSA Rej	0.50 (0.92)	0.78 (0.94)	0.97 (0.94)

7.3. Simulation 3: Estimating the treatment mechanism as well

In this simulation, the treatment mechanism, P̂(A|W) is estimated from the data using a logistic regression model with covariates that are predictive of the outcome Y. The simulated data were generated according to the following laws:

1. W₁ ~ N(1,2);

2. W₂ ~ U(1,4);

3. W₃ ~ U(0,20);

4. P(A = 1) = δ₀ = 0.5;

5. $Q_0(A,W)=P(Y=1|A,W)=1/1+\text{exp}[-(3A-2W_1^2-\text{log}(W_2)+0.5W_3)]$.

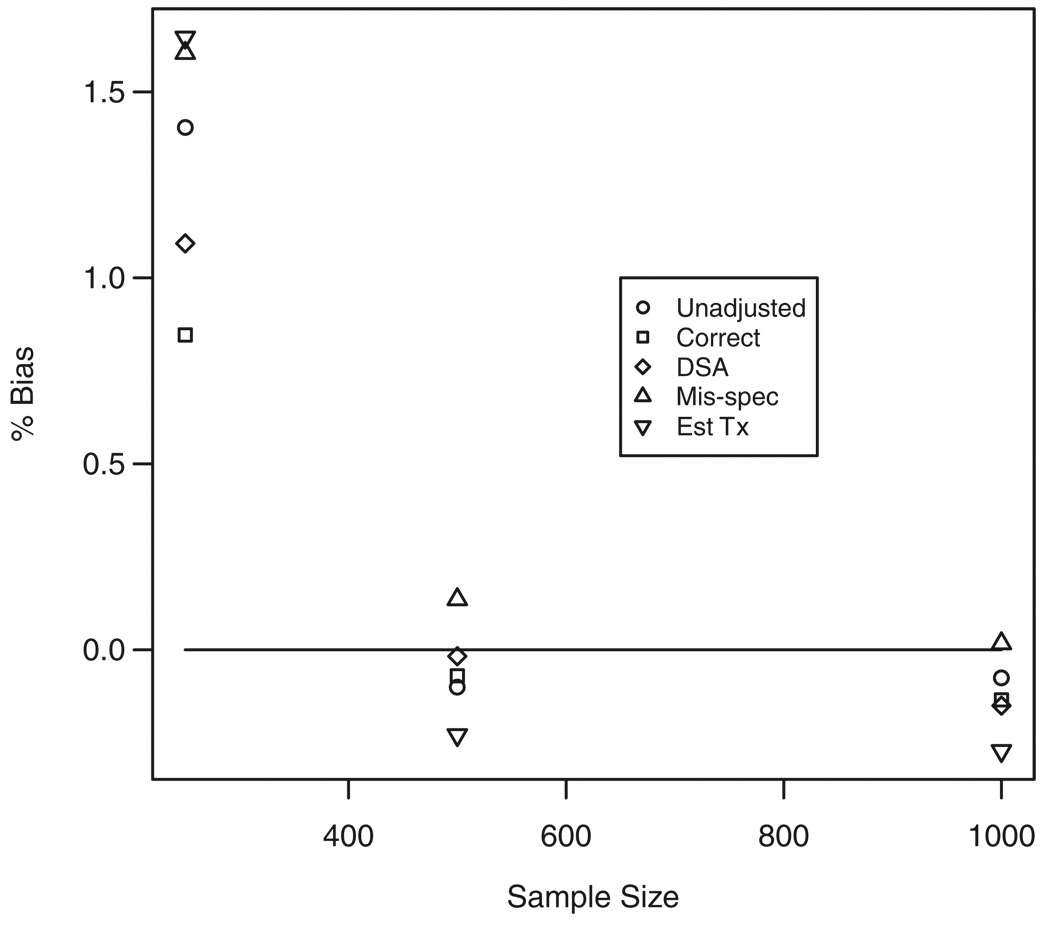
The true values were given by P(Y₁ = 1) = 0.569, P(Y₀ = 1) = 0.419 and RD = 0.150. The treatment mechanism was estimated with the logistic regression model given by g(A|W) = 1/{1+exp[−(γ₀+γ₁W₁+γ₂W₂+γ₃W₃)]}. The tMLE estimator, represented as ‘Est tx’ in Table IV and Figure 3, with the estimated treatment mechanism is no longer equivalent to the G-computation estimator. The mis-specified fit for Q(A, W) = 1/{1+exp[−(α₀+α₁A+α₂W₁)]} is used as the initial fit and the covariate h(A, W) provided in Section 3.4 is then added to this logistic regression. The tMLE is then estimated as usual. Thus, we are interested in comparing the mis-specified tMLE to the estimated treatment mechanism tMLE (Table IV). The efficiency is increased when estimating the treatment mechanism, from approximately 1.0 to 1.5. The power was approximately equal for the mis-specified and estimated treatment mechanism tMLE. The DSA tMLE method again shows a large improvement in efficiency and power over the unadjusted method.

Table IV.

Risk difference, estimated treatment mechanism.

	250	500	1000
Unadjusted MSE	2.6e−03	1.3e−03	6.5e−04
Correct RE	4.34	4.41	4.54
DSA RE	4.17	4.35	4.51
Mis-spec RE	1.01	1.03	1.01
Est tx RE	1.42	1.47	1.46
Unadjusted Rej	0.25 (0.94)	0.42 (0.95)	0.69 (0.94)
Correct Rej	0.79 (0.92)	0.97 (0.94)	1.00 (0.94)
DSA Rej	0.80 (0.92)	0.97 (0.93)	1.00 (0.94)
Mis-spec Rej	0.25 (0.94)	0.42 (0.95)	0.70 (0.95)
Est tx Rej	0.21 (0.98)	0.40 (0.98)	0.73 (0.98)

Figure 3.

Risk difference, estimated treatment mechanism: consistency graph.

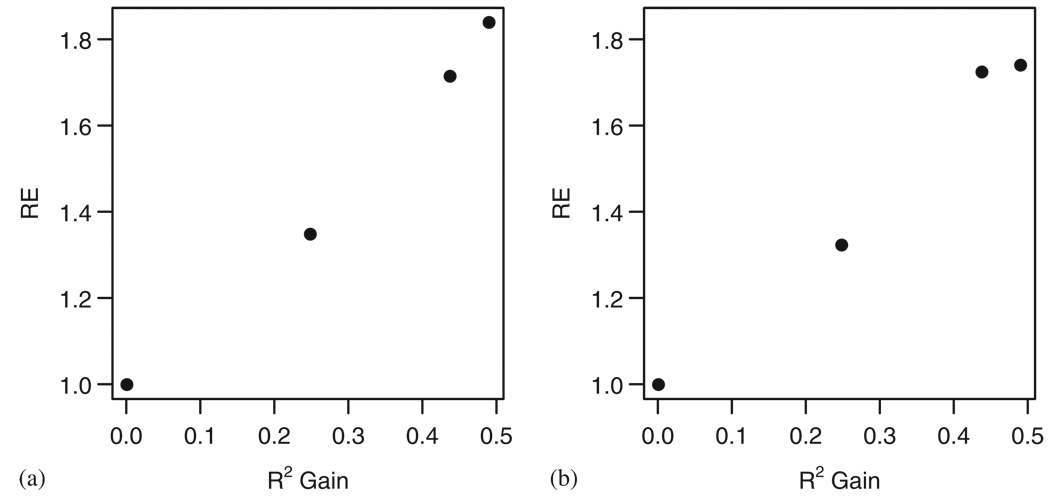
7.4. Efficiency gain and R²

To demonstrate the relation between efficiency gain and R², a simulation was run according to the following laws:

1. $\sqrt{W}\sim N(2,2);$

2. P(A=1)=δ₀=0.5;

3. Q₀(A, W)= P(Y =1|A, W)=1/1+exp[−(1.2A−cW)].

The data were sampled 5000 times with a sample size n = 1000 for each c = {0,0.25, 2,10}. That is covariate W is increasingly predictive. The R² was estimated in the ordinary least-squares sense,

$$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{[Y_i-\widehat{Q}(A,W)]}^2}}{{\displaystyle {\sum }_{i=1}^n{[Y_i-\overline{Y}]}^2}}$$

A gain in R² was computed as the difference between R² in the covariate-adjusted model and the covariate-unadjusted model. Figure 4 depicts the RE to the unadjusted model for the targeted MLE of the RD and OR against the gain in R². Clearly, a gain in RE comparing the tMLE with the unadjusted estimate corresponds with a gain in R².

Figure 4.

Efficiency Gain and R²: (a) risk difference and (b) odds ratio.

7.5. Simulation discussion

The simulations were based on relatively simple data generating distributions but were useful in demonstrating the following results:

• The tMLE shows a clear increase in both efficiency and power over the unadjusted method, even when Q(A, W) is not correctly specified.

• The DSA method for selecting Q(A, W) provides a significant increase in efficiency and power over the mis-specified fixed Q(A, W) method. The highest RE of approximately 13 was observed for the weak effect case with a sample size of n = 1000 in our simulations.

• The tMLE circumvents the singularity issue that occurs when using the adjusted method of extracting the coefficient from the logistic regression model Q(A, W).

• Interaction terms in the model for Q(A, W) fit entirely into the framework of the tMLE.

• Estimating the treatment mechanism provides a further small increase in efficiency over targeting only Q(A, W).

• There is a clear relation between increasing R² and efficiency gain.

• The method of covariate adjustment that extracts the coefficient for treatment from the conditional logistic model demonstrated a loss in efficiency with a gain in power due to the inflated point estimates, which corresponds with previous findings in the literature.

8. DISCUSSION

The tMLE provides a general framework that we applied to estimation of the marginal (unadjusted) effect of treatment in randomized trials. We observed that the traditional method of covariate adjustment in randomized trials using logistic regression models can be mapped, by averaging over the covariate(s), to obtain a fully robust and efficient estimator of the marginal effect, which equals the tMLE. We demonstrated that the tMLE does just this and results in an increase in efficiency and power over the unadjusted method, contrary to what has been reported in the literature for covariate adjustment for logistic regression. The simulation results demonstrated that data-adaptive model selection algorithms such as the DSA, which we used in this paper, or forward selection, should be applied if the algorithm is specified a priori. However, we showed that even adjusting by a mis-specified regression model results in gain in efficiency and power. Thus, using an a priori specified model, even if it is mis-specified, can increase the power, and thus reduce the sample size requirements for the study. This is particularly important for trials with smaller sample sizes. The tMLE framework can also address missing data, either in the outcome as we demonstrated in Section 4.3 for the RD, but also missingness in covariates and treatment as well for any of the parameters of interest. In these scenarios the tMLE covariate may not be as straightforward as those that were presented in this paper, but its derivation is analogous. We focused on logistic and RR regression, but the methodology can be extended to any other regression models for Q(A, W). The tMLE framework can also be applied to other parameters of interest in randomized trials such as an adjusted effect, for example by age or biomarker, and can also handle survival times as outcomes [6].

APPENDIX A

Details for derivations provided in the text are provided in this appendix.

A.1. Decomposition of efficient influence curve

Following the strategy of van der Laan and Rubin [6], the efficient influence curve D(p₀) can be decomposed as

$$\begin{array}{cc}D(p_0)=\hfill & D(p_0)-E(D(p_0)|A,W)+E(D(p_0)|A,W)-E(D(p_0)|W)\hfill \\ \hfill & +E(D(p_0)|W)-E(D(p_0))\hfill \end{array}$$

Let D₁(p₀) = D(p₀) − E(D(p₀)|A, W), D₂(p₀) = E(D(p₀)|A, W) − E(D(p₀)|W) and D₃(p₀) = E(D(p₀)|W) − E(D(p₀)). Then, D₁(p₀) is a score for p(Y|A, W), D₂(p₀) is a score for g₀(A|W) and D₃(p₀) is a score for the marginal probability distribution p(W) of W. Note that in this randomized trial setting, $g_0(A|W)=g_0(A)={\delta }_0^A{(1-{\delta }_0)}^{(1-A)}$.

A.2. Finding covariate for RD tMLE update based on logistic regression submodel

Consider an initial density estimator p̂⁰ of the density p₀ of O identified by a regression fit Q̂⁰(A, W), marginal distribution of A identified by $\widehat{\delta }=1/n{\displaystyle {\sum }_{i=1}^n{A}_i}$, the marginal distribution of W being the empirical probability distribution of W₁,…, W_n and A being independent of W. Since Y is binary, we have the following density:

$${\widehat{p}}^0(Y|A,W)={({\widehat{Q}}^0(A,W))}^Y{(1-{\widehat{Q}}^0(A,W))}^{1-Y}$$

where

$${\widehat{Q}}^0(A,W)=\frac{1}{1+\text{exp}-{\widehat{m}}^0(A,W)}$$

for some function m̂⁰. Now, consider the parametric submodel through p̂⁰ indexed by parameter ε

$${\widehat{p}}^0(\epsilon )(Y|A,W)={({\widehat{Q}}^0(\epsilon )(A,W))}^Y{(1-{\widehat{Q}}^0(\epsilon )(A,W))}^{1-Y}$$

where Q̂⁰(ε)(A, W) is given by the logistic regression model

$${\widehat{Q}}^0(\epsilon )(A,W)=\frac{1}{1+\text{exp}-({\widehat{m}}^0(A,W)+\epsilon h(A,W))}$$

with an extra covariate h(A, W), which needs to be chosen so that the score of ε at ε = 0 includes the efficient influence curve component D₁(p⁰) [6]. The required choice h will be specified below. We estimate ε with the maximum likelihood estimator $\widehat{\epsilon }={\text{arg max}}_{\epsilon }{\displaystyle {\sum }_{i=1}^n\text{log}{\widehat{Q}}^0(\epsilon )(A_i,W_i)}$. The score for this logistic regression model at ε = 0 is given by

$$\frac{\mathrm{d}}{\mathrm{d}{\epsilon }_1}\text{log}{p}^0(\epsilon ){(A,W)|}_{\epsilon =0}=h(A,W)(Y-{\widehat{Q}}^0(A,W))$$

We now set the score equal to the part of the efficient IC for p(Y|A, W), that is D₁, at p̂⁰ to obtain

$$h(A,W)(Y-{\widehat{Q}}^0(A,W))=(Y-{\widehat{Q}}^0(A,W))\left(\frac{I(A=1)}{\widehat{\delta }}-\frac{I(A=0)}{(1-\widehat{\delta })}\right)$$

This equality in h(A, W) is solved by

$$h(A,W)=\frac{I(A=1)}{\widehat{\delta }}-\frac{I(A=0)}{(1-\widehat{\delta })}$$

A.3. Relation between tMLE, DR and G-computation estimators

The efficient influence curve D(p₀) can be represented as an estimating function in ψ indexed by Q and g, D(p₀) = D(Q₀, g₀, Ψ(p₀)). In this randomized trial setting, $g_0={\delta }_0^A{(1-\delta )}^{1-A}$. The DR estimate is the solution to the corresponding estimating equation in ψ, $1/n{\displaystyle {\sum }_{i=1}^{n}D({\widehat{Q}}^0(A_i,W_i),\widehat{\delta },\psi )=0}$ and is given by

$$\begin{array}{ll}{\widehat{\psi }}_{\text{DR}}=\hfill & \frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{I(A_i=1)}{\widehat{\delta }}[Y_i-{\widehat{Q}}^0(1,W_i)]-\frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{I(A_i=0)}{1-\delta }[Y_i-{\widehat{Q}}^0(0,W_i)]}\hfill \\ \hfill & +\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Q}}^0(1,W_i)-\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Q}}^0(0,W_i)}}\hfill \end{array}$$

where $\widehat{\delta }=1/n{\displaystyle {\sum }_{i=1}^n{A}_i}$. In the logistic regression fit, log[Q̂ (A, W)/1−Q̂ (A, W)]=α̂X, where X = (1, A, W), the MLE α̂ solves the score equations given by

$$0={\displaystyle \sum _{i=1}^n{X}_{\mathit{\text{ij}}}[Y_i-\widehat{Q}(A_i,W_i)]}$$

for j = 1,…, p. The linear span of scores includes the covariate,

$$x_j=\frac{I(A=1)}{\widehat{\delta }}-\frac{I(A=0)}{1-\widehat{\delta }}$$

when A and an intercept are included in X. Thus, it follows that

$$0=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{I(A_i=1)}{\widehat{\delta }}[Y_i-{\widehat{Q}}^0(1,W_i)]-\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{I(A_i=0)}{1-\widehat{\delta }}[Y_i-{\widehat{Q}}^0(0,W_i)]}}$$

Hence,

$${\widehat{\psi }}_{\text{DR}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n[\widehat{Q}(1,W_i)-\frac{1}{n}}{\displaystyle \sum _{i=1}^n\widehat{Q}(0,W_i)]={\widehat{\psi }}_{\text{Gcomp}}={\widehat{\psi }}_{\text{RD-tMLE}}}$$

Thus, in this quite general scenario, we have that the double robust estimator, the G-computation estimator and the tMLE, all reduce to the same estimator.

A.4. Finding covariate for RR tMLE update based on logistic submodel

We apply the delta method to obtain the efficient influence curve of the log of the RR parameter, i.e. log(μ₁/μ₀) = log(μ₁)−log(μ₀). The efficient influence curve is given by

$$\begin{array}{cc}D(p_0)\hfill & =\frac{1}{{\mu }_1}\left(\frac{I(A=1)}{{\delta }_0}(Y-Q_0(1,W))+Q_0(1,W)-{\mu }_1\right)\hfill \\ \hfill & -\frac{1}{{\mu }_0}\left(\frac{I(A=0)}{(1-{\delta }_0)}(Y-Q_0(0,W))+Q_0(0,W)-{\mu }_0\right)\hfill \\ \hfill & =\frac{1}{{\mu }_1}\left(\frac{I(A=1)}{({\delta }_0)}(Y-Q_0(1,W))+Q_0(1,W)\right)\hfill \\ \hfill & -\frac{1}{{\mu }_0}\left(\frac{I(A=0)}{(1-{\delta }_0)}(Y-Q_0(0,W))+Q_0(0,W)\right)\hfill \end{array}$$

In order to find the covariate h(A, W) that is added to the regression model, we note the following equality given in [7]:

$$V(Y,A,W)=(V(1,A,W)-V(0,A,W))(Y-Q(A,W))$$ (A1)

if V is a function with conditional mean 0 given A and W. We apply this equality to D(p₀) = V(Y, A, W) to obtain h(A, W).

Let p̂⁰(ε₁) be the logistic regression fit with an extra covariate extension ε₁h(A, W). Based on (A1) we can immediately observe that the covariate h(A, W) added to the logistic regression is V(1, A, W) − V(0, A, W) since,

$$\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\epsilon }\text{log}{\widehat{p}}^0(\epsilon )(A,W){|}_{\epsilon =0}\hfill & =h(A,W)(Y-{\widehat{Q}}^0(A,W))\hfill \\ \hfill & =(V(1,A,W)-V(0,A,W))(Y-{\widehat{Q}}^0(A,W))\hfill \end{array}$$

Thus, evaluating D(p̂₀) at Y = 1 and Y = 0 gives,

$$h(A,W)=\frac{1}{{\mu }_1}\frac{I(A=1)}{\widehat{\delta }}-\frac{1}{{\mu }_0}\frac{I(A=0)}{(1-\widehat{\delta })}$$

A.5. Finding covariate for RR tMLE update based on RR regression submodel

Consider now the parametric submodel p̂⁰ indexed by parameter ε,

$${\widehat{p}}^0(\epsilon )(Y|A,W)={({\widehat{Q}}^0(\epsilon )(A,W))}^Y{(1-{\widehat{Q}}^0(\epsilon )(A,W))}^{1-Y}$$

where Q̂⁰(ε)(A, W) is given by the RR regression model,

$$\text{log}({\widehat{Q}}^0)(\epsilon )(A,W)={\widehat{m}}^0(A,W)+\epsilon h(A,W)$$

The score for this model evaluated at ε=0 is given by

$$\frac{\mathrm{d}}{\mathrm{d}\epsilon }\text{log}{\widehat{p}}^0(\epsilon )(A,W){|}_{\epsilon =0}=\frac{h(A,W)}{1-{\widehat{Q}}^0(A,W)}(Y-{\widehat{Q}}^0(A,W))$$

and it follows that the covariate added to the logistic regression model to obtain the tMLE is given by

$$h(A,W)=\left(\frac{1}{{\mu }_1}\frac{I(A=1)}{\widehat{\delta }}-\frac{1}{{\mu }_0}\frac{I(A=0)}{(1-\widehat{\delta })}\right)(1-{\widehat{Q}}^0(A,W))$$

A.6. Finding covariate for OR based on the logistic regression submodel

We apply the delta method to obtain the efficient influence curve of the log of this parameter, i.e.

$$\text{log}\left(\frac{{\mu }_1/(1-{\mu }_1)}{{\mu }_0/(1-{\mu }_0)}\right)=\text{log}\left(\frac{{\mu }_1}{(1-{\mu }_1)}\right)-\text{log}\left(\frac{{\mu }_0}{(1-{\mu }_0)}\right)$$

We have

$$\frac{\mathrm{d}}{\mathrm{d}{\mu }_1}\text{log}\left(\frac{{\mu }_1}{1-{\mu }_1}\right)=\frac{1}{{\mu }_1}+\frac{1}{1-{\mu }_1}$$

and thus the efficient influence curve is given by

$$\begin{array}{ll}D(p_0)=\hfill & \left(\frac{1}{{\mu }_1}+\frac{1}{1-{\mu }_1}\right)\left(\frac{I(A=1)}{{\delta }_0}(Y-Q_0(1,W))+Q_0(1,W)-{\mu }_1\right)\hfill \\ \hfill & -\left(\frac{1}{{\mu }_0}+\frac{1}{1-{\mu }_0}\right)\left(\frac{I(A=0)}{(1-{\delta }_0)}(Y-Q_0(0,W))+Q_0(0,W)-{\mu }_0\right)\hfill \end{array}$$

Applying equality (A1) to D(p̂⁰), we obtain

$$h(A,W)=\left(\frac{1}{{\mu }_1}+\frac{1}{1-{\mu }_1}\right)\frac{I(A=1)}{\widehat{\delta }}-\left(\frac{1}{{\mu }_0}+\frac{1}{1-{\mu }_0}\right)\frac{I(A=0)}{(1-\widehat{\delta })}$$

A.7. Finding covariate for RD with missing data based on logistic regression submodel

The efficient influence curve is given by

$$\begin{array}{ll}D(p_0)=\hfill & \frac{I(A=1)}{g_0(1,1|W)}[Y-Q_0(1,1,W)]\hfill \\ \hfill & -\frac{I(A=0)}{(g_0(0,1,W))}[Y-Q_0(0,1,W)]\hfill \\ \hfill & +Q_0(1,1,W)-Q_0(0,1,W)-\mathbf{\Psi }(p_0)\hfill \end{array}$$

where g₀(A = 1, c|W) = δ₀g(c|A=1, W) and g₀(A = 0, c|W) = (1 − δ₀) g(c|A = 0, W). We now present the analogue to the derivation of the tMLE for ψ₀. Consider the parametric submodel through p̂⁰ indexed by parameter ε

$${\widehat{p}}^0(\epsilon )(Y|A,C=1,W)={[{\widehat{Q}}^0(\epsilon )(A,C=1,W)]}^Y{[1-{\widehat{Q}}^0(\epsilon )(A,C=1,W)]}^{1-Y}$$

where Q̂⁰(ε)(A, C = 1, W) is given by the logistic regression model

$${\widehat{Q}}^0(\epsilon )(A,C=1,W)=\frac{1}{1+\text{exp}-[{\widehat{m}}^0(A,C=1,W)+\epsilon h(A,C=1,W)]}$$

At C = 0, the likelihood of P(Y | A, C, W) provides as contribution a factor 1, which can thus be ignored. The score for this logistic regression model at ε = 0 is given by

$$\frac{\mathrm{d}}{\mathrm{d}\epsilon }\text{log}{p}^0(\epsilon )(A,C,W){|}_{\epsilon =0}=I(C=1)h(A,C=1,W)(Y-{\widehat{Q}}^0(A,C=1,W))$$

We now set this score equal to the component of the efficient influence curve, which equals a score for P(Y |A, C = 1, W), at p̂⁰, to obtain the equality

$$\begin{array}{l}h(A,C=1,W)(Y-{\widehat{Q}}^0(A,C=1,W))\hfill \\ =(Y-{\widehat{Q}}^0(A,C=1,W))\left(\frac{I(A=1)}{\widehat{g}(1,1|W)}-\frac{I(A=0)}{\widehat{g}(0,1|W)}\right)\hfill \end{array}$$

Solving for h(A, C = 1, W) we obtain

$$h(A,C=1,W)=\frac{I(A=1)}{\widehat{g}(1,1|W)}-\frac{I(A=0)}{\widehat{g}(0,1,W)}$$