Abstract
The first step in DNA mismatch repair (MMR) is the recognition of DNA mismatches or nucleotide insertions/deletions (IDLs) by MutS and MutS homologs. To investigate the conformational properties of MutS-mismatch complexes, we used single-molecule fluorescence resonance energy transfer (smFRET) to examine the dynamics of MutS-induced DNA bending at a GT-mismatch. The FRET measurements reveal that the MutS-GT-mismatch recognition complex is highly dynamic, undergoing conformational transitions between many states with different degrees of DNA bending. Due to the complexity of the data, we developed an analysis approach, called FRET TACKLE, in which we combine direct analysis of FRET transitions with examination of kinetic lifetimes to identify all of the conformational states and characterize the kinetics of the binding and conformational equilibria. The data reveal that MutS-GT complexes can reside in six different conformations, which have lifetimes that differ by as much as 20-fold and exhibit rates of interconversion that vary by two orders of magnitude. To gain further insight into the dynamic properties of GT-MutS complexes and to bolster the validity of our analysis, we complemented our experimental data with Monte Carlo simulations. Taken together, our results suggest that the dynamics of the MutS-mismatch complex could govern the efficiency of repair of different DNA mismatches. Finally, in addition to revealing these important biological implications of MutS-DNA interactions, this FRET TACKLE method will enable the analysis of the complex dynamics of other biological systems.
Keywords: FRET, MutS, DNA mismatch repair, DNA-protein dynamics, single-molecule kinetics, transition density
MutS and MutS homologs are the primary cellular components to identify DNA mismatches and lesions and signal the cellular events that ultimately lead to either DNA mismatch repair or cell cycle arrest (1–9). It has been hypothesized that interactions between MutS and the DNA are lesion-dependent, where different DNA substrates introduce different contacts between MutS and the DNA as well as varied DNA flexibility and conformational changes in MutS (3, 4, 10–12). These different interactions are suggested to be fundamental for the ability of MutS to differentiate between distinct DNA defects and to signal different cellular fates in response (either MMR or cell cycle arrest) (10, 11).
The nature of the MutS-mismatch and MutS-DNA lesion recognition complexes has been identified in several high-resolution crystal structures (2, 5–7). In these structures MutS and hMutSα induce a well-defined kink in the DNA at a base-base mismatch, a base insertion/deletion (IDL), or a base lesion (2, 5–7). DNA bending by MutS has been suggested to serve an important role in mismatch identification, specificity, and response signaling (2, 3, 6, 13). However, structures of MutS bound to several different DNA mismatches, each of which repaired with a different efficiency in vivo, reveal mismatch-independent interactions between MutS homologs and the DNA, where the majority of contacts and DNA kinking are nearly identical in all structures (2, 5–7, 14, 15). A similar protein-DNA interface was also revealed in structures of MutSα bound to a DNA base lesion (2). The lack of differentiation between distinct DNA lesions and mismatches by MutSα in these studies has led to the proposal that downstream events, rather than specific MutS-DNA interactions in the initial recognition complex, control specific mismatch repair efficiency or signaling specific cellular pathways for the different DNA lesions (2). This model, however, creates a structure-function disconnect, as it is unclear why identical structures of MutS-DNA complexes would be repaired with different efficiencies or, furthermore, how they could signal different overall cellular responses.
Atomic force microscopy (AFM) studies provided hints that partially resolve this structure-function anomaly. AFM imaging of MutS binding at a mismatch identified two resulting DNA conformations, bent and unbent (3, 13). The existence of multiple mismatched DNA-MutS complex conformations supports a mechanism in which variable MutS-DNA interactions and conformational states allow MutS to differentiate between different types of mismatches or DNA lesions (3, 13). Distributions of DNA bend angles from AFM images of mismatched DNA-MutS complexes are broad, suggesting that these complexes could be dynamic. We used single-molecule fluorescence resonance energy transfer (smFRET) to investigate the potential of dynamic transitions among distinct bent and unbent DNA conformational states in mismatched DNA-MutS complexes.
In contrast to the static depictions of mismatched DNA-MutS complexes prevalent in leading models of DNA MMR and reinforced by the available high-resolution structures, single-molecule FRET reveals that T. aquaticus (Taq) MutS-DNA complexes are extremely dynamic, undergoing many transitions between multiple bent and unbent DNA conformations (Figure 1). To accurately identify the unique states sampled in these complexes and the transitions among them, we developed an analysis approach, FRET Transition Analysis Combined with Kinetic Lifetime Examination of states (FRET TACKLE), which applies multiple criteria (FRET efficiencies, transition density analysis, and kinetic lifetime analysis) to identify unique states buried in complex FRET efficiency data such as those observed for GT mismatched DNA-MutS complexes.
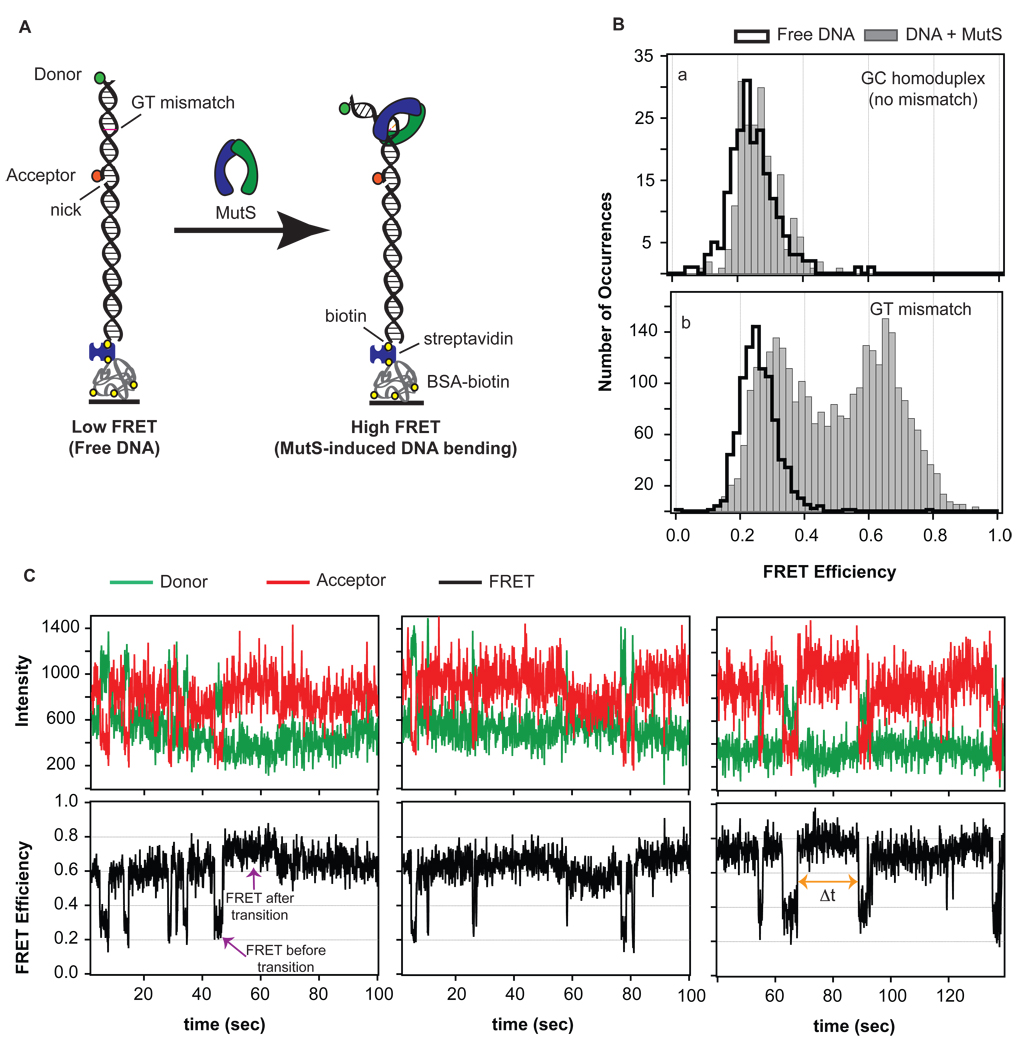
Figure 1.
(A) FRET reporter to measure MutS-induced DNA bending. A FRET donor and FRET acceptor are tethered to a 50 base-pair strand of DNA. The fluorescent dyes are located 19 base pairs apart with the GT-mismatch located about halfway between the two dyes. Upon MutS-induced DNA bending at the mismatch, the separation between the dyes decreases, and an increased FRET signal is observed. (B) FRET efficiency distribution of states in the absence (black cityscape) and presence (solid gray bars) of MutS for two DNA substrates: one without a mismatch (GC homoduplex, a) and one containing a mismatch (GT mismatch, b). The shift in the FRET distribution for MutS bound to a GT mismatch reveals mismatch-specific DNA bending induced by the protein. (C) Sample FRET donor, FRET acceptor, and corresponding FRET efficiency traces for GT mismatched DNA in the presence of MutS. Molecules sample a number of different FRET states, or bend angles, ranging from unbent (low FRET) to bent (high FRET) with very different kinetic rates of exchange among these states.
This analysis revealed a diverse DNA-protein conformational landscape and demonstrated that the MutS-mismatch recognition complex does not solely reside in a rigid bent conformation, as suggested from crystal structures (2–7), and does not simply interconvert between two states, as suggested from AFM studies (3, 13), but rather, samples a number of different bent and unbent DNA conformations with a variety of kinetic rates. Detailed analysis of the kinetics and stabilities of each state, complemented by Monte Carlo simulations of the complete kinetic scheme, suggests functional significances for the different conformations. The highly dynamic nature of this initial mismatch recognition complex revealed by single-molecule FRET TACKLE suggests that the dynamics and the kinetic behaviors of the different conformational states for MutS bound to different DNA mismatches or lesions may control the repair efficiencies of different mismatches in vivo and may also have a role in signaling downstream cellular responses.
EXPERIMENTAL PROCEDURES
Protein and DNA substrates
MutS from Thermus aquaticus was over-expressed in E. coli and purified as previously described (16). HPLC-purified labeled and unlabeled single-stranded oligonucleotides were purchased from Integrated DNA Technologies. DNA substrates contained a TAMRA-labeled oligonucleotide (5’-Biotin-TGT CGG GGC TGG CTT AAG GTG TGA AAT ACC TCA TCT CGA GCG TGC CGA TA-TAMRA-3’) annealed to a Cy5-labeled oligonucleotide (5’-TAT CGG CAC GTT CGA GATG-Cy5-3’) to create a duplex DNA fragment containing a GT base-base mismatch (Figure 1A). Oligonucleotides were annealed in buffer containing 20 mM Tris-HCl pH 7.8, 100 mM NaOAc, and 5 mM MgCl2 in a 1:1 ratio at 65°C for 20 minutes followed by slow cooling. When the temperature reached 55°C, an additional complementary strand was added and annealed to complete the duplex DNA substrate (5-AGG TAT TTC ACA CCT TAA GCC AGC CCC GACA-3’). The substrate was allowed to slowly cool to room temperature and was stored on ice or at 4°C. The annealed DNA substrate was assessed using gel electrophoresis and by observing localized donor and acceptor fluorescence signals once tethered to the surface for fluorescence analysis (described below). Molecules without both a FRET donor and a FRET acceptor were omitted from analysis. Control experiments were also performed using DNA substrates that did not contain a mismatch to ensure that the presence of the nick at the 5’ of the FRET acceptor (Figure 1A) did not affect observed fluorescence intensities and FRET efficiencies.
Fluorescence microscopy
Quartz microscope slides and flow channels were prepared as previously described (17). The surface in the channel was treated first with biotinylated-BSA (Sigma, 1 mg/mL, 5 minute incubation) followed by streptavidin (Invitrogen, 0.1 mg/mL, 5 minute incubation), similar to methods previously described (18). Annealed biotinylated, fluorescently-labeled, mismatched DNA was added to the treated surfaces at a concentration ranging between 10 and 30 pM for 5 minutes, and the unbound DNA was removed by rinsing with chilled buffer (20 mM Tris-HCl pH 7.8, 100 mM NaOAc, and 5 mM MgCl2). Samples were imaged at room temperature in the above rinsing buffer with the addition of enzymatic oxygen scavenging components (2% glucose (Sigma), 1% β-mercaptoethanol (Fluka), 0.1 mg/mL glucose oxidase (Sigma), and 0.025 mg/mL catalase (Sigma)) to enhance fluorophore lifetime and with the addition of triplet state quencher cyclooctatetraene (Aldrich) (~50 µM) to reduce dye blinking. Images were collected both in the presence and absence of MutS. Protein was allowed to bind the DNA for at least 5 minutes prior to image collection. Single-molecule FRET traces were also collected for mismatched DNA-MutS complexes bound to streptavidin-exposed, biotinylated polyethylene glycol (PEG)-coated quartz slides (19). Similar dynamics were observed for these complexes on both surfaces (Figures S1 and S6), ensuring that the dynamics were not the result of interactions of the protein and/or the DNA with the BSA-coated quartz surface. Furthermore, the consistency of the FRET TACKLE kinetics with bulk kinetics of MutS-DNA complexes also suggest limited interactions of MutS or the DNA with the surface that could affect the kinetics of the complexes.
Data were collected using a prism-type total internal reflection fluorescence (TIRF) laser microscope as described (17, 20). Two lasers were directed onto the prism, one at 532 nm to directly excite the donor dye (TAMRA) and one at 635 nm in an alternating sequence to directly excite the acceptor dye (Cy5) at the quartz-solution interface. Fluorescence emission was collected through a 60× 1.2 NA water immersion objective and split by a 645dcrx dichroic mirror (Chroma) into short and long wavelength paths. These paths were filtered for TAMRA and Cy5 emissions using HQ 585/70 and HQ 700/75 bandpass filters (Chroma), respectively. The spectrally-resolved emissions were relayed as side-by-side images onto a charge-coupled device camera (Cascade 512B, Roper Scientific). Images were exposed at 10 frames per second and collected using software written in-house.
Observed intensities of single-molecules were integrated with software written in-house to obtain individual fluorescence emission time traces as described previously (20). Emission traces were background subtracted and corrected for leakage of the donor signal into the acceptor channel (~ 5%). Molecules not confirmed to contain exactly one donor and one acceptor fluorophore were excluded from further analysis. FRET efficiencies were calculated from the respective donor and acceptor emissions as E = (IA)/(ID + IA), where ID and IA are the corrected intensities of the donor fluorophore and acceptor fluorophore, respectively.
FRET TACKLE data analysis
We apply a Gaussian derivative kernel algorithm to isolate FRET transitions in single-molecule traces (21). This algorithm (described in Supplemental Information and available at https://www.cs.unc.edu/Research/nano/cismm/download/edgedetector/index.html) yields each FRET efficiency sampled in a given FRET trace as well the time the molecule spends at that FRET efficiency (‘dwell time’, or Δt) and the transition sequence (Figure S2). Dwell times associated with the first and last FRET states in each trace are not accurately known and are discarded (Figure S2, states 1 and 12).
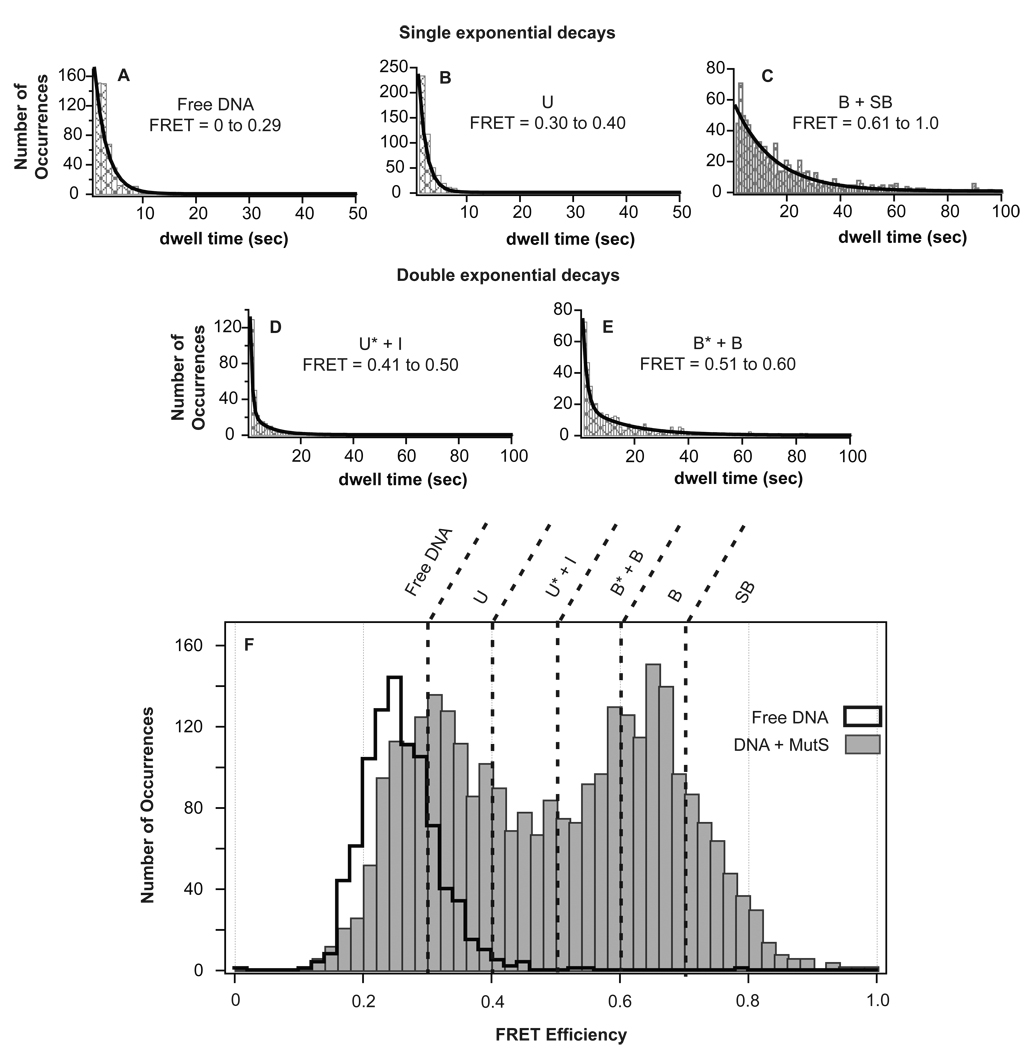
To perform kinetic lifetime analysis of states, FRET values across the entire distribution were grouped in small segments of FRET efficiencies (FRET +/− 0.005) and a dwell time distribution was generated for the state (plot of frequency vs. dwell time, Figure 3). The exponential fit to this plot provides the kinetic rate of the state (fit parameter 1/τ), and the inverse (τ) represents the ‘lifetime’ of the state. A single exponential fit represents a single lifetime, or single species, at that FRET efficiency. A double exponential fit would produce two kinetic rates and two lifetimes implying that two species reside at that FRET efficiency (Gelles and coworkers, submitted manuscript) (22). We applied an f-test to determine if a double exponential fit was warranted for the lifetime distributions shown in Figure 3D and 3E (Supplemental Information) (23). When two adjacent FRET efficiencies converge to the same lifetime (or lifetimes), those FRET efficiencies are grouped together and refit to produce a combined lifetime for that state. For example, the lifetime associated with FRET 0.33 is determined to be 1.9 seconds, and the lifetime associated with FRET 0.34 is determined to be 2.0 seconds (from the exponential fit parameters). These two FRET states have similar lifetimes (within error) and, as a result, are combined as the same state. This process is repeated across the FRET efficiency distribution until all states with unique lifetimes are isolated (Figure 3) (Additional details on this analysis are described in Supplemental Information).
Figure 3.
Determination of the number of unique species in the FRET efficiency distribution by lifetime analysis. (A–E) Plots of the distribution of dwell times showing fits to single or double exponentials for each group of FRET efficiencies with different lifetimes. The final range of FRET efficiencies that corresponded to unique states (shown in F) was determined by fitting the dwell time distributions for each distinct FRET efficiency (binned in 0.01 increments) and combining adjacent states if they had the same lifetimes (Supplemental Information). (F) The FRET efficiency distributions of GT-mismatched DNA in the absence of MutS (black cityscape, 895 molecules) and presence of MutS (gray bars, 2992 conformations (exemplified as numbers in Figure S2) sampled in 1095 molecules in two independent experiments at 200 nM MutS) showing the partition of individual states identified by unique lifetimes. Additional lifetime analysis of conformations B and SB, which were identified as two states by transition density analysis (Figure S4), is shown in Figure S3.
The lifetime and corresponding kinetic rate of SB was distinguished from the lifetime of B by separating these two FRET states into individual dwell time distributions (Figure S3) and refitting to obtain the exact lifetimes for each state (Table 1, Figure S3). As expected, the lifetimes for both states were similar (16 seconds and 14 seconds for B and SB, respectively).
Table 1.
FRET efficiency ranges and lifetimes for each unique GT-MutS state.
| State | FRET efficiency | Description | Lifetime from fits, independent experiments (τ, sec) |
(4) χ2 |
(3)Average Lifetime (τ, sec) |
|---|---|---|---|---|---|
|
Free DNA |
0 to 0.29 | Free DNA | 2.3 (1) | 2784 | 3.9 (± 2.3) |
| 5.5 (1) | 41 | ||||
| 37 (2) | 344 | ||||
| U | 0.30 to 0.40 | Low FRET, unbent GT-MutS complex |
1.4 (1) | 111 | 3.5 (± 2.1) |
| 6.3 (1) | 73 | ||||
| 3.0 (2 | 194 | ||||
| U* | 0.41 to 0.50 | Unstable intermediate GT-MutS complex (unbent) |
0.76 (1) | 88 | 0.53 (± 0.25) |
| 0.57 (1) | 29 | ||||
| 0.27 (2 | 105 | ||||
| I | 0.41 to 0.50 | Stable intermediate GT-MutS complex (intermediately bent) |
5.6 (1) | 88 | 8.7 (± 2.7) |
| 9.5 (1) | 29 | ||||
| 10.9 (2) | 105 | ||||
| B* | 0.51 to 0.60 | Unstable intermediate GT-MutS complex (bent) |
1.4 (1) | 242 | 2.2 (± 1.8) |
| 4.4 (1) | 22 | ||||
| 0.96 (2) | 185 | ||||
| B | 0.51 to 0.70 | High FRET, bent GT-MutS complex |
17 (1) | 1621 | 13 (± 3.3) |
| 13 (1) | 340 | ||||
| 10 (2 | 1581 | ||||
| SB | 0.70 to 1.0 | Very high FRET, super-bent GT-MutS complex |
20 (1) | 73 | 17 (± 4.1) |
| 18 (1) | 91 | ||||
| 11 (2) | 691 |
Lifetime of the DNA conformation determined at 200 nM MutS.
Lifetime of the DNA conformation determined at 20 nM MutS.
Average lifetimes for all states except Free DNA determined from the analysis of states in 3 independent experiments, two performed at 200 nM MutS and one at 20 nM MutS. The average lifetime of Free DNA is determined solely from the two independent experiments performed at 200 nM MutS.
χ2 of each exponential fit is calculated as Σ (yfit – ydata)2. For the distributions where a double exponential fit was applied, an f-test was performed to confirm the suitability of applying the double exponential fit versus a single exponential fit (Experimental Procedures, Supplemental Information).
Each 3-dimensional peak identified in the transition density distribution (Figure 2A) was fit to a 2-D Gaussian function following the equation:
| (1) |
where xo, yo, and zo are the offsets in the x, y, and z dimensions; xwidth and ywidth are the breadths of the Gaussians in both the x- and y- dimensions; A is the peak amplitude; and, cor is a correlation parameter representing deviation from the x–y orthogonal (angular skew in the peak). Each 2-D Gaussian peak isolated by applying this analysis across the entire transition density distribution (Figure S4) is shown in Figure 2B.
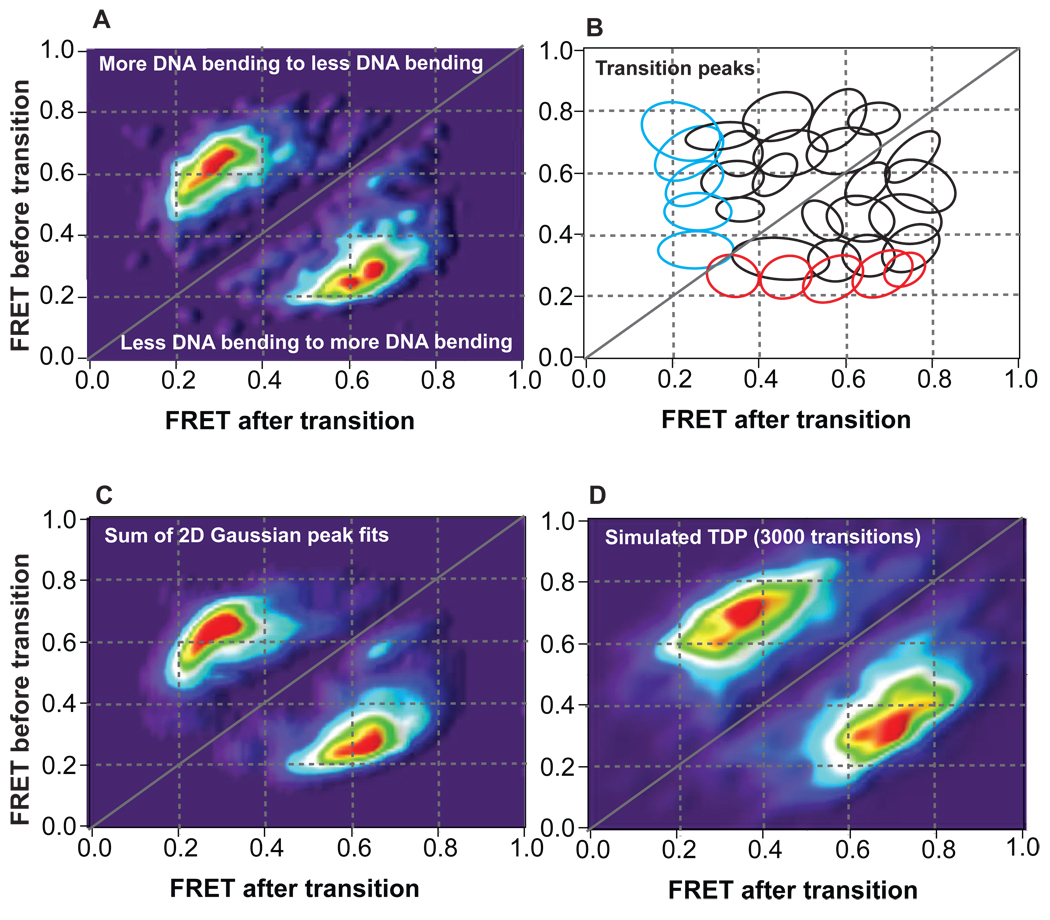
Figure 2.
Transition density distributions for conformational transitions induced by MutS on GT-mismatched DNA. (A) Raw transition density plot showing 2942 conformational transitions observed in 701 molecules. (B) Diagram outlining individual transition peaks embedded in the transition density plot determined from the 2-D analysis shown in Figure 4 and Figure S4. Each ellipse represents an individual transition peak. Red and cyan ellipses represent binding and unbinding transition peaks, respectively, while black ellipses represent conformational transitions among states with different FRET efficiencies. (C) Transition density plot generated from summing the 2-D Gaussian fits of each transition peak determined from the 2-D analysis shown in Figure 4 and Figure S4. The TDP of the sum of the individual transition peaks generates a smoother version of the TDP of the raw transition data (A). (D) Transition density plot generated from Monte Carlo simulations of 3000 transitions given the kinetic scheme determined using FRET TACKLE. The FRET efficiencies associated with each state were assigned based on the average FRET efficiencies determined from the 2-D Gaussian peak fits (Figure 4 and Figure S4), and the breadth associated with each FRET efficiency was set to 0.075 based on the breadth of the FRET efficiency of the distribution for free DNA (Figure 1B). The MC simulated TDP is very similar to the TDP of the raw data (A) when appropriate error and bias is applied to the simulated data (error parameter of 0.10 and bias parameter of 0.36 shown in (D)).
Based on a standard kinetic branching mechanism (24), the kinetic rates of each transition are determined by the following set of equations:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The rates of individual transitions are calculated by the probability of occurrence of a given transition by the branching ratios:
| (8) |
where x and y represent the states comprising the transition, and N represents the number of times a transition was observed from that state (Table 2). Additional details on the FRET TACKLE analysis approach are provided in Supplemental Information.
Table 2.
Kinetic rates, transition probability ratios (Nx→y / Nx,total), and partition ratios (Q) of GT-MutS binding, unbinding, and conformational transitions.
| (1)Transition rate (s−1) | (2)Nx→y / Nx,total | (3)Q = kf / kr | ||
|---|---|---|---|---|
|
GT-MutS complex transitions |
U to B | 0.38 | 0.56 | 15 |
| B to U | 0.026 | 0.42 | ||
| U* to B | 0.59 | 0.45 | 95 | |
| B to U* | 0.0062 | 0.099 | ||
| I to B | 0.039 | 0.25 | 14 | |
| B to I | 0.0027 | 0.043 | ||
| B* to B | 0.10 | 0.15 | 53 | |
| B to B* | 0.0019 | 0.030 | ||
| B to SB | 0.0039 | 0.063 | 0.28 | |
| SB to B | 0.014 | 0.19 | ||
| U to SB | 0.15 | 0.22 | 6.8 | |
| SB to U | 0.022 | 0.31 | ||
| U* to SB | 0.45 | 0.34 | 38 | |
| SB to U* | 0.012 | 0.17 | ||
| U to U* | 0.0094 | 0.014 | 0.12 | |
| U* to U | 0.077 | 0.059 | ||
| I to SB | 0.028 | 0.18 | 4.5 | |
| SB to I | 0.0062 | 0.087 | ||
| B* to SB | 0.16 | 0.23 | 21 | |
| SB to B* | 0.0075 | 0.10 | ||
| U to I | 0.047 | 0.07 | 2.5 | |
| I to U | 0.019 | 0.12 | ||
| U to B* | 0.036 | 0.053 | 0.21 | |
| B* to U | 0.17 | 0.25 | ||
| U* to B* | 0.028 | 0.021 | 0.8 | |
| B* to U* | 0.035 | 0.052 | ||
| I to B* | 0.0054 | 0.034 | nd | |
| B* to I | nd | |||
| KA (M−1) | ||||
|
4MutS Binding/ Unbinding transitions |
free to U | 0.041 | 0.096 | 3.8 × 106 |
| U to free | 0.054 | 0.081 | ||
| free to U* | 0.019 | 0.043 | 5.3 × 105 | |
| U* to free | 0.18 | 0.13 | ||
| free to I | 0.052 | 0.12 | 4.0 × 106 | |
| I to free | 0.065 | 0.42 | ||
| free to B* | 0.049 | 0.11 | 1.2 × 106 | |
| B* to free | 0.21 | 0.31 | ||
| free to B | 0.25 | 0.58 | 5.7 × 107 | |
| B to free | 0.022 | 0.35 | ||
| free to SB | 0.020 | 0.046 | 1.3 × 107 | |
| SB to free | 0.0098 | 0.14 |
Transition probability ratios were determined by the ratio of the number of times a given transition occurred versus the total number of transitions recorded from that state in total.
Partition ratios for each transition were calculated by the ratio of the forward and reverse rates and were used to calculate the relative free energies between each state (Supplemental Information).
Association constants for the binding and unbinding transitions are determined at a MutS concentration of 200 nM. These values result in an average dissociation constant of 13 nM, consistent with the dissociation constant determined in the bulk by fluorescence anisotropy (40 nM) (4).
RESULTS
We used single-molecule FRET (smFRET) to monitor the dynamics of Taq MutS-induced DNA bending. DNA substrates that have a FRET donor (TAMRA) and a FRET acceptor (Cy5) located 19 base pairs apart with a GT base-base mismatch located approximately halfway between the two fluorophores were annealed, tethered to a quartz surface, excited using prism-type total internal reflection fluorescence microscopy (Experimental Procedures, Figure 1A) (17), and the FRET efficiency between the dyes was measured in real time. In the absence of MutS, the DNA molecules exhibit a constant FRET efficiency for the duration of the trace, with an average FRET efficiency of 0.24 (Figure 1B). Based on a helical model of DNA (25–27), the FRET dye pair separation was determined to be 72 Å, yielding an approximate Förster distance (Ro) of 59 Å [ FRET = 1 / (1 + (r /Ro)6) ], similar to that determined for this pair in a previous study (25, 28). Using this Ro and geometric analysis of the DNA FRET reporter with a single kink located at the mismatch, this FRET assay is expected to be sensitive to changes in DNA bending ranging from 0° to 120°. Recent studies have shown that some fluorescent dyes stack on the ends of the DNA duplex, spending only a fraction of time in free rotation and invalidating the isotropic averaging of the κ2 rotational coefficient used to determine the exact Förster distance, and in turn FRET efficiency, for a FRET pair (29). In other words, both bending and twisting or untwisting of the DNA may contribute to observed changes in FRET efficiencies. Although this stacking prevents a direct interpretation of FRET efficiencies as quantitative DNA bend angles, it does not affect our ability to identify distinct conformational states of MutS-DNA complexes (described below).
To identify non-specific interactions of MutS with the DNA, with the fluorescent dyes, or with the nick on the 5’ side of the Cy5 dye (Figure 1A, Supplemental Information), we measured FRET efficiency traces using a non-mismatched DNA substrate in both the absence and presence of 200 nM MutS (Figure 1B, Figure S6). The FRET time traces are nearly identical with and without MutS and do not exhibit any transitions between distinct FRET states. This result is expected because insignificant binding of MutS to this DNA substrate is detected in bulk fluorescence anisotropy experiments (4). The slight shift in the center of the FRET efficiency distribution (Figure 1B) may reflect a change in local environment of the fluorescent dyes due to MutS nonspecifically interacting with the DNA without causing significant bending. No changes in the spectra or intensities of Cy5 (at the nick) or TAMRA (at the free end of the DNA) in the presence of 200 nM MutS were observed (Figure S6). These results are consistent with i) the low binding affinity of MutS for homoduplex DNA (KD ~ 20 µM) (4, 30), ii) AFM images of MutS and nicked DNA which did not reveal any preference for nicked sites (unpublished results), and iii) mismatch repair assays which demonstrated the efficiency of repair is independent of the position of the nick (from 10 to >100 base pairs from the mismatch (31)). Taken together, these results indicate that nonspecific binding by MutS to the DNA, if there is any, does not significantly alter the observed FRET efficiencies.
In contrast to homoduplex DNA FRET traces, individual time traces for many GT mismatched DNA molecules show transitions between different FRET states in the presence of MutS (Figure 1C and Figure S1), and the FRET distribution is significantly altered relative to free DNA (Figure 1B). Analysis of the individual time traces for hundreds of molecules using an edge-finding algorithm (described in Methods and Supplemental Information) reveals that GT-MutS complexes switch back and forth between several conformations with significantly different FRET efficiencies (Figure 1C), indicating large conformational transitions of the DNA. Intensity time traces for single dye-labeled GT mismatched DNA (containing the FRET donor in the absence of the FRET acceptor or the FRET acceptor in the absence of the FRET donor) in the presence of MutS did not show any fluctuations in the dye intensity (Figure S6), revealing that the anti-correlated intensity changes for dual-labeled GT mismatched DNA in the presence of MutS are the result of MutS-induced DNA bending and/or twisting and not fluctuations in the emission spectra or intensities of the dyes.
From these dynamic smFRET traces, we are able to determine the distribution of FRET states (Figure 1B) as well as identify the specific states before and after each transition, the dwell times (Δt) associated with each state, and the kinetics of interconversion between states (Figure S2).
Kinetics and thermodynamics of GT-MutS complexes revealed by FRET TACKLE
To characterize the transitions between different FRET states, we constructed 3-D histogram plots of the frequency of transitions between each of the states (called transition density plots, or TDPs) (Figure 2) (32, 33). Specifically, the number of times a given transition occurs (for example, from FRET 0.40 to FRET 0.60) is tabulated for all molecules, and the FRET efficiencies before (eg. 0.40) and after (eg. 0.60) the transitions are plotted on the y- and x-axes, respectively, with the number of times the transition occurs plotted on the z-axis (Figure 2). Peaks above the diagonal line represent transitions from higher FRET to lower FRET (more DNA bending to less DNA bending), while peaks below the diagonal line represent transitions from lower FRET to higher FRET (less DNA bending to more DNA bending) (Figure 2).
In a study of the dynamic binding and unbinding of RecA to DNA, transition densities were used to identify unique conformational states in the complexes (32, 33). The TDP for the GT-MutS molecules (Figure 2A), however, shows a complex distribution of transitions between multiple FRET states, with a number of overlapping transition peaks, making identification of the number of unique conformational states difficult from analysis of the transition densities alone. To overcome this limitation, we developed a modified analysis method called FRET TACKLE, which combines direct analysis of FRET transitions (32, 33) with kinetic lifetime analysis of individual states (34–36). As summarized below (and described in further detail in Supplemental Information), FRET TACKLE is not only a powerful method for isolating unique states from complex FRET efficiency distributions, but it also yields the rates of transitions among the different states as well as the relative stabilities of all the states, providing a complete quantitative picture of the dynamics of the GT-MutS complexes.
Kinetic lifetime examination of FRET states reveals six different states
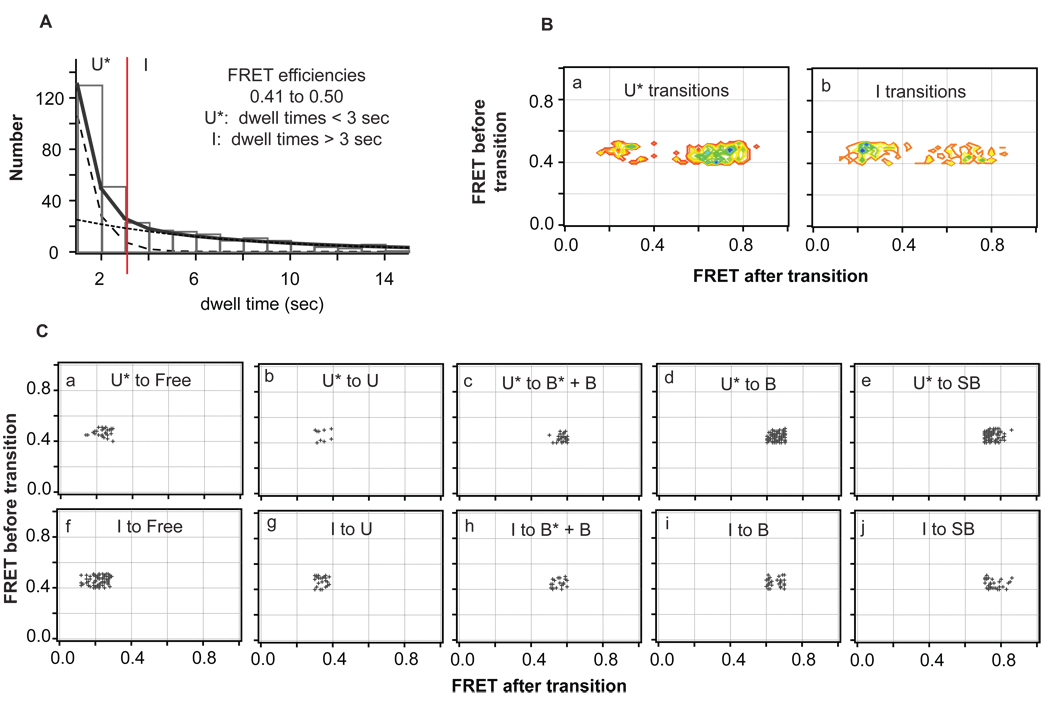
Previous single-molecule FRET studies have reported using lifetimes to identify and characterize different species among various FRET states or within a single range of FRET efficiencies (18, 22, 35, 37, 38). We employ a similar approach to identify a complete set of states with unique lifetimes for GT-MutS complexes. Briefly, the observed events are grouped by FRET values into bins with full width 0.01. The distribution of lifetimes within each bin is fit to an exponential decay function or the sum of two exponential decays (Figure 3) (Experimental Procedures, Supplemental Information) (23). If the lifetimes (τ−1) of the fits for adjacent bins are the same (within the errors of the parameters of the fits), those bins are pooled, and the resultant set of dwell times grouped by wider FRET bins is refit. This process is repeated until a unique set of states grouped into FRET bands that exhibit distinct lifetimes is obtained (Figure 3; Methods and Supplemental Information). From this analysis, we identified six unique conformational states for GT-mismatched DNA in the presence of MutS (Figure 3, Table 1).
The state comprising the lowest FRET range (FRET 0 to 0.29) overlaps with the FRET efficiencies observed for GT-mismatched DNA in the absence of MutS (Figure 3A). In addition, the lifetime of this state is consistent with bulk kinetic studies that determined the mismatch binding rate of Taq MutS to be 3 × 106 M−1sec−1 (39). Specifically, this bimolecular association rate predicts the lifetime of the unbound state at 200 nM MutS to be 1.7 seconds, which is very similar to our experimental result (τavg = 3.9 ± 2.3 seconds, Table 1). To verify that this state is indeed free DNA, we conducted the experiment at a reduced concentration of MutS. Lowering the MutS concentration results in a significant increase in the lifetime of the FRET state associated with free DNA (τ = 37 seconds, Table 1), while the lifetimes of the remaining GT-MutS conformations do not change significantly (Table 1). These results confirm the separation of FRET efficiencies representing unbound DNA from those representing MutS-bound, unbent DNA conformations using lifetime analysis.
The other five states represent different conformations of GT-MutS complexes, with the FRET values of these states loosely indicating the extent of DNA bending. We define the lower FRET conformations as ‘unbent’ or U. These states differ from free DNA by lifetime and also exhibit slightly different FRET efficiencies from free DNA, which may result from slight DNA bending or a change in the twist of the DNA induced by MutS. Higher FRET conformations, which clearly result from a significant decrease in the distance between the FRET donor and FRET acceptor, are defined as ‘bent’ or B (Figure 3, Table 1). The stable, intermediately bent state is denoted as conformation I. Conformational states with short lifetimes are predicted to be unstable states with respect to the other states and are denoted with asterisks (unstable, unbent (U*) or unstable, bent (B*)).
Although FRET values between 0.61 and 1.0 converged to a single lifetime, suggesting a single species, transitions between states within this FRET range are seen in the TDP (Figure 4A, discussed below), indicating that two species exist within this range of FRET efficiencies. This additional conformational state is denoted as conformation SB (‘super-bent’ GT-MutS complex, Table 1). This state appears to occupy very high FRET efficiencies (FRET 0.70 to 1.0) but does not have a lifetime unique from conformation B (Figure S3).
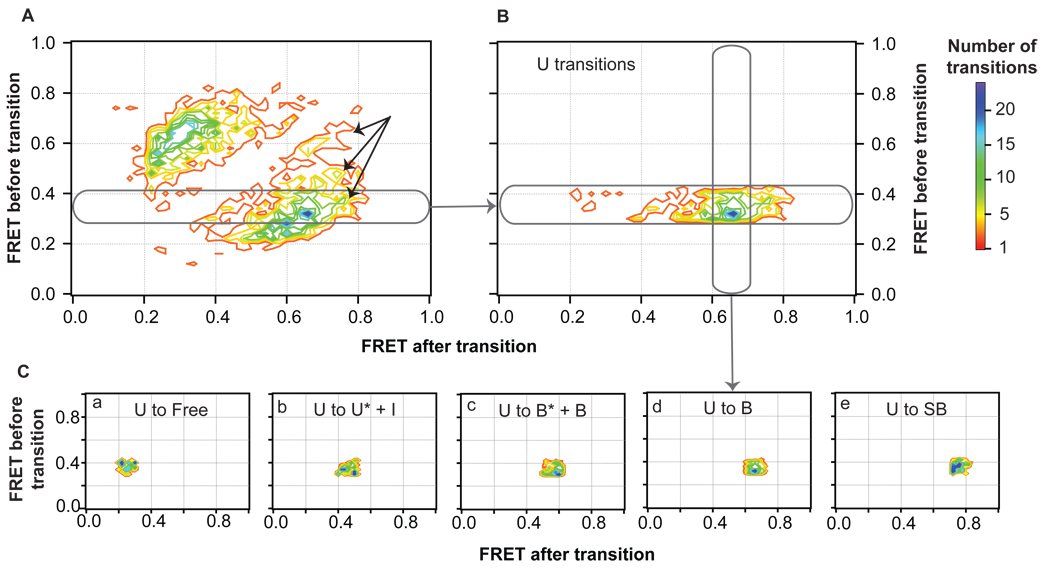
Figure 4.
Separation of transition peaks in the TDP by FRET efficiencies. (A) Contour image of the transition density distribution shown in Figure 2A. Black arrows represent transitions to a high FRET state not isolated by lifetime examination (conformation SB). (B) Transition density distribution for a section of transitions from an individual state (U). Individual peaks are cross-sectioned (C) and fit to 2D Gaussian distribution distributions. Complete documentation on this analysis across the entire TDP is shown in Figure S4.
Isolating unique states from transition density plots
Once states are identified by kinetic lifetime analysis, these states can be used to tease apart all transitions comprising the transition density distribution (Figure 2A and Figure 4A). As described in Experimental Procedures and the Supplemental Information, this analysis is performed in two parts. First, the TDP is sliced into individual FRET efficiency ranges that correspond to each FRET state, and each slice is cross-sectioned to isolate individual transition density peaks for every transition (Figure 4, Figure S4). Second, for those the peaks that contain two species (e.g., U* and I), the two species are separated by lifetime (Figure 5, Figure S5). Each of the peaks is then fit to a 2-D Gaussian, which are combined to generate the calculated TDP shown in Figure 2C. From the transition density analysis (Figures 4, 5, S4, and S5), the probabilities of transitions among every isolated state can be directly determined (Table 2).
Figure 5.
Separation of transition peaks for states with overlapping FRET ranges by lifetimes. (A) Dwell time distribution of a FRET efficiency state (0.41 to 0.50) comprised of two species (U* and I) determined from lifetime analysis (Figure 3D). The double exponential decay fit (solid black line) is deconvoluted into two single exponential decay fits (dashed black lines), and the two species are separated by dwell time (red line). (B) Transition density distributions for transitions identified when the two species in the mixed FRET state are separated by dwell time. (C) Scatter plots showing the transitions for the cross-section of each transition. The transition sequences of each species are not affected by altering the cutoff time (red line, A) between the two states to +/− 1 second.
Kinetic scheme and free energy diagram of DNA-MutS binding and conformational transitions
Because our FRET TACKLE analysis provides the lifetimes of all GT-MutS states (Table 1, Figure 3) as well as the probabilities for transitions between each of the states (Table 2), we can determine the rate constants for every observed transition (Experimental Procedures). The calculated kinetic rates (and the corresponding transition ratios) are shown in Table 2 and Figure 6. These rates fully characterize the kinetic scheme and were used to generate a free energy diagram for MutS interacting with GT-mismatched DNA (Figure 6 and Figure 7, Supplemental Information). Notably, the relative free energies of all the states were calculated for every transition pathway (for example, the relative free energy for B→B* was compared to that determined for B→U→B* and B→Free DNA→B*, etc.), and the relative free energies are consistent independent of path (to within a few tenths of a kcal/mol, Figure 7). This result strongly supports the kinetic scheme in Figure 6 and demonstrates the robustness of the FRET TACKLE analysis.
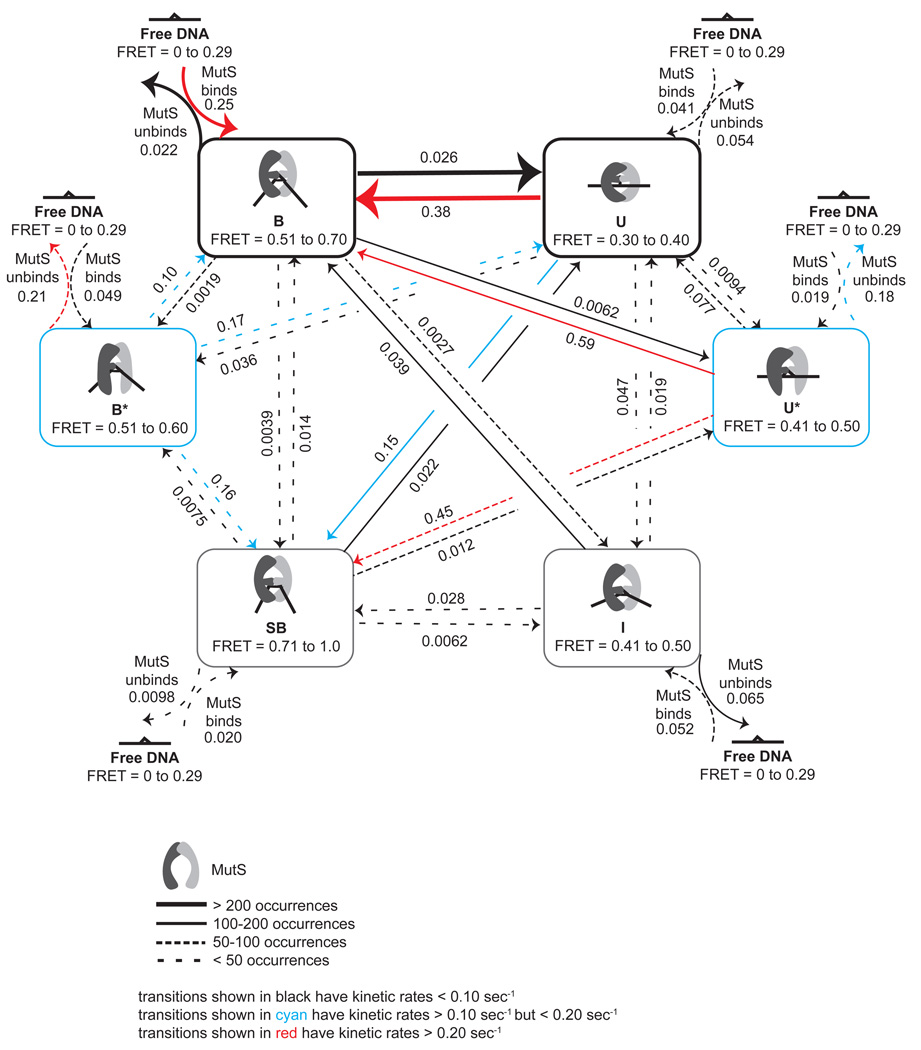
Figure 6.
Kinetic scheme of GT-MutS dynamics determined from the FRET TACKLE analysis of single-molecule FRET data. Arrows represent transitions that were observed, with decreasing line width representing a decreasing number of transitions observed between states. The rate constant (in seconds) for the transitions are shown above/below the arrows. The association rates are for 200 nM MutS. Black arrows represent transitions with kinetic rates less than 0.10 s−1; cyan arrows represent transitions with kinetic rates greater than 0.10 s−1 but less than 0.20 s−1; red arrows represent transitions with kinetic rates greater than 0.20 s−1 . The corresponding rates for each transition represented in this model are shown and are listed in Table 2.
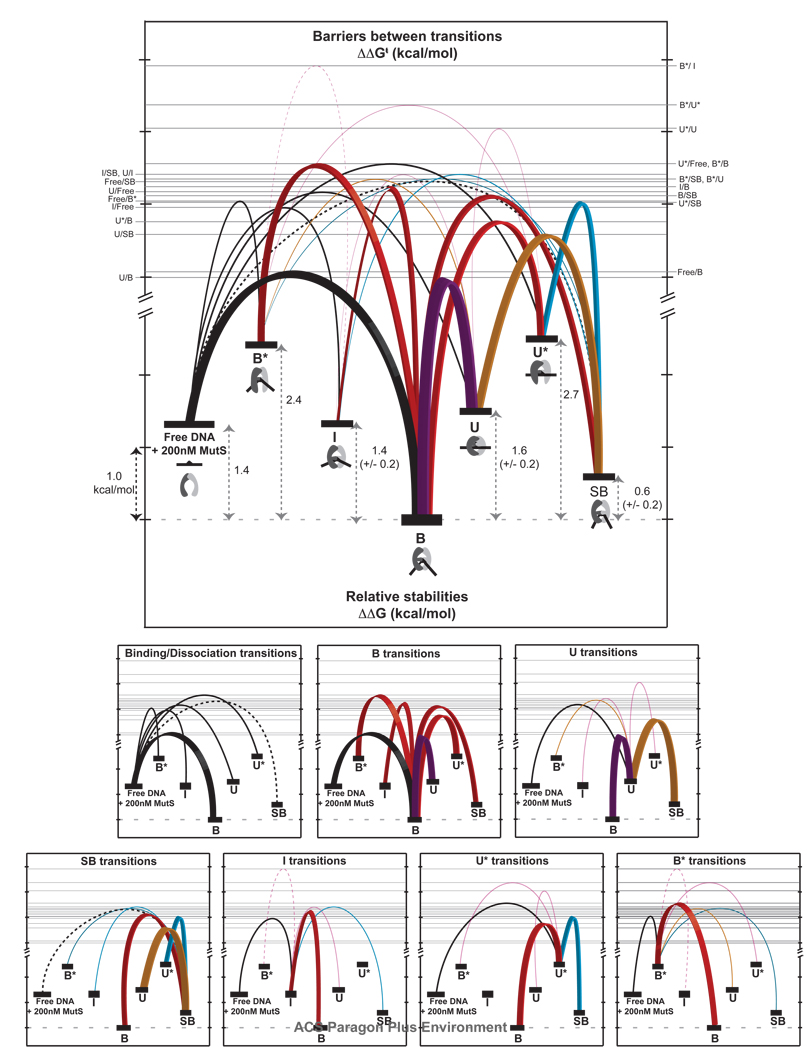
Figure 7.
Free energy diagram showing the relative stabilities (ΔΔG°) of each state and the relative free energy barriers (ΔΔG†) for each GT-MutS conformational, binding, and unbinding transition. The top diagram shows all transitions and the bottom diagrams show the transitions for each state. Tick marks represent ~ 1 kcal/mol. Binding and dissociation transitions are shown in black. Transitions down the energy funnel to the stable bent state B are shown in red with bold lines, with the most frequently observed transition (U↔B) shown in purple. The other dominant transitions in the kinetic scheme (U↔SB and U*↔SB) are shown with bold lines for emphasis. Transitions to state SB are shown in cyan; transitions to U are shown in orange. The error in the relative free energies of conformations UI, and SB result from differences in free energy calculations from different pathways. All other states yield the same free energy independent of path. All of the relative free energy barriers, with the exception of Free↔SBU↔IB*↔U*, and B*↔I, have an absolute variation from the average of the forward and reverse transitions of less than ± 0.1 kcal/mol. Transitions between Free↔SB (dashed black line), U↔I and B*↔U* (solid magenta lines) have an error of ± 0.2 kcal/mol, and the transition between B*↔I (dashed magenta line), which shows the fewest transitions, contains the largest error (± 0.6 kcal/mol). For simplicity, the relative free energies were calculated for a specific concentration of MutS (200 nM). However, addition of the concentration factor only changes the absolute free energy of the ‘Free DNA + MutS’ state and does not impose a difference in the relative free energies of the other conformations. For example, reducing the MutS concentration from 200 nM to 20 nM stabilizes the ‘Free DNA + MutS’ state by 1.4 kcal/mol (from ΔΔG = 1.4 kcal/mol to ΔΔG = 0 kcal/mol with respect to conformation B).
The complete kinetic scheme of these complexes identified by smFRET TACKLE is also consistent with bulk studies of these complexes. First, the average dissociation constant of these complexes determined from smFRET is 13 nM, comparable to results previously reported using EMSA, AFM, and fluorescence anisotropy (4, 40). Second, the lifetime of the unbound state is consistent with bulk kinetic studies (39).
Simulations of the kinetic mechanism determined from FRET TACKLE
To complement the experimental results and to further explore the dynamics and evolution of states visited during a single MutS binding event at a GT mismatch, we simulated the complete kinetic mechanism for the binding and conformational equilibria (Figure 6, Table 2) using two different methods: similarity transform and Monte Carlo. We used the similarity transform method (described in Supplemental Information) to perform ensemble simulations (41) and Metropolis Monte Carlo (MC) to simulate the conformational trajectories of single GT-MutS complexes (42). We examined the effect of different conditions, such as different MutS concentrations (Figure 8A–B), and different initially bound states, on the kinetic evolution of the GT-MutS complexes. As discussed below, these simulations offer interesting details that are difficult to capture by simply examining the experimental data (Supplemental Information). Furthermore, the agreement between the results from the simulations and the experimental data support and verify the kinetic scheme identified by FRET TACKLE and confirm that 3000 transitions are sufficient to define the kinetic mechanism (Supplemental Information and Table S2). Finally, to further examine the agreement between the simulations and experiment, we added error to the MC simulations to generate a TDP, and this MC TDP is very similar to the experimental TDP (Figure 2D vs. 2A).
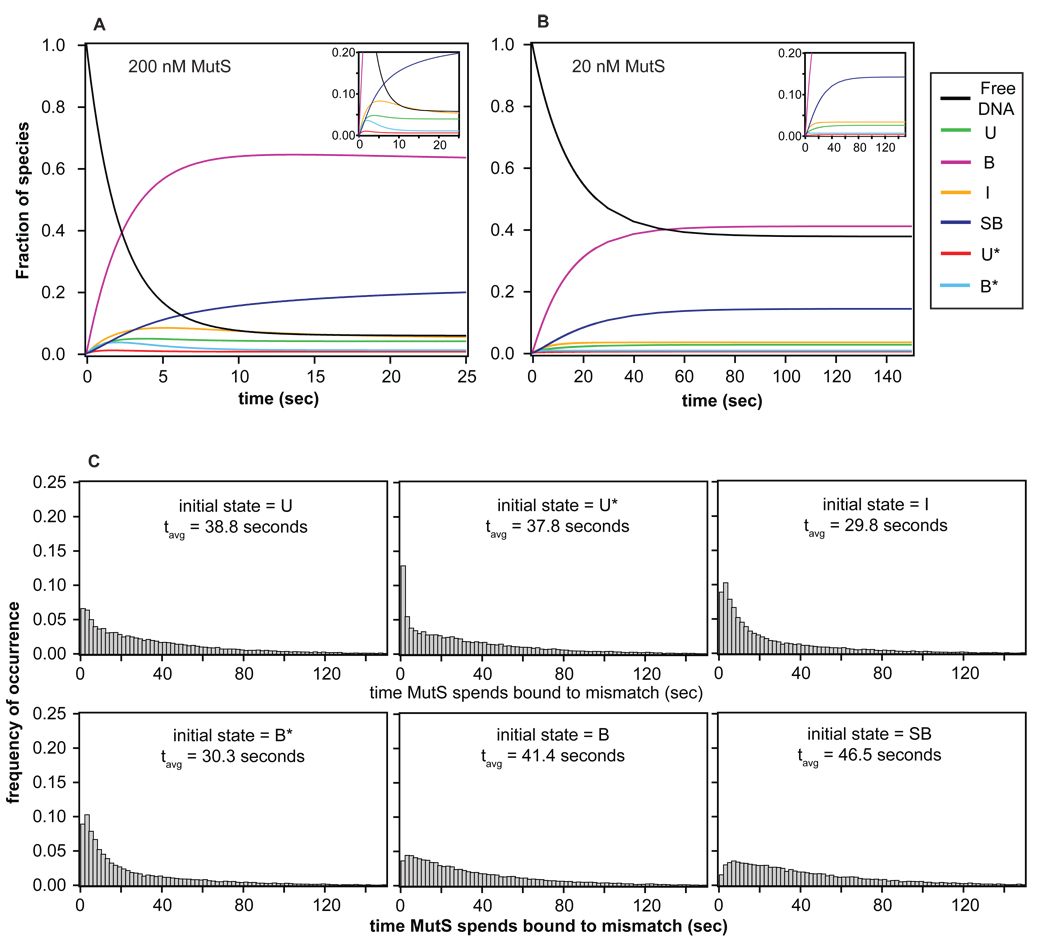
Figure 8.
Simulations of bulk and single molecule kinetic behavior. (A–B) Evolution of each species as a function of time for an ensemble of molecules using the similarity transform procedure. The inset shows the evolution of states with fractions less than 0.20. Results, shown as the fraction of species, reveal that the system reaches equilibrium in about 20 seconds at 200 nM MutS and in about 120 seconds at 20 nM MutS. The fraction of each species observed at equilibrium in the simulations are consistent with those determined from the experimental rates (Figure 7), confirming the accuracy in the FRET TACKLE kinetic calculations. (C) Distributions of the time MutS spends bound to the DNA generated from Monte Carlo simulations of single binding event (MCSBE) when each of the 6 different states is used as the initial state of the simulation. These results directly show that the time MutS spends bound to the DNA is highly dependent on the state in which the complexes start, where occupancy is highest when the starting state is the stable bent conformation B, and occupancy is the lowest when the starting state is the intermediately bent state I.
To gain insight into the properties of individual MutS-DNA complexes, we used MC to examine the fate of MutS when bound to DNA in each of the six different conformations (U, U*, I, B*, B, or SB). We performed Monte Carlo simulations (20,000) of single binding events (MCSBE), where each MutS-DNA conformation was used as the starting state and the simulation halted when MutS dissociated from the DNA. For a given starting state, these simulations yield information about the length of time MutS spends bound to the DNA, the number of conformational transitions and number of different states visited in a single binding event (SBE), and the likelihood that different states are visited (Figure 8C, Table 3).
Table 3.
Summary of MCSBE simulations showing the average lifetime MutS spends on the DNA (Figure 8C) as well as the total number of conformational transitions and states sampled in a single binding event for a given initial state in the simulation.
| MCSBE initial state | |||||||
|---|---|---|---|---|---|---|---|
| U | U* | I | B* | B | SB |
Average at equilibrium |
|
| Residence time on the DNA | 38.80 | 37.81 | 29.82 | 30.33 | 41.44 | 46.50 | 38.61 |
|
# conformational transitions in SBE |
4.97 | 4.94 | 3.60 | 4.34 | 4.19 | 4.96 | 4.28 |
|
# unique states sampled in SBE (including the initial state) |
2.91 | 3.12 | 2.45 | 2.85 | 2.43 | 3.05 | 2.59 |
The MCSBE reveals an average lifetime of MutS on the DNA of 38 seconds (Table 3), which is consistent with our smFRET experimental results. However, the average time that MutS spends on the DNA depends on the starting state in ways that are not easily predictable from the relative stabilities of the states (Figure 8C). For example, I is a relatively stable state (Figure 7), but MutS spends the least amount of time bound to the DNA (29.8 sec) when I is the starting conformation in the simulation; whereas, U* is one of the least stable states (Figure 7), but binding into U* results in relatively long residence time of MutS on the DNA (37.8 sec, Figure 8C). The distributions of the length of time MutS spends bound to the DNA, independent of the starting state in the simulation, are extremely broad, ranging from a few seconds to several minutes (Figure 8C). This heterogeneity in residence times of MutS on the DNA results from the large number of conformations that MutS-GT complexes can adopt coupled with the significant differences in barriers for transitions between states (Figure 7).
Notably, the MCSBE indicates that MutS rarely samples all six MutS-DNA conformations in a single binding event. Specifically, the average number of conformational transitions during a single binding event is 4.3, and the average number of different conformations visited during a single binding event is only 2.6 (Table 3). Consequently, the conformational states sampled by MutS, and therefore, the residence time on the DNA, are highly dependent on the initial conformational state. For example, starting in I, MutS visits on average only 1.6 other conformations and has the shortest residence time on the DNA (Table 3 and Table S3). However, if the complex does not readily dissociate, it may change conformation to a long-lived state (such as SB) and/or undergo repeated transitions between the bent and unbent states (Table S3). An extreme example of this phenomenon was observed in a simulation where MutS resided on the DNA for 450 seconds, and the complexes visited the unbent, bent, and superbent states 28, 33, and 18 times, respectively, before dissociation finally occurred. It is also interesting to note that there is no relation between the distribution of states visited and residence time of MutS on the DNA. Taken together, the MCSBE results show that conformations visited by MutS-DNA complexes, as well as the length of time MutS spends bound to the mismatch, is highly dependent on the initial conformation of the MutS-DNA complex (Tables 3 and S3).
DISCUSSION
Although there have been many biochemical and crystallographic studies of the mismatch repair protein MutS, the molecular mechanisms that underlie its cellular function remain unclear (2, 13, 43–46). This single enzyme must perform a number of different jobs, from identifying mismatched bases and signaling repair to identifying DNA damage due to oxidative or chemotherapeutic stresses and signaling apoptosis (8, 9, 47–50). In addition, MutS and MutS homologs play roles in other cellular processes, including double-strand break repair, meiotic and mitotic recombination, and transcription-coupled repair (13, 51–55). Crystal structures of MutS and MutSα bound to several different DNA mismatches and a DNA lesion are very similar, showing a single bent (or kinked) DNA conformation with similar MutS-DNA interfaces (2, 5–7). While these structures have provided invaluable information about MutS-DNA interactions, they do not provide an explanation for the observations that different mismatches are repaired with different efficiencies (2, 5–7, 14, 15, 56). In fact, the similarities of the structures of these complexes would suggest that all mismatches and some DNA lesions are recognized by MutS in a similar manner and would be repaired with similar efficiencies. Other studies have begun to address this conundrum. Experiments using AFM imaging have revealed that MutS-DNA complexes exist in more than a single conformation (3) and suggest that the dynamics of these complexes may be important for signaling DNA repair (3, 13).
To investigate the conformational and dynamic properties of the MutS-mismatch recognition complex, we used single-molecule FRET to characterize the DNA conformations of MutS-GT complexes and to monitor changes in conformation in real-time. Our results reveal that this complex is highly dynamic, with MutS inducing at least 6 different DNA conformations when bound to a GT mismatch. In addition, the lifetimes of the different conformations differ by as much as 20-fold (Table 1), and the rates of interconversion between different states vary by two orders of magnitude (Table 2). The complexity of the conformational properties of the MutS-mismatch DNA complex led us to develop an analysis approach called FRET TACKLE, which allowed us to identify all states sampled, the relative stability and lifetimes of all the states, and the rates of binding to and interconversion between the different states. Supplementing the kinetics identified from FRET TACKLE with Monte Carlo simulations of single molecules allows us to better understand the transition properties between the states and offers clues to the functional roles of these states in mismatch repair initiation by MutS.
FRET TACKLE reveals the potential roles of different conformational states in the MutS-mismatch recognition complex
The detailed kinetic scheme and relative stabilities determined for GT-MutS binding, unbinding, and conformational fluctuations (Figure 6 and Figure 7) demonstrate the complex dynamics that can govern interactions within the MutS-mismatch recognition complex. These data, combined with Monte Carlo simulations of single-binding events (Figure 8C, Table 3), provide substantial insight into the potential roles of the 6 different states in mismatch recognition by MutS.
MutS binding and DNA bending occur concomitantly
Inspection of the complete kinetic scheme of the GT-MutS complex (Figure 6, Table 2) reveals that MutS preferentially binds a GT mismatch in a bent conformation, with 59% of all binding transitions occurring directly into conformation B (Table 2). The rate of MutS binding into state B is at least five times faster than binding into any other state, and the bimolecular rate of binding into B (1.25 × 106 M−1s−1) is similar to the ensemble binding rate measured in bulk studies (3 × 106 M−1s−1) (39). In addition, in bulk studies, the rate of MutS binding to a mismatch exhibits a linear dependence on the concentration of MutS (150 nM – 500 nM) (39), and in our studies, lowering the concentration of MutS from 200 nM to 20 nM results in the expected increase in the lifetime of free DNA (Table 1). The MutS concentration-dependence on the rate of DNA binding follows the Law of Mass Action for MutS concentrations ranging from 20 nM to 500 nM, suggesting that MutS binding to DNA is “diffusion-limited”. Interestingly, although the binding of MutS to a mismatch appears to be diffusion-limited, the bimolecular rate is one to three orders of magnitude slower than would be expected for a protein the size of MutS (57, 58). A simple explanation for this relatively slow diffusion-limited binding rate is that MutS has a low probability of productive collision with the DNA (57, 59). Consistent with this idea, the DNA binding domains are disordered in the crystal structure of Taq MutS in the absence of DNA (6). Taken together, these results suggest that binding of MutS to DNA is an induced-fit process, in which both MutS and the DNA simultaneously undergo significant conformational rearrangements. Furthermore, the similarity in the rate of binding into conformation B with the rate of binding measured in the bulk studies (39) suggests that binding and bending are concerted processes (60). Our results show that binding directly into all other conformations is slower than binding in the bent conformation (B), indicating that the formation of the other states is likely not diffusion limited but limited by a conformational change after MutS binds the DNA. These results may suggest that MutS always passes through the bent state B upon DNA binding but in some cases, the residence time may be too short to be observed with current experimental capabilities.
MutS preferentially binds DNA in a bent conformation and then transitions to an unbent conformation
After binding into the stable bent state B, the GT-MutS complexes preferentially transition into the unbent DNA conformation U or MutS dissociates from the DNA, with all other transitions being 4 to 14 times slower (Figure 6, Table 2). Specifically, 39% of all conformational transitions of the GT-MutS complexes (not including binding and dissociation transitions) occur between states U and B. This preferred conformational pathway supports the previously proposed model for DNA mismatch recognition based on AFM studies, in which MutS searches for mismatches by bending the DNA and then undergoes a transition to an unbent state that is suggested to signal repair (3, 13). In addition, the higher stability of the bent state B relative to the unbent state U is also consistent with the AFM data (3, 61). Taken together, the AFM and single-molecule fluorescence results support the hypothesis that the bent DNA conformation represents an initial recognition complex and that the subsequent MutS-induced unbending of the DNA may be necessary to signal repair (3, 13).
SB and I may represent kinetically trapped alternate bent conformations
Once MutS-GT complexes enter conformation U, they most likely transition back to B or enter the conformation SB, with all other transitions being 4 to 16 times slower (Table 2, Figure 6 and Figure 7). Conformation SB is similar to B in that the two states exhibit nearly identical lifetimes (Figure S3), and they both transition preferentially to U (Figure 6, Figure S4). Although SB is only slightly less stable than B, the rate of MutS binding into SB is ten times slower than the rate of binding into B, and SB is rarely formed directly upon MutS binding to the DNA (Table 2, Figure 7). Interestingly, the lower stability of SB relative to B results from the slower rate of binding into SB and not a faster rate of dissociation. In fact, the rate of dissociation from SB is slower than that from any other conformation (Table 2, Figure 7). These results suggest that SB may be a kinetically-trapped alternate bent conformation. Perhaps as MutS-GT complexes transition out of the unbent state U back to the bent state B, which involves large changes in DNA bending, MutS forms an alternative set of protein-DNA contacts, resulting in the formation of SB. This hypothesis is plausible given that the DNA binding domains of MutS are disordered in the crystal structure in the absence of DNA (6), and these domains may therefore provide the necessary protein flexibility required to accommodate large DNA conformational changes, such as those from U to B.
While SB is rarely populated directly from free DNA, the predominant pathway to the formation of intermediately bent conformation I is via MutS binding to free DNA and directly forming I, although the rate of binding into I is 5 times slower than binding into B (Table 2). In addition, our Monte Carlo simulations reveal that when MutS is bound in conformation I, it is more likely to dissociate from the DNA than transition into any other conformational state, with ~ 40% of the transitions out of I resulting in MutS dissociation (Figure 6, Table 2). Additionally, MC simulations reveal that if MutS binds into I, it has the shortest average residence time on the DNA and undergoes the fewest conformational changes (Table 3, Figure 8C). This observation is consistent with the relatively high free energy barriers for transitions out of state I (Figure 7). These results, taken together with the observation that I is relatively stable compared to the other GT-MutS states (Table 1, Figure 7), imply that conformation I may comprise a stable set of protein-DNA contacts, unique from the other states, which must be broken for a transition to occur from I into one of the other states.
The kinetic properties of SB and I suggest that these are stable conformations in local free energy minima that are off the preferred transitional path (free DNA→B↔U aforementioned). A recent study following the sliding of MutS homolog Msh2-Msh6 along undamaged DNA revealed that the free energy landscape of one dimensional diffusion of MutS along DNA is rugged and contains a series of deep traps that may serve as a probing mechanism employed by MutS to distinguish between correctly paired DNA, mismatches, IDLs, and lesions (11). The energy landscape and kinetics that we observe for conformations SB and I suggest that these states may have a similar role for MutS bound to a GT mismatch. While these conformations may represent states that are off-path for mismatch repair, they could be on-path for some other cellular fate.
U* and B* represent unstable intermediate states
U* and B* have the highest relative free energies (Figure 7), comprise a small percentage of the equilibrium population of states (Figure 8A–B), and are short-lived (Table 1), with the lowest transition barriers (Table 2, Figure 7). Although U* and B* are similar in lifetime and stability, the formation of these states and their fates, once formed, are significantly different. U* most likely forms as an intermediate in transitions between B and SB; whereas, B* appears to form mainly as an intermediate between U and B or SB. Although both U* and B* have similarly fast dissociation rates (Figure 7, Table 2), MutS is much more likely to dissociate from the DNA if the MutS-GT complex is in conformation B* than U* (30% vs. 13% respectively), and the time MutS spends on the DNA is significantly shorter if it binds into state B* than into state U* (Table 3). Specifically, when the complexes are in conformation B*, MutS is more likely to dissociate from the DNA than to transition to any other state; whereas, complexes in state U* preferentially transition to other conformational states, especially B and SB, rather than result in dissociation of MutS (Figure 7). Taken together, these observations suggest that U* is an on-path, unstable intermediate state and that B* is an off-path, unstable intermediate state.
The dynamics of protein-DNA complexes follow similar trends to protein and RNA folding
The free energy diagram of GT-MutS complexes is similar to free energy landscapes of protein folding, suggesting that the rules that govern protein folding funnels may also apply to DNA-protein dynamics (62–64). The diagram of barriers between transitions dramatically demonstrates that these complexes have a ‘bumpy’ free energy landscape with a series of local free energy minima. The energy landscape reveals a preferred pathway of biomolecular complexes down the free energy funnel (Figure 7) despite the presence of unstable intermediate states that may form along the way, similar to protein-folding phenomena. The presence of local free energy minima, or kinetic traps, is also reminiscent of ‘off-path’, kinetically-trapped states identified in the folding transitions of ribozymes (65–67). In ribozyme folding, these states have been suggested to represent a number of phenomena, including misfolded conformations, structural intermediates, or states residing on alternative folding pathways (65–68). Perhaps similar trends apply to dynamics of protein-DNA complexes.
The dynamic trend: Large changes in DNA bending dominate the MutS-GT complex
A striking feature of the dynamics of GT-MutS complexes is that most transitions involve large changes in DNA bend angles. Specifically, the most frequently observed transitions within the complexes occur between states that reside on distant ends of the bending continuum (ie. B↔U, SB↔U, B↔U*, SB↔U*) even though I, which is intermediately bent, is stable. In addition, transitions between B and SB, which have similar extents of DNA bending, generally proceed through an unbent intermediate (U or U*). These large conformational changes may be related to energy associated with bending DNA and the apparent flexible nature of the DNA binding domains of MutS (6). The optimum conformation for MutS bound to DNA is one in which the DNA is bent, but the optimum conformation of DNA is unbent (3), which may result in metastable states where the optimum conformations of MutS and DNA are driving the interconversions, with MutS driving DNA bending and DNA driving unbending. Because the energy of DNA bending/unbending is greater the larger the angle change, the large conformational changes may be required to form the unbent states. This observation may explain the high likelihood for dissociation when the complexes form the intermediately bent state I. While state I may overcome the barriers to transition into a bent conformation (noting that other than dissociating, I is most likely to transition to SB or B), it does not readily transition to the unbent state. Perhaps the energy of unbending is insufficient to drive the transition from I to U and ultimately results in the complexes either sinking into a kinetic trap or dissociating.
The dynamics of the MutS-mismatch recognition complex could have a role in signaling repair or apoptosis
It has been suggested that the conformational dynamics of DNA-MutS complexes are important for signaling DNA repair and MutS-dependent damage-induced apoptosis (3, 10). In this work, we demonstrate that GT-MutS complexes can adopt several different conformations, with highly variable rates of interconversion between conformations, where the fastest rate is ~ 0.59 sec−1 (U*→B) and the slowest, 0.0019 sec−1 (B→B*). With the average lifetime of MutS on the DNA topping at ~ 40 seconds, the sampling of different states becomes largely dependent on the ‘starting’ conformational state (Table 3). Furthermore, the long lifetimes of the stable states (ie. conformations B and SB) prevent MutS from achieving conformational equilibrium during a single mismatch binding event, where the lifetime of MutS on the DNA is not long enough to sample all 6 conformational states in a single binding event. In fact, on average MutS only undergoes 4 to 5 conformational changes and samples 2 to 3 different states in a single binding event (Table 3). In addition, although MutS only samples the intermediate states for a fraction of its time spent on the DNA, the fact that the GT-MutS complex typically changes conformation 4 or 5 times after a binding event highlights the role of these less stable states in determining the states visited in a single binding event (Table 3). Furthermore, the bulk kinetic simulations reveal that the system is slow to reach equilibrium (20 seconds at 200 nM and 80 seconds at 20 nM), and prior to reaching equilibrium, the relative amounts of MutS-DNA complexes in the different states depend on the concentration of MutS (Figure 8). As a result, the distribution of states becomes an important feature of the mismatched DNA-MutS complex and may be different for MutS bound to different DNA mismatches or lesions. We can speculate that the relative distributions and kinetics of states sampled in these complexes may vary among different mismatches and DNA lesions and could play a role in the relative repair efficiencies or entry into different pathways in response to ATP.
For GT mismatched DNA bound by MutS, the kinetic scheme in conjunction with MC simulations suggest roles that each different state may play in the recognition pathway. Conformation B likely serves as the primary recognition state, and conformation U perhaps has a role as the repair signaling state (3, 13). The transition patterns and stability of states I and SB suggest that these conformational states may be kinetic mini-traps and are perhaps nonproductive for signaling repair of a GT mismatch, while conformation U* appears to be an unstable, on-path intermediate state, and B*, an unstable, off-path intermediate state. Although these complex dynamics could represent other localized events between MutS and the mismatch and nearby base pairs, or MutS transiently moving away from and returning to the mismatch, it is certain that complex protein-DNA dynamics are occurring. Additional studies of a number of different mismatches and DNA lesions, as well as studies of these complexes in the presence of cofactors such as ATP and MutL, will be interesting and will truly begin to unravel in further detail the functional roles of these states in overall mismatch recognition and signaling by MutS.
Conclusions
The broad distribution of conformational states and diverse kinetics that we observe for mismatched DNA-MutS complexes using single-molecule FRET encouraged the development of the FRET TACKLE analysis approach. This approach applies multiple criteria (FRET efficiency values, transition properties, and kinetic lifetime analysis) to identify the number of unique states, their relative stabilities, and the rates of exchange among multiple states in a diverse FRET distribution. FRET TACKLE allows the distinction between two states that have the same FRET efficiencies but different lifetimes and the distinction between two states that have identical lifetimes but different FRET efficiencies. This analysis approach was essential for identifying the 6 unique conformational states of GT-MutS DNA-protein complexes (in addition to the unbound DNA state), as well as for determining the complete kinetic scheme and free energy landscape of the dynamic, equilibrium fluctuations among these states. In addition, FRET TACKLE will be useful for teasing apart the dynamics and kinetics of other complex biological systems.
These results begin to address key questions regarding the roles of each of the MutS-mismatch DNA conformational states in the DNA mismatch repair pathway. The most stable states (B and U) may serve essential mismatch repair recognition and signaling roles, while other stable states (I and SB) could represent non-productive conformations or conformations that serve a different cellular function, with a number of intermediate states (U* and B*) sampled along the way. The many different conformational species and the dynamics between them require a new perspective on the way mismatch repair initiation is perceived. These results show the dynamic nature of mismatch repair initiation by MutS and reveal the fluidity of the MutS-mismatch recognition complex. The ability of these molecular complexes to sample a number of different states with a variety of interconversion kinetics may serve a fundamental role in how MutS leads to activation of repair of different mismatches, and furthermore, induces different cellular processes in response to ATP or different DNA mismatches or lesions, such as cisplatin and O-6-methyl guanine. This work sets the stage for future studies of MutS bound to a number of different DNA mismatches and lesions along with experiments to determine the fates of different conformations upon the addition of ATP, which will further elucidate the relationship between dynamic MutS-DNA structures and the function of MutS. These future directions will be telling regarding the role of different DNA conformational states in the MutS response-signaling mechanism. Overall, these studies provide a window into the complexities and dynamics of proteins interacting with DNA.
Supplementary Material
ACKNOWLEDGMENTS
The authors would like to acknowledge Brian Eastwood and Dr. Russell Taylor of the UNC Chapel Hill Center for Computer Integrated Systems for Microscopy and Manipulation (CISMM) for providing the 1D transition edge analysis algorithm and extending the software scripts to analyze FRET traces.
This work was supported in part by the American Cancer Society grant RSG-03-047 and NIH grants GM 079480 and GM 080294 from NIH awarded to DAE and by a fellowship from the Merck Research Laboratories awarded to LES. The research of KW is supported in part by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund.
ABBREVIATIONS
- MMR
mismatch repair
- IDL
insertion / deletion loop
- smFRET
single-molecule Fluorescence Resonance Energy Transfer
- FRET TACKLE
Fluorescence Resonance Energy Transfer Transition Analysis Combined with Lifetime Examination of States
- Taq
Thermus aquaticus
- TAMRA
tetra-methyl rhodamine
- BSA
bovine serum albumin
- TIRF
total internal reflection fluorescence
- TDP
transition density plot
- EMSA
electromobility gel shift assay
- AFM
atomic force microscopy
- MC
Monte Carlo
- MCSBE
Monte Carlo simulations of single binding events
- SBE
single binding event
Footnotes
Supporting Information Available
Additional experimental procedures, data analysis, results, and discussion, including a discussion of the limitations of the analysis. This information is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Modrich P. Methyl-directed DNA mismatch correction. J Biol Chem. 1989;264:6597–6600. [PubMed] [Google Scholar]
- 2.Warren JJ, Pohlhaus TJ, Changela A, Iyer RR, Modrich PL, Beese LS. Structure of the Human MutSalpha DNA Lesion Recognition Complex. Mol Cell. 2007;26:579–592. doi: 10.1016/j.molcel.2007.04.018. [DOI] [PubMed] [Google Scholar]
- 3.Wang H, Yang Y, Schofield MJ, Du C, Fridman Y, Lee SD, Larson ED, Drummond JT, Alani E, Hsieh P, Erie DA. DNA bending and unbending by MutS govern mismatch recognition and specificity. Proc Natl Acad Sci U S A. 2003;100:14822–14827. doi: 10.1073/pnas.2433654100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yang Y, Sass LE, Du C, Hsieh P, Erie DA. Determination of protein-DNA binding constants and specificities from statistical analyses of single molecules: MutS-DNA interactions. Nucleic Acids Res. 2005;33:4322–4334. doi: 10.1093/nar/gki708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Natrajan G, Lamers MH, Enzlin JH, Winterwerp HH, Perrakis A, Sixma TK. Structures of Escherichia coli DNA mismatch repair enzyme MutS in complex with different mismatches: a common recognition mode for diverse substrates. Nucleic Acids Res. 2003;31:4814–4821. doi: 10.1093/nar/gkg677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Obmolova G, Ban C, Hsieh P, Yang W. Crystal structures of mismatch repair protein MutS and its complex with a substrate DNA. Nature. 2000;407:703–710. doi: 10.1038/35037509. [DOI] [PubMed] [Google Scholar]
- 7.Lamers MH, Perrakis A, Enzlin JH, Winterwerp HH, de Wind N, Sixma TK. The crystal structure of DNA mismatch repair protein MutS binding to a G x T mismatch. Nature. 2000;407:711–717. doi: 10.1038/35037523. [DOI] [PubMed] [Google Scholar]
- 8.Au KG, Welsh K, Modrich P. Initiation of methyl-directed mismatch repair. J Biol Chem. 1992;267:12142–12148. [PubMed] [Google Scholar]
- 9.Duckett DR, Drummond JT, Murchie AI, Reardon JT, Sancar A, Lilley DM, Modrich P. Human MutSalpha recognizes damaged DNA base pairs containing O6-methylguanine, O4-methylthymine, or the cisplatin-d(GpG) adduct. Proc Natl Acad Sci U S A. 1996;93:6443–6447. doi: 10.1073/pnas.93.13.6443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salsbury FR, Jr, Clodfelter JE, Gentry MB, Hollis T, Scarpinato KD. The molecular mechanism of DNA damage recognition by MutS homologs and its consequences for cell death response. Nucleic Acids Res. 2006;34:2173–2185. doi: 10.1093/nar/gkl238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gorman J, Chowdhury A, Surtees JA, Shimada J, Reichman DR, Alani E, Greene EC. Dynamic basis for one-dimensional DNA scanning by the mismatch repair complex Msh2-Msh6. Mol Cell. 2007;28:359–370. doi: 10.1016/j.molcel.2007.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lebbink JH, Georgijevic D, Natrajan G, Fish A, Winterwerp HH, Sixma TK, de Wind N. Dual role of MutS glutamate 38 in DNA mismatch discrimination and in the authorization of repair. Embo J. 2006;25:409–419. doi: 10.1038/sj.emboj.7600936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kunkel TA, Erie DA. DNA mismatch repair. Annu Rev Biochem. 2005;74:681–710. doi: 10.1146/annurev.biochem.74.082803.133243. [DOI] [PubMed] [Google Scholar]
- 14.Kramer B, Kramer W, Fritz HJ. Different base/base mismatches are corrected with different efficiencies by the methyl-directed DNA mismatch-repair system of E. coli. Cell. 1984;38:879–887. doi: 10.1016/0092-8674(84)90283-6. [DOI] [PubMed] [Google Scholar]
- 15.Su SS, Lahue RS, Au KG, Modrich P. Mispair specificity of methyl-directed DNA mismatch correction in vitro. J Biol Chem. 1988;263:6829–6835. [PubMed] [Google Scholar]
- 16.Biswas I, Hsieh P. Identification and characterization of a thermostable MutS homolog from Thermus aquaticus. J Biol Chem. 1996;271:5040–5048. doi: 10.1074/jbc.271.9.5040. [DOI] [PubMed] [Google Scholar]
- 17.Weninger K, Bowen ME, Chu S, Brunger AT. Single-molecule studies of SNARE complex assembly reveal parallel and antiparallel configurations. Proc Natl Acad Sci U S A. 2003;100:14800–14805. doi: 10.1073/pnas.2036428100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McKinney SA, Freeman AD, Lilley DM, Ha T. Observing spontaneous branch migration of Holliday junctions one step at a time. Proc Natl Acad Sci U S A. 2005;102:5715–5720. doi: 10.1073/pnas.0409328102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ha T, Rasnik I, Cheng W, Babcock HP, Gauss GH, Lohman TM, Chu S. Initiation and re-initiation of DNA unwinding by the Escherichia coli Rep helicase. Nature. 2002;419:638–641. doi: 10.1038/nature01083. [DOI] [PubMed] [Google Scholar]
- 20.Bowen ME, Weninger K, Ernst J, Chu S, Brunger AT. Single-molecule studies of synaptotagmin and complexin binding to the SNARE complex. Biophys J. 2005;89:690–702. doi: 10.1529/biophysj.104.054064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Canny J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986;8:679–698. [PubMed] [Google Scholar]
- 22.Zhuang X, Kim H, Pereira MJ, Babcock HP, Walter NG, Chu S. Correlating structural dynamics and function in single ribozyme molecules. Science. 2002;296:1473–1476. doi: 10.1126/science.1069013. [DOI] [PubMed] [Google Scholar]
- 23.Foster JE, Holmes SF, Erie DA. Allosteric binding of nucleoside triphosphates to RNA polymerase regulates transcription elongation. Cell. 2001;106:243–252. doi: 10.1016/s0092-8674(01)00420-2. [DOI] [PubMed] [Google Scholar]
- 24.Atkins PW. Physical Chemistry. Oxford University Press; 1978. [Google Scholar]
- 25.Deniz AA, Dahan M, Grunwell JR, Ha T, Faulhaber AE, Chemla DS, Weiss S, Schultz PG. Single-pair fluorescence resonance energy transfer on freely diffusing molecules: observation of Forster distance dependence and subpopulations. Proc Natl Acad Sci U S A. 1999;96:3670–3675. doi: 10.1073/pnas.96.7.3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Clegg RM, Murchie AI, Zechel A, Lilley DM. Observing the helical geometry of double-stranded DNA in solution by fluorescence resonance energy transfer. Proc Natl Acad Sci U S A. 1993;90:2994–2998. doi: 10.1073/pnas.90.7.2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jares-Erijman EA, Jovin TM. Determination of DNA helical handedness by fluorescence resonance energy transfer. J Mol Biol. 1996;257:597–617. doi: 10.1006/jmbi.1996.0188. [DOI] [PubMed] [Google Scholar]
- 28.Lakowicz JR. Topics in Fluorescence Spectroscopy. 2nd ed. New York: Kluwe Academic/Plenum Publishers; 1999. [Google Scholar]
- 29.Iqbal A, Arslan S, Okumus B, Wilson TJ, Giraud G, Norman DG, Ha T, Lilley DM. Orientation dependence in fluorescent energy transfer between Cy3 and Cy5 terminally attached to double-stranded nucleic acids. Proc Natl Acad Sci U S A. 2008;105:11176–11181. doi: 10.1073/pnas.0801707105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huang SN, Crothers DM. The role of nucleotide cofactor binding in cooperativity and specificity of MutS recognition. J Mol Biol. 2008;384:31–47. doi: 10.1016/j.jmb.2008.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Larson ED, Nickens D, Drummond JT. Construction and characterization of mismatch-containing circular DNA molecules competent for assessment of nick-directed human mismatch repair in vitro. Nucleic Acids Res. 2002;30:E14. doi: 10.1093/nar/30.3.e14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.McKinney SA, Joo C, Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Joo C, McKinney SA, Nakamura M, Rasnik I, Myong S, Ha T. Realtime observation of RecA filament dynamics with single monomer resolution. Cell. 2006;126:515–527. doi: 10.1016/j.cell.2006.06.042. [DOI] [PubMed] [Google Scholar]
- 34.Zhuang X, Bartley LE, Babcock HP, Russell R, Ha T, Herschlag D, Chu S. A single-molecule study of RNA catalysis and folding. Science. 2000;288:2048–2051. doi: 10.1126/science.288.5473.2048. [DOI] [PubMed] [Google Scholar]
- 35.Liu S, Bokinsky G, Walter NG, Zhuang X. Dissecting the multistep reaction pathway of an RNA enzyme by single-molecule kinetic "fingerprinting". Proc Natl Acad Sci U S A. 2007;104:12634–12639. doi: 10.1073/pnas.0610597104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xie XS, Lu HP. Single-molecule enzymology. J Biol Chem. 1999;274:15967–15970. doi: 10.1074/jbc.274.23.15967. [DOI] [PubMed] [Google Scholar]
- 37.Lee JY, Okumus B, Kim DS, Ha T. Extreme conformational diversity in human telomeric DNA. Proc Natl Acad Sci U S A. 2005;102:18938–18943. doi: 10.1073/pnas.0506144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wong OK, Guthold M, Erie DA, Gelles J. Interconvertible Lac Repressor-DNA Loops Revealed by Single-Molecule Experiments. PLoS Biology. 2008;6:e232. doi: 10.1371/journal.pbio.0060232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jacobs-Palmer E, Hingorani MM. The effects of nucleotides on MutS-DNA binding kinetics clarify the role of MutS ATPase activity in mismatch repair. J Mol Biol. 2007;366:1087–1098. doi: 10.1016/j.jmb.2006.11.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schofield MJ, Brownewell FE, Nayak S, Du C, Kool ET, Hsieh P. The Phe-X-Glu DNA binding motif of MutS. The role of hydrogen bonding in mismatch recognition. J Biol Chem. 2001;276:45505–45508. doi: 10.1074/jbc.C100449200. [DOI] [PubMed] [Google Scholar]
- 41.Davis JH. Differential Equations with Maple: An interactive approach. Birkhauser; 2001. [Google Scholar]
- 42.Gillespie DT. A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions. Journal of Computational Physics. 1976;22:403–434. [Google Scholar]
- 43.Schofield MJ, Hsieh P. DNA mismatch repair: molecular mechanisms and biological function. Annu Rev Microbiol. 2003;57:579–608. doi: 10.1146/annurev.micro.57.030502.090847. [DOI] [PubMed] [Google Scholar]
- 44.Mojas N, Lopes M, Jiricny J. Mismatch repair-dependent processing of methylation damage gives rise to persistent single-stranded gaps in newly replicated DNA. Genes Dev. 2007;21:3342–3355. doi: 10.1101/gad.455407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Iyer RR, Pluciennik A, Burdett V, Modrich PL. DNA mismatch repair: functions and mechanisms. Chem Rev. 2006;106:302–323. doi: 10.1021/cr0404794. [DOI] [PubMed] [Google Scholar]
- 46.Iyer RR, Pohlhaus TJ, Chen S, Hura GL, Dzantiev L, Beese LS, Modrich P. The MutSalpha-proliferating cell nuclear antigen interaction in human DNA mismatch repair. J Biol Chem. 2008;283:13310–13319. doi: 10.1074/jbc.M800606200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Stojic L, Brun R, Jiricny J. Mismatch repair and DNA damage signalling. DNA Repair (Amst) 2004;3:1091–1101. doi: 10.1016/j.dnarep.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 48.Hickman MJ, Samson LD. Apoptotic signaling in response to a single type of DNA lesion, O(6)-methylguanine. Mol Cell. 2004;14:105–116. doi: 10.1016/s1097-2765(04)00162-5. [DOI] [PubMed] [Google Scholar]
- 49.Li GM. DNA mismatch repair and cancer. Front Biosci. 2003;8:d997–d1017. doi: 10.2741/1121. [DOI] [PubMed] [Google Scholar]
- 50.Drotschmann K, Topping RP, Clodfelter JE, Salsbury FR. Mutations in the nucleotide-binding domain of MutS homologs uncouple cell death from cell survival. DNA Repair (Amst) 2004;3:729–742. doi: 10.1016/j.dnarep.2004.02.011. [DOI] [PubMed] [Google Scholar]
- 51.Smith JA, Waldman BC, Waldman AS. A role for DNA mismatch repair protein Msh2 in error-prone double-strand-break repair in mammalian chromosomes. Genetics. 2005;170:355–363. doi: 10.1534/genetics.104.039362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Datta A, Adjiri A, New L, Crouse GF, Jinks Robertson S. Mitotic crossovers between diverged sequences are regulated by mismatch repair proteins in Saccaromyces cerevisiae. Mol Cell Biol. 1996;16:1085–1093. doi: 10.1128/mcb.16.3.1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Drummond JT, Anthoney A, Brown R, Modrich P. Cisplatin and adriamycin resistance are associated with MutLalpha and mismatch repair deficiency in an ovarian tumor cell line. J Biol Chem. 1996;271:19645–19648. doi: 10.1074/jbc.271.33.19645. [DOI] [PubMed] [Google Scholar]
- 54.Mellon I, Champe GN. Products of DNA mismatch repair genes mutS and mutL are required for transcription-coupled nucleotide-excision repair of the lactose operon in Escherichia coli. Proc Natl Acad Sci U S A. 1996;93:1292–1297. doi: 10.1073/pnas.93.3.1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mellon I, Rajpal DK, Koi M, Boland CR, Champe GN. Transcription-coupled repair deficiency and mutations in human mismatch repair genes. Science. 1996;272:557–560. doi: 10.1126/science.272.5261.557. [DOI] [PubMed] [Google Scholar]
- 56.Fazakerley GV, Quignard E, Woisard A, Guschlbauer W, van der Marel GA, van Boom JH, Jones M, Radman M. Structures of mismatched base pairs in DNA and their recognition by the Escherichia coli mismatch repair system. Embo J. 1986;5:3697–3703. doi: 10.1002/j.1460-2075.1986.tb04702.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Berg OG, Winter RB, von Hippel PH. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 58.Winter RB, Berg OG, von Hippel PH. Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor--operator interaction: kinetic measurements and conclusions. Biochemistry. 1981;20:6961–6977. doi: 10.1021/bi00527a030. [DOI] [PubMed] [Google Scholar]
- 59.von Hippel PH, Berg OG. Facilitated target location in biological systems. J Biol Chem. 1989;264:675–678. [PubMed] [Google Scholar]
- 60.Dhavan GM, Crothers DM, Chance MR, Brenowitz M. Concerted binding and bending of DNA by Escherichia coli integration host factor. J Mol Biol. 2002;315:1027–1037. doi: 10.1006/jmbi.2001.5303. [DOI] [PubMed] [Google Scholar]
- 61.Tessmer I, Yang Y, Zhai J, Du C, Hsieh P, Hingorani MM, Erie DA. Mechanism of MutS searching for DNA mismatches and signaling repair. J Biol Chem. 2008 doi: 10.1074/jbc.M805712200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 63.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: the energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 64.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 65.Pan T, Fang X, Sosnick T. Pathway modulation, circular permutation and rapid RNA folding under kinetic control. J Mol Biol. 1999;286:721–731. doi: 10.1006/jmbi.1998.2516. [DOI] [PubMed] [Google Scholar]
- 66.Russell R, Herschlag D. Probing the folding landscape of the Tetrahymena ribozyme: commitment to form the native conformation is late in the folding pathway. J Mol Biol. 2001;308:839–851. doi: 10.1006/jmbi.2001.4751. [DOI] [PubMed] [Google Scholar]
- 67.Saksmerprome V, Burke DH. Deprotonation stimulates productive folding in allosteric TRAP hammerhead ribozymes. J Mol Biol. 2004;341:685–694. doi: 10.1016/j.jmb.2004.06.027. [DOI] [PubMed] [Google Scholar]
- 68.Solomatin SV, Greenfeld M, Chu S, Herschlag D. Multiple native states reveal persistent ruggedness of an RNA folding landscape. Nature. 463:681–684. doi: 10.1038/nature08717. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.