Abstract
An integer linear optimization model is presented to predict residue contacts in β, α + β, and α/β proteins. The total energy of a protein is expressed as sum of a Cα – Cα distance dependent contact energy contribution and a hydrophobic contribution. The model selects contacts that assign lowest energy to the protein structure while satisfying a set of constraints that are included to enforce certain physically observed topological information. A new method based on hydrophobicity is proposed to find the β-sheet alignments. These β-sheet alignments are used as constraints for contacts between residues of β-sheets. This model was tested on three independent protein test sets and CASP8 test proteins consisting of β, α + β, α/β proteins and was found to perform very well. The average accuracy of the predictions (separated by at least six residues) was approximately 61%. The average true positive and false positive distances were also calculated for each of the test sets and they are 7.58 Å and 15.88 Å, respectively. Residue contact prediction can be directly used to facilitate the protein tertiary structure prediction. This proposed residue contact prediction model is incorporated into the first principles protein tertiary structure prediction approach, ASTRO-FOLD. The effectiveness of the contact prediction model was further demonstrated by the improvement in the quality of the protein structure ensemble generated using the predicted residue contacts for a test set of 10 proteins.
Keywords: αBB, CSA, CASP8, Integer Linear Optimization, Force Field, Hydrophobic
1 Introduction
Given the primary structure of a protein, the prediction of its three dimensional structure is referred as the protein structure prediction problem. Protein structure prediction is one of the most important problems in the field of computational biology with its importance and application in the fields of drug design and biotechnology. Various computational techniques have been developed for protein structure prediction. These techniques can be broadly classified into four categories: (a) comparative modeling, (b) fold recognition, (c) first principles methods that use database information, and (d) first principles methods without database information. Comparative modeling and fold recognition methods use the sequence and fold similarity of the existing protein structures as a basis for structure prediction. On the other hand, first principles based methods rely on physical/chemical laws for the three dimensional structure prediction. A review of these methods can be found in (Floudas et al., 2006; Floudas, 2007; Zhang, 2008).
First principles methods that do not use database information are the most difficult types because these methods attempt to build three dimensional structures without any knowledge of existing structures. The two main challenges of the prediction methodology are 1) generation of an ensemble of high quality structures and 2) a method to identify conformers that are close to the native structure. The number of possible protein structures for a given primary structure is very large. Thus, it is of vital importance to search the conformational space efficiently to find energetically stable and physically realizable structures. Any additional information that can be used to restrict the conformational search space can potentially help in better structure prediction.
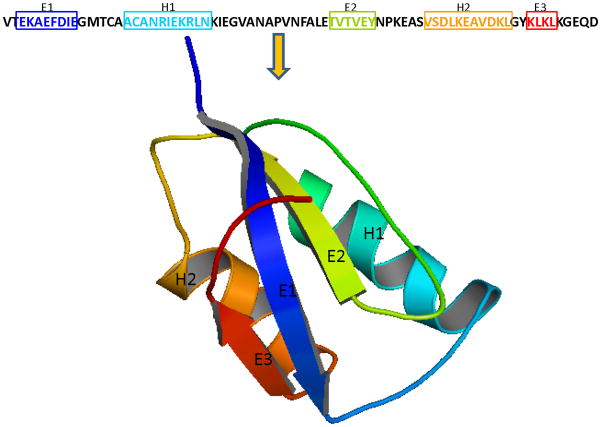
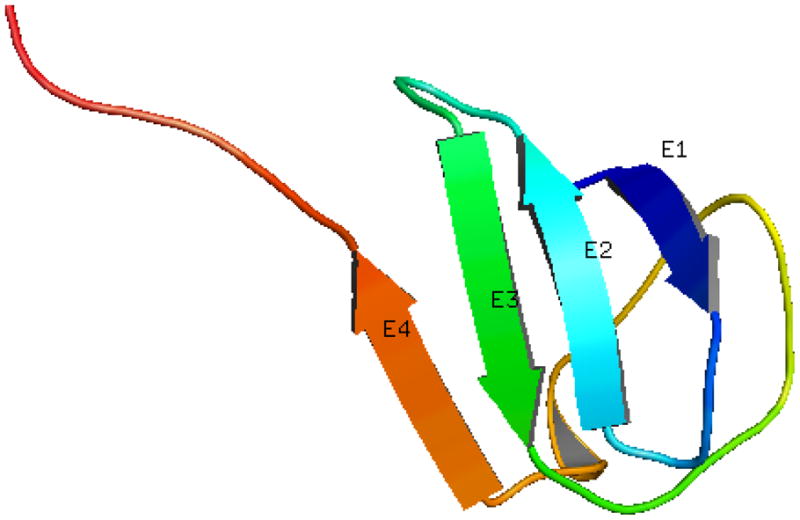
Protein contact prediction problem aims to predict contacts between non-local residues of a protein that are close to each other in the three dimensional structure. Figure 1 illustrates the contact prediction problem where the strand residues (E1-E2 or E1-E3) are non-local but they make close “contact” in the three-dimensional structure. These residue contacts can be explicitly used as restraints in structure prediction algorithms. A well restrained problem can significantly reduce the feasible search space of a protein. These also ensure that the predicted structures have these non-local contacts thereby producing more plausible structures and making the structure prediction algorithm more efficient. Thus, the development of an effective residue contact prediction model can play a vital role in protein structure prediction (Ortiz et al., 1998a,b,c; Olmea et al., 1999; Bonneau et al., 2002; McAllister et al., 2006; McAllister and Floudas, 2007).
Figure 1.
A cartoon illustrating the residue contact prediction problem. The residues of these two β-strands are far-off in the primary structure of the protein. However, they are very close to each other in the three dimensional structure.
In a seminal work, Wako and Scheraga (1981) assessed the quality of predicted contacts for protein folding. A quantity, H, was introduced to assess the effect of number, quality and type of the distance constraints on the quality of the computed conformation. An empirical relation was found between the quantity H and RMSD value of the computed structure for protein BPTI, and this relation was used to estimate the required number of constraints, constraint type and accuracy in order to determine the structure within a given RMSD value.
MODELLER, a comparative modeling based approach, generates distance restraints from homologous proteins of known structure and then uses them to predict three dimensional structures of unknown proteins (Sali and Blundell, 1993; Marti-Renom et al., 2000). Similarly, Ortiz et al. (1998a) used multiple sequence alignments to derive distance restraints that were used in Monte Carlo simulations. Floudas and coworkers used bounds on the distance between the Cα atoms of the helical residues and β-sheet residues to enforce the secondary structure geometry in predicted protein structures (Klepeis and Floudas, 2003b; Klepeis et al., 1999, 2005; McAllister and Floudas, 2009). In a similar effort, Vendruscolo (2002) and Vassura et al. (2003) developed methods to construct the three dimensional structure of the protein backbone given its residue contact map.
Various research groups have introduced different approaches to develop residue contact prediction methods. These techniques can be broadly divided into three categories. The first category is based on correlated mutations analysis (Göbel et al., 1994; Olmea and Valencia, 1997; Singer et al., 2002; Hamilton et al., 2004; Vicatos et al., 2005; Kundrotas and Alexov, 2006). The second category uses machine learning approaches (Fariselli and Casadio, 1999; Fariselli et al., 2001a,b; Lund et al., 1997; Zhao and Karypis, 2003; Shao and Bystroff, 2003; Zhang and Huang, 2004; Punta and Rost, 2005; Vullo et al., 2006; Cheng and Baldi, 2007; Shackelford and Karplus, 2007; Wu and Zhang, 2008) and the last category is based on the use of optimization techniques for contact prediction (Klepeis and Floudas, 2003a; McAllister et al., 2006; Rajgaria et al., 2009).
Correlated mutations analysis (CMA) is based on the premise that mutations in proximal residues occur in a covariant fashion. It is believed that when a critical residue (i.e., important for protein function) of a protein is mutated, the proximal residues are likely to undergo mutations in order to keep the functionality intact (Vicatos et al., 2005). CMA based methods estimate correlated mutations using a set of training proteins and then use the derived information for residue contact prediction. Some of the initial CMA based methods were developed by Göbel et al. (1994) and Taylor and Hatrick (1994). Olmea and Valencia (1997) included some other sources of sequence related information (residue contact preferences, residue contact density etc.) in their correlated mutations analysis method and found better contact prediction results. Hamilton et al. (2004) reported an overall accuracy value of 30.7% for their CMA based method when they considered the best L/10 predictions. Vicatos et al. (2005) developed a CMA based method starting with a vector of 142 descriptors (based on the physio-chemical properties) for residue similarity comparison. These 142 descriptors were subsequently reduced to a set of 19 descriptors using Principal Component Analysis. Finally, a set of 3 main descriptors was selected for correlated mutations analysis. This method was tested on all protein structural classes and produced an average accuracy of ~15% for α-helical proteins, ~21% for β proteins, and ~27% for α - β proteins. A review and comparison of different methods for contact prediction using CMA can be found in Horner et al. (2008).
Machine learning based approaches for residue contact prediction use techniques like hidden Markov models, self organizing maps, neural networks and support vector machines (Pollastri and Baldi, 2002; Zhao and Karypis, 2003; Cheng and Baldi, 2007). Zhao and Karypis (2003) used a support vector machine based method which incorporated features such as sequence profiles and their conservation, secondary structure etc. They demonstrated and concluded that different structural features produced best results for different structural classes. Overall, they reported an average accuracy of of 22.4%. Lund et al. (1997); Fariselli and Casadio (1999); Fariselli et al. (2001a,b); Shackelford and Karplus (2007) combined neural network techniques with correlated mutations analysis for residue contact prediction. Cheng and Baldi (2007) proposed a support vector machine based method (SVMcon) for residue contact prediction. This method uses a set of five features (local window feature, pairwise information feature, residue type feature, central segment window feature, and protein information feature) as input to predict the likelihood of contact between two residues (Cheng and Baldi, 2007). The use of the enhanced feature set enabled the authors to attain a higher level of accuracy. SVMcon was also tested on all protein structural classes and an overall average accuracy of 37%, 30%, and 21% was obtained for residue separation value of 6, 12, and 24, respectively. Wu and Zhang (2008) developed two machine learning based methods for residue contact prediction. The first method, SVM-SEQ, uses sequence information, solvent accessibility, and position specific scoring matrices for contact prediction. The second method, SVM-LOMETS, uses the consensus of predicted contacts obtained from various threading templates. After comparing the prediction results obtained using these two methods, the authors concluded that the SVM-SEQ method is better than the SVM-LOMETS for free modeling targets.
It has been shown that a set of good contacts can improve the quality of a protein structure by providing a set of restraints that narrows the conformational search space and guides the search algorithm toward the correct energetic funnel (Marti-Renom et al., 2000; Bonneau et al., 2002; McAllister and Floudas, 2007).
Although advances have been made, the protein residue contact prediction problem is still largely unsolved (Grãna et al., 2005; Izarzugaza et al., 2007). There are a lot of residue contact prediction methods that suffer from low predictive accuracy. A large number of false positive predictions can impose undesirable distance bounds between certain residues of a protein, thereby changing the topology of predicted structure. This can have detrimental effect on the quality of predicted structures. It is certainly desirable to have a contact prediction method that produces highly accurate contacts. It is also important that it does not predict too many false positive contacts. A high number of false positive predictions typically render such methods of little use in the ab initio prediction of protein structure.
The problem of improving accuracy of predicted contacts has been addressed by some research groups. A lot of this effort has been dedicated towards improving the method of prediction itself. However, very little has been done to enrich the predictions once the predictions have been made. This can be treated as a “post-processing” problem and can be completely decoupled from the original problem of contact prediction. This requires developing methods that would take a set of predicted contacts as an input and produce only a subset of these predictions. The predicted contacts are selected or rejected based on a “selection criteria” which is method dependent. If the accuracy of the subset of predictions is more than the accuracy of the original predictions, then the overall accuracy has been increased.
In one of the early works, Olmea and Valencia (1997) explored the possibility of increasing the accuracy of their previously developed contact prediction method (Göbel et al., 1994). To increase the accuracy of their correlated mutations based approach, they included various other factors like sequence conservation, contact density, alignment stability, sequence separation along the chain among others. They found that that presence of these new factors increased their accuracy.
Frenkel-Morgenstern et al. (2007) developed a method, GARP, to refine protein residue contacts through the use of graph analysis. In this approach they use the predicted contacts between any two residues as edges. The contacting amino acids were denoted as nodes and an edge between any two nodes denoted a contact between these two amino acids. Through the use of graph analysis they were able to identify regions of high connectivity that characterize protein structures. Frenkel-Morgenstern et al. (2007) also reported that the accuracy of their method increased from 12% to 18%.
Kundrotas and Alexov (2006) addressed the problem of reducing false positives by developing a set of filters based on the identity of contacting amino acids. These filters were meant to remove predicted pairs that do not have complementary physical-chemical properties. They were decided based on the nature of various interactions between different amino acids (e.g. hydrophobicity, polarity etc.). The optimal parameters for these filters were optimized on a set of 15 high resolution crystal structures and produced an average accuracy of 0.09 (0.07 without filters) on a set of 65 high resolution structures. Vicatos and Kaznessis (2008) proposed a Monte Carlo simulation based approach for α-helical proteins to separate true positive predictions from false positive predictions thereby increasing the overall accuracy.
The third category of optimization based residue contact prediction method was recently proposed by Rajgaria et al. (2009). This method was developed to predict contacts between hydrophobic residues of α-helical proteins and it produced an average accuracy of 66% when tested on multiple test sets of α -helical proteins. The presented formulation is an extension of the successful method of Rajgaria et al. (2009). It has been enhanced to predict residue contacts for β, α/β, and α + β proteins.
One important application of residue contact prediction is to reduce the conformational search space of protein structure prediction. The usefulness of residue contact prediction is tested by applying these predicted contacts to three dimensional structure prediction for proteins. All different protein structure prediction techniques mentioned in the first paragraph could use these predicted residue contacts to improve its prediction performance. In this paper, the residue contact prediction model is incorporated into an ab initio protein tertiary structure prediction algorithm, ASTRO-FOLD (Klepeis and Floudas, 2002b, 2003b,c; Klepeis et al., 2003a,b). ASTRO-FOLD uses a multi-stage process to predict protein tertiary structure: secondary structure prediction, distance and angle restraints prediction and final tertiary structure prediction. Ten proteins with different topologies including two CASP8 proteins are chosen as the test proteins to verify the usefulness of the residue contact prediction method.
2 Contact Prediction Model
The presented formulation is an optimization based method to predict residue contacts of a protein. The primary sequence and the secondary structure information is input to the model. The secondary structure information is obtained using the Dictionary of Protein Secondary Structure (DSSP)(Kabsch and Sander, 1983). It assigns secondary structure through the identification of hydrogen bonding patterns indicative of α-helices, β-sheets, and turns.
The model then uses a Cα-Cα distance dependent force field to calculate the energetic contribution of each of the possible contacts of a protein. Contacts are predicted by formulating this problem as an optimization problem where the objective is to minimize the sum of contact energy and a hydrophobicity contribution. These predicted contacts correspond to the protein conformation that has the lowest energy. A set of constraints, based on geometric considerations and experimental observations, is also included in the model to produce physically realistic contacts.
2.1 High Resolution Cα-Cα Distance Dependent Force Field
The energy function used in this formulation is a high resolution Cα-Cα distance dependent force field generated using a linear optimization formulation (Rajgaria et al., 2006). The force field is denoted as high resolution because it has been trained on a large set of high resolution decoys (small RMSDs with respect to the native) and it was generated by requiring that the native structure always has a lower energy value than the similar non-native structures. This type of training ensures that the force field will assign a contact energy that would result in a lower energy configuration.
The Cα-Cα high resolution force field (HRFF) is a distance dependent force field and the energy corresponding to an interaction between two residues depends on the “contact” distance between the two Cα atoms. A contact exists when the Cα carbons of two amino acids are within 3 and 9 Å of each other. This contact distance range is divided into 8 bins. Hence, the energy of each interaction is a function of the Cα-Cα distances and the identity of the interacting amino acids. For 20 naturally occurring amino acids, there are 210 amino acid combinations and for 8 distance bins there are 1680 energy parameters. In this model these energy parameters are denoted as Ei,j,b, where i and j are the interacting amino acids and b is the contact distance. The Cα-Cα HRFF is then simply used as a lookup table and the interaction energy between any two amino acids of given identities and distance is a parameter. For more detailed information on force field generation, readers are referred to the original work (Rajgaria et al., 2006).
2.2 Model Formulation
2.2.1 Nomenclature
The following gives a listing of the sets, parameters and binary variables used in this model.
Sets
i, j: set of residue positions
r, s: set of strands
p, q: set of helices
si, sj: set of strand positions
hi, hj: set of helical positions
b: set of distance bins
Parameters
Ei,j,b: energy value for contact between residues i,k in distance bin b
HP (si): hydrophobicity value of strand residue si
N umHP (r): number of hydrophobic residues in strand sr
lenr: length of strand sr
Binary Variables
wi,j,b: contact between residue pair (i, j) in distance bin b
yci,j: contact between residue pair (i, j) in bin 1–8
ysr,s: contact between strand sr and strand ss
ysAPr,s: anti-parallel contact between strand sr and strand ss
ysPr,s: parallel contact between strand sr and strand ss
yhp,q: contact between helix hp and helix hq
A binary variable, wi,j,b is defined for each residue pair and this variable is active only when the pair (i, j) forms a residue contact in the given distance bin b. Although, the definition of a contact is method dependent, in a broad sense a contact is said to exist between a pair of residues/atoms when the spatial distance is below a certain threshold. The definition of a contact can be based on the distance between two Cα atoms, or between two Cβ atoms or may be a combination of both (Fariselli et al., 2001b).
For the proposed method a Cα-Cα distance dependent contact definition is employed. This distance dependence is divided into 8 bins. The model uses an extra bin, bin 9, to identify these no-contacts. Table 1 shows the relation between the contact bin and the distance range in which the predicted contact is likely to occur. For all bins, a distance dependent prediction range is defined with a maximum width of 8.0 Å. For bin 1, the prediction range is from 3.0–8.0 Å with a prediction width of 5 Å. If a contact is predicted in bin 1, then it means that the model predicts this contact to be in a distance range of 3.0–8.0 Å in the native structure of the protein. For bin 2, a prediction width of 6.0 Å is used with distance between 3.0–9.0 Å. For bin 3 and 4, the prediction range is from 3.0–10.0 Å and 3.0–11.0 Å respectively. For the last 4 bins (bin 5–8) the prediction range is between 4.0 and 12.0 Å. It is important to emphasize the motivation behind the selection of this contact definition. A set of bin dependent contact definition was chosen because the energy function employed in the model is also distance dependent. The main goal of this contact prediction model is to enhance ASTRO-FOLD, a first principles protein structure prediction framework, by providing a set of distance bounds between contacting residue pairs (Klepeis and Floudas, 2003b). A tight contact definition is not always desirable from the protein structure prediction point of view. A tight distance bound corresponding to false predictions can potentially misdirect the conformational search. The contact definition used in this work generates a set of distance bounds that are very useful for protein structure prediction using ASTRO-FOLD.
Table 1.
Distance dependent contact definition based on predicted bin.
| Bin ID | Predicted Cα-Cα Contact Distance Range [Å] |
|---|---|
| 1 | 3.0–8.0 |
| 2 | 3.0–9.0 |
| 3 | 3.0–10.0 |
| 4 | 3.0–11.0 |
| 5 | 4.0–12.0 |
| 6 | 4.0–12.0 |
| 7 | 4.0–12.0 |
| 8 | 4.0–12.0 |
2.3 Objective Function
The goal of this formulation is to find the non local contacts between residues of various secondary structures elements of a protein. As mentioned earlier, the contact between every residue pair is denoted by a binary variable, wi,j,b (representing the existence of a residue-residue contact between pair (i, j) at a distance bin b). The objective function of this formulation is shown in Equation 1. The first term of this function is the energetic contribution from all the contacting residues. Each of the binary variables wi,j,b, are assigned an energy value Ei,j,b, based on the identity of the contacting residues (i, j) and the distance (bin b) at which they contact. If the predicted distance bin for residue pair (i, j) is in bin 1–8 then it means that these two residues are contacting. An extra bin, bin 9, is used to denote a “no-contact” between a pair of residues. Thus, a contact between two residues (i, j) in bin ‘9’ (wi,j,9 = 1) implies the residue pair is not contacting. An energy value of zero is assigned for all contacts in bin ‘9’ (Ei,j,b = 0). Thus, the total energy of a protein can be calculated by taking the sum of such energy contributions over all the residue pairs (as shown in the first term of Equation 1).
The second term of Equation 1 is the hydrophobic contribution when the residues of two different strands contact each other to form a β-sheet. The residue pair (si, sj), denote all pairs of residues that are in different β-strands (i.e., si ∈ sr ∧ sj ∈ sj ). PRIFT, a hydrophobicity scale, (Cornette et al., 1987) is used to assign hydrophobicity value to every amino acid (Table 2). A binary variable yci,j, is defined for each residue pair and this variable is active only when the pair (i, j) forms a residue contact in the first 8 bins. In the second term of Equation 1, hydrophobicity for a strand pair is added only when they are contacting (i.e., ycsi,sj =1). For every contact, the hydrophobic contribution from both participating residues is considered by taking their sum. To calculate the overall hydrophobic contribution, an arithmetic sum is taken over all such strand pairs. The hydrophobic contribution is then multiplied with an optimal weight and added to the first term.
Table 2.
Hydrophobicity Values for all residues using PRIFT scale (Cornette et al., 1987).
| No | Residue | Hydrophobicity Value (HP) | No | Residue | Hydrophobicity Value (HP) |
|---|---|---|---|---|---|
| 1 | Ala (A) | 0.22 | 11 | Met (M) | 4.23 |
| 2 | Cys (C) | 4.07 | 12 | Asn (N) | −0.46 |
| 3 | Asp (D) | −3.08 | 13 | Pro (P) | −2.23 |
| 4 | Glu (E) | −1.81 | 14 | Gln (Q) | −2.81 |
| 5 | Phe (F) | 4.44 | 15 | Arg (R) | 1.42 |
| 6 | Gly (G) | 0.00 | 16 | Ser (S) | −0.45 |
| 7 | His (H) | 0.46 | 17 | Thr (T) | −1.90 |
| 8 | Ile (I) | 4.77 | 18 | Val (V) | 4.67 |
| 9 | Lys (K) | −3.04 | 19 | Trp (W) | 1.04 |
| 10 | Leu (L) | 5.66 | 20 | Tyr (Y) | 3.23 |
A residue pair (i, j) has to form one (and only one) contact in one of the 9 bins. This means that wi,j,b will be equal to 1 for only one bin and it will be equal to 0 for all other bins. This is incorporated in the model as Equation 2. Similarly, ycsi,sj is related to wi,j,b through Equation 3.
| (1) |
| (2) |
| (3) |
| (4) |
2.4 Beta Strand Based Constraints
A binary variable ysr,s, is used to represent a contact between two strands sr and ss. This binary variable is set equal to one (ysr,s = 1) if strand sr and ss contact each other otherwise, it is set to zero. The following equations are used to relate the topology variable ysr,s to residue pair contact variable wi,j,b. If wi,j,b is active for a residue pair (i, j) where i and j are residues of two different strands (r and s) and b is in the first 8 bins (denoting a contact) then ysr,s is activated. This condition is presented in Equation 5.
Similarly, if two strands are contacting then at least some of the residues of these strands should contact each other. The minimum number of required contacts have been set equal to min(lenr, lens) − 1 where, lenr and lens denote the length of strand r and s respectively. This condition is incorporated through Equation 6. If ysr,s is equal to one then the left hand side of Equation 6 requires at least min(lenr, lens) − 1 number of wi,j,b variables to be active. On the other hand, if ysr,s is equal to zero then this equation is relaxed.
| (5) |
| (6) |
Equation 7 limits the number of non-local contacts a strand residue si, can have with other residues. A maximum limit of 10 non-local contacts (separated by at least 3 residues) is imposed on all strand residues.
| (7) |
Equations 8–9 relate the contact between a pair of strand residues and their neighboring residues. If two non-local residues si (si ∈ sr ) and sj (sj ∈ ss) make a “close” contact (between bin 2 and 6) then at least one of the neighboring residues of strand residue si and sj should make a contact. The neighboring residue contact constraint corresponding to residue sj is Equation 8 and a similar equation corresponding to residue si is Equation 9.
| (8) |
| (9) |
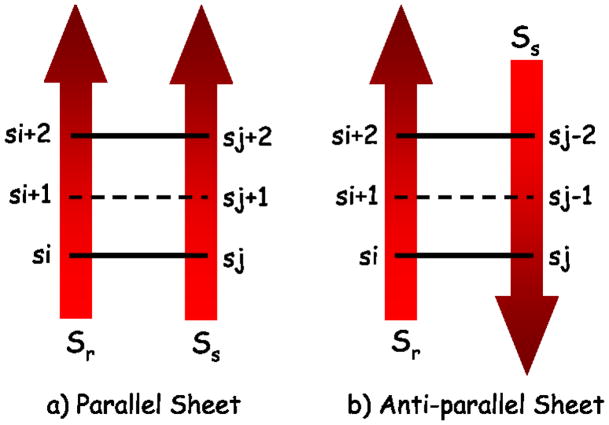
If two strands (sr and ss) contact each other to make a β-sheet, then they can contact in a parallel or an anti-parallel fashion. These two topologies are shown in Figure 2. The following equation states that if residue si and si + 2 of strand sr contact residue sj and sj + 2 of strand ss in bin 2–6, then residue si + 1 should also contact residue sj + 1 in bin 2–6. This equation (Equation 10) is motivated from the geometry of the parallel topology. A similar equation (Equation 11) is included to account for the potential anti-parallel topology (Figure 2).
Figure 2.
Cartoon depicting contact between two strands in a) a parallel fashion and b) an anti-parallel fashion. If the strands form a parallel β-sheet and residue si contacts sj and residue si + 2 contacts sj + 2 then residue si + 1 should also contact residue sj + 1. Similarly, residue si + 1 should contact residue sj − 1 if the two strands form an anti-parallel β-sheet.
| (10) |
| (11) |
2.5 Beta Topology Based Constraints
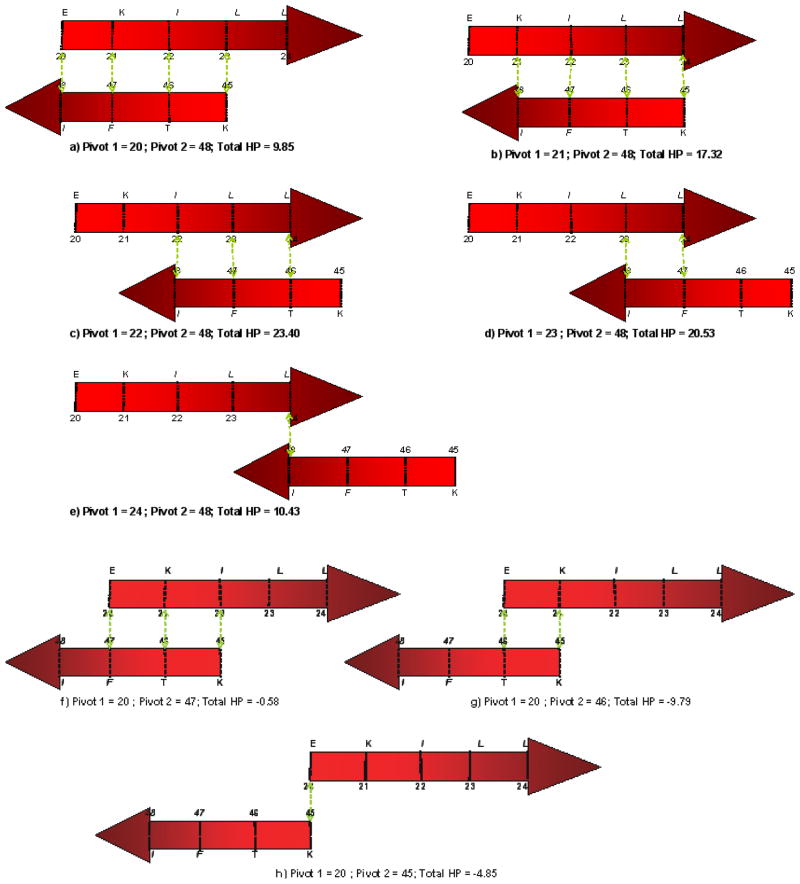
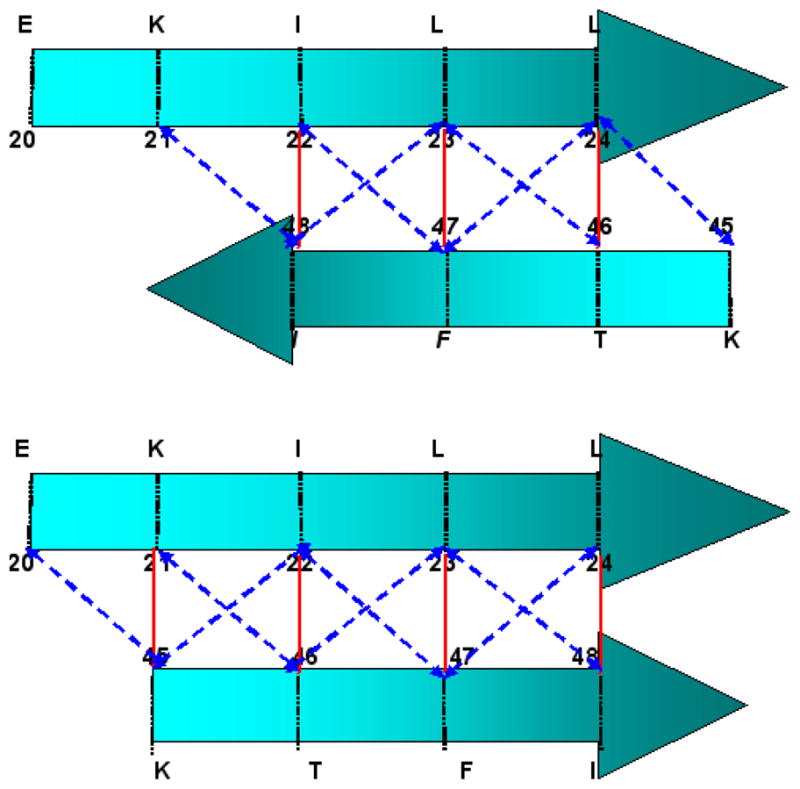
In this section we present a set of constraints for β-sheet topology. When two β-strands contact each other, they can contact in various possible alignments as well as in two different directional orientation (parallel and anti-parallel). We have developed a hydrophobicity based method to specify the most likely alignment given a strand pair and their orientation. This most likely alignment is characterized by “pivots”. The pivots are residue positions in two contacting strands (one in each strand) that act as anchors in bringing the strands together to make a β-sheet. To explain the possible alignments and pivot calculation, we will use a hypothetical protein segment with two β-strands. Let strand 1 be a 5 residue strand (EKILL) and strand 2 be a 4 residue strand (IFTK). Figure 3 shows the possible alignments when these two strands contact each other in an anti-parallel fashion. Alignments (a–e) are created by keeping strand one fixed and right-shifting the second strand. The dotted green lines between the two strands denote the vertical contact between corresponding residues of these strands. Similarly, alignments (f–h) are created by keeping strand one fixed and left-shifting the second strand. Alignments (a–h) are the only possible alignments for these two strands to contact in an anti-parallel fashion. A similar procedure can be adopted to obtain all possible alignments for parallel topology. Note there are other ways to study and determine the β-sheet topology. One example is based on statistical method to get the occurrence of different amino acid pairs in anti-parallel and parallel β-sheets (Lifson and Sander, 1979, 1980).
Figure 3.
Possible anti-parallel alignments of a hypothetical protein segment with two β-strands. Alignments (a–e) are generated by right-shifting the lower strand while keeping the upper strand fixed. Whereas, alignments (f–h) are generated by left-shifting the lower strand while keeping the upper strand fixed. The dotted green lines between two strands denote a contact between the two residues.
Once all alignments are enumerated for a β-strand pair of a protein, hydrophobicity value of each of these alignments is calculated using the PRIFT (Cornette et al., 1987) scale. There have been various attempts in the literature to assign hydrophobicity values to the amino acids. These hydrophobicity values are used to identify hydrophobic regions of a protein. Cornette et al. (1987) compared thirty-eight published hydrophobicity scales and recommended the PRIFT scale for hydrophobicity estimation (Table 2). The hydrophobicity of a particular alignment is then calculated by taking the arithmetic sum of hydrophobicity value of all overlapping residues of both the strands. For example, the hydrophobicity corresponding to the alignment (d) of Figure 3 is calculated by taking the sum of hydrophobicity values of two Leucines, one Isoleucine and one Phenylalanine (2 * 5.66 + 4.77 + 4.44 = 20.53). Similarly, the hydrophobicity value of other alignments shown in Figure 3 is written below the corresponding alignment.
Pivots for a particular strand pair are decided based on the alignment which has the highest hydrophobicity value. In the foregoing example, alignment (c) has the highest hydrophobicity value of 23.40 when these two strands contact in anti-parallel fashion. Pivots are then defined as the residue positions in the contacting strands that make vertical contacts (as denoted by dotted green lines in Figure 3). According to this definition, residue pair (22,48), (23,47), and (24,46) each are classified as pivots for these two strands. However, for the ease of nomenclature, the smallest residue position among all these pairs is chosen as pivot 1 and the corresponding vertical residue is chosen as pivot 2. Thus, the residue pair (22,48) is the pivot pair when these two strands make an anti-parallel contact. It is also clear that if one pair of pivots is given then the other pivot positions can be easily inferred. Thus, only one unique pivot pair is associated with each strand pair. If two alignments have the same hydrophobicity value then the pivot pair is calculated from the alignment which has more overlapping residue pairs (more number of dotted green lines). Pivots are then calculated for each strand pair combination of a protein for both parallel and anti-parallel topology. In the following paragraphs we use protein 1AUU as an example to illustrate pivot calculation.
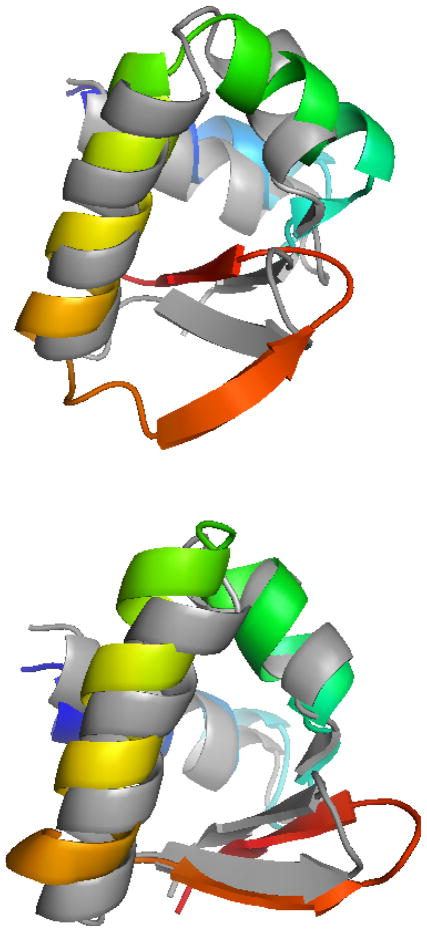
Protein 1AUU is a 55 residue β-protein with four β-strands. These four strands contact each other in an anti-parallel fashion (Figure 4). The location and residue composition of these strands are given in Table 3. These four strands can make 6 unique strand pairs. Moreover, each of these strand pairs can contact in either a parallel or an anti-parallel fashion resulting in 12 different strand pair arrangement. The pivots corresponding to each of these arrangements are given in Table 4.
Figure 4.
Three dimensional structure of the native structure of protein 1AUU.
Table 3.
Secondary structure information of protein 1AUU
| No | Location | Length | Residue Composition |
|---|---|---|---|
| β1 | 2–3 | 2 | KI |
| β2 | 11–15 | 5 | AIVVK |
| β3 | 20–24 | 5 | EKILL |
| β4 | 45–48 | 4 | KTFI |
Table 4.
Twelve possible strand pair combinations corresponding to four β-strands of protein 1AUU.
| Parallel Contact | ||||
|---|---|---|---|---|
| No | Strand Pair | Pivots | Total HP | Overlap |
| 1 | β1-β2 | P1=2; P2=12 | 11.17 | 2 |
| 2 | β1-β3 | P1=2; P2=23 | 13.05 | 2 |
| 3 | β1-β4 | P1=2; P2=47 | 10.94 | 2 |
| 4 | β2-β3 | P1=11; P2=21 | 27.38 | 4 |
| 5 | β2-β4 | P1=11; P2=45 | 18.60 | 4 |
| 6 | β3-β4 | P1=21; P2=45 | 17.32 | 4 |
| Anti-Parallel Contact | ||||
| No | Strand Pair | Pivots | Total HP | Overlap |
| 1 | β1-β2 | P1=2; P2=13 | 11.17 | 2 |
| 2 | β1-β3 | P1=2; P2=24 | 13.05 | 2 |
| 3 | β1-β4 | P1=2; P2=48 | 10.94 | 2 |
| 4 | β2-β3 | P1=12; P2=24 | 24.12 | 4 |
| 5 | β2-β4 | P1=11; P2=48 | 18.60 | 4 |
| 6 | β3-β4 | P1=22; P2=48 | 23.40 | 3 |
It is important to emphasize the significance and use of these pivots in the context of residue contact prediction. Specifying a pivot pair means that if the two strands were to contact each other to make a β-sheet then the strands would align according to the alignment dictated by the pivot pair associated with the corresponding strand pair. As mentioned earlier, given a pivot pair, the alignment corresponding to it is created by aligning the strands in such a way that all the pivots make vertical contacts with each other.
It must be understood that the pivot analysis does not fix/preclude contact between any pair of strands. It is only used to identify the most likely alignment (because hydrophobicity is believed to be the main driving force behind the β-sheet formation) for all possible strand pairs. This pivot information is then used to allow/disallow certain contacts between a pair of strands. The pivots based constraints are discussed in the next section.
2.5.1 Pivot Based Constraints
The top part of Figure 5 shows the most likely alignment (based on the pivot analysis) when strand 3 and 4 of protein 1AUU contact in an anti-parallel fashion. The residue pairs (22,48), (23,47), and (24,46) are the three pivot pairs (pivot1, pivot2) for this alignment. It was observed that all residues that are three or more residues apart (in both directions) from a pivot (say pivot 1) are rarely within 9 Å distance from the other pivot (pivot 2). Also, residues that are within ±1 residue distance from pivot 1 are mostly within 9 Å distance from pivot 2. This observation is used to write a set of likely contacts and disallowed contacts for a given pivot pair. It was also observed that residues that are ±2 residues apart may or may not fall within the 9 Å contact range. Thus, ±2 residues are not disallowed to make contacts.
Figure 5.
Cartoon depicting an anti-parallel (Pivots: 22,48) and a parallel (Pivots: 21,45) contact between strand 3 and strand 4 of protein 1AUU. These alignments can be used to infer a set of allowed and disallowed contacts. The vertical contacts (bold red lines) and ±1 slant contacts (dashed blue lines) are allowed contacts. Contacts that are ±3 or more residues apart (not shown in this figure) from the pivots are not allowed.
The likely contacts corresponding to the strand pair (3,4) of protein 1AUU is shown in the top part of Figure 5. The vertical contact between the three pivots are shown in bold red lines. The contacts that are ±1 residues apart are shown in blue dashed lines. The ±1 contact between residue (22,49) and (25,46) for anti-parallel arrangement is not shown in this figure because residue 25 and 49 are not β-strand residues. The contacts that are ±3 or more residues apart are very likely to fall in bin 9 (beyond 9 Å distance). Thus, these contacts are classified as disallowed. A complete list of these allowed and disallowed contacts corresponding to this strand pair is given in Table 5.
Table 5.
A list of allowed and disallowed contacts when β3 and β4 of protein 1AUU contact each other.
| Parallel Contact | Likely Contacts | Disallowed | ||
|---|---|---|---|---|
| No | Pivots | Vertical | ±1 residues | Contacts |
| 1 | P1=21; P2=45 | 21–45 | 20–45; 21–46; 22–45 | 24–45 |
| 2 | P1=22; P2=46 | 22–46 | 22–47; 23–46 | 20–48 |
| 3 | P1=23; P2=47 | 23–47 | 23–48 | 20–47 |
| 4 | P1=24; P2=48 | 24–48 | 24–47 | 21–48 |
| Anti-parallel Contact | Likely Contacts | Disallowed | ||
| No | Pivots | Vertical | ±1 residues | Contacts |
| 1 | P1=22; P2=48 | 22–48 | 22–47; 21–48; 23–48 | 20–45; 21–45; 22–45 |
| 2 | P1=23; P2=47 | 23–47 | 23–46 | 20–47 |
| 3 | P1=24; P2=46 | 24–46 | 24–45; 24–47 | 20–46; 21–46 |
Once a set of allowed and disallowed contacts are determined for each strand pair, constraints are written to fix these contacts. Two other binary variables, ysPr,s and ysAPr,s, are introduced to denote a parallel and an anti-parallel contact between strands sr and ss. Variable ysPr,s is set equal to 1 if the strands contact in a parallel fashion. Similarly, ysAPr,s is set equal to 1 if the strands contact in an anti-parallel fashion. Equation 12 states that if the strand pair (3,4) contact each other in an anti-parallel fashion then all of the allowed contacts given in Table 5 should be active. For an anti-parallel contact, ysAP would become equal to 1 forcing every term in the left hand side to be equal to 1. If the strands do not contact in an anti-parallel fashion then the right hand side would be equal to zero, thus relaxing the equation. Similarly, Equation 13 disallows the contacts corresponding to residue pairs that are ±3 or more residues apart from the pivots. A similar set of equations for allowed and disallowed contacts is included for a parallel contact between these two strands (Equations 14 and 15). Similar equations (not shown) are written for all possible strand pairs. These equations do not fix any topology but merely disallow certain contacts if any of these strand contacts were to occur.
| (12) |
| (13) |
| (14) |
| (15) |
2.5.2 Other Topology Based Constraints
Equation 16 is included in the model to limit the maximum number of interactions a strand can have with other strands of the protein. In the proposed model, a strand is only allowed to contact two other long strands (length ≥ 3). This limit on the maximum number of strand contacts can be changed but a maximum value of two was used because a strand can at most contact two other strands to make a β-sheet. Although, it is possible for a strand to be in spatial proximity of another sheet, an upper limit of two was set in order to require that the model choose the most important contacts.
| (16) |
Equation 17 limits the total number of strand contacts allowed for a protein. In the absence of such a constraint, the model might select a β-barrel like topology where each strand makes two contacts with the neighboring strands (one on each side) thereby satisfying Equation 16. Equation 17 prohibits this kind of topology by requiring the total number of strand contacts being less than or equal to the right hand side of Equation 17. The first term on the right hand side is the sum of all strands that have two or more hydrophobic residues. All such strands are allowed to make contacts and they are included in the first term. The second term includes contacts for long strands (length ≥ 3) with only one hydrophobic residues. If a protein has zero or one strand (that qualifies this criterion) then the maximum limit is set to one (as given in Equation 17) for both the terms. In the following equation, N umHP (r) is a parameter denoting the total number of hydrophobic residues in strand sr.
| (17) |
The strand to strand contacts are further constrained based on the number of hydrophobic residues in the contacting strands. If a strand has “adequate” number of hydrophobic residues then it should make at least one strand to strand contact. A strand is said to have adequate hydrophobic residues if the length of the strand is at least two residues and it has two or more hydrophobic residues or the length of the strand is at least three residues if it has only one hydrophobic residue (Equation 18). On the other hand, if a strand “does not have adequate” number of hydrophobic residues then it should not contact any other strand. Strands of length two or less residues with only one hydrophobic residue or strands with no hydrophobic residues are restricted to not make any strand to strand contacts. This constraint is included using Equation 19. In the following two equations lenr, is a parameter that denotes the length of strand sr.
| (18) |
| (19) |
Another constraint (Equation 20) is included to limit strand to strand contact between small strands and big strands. Equation 20 states that strands of length two residues should not contact long strands (length ≥ 3). This equation should be seen in tandem with Equation 17, which puts a limit on the maximum number of strand contacts for a protein. Equation 20 ensures that the contact between a small strand and big strands is not chosen over contacts between big strands that might result in a lower energy configuration. However, it was observed that strands of length two residues contact each other. To account for this observation, Equation 20 is not applied for strands of length two residues.
| (20) |
The binary variables, ysPr,s and ysAPr,s, are related to the strand contact variable ysr,s through Equations 21–23. Equation 23 requires that two strands sr and ss can only contact in either a parallel or an anti-parallel fashion. Thus only one of these two variables are activated.
| (21) |
| (22) |
| (23) |
2.6 General Constraints
As mentioned earlier, a high accuracy is good but it is equally important to have a small number of false predictions. Equations 24–25 are added in the model to restrict the total number of predictions. It has been observed that the predicted contacts are usually less accurate for long proteins. This is due to the increased combinatorial complexity because of the long length. This equation is included in the model to restrict total number of predicted contacts for long proteins. For proteins that are less than 150 residues in length are allowed to make N res number of non-local contacts. However, proteins with length higher than 150 residues are only allowed to make 0.75 * N res number of non-local contacts. Here, N res is the length of the protein under consideration.
| (24) |
| (25) |
Equations 26–27 are very similar to Equations 8–9. If a residue pair (i, j | abs(i − j) ≥ 2) makes a “very close” contact (in bin 2 or bin 3) then both neighbors (on each side) of strand residue i and j should make a contact. A coefficient of 2 is multiplied on the left hand side of the following equations to activate both binary variables on the right hand side when i and j make a contact.
| (26) |
| (27) |
Equations 28 and 29 require that no three consecutive contacts should take place in the same bin. This equation is motivated from the observation that it is not very common to find three consecutive residues forming contacts with a common residue at approximately same distance. Although, it is possible to find such uncommon occurrences, this model aims at predicting typical (common) contacts using a mathematically rigorous framework.
| (28) |
| (29) |
2.6.1 Helix Contact Constraints
A set of constraints corresponding to contacts between α-helical residues, loop residues, and Cysteine residues are also included in the model. These constraints were part of the formulation presented in Rajgaria et al. (2009). Equations 4–22 of this publication are also part of this model. These equations are not presented in this article to avoid repetition. Readers are referred to the original work for detailed information (Rajgaria et al., 2009).
2.6.2 Integer Cut Constraints
This optimization based formulation offers the ability to generate a rank-ordered list of solutions. A single optimal solution obtained using this formulation corresponds to the one with the lowest objective function value. However, it is possible to generate a rank-ordered list of solutions by using the following integer cut constraint (Equation 30). The addition of this constraint allows the user to generate a specified number of contact results in increasing order of optimal value (the objective function is being minimized). Sometimes, the objective function value of these solutions is very close to the objective function value of the optimal solution. This ability to generate a rank ordered list of results in a mathematically rigorous way adds to the algorithmic advantage of the model. The use of Equation 30 excludes the previous solution from the feasible solution space for every subsequent iteration and a unique solution is obtained for each of the iterations.
| (30) |
Set A in Equation 30 represents the set of all active ysr,s and yhp,q (i.e., ysr,s = 1; yhp,q = 1) variables. The cardinality of set A, card(A), is the total number of elements in set A. I represents the set of inactive variables.
2.7 Preprocessing
It has been observed that the distance between intra-strand residues si and si + 3 is always more than 9 Å. This observation can be used to restrict binary variables that denote a contact between an intra-strand pair (si,si + 3) and beyond at less than 9 Å. Equation 31 is included in the model to fix such binary variables.
| (31) |
Similarly, a set of preprocessing steps are included to fix contacts between α-helical residues and loop residues. These preprocessing steps can be found in Equations 24–37 of Rajgaria et al. (2009).
3 Results and Discussion
An integer linear optimization based contact prediction method has been presented. This method can be used to predict residue contacts for all structural classes of a protein. It not only offers the advantage of finding the contacts corresponding to the global minima, but it can also produce a rank-ordered list of residue contacts. It also offers the flexibility of incorporating additional constraints where a user can add unique and problem specific constraints to the model. The complete model forms an ILP problem that can be solved to optimality using commercial solvers (e.g. CPLEX (ILOG, 2003)).
The effectiveness of a contact prediction can be measured by calculating its accuracy. Accuracy is defined as the ratio of correct predictions to total predictions. Accuracy can also be written in terms of true positives (TP) and false positives (FP) as shown in Equation 32. A higher value of accuracy means a better contact prediction model.
| (32) |
Another useful criterion to evaluate contact prediction effectiveness is the average distance of true positives (avgTPdis) and false positives (avgFPdis). This criterion aims to estimate the usefulness of predicted contacts in protein structure generation. As mentioned earlier, these contacts can be used as search/guiding criteria to limit the protein conformational search space. While TP contacts will guide the search towards the actual structure of a protein, FP contacts corresponding to large unrealistic distances in the native structure might misguide the search. Thus, a good contact prediction scheme should not only have a high accuracy value but the number of false positives as well as the avgFPdis should be small.
Some of the local contacts (within the secondary structure of a protein) can be determined a priori because of the geometry of the secondary structure elements. However, the goal is to predict non-local contacts that can not be determined a priori. For these reasons, accuracy corresponding to contacts that are separated by less than 6 residues are not reported. Instead, accuracy corresponding to residue separation of 6, 12, and 24 is reported to demonstrate the efficacy of the method for residue pairs that are far-off in the sequence space.
This method has been tested on proteins from three independent test sets. The test proteins were further divided into smaller sets depending on the structural class. Three to five predictions were obtained for every test protein. In most of the cases, the best prediction was in the top three predictions. Prediction results on these test sets are presented in the following subsections.
3.1 Protein Test Set 1
The first test set was taken from the work of Cheng and Baldi (2007). In this work, the authors developed a residue contact prediction method (SVMcon) using Support Vector Machines. They incorporated a set of five residue information based input features to predict contact between a pair of residues. This method was trained on a set of 485 proteins while accounting for the unbalanced nature of the problem (with far more examples of non-contacts than contacts). They used a 8 Å criterion to define a contact between Cα atoms of two residues. SVMcon was tested on a set of 48 proteins covering all SCOP (Murzin et al., 1995) structural classes and the accuracy results were reported for non-local contacts that were 6, 12, and 18 residues apart. SVMcon was found to perform best for the contacts that are 12 residues apart. The proposed method was tested on β, α/β, and α + β proteins of this test set. The test results on α-helical proteins have been reported elsewhere (Rajgaria et al., 2009). In the remainder of this document, this set of test proteins will be referred as test set 1.
3.1.1 β Proteins
There are 8 single domain β proteins in this test set with length ranging from 98 to 170 residues. Table 1 of the supplementary material presents the performance of our method on these 8 β proteins for residue separation of 6, 12 and 24 residues. The third column of this table reports the accuracy for contacts that are 6 residues apart. The number of true positive contacts (TP) and total contacts (TP+FP) are also listed in the same column. The accuracy for separation of 12 and 24 residues is given in the next two columns. The average accuracy on this test set is 0.563, 0.532, and 0.612 for separation of 6, 12, and 24 residues.
Protein 1HE7 is a 107 residue protein with seven β-strands and one 310-helix. The β-strands contact each other to make two β-sheets of 3 strands each [sheet 1: β1-β5, β4-β5; sheet 2: β2-β6, β6-β7]. β3 is a two residue strand that does not participate in β-sheet formation. The contact prediction model correctly predicted the contacts of β-sheet 2 [contact between β2, β6 and β6, β7]. For β-sheet 1, contact between β4, β5 was also predicted. One wrong contact was predicted between β1, β4 instead of β4, β5. An accuracy of 0.636 was obtained for this protein with 68 correct predictions. Since, most of the predicted contacts between β-strands are correct, a small avgFPdis of 13.5 Å is obtained for this protein.
The highest accuracy is obtained for proteins 1QJP (0.810). Protein 1QJP has a β-barrel like structure. It is interesting to observe that a high value of accuracy is obtained for this protein because the presented formulation has a constraint (Equation 17) that prohibit a β-barrel like structure. Because of this constraint, the correct topology is not predicted by the proposed model. However, correct anti-parallel sheet topology is predicted for some pairs of β strands producing a high value of accuracy of 0.810 for separation of 6 residues.
For all of these proteins, the average distance of true positives (avgTPdis) and false positives (avgF-Pdis) was calculated from the native structure. These values are reported in column four and five of Table 1 of the supplementary materials. The average value of avgTPdis for single domain proteins is 7.7 Å and the average value of avgFPdis is 16.9 Å. As mentioned earlier, protein 1QJP has a β-barrel like structure and this model can not predict correct contacts for this kind of topology. Thus, some incorrect β-strand contacts are predicted which are far-off in the three dimensional structure of the protein. These incorrect predictions result in a high value of avgFPdis value of 21.1 for protein 1QJP.
3.1.2 α + β and α/β Proteins
This test set consists of 21 α + β and α/β proteins. All of these proteins are single domain proteins ranging from 76 to 198 residues in length. The test results on this test set is presented in Table 2 of the supplementary materials. The average accuracy on this test set is 0.602, 0.581, and 0.536 for separation of 6, 12, and 24 residues. The average true positive distance and false positive distance for this test is 7.6 and 16.4 Å.
One of the highest accuracies is obtained for protein 1DZO. It is a 120 residue α + β protein with 6 β strands and 2 α-helices (Figure 6). Strand 1 and 2 contact each other in a parallel fashion and rest of the strands make a β-sheet by contacting in an anti-parallel fashion. The α-helices do not make non-local contacts. Instead, helix 2 extends in the same direction as helix 1 thereby not making a parallel or an anti-parallel contact. Our method predicted 74 non-local contacts for this protein and 64 of these contacts are correct, producing an accuracy of 0.865 for separation of 6 residues. Figure 6 shows all predicted contacts for protein 1DZO. The correct contacts are shown in black bold lines and the incorrect contacts are shown in red dotted lines.
Figure 6.
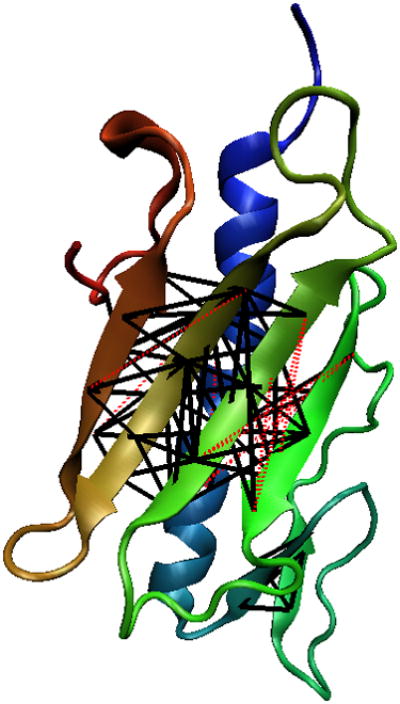
The three-dimensional structure of protein 1DZOA. The black bold lines denote a correctly predicted contact whereas the red dotted lines denote an incorrect contact.
Protein 1G2R is another α + β protein of this test set. It is a 94 residue protein with 3 strands and 3 α-helices. Strand 1, 2, and 3 make a β-sheet with strand 1 (in the middle) making anti-parallel contacts with strand 2 and 3. Similarly, helix 2 contacts helix 3 in an anti-parallel fashion. Our method correctly predicts a contact between strand 1–2 and strand 1–3 producing an accuracy of 0.763. However, it identifies the contact between 1–3 as parallel instead of anti-parallel. The contact between strand 1–2 is correctly predicted as an anti-parallel contact.
Protein 1XER is an example from this test set where this method did not produce a good accuracy. This protein is 103 residue α + β protein with 7 strands and 4 α-helices. Our method did not predict the correct topology thereby predicting incorrect contacts. Overall the method has produced good accuracy for these test proteins. Accuracy is higher than 50% for 16 out of the 21 test proteins. On an average, the accuracy on α + β proteins is more than α/β proteins.
3.2 Protein Test Set 2
Test set 2 was taken from the work of Vicatos et al. (2005). This test set was used by them to test their correlation mutations analysis based residue contact prediction method. They applied CMA using a set of descriptors based on the physio-chemical properties of residues. Principal Component Analysis was performed on a large set of descriptors to reduce this to a small set of descriptors that accounted for most of the variations. They found that the use of new descriptors resulted in more accurate predictions compared to other CMA methods. They used a 6 Å cutoff distance to define a contact. Also, only non-local contacts that were separated by 8 or more residues were considered. We test our method on 54 β, α + β, and α/β proteins of their test set. Proteins with more than 250 residues were not included in our test set. The remainder of this document will refer to this as test set 2. This set has been further divided into two test sets based on the structural classification of test proteins. The test results on 25 α-helical proteins have been reported elsewhere (Rajgaria et al., 2009) and the results on rest of the proteins are presented below.
3.2.1 β Proteins
Table 3 of the supplementary materials presents the testing results of our method on 25 β proteins of test set 2. An additional column reporting accuracy values for contacts separated by 8 or more residues is also included in this table (as published in Vicatos et al. (2005)). The average accuracy for residues separation of 6 is 0.579. This accuracy is in the same range of accuracy obtained for β proteins of test set 1. The accuracy for residue separation of 8, 12, and 24 is 0.564, 0.525, and 0.449 respectively.
High accuracy is obtained for protein 1AUU, 1BBZ, 1CDQ and 1JPC. Protein 1AUU is a small protein of 55 residues. It has 4 strands (S1(2–3), S2(11–15), S3(20–24), S4(45–48)) with only one hydrophobic residue in strand 1. These strands contact each other in an alternating fashion to make a β-sheet. One of the model constraint disallows contacts for a stand of length 2 with only one hydrophobic residues. Thus, no contacts are predicted for this strand. For other strands, the correct anti-parallel topology is predicted.
Protein 1JPC (108 residues, 11 strands) has three β-sheets making a three-dimensional triangular structure (with each sheet as a side of a triangle). The strands contact in anti-parallel fashion to make each of these β-sheets. This is a difficult topology to predict. Although, our method did not correctly predict the topology of all three β-sheets, it predicted most of the correct contacts resulting in an accuracy of 0.861 (93 correct contacts out of 108 predicted contacts). This protein also has a disulfide bridge between residue 29 and residue 52. This model successfully identified the disulfide bridge between these two Cysteine residues.
The lowest accuracy on this test set is obtained for protein 1F3Z. It is a 150 residue protein with 5 α-helices and 16 β-strands. Although the length of protein 1F3Z is smaller compared to other proteins of this test set, the number of secondary structure elements is large. This increases the combinatorial complexity of the problem. The number of possible strand contacts is large for this protein and our method did not identify the correct topology for this protein, resulting in a very low accuracy and high average false positive distance. The average false positive distance for this test set is 15.3 Å which is less than the average false positive distance found on β proteins of test set 1.
3.2.2 α + β and α/β Proteins
This test set consists of 29 α + β, and α/β proteins ranging from 45 to 249 residues in length. The testing results on this set are given in Table 4 of the supplementary materials. The average accuracy on this test is 0.643 for residue separation of 6 or more. This is the highest average accuracy among all test sets. The average false positive distance is 15.8 Å for this test set. The average accuracy for separation 8, 12, and, 24 is 0.646, 0.641, and 0.604 respectively.
The highest accuracy is achieved for protein 1DIV. It is a small protein of 55 residues. Our method correctly identifies the topology and all the contacts are predicted correctly. The proposed method has also been modeled to identify disulfide bridges (if any) between Cysteine residues of a protein. Protein 1F5M is a 176 residue protein with 6 α-helices and 6 β-strands. There is a disulfide bridge between residue 88 and residue 122 of this protein. Our method correctly identifies this disulfide bridge.
The highest avgFPdis is obtained for protein 1BP1. It is a 217 residue long α/β protein. The three dimensional structure of this protein has a cylindrical shape (like a β barrel) with a α-helix in between. The model predicted a β-sheet between β1 and β3 which are far off in the native structure. This incorrect prediction caused the avgFPdis to be so high. Although, the contact prediction model failed (either low accuracy or high avgFPdis) for some of the test cases, 22 out of 29 test proteins have accuracy higher than 0.500.
3.3 Protein Test Set 3
The third test set was taken from the work of Wu and Zhang (2008). In this work, the authors have compared different machine learning methods (sequence based and template-based) for residue contact prediction. They tested different contact prediction methods on a test set of 554 non-homologous proteins with a pair-wise sequence identity less than 25%. The length of these proteins varies from 50 to 300 residues. They classified these proteins into “Easy” (220 proteins), “Medium” (98 proteins), “Hard” (220 proteins) and “Very Hard” (16 proteins) targets based on the threading significance score [refer Wu and Zhang (2008) for a complete description of their method].
This test set was created from the set of “Hard” and “Very Hard” proteins of Wu and Zhang (2008) test set. There were 144 β, α + β, and α/β proteins in a set of 236 proteins. Out of these 144 proteins, 100 proteins were randomly selected as our test set. The test results are shown in Tables 6–8 of the supplementary materials. The average accuracy on this test is 0.646 for residue separation of 6 and the average false positive distance is 15.0 Å. The average accuracy for separation 12, and, 24 is 0.603, and 0.675 respectively.
The summary of all test results is presented in Table 6. The average accuracy of all three tests is 0.607 for residue separation of 6. It can be seen from this table that our method consistently produces an accuracy value of ~ 60% across all test sets. Similarly, the average false positive distance is 15.88 Å, which is also approximately the same for all test sets.
Table 6.
Summary results of the proposed contact prediction model on single domain proteins of the three test sets.
| Residue Seperation=6 | ResSep=12 | ResSep=24 | |||
|---|---|---|---|---|---|
| Test Set | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy |
| Test Set 1: β Proteins | 0.563 | 7.7 | 16.9 | 0.523 | 0.612 |
| Test Set 1: Mixed α/β Proteins | 0.602 | 7.6 | 16.4 | 0.581 | 0.536 |
| Test Set 2: β Proteins | 0.579 | 7.5 | 15.3 | 0.525 | 0.449 |
| Test Set 2: Mixed α/β Proteins | 0.643 | 7.6 | 15.8 | 0.641 | 0.604 |
| Test Set 3: β & Mixed α/β Proteins | 0.646 | 7.5 | 15.0 | 0.603 | 0.675 |
| Average | 0.607 | 7.58 | 15.88 | 0.575 | 0.575 |
3.4 Predictions Without Knowledge of Secondary Structure
3.4.1 α + β and α/β Proteins of Test Set 2
As described earlier, secondary structure information of a protein is input to the model. For all the previous results, secondary structure information was derived using DSSP which in turn uses the tertiary structure of a protein. For any “blind” test, the tertiary structure will not be available. In such a scenario, DSSP can not be used to determine the location of secondary structure elements. For all new proteins, one will have to rely on secondary structure prediction techniques that only use the sequence information. An analysis was carried out to estimate the sensitivity of the proposed model with respect to the accuracy of secondary structure information. PSIPRED (Jones, 1999), a very successful method for secondary structure prediction, is a multi-stage neural network based approach that uses profile information derived from position specific scoring matrices. It was used to generate the secondary structure information for 29 mixed α/β proteins of test set 2. The accuracy results calculated using the predicted secondary structure information is given in Table 5 of the supplementary materials. An average accuracy of 0.605, 0.589, and 0.570 was obtained for residue separation of 6, 12, and 24.
The accuracy of a secondary structure prediction can be evaluated using Q3 and Segment Overlap Accuracy (SOV) measures. The Q3 accuracy is calculated by taking the average of prediction accuracy at individual residue positions. On the other hand, SOV score is calculated using the average overlap between the actual and predicted segments instead of average accuracy calculated using individual residues (Rost et al., 1994). This is a more meaningful assessment metric compared to Q3 as it also accounts for the type and position of secondary structure segment.
For most of the 29 test cases, the change in accuracy is small. However, there are cases such as protein 1DBD where the accuracy decreases from 0.962 to 0.650 when secondary structure information from PSIPRED is used. The native structure of this protein has 3 α-helices and 4 β-strands. However, PSIPRED prediction for this protein consists of only 1 α-helix and 6 β-strands. The Q3 accuracy and SOV measure for this prediction is 74.10% and 54.0% respectively. This prediction accuracy is very low compared to an average secondary structure prediction accuracy of ~80%. The location of α-helices and β-strands plays an important role in constraints of the contact prediction model. Thus, the difference in secondary structure prediction for protein 1DBD is quite significant and a decrease in the accuracy of predicted contacts can be attributed to it. Similarly, a low SOV accuracy is obtained for proteins 2HGF, 1ONE, 1APY, 1DEF, 1GLU, and 1BP1. The poor secondary structure prediction accuracy results in a decreased contact prediction accuracy and increased average false positive distance (avgFPdis). Overall, the accuracy of predicted contacts did not change by more than ~6%.
3.4.2 Residue Contact Prediction of CASP8 Proteins
A major test of contact prediction methods is done through a biennial world wide competition, Critical Assessment of Techniques for Protein Structure Prediction (CASP). The contact prediction accuracies for L/5 contacts, L/10 contacts, and best 5 contacts (according to the confidence score) are calculated and used for comparison between different groups. It is concluded that the contact prediction accuracy improves as the number of contacts decreases, meaning the accuracy for L/10 is higher than that of L/5 contacts, and the accuracy for the best 5 contacts is the highest. Across all the groups the best contact prediction accuracy for the best 5 contacts is less than 45% (Grãna et al., 2008).
In order to evaluate our contact prediction methods, 20 single domain proteins from CASP8 are selected. Since our method requires secondary structure information, PSIPRED is used to provide the secondary structures for these 20 proteins. The contact prediction results for the CASP8 proteins are shown in Table 9 of the supplementary materials. The average prediction accuracies of the CASP8 proteins are 51.8%, 51.0%, 48.6% and 38.9 % for residue separations of 6, 8, 12 and 24, respectively. This compares favorably with the highest accuracy of less than 45% which is based on the top 5 predictions in CASP8.
Helical proteins are also included in the 20 proteins, which allows us to have a comprehensive assessment of our prediction method. The highest contact prediction accuracy, 90%, is obtained for T469. The two proteins that have the lowest accuracies are T476 of 16.7% and T480 of 15.2%. T476 is a mixed α/β protein with 4 helices and 2 strands. The Q3 value is 62.5% and SOV value is 40.0% for helix; while the Q3 value and SOV values for strand are 50%, 50% respectively. These relatively small values of Q3 and SOV from PSIPRED prediction is one of the reasons for the low prediction accuracy of T476. Similarly for T480, a pure β protein, the Q3 and SOV values for strand prediction are only 20% and 30%.
4 Protein Tertiary Structure Prediction Using ASTRO-FOLD with Residue Contact Prediction
The main goal behind the development of a residue contact prediction model is to aid protein structure prediction by providing a set of accurate distance bounds which reduces the conformational search space. The residue contact prediction model is incorporated into our ab initio protein tertiary structure prediction method, ASTRO-FOLD (Klepeis and Floudas, 2002b, 2003c,b; Klepeis et al., 2003a,b). The goal of this section is to examine the usefulness of the proposed residue contact prediction model in protein tertiary structure prediction.
4.1 ASTRO-FOLD for Protein Tertiary Structure Prediction
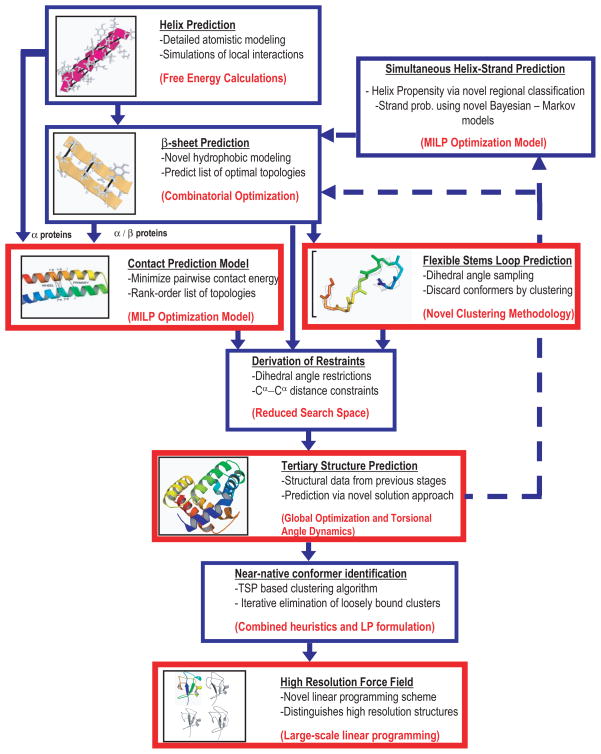
The ASTRO-FOLD approach is an ab initio method for the tertiary structure predictions of proteins from their primary amino acid sequences. It consists of several steps which are discussed in the following paragraphs. The overall flowchart of most recent version of ASTRO-FOLD is dipicted in Figure 7.
Figure 7.
Overall schematic of the enhanced ASTRO FOLD approach for tertiary structure prediction of proteins.
The first stage of ASTRO-FOLD method is the identification of α-helical regions and β-strand regions of a protein (Klepeis and Floudas, 2002a, 2003a). The prediction method of α-helices divides the amino acid sequence into a series of overlapping oligopeptides and then atomistic level modeling is performed to calculate the helical propensity for every oligopeptide sequence. A semi-empirical force field ECEPP/3 (Empirical Conformational Energy Program for Peptides) is used for the atomistic level modeling (Némethy et al., 1992). The identification of the native peptide conformation translates into a problem of global optimization where the goal is to identify the conformation with the lowest free energy (Klepeis and Floudas, 1999, 2002a). After α-helices are determined, the remaining residues are analyzed for the location of β-strands (Klepeis and Floudas, 2003a). Hydrophobic collapse is used as the main driving force for the prediction of β-sheets. An integer linear optimization method is developed to maximize the sum of the hydrophobic contributions for both residue-residue contacts as well as strand-to-strand contacts.
Recently, a new secondary structure prediction method, HELIOS, has been developed in our group and this has been incorporated into ASTRO-FOLD (Subramani and Floudas, 2009a). HELIOS predicts α-helical region of a protein by maximizing the hydrogen bonding propensity. The model also includes hydrophobicity effects and the effect of hydrogen bonding between the side chain and main chain atoms. In another work, Subramani and Floudas (2009b) developed a method, BEST-PRED, that uses naive Bayesian and first order Markov models for the prediction of β-strand locations. The first order Markov model is used to calculate pairwise occurrence of alternate amino acids in β-strands. On the other hand, a naive Bayesian model, assuming independence of neighboring residues, is used to calculate the probability that a particular residue is in a β-strand. An integer linear programming formulation that maximizes the strand probability for the entire protein is used to predict the location of β-strands.
The second stage of ASTRO-FOLD is to derive a set of dihedral and distance constraints in order to reduce the conformational search space of a protein. Restraints are derived from the predicted protein secondary structures. The secondary structures of proteins have special geometry that can be used to derive bounds on dihedral angles and Cα-Cα distances. Restraints for the loop region are derived through dihedral angle sampling and a novel clustering approach (Monnigmann and Floudas, 2005).
Additional and tighter constraints can be derived for a protein. The residue contact prediction model proposed in this paper is used to derive the residue contact constraints. This proposed method can predict inter-residue contacts for α, β, α + β, and α/β proteins. In another work, McAllister and Floudas (2009) developed enhanced bounding techniques to reduce the protein conformational search space. The bounds on dihedral angles, φ and ψ, were developed using the predicted secondary structure and allowed φ/ψ space. Another distance bounding technique is developed in this work for β-sheet topology.
The final step of ASTRO-FOLD approach involves the prediction of the tertiary structure of the full protein sequence. ASTRO-FOLD combines a deterministically based αBB global optimization algorithm, conformational space annealing (a stochastic global optimization), molecular dynamics in torsion-angle space, and rotamer optimization to solve a non-convex constrained problem. The information predicted from the first two states are used as the input to the final stage. The use of the deterministic global optimization algorithm, αBB, guarantees convergence to the global minimum solution by a convergence of upper and lower bounds on the potential energy minimum (Adjiman et al., 1996, 1997, 1998a,b; An-droulakis et al., 1995; Floudas, 2000; Floudas and Pardalos, 1995). This method converges to the global minima by developing a converging sequences of upper and lower bounds. Upper bounds are obtained by the local minimization of the original non-convex problem. Whereas, a convex lower bounding function is obtained by augmenting the objective and constraint function with a quadratic term. With these bounding functions, the problem is iteratively solved using the branch and bound technique where a region is fathomed if the lower bound rises above the best upper bound.
Applying torsion angle dynamics (TAD) as an initialization step and a stochastic global optimization method such as conformation space annealing (CSA)(Lee et al., 1997, 1998, 2000; Lee and Scheraga, 1999; Ripoll et al., 1998) leads into the quick determination of low energy conformations. ASTRO-FOLD is such a hybrid approach, and by using this hybrid method, the search for the native state becomes much efficient, while still retaining the deterministic guarantees of convergence (Klepeis and Floudas, 2002b, 2003c,b; Klepeis et al., 2003a,b).
The latest improvement of ASTRO-FOLD focus on efficient local minimization strategy. This strategy combines torsional angle dynamics and rotamer optimization for identifying and improving the quality of the conformations. It ensures that the steric clashes between protein side chains are removed thus providing a better starting point (McAllister and Floudas, 2009b).
4.2 Evaluation of Protein Tertiary Structure Prediction
A variety of metrics exist to evaluate the quality of predicted protein tertiary structures. The most commonly used metric to estimate the similarity between two protein structures is the root mean square deviation (RMSD) between two sets of atoms that represent the protein structure. The RMSD between two protein structures can be calculated using all atoms, all heavy atoms or Cα atoms of the protein. For this study, RMSD based only on the Cα atoms of the protein was used. The RMSD is a widely used metric to evaluate the quality of a protein structure. However, a high RMSD value can be obtained because of incorrect prediction of a small number of atoms, possibly in the loop or coil region of the protein. For such cases, where only a small number of atoms are not aligned, the RMSD is not an effective descriptor of the quality of the conformer.
Another measure, GDT(Global Distance Test), calculates the similarity between two structures by iteratively maximizing the number of Cα atoms (not necessarily continuous) that are within a specified distance d (Zemla et al., 1999; Zemla, 2003). The template modeling (TM) score is another metric to evaluate the quality of a protein tertiary structure (Zhang and Skolnick, 2004). This scoring method removes the need to have distance dependent cutoff values (as in GDT TS score) and protein length dependence. For this analysis, RMSD, GDT TS score, TM-score will be used to evaluate the quality of protein structures.
4.3 Results and Discussion of Protein Tertiary Structure Prediction
The effectiveness and usefulness of the residue contact prediction method is tested using 10 proteins including some ”blind” targets (T473 and T499) from recently concluded CASP8 experiments. The testing results are reported in Table 7 where Columns 3–6 correspond to the quality of ensemble of protein structures generated using residue contacts. Similarly, Columns 7–10 correspond to structures generated without using any residue contacts. It can be seen from this table that the quality of the best structure (in terms of RMSD, TM-score, GDT score) is much better when residue contacts are used in ASTRO-FOLD. On an average, the RMSD of the best structure is 1.65 Å less when residue contacts are used during structure prediction. Similarly, the average TM and GDT score improvement is 7% and 8% respectively. In order to simplify the description, the WITHSET is used to represent the structures generated by using the predicted contacts and the WITHOUTSET is used to represent the structures generated by without using the predicted contacts in the article.
Table 7.
Comparison of predicted tertiary structures 1) using predicted residue contacts and 2) without using predicted contacts. Column 4 and 8 show the best RMSDs of the clustering results and the numbers in parentheses denote the ranking of the corresponding picked structures.
| With Predicted Contacts | Without Predicted Contacts | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Protein | size | best RMSD | best RMSD of clustering | best TM | best GDT | best RMSD | best RMSD of clustering | best TM | best GDT |
| 1J75 | 57 | 2.98 | 4.10 (5.8%) | 0.57 | 0.67 | 5.06 | 6.41 (8.3%) | 0.52 | 0.61 |
| 1CTJ | 89 | 5.26 | 9.08 (13.0%) | 0.44 | 0.45 | 7.99 | 9.24 (2.1%) | 0.40 | 0.40 |
| 1ELR | 128 | 4.59 | 7.27 (2.6%) | 0.57 | 0.49 | 8.63 | 13.62 (18.7%) | 0.41 | 0.36 |
| 1R69 | 69 | 3.74 | 4.87 (1.6%) | 0.49 | 0.56 | 4.58 | 6.41 (4.3%) | 0.44 | 0.54 |
| 1AUU | 55 | 4.31 | 6.15 (6.1%) | 0.48 | 0.59 | 6.93 | 8.20 (2.3%) | 0.31 | 0.38 |
| T499 | 58 | 5.20 | 6.06 (4.4%) | 0.39 | 0.54 | 6.58 | 7.25 (0.5%) | 0.38 | 0.46 |
| T473 | 68 | 5.01 | 6.91 (6.3%) | 0.42 | 0.54 | 5.90 | 7.78 (2.3%) | 0.40 | 0.47 |
| 1C75 | 71 | 5.11 | 6.16 (0.5%) | 0.41 | 0.47 | 5.91 | 7.41 (7.7%) | 0.39 | 0.44 |
| 1HCR | 52 | 4.05 | 6.02(4.8%) | 0.62 | 0.70 | 4.83 | 6.52(13.1%) | 0.49 | 0.59 |
| 1ROP | 56 | 0.99 | 1.42(0.3%) | 0.90 | 0.96 | 1.34 | 1.61(0.3%) | 0.85 | 0.93 |
ASTRO-FOLD identifies the near-native structures by using a travelling-salesman-problem based clustering approach, ICON(Subramani et al., 2009). The predicted 3D structures from both the WITH-SET and the WITHOUTSET are subject to this clustering method. The top five structures which are closest to the top five cluster centroids are selected. The corresponding best RMSD structures of the top five structures are presented in Columns 4 and 8 of Table 7. Overall the ICON clustering method selects better structures in terms of RMSD values for the WITHSET protein structures than the WITH-OUTSET structures, as indicated by the smaller RMSD values in Column 4 than the RMSD values in Column 8 of Table 7. This shows that the predicted residue contacts improve the protein tertiary structure prediction in ASTRO-FOLD. In the parentheses of the Columns 4 and 8 shows the RMSD rankings of the best structures from the clustering method. The ranking is calculated as the relative position of the RMSD value of the selected structure among the corresponding structure ensemble. 1% indicates that the selected structure has a RMSD within top 1% of all the structures, thus the smaller the ranking value, the better the clustering method does. In most cases, the clustering method is able to pick a top 5% structure. On average, a 4.54% ranking is obtained for the WITHSET structures, and an average ranking of 5.96% is obtained for the WITHOUTSET structures. The better ranking for the WITHSET structures indicates that the structures generated are more concentrated.
The distributions of the RMSD values, TM and GDT scores of the predicted 3D structures show how good the conformational sampling is in the protein tertiary structure prediction framework. By comparing the distributions of RMSD, TM and GDT values between the WITHSET structures and the WITHOUTSET structures, the effect of the residue contact prediction on the protein tertiary structure predictions can be easily shown. The distributions are shown in Table 10 of the supplementary materials. In this table, Columns 2–4 show the RMSD, TM and GDT distributions for the WITHSET structures, and Columns 5–7 show the corresponding distributions for the WITHOUTSET structures. The best RMSD structures, TM structures and GDT structures for the WITHSET are consistently better than those of the WITHOUTSET. Even the worst structures in terms of RMSD, GDT and TM scores of the WITHSET structures are better than those of the WITHOUTSET, indicating the improvement in the structure quality by using the predicted residue contacts. For example, the best RMSD structures of the WITHSET are on average 1.65 Å better than the WITHOUTSET.
The improvement in the structure quality can also be seen from the comparison between the numbers of meaningful structures generated in the WITHSET and the WITHOUTSET. Table 11 of the supplementary materials shows this comparison. A structure in this article is considered as meaningful if its RMSD value is less than 6 Å, or if its TM score is greater than 0.4, or if its GDT score is greater than 0.4. As shown in Table 11 of the supplementary materials, the WITHSET structures have more meaningful structures than the WITHOUSET for most of the proteins.
The best prediction over all the proteins is obtained for protein 1ROP. It is a 56 amino acid protein with a simple 2 helical bundle topology. For this topology, ASTRO-FOLD is able to determine a structure within 1 Å using predicted residue contacts. And the clustering method selects a 1.42 Å structure with a ranking of 0.3%. For all other proteins, the best predicted structures have RMSD values ranging from 2.98 Å to 5.26 Å. In the sequel, a mixed α/β protein 1J75 is taken as an example to analyze the tertiary structure predictions and the effect of residue contact prediction on tertiary structure prediction.
Protein 1J75 is the ZαDLM domain of protein DLM-1 that binds to left-handed Z-DNA (one of the various possible double helical structures of DNA). It is a 57 residue protein with an α/β architecture. There are three α-helices [H1: 2–13, H2: 19–26, H3: 30–42] and three β-strands [B1: 17–18, B2: 46–50, B3: 53–56] in this protein. In the native structure of protein 1J75, the three helices are packed against three anti-parallel β-strands. Helix 1 is connected to Helix 2 by β1. β1,β3 and β2,β3 contact each other to make a 3 strand anti-parallel β-sheet. The overall sequence of secondary structures for protein 1J75 is α1β1α2α3β2β3. The residue contact prediction model correctly predicted an anti-parallel sheet formed by contacts between β1,β3 and β2,β3. The model also correctly identified contacts between Helix 1–2 and Helix 2–3. The prediction accuracy on this protein is 0.885 with 23 correct and 3 incorrect predictions.
A comparison of the quality of tertiary structures between the WITHSET and the WITHOUTSET is shown in Table 8. It can be seen from this table that the use of predicted residue contacts increases the quality of predicted tertiary structures, as well as the quality of the structure ensemble. The RMSD of the best structure in the WITHOUTSET is 5.06 Å. Whereas, the RMSD of the best structure of the WITHSET is only 2.98 Å. In terms of the quality of the ensemble, the WITHSET has 14262 structures with RMSD < 6 Å, whereas the WITHOUTSET has only 383 structures with RMSD < 6 Å. The predicted structures of the WITHSET also have a higher TM-score and a higher GDT_TS score compared to structures from the WITHOUTSET. Protein structures with TM-score of 0.4 and above are considered meaningful predictions (Zhang and Skolnick, 2004). There are 5999 structures in the WITHSET with a TM-score more than 0.4 whereas, there are only 18 such structures in the WITHOUTSET. Similarly, there are 25361 structures in the WITHSET with a GDT_TS score more than 0.4 whereas, there are only 13742 structure in the WITHOUTSET with a GDT_TS score more than 0.4.
Table 8.
A comparison of predicted tertiary structures of protein 1J75 generated 1) using predicted residue contacts and 2) without using predicted contacts.
| Evaluation Metric | With Contacts | Without Contacts |
|---|---|---|
| RMSD Range of Conformers | 2.98–12.15 | 5.06–22.56 |
| Best RMSD (Å) | 2.98 | 5.06 |
| Best TM-score | 0.573 | 0.522 |
| Best GDT_TS score | 0.667 | 0.605 |
| Conformers with RMSD <6.0Å | 14262 | 383 |
| Conformers with TM-score > 0.4 | 5999 | 18 |
| Conformers with GDT_TS score > 0.4 | 25361 | 13742 |
Figure 8 shows the native structure of protein 1J75 along with the lowest RMSD structures from the WITHSET and the WITHOUTSET. The top part of Figure 8 shows the native structure (gray) along with the lowest RMSD structure (color) from the WITHOUTSET. The overall topology of the predicted structure is close to the native structure of the protein. However, β2 of the predicted structure is not aligned with the corresponding strand of the native structure. Similarly, helix 2 is also not well aligned with the native structure.
Figure 8.
Best RMSD predicted structure of protein 1J75(color) versus native 1J75(gray). The structure on the top is generated without using any residue contacts. The structure on the bottom is generated using predicted residue contacts.
The bottom part of Figure 8 shows the native structure (gray) along with the lowest RMSD structure (color) from the WITHSET. β2 of the best structure of the WITHSET has almost a perfect alignment with the corresponding strand of the native structure. Similarly, helix 2 is also in structural agreement with the native structure. The presence of distance bounds for pairs of residues between β2 and β3 requires the ASTRO-FOLD approach to produce structures with contacts between β2 and β3. Apart from minor shifts in the α-helical and loop regions, the best structure of the WITHSET aligns very well with the native structure of protein 1J75. From these comparisons it is clear that the quality of protein structures and the quality of the ensemble improved when the predicted residue contacts are used in protein structure prediction.
5 Conclusions
An optimization based residue contact prediction method has been presented. It is an integer linear programming based method that can be used to predict residue contacts for β, α + β, and α/β proteins. The contact prediction problem is solved by optimizing an objective function which is a combination of energetic contribution corresponding to every residue pair contact and a hydrophobic contribution for contacts between β-strand residues. The optimal solution is obtained while satisfying a set of constraints. These constraints are included in the model to produce physically realistic contacts. A new hydrophobicity based method has been presented to find optimal alignments of β-strands in β-sheets. The alignments are used to allow/disallow contacts between certain residues from a pairs of β-strands. Integer cut constraints have been included in the model to produce a rank-ordered list of most optimal contacts. This formulation also offers the flexibility of incorporating additional constraints where a user can add unique and problem specific constraints to the model. The presented method was tested on three different test sets consisting of β, α + β, and α/β proteins and produced an average accuracy of 0.607 for single domain proteins.
This proposed residue prediction model has been incorporated into our ab initio protein tertiary structure prediction algorithm, ASTRO-FOLD. The usefulness of the residue contact prediction model was further illustrated by comparing the quality of two ensembles of protein structures that were generated with and without using the predicted contacts for a test set of 10 proteins. The ICON clustering method is applied to these two ensembles of structures as in a blind prediction and the average clustering rankings of 4.54% and 5.96% were obtained for the clustering process. The quality of the ensemble, as well as the quality of individual protein structures was better when predicted residue contacts were used as distance bounds during the structure prediction. These results along with the test results on 20 CASP8 proteins are very encouraging and suggested that these predicted contacts can be used as explicit restraints in protein structure prediction methods to produce better quality structures.
Supplementary Material
Acknowledgments
CAF gratefully acknowledges financial support from National Science Foundation, National Institutes of Health (R01 GM52032; R24 GM069736) and U.S. Environmental Protection Agency, EPA (GAD R 832721-010). Although the research described in the article has been funded in part by the U.S. Environmental Protection Agency’s STAR program through grant (R 832721-010), it has not been subjected to any EPA review and does not necessarily reflect the views of the Agency, and no official endorsement should be inferred.
References
- Adjiman CS, Androulakis IP, Floudas CA. Global Optimization of MINLP Problems in Process Synthesis and Design. Computers and Chemical Engineering. 1997;21:S445–S450. [Google Scholar]
- Adjiman CS, Androulakis IP, Floudas CA. A Global Optimization Method for General Twice-differentiable NLPs - II. Implementation and Computational Results. Computers and Chemical Engineering. 1998a;22:1159–1179. [Google Scholar]
- Adjiman CS, Androulakis IP, Maranas CD, Floudas CA. A Global Optimization Method, αBB, for Process Design. Computers and Chemical Engineering. 1996;20:S419–S424. [Google Scholar]
- Adjiman CS, Dallwig S, Floudas CA, Neumaier A. A Global Optimization Method for General Twice-differentiable NLPs - I. Theoretical Advances. Computers and Chemical Engineering. 1998b;22:1137–1158. [Google Scholar]
- Androulakis IP, Maranas CD, Floudas CA. αBB: A Global Optimization Method for General Constrained Nonconvex Problems. Journal of Global Optimization. 1995;7:337–363. [Google Scholar]
- Bonneau R, Ruczinski I, Tsai J, Baker D. Contact Order and ab-initio Protein Structure Prediction. Protein Science. 2002;11:1937–1944. doi: 10.1110/ps.3790102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J, Baldi P. Improved Residue Contact Prediction Using Support Vector Machines and a Large Feature Set. BMC Bioinformatics. 2007;8:113–121. doi: 10.1186/1471-2105-8-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornette JL, Cease KB, Margalit H, Spouge JL, Berzofsky JA, DeList C. Hydrophobicity Scales and Computational Techniques for Detecting Amphipathic Structures in Proteins. Journal of Molecular Biology. 1987;195:659–685. doi: 10.1016/0022-2836(87)90189-6. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Casadio R. A Neural Network Based Predictor of Residue Contacts in Proteins. Protein Engineering. 1999;12:15–21. doi: 10.1093/protein/12.1.15. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Olmea O, Valencia A, Casadio R. Prediction of Contact Maps with Neural Networks and Correlated Mutations. Protein Engineering. 2001a;13:835–843. doi: 10.1093/protein/14.11.835. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Olmea O, Valencia A, Casadio R. Progress in Predicting Inter-Residue Contacts of Proteins With Neural Networks and Correlated Mutations. Proteins: Structure, Function, and Bioinformatics. 2001b;5:157–162. doi: 10.1002/prot.1173. [DOI] [PubMed] [Google Scholar]
- Floudas CA. Computational Methods in Protein Structure Prediction. Biotechnology and Bioengineering. 2007;97(2):207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- Floudas CA, Fung HK, McAllister SR, Mönnigmann M, Rajgaria R. Advances In Protein Structure Prediction and De Novo Protein Design: A Review. Chemical Engineering Science. 2006;61:966–988. [Google Scholar]
- Floudas CA. Nonconvex Optimization and its Applications. Kluwer Academic Publishers; 2000. Deterministic Global Optimization: Theory, Methods and Applications. [Google Scholar]
- Floudas CA, Pardalos PM. State of the Art in Global Optimization: Computational Methods and Applications - preface. Journal of Global Optimization. 1995;7:113. [Google Scholar]
- Frenkel-Morgenstern M, Magid R, Eyal E, Pietrokovski S. Refining Intra-Protein Contact by Graph Analysis. BMC Bioinformatics. 2007;8:S56–S60. doi: 10.1186/1471-2105-8-S5-S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göbel U, Sander C, Schneider R, Valencia A. Correlated Mutations and Residue Contacts in Proteins. Proteins: Structure, Function, and Bioinformatics. 1994;18:309–317. doi: 10.1002/prot.340180402. [DOI] [PubMed] [Google Scholar]
- Grãna O, Baker D, MacCallum R, Meiler J, Punta M, Rost B, Tress M, Valencia A. CASP6: Assessment of Contact Predictions. Proteins: Structure, Function, and Bioinformatics. 2005;61:214–224. doi: 10.1002/prot.20739. [DOI] [PubMed] [Google Scholar]
- Grãna O, Gonzalez-Izarzugaza T, Tress M. CASP8 Contact Prediction; CASP8 Meeting; 2008. [Google Scholar]
- Hamilton N, Burrage K, Ragan MA, Huber T. Protein Contact Prediction Using Patterns of Correlation. Proteins: Structure, Function, and Bioinformatics. 2004;56:679–684. doi: 10.1002/prot.20160. [DOI] [PubMed] [Google Scholar]
- Horner DS, Pirovano W, Pesole G. Correlated Substitution Analysis and the Prediction of Amino Acid Structural Contacts. Briefings in Bioinformatics. 2008;9:46–56. doi: 10.1093/bib/bbm052. [DOI] [PubMed] [Google Scholar]
- ILOG. CPLEX User’s Manual 9.0. 2003. [Google Scholar]
- Izarzugaza JMG, Grana O, Trees ML, Valencia A, Clarke ND. Assessment of Intramolecular Contact Predictions for CASP7. Proteins: Structure, Function, and Bioinformatics. 2007;18:152–158. doi: 10.1002/prot.21637. [DOI] [PubMed] [Google Scholar]
- Jones DT. Protein Secondary Structure Prediction Based on Position-Specific Scoring Matrices. Journal of Molecular Biology. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Floudas CA. Free Energy Calculations for Peptides via Deterministic Global Optimization. Journal of Chemical Physics. 1999;110:7491–7512. [Google Scholar]
- Klepeis JL, Floudas CA. Ab initio Prediction of Helical Segments in Polypeptides. Journal of Computational Chemistry. 2002a;23:245–266. doi: 10.1002/jcc.10002. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Floudas CA. ASTRO-FOLD: Ab Initio Secondary and Tertiary Structure Prediction in Protein Folding. European Symposium on Computer Aided Process Engineering-12; 2002b. [Google Scholar]
- Klepeis JL, Floudas CA. Prediction of beta-sheet Topology and Disulfide Bridges in Polypeptides. Journal of Computational Chemistry. 2003a;24:191–208. doi: 10.1002/jcc.10167. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Floudas CA. ASTRO-FOLD: A Combinatorial and Global Optimization Framework for Ab Initio Prediction of Three-Dimensional Structures of Proteins from the Amino Acid Sequence. Biophysical Journal. 2003b;85:2119–2146. doi: 10.1016/s0006-3495(03)74640-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klepeis JL, Floudas CA. Ab Initio Tertiary Structure Prediction of Proteins. Journal of Global Optimization. 2003c;25:113–140. [Google Scholar]
- Klepeis JL, Floudas CA, Morikis D, Lambris JD. Predicting Peptide Structures Using NMR Data and Deterministic Global Optimization. Journal of Computational Chemistry. 1999;20:1354–1370. [Google Scholar]
- Klepeis JL, Wei Y, Hecht MH, Floudas CA. Ab Initio Prediction of the 3-Dimensional Structure of a De Novo Designed Protein: A Double Blind Case Study. Proteins: Structure, Function, and Bioinformatics. 2005;58:560–570. doi: 10.1002/prot.20338. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Pieja MT, Flouda CA. A New Class of Hybrid Global Optimization Algorithms for Peptide Structure Prediction: Integrated Hybrids. Computer Physics Communication. 2003a;151:121–140. [Google Scholar]
- Klepeis JL, Pieja MT, Flouda CA. A New Class of Hybrid Global Optimization Algorithms for Peptide Structure Predic tion: Alternating Hybrids and Application fo Met-Enkephalin and Melittin. Biophysical Journal. 2003b;84:869–882. doi: 10.1016/S0006-3495(03)74905-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundrotas P, Alexov EG. Predicting Residue Contacts Using Pragmatic Correlated Mutations Method: Reducing the False Positives. Bioinformatics. 2006;7:503–512. doi: 10.1186/1471-2105-7-503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Pillardy J, Czaplewski C, Arnautova Y, Ripoll DR, Liwo A, Gibson KD, Wawak RJ, Scheraga HA. Efficient Parallel Algorithms in Global Optimization of Potential Energy Functions for Peptides, Proteins and Crystals. Computer Physics Communication. 2000;128:399–411. [Google Scholar]
- Lee J, Scheraga HA. Conformational Space Annealing by Parallel Computations: Extensive Conformational Search of Met-enkephalin and the 20-Residue Membrane-Bound Portion of Melittin. International Journal of Quantum Chemistry. 1999;75:255–265. [Google Scholar]
- Lee J, Scheraga HA, Rackovsky S. New Optimization Method for Conformational Energy Calculations on Polypeptides: Conformational Space Annealing. Journal of Computational Chemistry. 1997;18:1222–1232. [Google Scholar]
- Lee J, Scheraga HA, Rackovsky S. Conformational Analysis of the 20-Residue Membrane-Bound Portion of Melittin by Conformational Space Annealing. Biopolymers. 1998;46:103–115. doi: 10.1002/(SICI)1097-0282(199808)46:2<103::AID-BIP5>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- Lifson S, Sander C. Antiparallel and Parallel β-strands Differ in Amino Acid Residue Preferences. Nature. 1979;282:109–111. doi: 10.1038/282109a0. [DOI] [PubMed] [Google Scholar]
- Lifson S, Sander C. Specific Recognition in the Tertiary Structure of beta-Sheets of Proteins. Journal of Molecular Biology. 1980;139:627–639. doi: 10.1016/0022-2836(80)90052-2. [DOI] [PubMed] [Google Scholar]
- Lund O, Frimand K, Gorodkin J, Bohr H, Bohr J, Hansen J, Brunak S. Protein Distance Constraints Predicted by Neural Networks and Probability Density Functions. Protein Engineering. 1997;10:1241–1248. doi: 10.1093/protein/10.11.1241. [DOI] [PubMed] [Google Scholar]
- Marti-Renom MA, Stuart A, Fiser A, Snchez R, Melo F, Sali A. Comparative Protein Structure Modeling of Genes and Genomes. Annu Rev Biophys Biomol Struct. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
- McAllister SR, Floudas CA. Alpha Helical Topology and Tertiary Structure Prediction in Globular Proteins. Proceedings of 46th IEEE Conference on Decision and Control. 2007;46:4551–4556. [Google Scholar]
- McAllister SR, Floudas CA. Enhancing Bounding Techniques to Reduce the Protein Conformational Search Space. Optim Method Softw. 2009;24(4,5):837–855. doi: 10.1080/10556780902753486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAllister SR, Floudas CA. An Improved Hybrid Global Optimization Method for Protein Tertiary Structure Prediction. Computational Optimization and Applications. 2009b doi: 10.1007/s10589-009-9277-y. Appeared online, 21 July 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAllister SR, Mickus BE, Klepeis JL, Floudas CA. A Novel Approach for Alpha-Helical Topology Prediction in Globular Proteins: Generation of Interhelical Restraints. Proteins: Structure, Function, and Bioinformatics. 2006;65:930–952. doi: 10.1002/prot.21095. [DOI] [PubMed] [Google Scholar]
- Monnigmann M, Floudas CA. Protein Loop Structure Prediction with Flexible Stem Geometries. Proteins: Structure, Function, and Bioinformatics. 2005;61:748–762. doi: 10.1002/prot.20669. [DOI] [PubMed] [Google Scholar]
- Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: A Structural Classification of Proteins Database for the Investigation of Sequences and Structures. Journal of Molecular Biology. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- Némethy G, Gibson KD, Palmer KA, Yoon CN, Paterlini G, Zagari A, Rumsey S, Scheraga HA. Energy Parameters in Polypeptides. 10. Improved Geometrical Parameters and Nonbonded Interactions for Use in the ECEPP/3 Algorithm, with Application to Proline-Containing Peptides. Journal of Physical Chemistry. 1992;96:6472–6484. [Google Scholar]
- Olmea O, Rost B, Valencia A. Effective Use of Sequence Correlation and Conservation in Fold Recognition. Journal of Molecular Biology. 1999;295:1221–1239. doi: 10.1006/jmbi.1999.3208. [DOI] [PubMed] [Google Scholar]
- Olmea O, Valencia A. Improving Contact Prediction by the Combination of Correlated Mutations And Other Sources of Sequence Information. Folding and Design. 1997;2:S25–S32. doi: 10.1016/s1359-0278(97)00060-6. [DOI] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Nativelike Topology Assembly of Small Proteins Using Predicted Restraints in Monte Carlo Folding Simulations. Proceedings of the National Academy of Sciences of the United States of America. 1998a;95:1020–1025. doi: 10.1073/pnas.95.3.1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Fold Assembly of Small Proteins Using Monte Carlo Simulations Driven by Restraints Derived from Multiple Sequence Alighments. Journal of Molecular Biology. 1998b;277:419–448. doi: 10.1006/jmbi.1997.1595. [DOI] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Tertiary Structure Prediction of the KIX Domain of CBP Using Monte Carlo Simulations Driven by Restraints Derived from Multiple Sequence Alignments. Proteins: Structure, Function, and Bioinformatics. 1998c;30:287–294. doi: 10.1002/(sici)1097-0134(19980215)30:3<287::aid-prot8>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Pollastri G, Baldi P. Prediction of Contact Maps By Recurrent Neural Network Architecture and Hidden Context Propagation From All Cardinal Corners. Bioinformatics. 2002;18:S62–S70. doi: 10.1093/bioinformatics/18.suppl_1.s62. [DOI] [PubMed] [Google Scholar]
- Punta M, Rost B. PROFcon: Novel Prediction of Long-range Contacts. Bioinformatics. 2005;21:2960–2968. doi: 10.1093/bioinformatics/bti454. [DOI] [PubMed] [Google Scholar]
- Rajgaria R, McAllister SR, Floudas CA. A Novel High Resolution Cα-Cα Distance Dependent Force Field Based on a High Quality Decoy Set. Proteins: Structure, Function, and Bioinformatics. 2006;65:726–741. doi: 10.1002/prot.21149. [DOI] [PubMed] [Google Scholar]
- Rajgaria R, McAllister SR, Floudas CA. Towards Accurate Residue-Residue Hydrophobic Contact Prediction for Alpha Helical Proteins Via Integer Linear Optimization. Proteins: Structure, Function, and Bioinformatics. 2009;74:929–947. doi: 10.1002/prot.22202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripoll D, Liwo A, Scheraga HA. New Developments of the Electrostatically Driven Monte Carlo Method: Tests on the Membrane-Bound Portion of Melittin. Biopolymers. 1998;46:117–126. doi: 10.1002/(SICI)1097-0282(199808)46:2<117::AID-BIP6>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Rost B, Sander C, Schneider R. Redefining the Goals of Protein Secondary Structure Prediction. Journal of Molecular Biology. 1994;235:13–26. doi: 10.1016/s0022-2836(05)80007-5. [DOI] [PubMed] [Google Scholar]
- Sali A, Blundell TL. Comparative Protein Modelling by Satisfaction of Spatial Restraints. Journal of Molecular Biology. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- Shackelford G, Karplus K. Contact Prediction Using Mutual Information and Neural Nets. Proteins: Structure, Function, and Bioinformatics. 2007;69:159–164. doi: 10.1002/prot.21791. [DOI] [PubMed] [Google Scholar]
- Shao Y, Bystroff C. Predicting Interresidue Contacts Using Templates and Pathways. Proteins: Structure, Function, and Bioinformatics. 2003;53:497–502. doi: 10.1002/prot.10539. [DOI] [PubMed] [Google Scholar]
- Singer MS, Vriend G, Bywater RP. Prediction of Protein Residue Contacts with a PDB-derived Likelihood Matrix. Protein Engineering. 2002;15:721–725. doi: 10.1093/protein/15.9.721. [DOI] [PubMed] [Google Scholar]
- Subramani A, Floudas CA. HELIOS: A Novel Method for the Prediction of α-helical Regions of a Protein. 2009a. In Preparation. [Google Scholar]
- Subramani A, Floudas CA. BEST-PRED: A Naive Bayesian and First Order Markov Model for the Prediction of β-strand Regions of a Protein. 2009b. In Preparation. [Google Scholar]
- Subramani A, DiMaggio P, Jr, Floudas C. Selecting High Quality Protein Structures from Diverse Conformational Ensembles. Biophysical Journal. 2009;97(6):1728–1736. doi: 10.1016/j.bpj.2009.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor WR, Hatrick K. Compensating Changes in Protein Multiple Sequence Alignments. Protein Engineering. 1994;7:341–348. doi: 10.1093/protein/7.3.341. [DOI] [PubMed] [Google Scholar]
- Vassura ML, Margara L, Di Lena P, Medri F, Fariselli P, Casadio R. Reconstruction of 3D Structures from Protein Contact Maps. IEEE-ACM Transactions on Computational Biology and Bioinformatics. 2003;5(3):357–367. doi: 10.1109/TCBB.2008.27. [DOI] [PubMed] [Google Scholar]
- Vendruscolo M. Protein Folding Using Inter-Residue Contacts. First International Symposium on 3D Data Processing Visualization and Transmission. 2002;3dpvt:724–728. [Google Scholar]
- Vicatos S, Kaznessis YN. Separating True Positive Predicted Residue Contacts from False Positive Ones in Mainly α Proteins, Using Constrained Metropolis MC Simulations. Proteins: Structure, Function, and Bioinformatics. 2008;70:539–552. doi: 10.1002/prot.21553. [DOI] [PubMed] [Google Scholar]
- Vicatos S, Reddy BVB, Kaznessis Y. Prediction of Distant Residue Contacts With the Use of Evolutionary Information. Proteins: Structure, Function, and Bioinformatics. 2005;58:935–949. doi: 10.1002/prot.20370. [DOI] [PubMed] [Google Scholar]
- Vullo A, Walsh I, Pollastri G. A Two-stage Approach for Improved Prediction of Residue Contact Maps. Bioinformatics. 2006;7:180–192. doi: 10.1186/1471-2105-7-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wako H, Scheraga HA. On the Use of Distance Constraints to Fold a Protein. Macromolecules. 1981;14:961–969. [Google Scholar]
- Wu S, Zhang Y. A Comprehensive Assessment of Sequence-based and Template-based Methods for Protein Contact Prediction. Bioinformatics. 2008;24:924–931. doi: 10.1093/bioinformatics/btn069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemla A. LGA: A Method for Finding 3D Similarities in Protein Structures. Nucleic Acids Research. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemla A, Venclovas Č, Moult J, Fidelis K. Processing and Analysis of CASP3 Protein Structure Predictions. Proteins: Structure, Function, and Bioinformatics. 1999;S3:22–29. doi: 10.1002/(sici)1097-0134(1999)37:3+<22::aid-prot5>3.3.co;2-n. [DOI] [PubMed] [Google Scholar]
- Zhang GZ, Huang DS. Prediction of Inter-Residue Contacts Map Based on Genetic Algorithm Optimized Radial Basis Function Neural Network and Binary Input Encoding Scheme. Journal of Computer-Aided Molecular Design. 2004;18:797–810. doi: 10.1007/s10822-005-0578-7. [DOI] [PubMed] [Google Scholar]
- Zhang Y. Progress and Challenges in Protein Structure Prediction. Current Opinon in Structural Biology. 2008;18:342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. Scoring Function for Automated Assessment of Protein Structure Template Quality. Proteins: Structure, Function, and Bioinformatics. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Karypis G. Prediction of Contact Maps Using Support Vector Machines. Proc of the IEEE Symposium on Bioinformatics and Bioengineering; 2003. pp. 26–36. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.