Somatosensory Plasticity and Motor Learning

Abstract

Motor learning is dependent upon plasticity in motor areas of the brain, but does it occur in isolation, or does it also result in changes to sensory systems? We examined changes to somatosensory function that occur in conjunction with motor learning. We found that even after periods of training as brief as 10 min, sensed limb position was altered and the perceptual change persisted for 24 h. The perceptual change was reflected in subsequent movements; limb movements following learning deviated from the prelearning trajectory by an amount that was not different in magnitude and in the same direction as the perceptual shift. Crucially, the perceptual change was dependent upon motor learning. When the limb was displaced passively such that subjects experienced similar kinematics but without learning, no sensory change was observed. The findings indicate that motor learning affects not only motor areas of the brain but changes sensory function as well.

Introduction

Neuroplasticity is central to the development of human motor function and, likewise, to skill acquisition in the adult nervous system. Here we assess the possibility that human motor learning also alters somatosensory function. We show that after brief periods of movement training, there are not only changes to motor function but also persistent changes to the way we perceive the position of our limbs.

Work to date on motor learning has focused almost exclusively on plasticity in motor systems, that is, on how motor systems acquire new abilities, how learning occurs during motor development, and how learning is compromised by trauma and disease. The extent to which these changes in motor function affect the somatosensory system is largely unknown. An effect of motor learning on sensory systems is likely since activity in somatosensory cortex neurons varies systematically with movement (Soso and Fetz, 1980; Chapman and Ageranioti-Bélanger, 1991; Ageranioti-Bélanger and Chapman, 1992; Cohen et al., 1994; Prud'homme and Kalaska, 1994; Prud'homme et al., 1994) and also because of the presence of ipsilateral corticocortical pathways linking motor to somatosensory areas of the brain (Jones et al., 1978; Darian-Smith et al., 1993). It is also likely since sensory experience on its own results in structural change to somatosensory cortex (Jenkins et al., 1990; Recanzone et al., 1992a,b; Xerri et al., 1999). Indeed there are a number of pieces of evidence suggesting perceptual change related to movement and learning. These include proprioceptive changes following visuomotor adaptation in reaching movements and in manual tracking (van Beers et al., 2002; Simani et al., 2007; Malfait et al., 2008; Cressman and Henriques, 2009) and visual and proprioceptive changes following force-field learning (Brown et al., 2007; Haith et al., 2008).

Here we describe studies involving human arm movement that test the idea that sensory function is modified by motor learning. Specifically, we show that learning to correct for forces that are applied to the limb by a robot results in durable changes to the sensed position of the limb. We obtain estimates of sensed limb position before and after motor learning, using two different techniques. We find that following periods of training as brief as 10 min, the sensed limb position shifts reliably in the direction of the applied force. We obtain a similar pattern of perceptual change for both left–right movements and forward–back movements. The change is also similar following perceptual tests conducted in statics and during movement. The perceptual shifts that we observe are squarely grounded in motor learning. Subjects show no evidence of sensory change when the robot is programmed to passively move the hand through the same kinematic trajectories as subjects who actually experience motor learning. Moreover, we find that the perceptual shifts are reflected in subsequent movements. Following learning, movement trajectories deviate from their prelearning path by an amount similar in magnitude and in the same direction as the perceptual shift.

Materials and Methods

Subjects and tasks.

In total, 91 subjects were tested: 30 in experiment 1, 36 in experiment 2, and 25 in three different experiment 1 control studies. The subjects were all right handed and reported no history of sensorimotor disorder. All procedures were approved by the McGill University and The University of Western Ontario Research Ethics Boards.

Subjects performed reaching movements while holding the handle of a two degree-of-freedom planar robotic arm (InMotion2, Interactive Motion Technologies). Subjects were seated and arm movements occurred in a horizontal plane at shoulder height. An air sled supported the subject's arm against gravity, and a harness restrained the subject's trunk. Vision of the arm was blocked by a horizontal semisilvered mirror, which was placed just above the hand. During reaching movements, visual feedback was provided by a computer-generated display that projected target positions and a cursor representing hand position on the mirror. This resulted in a visual image that appeared in the same plane as the hand. Hand position during the experiment was measured using 16-digit optical encoders (Gurley Precision Instruments) located in the robot arm. A force-torque sensor (ATI Industrial Automation) mounted below the robot handle measured forces applied by the subject.

Experiment 1.

Subjects were tested on 2 separate days. The first day was used only to familiarize subjects with the experimental procedures, and the data were not included in our analyses. The first day of the experiment was divided into two parts. In the first part, subjects were trained to make straight reaching movements to a visual target in the absence of load. In the second phase, subjects' perception of limb position was estimated using an iterative algorithm known as parameter estimation by sequential testing (PEST) (Taylor and Creelman, 1967), which is described below.

The second day involved the experimental manipulation. It was divided into several parts in which tests of sensed limb position were interleaved with different phases of a standard dynamics-learning task (Fig. 1A). Day 2 began with an initial baseline estimate of sensed limb position. Subjects then made 150 movements during which the robot applied no force to the hand (null condition). Immediately following null-field training, a second baseline estimate of sensed limb position was obtained. Subjects then began the training phase, during which they made 150 movements in a velocity-dependent force field. An estimate of the sensed limb position was obtained immediately after force-field learning. Subjects then made 50 movements in a null field, to measure aftereffects and to wash out the kinematic effects of learning. After these aftereffect trials, a final estimate of the sensed limb position was obtained. The design thus yielded two baseline estimates of sensed limb position, one estimate immediately after force-field learning and one following aftereffect trials.

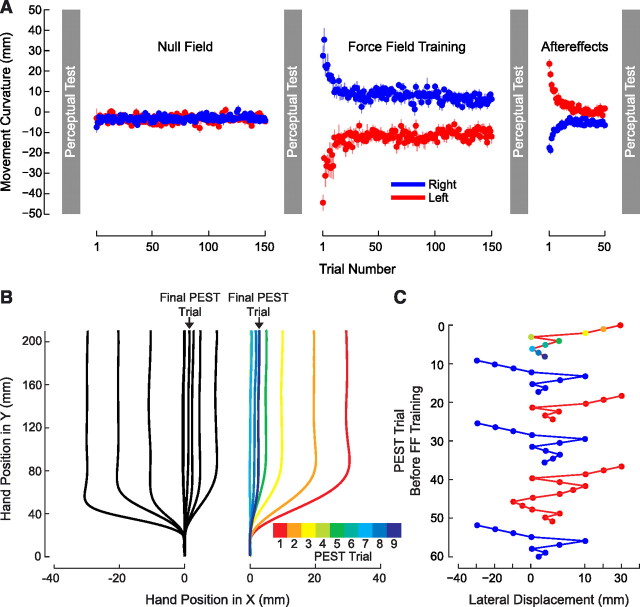
Figure 1.

Force-field learning and the perception of limb position. A, Subjects adapt to mechanical loads that displace the limb to the right or the left in proportion to hand velocity. Perceptual tests (gray) that estimate sensed limb position are interleaved with force-field training. Average movement curvature (±SE) is shown for null-field, force-field, and aftereffect phases of the experiment. B, The perceptual boundary between left and right is estimated using an iterative procedure known as PEST. The limb is displaced laterally by a computer-generated force channel, and subjects are required to indicate whether the limb has been deflected to the right. Examples are shown of individual PEST runs starting from left and right, respectively. The sequence beginning to the right is color coded to indicate the sequence of trials. C, A sequence of six PEST runs (starting from the top) with the lateral position of the hand shown on the horizontal axis and the PEST trial number on the vertical. The colored sequence of positions shown at the top is the same as that shown on the right side of B. PEST runs alternately start from the right and the left and result in similar estimates of the perceptual boundary. Note that the horizontal axis highlights lateral hand positions between 0 and 10 mm.

In the dynamics-learning task, subjects made reaching movements to a single visual target. Two white circles, 1.5 cm in diameter, marked the movement start and end points. The start point was situated in the center of the workspace, ∼25 cm from the subject's chest along the body midline. The target was located 20 cm in front of the start position in the sagittal plane. A yellow circle, 0.75 cm in diameter, provided the subject with feedback on the hand's current position. Subjects were instructed to make reaching movements in 1000 ± 50 ms. Subjects were also asked to move as straight as possible. Visual feedback of movement speed was provided at the end of each movement. The feedback was used to help subjects achieve the desired movement duration, but no trials were removed from analysis if subjects failed to comply with the speed requirement. At the end of each trial, the robot returned the subject's hand to the start position. An interval ranging from 500 to 1000 ms, chosen randomly, was included between trials.

In the force-field-learning phase, subjects were randomly divided in two groups. For one group, the robot applied a clockwise load to the hand that primarily acted to deflect the limb to the right. The second group was trained in a counterclockwise force field that deflected the limb primarily to the left. The force field was applied to the hand according to the following equation:

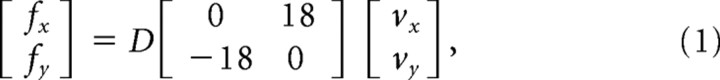where x and y are the lateral and sagittal directions, f_x and f_y are the commanded force to the robot in newtons, v_x and v_y are hand velocities in Cartesian coordinates in meters per second, and D defines the direction of the force field. For the clockwise force field, D was 1; for the counterclockwise condition, D was −1.

Estimates of sensed limb position were obtained in separate experimental blocks by asking subjects to reach to the same visual target as in the motor-learning phase of the experiment. When the subject's hand was 0.5 cm beyond the start point, all visual feedback (the target location and the yellow dot representing the subject's hand location) was removed. The robot applied a force channel throughout the movement that determined the lateral position of the hand. The parameters of the force channel were similar to those used in Scheidt et al. (2000). The equation for the force channel was f_x = 3000δ_x − 90v_x, where f_x is the force applied by the robot in newtons, δ_x is the difference in meters between the current lateral position of the hand and the center of the channel, and v_x is the lateral velocity of the hand in meters per second. Stiffness is in newtons per meter, and viscosity is in newton-seconds per meter. No force was applied in the y direction. The force channel was programmed to be straight for the initial 1.5 cm of the outward movement. At 1.5 cm, the force channel was programmed to shift laterally over 300 ms and remain at the new lateral position until the end of the movement. The change in the lateral position occurred according to a minimum jerk profile. Subjects were instructed not to oppose the lateral deflections and to continue the outward movement until a virtual soft wall at 20 cm indicated the end of movement. When subjects reached the haptic target, they were asked to maintain the position of the limb. At this point, subjects answered the question “Was your hand pushed to the right?” Subjects had been briefed previously that if they felt the hand had been deflected to the right they should respond yes, and otherwise they should respond no. Following a response, the limb was returned to the start location by the robot.

The PEST procedure (Taylor and Creelman, 1967) was used to manipulate the magnitude of the lateral deviation of the hand for purposes of estimating the perceptual boundary between left and right. PEST is an efficient algorithm for the estimation of psychophysical thresholds. Each PEST run begins with a suprathreshold displacement and, based on the subject's response, progressively decreases the displacement until a threshold displacement is reached. Based on a pilot study, we used 3 cm as an initial lateral deviation, which all subjects could correctly identify. On the next trial, the deviation was reduced by 1 cm, and this was repeated until the subject detected a change in the direction of lateral deviation. At this point, the step size was reduced by half, and the next displacement was in the opposite direction. The algorithm terminated whenever the upcoming step size fell below 1 mm.

Each block of perceptual tests had six PEST runs that yielded six separate estimates of the right–left boundary. Three of the six PEST runs started from the right (3 cm to the right as a first lateral displacement and −1 cm as the first step size), and three runs started from left (3 cm to the left and 1 cm as the first step size). Figure 1B shows two sets of PEST runs for one representative subject, one starting from left and the other starting from the right.

The data from all six PEST runs in each phase of the experiment were used to estimate the perceptual boundary between left and right. The entire set of measured lateral deviations and associated binary responses were fitted on a per-subject basis with a logistic function that gave the probability of responding “yes, the hand was deviated to the right” as a function of the lateral position of the hand. We used a least-squared error criterion (glmfit in Matlab) to obtain the fit. The 50% point of the fitted function was taken as the perceptual boundary and used for purposes of statistical analysis. Measures of the perceptual boundary, based on the lateral position of the hand in the final trial of each PEST sequence, gave results similar to those derived from the fitted psychometric functions.

We verified that the force channel produced the desired displacements by comparing the difference between the actual and commanded positions of the limb. We focused on the largest commanded displacement, the 3 cm deviation that occurs at the start of each PEST run. The absolute difference between actual and commanded displacements was 0.46, 0.42, 0.77, and 0.40 mm for the two sequences of PEST trials that occurred before learning and the sequences following force-field training and following aftereffect trials, respectively. These values are averaged over subjects, over PEST runs that began from the left and the right, and over force-field directions.

Experiment 2.

Subjects were tested in a 1-h-long session. Each subject completed tests of sensed limb position, using the method of constant stimuli, before and after force-field learning. In the dynamics-learning phase of the study, subjects were asked to make side-to-side movements between two 2 cm targets. The targets were placed on a lateral axis 25 cm in front of the body and centered on the subject's midline. The total movement distance was 20 cm. A small filled circle 0.8 cm in diameter indicated the position of the subject's hand during the movement. The start of each trial was indicated visually by the appearance of the target circle. Subjects were instructed to make straight movements between targets in 600 ± 100 ms. Visual feedback of movement speed was provided at the end of each trial. The feedback was not used to exclude any movements from analysis.

Subjects completed 400 movements in four experimental blocks. In the force-field-learning phase, subjects were assigned at random to one of two groups. One group trained with a load that pushed the hand outward during movement, away from the body. The other trained with a field that pushed the hand inward, toward the body. The force field was defined by the following equation:

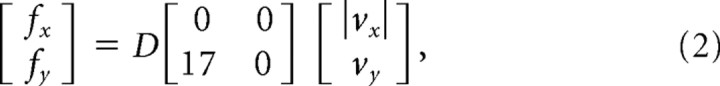where x and y are the lateral and sagittal directions, f_x and f_y are the commanded force to the robot in newtons, v_x and v_y are hand velocities in Cartesian coordinates in meters per second, and D defines the direction of the force field. For the outward force field, D was 1; for the inward condition, D was −1.

In perceptual tests, subjects were required to compare the felt position of their right hand with that of their left index finger. The subject's left index finger was fixed in position 0.5 cm to the left of the moving right hand. On each perceptual trial, the right hand was positioned by the robot at a location along the subject's midline in the sagittal plane. Subjects were instructed to indicate whether their right hand was closer or farther from their body relative to the left index finger. The hand was not moved directly between test locations, since information related to the sequence of hand positions might be used as a basis for their perceptual decision. Instead, for each successive hand position in the perceptual test, the robot moved the right hand first away and then back to the next test position in sequence. This distractor movement was used between all perceptual judgments. The movement away and back followed a bell-shaped velocity profile, and was randomized in terms of the distance traveled (14 ± 2 cm SD), duration (1000–1600 ms), and direction (away from or toward the body).

Perceptual judgments were collected for each subject before and after motor learning. Seven fixed locations on a sagittal axis were used for perceptual testing. The test points were all at the midpoint of the lateral movement axis and differed in their inward–outward position. Relative to the left index finger, which was held at 0.0 cm, the right hand was positioned at −3.0, −1.3, −0.7, 0.0, 0.7, 1.3, and 3.0 cm along the sagittal axis. Each position was tested multiple times, 6, 12, 12, 14, 12, 12, and 6, respectively. The locations farthest from the midpoint were tested less often because subjects performed at almost 100% at these locations. The ordering of test locations was randomized. The direction of the distractor movement between judgments (outward or inward) was pseudorandomly ordered such that each position was approached from each of the two directions an equal number of times. As in experiment 1, the actual positions of the right limb (as measured by the encoders of the robot) and subjects' binary verbal responses were fit with a logistic function (glmfit in Matlab) for each subject separately to produce psychometric curves. The position on the curve at which the subject responded “close” and “far” with equal probability determined the perceptual boundary.

Data analysis.

In experiment 1, hand position and the force applied to the robot handle were sampled at 400 Hz. In experiment 2, the sampling rate was 600 Hz. The recorded signals were low-pass filtered at 40 Hz using a zero phase lag Butterworth filter. Positional signals were numerically differentiated to produce the velocity estimates. The start and end of each trial was defined as the time that hand tangential velocity went above or fell below 5% of maximum velocity. The maximum perpendicular deviation of the hand (PD) from a straight line connecting movement start and end of movement was calculated on a trial-by-trial basis and served as a measure of motor learning.

To statistically quantify our data, our general approach was to use repeated-measures ANOVAs. When appropriate, the ANOVA included a between-subjects factor that specified the direction of the force field in which subjects were trained. ANOVAs were followed by Bonferroni-corrected post hoc tests. We applied this ANOVA approach to the following analyses. To quantify motor learning in both experiments 1 and 2, we analyzed the change in PD between the first 10 and the last 10 movements made in the force field. To quantify perceptual shifts in experiment 1, we analyzed the change in perceptual boundary between the second baseline measurement and those that were subsequently obtained. The perceptual shift in experiment 2 was quantified as the difference between the prelearning and postlearning perceptual boundaries, and was evaluated using a one-way ANOVA. A repeated-measures ANOVA was used to show differences in the extent to which subjects showed aftereffects in the passive control experiment. Changes in movement kinematics following learning were quantified as the difference in movement curvature between the final 10 movements in the aftereffect phase and the final 50 null-field movements before motor learning. A repeated-measures ANOVA was used to compare the magnitude of the shift in kinematics with the shift in perceptual boundary following learning and after washout. ANOVA was used to determine how force production changed over the course of the experiment, and differed depending on the force-field direction. Lateral forces applied to channel walls were measured over the first 100 ms of the first movement in each sequence of perceptual testing.

We also performed analyses to determine whether motor learning led to a change in perceptual acuity. For these analyses, we quantified acuity on a per-subject basis using the distance between the 25th and 75th percentiles of the fitted psychometric function. For both experiments 1 and 2, we used ANOVA to assess changes between prelearning and postlearning acuity for the different force-field directions.

Results

We used two different techniques in two different laboratories to assess sensory change associated with motor learning. In experiment 1, we assessed the sensed position of the limb in the absence of visual feedback by having subjects indicate whether the robot deflected straight ahead movements to the left or the right. Experiment 2 used an interlimb matching procedure also in the absence of visual feedback to obtain estimates of the sensed limb position. In both cases, sensed limb position was assessed before and after subjects learned to reach to targets in the presence of a force field that displaced the limb laterally in proportion to movement velocity. Experiment 1 involved outward movements along the body midline. Experiment 2 tested lateral movements. We varied the measurement technique and the movement direction to assess the generality of the observed perceptual changes.

Figure 1A shows the experimental sequence for the study in which we obtained estimates of sensed limb position during movement. We interleaved blocks of trials in which we estimated limb position (shown in gray) with blocks of trials in a standard force-field-learning procedure. We also assessed whether the perceptual change persisted after the effects of motor learning were eliminated using washout trials.

Estimates of limb position were obtained in the absence of visual feedback using an iterative procedure known as PEST (Taylor and Creelman, 1967), where on each movement the limb was displaced laterally using a force channel (Scheidt et al., 2000) (Fig. 1B). At the end of each movement, the subject gave a binary response that indicated whether the limb had been deflected to the left or the right. The magnitude of the deflection was adaptively modified based on the subject's response to estimate the sensed boundary between left and right (Taylor and Creelman, 1967). Figure 1B shows PEST runs for a representative subject before force-field learning. The left panel gives trials in which the testing sequence began with a deflection to the left. The right panel shows a sequence for the same subject that started from the right. Figure 1C shows a sequence of six PEST runs. Each run converges on a threshold for the perceived left–right boundary that remains stable across successive estimates.

In the motor-learning phase of the study, subjects were trained to make movements in a clockwise or a counterclockwise force field, whose main action was to push the hand to the right (blue) or the left (red) during movement. Performance over the course of learning was quantified by computing the maximum PD from a line joining movement start and end. Values for PD in each phase of the experiment are shown in Figure 1A, averaged over subjects. It can be seen that movements are straight under null conditions. They are deflected laterally with introduction of load and reach asymptotic levels at the end of training that approach null-field levels. A repeated-measures ANOVA found that the reduction in curvature was reliable for both directions of force (p < 0.001 in each case). Curvature in aftereffect trials is opposite to that observed early in learning and reflects the adjustments to motor commands needed to produce straight movements in the presence of load. Curvature at the end of the washout trials differs from that under null conditions; movements remain curved in a direction opposite to that of the applied force.

Perceptual performance was quantified for each subject separately by fitting a logistic function to the set of lateral limb positions and associated binary responses that were obtained over six successive PEST runs in each phase of the experiment. For example, the entire sequence in Figure 1C would lead to a single psychometric function relating limb position to the perceptual response. Figure 2A shows binned response probabilities, averaged across subjects, and, for visualization purposes, psychometric functions fit to the means for the rightward and leftward force fields. Separate curves are shown for estimates obtained before and after force-field learning. It can be seen that following learning, the psychometric function and hence the perceptual boundary between left and right shifts in a direction opposite to the applied load. Thus, if the force field acts to the right (Fig. 2A, right), the probability of responding right increases following learning. This means that the hand feels farther to the right than it did before learning.

Figure 2.

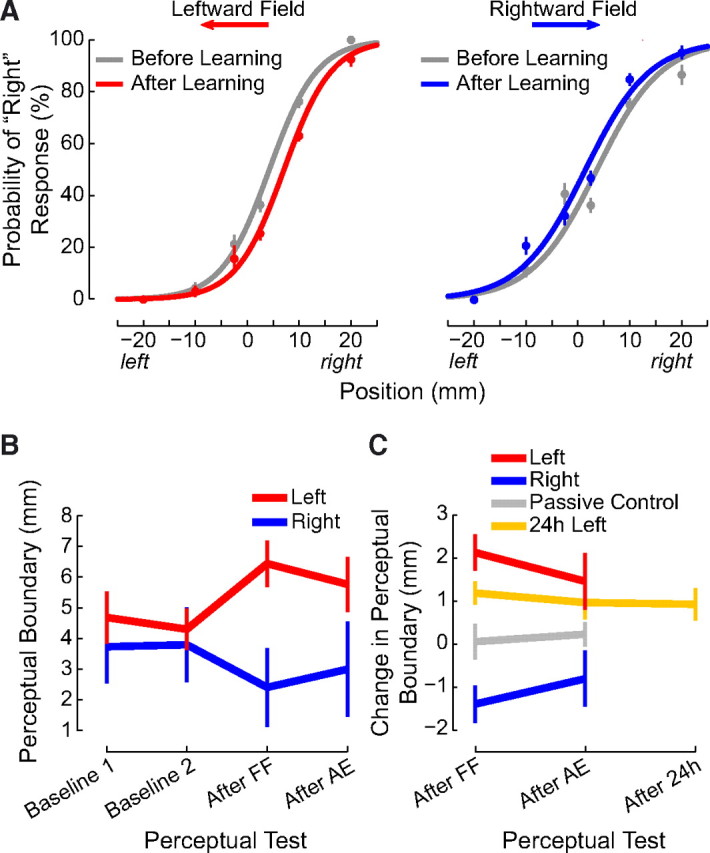
Following motor learning, the perceptual boundary shifts in a direction opposite to the applied force. A, Binned response probabilities averaged over subjects (±SE) before (gray) and after (red or blue) learning and fitted psychometric functions reflecting perceptual classification for each force-field direction. B, Mean estimates of the perceptual boundary between left and right (±SE) are shown for baseline estimates (Baseline 1 and Baseline 2) and for estimates obtained following force-field learning (After FF) and following aftereffect trials (After AE). The sensed position of the limb changes following learning, and the change persists following aftereffect trials. C, The perceptual shift depends on the direction of the force field (left vs right). The change in the perceptual boundary persists for at least 24 h (24 h Left). A perceptual shift is not observed when the robot passively moves the hand through the same sequence of positions and velocities as in the left condition such that subjects do not experience motor learning (Passive Control).

Figure 2B quantifies perceptual performance at various stages of learning. The dependent measure for these analyses is the 50% point on the psychometric function that was obtained by fitting the curve to the set of binary responses. This is the limb position associated with the perceived left–right boundary, that is, the position on the lateral axis at which the subject responds left and right with equal probability. Figure 2B shows mean values for this perceptual measure over the course of the experiment. Perceptual estimates are seen to be similar for the two prelearning measures (labeled baseline 1 and baseline 2). The sensed position of the limb shifts following force-field training, and the changes persist following aftereffect trials.

We evaluated changes in sensed limb position as a consequence of learning by computing the perceptual shift on a per-subject basis (Fig. 2C). We computed the shift in the perceptual boundary as a difference between the final null condition estimate and the estimate following training. We computed the persistence of the shift as the difference between the final null condition measure and the estimate following aftereffect trials. A repeated-measures ANOVA found that immediately after force-field learning, there was a shift in the sensed position of the limb that was reliably different from zero (p < 0.01). The shift decreased (F_(1,28) = 5.063, p < 0.05) following washout but remained different from zero (p < 0.05). The magnitude of the shift was the same in both directions (F_(1,28) = 0.947, p > 0.3). Thus force-field learning is associated with changes in the sensed position of the limb that persist even after washout trials.

To examine the persistence of the perceptual change, we tested 15 new subjects in a procedure that was identical to the main experiment with the addition of another perceptual test 24 h after motor learning. As in the previous analyses, we calculated the perceptual shift as the difference between the final baseline estimate and each of the estimates following training (Fig. 2C). A repeated-measures ANOVA found that the force field resulted in a reliable shift in the perceptual boundary that was similar for the three time points (F_(2,28) = 0.298, p > 0.7). Moreover, at each of the time points, the mean shift was reliably different from zero (p < 0.05 in each case). Thus, brief periods of force-field learning result in shifts in the perceptual boundary that persist for 24 h.

We quantified the magnitude of the perceptual change in relation to the extent of learning. For this analysis, we took measures of perceptual change from the data shown in Figure 2C. We obtained estimates of the magnitude of learning by measuring lateral deviation on aftereffect trials following training. We used both maximum PD and the average perpendicular distance for each movement as measures of learning. Averaged over subjects and force-field directions, we found that the perceptual shift was 33% as large as the extent of learning based on average PD for the first three aftereffect trials, and 11% as large as the extent of learning using maximum PD on these same trials.

In a control analysis, we assessed the possibility that the estimated perceptual shift might differ depending on whether testing began from the right or the left. For purposes of this analysis, we computed estimates of the perceptual shift separately for PEST runs that began from the left and the right using the final position of each PEST run in each condition. A repeated-measures ANOVA found that there were no differences in the perceptual shift for PEST runs beginning from the left or the right (F_(1,28) = 0.03, p > 0.85). None of the interactions between force-field direction, the phase of the experiment at which perceptual shifts were measured, and whether PEST runs began from the left or the right were significant (p > 0.2 or more in all cases).

Psychometric functions shown in Figure 2A can be characterized by two parameters. One parameter represents the sensitivity of the subject's response to the lateral position of the limb (slope), and the other parameter gives the position on the lateral axis at which the subject responds left and right with equal probability (left–right boundary). We tested whether learning resulted in differences in the slope of the psychometric function, using the distance between the 25th and 75th percentiles as a measure of perceptual acuity (or sensitivity). We assessed possible differences in sensitivity following force-field learning and following aftereffect trials in both leftward and rightward force fields using a repeated-measures ANOVA. We observed no differences in sensitivity in measures obtained following force-field training or after washout trials (F_(1,28) = 0.7, p > 0.4), nor for leftward versus rightward force fields (F_(1,28) = 0.28, p > 0.85). None of the individual contrasts assessing possible interactions was reliable by Bonferroni comparisons (p > 0.1 or more in all cases). This suggests that dynamics learning modified the sensed position of the limb in space without modifying perceptual acuity.

We conducted a separate experiment involving 10 subjects to determine the extent to which the observed perceptual change is tied to motor learning. The methods were identical to those in experiment 1 except that the force-field-learning phase was replaced with a task that did not include motor learning. In the null and aftereffect phases of the control experiment, subjects moved actively as in experiment 1. The force-field phase of the experiment was replaced with a passive task in which the robot was programmed to reproduce the active movement of subjects in the leftward force-field condition of experiment 1. We used this condition for the passive control because it resulted in the largest perceptual change following motor learning. We computed on a trial-by-trial basis the mean movement trajectory experienced by subjects during the training phase in experiment 1. The robot produced this series of movements under position servo control in which the subject's arm was moved along the mean trajectory for each movement in the training sequence. As in the active movement condition, the hand path was also displayed visually during the passive movement. Thus, subjects experienced a series of movements that were the same as those in experiment 1, but they did not experience motor learning. As in experiment 1, perceptual tests were conducted before and after this manipulation.

To ensure that subjects in the passive control experiment were attending to the task, we randomly eliminated visual feedback during either the first or the second half of the movement in 15 of 150 movements in the passive condition. Subjects were instructed to report all such instances after the trial ended and to indicate whether the first or the second half of the movement had been removed. Six of the ten subjects tested in this condition missed none of these events, two subjects missed one, and two subjects missed two. This suggests that in the passive control experiment, subjects attended to the task.

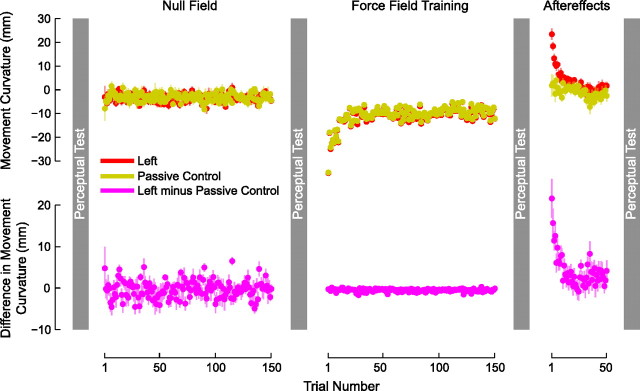
Figure 3 (top) shows the mean movement curvature (PD) of the hand for subjects tested in the passive control experiment (yellow) and for subjects in the original experiment (red). Figure 3 (bottom) shows the average difference between PD measured in the passive control experiment and PD as measured in the original leftward force-field condition. Note that a value of zero indicates an exact match in the PD measures of the two experiments. The subtraction, given in the bottom of Figure 3, shows that movement kinematics were well matched in the null phase, when subjects in both experiments made active movements. In the force-field phase of the experiment, the near-zero values in the bottom indicate that subjects in the passive control experienced kinematics that closely matched the mean trajectory in the original experiment. The nonzero values at the start of the aftereffect phase indicate that the passive control condition resulted in aftereffects that were smaller than those in the main experiment. A repeated-measures ANOVA based on the first 10 and last 10 trials in the null field and aftereffect phases showed that PD differed depending on whether subjects actively learned the force field or were tested in the passive control experiment (F_(3,69) = 14.194, p < 0.001). Differences in PD were reliable on initial aftereffect movements; subjects trained in the force field showed more curvature on initial aftereffect movements than subjects in the passive control (p < 0.001). Curvature on initial aftereffects for passive control subjects was no different from curvature on initial or final null-field movements (p > 0.2 for both comparisons). Thus, there was no evidence of motor learning in the passive control experiment.

Figure 3.

The presence of a perceptual shift depends on motor learning. In a control experiment, subjects experience the same trajectories as individuals that display motor learning. Subjects make active movements in the null and aftereffect phases of the study. In the force-field training phase, they are moved passively by the robot to replicate the average movement path experienced by subjects in the leftward condition that show motor learning. The top shows mean movement curvature (±SE) over trials for subjects in the original active learning condition (red) and the passive control condition (yellow). The bottom (magenta) gives the difference between active and passive movements. Movement aftereffects are not observed in the passive condition (yellow), indicating there is no motor learning.

We measured perceptual change in the passive control study in exactly the same manner as in experiment 1. Figure 2C shows measures of perceptual change in both the original active learning condition and comparable measures taken from the passive control. A repeated-measures ANOVA compared the perceptual shifts in the two experiments. Perceptual shifts differed depending on whether or not subjects experienced motor learning (F_(1,23) = 5.619, p < 0.05). As described above, subjects in the original experiment who learned the leftward force field showed perceptual shifts that were reliably different from zero both immediately after learning and after washout trials as well (p < 0.05 in both cases). In contrast, subjects tested in the passive control experiment showed shifts that were not different from zero at either time point (p > 0.7 in both cases).

The passive control experiment rules out the possibility that the shifts in the perceptual boundaries that we observed are due to the movement kinematics experienced during training. The passive control also argues against the idea that the perceptual shifts depend on the forces experienced during training and not on motor learning. Under passive conditions, it is not possible to equate fully both trajectory and force simultaneously. Thus, forces at the hand during the passive control study differed from those experienced during learning in the main experiment. On average, subjects in the passive condition experienced a maximum lateral force at the hand of 2.44 N, whereas during active force-field learning, the maximum lateral force averaged 5.14 N. However, if the perceptual shift that we have observed was linked to experienced force, then a nonzero perceptual change should have been seen in passive control manipulation, since subjects experienced nonzero forces. As reported above, this was not the case. Instead, the passive control experiment suggests that the perceptual shifts depend on motor learning.

We found that following learning, subsequent movements were modified in a fashion that was consistent with the perceptual change. The modification can be seen in Figure 4, which gives movement curvature (replotted from Fig. 1) during null-field movements before and after motor learning (note that the force-field-learning phase is not shown in this figure). It can be seen that relative to movements before learning, which were straight, movements after learning are more curved. The difference in curvature between null-field movements before learning and the final 10 aftereffect movements was reliable for both force-field directions (p < 0.01 in both cases). This suggests that following learning, movement trajectories do not return to their prelearning values.

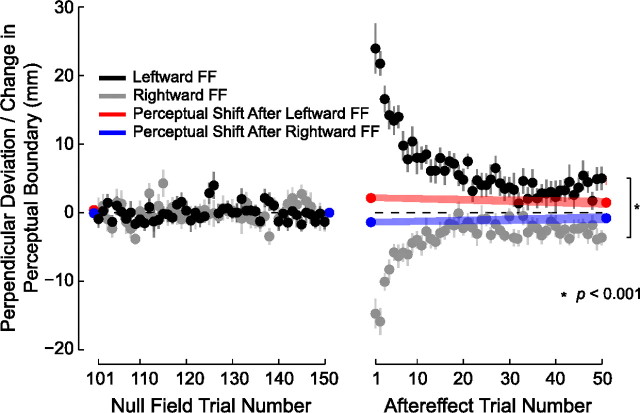
Figure 4.

After motor learning, movements follow trajectories that are aligned with shifted perceptual boundaries. Mean movement curvature (±SE) is shown in gray (replotted from Fig. 1). The left side shows the final 50 null field movements before force-field training. The data have been shifted such that the mean movement curvature in the null field is zero. The right side shows curvature on the 50 aftereffect trials, plotted relative to curvature on the null field trials. Curvature during the final aftereffect movements differs from baseline curvature. Changes in curvature following learning are not statistically different in magnitude and in the same direction as the shift in the perceptual boundary. The red and blue data points show the shift following force-field learning and aftereffect trials, replotted from Figure 3 (±SE shown in the red and blue bands).

We compared the change in movement trajectory to the observed shift in the perceptual boundary (shown in red and blue in Fig. 4, replotted from Fig. 3). We performed a repeated-measures ANOVA and found that depending on the force-field direction, there were differences in the kinematic and perceptual measures (F_(2,56) = 8.35, p < 0.01). For the rightward field, Bonferroni-corrected comparisons found no differences between the kinematic change and the perceptual shift, following learning (p > 0.35) and following aftereffect trials (p > 0.10). For the leftward field, the kinematic change was no different from the perceptual shift immediately following learning (p > 0.20) but was marginally greater than the perceptual shift following aftereffect trials (p = 0.054). Nevertheless, despite the marginal statistical effect, it can be seen that the perceptual shift is somewhat smaller in size. Thus, we performed two further analyses to assess whether the movement trajectories shown in Figure 4 were similar to the perceptual shifts or whether indeed there was a difference. In these analyses, we computed two different kinematic measures and repeated the statistical comparison between the lateral shift in the movement trajectory and the shift in the perceptual boundary. One measure was the perpendicular deviation at maximum velocity. The second was the average perpendicular deviation throughout the movement trajectory. We performed separate repeated-measures ANOVAs using these new variables and found that lateral changes in the perceptual boundary, following learning and also following aftereffect trials, did not differ from the lateral shift in movement kinematics measured over the final 10 aftereffect trials (F_(2,56) = 0.25, p > 0.75 for perpendicular deviation at maximum velocity, F_(2,56) = 0.72, p > 0.9 for average perpendicular deviation). Thus, based on these analyses, postlearning movements follow trajectories that are no different from shifted perceptual boundaries.

Above we show persistent shifts in the perceptual boundary between left and right. The shifts were present following 50 washout trials and also 24 h later. One possible explanation for the persistence of the shifts is that there were too few washout trials for performance to return to asymptotic levels. To verify that performance on aftereffect trials had reached asymptotic values, we divided the 50 trials into 10 bins of 5 trials each (trials 1–5, 6–10, and so forth) and examined changes in movement curvature over successive bins. We repeated the analysis dividing the aftereffect trials into bins of 10 movements each and found similar results to those reported below. We conducted a repeated-measures ANOVA to compare how movement curvature changed over the course of the aftereffect trials. For subjects trained in the leftward field, we found no changes in movement curvature beyond the 16th aftereffect trial (p > 0.7 for 20 of 21 possible comparisons, p > 0.05 for the remaining comparison). The same was true for the rightward field (p > 0.9 for all 21 comparisons). This suggests that performance returned to asymptotic levels well before the end of the washout phase.

Our procedure for testing the effects of motor learning on the sensed limb position involved a series of movements in force channels (Scheidt et al., 2000) that deflected the limb laterally and allowed us to estimate the perceived left–right boundary. The force channels were sufficiently stiff that they prevented lateral deflections of the hand and thus could be used to measure lateral forces applied by the subject following learning. This, however, raises the possibility that the changes in the sensed position of the hand following learning may have resulted from the production of isometric lateral force, as has been shown previously (Gandevia et al., 2006). The analyses described below rule out this possibility.

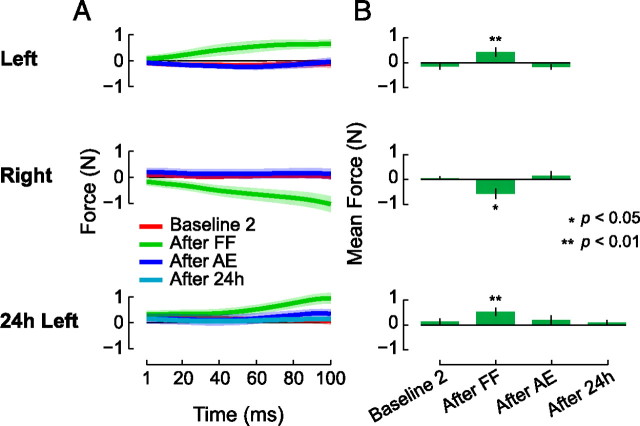
Figure 5 shows the lateral force applied to the channel wall during perceptual testing. For purposes of this analysis, we used forces during the first 100 ms of movement, just before the force channel deviated the hand to the left or right. For each subject, we measured lateral forces on the first channel movement in each of the four perceptual tests. Figure 5A gives the mean force profile before motor learning (red), following learning (green), following aftereffect trials (blue), and in the perceptual tests conducted 24 h later (cyan). Figure 5B shows mean values for the force profiles shown at the left.

Figure 5.

During perceptual tests, subjects only apply lateral force immediately after force-field learning. In other phases of the experiment, lateral force during perceptual tests is not different from zero. Thus, perceptual measurements are not contaminated by active force production in a lateral direction. A, Mean lateral force applied to the force channel walls (±SE) in the first 100 ms of the first perceptual test movement. B, Summary plot showing mean lateral force production (±SE) on the four perceptual tests.

We performed a repeated-measures ANOVA to evaluate the extent to which lateral force production changed over the course of the experiment. We performed a single ANOVA to assess differences in lateral force production in perceptual trials that followed baseline, force-field training, aftereffects, and 24 h perceptual tests. ANOVA revealed that lateral force production differed for the four perceptual tests (F_(6,126) = 8.168, p < 0.001). Immediately following force-field training, subjects produced lateral forces during perceptual testing that were different from zero (p < 0.05 for the leftward, p < 0.01 for the rightward and 24 h subjects). For all other perceptual tests, lateral force production was not reliably different from zero (p > 0.05 for all comparisons). Thus, lateral force is observed immediately following learning but at no other time. Accordingly the observed changes in the sensed position of the hand are not due to lateral force production during perceptual testing.

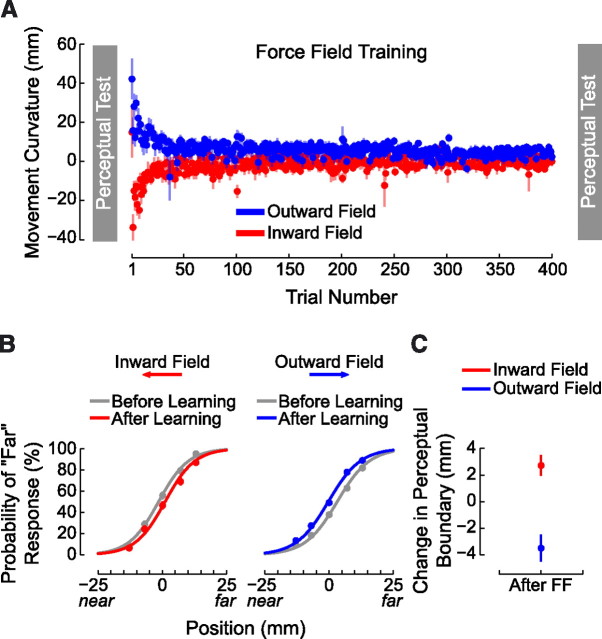
To assess the generality of the perceptual changes that we observed, we conducted a second experiment in which movements were made in a different direction and perceptual estimates were obtained with the limb stationary, using a different procedure to assess sensed limb position. In experiment 2, subjects made movements in a lateral direction between two targets centered about the body midline. A velocity-dependent force field displaced the limb, for one group of subjects toward the body, and for a second group, away from the body. Sensed limb position was estimated before and after force-field training using an interlimb matching technique. Perceptual tests involved the method of constant stimuli in which the left hand was held in position midway between the two targets while the robot positioned the right hand that had been used for motor learning at a series of locations on a forward–backward axis. At each position, the subject was asked to judge whether the right hand was located farther or closer to the body than the left hand.

We assessed motor learning by measuring movement curvature (Fig. 6A). A repeated-measures ANOVA found that for both the inward and outward force field, mean PD decreased reliably over the course of training (p < 0.001 in each case) indicating that subjects adapted to the load. The average perceptual performance associated with these training directions is shown in Figure 6B. For visualization purposes, logistic functions were fit to the set of mean response probabilities (averaged over subjects) at each of the seven test locations. As in experiment 1, it can be seen that the perceptual boundary shifted in a direction opposite to the force field. Thus, when the right hand was positioned coincident with the left, following training with an outward force field, subjects were more likely to respond that their right hand was farther from the body than their left. A perceptual shift in the opposite direction was observed when the force field acted toward the body.

Figure 6.

Force-field learning and perceptual testing with lateral movements. A, Mean perpendicular deviation over the course of training is shown for inward and outward loads. B, Binned response probabilities averaged across subjects (±SE) at each of the test locations and fitted psychometric functions show perceptual classification before (gray) and after (red or blue) learning force fields that act toward and away from the body. As in experiment 1, following motor learning the perceptual boundary shifts in a direction opposite to the applied force. C, Mean perceptual change (±SE) following force-field learning (After FF) with loads that act toward or away from the body.

Figure 6C shows the mean change in sensed limb position for each force-field direction. For statistical analysis, the sensed position of the limb was computed before and after learning for each subject separately. Figure 6C shows the mean change in sensed limb position for each force-field direction. The outward force field moved the perceptual boundary closer to the body. The inward force field shifted the boundary outward. A one-way ANOVA found that outward and inward perceptual shifts were significantly different from one other (F_(1,35) = 16.092, p < 0.001) and that each shift was reliably different from zero (p < 0.01 in each case).

As in experiment 1, the measured perceptual changes did not involve changes in perceptual acuity. Perceptual acuity was quantified on a per-subject basis using the distance between the 25th and 75th percentiles of the fitted psychometric function. A repeated-measures ANOVA assessed possible changes in acuity before and after force-field learning in both inward and outward force fields. No changes were observed from before to after learning (F_(1,34) = 0.77, p > 0.35), nor for inward versus outward force fields (F_(1,34) = 1.52, p > 0.2). Thus dynamics learning primarily affects the sensed position of the limb without affecting perceptual acuity.

Discussion

In summary, we have shown that motor learning results in a systematic change in the sensed position of the limb. The perceptual change is robust; we observe similar patterns of perceptual change for different movement directions, using different perceptual estimation techniques and also when perceptual estimates are obtained during movement and when the limb is stationary. The persistence of the perceptual change for 24 h and its presence under stationary conditions not experienced during training point to the generality of the perceptual recalibration.

The magnitude of the perceptual shift was between 11 and 33% of the estimated magnitude of learning. However, these calculations may well underestimate the magnitude of the perceptual effect. First, our measure of motor learning was based on deviation measures that were obtained from the initial aftereffect trials. While these are standard measures of learning in experiments such as these, they are also measures that are particularly transient and dissipate rapidly over trials. A better measure for this purpose would be an estimate of motor learning that reflects more durable effects, such as one obtained at longer delays following training. We anticipate that perceptual change would constitute a larger proportion of a less transient measure of motor learning. A second consideration is that the perceptual change that we have observed is a measure that was taken after relatively little training. The measured perceptual change may constitute a more substantial portion of the estimated learning if more extensive training had taken place.

It is known that sensory experience in the absence of movement results in a selective expansion of the specific regions of somatosensory cortex that are associated with the sensory exposure and also leads to changes in sensory receptive field size that reflect the characteristics of the adaptation (Recanzone et al., 1992a, 1992b). Structural change to somatosensory cortex is observed when sensory training is combined with motor learning in a task that requires precise contact with a rotating disk (Jenkins et al., 1990) and when animals are required to make finger and forearm movements to remove food from a narrow well (Xerri et al., 1999). In these latter cases it is uncertain whether it is the sensory experience, the motor experience, or both factors in combination that leads to remapping of the sensory system. The findings of the present paper help in the resolution of this issue. The sensory change observed here is dependent on active movement. When control subjects experience the same movements but without motor learning, perceptual function does not change. The present findings thus point to a central role of motor learning in plasticity in the sensorimotor system.

We observed that movement kinematics change following motor learning. In particular, movement curvature in the absence of load is greater than that present before learning. Moreover, movements following learning deviate from their prelearning trajectories by an amount that is not statistically different in magnitude and in the same direction as the sensory recalibration. This suggests that, following learning, movements follow altered perceptual boundaries. The sensory change that we observe in conjunction with motor learning thus appears to have functional consequences in sensorimotor behaviors.

The findings of the present paper bear on the nature of adaptation in sensory and motor systems. Most approaches to neuroplasticity treat sensory and motor adaptation in isolation (Gomi and Kawato, 1993; Ghahramani et al., 1997; Wolpert and Kawato, 1998; Gribble and Ostry, 2000). An alternative possibility supported by the data in the present study is that plasticity in somatosensory function involves not only sensory systems but motor systems as well (Haith et al., 2008; Feldman, 2009). Evidence in support of the idea that somatosensory perception depends on both sensory and motor systems would be strengthened by a demonstration that changes in perceptual function parallel changes in learning over the course of the adaptation process. Comparable patterns of generalization of motor learning and generalization of the associated sensory shift would also support this possibility. Other studies might use cortical stimulation to enhance (Reis et al., 2009) or suppress (Cothros et al., 2006) retention of motor learning, to show a corresponding enhancement or suppression of the change in somatosensory perception.

Other researchers have proposed that sensory perception depends on both sensory and motor systems (Haith et al., 2008; Feldman, 2009). Learning can lead to changes in sensory perception via changes to motor commands, sensory change, or the two in combination. One possibility is that motor learning involves adjustments to motor commands that recalibrate the central contribution to position sense [see Feldman (2009) for a recent review of central and afferent contributions to position sense]. In effect, signals from receptors are measured in a reference frame that has been modified by learning. A somewhat different possibility is that the learning involves a recalibration of both sensory and motor processes. Haith et al. (2008) propose that changes in performance that are observed in the context of learning depend on error-driven changes to both motor and sensory function.

The passive control experiment suggests that it is unlikely that sensory experience alone could contribute to the observed perceptual changes. However, prolonged exposure to lateral shifts in the position of the limb due to force-field learning might in principle lead subjects to modify their estimates of limb position and to interpret somatosensory feedback during subsequent perceptual testing in terms of this updated estimate (Körding and Wolpert, 2004). While the distribution of sensory inputs experienced during movement could play a role in subsequent perceptual measures, in the present study perceptual change is not observed in the context of passive movement. This suggests that active involvement of the participant in the context of movement production is required for the observed sensory shift.

The cortical areas that mediate somatosensory changes that accompany motor learning are not known. Changes to primary and second somatosensory cortex would seem most likely. However the involvement of primary motor cortex in somatic perception (Naito, 2004), and the involvement of premotor and supplementary motor areas in somatosensory memory and decision-making processes (Romo and Salinas, 2003), suggests that sensory remodeling in the context of motor learning may also occur in motor or perhaps even prefrontal areas of the brain.