Abstract
Optical imaging has been widely applied in preclinical and clinical applications. Fifteen years ago, an efficient Monte Carlo program ‘MCML’ was developed for use with multi-layered turbid media and has gained popularity in the field of biophotonics. Currently, there is an increasingly pressing need for simulating tools more powerful than MCML in order to study light propagation phenomena in complex inhomogeneous objects, such as the mouse. Here we report a tetrahedron-based inhomogeneous Monte Carlo optical simulator (TIM-OS) to address this issue. By modeling an object as a tetrahedron-based inhomogeneous finite-element mesh, TIM-OS can determine the photon– triangle interaction recursively and rapidly. In numerical simulation, we have demonstrated the correctness and efficiency of TIM-OS.
1. Introduction
The combination of improved optical molecular probes (such as those based on bioluminescence and fluorescence) and optical imaging techniques has led to the development of optical molecular imaging tools that allow the visualization and analysis of cellular and molecular features in biological, preclinical and clinical applications (Contag and Bachmann 2002, Ntziachristos et al 2005, Ray et al 2003, Rice et al 2001, Jaffer and Weissleder 2005, Thakur and Lentle 2006, Weissleder and Ntziachristos 2003). To overcome the limitations of planar optical molecular imaging, fluorescence molecular tomography (FMT) and bioluminescence tomography (BLT) were developed to localize and quantify target probe distributions within living systems (Wang et al 2006, Weissleder and Ntziachristos 2003, Vinegoni et al 2008).
The solution to these FMT and BLT problems requires an accurate model of the photon propagation in the biological tissue, which is a turbid medium that scatters and absorbs photons significantly. It is well known that the radiative transfer equation (RTE) is highly accurate for description of the propagation of photons in a turbid medium (Busbridge 1960, Case and Zweifel 1967, Chandrasekhar 1950, Prahl 1988). However, RTE is computationally challenging even with a high-performance computer (Klose et al 2005). Thus, various approximate models, such as diffusion approximation (Arridge 1999, Arridge et al 1993, Boas 1996), phase approximation (Cong et al 2007a, 2007b, 2008), high order spherical harmonics (Fletcher 1983) and simplified spherical harmonics models (Klose and Larsen 2006), have been developed to solve RTE efficiently. On the other hand, Monte Carlo simulation can solve RTE with any desired accuracy (Flock et al 1989a, 1989b, Keijzer et al 1989, Li et al 2004, Manno 1999, Wang et al 1995, Wilson and Adam 1983). This is achieved by tracing the propagation of photons one by one based on their statistical scattering and absorption behaviors. Hence, Monte Carlo simulation can be used as a gold standard to verify other RTE solving methods, and as an additional tool to study the photon transport phenomena.
Monte Carlo simulation is a widely applied method used to solve complex problems by simulating the statistical behavior of a large number of individual entities and analyzing their collective features. For example, it can be used to compute highly complex integrals over irregular domains, such as in the semiconductor industry (Aldegunde et al 2008). The Monte Carlo simulation technique has been extensively studied in the field of high energy physics to investigate particle transfer in Hirayama et al (2005), Allison et al (2006) and Agostinelli et al (2003). EGS5 and Geant4 are exemplary software simulation packages developed for this purpose and have been used in numerous studies. Typically, the photon scattering in turbid media is very complex. In some photon transport processes, the number of scattering events for each photon is limited, such as in the case of x-ray and tissue interaction. For other transport processes, the photon will move in a pronounced zigzag pattern. For example, biological tissues generally have a relatively high scattering coefficient for visible light, and the behavior of the photon can be described by the average scattering angle without the detailed scattering profile. Based on key optical parameters including the absorption coefficient, scattering coefficient and anisotropy factor, efficient optical Monte Carlo simulation is feasible for use in biological tissues.
Biophotonic transport was first simulated in relatively simple geometric settings, such as in tissue slabs (Prahl et al 1989). In 1995, Wang et al (1995) introduced a Monte Carlo simulation program, referred to as ‘MCML’, for multi-layered specimens. Due to the parallel nature of the Monte Carlo simulation, the trajectories of any two photons are actually independent. Hence, various efforts were made to improve the simulation speed via parallel computing using computer cluster (Chen et al 2007), graphics processing unit (GPU) (Alerstam et al 2008) and field-programmable gate array (FPGA)-based programming (Lo et al 2009).
In recent years, several groups have made efforts to develop Monte Carlo programs for complex heterogeneous specimens. In 1996, Pfefer et al (1996) introduced a Monte Carlo method based on a cubic voxel model and demonstrated its utility in a semi-infinite multi-layered slab geometry with embedded blood vessels. In 2002, Boas et al (2002) presented a time-domain Monte Carlo code also based on a cubic voxel model and applied it in a 3D model of the head. In the voxel model, each voxel can be assigned with different optical parameters, making this approach very flexible. The major problem with this method is that it is difficult to incorporate precise boundary information, and this may introduce significant errors due to mismatched boundaries (Binzoni et al 2008). Li et al developed a Monte Carlo optical simulation environment (MOSE) based on standard building blocks such as ellipsoids, cylinders and polyhedrons which approximate the shapes of biological tissues (Li et al 2004). A major problem with this program is that biological structures usually have non-standard boundaries/interfaces, which cannot be easily defined in terms of standard geometrical building blocks.
Recently, Cote and Vitkin (2005) and Margallo-Balbas and French (2007) proposed the use of a surface mesh to more accurately define the interface between tissues in Monte Carlo simulation. A triangle-based surface mesh, which is widely used in mechanical engineering and can be extracted from a finite element tetrahedral mesh, approximates complex boundaries/interfaces well. In the context of Monte Carlo simulation, the program needs to determine whether a triangle will be hit by a photon prior to it is moved. Given that the large number of triangles need to be tested for each step, an efficient algorithm is required to evaluate possible photon–triangle interactions. Margallo-Balbas and French (2007) employed a spatial hierarchy algorithm in their program. This is a standard technique in the field of computer graphics to perform ray tracing operations and accelerate photon propagation modeling. The goal of the spatial hierarchy algorithm is to reduce the average number of operations per step. Recently, MOSE also utilized this idea in its new version. There are two main drawbacks for the triangle-based surface mesh scheme. First, it is still quite slow because of the large number of tracing operations and associated computational costs. The program by Margallo-Balbas and French (2007) simulated 8 million photons in 1 h on a 3.2 GHz Pentium 4 PC, whereas our program can simulate 250 million photons in 1 h in the essentially same setting. Second, the triangle-based mesh is not as flexible as the voxel-based scheme. In the voxel scheme, the optical parameters of even a single voxel can easily be changed. In the triangle-based mesh, a new surface mesh must be generated each time the optical parameters are modified for a new region.
In this paper, we report a novel tetrahedron-based inhomogeneous Monte Carlo optical simulation (TIM-OS) scheme. The program is faster than the surface mesh scheme and more flexible than the voxel scheme. The key idea underlying this scheme is that by modeling a geometry as a tetrahedron-based finite element mesh, TIM-OS can determine the photon– triangle interaction recursively and rapidly. Because the mean free path of a photon in biological tissues is usually much smaller than the size of a tetrahedron, most photon steps will be made within a tetrahedron and only a small portion of these random walks will go across a tetrahedron surface. In other words, since the photon starts its movement inside a tetrahedron, the ray triangle interaction could only happen with one of the four triangles, reducing the searching space significantly. Therefore, the TIM-OS approach represents a significant improvement over the current methods, allowing accelerated photon propagation modeling in complex geometry.
2. Methodology
The rules used in TIM-OS are similar to those described by Wang et al (1995). The major difference is outlined in the red dashed box in figure 1. In the following, for convenience when we talk about a photon, we are referring to a packet of photons with a corresponding weight, which is treated as continuous. It is also possible to perform the Monte Carlo simulation one photon by one photon in a quantum fashion but in this case many more photons are needed to produce a smooth profile (Kahn and Harris 1951, Wang et al 1995).
Figure 1.
Flowchart for the tetrahedron-based inhomogeneous Monte Carlo optical simulation (TIM-OS) scheme.
2.1. Photon-triangle interaction
The most demanding task required to trace a photon through complex heterogeneous structures is to identify photon–surface interactions. The tetrahedron-based representation provides a balance between the complexity and flexibility of a geometrical model. A tetrahedron is a solid shape with four triangular faces. In finite element analysis, a complex shape can be broken down into a mesh of irregular tetrahedra. Given a location (tetrahedron) and the direction of a photon in such a tetrahedral mesh, a free fly step size, in which there will be neither absorption nor scattering applied to the photon, can be computed according to the local optical parameters. Then, the four triangular surfaces of the tetrahedron will be examined to identify a possible photon–triangle interaction. This process can be repeated until the photon dies or escapes the object. In each cycle prior to the photon being moved, the program will check whether the photon will hit one of the triangles. The blue dotted box shown in figure 1 illustrates the photon–triangle interaction. Since the tetrahedron in which the photon is currently contained is already known, in each step the photon–triangle interaction testing is limited to the four triangles of the current tetrahedron. If the photon does not hit a triangle, it will be moved by the current step size. If the photon does hit a triangle, it will be placed on the first intersection point on the triangle. Because a neighboring tetrahedron or the surrounding medium may have a different refractive index, the photon may be reflected or transmitted. If it is reflected, a reflection direction and a new step size will be computed, and whether the photon will hit another triangle will be similarly checked but under the new conditions. If the photon passes through a boundary triangle, fluence information will be updated for this surface triangular element and the program will launch a new photon if there are more. If the triangle is not on a boundary, it will be moved into a new tetrahedron. A refractive direction and a new step size will be computed, and whether the photon hits a triangle or not will be similarly checked in the new tetrahedron.
Note that in the above photon–triangle interaction procedure, when a photon hits an interface between two media, the photon is either reflected or refracted in an all or none manner. It is certainly possible to divide the photon packet into two parts: one being reflected and the other refracted (Wang et al 1995). The energy of the two parts will be computed based on a ratio between reflected/refracted photons. We will study this approach in a future version of TIM-OS.
More specifically, if P⃗ is the position of the photon and U⃗ the unit direction of the photon movement, the path of the photon can be described as a line function: P⃗′ = P⃗ + U⃗ t for t > 0. For each triangle in the finite element mesh, we can find an equation in advance: N⃗ · Q⃗ + d = 0, where N⃗ is the inward unit normal vector of the triangle, Q⃗ is a point on the plane, N⃗ · Q⃗ is the dot product of vectors N⃗ and Q⃗ and d is a scalar for the plane function. The intersection point of the photon path and the plane of the triangle can be solved by combining the line and the triangle functions as
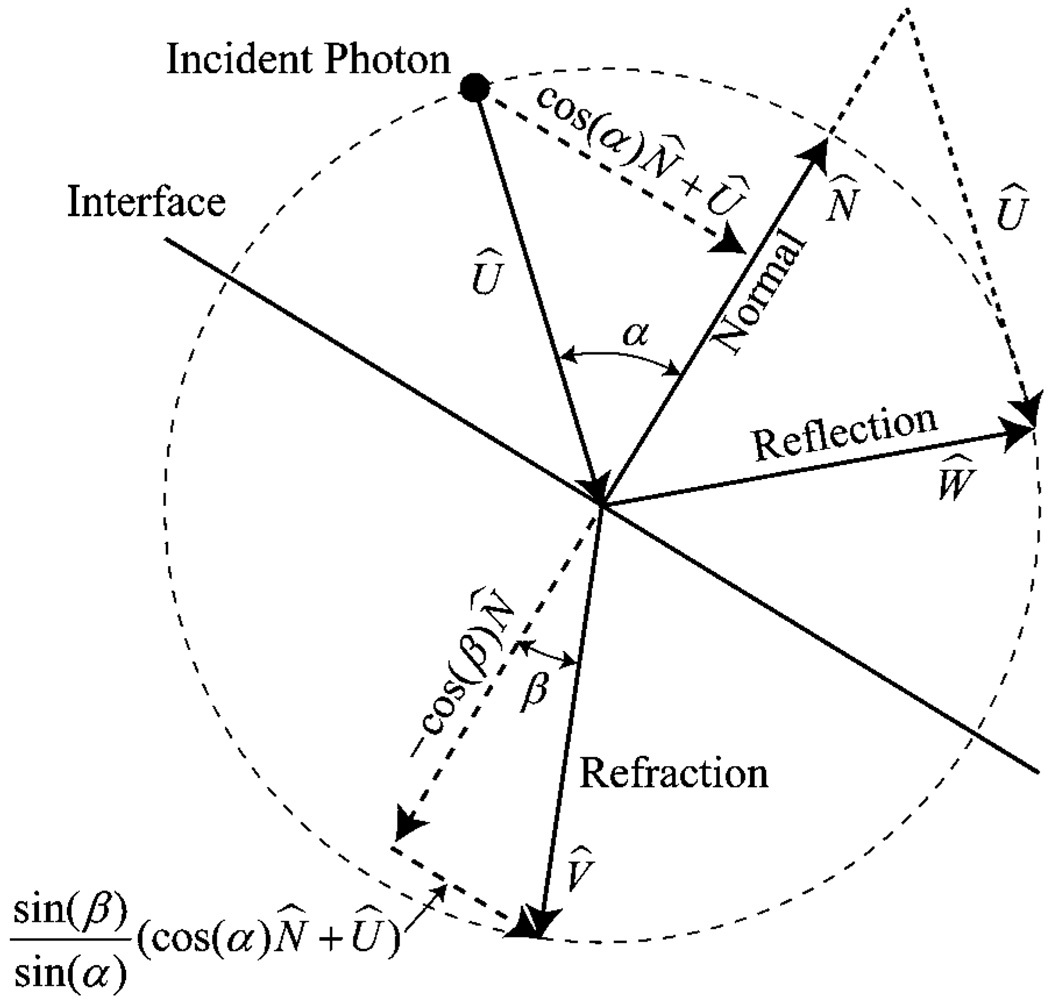
where t is the distance from the photon’s current point to the intersection point. If the photon’s step size is smaller than the smallest positive t, then the photon will not hit any triangle within this step; otherwise, the triangle with the smallest positive t will be hit by the photon first. Based on the photon incident vector U⃗ and the triangle normal vector N⃗, the incident angle α can be computed as cos(α) = abs(U⃗ · N⃗). The probability with which the photon will be reflected can then be estimated as in MCML (Wang et al 1995). If the photon is reflected, the reflection direction W⃗ will be computed. As shown in figure 2, it is easy to find that W⃗ = 2 cos(α)N⃗ + U⃗. If the photon is transmitted, the mismatched refractive indices must be taken into account when the refraction direction is computed. Clearly, the refraction direction can be found according to
where β is the refractive angle. All the values of sin (α), cos(α), sin(β) and cos(β) are already known while the probabilities for reflection and refraction are estimated.
Figure 2.
Geometry for reflection and refraction.
Note that in the computation of the incident angle, if a photon hits exactly at a corner or an edge of a tetrahedron, theoretically the incident angle is not defined. In our program, we break this uncertainty by selecting the first triangle of that corner or edge if the photon is extremely close to it; for example, within 10−10 mm. In general, it is very rare that a photon can be that close to a corner or edge because the volume that is close to a corner or an edge is negligible compared to the whole problem domain. Furthermore, to reduce the probability of this uncertainty occurring, we should not define a source position exactly on a node or an edge. In case this happens, we can shift the node or the two nodes of the edge to avoid this problem.
The rest of the flowchart is similar to MCML. Let us briefly recall those steps here; after we move the photon packet, the weight of the photon packet will be reduced for absorption. The lost weight will be scored into the tetrahedron in TIM-OS. It is also possible to establish a separate grid to store absorption information. Then, TIM-OS will check the weight of the photon packet. If it is below a threshold (say, 0.000 01), a survival roulette test will be performed on the photon packet (Hendricks and Booth 1985, Carter and Cashwell 1975, Wang et al 1995). This test gives the photon packet one chance in m (say, 10) to survive with a new weight of m times the current weight for energy conservation. If the photon packet does not survive, TIM-OS will jump out of the loop and launch a new photon packet. If the photon packet has a significant weight or it survives the roulette test, TIM-OS will scatter the photon packet into a new direction based on the local anisotropy factor.
There are a few additional computational steps used in TIM-OS relative to the original MCML scheme. If the geometry of the specimen is that of a multi-layered tissue, the amount of the additional computational cost is relatively small as compared to that of the expensive functions used in the Monte Carlo simulation, such as sine, cosine, logarithm and random number generation. Hence, the speed of TIM-OS will be comparable to that of MCML in this case.
3. Numerical results
3.1. Simulation with multi-layered tissue
First, we compared TIM-OS with MCML, a default standard in this area. The test bed was a dual quad-core Xeon (2.5 GHz) machine running an Ubuntu 64-bit Linux system with eight CPU cores. The TIM-OS program was written in C/C++ and compiled using the Intel C/C++ compiler. MCML was downloaded and compiled using the same compiler. For each run, TIM-OS used eight CPU cores, while MCML used only one CPU core. While MCML utilized the geometrical symmetry of a multi-layered tissue, we made TIM-OS record the transmittance fluence and diffuse reflectance fluence in the same fashion: fluence was recorded with respect to the distance to the center of the surface using a set of ring-type sensors. The distance between the outer radius and the inner radius of a ring sensor is 0.01 mm. To validate the TIM-OS program, we applied TIM-OS to both single-layered and multi-layered cases and compared the results with their counterparts from MCML. In the following simulation experiments, 108 photons were launched at the position (0, 0, 0) in the direction (0, 0, 1) in each simulation. In this paper, we use mm for all the sizes and positions, and mm−1 for the absorption and scattering coefficients. In all the experiments, we let the environment be air, with a refractive index of 1.0.
In the single-layered case, we tested all the 18 combinations of two different absorption coefficients: µa = (0.05, 0.4), three different scattering coefficients: µs = (20, 80, 320), and three different thicknesses (0.5, 1, 2). All the tissues shared a refractive index of 1.46 and an anisotropy factor of 0.9. A finite element mesh was generated for each tissue using our own finite element mesh generator. In TIM-OS, we have to limit the size of the semi-infinite slab to some finite size but this should still be large enough not to significantly affect the fluence in the center. In the MCML simulation, we noted that while r (the distance from the point of measurement to the center) is larger than 10 mm, there are almost no photons in all the simulations. Hence, we chose the width of the slab to be 20 mm in the X and Y axes. For the slab with 1 mm thickness, we first partitioned it into a set of 1 mm cubes. Then we broke down each cube into 6 tetrahedra and obtained a finite element mesh with 2400 tetrahedra. For layers of different thicknesses, we just squashed or extended the slab along the Z axis. TIM-OS can work over a range of complexity from a very simple mesh with a few tetrahedra to an extremely complex mesh with millions of tetrahedra. The only requirement for TIM-OS to work effectively is that the tetrahedral mesh should approximate the shape of each structural component well. In practical applications, there are many factors that influence the choice of a finer or a coarser mesh. If we want to compare and validate other RTE solvers with TIM-OS, it is easier to reuse the tetrahedral mesh used in those RTE solvers. If we just need a simulation result, we can use a coarse mesh to save some computational time. In our experiments, we noted that the difference between the computational time for a coarse mesh and a fine mesh is very little in most cases. Therefore, there is no need to simplify the mesh. Since the purpose of this paper is to demonstrate the power of TIM-OS, we have used a much finer mesh to represent the selected phantoms.
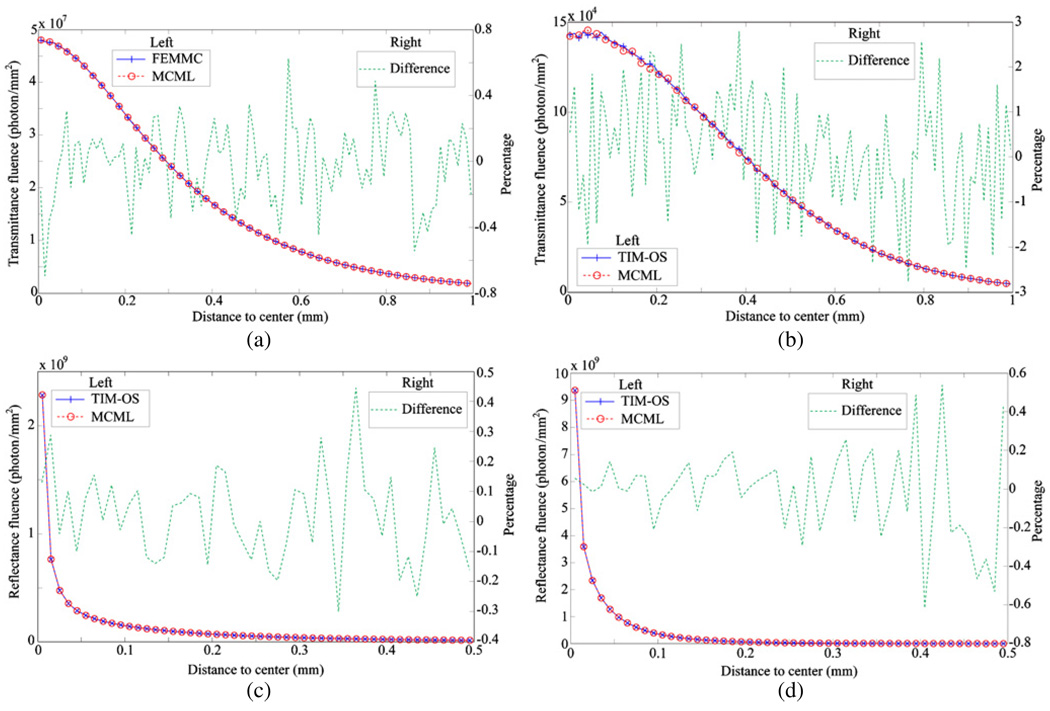
In the case of single-layered tissue, it was observed that the total transmitted energy of TIM-OS was always smaller than that of MCML. We hypothesized that the problem was due to the bias of the pseudorandom number generator. Thus, the random number generator in the original MCML was replaced with a Mersenne Twister pseudorandom number generator provided by the Intel Math Kernel Library (MKL), and all the simulation tests were repeated under the same conditions. This time the average difference between the two Monte Carlo simulators was less than 0.02% in the total transmitted energy, and the average difference in the total diffuse reflectance energy was similar. Note that the total transmitted energy of the original MCML was about 0.4% higher than that obtained by the MCML with the new random number generator. This confirmed that the random generator in the original MCML has some bias. The MCML results shown in this paper were therefore based on MCML with a new random number generator. Figure 3 compares the transmittance fluence profiles and diffuse reflectance fluence profiles between TIM-OS and MCML in two typical experiments from the above 18 cases.
Figure 3.
Comparison of transmittance and reflectance fluence profiles of TIM-OS and MCML in the case of a single tissue layer. (a) Transmittance profile with thickness 0.5 mm, µa = 0.05 and µs = 80, (b) transmittance profile with thickness 1 mm, µa = 0.4 and µs = 320, (c) reflectance profile with the same parameters as (a), and (d) reflectance profile with the same parameters as (b).
Next, we compared the two simulators in the case of a four-layered tissue with two different materials: (µa = 0.05, µs = 10, g = 0.9, n = 1.3) and (µa = 0.1, µs = 20, g = 0.95, n = 1.5), where n is the refractive index. Each layer was 1 mm in thickness. The order of the layer types was 1, 2, 1 and 2 sequentially. The finite element mesh of the four-layer phantom had 2205 nodes and 9600 tetrahedra. The transmittance fluence profiles from the two programs were in excellent agreement, as shown in figure 4(a). The difference between those two simulators was about 0.04% in the total transmitted energy. The difference was primarily from the Poisson noise embedded in the simulation since two separate runs of MCML with different startup random seeds produced a similar difference. This multi-layered simulation experiment shows that there is no significant difference between TIM-OS and MCML.
Figure 4.
Comparison of the transmittance fluence profiles generated by TIM-OS and MCML in the case of a four-layered tissue.
Moreover, we performed a different multi-layered simulation experiment to further check the accuracy of TIM-OS. In the previous simulation, the interfaces between different layers were parallel to the X–Y plane. To avoid the case that TIM-OS may favor an interface parallel to the X–Y, X–Z, or Y–Z planes, in this simulation, we first rotated the four-layered finite element mesh around the X axis by 30° and around the Z axis by 45° to produce a new finite element mesh such that the interfaces are not parallel to these planes. Since we already verified that TIM-OS is correct under the original multi-layered setting, this simulation is considered as an extra precaution. In other words, if TIM-OS can produce the same result in the original setting and rotated setting, we will feel even more confident on the correctness of TIM-OS in a general case. The location of the source was still (0, 0, 0) but its direction was rotated by the same angles as the mesh to be perpendicular to the bottom surface of the phantom. Then, we ran TIM-OS in the rotated setting with the same random seed and obtained the surface fluence. The results from the two settings matched precisely, with a difference of 0.0074% in the total surface fluence.
Even though TIM-OS and MCML work in different presentation domains, we still compared their speeds. On average, TIM-OS is about eight to ten times faster than MCML. For example, while MCML spent a total of 6340 s to handle the four-layered tissue model, TIM-OS used only 738 s, a speed gain of more than eight times. Hence, if TIM-OS used only one CPU core, it would have almost the same speed as MCML.
For curiosity, we also compared TIM-OS with the GPU-based MCML implementation: ‘CUDAMCML’ (Alerstam et al 2008, 2009). In the newest manual (Alerstam et al 2009), CUDAMCML was compared with the original MCML and showed a speed increase of more than 50 times, in contrast with the 1000-fold increase in speed that was originally reported (Alerstam et al 2008). To compare TIM-OS with CUDAMCML, we ran the single-layer case described in the CUDAMCML manual: n = 1.5, µa = 0.1, µs = 90, g = 0.9 and a thickness of 100 mm. Because the downloaded CUDAMCML program did not perform well on our workstation, which has a Quadro FX570 workstation graphic card from Nvidia, we have cited all the CUDAMCML data from the CUDAMCML manual (Alerstam et al 2009) (downloaded on 26 September 2009). Since CUDAMCML works in single precision floating numbers, we rewrote TIM-OS in single precision floating numbers for comparison. In this case, TIM-OS took 252 s while CUDAMCML took 64 s for 10 million photons—about four times faster. We then compared a multi-thread implementation of MCML (also in single floating point numbers) with CUDAMCML and found that the multi-thread MCML took 114 s. That is, CUDAMCML was only two times faster than highly optimized MCML on an eight-core machine. Based on this comparison, given the overheads due to complex geometry and the GPU memory bottleneck, it appears that there is not enough potential for a gain of speed for us to move our TIM-OS code to a middle range GPU card, such as the Nvidia 9800GT used for CUDAMCML. However, a high-end GPU workstation with a Tesla S1070 graphic card might perform much better.
3.2. Simulation in complex geometry
First, we compared TIM-OS with MOSE in a relatively simple heterogeneous geometry. A Windows machine with a 2.66 GHz Intel Core 2 Duo processor and 3 GB memory was used to run MOSE. The single core performance of the Windows machine is comparable to the Linux machine with a 2.5 GHz Xeon processor. The performance of TIM-OS was then evaluated with a highly complex mouse model. Also, we tried to compare TIM-OS with triMC3D (Margallo-Balbas and French 2007) but we were unable to make it work, because a runtime version was unavailable, and a number of necessary components were from different vendors and difficult to compile.
The heterogeneous model we used was a cube centered at (0, 0, 0) with five different regions, as shown in figure 5 (a). The side length of the cube was 10 mm. Four small 1 mm3 cubes were centered in the large cube at the four locations: (2, 2, 2), (2, −2, −2), (−2, 2, 2) and (−2, −2, −2) respectively. The optical parameters are listed in table 1. An isotropic point source with 107 photons was placed at the position (0.3, 1.31, 1.3333). The finite element model contained 21 × 21 × 21 = 9261 nodes and 48 000 tetrahedrons. Because MOSE is based on triangular mesh, we extracted the triangular mesh model with 4992 triangles from the finite element model. TIM-OS spent 330 s on the simulation. Figure 5(b) shows the surface fluence obtained from TIM-OS. MOSE was much slower than TIM-OS. To shorten computational time, we reduced the number of photons to 106 for MOSE, but it still spent approximately 4 h (there is no timer in MOSE to return the exact simulation time). Hence, TIM-OS was more than 400 times faster than MOSE. If both the programs used only one CPU core, TIM-OS would be still more than 50 times faster than MOSE. Hence, we did not compare TIM-OS with MOSE in the following more complex experiment. For comparison, two boundary datasets are measured using the nodes at the planes of x = 0 and x = −4, as shown by the two dotted lines in figure 5(a). A comparison of the surface fluence readings from TIM-OS and MOSE on the selected datasets is shown in figures 5(c) and (d) demonstrating that the two simulators fit well. It is necessary to note that since both MOSE and TIM-OS used a surface triangle as a detector in this experiment, the fluence value for a given node came from the nearby triangles through interpolation. This has certainly smoothed the data to some degree. In this experiment, we also categorized the types of photon–triangle interactions. There were approximately 21% steps that hit one triangle and 5% of steps that hit two triangles. For a stronger scattering coefficient and a larger tetrahedral mesh, these percentages will be even lower, and TIM-OS will spend even less time in checking photon–triangle interactions. If scattering is weak, the number of steps needed for a photon to escape from an object will be much smaller, the simulation problem will be much easier for all MC simulators and TIM-OS can still perform well.
Figure 5.
Numerical simulation with a heterogeneous cube. (a) The geometry of the cube, (b) the surface fluence computed with TIM-OS, (c) and (d) comparison of surface fluence readings between TIM-OS and MOSE for the nodes on the plane x = 0 (c) and x = −4 (d).
Table 1.
Optical parameters of the heterogeneous cube.
| Region index |
Absorption coefficient (mm−1) |
Scattering coefficient (mm−1) |
Anisotropy factor |
Refractive index |
|---|---|---|---|---|
| 1 | 0.05 | 20 | 0.9 | 1.3 |
| 2 | 0.1 | 10 | 0.7 | 1.1 |
| 3 | 0.2 | 20 | 0.8 | 1.2 |
| 4 | 0.1 | 10 | 0.9 | 1.4 |
| 5 | 0.2 | 20 | 0.9 | 1.5 |
In the following experiment, we used TIM-OS to simulate a realistic bioluminescence imaging experiment with a bioluminescence source embedded inside a mouse digital atlas, downloaded from the DIGIMOUSE website (Dogdas et al 2007, Stout et al 2002). This digital mouse model contains all the major organs with 58 244 nodes and 306 773 tetrahedra. The optical parameters of the mouse were listed in table 2. In this simulation, a total of 109 photons were launched from the source region. TIM-OS spent a total of 12 772 s (3.53 h) for the simulation. Figure 6(a) illustrates the major organs near the source. Figure 6(b) shows the surface fluence mapped on the mouse surface. This experiment shows that TIM-OS can efficiently handle a highly complex geometry with a large number of photons in a reasonable amount of time.
Table 2.
Optical parameters of the digital mouse.
| Region name |
Absorption coefficient (mm−1) |
Scattering coefficient (mm−1) |
Anisotropy factor |
Refractive index |
|---|---|---|---|---|
| Muscle | 0.23 | 10 | 0.9 | 1.37 |
| Heart | 0.11 | 11 | 0.9 | 1.37 |
| Stomach | 0.21 | 17 | 0.9 | 1.37 |
| Spleen | 0.23 | 10 | 0.9 | 1.37 |
| Kidneys | 0.12 | 12 | 0.9 | 1.37 |
| Lungs | 0.35 | 23 | 0.9 | 1.37 |
| Liver | 0.45 | 20 | 0.9 | 1.37 |
Figure 6.
Numerical simulation with a heterogeneous mouse. (a) The geometry of the mouse with major organs near the source, and (b) the surface fluence computed with TIM-OS.
4. Discussions and conclusion
The modern CPU is significantly different from that available in the early 1990s when MCML was developed. Currently, one of the most important CPU features is the single instruction multiple data (SIMD) support; for example, the Intel processor provides Streaming SIMD Extensions (SSE), which handles two double-precision floating-point numbers or four single-precision floating-point numbers in one instruction. This suggests that the modern CPU may run faster if the same instructions are grouped and applied together to an array of data. In the Monte Carlo simulation, there are multiple places where we can apply this technique. For example, the random number generation, a core function in the Monte Carlo simulation, is a time-consuming procedure in all the Monte Carlo simulation programs, because for each step or scattering a new random number is needed. Instead of generating one random number each time as in MCML, a better way is to generate an array of random numbers in one function call and use them one by one as needed. The Intel Math Kernel Library provides a function to generate an array of uniformly distributed random numbers, which gives a significant performance improvement over the use of a classic random number generator. We found that the speed of MCML can be improved 10–20% by simply replacing the original random number generator in MCML with an Intel vector random number generator. In addition to the random number generation, the Intel Math Kernel Library also provides vector implementations for certain computationally expensive core mathematical functions, such as log, power and trigonometric functions. These vector mathematical functions can be adapted to improve the Monte Carlo simulation. For example, when generating a random step for a photon, the computation involves a log function. After the generation of the array of random numbers, we can directly apply the vector log function on the array. By doing this, we obtained 30–50% improvement in speed, which was machine dependent. It is also possible to replace the Intel MKL library with the AMD math library for optimal performance on an AMD machine.
Another important trend is multi-core computer architecture. It becomes difficult to boost the CPU speed significantly by increasing the working frequency. A natural alternative way to increase computer speed is to pack more processor cores in one single CPU. For example, the current Intel Xeon and AMD Opteron CPUs have 4–6 computational cores. In the near future, general CPUs may likely have 8 or even 128 cores. Thus, there will be more leverage for us to utilize the power of multi-core techniques. It is fortunate that the Monte Carlo simulation is one of the most attractive parallel computing applications. In the real world, the trajectories of photons are essentially independent. In an ideal case, let us suppose that the number of processors is the same as the number of photons. Then, we can simulate the photon propagation in a single run. In the context of the current TIM-OS software, we use multi-thread programming to the degree the PC allows, that is, each of all available threads runs part of the simulation job. As a result, multi-thread programming improves the performance by almost eight times on an eight-core PC.
It is also natural to extend the parallelization to a cluster of machines each with multiple cores. We can always generate multiple TIM-OS runs on various machines, each of which is initialized with a different random seed and all of which collectively produce an improved outcome. In this way, we can even extend the parallelization to a large computer heterogeneous grid (under Windows, Linux, Unix, and so on). Note that a good parallel random generator is critical to manage the random number sequence for all the parallel threads. In our TIM-OS program, the MT2203 pseudorandom number generator (Marsaglia and Tsang 2000, Intel 2009a, 2009b) is used. This pseudorandom number generator provides a way to generate up to 1024 independent sequences. Hence, we can have up to 1024 independent threads in a parallel environment.
While the shared memory machine has more and more computational cores, this scheme may encounter a memory bandwidth bottleneck. Each time a photon enters into a new tetrahedron, the program needs to fetch information on the tetrahedron, including the geometry of the tetrahedron and its optical coefficients. By organizing these tetrahedrons in such a way that neighboring tetrahedrons are close to each other in the memory, the cache missing rate can be reduced to improve the simulation performance. This problem is exactly the same as the bandwidth problem in the area of sparse symmetric matrices. The bandwidth problem is NP-hard, and a complete search method is not suitable in our case. In our implementation, we reorder all the tetrahedrons on a preprocessor using the so-called reverse Cuthill–McKee algorithm (Cuthill and McKee 1969). Even though we did not observe any significant improvement of the performance on our eight-core machine, it could be useful when the number of cores is increased in a shared memory machine. While our current SMP system has only eight cores, the current GPU system has already integrated up to 960 cores in one single machine. A total of 960 cores reading and writing memory randomly will greatly reduce the performance of the GPU machine. A recent GPU-based MCML implementation (Alerstam et al 2009) on a Nvidia 9800GT graphic card showed a performance gain of about 58–137 times compared with the original MCML on a Core i7 CPU. It was observed that half of the running time was used to store the photon absorption information for a simple multi-layered geometry. For a complex geometry, such as the anatomy of a mouse, the memory bottleneck problem will be much worse than that with a multi-layered geometry. Organizing those data wisely will help reduce this problem.
The algorithm presented here is not limited to a traditional CPU-based machine. We can apply it to a GPU-based machine. The current mainstream eight-core workstation can reach 75G FLOPS for double-precision floating-point operations and 150G FLOPS for single-precision floating-point number operations. The current best GPU-based workstation has four Tesla S1070 graphic cards with 300G FLOPS for double-precision floating-point number operations and 4000G FLOPS for single-precision floating-point number operations. Hence, we will also work along this path, which may provide more than tenfold acceleration with an approximate fourfold increase in hardware cost.
The application of tetrahedron-based inhomogeneous Monte Carlo simulation is not limited to optical imaging. The TIM-OS scheme can also be adapted in x-ray studies, such as x-ray dual energy, backscattering and dark field imaging. X-ray small-angle scattering is a unique contrast technique that reveals subtle structural variations within soft tissues. By incorporating small-angle scattering phase functions in our TIM-OS software, we can accurately model the small-angle scattering process in a biomedically relevant environment. Since the number of x-ray scattering events is much smaller than the number of optical scattering events, it is possible to simulate dark field imaging in real time on a regular PC.
In conclusion, we have developed a new Monte Carlo scheme based on a relatively simple yet quite flexible tetrahedron-based optically inhomogeneous finite element mesh. This scheme greatly reduces the computational cost to solve optical radiative transport problems in the Monte Carlo simulation of complex heterogeneous biological tissues. The high performance of this scheme stems from the tetrahedron representation. In each tetrahedron, there are only four triangles. If a photon is in a tetrahedron, for each Monte Carlo propagation step the program only needs to test four triangles for a possible photon–triangle interaction. This type of interaction test is much simpler than traditional ray triangle interaction in the ray tracing scheme associated with a triangle-based surface mesh such as in triMC3D. Our numerical simulation results have confirmed the advantages of our tetrahedron-based approach. For a multi-layered tissue, TIM-OS is faster than the original MCML even if both the programs use only one CPU core. For highly complex mouse geometry, TIM-OS is capable of solving the optical forward propagation problem on a current desktop PC. This type of capability has never been previously demonstrated on a desktop PC.
Acknowledgments
The work is partially supported by NIH/CA127189 and NIH/EB004287.
References
- Agostinelli S, et al. GEANT4-a simulation toolkit. Nucl. Instrum. Methods. A. 2003;506:250–303. [Google Scholar]
- Aldegunde M, García-Loureiro AJ, Martinez A, Kalna K. Tetrahedral elements in self-consistent parallel 3D Monte Carlo simulations of MOSFETs. J. Comput. Electron. 2008;7:201–204. [Google Scholar]
- Alerstam E, Svensson T, Andersson-Engels S. Parallel computing with graphics processing units for highspeed Monte Carlo simulation of photon migration. J. Biomed. Opt. 2008;13:1–3. doi: 10.1117/1.3041496. [DOI] [PubMed] [Google Scholar]
- Alerstam E, Svensson T, Andersson-Engels S. CUDAMCML User manual and implementation notes. 2009 http://www.atomic.physics.lu.se/biophotonics/our_research/monte_carlo_simulations/gpu_monte_carlo/
- Allison J, et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006;53:270–278. [Google Scholar]
- Arridge S. Optical tomography in medical imaging. Inverse Problems. 1999;15:R41–R93. [Google Scholar]
- Arridge SR, Schweiger M, Hiraoka M, Delpy DT. A finite-element approach for modeling photon transport in tissue. Med. Phys. 1993;20:299–309. doi: 10.1118/1.597069. [DOI] [PubMed] [Google Scholar]
- Binzoni T, Leung TS, Giust R, Rufenach D, Gandjbakhche AH. Light transport in tissue by 3D Monte Carlo: influence of boundary voxelization. Comput. Methods Programs Biomed. 2008;89:14–23. doi: 10.1016/j.cmpb.2007.10.008. [DOI] [PubMed] [Google Scholar]
- Boas DA. Dissertation. Graduate School of Arts and Sciences, University of Pennsylvania; 1996. Diffuse photon probes of structural and dynamical properties of turbid media : theory and biomedical applications; p. xix. [Google Scholar]
- Boas DA, Culver JP, Stott JJ, Dunn AK. Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head. Opt. Express. 2002;10:159–170. doi: 10.1364/oe.10.000159. [DOI] [PubMed] [Google Scholar]
- Busbridge IW. The Mathematics of Radiative Transfer. Cambridge: Cambridge University Press; 1960. [Google Scholar]
- Carter LL, Cashwell ED. Particle Transport Simulation with the Monte Carlo Method. Oak Ridge, TN: US Energy Research and Development Administration; 1975. [Google Scholar]
- Case KM, Zweifel PF. Linear Transport Theory. Reading, MA: Addison-Wesley; 1967. [Google Scholar]
- Chandrasekhar S. Radiative Transfer. Oxford: Clarendon; 1950. [Google Scholar]
- Chen C, Lu JQ, Li K, Zhao SS, Brock RS, Hu XH. Numerical study of reflectance imaging using a parallel Monte Carlo method. Med. Phys. 2007;34:2939–2948. doi: 10.1118/1.2745241. [DOI] [PubMed] [Google Scholar]
- Cong W, Cong A, Shen H, Liu Y, Wang G. Flux vector formulation for photon propagation in the biological tissue. Opt. Lett. 2007a;32:2837–2839. doi: 10.1364/ol.32.002837. [DOI] [PubMed] [Google Scholar]
- Cong W, Shen H, Cong A, Wang G. Integral equations of the photon fluence rate and flux based on a generalized Delta–Eddington phase function. J. Biomed. Opt. 2008;13:024016. doi: 10.1117/1.2907168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong W, Shen H, Cong A, Wang Y, Wang G. Modeling photon propagation in biological tissues using a generalized Delta–Eddington phase function. Phys. Rev. E. 2007b;76:051913. doi: 10.1103/PhysRevE.76.051913. [DOI] [PubMed] [Google Scholar]
- Contag CH, Bachmann MH. Advances in in vivo bioluminescence imaging of gene expression. Annu. Rev. Biomed. Eng. 2002;4:235–260. doi: 10.1146/annurev.bioeng.4.111901.093336. [DOI] [PubMed] [Google Scholar]
- Cote D, Vitkin IA. Robust concentration determination of optically active molecules in turbid media with validated three-dimensional polarization sensitive Monte Carlo calculations. Opt. Express. 2005;13:148–163. doi: 10.1364/opex.13.000148. [DOI] [PubMed] [Google Scholar]
- Cuthill E, McKee J. Reducing the bandwidth of sparse symmetric matrices. 24th Nat. Conf. ACM. 1969:157–172. [Google Scholar]
- Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digimouse: a 3D whole body mouse atlas from CT and cryosection data. Phys. Med. Biol. 2007;52:577–587. doi: 10.1088/0031-9155/52/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher JK. A solution of the neutron-transport equation using spherical-harmonics. J. Phys. A: Math. Gen. 1983;16:2827–2835. [Google Scholar]
- Flock ST, Patterson MS, Wilson BC, Wyman DR. Monte-Carlo modeling of light-propagation in highly scattering tissues: 1. Model predictions and comparison with diffusion theory. IEEE Trans. Biomed. Eng. 1989a;36:1162–1168. doi: 10.1109/tbme.1989.1173624. [DOI] [PubMed] [Google Scholar]
- Flock ST, Wilson BC, Patterson MS. Monte-Carlo modeling of light-propagation in highly scattering tissues: 2. Comparison with measurements in phantoms. IEEE Trans. Biomed. Eng. 1989b;36:1169–1173. doi: 10.1109/10.42107. [DOI] [PubMed] [Google Scholar]
- Hendricks JS, Booth TE. Monte-Carlo Methods and Applications in Neutronics, Photonics and Statistical Physics Lecture Notes in Physics. vol 240. Berlin: Springer; 1985. MCNP variance reduction overview; pp. 83–92. [Google Scholar]
- Hirayama H, Namito Y, Bielajew AF, Wilderman SJ, Nelson WR. The EGS5 code system. Stanford Linear Accelerator Center Report SLAC-R-730. 2005 [Google Scholar]
- Intel. Intel Math Kernel Library Reference Manual. 2009a http://software.intel.com/en-us/articles/intel-math-kernel-library-documentation/
- Intel. Intel Math Kernel Library Vector Statistical Library Notes. 2009b http://software.intel.com/en-us/articles/intel-math-kernel-library-documentation/
- Jaffer FA, Weissleder R. Molecular imaging in the clinical arena. JAMA. 2005;293:855–862. doi: 10.1001/jama.293.7.855. [DOI] [PubMed] [Google Scholar]
- Kahn H, Harris TE. Estimation of particle transmission by random sampling. Monte Carlo Methods (National Bureau of Standards Applied Mathematics Series. 1951;vol 12:27–30. [Google Scholar]
- Keijzer M, Jacques SL, Prahl SA, Welch AJ. Light distributions in artery tissue: Monte Carlo simulations for finite-diameter laser beams. Lasers Surg. Med. 1989;9:148–154. doi: 10.1002/lsm.1900090210. [DOI] [PubMed] [Google Scholar]
- Klose AD, Larsen EW. Light transport in biological tissue based on the simplified spherical harmonics equations. J. Comput. Phys. 2006;220:441–470. [Google Scholar]
- Klose AD, Ntziachristos V, Hielscher AH. The inverse source problem based on the radiative transfer equation in optical molecular imaging. J. Comput. Phys. 2005;202:323–345. [Google Scholar]
- Li H, Tian J, Zhu F, Cong W, Wang LV, Hoffman EA, Wang G. A mouse optical simulation environment (MOSE) to investigate bioluminescent phenomena in the living mouse with the Monte Carlo method. Acad Radiol. 2004;11:1029–1038. doi: 10.1016/j.acra.2004.05.021. [DOI] [PubMed] [Google Scholar]
- Lo WCY, Redmond K, Luu J, Chow P, Rose J, Lilge L. Hardware acceleration of a Monte Carlo simulation for photodynamic therapy treatment planning. J. Biomed. Opt. 2009;14:014019. doi: 10.1117/1.3080134. [DOI] [PubMed] [Google Scholar]
- Manno I. Introduction to the Monte Carlo Method. Budapest: Akadémiai Kiadó; 1999. [Google Scholar]
- Margallo-Balbas E, French PJ. Shape based Monte Carlo code for light transport in complex heterogeneous tissues. Opt. Express. 2007;15:14086–14098. doi: 10.1364/oe.15.014086. [DOI] [PubMed] [Google Scholar]
- Marsaglia G, Tsang WW. A simple method for generating gamma variables. ACM Trans. Math. Softw. 2000;26:363–372. [Google Scholar]
- Ntziachristos V, Ripoll J, Wang LHV, Weissleder R. Looking and listening to light: the evolution of whole-body photonic imaging. Nature Biotechnol. 2005;23:313–320. doi: 10.1038/nbt1074. [DOI] [PubMed] [Google Scholar]
- Pfefer TJ, Barton JK, Chan EK, Ducros MG, Sorg BS, Milner TE, Nelson JS, Welch AJ. A three-dimensional modular adaptable grid numerical model for light propagation during laser irradiation of skin tissue. IEEE J. Sel. Top. Quantum. 1996;2:934–942. [Google Scholar]
- Prahl S. PhD Thesis. University of Texas at Austin; 1988. Light transport in tissue. [Google Scholar]
- Prahl SA, Keijzer M, Jacques SL, Welch AJ. A Monte Carlo model of light propagation in tissue. Proc. SPIE. 1989;5:102–111. [Google Scholar]
- Ray P, Wu AM, Gambhir SS. Optical bioluminescence and positron emission tomography imaging of a novel fusion reporter gene in tumor xenografts of living mice. Cancer Res. 2003;63:1160–1165. [PubMed] [Google Scholar]
- Rice BW, Cable MD, Nelson MB. In vivo imaging of light-emitting probes. J. Biomed. Opt. 2001;6:432–440. doi: 10.1117/1.1413210. [DOI] [PubMed] [Google Scholar]
- Stout D, Chow P, Silverman R, Leahy RM, Lewis X, Gambhir S, Chatziioannou A. Creating a whole body digital mouse atlas with PET, CT and cryosection images. Mol. Imaging Biol. 2002;4:S27. [Google Scholar]
- Thakur M, Lentle BC. Report of a summit on molecular imaging. Radiology. 2006;236:753–755. doi: 10.1148/radiol.2363051160. [DOI] [PubMed] [Google Scholar]
- Vinegoni C, Pitsouli C, Razansky D, Perrimon N, Ntziachristos V. In vivo imaging of Drosophila melanogaster pupae with mesoscopic fluorescence tomography. Nat. Methods. 2008;5:45–47. doi: 10.1038/nmeth1149. [DOI] [PubMed] [Google Scholar]
- Wang G, Cong WX, Durairaj K, Qian X, Shen H, Sinn P, Hoffman E, McLennan G, Henry M. In vivo mouse studies with bioluminescence tomography. Opt. Express. 2006;14:7801–7809. doi: 10.1364/oe.14.007801. [DOI] [PubMed] [Google Scholar]
- Wang L, Jacques SL, Zheng L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995;47:131–146. doi: 10.1016/0169-2607(95)01640-f. [DOI] [PubMed] [Google Scholar]
- Weissleder R, Ntziachristos V. Shedding light onto live molecular targets. Nat. Med. 2003;9:123–128. doi: 10.1038/nm0103-123. [DOI] [PubMed] [Google Scholar]
- Wilson BC, Adam G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983;10:824–830. doi: 10.1118/1.595361. [DOI] [PubMed] [Google Scholar]