Abstract
Background
Genome-wide association studies (GWAS) are now feasible for studying the genetics underlying complex diseases. For many diseases, a list of candidate genes or regions exists and incorporation of such information into data analyses can potentially improve the power to detect disease variants. Traditional approaches for assessing the overall statistical significance of GWAS results ignore such information by inherently treating all markers equally.
Methods
We propose the prioritized subset analysis (PSA), in which a prioritized subset of markers is pre-selected from candidate regions, and the false discovery rate (FDR) procedure is carried out in the prioritized subset and its complementary subset, respectively.
Results
The PSA is more powerful than the whole-genome single-step FDR adjustment for a range of alternative models. The degree of power improvement depends on the fraction of associated SNPs in the prioritized subset and their nominal power, with higher fraction of associated SNPs and higher nominal power leading to more power improvement. The power improvement can be substantial; for disease loci not included in the prioritized subset, the power loss is almost negligible.
Conclusion
The PSA has the flexibility of allowing investigators to combine prior information from a variety of sources, and will be a useful tool for GWAS.
Key Words: Association analysis, False discovery rate, HapMap
Introduction
Genome-wide association studies (GWAS) have now become feasible due to recent developments in genotyping technologies, a rapid decline in genotyping costs [1,2,3], and the completion of the International HapMap Project [4]. In GWAS, investigators typically rely on commercial genotyping products that attempt to provide adequate coverage across the genome. However, many times an investigator may have prior knowledge, e.g., candidate genes or evidence for linkage, where dense coverage might be desirable. Unfortunately, commercial genotyping products for GWAS typically have variation in coverage across the genome and do not allow for flexible selection of SNPs, leaving investigators with little control over what regions should receive high coverage. In the face of such restrictions, the commonly used approach of carrying out a single multiple-testing adjustment may not be efficient because regions with little relevance to a study might receive dense coverage and unnecessarily increase the number of hypothesis tests. The standard single-step adjustment ignores prior knowledge of potentially promising regions, and as a result, tests of significance for SNPs in such regions may be overly down-weighted due to the other relatively unpromising SNPs. In this situation, it could be more powerful to use prior information to prioritize genomic regions in data analysis.
Recognizing this problem, Genovese et al. [5] and Roeder et al. [6] introduced a method in which the association analysis p value for each SNP is up- or down-weighted and then the resulting weighted p values are subsequently used in the false discovery rate (FDR) procedure [7]. Roeder et al. [6] illustrated this weighted FDR approach by defining weights according to linkage analysis information, and showed that their method is more powerful than the standard FDR procedure using the original p values. However, in many studies, linkage information is not available for the disease and population of interest, and even when available, linkage evidence may be contradictory across different linkage studies. In addition, an investigator might wish to incorporate information on biologically relevant candidate genes, which do not necessarily fall within linkage peak regions, in the analysis. While the proposed method of Roeder et al. [6] can be applied outside the linkage setting to give increased weight to candidate SNPs, it remains unclear how such weights should be assigned, especially when multiple sources of prior information with different levels of evidence are available.
Sun et al. [8] proposed a stratified FDR method in which the genome is partitioned into subsets based on a set of criteria and the FDR procedure is applied to each subset. They evaluated the performance of this approach on 198,345 SNPs typed to test for association with Parkinson's disease [9]. They partitioned the association results into two subsets based on the minor allele frequencies (MAFs) and applied the FDR procedure separately to the two subsets. While MAF is related to the power to detect disease association, it has little relevance with prior biological information and thus partitioning based on MAF probably would not lead to noticeable power improvement. In fact, using the stratified FDR approach, Sun et al. [8] demonstrated that stratification on MAF provided no distinct advantage over non-stratified analysis. Although Sun et al. [8] mentioned the potential of using alternative stratification approaches, such as candidate genes and linked regions, they did not evaluate the advantage of these alternatives.
In this paper, we propose Prioritized Subset Analysis (PSA) in which the genome is partitioned into regions of high and low priority, with high priority regions defined on the basis of prior evidence for disease variants, and the FDR procedure is performed separately on the prioritized subset and in the complementary, non-prioritized subset. Unlike the weighted FDR approach [5, 6], PSA does not explicitly assign weights to the SNPs. We demonstrate that the PSA, an approach that is intuitive and easy to implement, is more powerful than the whole-genome single-step FDR adjustment. We also investigate factors – sizes of prioritized regions, fraction of disease regions and their effect sizes in the prioritized subset – that influence the power of the PSA and their effect on the overall FDR.
Methods
Prioritized Subset Analysis
A commonly used multiple-comparison adjustment in GWAS is the whole-genome single-step FDR adjustment (abbreviated as whole-genome adjustment or WGA). When prior information such as candidate genes or regions of linkage is available, results within highly promising genomic regions might be overly down-weighted due to inclusion of tests in relatively unpromising genomic regions. To address this problem, we propose to partition the complete set of SNPs into two distinct subsets of SNPs. The ‘prioritized’ subset of SNPs consists of SNPs in regions that have been identified to be more likely to harbor disease susceptibility variants. The ‘complimentary’ subset of SNPs consists of all remaining SNPs not assigned to the ‘prioritized’ subset. We then perform the FDR adjustment twice, once on the prioritized subset of SNPs and once on the complementary, non-prioritized subset, of SNPs. The two FDR procedures use the same error rate, which is the overall target error rate. We call this approach the Prioritized Subset Analysis (PSA). We note that this approach does not involve assigning weights to either the prioritized or complimentary set of SNPs. By defining the prioritized subset, we wish to incorporate prior knowledge pertaining to the genetics of the phenotype of interest into GWAS, with the hope of improving the power while controlling the genome-wide error rate at desired level.
FDR Procedure
The FDR procedure, originally introduced by Benjamini and Hochberg [7], is commonly used to control the global error rate in multiple-testing problems. The FDR controls the expected fraction of false positives among significant findings. Let R be the total number of rejections, Vbe the number of false rejections, and Q = V/R when R > 0 and Q = 0 otherwise. The FDR is the expectation E(Q) of Q. The number of true positives is R – V. In practice, the FDR procedure operates as follows. Let m be the total number of genetic markers, and Hi (i = 1, …, m) be the null hypothesis of no association between marker i and the outcome of interest. For each null hypothesis Hi, a statistical test is carried out. Let P(1) ≤ P(2) ≤ … ≤ P(m) denote the ordered p values obtained from these m hypothesis tests. For a given FDR level q, the ordered p value P(i) is compared with the critical value i · q/m. Let k = max{i: P(i) ≤ i ·q/m} be the largest index i such that P(i) ≤ i · q/m. If such a k exists, then the hypotheses corresponding to the k smallest p values are rejected.
Benjamini and Hochberg [7] proved that when the tests are mutually independent, the FDR of this procedure will be under control, that is, E(Q) ≤ qm0/m ≤ q, where m0 is the number of tests for which the null hypothesis is true. However, in GWAS, nearby SNPs are often in linkage disequilibrium (LD), leading to dependency among tests. Benjamini and Yekutieli [10] proved that the FDR will be under control when the test statistics have positive regression dependency. Because markers in LD tend to result in positively correlated tests, one intuitively would expect this property to hold for genetic association analysis and hence the FDR to be under control. Using simulations, Sabatti et al. [11] showed this to be true for case-control studies.
Properties of the PSA
Let R1 be the number of rejections and V1be the number of false rejections in the prioritized subset. Similarly, let R2 and V2 denote the corresponding numbers for the non-prioritized subset. Then, the total number of rejections is R = R1 + R2, and the total number of false rejections is V = V1 + V2. For each subset, the FDR will be under control. Intuitively, one might expect that the overall FDR is also under control, because for a data set, if Q1 = V1/R1 ≤ q and Q2 = V2/R2 ≤ q, then Q = V/R = (V1 + V2)/(R1 + R2) ≤ (R1q + R2q)/(R1 + R2) = q. However, the FDR procedure only guarantees E[Q1] ≤ q and E[Q2] ≤ q, which does not necessarily lead to E[Q] ≤ q. Therefore, we carried out simulations to investigate the effect of PSA on the overall FDR.
One interesting aspect of the FDR procedure is that the chance of rejecting a test depends not only on the test itself, but also on other tests. The chance increases when the fraction of tests under the alternative hypotheses or their nominal power increases; in other words, a test can ‘borrow the strength’ from the other tests. In the PSA, when the prioritized subset is defined such that it includes most disease gene regions or disease loci with relatively strong effect, the prioritized subset will, compared to the whole set, have a higher fraction of tests under the alternative hypotheses or relatively higher nominal power. As a result, for a SNP that is included in the prioritized subset, the PSA will likely have higher power to detect association with the disease than the WGA. On the other hand, if a disease gene region is not included in the prioritized subset, the PSA might lead to a loss of power compared to the WGA. We carried out simulations to demonstrate this power loss is often negligible. A similar phenomenon was also observed for the weighted FDR procedure proposed by Genovese et al. [5] and Roeder et al. [6].
Simulations
We carried out simulations to evaluate the performance of the PSA, its effect on the overall FDR, and the change in power when a disease gene region is not included in the prioritized subset. To give a practical evaluation of the PSA, we analyzed simulated GWAS data sets with LD patterns resembling real data as derived from the HapMap.
HapMap Data
Phased genotype data for the 60 CEU (CEPH samples with ancestry from northern and western Europe) founder subjects were obtained from HapMap release #21 (www.hapmap.org). We also obtained SNP names and positions for Illumina Sentrix® HumanHap300 BeadChips (317,503 SNPs). After merging with the HapMap phased data, 314,174 (99.0%) SNPs remained and were used for our simulations.
Disease Model
We considered a six-locus disease model assuming the disease loci are independent and reside on different chromosomes. We generated a model in which three of these disease loci have small effect (locus-specific sibling recurrence risk λs = 1.02, genotypic relative risk or GRR ≈ 1.34) and the others have relatively large effect (locus-specific λs = 1.05, GRR ≈ 1.57). We note that λs = 1.05 is similar to the effect size of TCF7L2,arecently identified type 2 diabetes susceptibility gene [12]. To assess the impact of local LD on power, the three small effect disease loci were placed in regions with weak, moderate, and strong LD, respectively, and the three large effect disease loci were placed similarly. Using these criteria, we picked three SNPs on chromosomes 6, 10, and 5 (MAF = 0.25, 0.36, 0.33), as the disease loci that confer small disease risk, and three SNPs on chromosomes 3, 11, and 4 as the disease loci with relatively large effect (MAF = 0.43, 0.31, 0.30). These minor allele frequencies are similar to putative disease variants identified in the first GWAS reported for type 2 diabetes [13]. The disease chromosomes were randomly chosen according to desired LD levels and the results would not change dramatically if other chromosomes with similar LD patterns were chosen as disease loci.
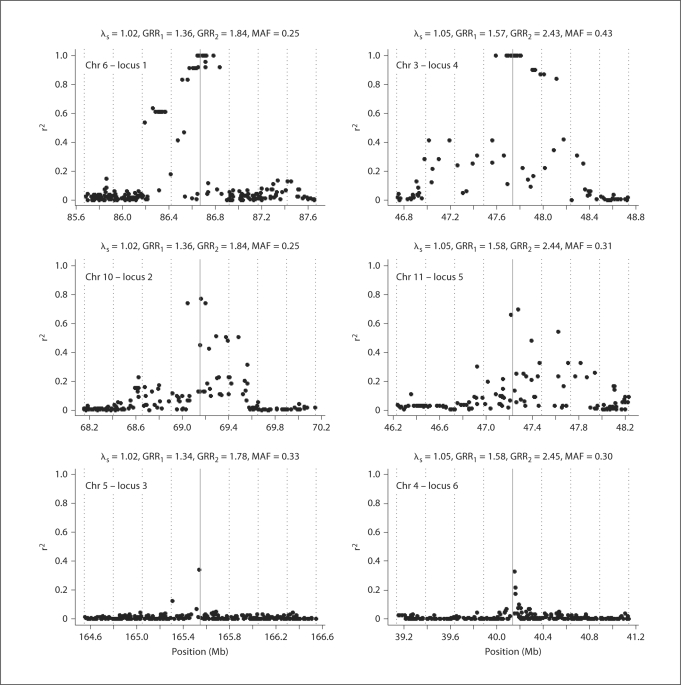
The minor alleles were designated as the risk alleles. We assigned penetrances as Pr(affected∣genotype) = 1/[1 + exp (–β0 – Σ6i= 1 βigi)], where gi ∈ {0,1,2} is the number of risk alleles at disease locus i. This is equivalent to assuming multiplicative effect across disease loci on the odds scale. The parameters βi were chosen so that the locus-specific λs = 1.02 for i = 1, 2, 3 and λs = 1.05 for i = 4, 5, 6; the intercept β0 was chosen so that the population disease prevalence was 5%. Figure 1 shows the locations of disease loci and nearby SNPs on the Illumina HumanHap300 SNP panel, and the LD as measured by r2 between the disease loci and the nearly SNPs.
Fig. 1.
Local LD patterns around the six disease loci used in simulations. Displayed is the pairwise r2 between the disease locus (solid grey line) and the SNPs on the HumanHap300 within 1 Mb from the disease locus (black dots).
Simulation of Case-Control Data
We generated 1,000 replicate data sets containing genotype data from 500 unrelated cases and 500 unrelated controls. For each individual, we first generated the genotypes at the pre-determined disease loci according to the disease model described above, and assigned one allele to each of the two chromosomes carried by that individual. The remaining genotypes of each chromosome were generated using the algorithm of Durrant et al. [14]. Letd denote the disease locus. For each chromosome, given the allele at d, the algorithm starts by picking, at random, a five-SNP haplotype at loci [d − 2, d + 2] from the 120 CEU founder chromosomes that has the same allele at d. The algorithm then gradually grows the whole chromosome as follows: for markers on the right side of the disease locus, it generates an allele at locus d + i given the haplotype at [d + i– 4, d + i − 1] for i ≥ 3; the conditional probabilities for the alleles at locus d + i given the haplotype at [d + i– 4, d + i − 1] are determined based on the HapMap phased data. Similarly, for markers on the left side of the disease locus, it generates an allele at locus d– igiven the haplotype at [d – i + 1, d – i + 4] for i ≥ 3. Genotypes for non-disease chromosomes were generated similarly except that a randomly selected SNP was designated as the starting SNP.
Note that the simulated chromosomes generated by this algorithm are not exact copies of those in the original HapMap samples. Rather, the 120 CEU founder chromosomes are used to generate plausible haplotypes in a wider population. This algorithm retains short-range LD patterns [14], upon which power is mostly determined.
Test of Association and Power Estimation
The disease locus genotypes were removed prior to data analysis. Allele frequencies in cases and controls were compared using a 1-d.f. chi-squared test. Markers with total allele count <5 for any allele were excluded from analyses. On average, only two to three such SNPs were excluded because the HumanHap300 chip consists mostly of SNPs with MAF ≥ 0.05. The FDR level used in all the procedures was q = 0.05. A success was declared if a significantly associated SNP was within 1 Mb from the disease locus. The power to detect association was computed as the fraction of successes among all replicate data sets.
Definition of Prioritized Subset
When defining the prioritized subset, we considered the following combinations: (i) the number of candidate regions in the prioritized subset (6, 14, 22); (ii) the size of the candidate regions (2 Mb, 20 Mb), and (iii) the number of disease loci included in the prioritized subset. The 2 Mb regions may resemble those determined on the basis of candidate genes, whereas the 20 Mb regions may be typical for those identified through linkage studies. If a region contained a disease locus, it was defined to be centered on the disease locus; candidate regions not containing any disease locus were picked randomly in the genome. All the candidate regions were unlinked to each other.
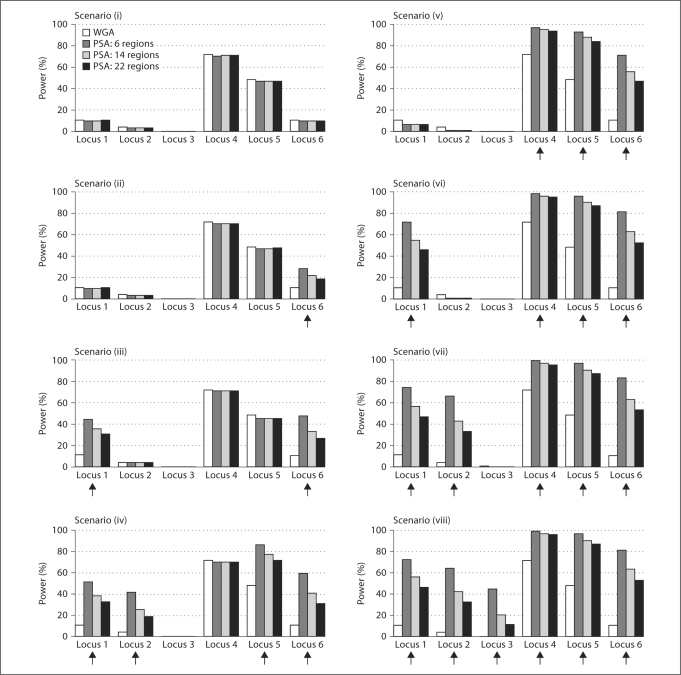
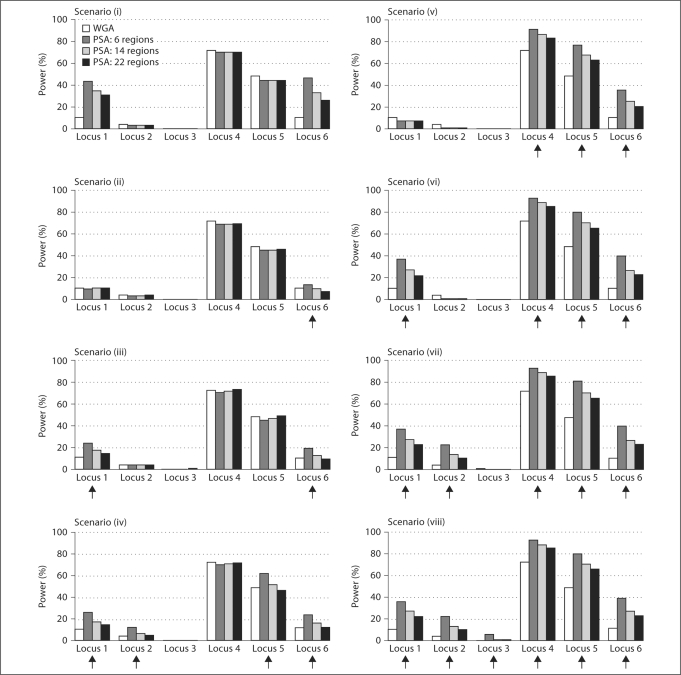
Several criteria can guide the choice of how many disease loci are included in the prioritized subset. Because the prioritized subset will likely include regions identified through previous linkage or associated studies, we considered the relative likelihood for our simulated disease loci to be identified in previous studies. Disease loci with strong effects are more likely to be identified than those with weak effects, and given the same marginal effect, disease loci in regions of strong LD are more likely to be identified in association studies than those in regions of weak LD. Following these rationale, we considered a variety of scenarios and defined the prioritized subset to include the three large effect disease loci and various numbers of the small effect disease loci. We also considered scenarios to examine the effect of exclusion of disease loci from the prioritized subset. Altogether, the following eight scenarios were considered (fig. 2, 3), with increasing number of disease loci included in the prioritized subset: (i) no disease loci; (ii) one large effect disease locus (locus 6); (iii) one large and one small effect disease loci (loci 1 and 6); (iv) two large and two small effect disease loci (loci 1, 2, 5, and 6); (v) the three large effect disease loci (loci 4, 5, and 6); (vi) the three large effect and one small effect disease loci (loci 1, 4, 5, and 6); (vii) the three large effect and two small effect disease loci (loci 1, 2, 4, 5, and 6), and (viii) all six disease loci. Note that our current knowledge may be limited so that only a small fraction of disease loci will be included in the prioritized subset. Nonetheless, these eight scenarios allow us to evaluate PSA under a broad range of possibilities.
Fig. 2.
Power comparison between the PSA and the WGA when the candidate region sizes were 2 Mb. The arrows indicate the disease loci that were included in the prioritized subset.
Fig. 3.
Power comparison between the PSA and the WGA when the candidate region sizes were 20 Mb. The arrows indicate the disease loci that were included in the prioritized subset.
Results
Power of the PSA
Figure 2 displays the estimated power of the PSA and the WGA when candidate region sizes were 2 Mb, and figure 3 displays the power when candidate region sizes were 20 Mb. As expected, the PSA is more powerful than the WGA for the disease loci that are included in the prioritized subset. For example, the power to detect disease locus 1 was 12% in the WGA, but it increased substantially when disease locus 1 was included in the prioritized subset. In scenarios (vi)–(viii) in which the prioritized subset had six candidate regions including disease locus 1 and the three large-effect disease loci, the power to detect disease locus 1 increased to 38% when the region sizes were 20 Mb (fig. 3), and further increased to 72% when the region sizes were 2 Mb (fig. 2). Clearly, if a prioritized region contains a disease locus, then a narrower region will lead to greater power improvement due to increased precision and a resulting smaller proportion of non-associated markers in the prioritized subset.
The power improvement also depended on how many other disease loci were included in the prioritized subset. For example, when the prioritized subset had six candidate regions and the region sizes were 2 Mb (fig. 2), the power to detect disease locus 6 increased from 12% in the WGA to 28% when it was the only disease locus included in the prioritized subset (scenario (ii)), to 46% when disease locus 1 was also included (scenario (iii)), to 59% when disease loci 1, 2, 5 were included (scenario (iv)), and to 81% when all the other disease loci were included (scenario (viii)).
The effect size of the other disease loci that were included in the prioritized subset also played a role. As an example, let us compare scenarios (iv) and (vi). Although both scenarios included disease locus 1 and three other disease loci, and both improved the power to detect disease locus 1 substantially, the magnitude of power improvement was quite different. When the prioritized subset had six candidate regions and the region sizes were 2 Mb, for scenario (vi), which included all three relatively large effect disease loci, the power increased from 12% in the WGA to 72% in the PSA, whereas the power increased to only 52% for scenario (iv) in which disease locus 4 was replaced by disease locus 2, a locus with smaller effect.
Moreover, the power improvement depends on how many non-disease regions were included in the prioritized subset; the more non-disease regions in the prioritized subset, the less improvement in power due to a higher proportion of non-associated markers in the prioritized subset. For each of the scenarios we considered, as the number of candidate regions increased from 6 to 22, the magnitude of power improvement decreased (fig. 2, 3). Nonetheless, if all six disease loci were correctly included in the prioritized subset (scenario (viii)), even when 16 other non-disease regions were also included, dramatic improvements in power could still be observed, especially when the prioritized region sizes were small.
While inclusion of disease loci in the prioritized subset often leads to substantial improvement in power, their exclusion incurs negligible power loss (fig. 2, 3). For example, when none of the disease loci were included in the prioritized subset (scenario (i)), the power of detecting association for all disease loci was almost the same as that of the WGA, regardless of the prioritized region size and the number of candidate regions in the prioritized subset. A similar phenomenon was observed for the weighted FDR procedure [5, 6] in which down weighting disease variants resulted in almost negligible power loss.
As expected, the power of detecting association with a disease locus depends not only on the effect of the variant, but also on the LD pattern surrounding the disease locus. A consequence of high LD around a disease locus is that many SNPs on the chip may tag the disease locus with high r2, providing multiple opportunities for the disease association to be detected, especially when the disease locus genotypes are not directly observed. For example, when all six disease loci were included in the prioritized subset (scenario (viii)), the power was 72% for disease locus 1 (in a strong LD region), whereas it was only 43% for disease locus 3 (in a weak LD region), despite the fact that they had the same genetic effect size. In either situation, our results showed that the PSA could substantially increase power, especially for disease loci in a weak LD region or with small genetic effect.
We repeated simulations with different MAFs and disease models, and observed similar pattern of power improvement for the PSA. These results suggest that the performance of PSA is robust to MAF and disease model (data not shown). We also repeated simulations with 100 cases and 100 controls, and observed similar patterns of power improvement, but the magnitude of power was near zero for the genetic effect sizes we simulated.
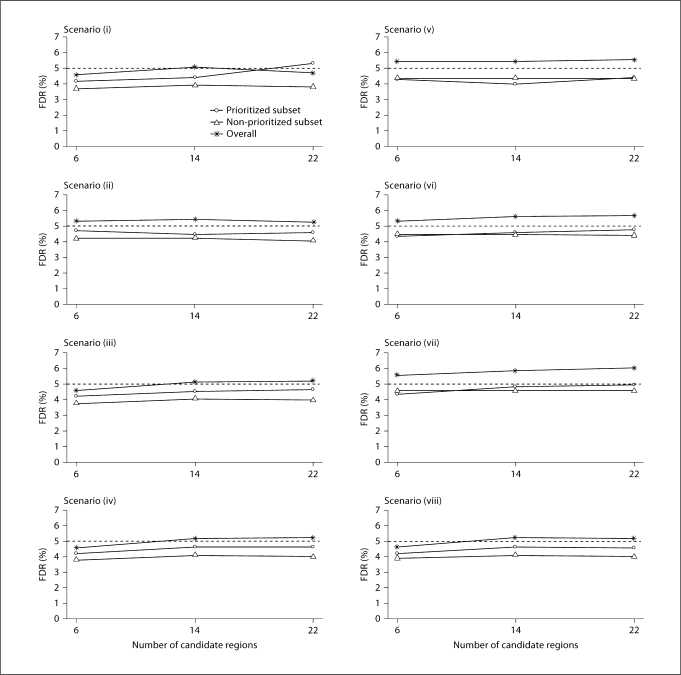
Overall FDR in the PSA
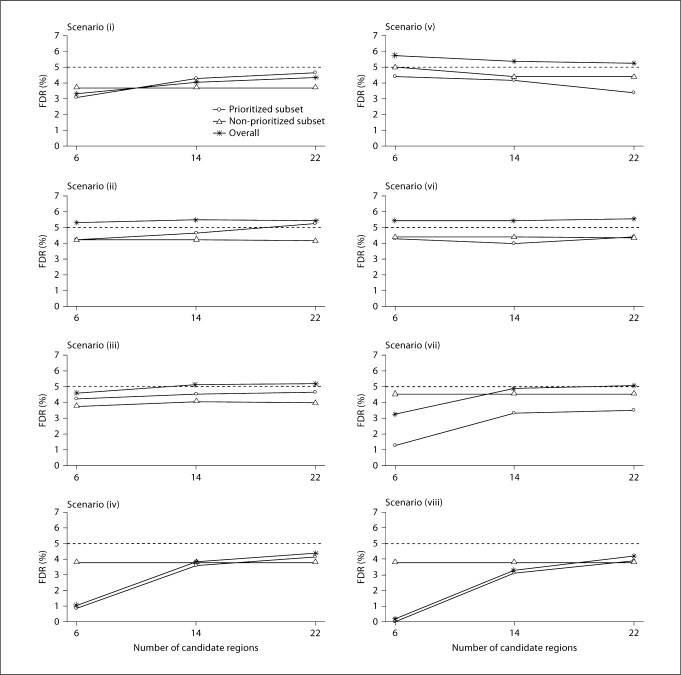
Our results (fig. 4 and 5) indicate that the overall FDR is under control. In the scenarios we considered, the FDR in the prioritized subset was even smaller than the overall FDR. In general, informative partitioning and accurate prior knowledge about disease gene regions tend to yield smaller overall FDR. In the extreme situation in which the prioritized subset consisted of the six disease loci and the size of each candidate region was 2 Mb, the overall FDR was near 0%. When the number of candidate regions and the region sizes increased, i.e., when the prior knowledge about the disease became less certain, the overall FDR increased. In most scenarios we considered, the overall FDR was greater than the FDR in both subsets, presumably because the overall fraction of false rejections tended to be dominated by the higher value of the fractions for the two subsets.
Fig. 4.
Overall FDR of the PSA when the candidate region sizes were 2 Mb.
Fig. 5.
Overall FDR of the PSA when the candidate region sizes were 20 Mb.
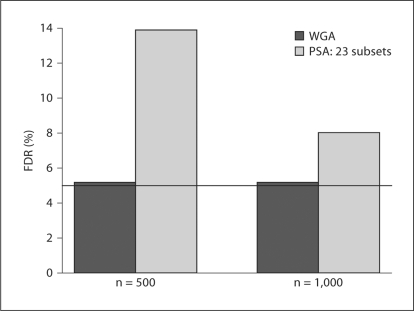
The tendency that the overall FDR is greater than the FDR in each subset may be stronger when the number of subsets is greater than two, which might lead to non-negligible inflation of the overall FDR when the genome is partitioned into many subsets. Examination of this issue is important because, for example, one might choose to carry out the FDR procedure separately for each chromosome, effectively splitting the genome into 23 subsets. Therefore, we carried out further simulations. We simulated 1,000 replicate data sets of n cases and n controls (n = 500, 1,000), and partitioned the SNPs into 23 subsets, one for each chromosome. We then carried out the FDR procedure in each subset and calculated the overall FDR. Figure 6 shows that this led to a substantial inflation in the overall FDR. When n = 500, the overall FDR was 13.9%, almost three times as much as the target FDR control level q = 5%. As the sample size increased to n = 1,000, the overall FDR was less inflated, but still was at about 8%.
Fig. 6.
Overall FDR for analysis on 23 subsets.
Sun et al. [8] demonstrated that the expected total number of true discoveries may increase as a result of the stratified FDR analysis. Here, we showed that the overall FDR also can increase as a result of stratification, presumably because the number of false discoveries might increase at a faster rate than the number of true discoveries as the number of subsets increases.
Discussion
GWAS generates massive amounts of data and as a result leads to a substantial multiple-testing problem. On the one hand, SNP panels with hundreds of thousands of SNPs are desired to ensure good coverage of the whole genome. On the other hand, these products result in a huge number of hypothesis tests that require appropriate adjustment. This problem is especially serious in GWAS, in which the SNP panels have variation in coverage across the genome and investigators typically have little control over what SNPs to type and what regions receive dense coverage, but at the same time are obligated to adjust for many tests. Regions with little relevance to a study might receive dense coverage and unnecessarily increase the number of tests. A common analysis strategy for GWAS is to perform association analysis for each SNP and adjust for multiple comparisons for all the tests in a single step, in which all SNPs are inherently treated equally. Such equal treatment of all SNPs is optimal only when all the SNPs have an equal chance, a priori, to be associated with the outcome, which is often not true given our prior knowledge about candidate genes and linked regions. We proposed the prioritized subset analysis (PSA) in which we define a prioritized subset to be comprised of SNPs in regions that may harbor disease genes and then carry out the FDR procedure in the prioritized subset and in the complementary non-prioritized subset, respectively.
We have demonstrated that the PSA is more powerful than the whole-genome single-adjustment approach under a variety of alternative models. The power improvement can be substantial depending on how much prior information is available. More accurate prior information leads to greater improvement in power. One consequence of this power improvement is that the sample sizes required to achieve a certain power can be greatly reduced for SNPs included in the prioritized subset. For example, disease locus 1 from our simulation would require about 1,200 cases and 1,200 controls to achieve 70% power to detect association. When prior information on candidate genes is mostly correct so that the prioritized subset consists of all disease genes, then the PSA can achieve similar level of power with only 500 cases and 500 controls. A nice property of the PSA is that even if the prior knowledge is not accurate, for example, in the worst situation, when none of the disease variants are included in the prioritized subset, the power loss of the PSA is negligible. Similar phenomenon has been observed in weighted FDR analysis [5, 6].
The power of the PSA depends not only on the effect of the disease locus itself, but also on other factors, including the sizes of the prioritized regions, the numbers of disease and non-disease regions in the prioritized subset, and the effect sizes of the other disease loci included in the prioritized subset. All these factors determine the fraction of associated SNPs in the prioritized subset and their nominal power. In the FDR procedure, a test can ‘borrow the strength’ of the other tests: the power increases when the fraction of tests under the alternative hypotheses or their nominal power increases. The PSA improves power by taking advantage of this property. When the prioritized subset is defined such that it includes most disease gene regions or disease loci with relatively strong effect, the prioritized subset will, compared to the whole set, have a denser fraction of tests under the alternative hypotheses or relatively higher nominal power among such tests. As a result, for a SNP that is included in the prioritized subset, the PSA will likely have higher power to detect association with the disease than the WGA.
The PSA differs from the previously proposed approaches [5, 6, 8]. Genovese et al. [5] and Roeder et al. [6] proposed a weighted FDR approach and illustrated it by using prior linkage information to define weights for individual SNPs, effectively resulting in a less stringent threshold for SNPs within linkage peaks versus those outside. However, prior information regarding disease susceptibility loci often comes from multiple sources other than linkage. For example, we often have some biological hypotheses about the disease, which facilitate identification of candidate genes (e.g., KCNJ11 and ABCC8 may be candidate genes for type 2 diabetes because they are the two subunits of the β-cell KATP channel). Results also may be available from previous association studies for the trait of interest or other related traits (e.g., for type 2 diabetes, CAPN10[15], HNF4α [16], and SLC30A8 and HHEX[13]). Although the weighted FDR approach can be applied to SNPs outside linkage regions, it may be difficult to choose appropriate weights from among a variety of possible weighting schemes. As a result, researchers might find it daunting to use because they must not only choose which SNPs to receive higher weights as well as which weighting scheme to utilize, but they are also compelled to justify and interpret the impact of all of the different weights. The PSA does not assign different weights to different subsets of SNPs, rather the PSA simply involves categorizing SNPs into two different risk subsets (presumed high risk versus low risk). The weighted FDR could use a binary weighting scheme to differentiate between presumed high risk and low risk SNPs. However, it is important to note that the weighted FDR still performs a single FDR adjustment (for a set containing both up-weighted high risk SNPs and down-weighted low risk SNPs) while the PSA performs two separate FDR adjustments (one for the subset containing high risk SNPs and one for the subset containing low risk SNPs). It has been proven previously that the FDR for the weighted FDR method is well controlled [5] and we have demonstrated via simulation that the overall FDR for PSA is also well controlled. Future studies should compare the two different approaches in terms of statistical power over a wide range of alternative models and different weighting schemes for the weighted FDR.
Sun et al. [8] stratified SNPs on their ‘qualities’ such as minor allele frequency, which has little to do with the SNPs’ potential functionality or the prior knowledge of trait-marker associations. As a result, their approach does not lead to noticeable power improvement. In practice, one would like to select out SNPs that are non-synonymous, have known functionality, or lie within candidate genes. In this paper, we showed that stratifying based on prior information pertaining to the genetics of the trait can be quite helpful. In addition, Sun et al. [8] did not evaluate the effect of stratification on the overall FDR. They showed the stratified analysis may have the advantage of having more true positives. However, at the same time, the number of false positives may also increase as the number of subsets increases, leading to inflation of the overall FDR, a quantity that we desire to control. Our results suggest that it is best to have a single prioritized subset so that a SNP can borrow the strength of the other SNPs included in the same subset. If the potentially associated SNPs were to be split into more than one subset, the overall strength may be diluted and the power advantage of the PSA could be diminished.
We feel it is necessary to provide some recommendations on how the PSA will be applied in practice. One of the major advantages of GWAS using commercial genotyping platforms is the transparency of the analytic design. Unlike individual candidate gene association studies, it is typically known how many SNPs, in total, have been studied in a GWAS. This transparency allows the scientific community to put into proper perspective the overall statistical significance of the findings. We believe the benefit of applying the PSA to GWAS data is compelling. However, without careful consideration, the PSA could be exploited to show seemingly superior results, especially when one seeks to define the prioritized subset after looking at the data. A priori determination of the prioritized subset is necessary to maintain valid estimates of statistical significance. To keep the transparency of GWAS, we recommend documenting the SNP subset assignments prior to conducting PSA. This can help ensure that the information used in prioritization is independent of the observed p values [8]. The prioritized subset can be defined based on information from multiple sources. For example, linkage analysis results are useful for defining candidate regions, and genome annotation databases or previous published association findings are useful resources for defining candidate genes. Moreover, one might partition the genome in a greedy way such that the prioritized subset contains a small number of regions. Although this increases the power for the SNPs included in the prioritized subset, it offers no power gain for other potential genes and regions that are excluded. Thus, in the absence of good a priori information, such greedy partitioning likely will not help much and should be discouraged.
For multiple outcome variables, the need to partition the tests into more than two subsets may arise. Sun et al. [8] described a situation in which 1,500 SNPs were analyzed to look for correlation with five outcome variables. For each outcome variable, there were 1,500 tests. One could carry out a single FDR adjustment for all 7,500 tests, or five separate FDR adjustments, one for each outcome variable. Because the numbers of associated SNPs may vary substantially across the five variables, Sun et al. [8] demonstrated it would be more powerful to carry out separate adjustment. However, we caution that analysis on many subsets may lead to inflation of the overall FDR.
In principle, the PSA can be applied to situations in which multiple hypothesis tests are performed and the investigator has a prior knowledge on the relative likelihood for the tests to lead to significant results. For example, when studying gene-gene or gene-environment interactions, it would be desirable and probably more powerful to define a prioritized subset consisting of plausible combinations of gene-gene or gene-environment pairs than considering all possible pairs in a single adjustment. In candidate gene studies, investigators may rely on cost-efficient multiplex genotyping assays that will genotype a fixed number of SNPs at a time. Often the number of SNPs an investigator is willing to genotype is not exactly the allowed number on the assay, and adding SNPs to fill the assay would incur little additional costs. In this situation, investigators often choose to fill in the spaces with ‘extra’ SNPs, which they may not have chosen to genotype if substantial cost were involved. In other words, these additional SNPs may have relatively lower priority compared to the originally selected ones. In this situation, a single adjustment for multiple testing for all the SNPs may lower the power for the originally selected SNPs, and the PSA would be a more powerful alternative.
When external information is available, it is often desirable to incorporate such information into analysis so that more efficient use of the full genomic data can be achieved. The PSA takes into account prior information on candidate genes and linked regions by defining a prioritized subset to comprise the SNPs falling in these regions. Some other methods have also been developed to combine prior information into analysis, for example, genomic convergence [17] and the weighted FDR procedure [5, 6]. The PSA is a powerful, intuitive, and easily implemented approach for GWAS. Furthermore, the PSA has the flexibility of allowing the investigators to combine prior information from a variety of sources and does not require assigning different combinations of weight factors. We believe that the PSA will be a useful addition to the existing toolbox of statistical methods.
Acknowledgements
This work was supported by an internal grant from the Center for Human Genetics Research at Vanderbilt University (to C.L.), the University Research Foundation grant and the McCabe Pilot Award from the University of Pennsylvania (to M.L.), National Institutes of Health grants P20 RR020751-01-02 and R01 DK066368-03 (to E.M.L.), and American Diabetes Association research grant 1-05-RA-140 (to R.M.W.). This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, Tenn., USA.
References
- 1.Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nat Rev Genet. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
- 2.Wang WY, Barratt BJ, Clayton DG, Todd JA. Genome-wide association studies: theoretical and practical concerns. Nat Rev Genet. 2005;6:109–118. doi: 10.1038/nrg1522. [DOI] [PubMed] [Google Scholar]
- 3.Hinds DA, Stuve LL, Nilsen GB, Halperin E, Eskin E, Ballinger DG, Frazer KA, Cox DR. Whole-genome patterns of common DNA variation in three human populations. Science. 2005;307:1072–1079. doi: 10.1126/science.1105436. [DOI] [PubMed] [Google Scholar]
- 4.The International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Genovese CR, Roeder K, Wasserman L. False discovery control with p-value weighting. Biometrika. 2006;93:509–524. [Google Scholar]
- 6.Roeder K, Bacanu SA, Wasserman L, Devlin B. Using linkage genome scans to improve power of association in genome scans. Am J Hum Genet. 2006;78:243–252. doi: 10.1086/500026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc B. 1995;57:289–300. [Google Scholar]
- 8.Sun L, Craiu RV, Paterson AD, Bull SB. Stratified false discovery control for large-scale hypothesis testing with application to genome-wide association studies. Genet Epidemiol. 2006;30:519–530. doi: 10.1002/gepi.20164. [DOI] [PubMed] [Google Scholar]
- 9.Maraganore DM, de Andrade M, Lesnick TG, Strain KJ, Farrer MJ, Rocca WA, Pant PV, Frazer KA, Cox DR, Ballinger DG. High-resolution whole-genome association study of Parkinson disease. Am J Hum Genet. 2005;77:685–693. doi: 10.1086/496902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Benjamini Y, Yekutieli D. False discovery rate-adjusted multiple confidence intervals for selected parameters (with discussions) J Am Stat Assoc. 2005;100:71–93. [Google Scholar]
- 11.Sabatti C, Service S, Freimer N. False discovery rates in linkage and association genome screens for complex disorders. Genet. 2003;164:829–833. doi: 10.1093/genetics/164.2.829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grant SF, Thorleifsson G, Reynisdottir I, Benediktsson R, Manolescu A, Sainz J, Helgason A, Stefansson H, Emilsson V, Helgadottir A, Styrkarsdottir U, Magnusson KP, Walters GB, Palsdottir E, Jonsdottir T, Gudmundsdottir T, Gylfason A, Saemundsdottir J, Wilensky RL, Reilly MP, Rader DJ, Bagger Y, Christiansen C, Gudnason V, Sigurdsson G, Thorsteinsdottir U, Gulcher JR, Kong A, Stefansson K. Variant of transcription factor 7-like 2 (TCF7L2) gene confers risk of type 2 diabetes. Nat Genet. 2006;38:320–323. doi: 10.1038/ng1732. [DOI] [PubMed] [Google Scholar]
- 13.Sladek R, Rocheleau G, Rung J, Dina C, Shen L, Serre D, Boutin P, Vincent D, Belisle A, Hadjadj S, Balkau B, Heude B, Charpentier G, Hudson TJ, Montpetit A, Pshezhetsky AV, Prentki M, Posner BI, Balding DJ, Meyre D, Polychronakos C, Froguel P. A genome-wide association study identifies novel risk loci for type 2 diabetes. Nature. 2007;445:881–885. doi: 10.1038/nature05616. [DOI] [PubMed] [Google Scholar]
- 14.Durrant C, Zondervan KT, Cardon LR, Hunt S, Deloukas P, Morris AP. Linkage disequilibrium mapping via cladistic analysis of single-nucleotide polymorphism haplotypes. Am J Hum Genet. 2004;75:35–43. doi: 10.1086/422174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Horikawa Y, Oda N, Cox NJ, Li X, Orho-Melander M, Hara M, Hinokio Y, Lindner TH, Mashima H, Schwarz PE, del Bosque-Plata L, Horikawa Y, Oda Y, Yoshiuchi I, Colilla S, Polonsky KS, Wei S, Concannon P, Iwasaki N, Schulze J, Baier LJ, Bogardus C, Groop L, Boerwinkle E, Hanis CL, Bell GI. Genetic variation in the gene encoding calpain-10 is associated with type 2 diabetes mellitus. Nat Genet. 2000;26:163–175. doi: 10.1038/79876. [DOI] [PubMed] [Google Scholar]
- 16.Silander K, Mohlke KL, Scott LJ, Peck EC, Hollstein P, Skol AD, Jackson AU, Deloukas P, Hunt S, Stavrides G, Chines PS, Erdos MR, Narisu N, Conneely KN, Li C, Fingerlin TE, Dhanjal SK, Valle TT, Bergman RN, Tuomilehto J, Watanabe RM, Boehnke M, Collins FS. Genetic variation near the hepatocyte nuclear factor-4 alpha gene predicts susceptibility to type 2 diabetes. Diabetes. 2004;53:1141–1149. doi: 10.2337/diabetes.53.4.1141. [DOI] [PubMed] [Google Scholar]
- 17.Hauser MA, Li Y-J, Takeuchi S, Walters R, Noureddine M, Maready M, Darden T, Hulette C, Martin E, Hauser E, Xu H, Schmechel D, Stenger JE, Dietrich F, Vance J. Genomic convergence: identifying candidate genes for Parkinson's disease by combining serial analysis of gene expression and genetic linkage. Hum Mol Genet. 2003;12:671–677. [PubMed] [Google Scholar]