Collective behaviour in gene regulation: The cell is an oscillator, the cell cycle a developmental process

Abstract

The finding of a genome-wide oscillation in transcription that gates cells into S phase and coordinates mitochondrial and metabolic functions has altered our understanding of how the cell cycle is timed and how stable cellular phenotypes are maintained. Here we present the evidence and arguments in support of the idea that everything oscillates, and the rationale for viewing the cell as an attractor from which deterministic noise can be tuned by appropriate coupling among the many feedback loops, or regulons, that make up the transcriptional-respiratory attractor –cycle (TRAC). The existence of this attractor also explains many of the dynamic macroscopic properties of the cell cycle and appears to be the timekeeping oscillator in both cell cycles and circadian rhythms. The path taken by this primordial oscillator in the course of differentiation or drug response may involve period doubling behavior. Evidence for a relatively high frequency timekeeping oscillator in yeast and mammalian cells comes from expression array analysis and GCMS in the case of yeast and primarily from macroscopic measures of phase response to perturbation in the case of mammalian cells. Low-amplitude, genome-wide oscillations, a ubiquitous but often unrecognized attribute of phenotype, could be a source of seemingly intractable biological noise in microarray and proteomic studies. These oscillations in transcript and protein levels and the repeated cycles of synthesis and degradation they require, represent a high energy cost to the cell which must, from an evolutionary point of view, be recovered as essential information. We suggest that the information contained in this genome wide oscillation is the dynamic code that organizes a stable phenotype from an otherwise passive genome.

The temporal organization of cellular phenotype is oscillatory not stochastic

The idea that regulation of gene expression and protein synthesis are stochastic endures despite computational studies and a significant body of experimental evidence for viewing the cell as a network of coupled oscillators. Stochasticity in gene regulation is driven principally by the low message copy number conundrum but lacks the predictive power of attractor models when extended beyond a few genes to a consideration of the precision of cellular clocks and circadian rhythms (1-4) Genome wide oscillations in transcription bring into question models of cellular phenotype that assume steady state, stochastic based mechanisms for regulation of protein and transcript levels (5-7). Instead, this precise temporal organization favors a view of cellular phenotype as a globally coupled dynamic structure, a periodic attractor (8-10). Here, we can focus the argument for one or the other of these two alternative models for regulation of gene expression by a close analysis of a recent study by Newman and his colleagues (7) These workers, examined the contribution of extrinsic and intrinsic noise (5) to the regulation of protein levels in Saccharomyces cerevisiae. By flow cytometric sorting of 4130 cultures, each with a different green fluorescent protein (GFP) tagged protein, they were able to compare relative levels of about 2500 proteins under several different growth conditions and different media. Based on the assumption of steady state kinetics, that is that protein expression varied in a way that was independent of any underlying intrinsic oscillatory dynamics, they identified several processes and a number of genes whose behavior was classified as nosy or quiet. Genes involved in protein synthesis and degradation were quiet while those that functioned in the peroxisome or amino acid biosynthesis were noisy. Additionally, they found several paradoxical relationships – most notably instances where protein levels were high when the corresponding message was low. While this work was a technical tour de force, it does admit of another interpretation, one that is both predictive of the apparent noisiness of gene regulation and consistent with the precision of known biological rhythmicities. .

A transcriptional attractor explains apparent noise in protein regulation

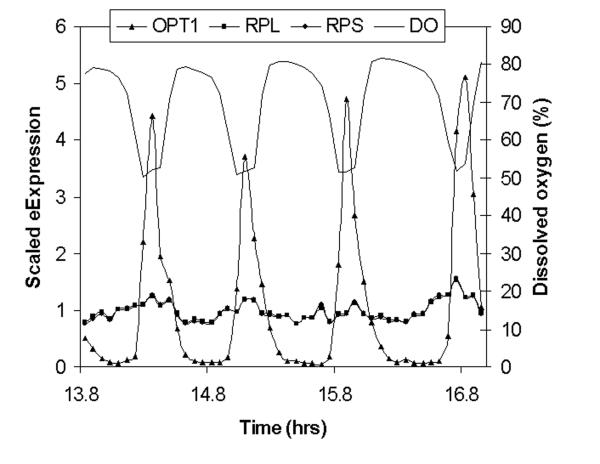
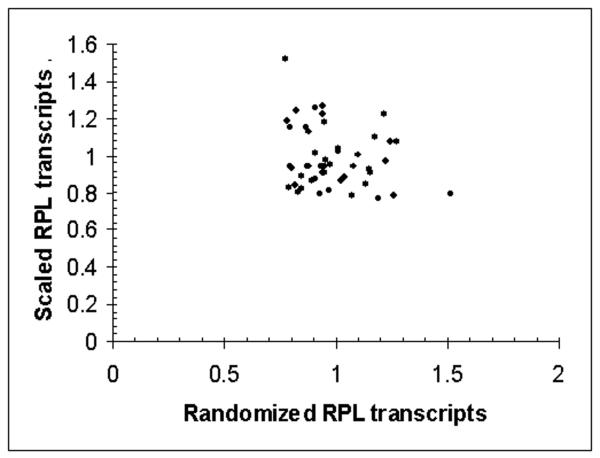
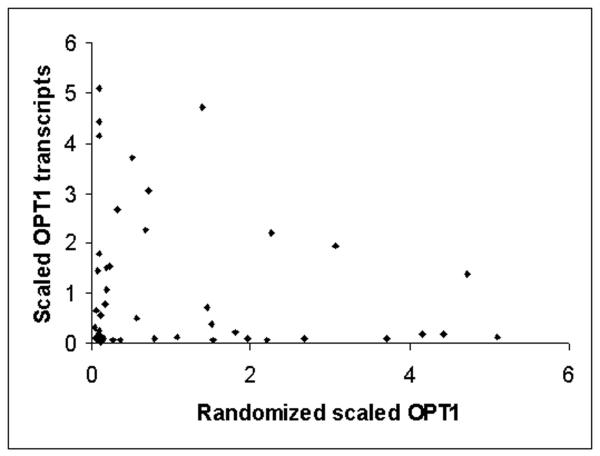
Using the classifications of Newman et al (7) to identify proteins whose regulation was “noisy” or” quiet”; we examined the patterns of expression in our gated synchrony culture system (1). Functionally related groups of proteins whose regulation was found to be quiet such as Golgi, ribosomal and other translation related functions showed regular low amplitude (1.1-2.1 fold) oscillations in transcription, while stress, respiratory, peroxisomal, and other proteins classed as noisy, were characterized by precise but very high amplitude (2 to 72-fold) oscillations. In figure 1A, the pattern of expression through four transcriptional cycles of the TRAC of transcripts whose protein regulation in temporally uncharacterized cultures of S. cerevisiae were classified as noisy are shown. These transcripts were also identified as having high coefficients of variation (CV) values in flow cytometric analysis of GFP fluorescence distributions. This pattern generalizes throughout the transcriptome – quiet genes show low amplitude oscillations noisy genes express transiently at high amplitudes. In figure 1B n example of a single transcript, OPT1 and the averages of all the large ribosomal proteins (RPL) and small ribosomal proteins (RPS) transcripts are shown. In figures 1C and 1D the expression values of OPT1 and the ribosomal transcripts are randomized and a scatter plot of the randomized values are shown to simulate how these genes might appear if analyzed in flow. It is clear that the apparent variation in OPT1 is much greater than the average of the ribosomal transcripts and OPT1 might be incorrectly scored as having a low abundance or as having “quality control” problems.

Figure 1. Noisy and quiet genes represent high and low amplitude oscillations.

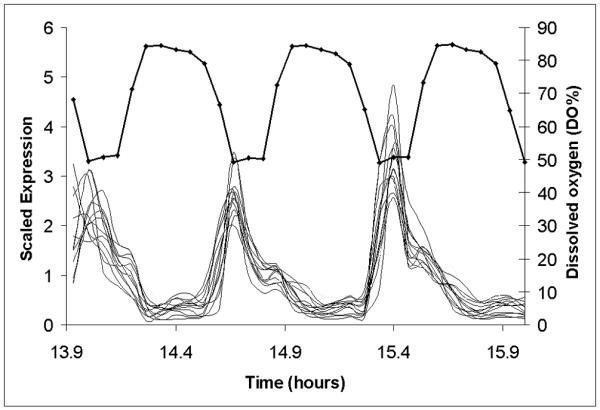
In figure 1A, transcripts from the gated synchrony culture system, whose proteomic patterns and CV classed them as noisy are shown in relationship to the benchmark oscillation in dissolved oxygen. Sixteen transcripts maximally expressed in the respiratory phase are shown (solid lines) in relationship to dissolved oxygen (filled circles-). In figure 1B, one of these transcripts, OPT1 (filled triangles), is shown relative to the averages of all 52 of the small ribosomal protein transcripts (filled circles)) and all 74 of the large ribosomal protein transcripts (filled squares). In both figures the expression for each gene is scaled by dividing each value by the average of all values for that gene in the first or control cycle of the experiment (first 11 samples). Intensity values for the high amplitude oscillation transcript OPT1 range from 200 to 6000 intensity units. Scatter plots of the randomized expression values for OPT1 (figure 1D) and RPS (figure 1C) indicate the differences in variance that might be expected if sampling was done on a temporally uncharacterized culture.

In an earlier work (2) we Fourier filtered the transcripts scored as present in all the samples taken for the time series analysis, and then ordered them according to power shown at 40 minutes, the period of the transcriptional oscillation in our strain IFO0233. Of the 4429 transcripts scored as present, 4328 showed maximum power in the 40-minute range by FFT analysis (2). This is very similar to the number (4311) found with maximum power at 40 minutes in our previously published control series (1). This analysis suggests that 4328 (97.7 %) of the 4429 expressed genes show maximal power in the 40 minute range. From this set, we have matched the 500 most periodic against the Table 1 of the Newman study and find 155 of these made the discrimination categories and were further analyzed by these authors. The variance in this group was much greater than that in the population of GFP labeled proteins as a whole. What is most important is the observation that of the 50 most periodic in our work, only 16 were able to be analyzed by Newman and all but two of these were among the least periodic of the group. Those eliminated from that study were often eliminated due to low abundance. In some instances these were proteins whose messages in our synchronous cultures showed very high intensities. We reason that these proteins are made periodically, as their messages are, and in many instances catabolized rapidly. In our transcript group, only 3 of every 12 samples show levels much above background and only one in 12 show high levels. In a random or temporally uncharacterized population only 8-20% of the cells would give good signals. To illustrate this, a set of 15 genes have been selected that show periodic expression at rather high levels and yet appeared to be of low abundance (Figure 1A).One of these, MET14 reaches intensity levels of more than 17000 and then rapidly falls to levels of 300 units. The tendency in flow analysis of GFP tagged proteins in a population of cells may have been to exclude the most periodic proteins based on assumptions of stochastic regulation, constitutive synthesis or random variations in level around the steady state

These high amplitude oscillations, where expression levels go from background to maximum and return to background level very quickly, are characteristic of about 20% of the transcriptome. This pattern would seem to provide direct visual evidence of the low level of combined biological and measurement noise that is possible in a well controlled biological system. Newman noted that for some proteins, levels of the coding transcript were inversely correlated with the level of protein. Such a seemingly paradoxical outcome is understandable from the pattern of expression in the high amplitude oscillations shown in Figure 1 and is a predicted consequence of periodic zero order synthesis and constant first order decay of the message under almost any circumstance where the protein has a longer half-life than the message. . Calculations based on this assumption yields a signal to noise ratio of greater than 50 db for many of the transcripts showing this pattern of oscillation. Note that the data used for figure above was taken from the phenelzine treatment experiment so that cycles 2-4 are post treatment. The increase in level of the transcripts is associated with the treatment.

One caveat remains – it is possible that the oscillations are driven by the process that causes the cultures to synchronize. Evidence of quantized generation times in mammalian cells tends to refute this idea but it does seem plausible that synchronization might increase the amplitude of the oscillation. Inherent in many of the starting points for analysis of microarray data is the idea that the underlying process involves cells that exist at a steady state and that the values obtained come from an ergodic process. The distinction between what can be found in high throughput data from temporally uncharacterized biological systems by the application of appropriate methods such as singular value decomposition (SVD) or principle component analysis (PC) and the relevance of this to ergodic theory has been addressed in detail by Giuliani and his colleagues (11).

Evidence for genome wide oscillations in transcription

Expression levels were determined using Affymetrix microarrays in two separate experiments during which a total of 80 time series samples were taken through 7 cycles (4 control cycles - 3 treated) of the oscillation. We showed that oscillations are a ubiquitous property of yeast transcripts (1, 2). The temporal organization that gives rise to the well characterized 40 minute oscillation in dissolved oxygen (DO) is manifested in the sequestering of transcripts into those maximally expressed in the reductive phase and those maximally expressed in the respiratory phase. Typically, the reductive phase is roughly twice the length of the respiratory phase and expression maxima are largely restricted to three equally spaced intervals in the cycle—one in the respiratory phase and two in the reductive phase. We have suggested that this TRAC is responsible for the temporal organization of phenotype and for the timing of developmental processes such as the cell cycle. The temporal coordination manifested by the TRAC appears to involve essentially all cellular functions thus far examined. Given the alternation of the redox state, it should not be surprising to find that the alternation of respiration and reduction also extends to the functional state of the mitochondria (4, 27, 28). Of current interest is the role that these high amplitude oscillations play in protein synthesis, degradation and functional state. Transcripts for ubiquitin-proteosome function are made at just one phase of the cycle suggesting that protein catabolism is temporally organized and oscillatory. Additionally, transcripts for mitochondrial and cytosolic ribosomal proteins, sulfur metabolism, amino acid biosynthesis and most of the Golgi and peroxisome related transcripts are made together at particular points in the cycle. This temporal organization extends to the synchronous gating of cells into S-phase. DNA replication in these cells begins abruptly at the end of the respiratory phase as oxygen consumption decreases and H2S levels rise. The restriction of DNA replication to the reductive phase of the cycle is seen as an evolutionarily important mechanism for preventing oxidative damage to DNA during replication. The time sharing that occurs in each redox cycle reproduces the two antithetical environments that are thought to have led to the fusion of primitive unicells – one an Archaeal host capable of producing H₂S from environmental sulphate and a proteobacterial H₂S oxidizing endosymbiont engulfed by phagocytosis (12, 13). This circa 40 minute metabolic cycle has been observed in essentially every unicellular system examined. Making the connection between this well known metabolic cycle, transcription, DNA replication and the cell cycle heightened interest in the relationship between oscillations and the organization of phenotype. The evidence that the cell is a coupled oscillatory system has been further strengthened since the original observation discussed above by studies by Murray and his colleagues on the oscillation in a large proportion of the metabolites of S. cerevisiae growing in gated synchrony cultures and displaying a 40 minute period (3).

Are the dynamics underlying oscillating culture systems in all cases similar?

Following on our original report (1), other laboratories took up the system and repeated most of the generalizations including the genome wide nature of the transcriptional oscillation and the restriction of DNA replication to a phase of the cycle when hydrogen sulfide levels were providing a reducing environment. However, the metabolic cycle of these cells was 5 hours long and the amplitude of the ribosomal protein transcripts was very high. Whereas our gated synchrony system maintains glucose levels in the range optimal for production of aromatic alcohols, these 5 hour cultures were growing in medium containing half the initial glucose and were described as nutrient limited. (14). The very high level of synthesis and degradation of the ribosomal transcripts, the relatively higher levels of transcripts made at restricted points in the cell cycle and the lack of phase correspondence (Figure 2) between our studies and theirs lead us to suggest that system is In most ways more like reversal of an arrested cell cycle than a stochastic tissue. Experimentally there seems little doubt that cells do display genome wide oscillations in transcription despite statistical arguments which would limit the number of oscillatory transcripts to some significant fraction of all transcripts. This quickly degenerates into an argument regarding the best method of describing a transcriptome. If we start we the belief that cells are at equilibrium unless driven or perturbed away from that state then it is natural to assume that the variability in transcript or protein levels in temporally uncharacterized cultures is a measure of regulatory noise and if some processes or cellular components seem to have more or less of this noise it is natural to attempt to incorporate this phenomenon into the regulatory machinery of the cell. The correlation between noisy proteins and precise high amplitude oscillations is very good and the evidence that one can say that transcripts with low amplitude oscillations are oscillatory is strong. It comes down to the idea that in expression microarrays certain platforms and methods of amplifying and detecting levels of message are much better than we might have thought which implies that in many cases the underlying cell biology is poorly defined in the time domain.

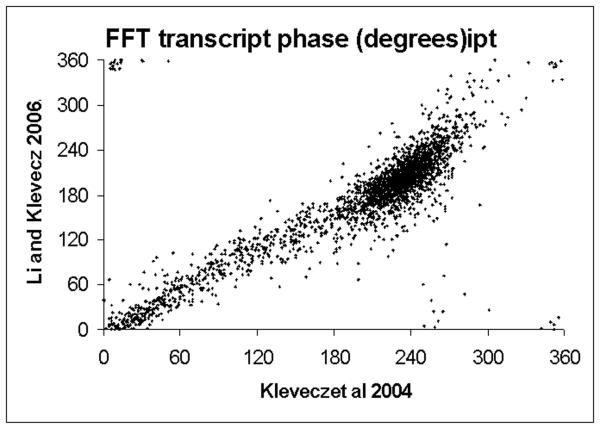
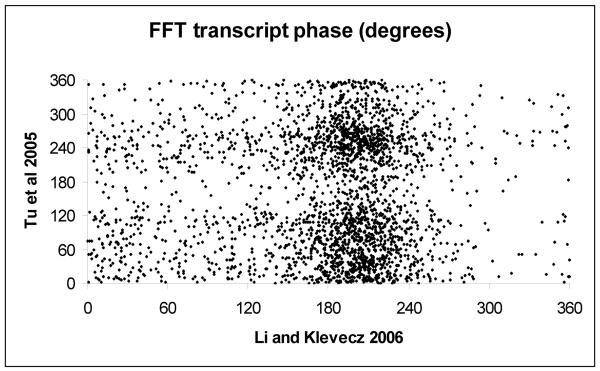
Figure 2. Phase relationships of transcripts from short and long period metabolic cycles.

Scatter plots of all periodic transcripts found to be present in all three of the time series data sets considered are shown (1, 2, 14). In figure 2A the results of the original control series are paired with the results from the phenelzine perturbation experiment. Perfect correspondence would appear as a dotted line with a slope of one. In the original phenelzine it was noted that the major effect of the drug initially delay the phase of maximum expression in the mid-reductive phase transcripts. This led to a transient increase in period length in the oscillation. The delay in phase is manifested in a population of transcripts displaced downward from the line of correspondence. Slight differences in phase from near zero to near 360 degrees are a plotting artifact. In figure 2B the results of Li and Klevecz (2) are plotted against those of Tu et al (14).

To further this crucial recognition of the new paradigm we urge increased attention to source and sampling of biological systems and the application of analytical tools more appropriate to time series data a or extraction of the global properties of the system such as singular value decomposition (SVD), principle component analysis (PCA), self organizing maps (SOM), wavelet multiresolution decomposition (WMD) and for high quality time series data Fourier analysis (FFT). As discussed in detail below, prior to the exploitation of the gated synchrony culture system to collect true time series data sets, expression arrays were applied to cells in forced synchronization methods and involved data sets too short and noisy for comfortable application of Fourier analysis. We now have the capacity to follow the transcriptional patterns of all expressed genes to construct a system-wide dynamic network. By assessing the temporal pattern of gene expression in all of the transcripts closely through time following perturbation, we can begin to construct the dynamic architecture of phenotype and to derive the first measurements of coupling strength among genes. Such information is essential to constructing a detailed formal representation of the cellular attractor. Network representations based on two-hybrid, chip-chip or mass spectrometry interactions (15-20) give us a sparse mapping of genes that interact but have not offered clear insights into dynamic connectivity among genes and their transcripts. One effort here is to bring together genome-wide changes through time and the more traditional gene centered steady-state network perspective.

Some details of the analysis of time series data from the gated synchrony system

Application of Fourier analysis and wavelet decomposition to the available time series data sets finds that more than three quarters of all transcripts expressed in S. cerevisiae can be shown to oscillate. Limiting such time series analysis to transcripts found to be present in all samples from a time series study finds that all but 2% are oscillatory Those that fail the test frequently show higher frequency oscillations or are of such low expression as to make them practically unanalyzable. Alternatively, by setting the p-value for significance of the variance obtained through classical statistical processes sufficiently high, greater than .001, it is possible to make the claim that just a few hundred transcripts oscillate. Better than any other argument, this shows the chasm between statisticians and dynamicists and the importance of having the correct model through which the data analysis is pursued. .

Using the data from the three time series data sets with sufficient sample length and density to permit Fourier analyses, we find that the original report has 4169 transcripts that show a 40 minute period (Klevecz et al), where each of the three cycles were scaled prior to analysis. This was done as described in the original paper because the data were taken from two separate experiments with slightly different amplitudes and periods of oscillation. In the second study by Li and Klevecz (2) using what we regard as the optimal adjustment for hybridization efficiency we get 4328 transcripts with a 40 minute periodicity. Using this same adjusted data and applying an adjustment for sequence that number goes to 4780. In the case of the Tu et al (14) data, using their raw CEL files we find 4832 transcripts with a period of ~5 hours, equal to that of the dissolved oxygen, while using the GSM files we find 4910 periodic transcripts. One major difference between the findings from the two laboratories is in the period of the oscillation. This makes difficult any conclusion beyond the obvious one that in both systems most all transcripts oscillate The standard strain, IFO0233, used in many of the earlier works has a period of ~40 minutes and it must be noted that all of the earlier studies on what was called an ultradian or metabolic oscillation reported an oscillation in oxygen consumption in the 40 minute range. The CEn.PK strain cells in our hands have a period that varies, quantally between 2 hours and 4 hours. The report from Tu et al (14) describes an oscillation with a period of 5 hours. The greatest differences in the results from the two strains are in the phase of maximum expression. This difference appears to be emphasized if the phase is determined from the FFT analysis. Even though the sampling density and length is greater than anything done previously, it appears insufficient to allow FFT analysis to dissect the correct phase s. Reductive phase transcripts in our studies frequently had two maxima, one in early reductive and one in late reductive. Fourier is unable in most instances to distinguish these and instead finds a mid-reductive maximum (Figure 2B). However, this by itself is not sufficient to account for the phase differences between our data (1, 2) and that of Tu (14). Here we show the genome scale comparison of the phases of maximum expression in the three data sets (figure 2). The comparison between our 2004 and 2006 data sets is quite good considering that the 2006 data set was taken prior to and following a treatment with phenelzine a drug that alters the period of the oscillation. Indeed, the beginnings of the phase response to the drug treatment can be seen in the cluster of transcripts the fall away from the line of perfect correspondence of phase. Plotting as a scatter plot either of our results against the Tu data yields a pattern with little correlation. Of interest is the somewhat different result that comes out of a matching of phases from the scaled data from the three sets using a simple calculation of maximum expression (data not shown).

In many ways the simplest projection, a color temperature map in which the level of gene expression, from red maxima to blue minima (1,2)is the most informative of the overall behavior of the transcriptome and shows very clearly that expression maximums sequestered temporally to certain phases of the oscillation. SOM analysis tends to associate transcripts with similar phases of expression and when embodied as it is the GEDI analysis (15) enables one to use the color temperature map dynamically and in effect make a movie of the phase and amplitude relationships among the transcripts through the cycles of oscillation (2). Thus far we have been considering only individual transcripts analytically and then putting them into a system wide perspective by the method of presentation. PC and SVD analysis use the collective properties of the system to extract the information content and present it a set of vectors of reduced dimensionality. All of these methods lead one to conclude that the cell is an oscillator. For those few constituents that cannot be shown to oscillate, we will point to dynamic systems theory, which says that as more things oscillate in a coupled system the likelihood that everything oscillates increases (16). . We would conclude that if more than half of all expressed transcripts oscillate then this probability becomes a near certainty.

Picturing the cellular phenotype in concentration space and time

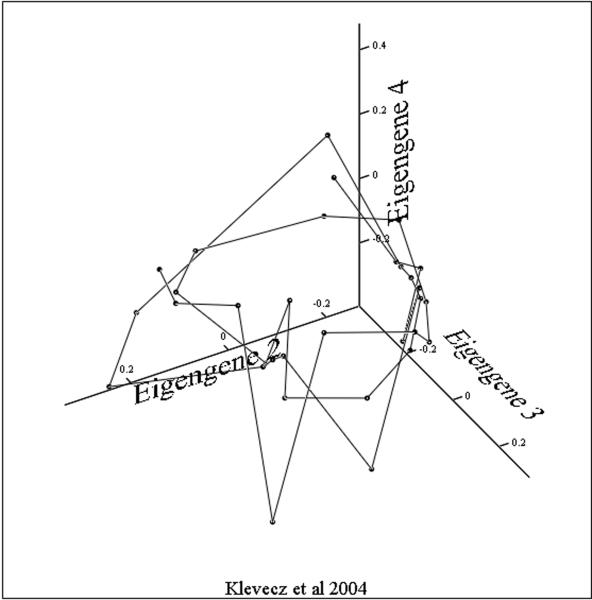
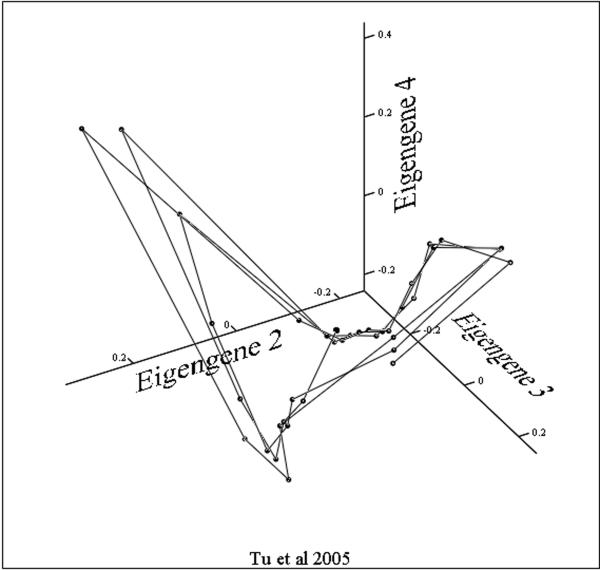
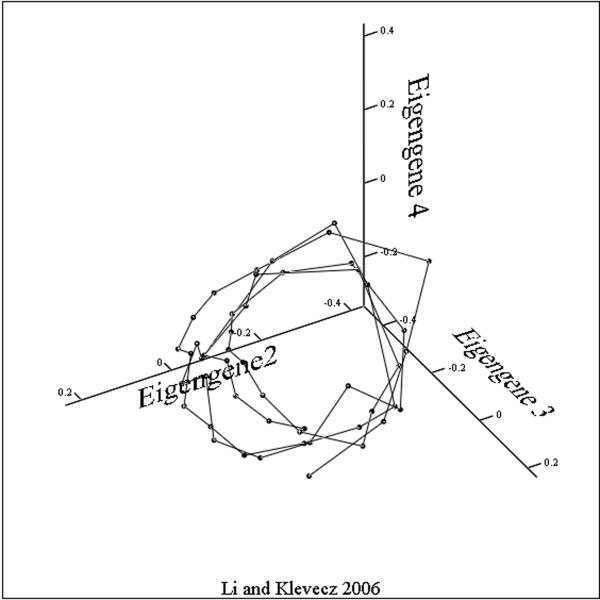
Viewed from a temporal perspective, the patterns of expression are less complex than we might have expected from a consideration of the combinatorial potential. The trajectories through concentration space followed by most of the 5000 expressed yeast genes can be modeled as a thick surface with some loss of information but greatly increased accessibility .What such a presentation does not give us are the detailed gene by gene connectivity relationships. However, it does suggest an experimental path to determining such relationships. If by treating cells with a drug such as phenelzine and following the changes that occur in the surface as the system responds, we have at least the beginnings of a map of the coupling and/or co regulation among differing genes. Recent studies have shown that changes in gene expression in response to perturbation by drugs occur through a folding or unfolding of the surface described by this circle of transcripts, and suggests, as a generalization, that the path from this 40-minute oscillation to the cell cycle and circadian rhythms takes place through a series of period two or period three bifurcations. These foldings in the surface of the putative attractor result in an increasingly dense set of nested trajectories in the concentrations of message and protein. In some expression array studies it appears that there are times in the attractor cycle when large clusters of transcripts are synthesized while at other times there are relatively few. This has suggested that the maintenance of a stable phenotype requires a specific spatio-temporal structure with synthetic events occurring at antipodal phases around the steady state – what we might call the dynamic architecture of phenotype. Likewise, singular value decomposition (SVD) shows that the principle Eigengenes (20) yield a similar picture of the attractor surface. How this surface might change as period lengthens or as a cell differentiates is one of two important and closely related questions that should form the focus of future studies. If we examine the three principle eigengenes derived from an SVD analysis of the entire population of transcripts and plot these as a three dimensional figure we can see the dynamic surface generated. SVD and PC give us a global measure of the information content of the system as expressed in the vectors and it is clear that in all three experiments the system is globally oscillatory. The disadvantage of SVD analysis is the difficulty of getting an intuitive understanding of the difference in the surfaces generated beyond saying that it appears to be an oscillatory system. Again, the surfaces generated by SVD analysis from the ~40 minute cycles (figures 3A and 3C)are similar to one another in forming a bowl or conical shape around the steady state. In other projections of the phenelzine treated cells the increase in cycle time following treatment can be clearly seen (2). In figure 3B the same three eigengenes are shown for the data of Tu et al. This structure is interesting in its simple butterfly shape and gives the appearance of being composed of two identical halves. In other projections the surface appears as a line shaped as an inverted “V”.

Figure 3. The Eigensurfaces of the genome wide oscillations in transcription.

Data from all transcripts scored as present in each of the three experiments were analyzed. In each case eigengene 1 is a near constant and serves to normalize the results. Eigengenes 2, 3 and 4 were plotted with identical projection axes.

Reanalysis of the early expression array data

Prior to the discovery of genome-wide oscillations in transcription - at a time when the first microarray studies of the yeast cell cycle were published as part of the Stanford cell cycle project (17,19) - it seemed clear that the prevailing model, the model against which the results were interpreted followed the pathways paradigm---the cycle as a series of branched and connected linear sequential steps, or perhaps “the just in time notion” - an assembly line along which the cell chugged on its way to division. This binarized model is a perfectly logical extension of mutational analyses that gives a sparse mapping of cellular processes - a mapping of the necessary but not sufficient steps - through the cycle. Such an analysis is discrete and uncomplicated by the moment-to-moment, or hour-to-hour changes in metabolites or macromolecules. To a large degree this old paradigm was responsible for our success in the molecular genetic dissection of the genome. .At that time, and despite solid theoretical underpinnings, the notion of the cell as a dynamical system was not much in evidence. But the cell is a coupled complex system and, in such systems, when the concentration of one constituent changes, it tugs, to a greater or lesser degree, on the entire network. One can speculate that in this post-genomic era, the elaboration of this tugging response to intentional perturbations will allow us to predict and control phenotype.

Given the prevailing models at the beginning of the microarray era, one can imagine that the single greatest surprise coming out of Wavelet and SVD analyses of cell cycle data was the consensus finding that much of the transcriptome oscillated (19-25), not just the 400 or 800 “cell cycle regulated” genes. Following on the initial reports (17,18), where data analysis involved either linear clustering or Fourier analysis of these very short data sets, there appeared a series of re-analyses of the Stanford cell cycle data where methods more suited to short, sparse and noisy data were employed Alter et al 20,24,25) and Rifkin and Kim (23) in their SVD-based analyses, and Klevecz and Douse (21) and Klevecz (22) using wavelet decomposition, all concluded that there was evidence for a genome wide oscillation in transcription. It was in these early studies that SVD was shown to be an excellent method for developing a global representation of the expression profiles. It seemed as well to identify both biological perturbations and measurement variability. Perturbations due to serum or media additions were detected in the Alter et al. analysis (8), and two major oscillatory components contributing to the global pattern of expression were seen as well in the analysis of synchronized mammalian cell cultures (24).

Using an entirely different approach involving wavelet decomposition (21,22), it was possible to partition away high frequency noise and low frequency trends in the Stanford yeast cell cycle data to uncover genome-wide oscillations in expression in about 4500 of the 6178 gene expression profiles. These were typically of cell cycle or half cell cycle duration, with periods of 40 and 80 minutes in these rapidly dividing cultures grown on high glucose. Because the Stanford data set lacked replicates, an image processing strategy was employed to enhance the pattern of peaks and troughs in the noisy low amplitude oscillations: the wavelet decomposition for each gene at each level was aligned side-by-side with all other genes at that level. The resulting pattern in color contour maps showed a series of bands or peaks with a great deal of phase coherence, with periods of either 40 or 80 minutes. In agreement with the SVD analysis, this finding suggested that there are large-scale oscillations in transcription but also finds evidence of higher frequency 40-minute oscillations in mRNA levels through the cell cycle. It was this finding that led to our time series analysis of transcription in the gated synchrony culture system. If the cell is an oscillator whose behavior is revealed by synchronization techniques, is it safe to assume that we have a random population if no particular effort has been made to synchronize the cell culture or the tissue? I think the answer must be no under circumstances where there is significant cell-to-cell communication. We should pause to consider what it means to so many standard paradigms and methods of analysis if it is true that everything oscillates

When everything oscillates

• Economy of explanation requires that the cell be viewed as periodic an attractor

• Calculations of drug response, message and protein half-lives based on steady state assumptions may be wrong.

• The canonical 2-fold boundary for significance is not “noise in the conventional sense but signal expressed with oscillatory dynamics.

• Stable and precise mammalian cell culture systems where these oscillations can be more thoroughly studied are urgently needed.

The cell cycle is a developmental process not a cycle

If everything oscillates and does so with a period that is an integral submultiple of the cell cycle, then the cell cycle, as it is conventionally understood, is a developmental process not a cycle. It is timed but does not keep time. We and others (26,27) published several reviews of cell cycle regulation that presented the fundamentally different view of the timing of cell cycle events by an attractor

From the 1950s onward four different conceptual pictures of the cell cycle in eukaryotes emerged. Each is based on a relatively distinct body of data and has spawned a relatively distinct research tradition. Briefly, these four views are as follows: 1. An image of the cell cycle as an interlocked and partially branched sequence of discrete events, linked in more or less complex causal chains. The primary evidence comes from genetic experiments on the budding yeast, S. cerevisiae, Hartwell (28) in which a number of temperature-sensitive cell division cycle (cdc) mutants that prevent normal cycling at the restrictive temperature were collected and studied. Many of these mutants have the property that cells cannot initiate or complete some easily measured event associated with the mutated gene. This is an easily grasped model and is similar in many ways to the later “just in time” models. In the time before high throughput technologies a few did challenge the notion that the cell cycle was blocked by the mutant in question by pointing out that in the cases where it has been studied essentially everything the cell did except for those few processes downstream from the mutational block when on, with the period of the cell cycle. To put it in modern terms, cell cycle mutants cause the attractor to be sub-threshold with respect to the mutant-blocked event. 2. A strictly stochastic state model with two or more discrete states and random transitions between them. This began as the transition probability model (29) and emphasized analysis of the distribution of cell age at mitosis in a population of presumptive identical cells in which some limiting material. Events within the cycle are initiated when this material is present in sufficient quantity. Conceptually this view is now taken up in the low message copy number problem and the resulting view of regulation as stochastic. With a few exceptions this type of model is forced to ignore the many dynamic behaviors seen in cellular oscillators and circadian biological clocks. 3. “Sizer” models, based on the concept that a reliable ratio of cytoplasmic mass to nuclear content must be maintained, and hence that this ratio plays a critical role in the timing of cycle events. This was an adequate representation in the early days of cell cycle modeling but apart from efforts to couple this to limit cycle oscillators (30) has no standing today. 4. Biochemical oscillator models, which in a variety of forms have been based on the view that essential variables wax and wane in concentration during the cell cycle and trigger events when they reach appropriate thresholds of concentration (26, 27). This tradition has explored phenomena suggestive of smooth alterations in concentrations by external perturbations, leading to phase-resetting phenomena or to phase conflicts when cells at different phases are brought together to allow cell to cell communication.

Quantized generation times (31), together with perturbation analyses, formed the experimental foundation of efforts to synthesize a model of the cell cycle in which such disparate concepts as check points, and limit cycles or complex attractors were fused (26,27). The basic idea was that checkpoints represent sub-threshold oscillations in an attractor that underlies the cell cycle. The oscillator that gave rise to gated cell divisions in mammalian cells was shown to be phase responsive and temperature compensated. The quantized generation time model was extended to other cell types and to gating of circadian rhythm-based cell division in plants, dinoflagellates and a variety of mammalian cells in culture. One prediction of the attractor models was that all cell cycle events would be gated by the attractor, and this period would be an integral sub-multiple of the cell cycle or circadian rhythm it timed. Quantized generation times were the first direct evidence of a cellular clock, but the more recent finding that the continuous culture system in yeast appears to be timed by a similar oscillator that can be tuned or driven to “fold” (i.e., undergo a series of period two or period three bifurcations), and that cell cycle events in S. cerevisiae appear to be gated by this transcriptional cycle suggests that a similar phenomenon, although on a different time scale, is operating in all systems from yeast to mammalian cells. This realization has opened a new and experimentally more accessible path to investigations of synchronous gating and the role of oscillations in generating and maintaining a stable phenotype.

Are equal numbers of genes transcribed at all points in the cycle?

In their analysis of the alpha factor synchrony, Alter et al (25) built a color mapping of the pattern of change for all transcripts through the cycle that suggests that there are phases in the cycle when relatively greater numbers of genes are maximally expressed than at other times. This is clearer in the cdc15 synchrony, where the two principle components or “arraylets” tend to be maximally expressed at just two points in the cycle. This phase coherence was also seen in the wavelet decomposition analysis for the cdc28 and alpha factor synchronies (21, 22). This restriction of transcription to distinct points in the TRAC is clearly seen in the two papers published using the gated synchrony culture system. Given that there are large variations in the number of messages being synthesized at any point in the cycle, a potential artifact exists with respect to the assignment of phase of maximum transcript level in the standard methods of expression array analysis using either Affymetrix chips or spotted arrays. Consider the hypothetical instance where 90% of the transcripts are made at one brief phase of the cycle with the remaining transcripts made uniformly through the remainder of the cycle. Adding equal amounts of message to the hybridization mix will reduce the contribution of the high transcript phase significantly. If we further normalize by requiring equal total hybridization in all samples then we have pretty much insured that all phases of the cycle will have the same total message and therefore, that the points with few messages may cause these to be over-represented The only sure way to avoid this is to spike into the samples at the time of RNA isolation a set of standards not expressed by the cells of interest and to normalize each microarray to constant expression in these standards. In two color assays, the post-amplification normalization against a randomized composite of all samples eliminates only the second normalization as a source of error. We are exploring the addition of constant amounts of S. pombe purified mRNA to the samples at the beginning of RNA isolation.

The use of actin and other constitutive, maintenance or housekeeping genes as normalizing standards is a time honored practice in PCR and other amplification assays. Warrington et al (32) have addressed this question in an analysis of human adult and fetal tissues. Of the 535 genes identified as highly expressed in all tissues examined, all but 47 varied by greater than 1.9 fold. They caution that further analysis might find regular variations in these low amplitude transcripts as well. That a gene is expressed constitutively does not mean that its transcript is maintained at a constant level through the cycle. It is important to know in any system, whether these genes show regular oscillations in expression. If so, then they become a questionable standard.

Viewing continuous cultures of yeast as a stochastic tissue

The details of the cellular dynamics that lead to the emergence of redoxand TRAC oscillations and the gating of cells into cell cycle stages are still not completely known. What seems clear is that at the cell densities required for emergence of the oscillation - between 2-8×10⁸ cells/ml - the cultures are in effect tissues. The distance between cells is less than one cell diameter so that there is the potential for constant exchange of materials directly as well as through diffusion. The collisions are random and in some sense global rather than local as in a mammalian tissue. Moreover, because of the balance between new cells appearing by division and the removal of cells by dilution there are always a disproportionate fraction of newly divided cells – the exponential growth distribution. Further complicating the simulation or calculation of cell cycle times within the gated synchrony population is the clear indication that newly divided daughter (virgin) cells have longer cycle times then the newly divided mother. How that signaling of a cell not yet ready to replicate or divide effects a cell that would otherwise be ready to divide is central to understanding how cells with adequate nutrients are prevented from replicating and dividing with the minimal generation times. Kinetically, the yeast stochastic tissue and a mammalian tissue such as the epithelial cells of the gastro-intestinal tract are similar – if on different time scales. In the GI tract of mammals the cell cycle time of a particular cell is in the range of 5-10 days, even though fraction, typically 10-15% of the cells in that tissue divides each day at the same time of day. In the yeast gated synchrony system, where the TRAC is 40 minutes long, 8-10% of the cells divide in each turn of the cycle, even though the cell cycle time of these cells is ~8 hours. Mammalian cells when explanted to culture exhibit an ability to grow with generation times much shorter than 10 days, typically 24 hours. Similarly in yeast cells diluted and refed with the conditioned medium, the cells divide with a 2 hour generation time.

Quorum sensing, quorum conflicts and quorum compromise

In simulations of tissue growth we have suggested that the slowing of growth occurs by virtue of phase conflicts between coupled neighboring cells, with the “younger” cells retarding the kinetics of the older cells. We have called this a quorum conflict. Fink (33) has suggested that it is likely that many lab strains of cerevisiae, some of which oscillate poorly, have been inadvertently selected for properties that minimize the ability to respond to signaling compounds such as the aromatic alcohols to form biofilms. Because biofilm formation involves cell to cell signaling growth in non-repressing concentrations of glucose and requires high cell densities, all attributes of the gated synchrony culture system. We believe that this is a potentially fruitful path to follow. When grown to sufficient cell densities – generally greater than 2×10^8 – cells to cell communication via acetaldehyde and H2S and, we speculate other as yet unknown signals related to pseudo-hyphal growth such as phenylethanol and tryptophol Signaling caused the cells to become synchronous with respect to their respiratory – reductive cycle while remaining partially synchronous with respect to DNA synthesis and cell division. So while it is known that acetaldyde and hydrogen sulfide might be sufficient to explain the onset of respiratory – reductive cycle synchrony, they are not sufficient to explain the partial synchrony seen in the cell cycle and more to the point why it is that cultures do not always begin respiratory reductive cycling. One idea developed below is that there are stable nodes of oscillation that require a particular phase relationship between the TRAC and the cell cycle. The release of hydrogen sulfide by a significant fraction of the cells in the fermenter ensures that no cells in the fermenter will be able to respire. We have suggested that the time sharing that occurs within every cell with DNA replication taking place only during the time that H2S release has poisoned mitochondria and prevented respiration is an evolutionarily important event. It is not so clear that the inverse is true, that is, that cells that are early in the cell cycle and not ready to replicate DNA must do so just because H2S levels are high and respiration is not occurring.

Stochastic noise is swept up and damped by appropriate phase arrangements in a population of individually noisy oscillators

The idea that cell division and other events might be retarded by the interaction of cell-cell signaling is based on simulations of fields of cells coupled through diffusion of one of the products of the reaction used to represent the cell cycle in each of the cells. In this case the attractor used to represent each cell was the Rossler attractor and each cell ran the identical oscillator with respect to all parameters. To test the effect of diffusive coupling on each of these “regulons” of noise the system was run in the chaotic domain. In addition to this deterministic noise, Gaussian noise was also added at each time step in the simulation (34-36). The difference in the fields was the starting phase of the oscillation. It was discovered that for certain initial phases, differing patterns emerged across the field. The most interesting of these were the “target pattern” associated with the classic findings in bacterial colonies expressing quorum sensing and spirals in which remarkably, the variability in the attractor was largely damped and the inner members of the spiral near the core of the spiral were essentially periodic and showed near limit cycle kinetics. It turned out that these innermost oscillators had by chance been arranged so that they were poised at antipodal phases around the steady state or singularity. This phase arrangement once established was very stable to perturbation and could be “transplanted” into turbulent fields where it would organize them into spirals. In essence spiral patterns form when there is not a quorum but a quorum conflict in either space or space and time. We suggest that the theoretical basis for stochastic regulation, the difficulty in formally representing a genetic regulatory loop with a continuous system of ordinary differential equations when one of the constituents falls to near zero values is obviated by thee findings in coupled oscillatory systems. Indeed, in such a coupled system, low copy numbers may be permitted or selected for so long as a significant proportion of the transcriptome is expressed with high amplitude oscillations. As a specific example, in the Rossler attractor, regulation of the high amplitude component where the peak to trough ratio of the variable is in the range of 100, the X and Y variables can have peak to trough ratios of 1.3. In such a coupled system any propensity to stochasticity is swept up by the high amplitude components.

Although the earlier modeling was intriguing, it was startling to find in our expression array analysis of the gated synchrony system direct experimental evidence that transcripts were being made in somewhat restricted patterns through the TRAC and that the times of transcript maxima were clustered in 3 or four phases in the cycle. That is, that they were poised at antipodal phases around the steady state. So in both theoretical and experimental systems it appears that in a coupled system, as a cell must be, any tendency to stochasticity will be swept up into the attractor surface and show periodic expression, even under conditions where a significant fraction of the transcripts express at low levels. Golbeter and his colleagues (37) have addressed the low message copy number problem directly for a single three variable reaction-diffusion system and find that sustained oscillations are possible for message levels in the range of 10 mRNAs per cell (37). Going beyond that, we would argue that in the case of a system wide oscillation with maximums in expression at differing phases, it is the collective copy number that is critical to sustained oscillations

What’s next? What is needed?

As impressive as the yeast gated synchrony is, there are some unresolved questions regarding the population dynamics that confound an exact mapping of expression array data to the dynamics of cellular phenotype. The application of analytical methods that are suited to non-linearities in time series data should find a wider use. It seems clear that the most successful and widely applied method so far is SVD (PCA). .Wavelet analysis has many advantages over FFTs for the data length and densities likely to be encountered in expression array studies. It will be much improved if optimized wavelet families are found that can represent complex patterns in time of transcripts or other biological signals of interest efficiently and accurately. Wavelet optimization and match filtering would be expected to remove some of the limitations found in analysis using off-the –shelf wavelets (40).