Theory of “Selectivity” of label-free nanobiosensors: A geometro-physical perspective

Abstract

Modern label-free biosensors are generally far more sensitive and require orders of magnitude less incubation time compared to their classical counterparts. However, a more important characteristic regarding the viability of this technology for applications in genomics∕proteomics is defined by the “Selectivity,” i.e., the ability to concurrently and uniquely detect multiple target biomolecules in the presence of interfering species. Currently, there is no theory of Selectivity that allows optimization of competing factors and there are few experiments to probe this problem systematically. In this article, we use the elementary considerations of surface exclusion, diffusion limited transport, and void distribution function to provide guidance for optimum incubation time required for effective surface functionalization, and to identify the dominant components of unspecific adsorption. We conclude that optimally designed label-free schemes can compete favorably with other assay techniques, both in sensitivity as well as in selectivity.

INTRODUCTION

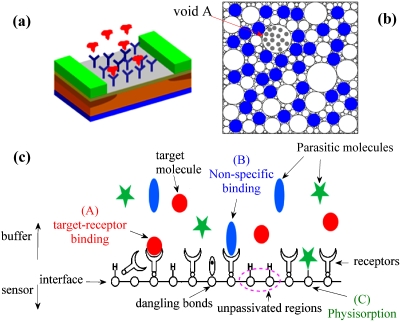
Modern label-free biosensors based on nanoscale devices allow highly sensitive detection of target biomolecules^{1, 2, 3, 4, 5} and are considered as a technology alternative to the existing chemical and biological detection schemes. These label-free schemes detect the presence of target biomolecules based on their intrinsic characteristics [e.g., field-effect transistor (FET) biosensor is a charge based detection scheme], not through the presence of extrinsic labels (e.g., magnetic nanoparticle⁶ or fluorophore) attached to the target molecule in a previous labeling step. The sensitivity of label-free nanobiosensors are often demonstrated by detection of single target species at extraordinarily low concentrations; the practical system-level considerations for massively parallel detection schemes are, however, left as future work and often not elucidated clearly. A basic consideration for parallel detection of multiple target molecules is defined by the “Selectivity” of the sensor technology [Fig. 1a], which quantifies the ability of a sensor to detect the desired target via “lock-and-key” principle in the presence of a host of almost similar molecules (called parasitic or interfering molecules). To illustrate the significance of the Selectivity, consider the problem of prostate specific antigen (PSA) detection in blood:⁵ human blood contains about 70 mg∕ml of proteins while PSA concentration⁷ is about 2 ng∕ml. Therefore even if detection scheme provides a sensitivity of 1 ng∕ml of PSA, it would still not qualify as a viable technology option unless the sensor simultaneously achieves a Selectivity ratio greater than 1 ppm.⁵ This is particularly important for label-free schemes that sense the presence of target molecules via remote electrostatic interaction, e.g., FET biosensors, which detect the presence of target molecules by the electrostatic interaction of the charge of biomolecule (like DNA) with the sensor. As electrostatics is a long range interaction, even molecules which are physisorbed on the sensor surface or weakly bound to the capture probes can still modulate sensor characteristics. Such schemes cannot distinguish between target molecule locked to capture probe versus an interfering species adsorbed onto the surface [on regions not covered by the receptor molecules, see Fig. 1b]. Without high degree of Selectivity, one might require extensive sample preparation and prefiltration that would easily offset the perceived cost advantages of the label-free technology. Therefore, Selectivity of label-free biosensors represents an important optimization problem where theoretical models can play a defining role in reducing the experimental overhead in evaluating technology options.

Figure 1.

A modern biosensor system. (a) Schematic of the sensor with receptors functionalized to the surface. (b) Top view of the sensor shown in (a). Receptor molecules are shown as solid dots. The random sequential attachment of receptors introduces voids (open circles) of varying sizes on sensor surface over which parasitic adsorption can occur (illustrated as shaded dots in the void A). (c) Cross-section of a sensor system illustrating the various components that contribute towards Selectivity.

In this paper we suggest that many fundamental aspects of the Selectivity problem is accessible to intuitive geometrical considerations based on random sequential absorption (RSA) (Ref. ⁸) and circle packing problem^{9, 10} combined with kinetics of diffusion limited Langmuir process. This simple intuitive model allows us to frame and answer, for the first time, a series of very interesting questions regarding nanobiosensors. (i) How long should one wait (optimum incubation time) for surface passivation∕receptor functionalization and the dependence of incubation time on Selectivity of biosensors? (ii) How does the size of the parasitic molecule affect the Selectivity of a sensor? (iii) How does the label-free methods (i.e., schemes based on the intrinsic characteristic of molecules like the net charge of a DNA strand, etc.) compare with the sensors based on optical labeling? – are there inherent advantages or disadvantages? etc.

We provide a phenomenological definition of Selectivity in Sec. 2 and develop an analytical and numerical model for Selectivity in Sec. 3. The model is then used in Sec. 4 to study the functional dependence of various parameters like incubation time on Selectivity and is used to estimate the ability of label-free sensors in selective detection of target biomolecules.

A phenomenological definition of Selectivity

Before getting into the details of the numerical model, let us briefly consider the phenomenological definition of the Selectivity. Detection of target biomolecules in a solution is a two step process. The first step involves functionalization of the sensor surface with receptor molecules specific to the desired target. In this step, the solution containing the receptor molecules is introduced to the sensor surface. Subsequently these receptor molecules diffuse within the fluidic volume to eventually (and sequentially) attach to the sensor surface at random locations. Generally, steric hindrance due to the finite size of receptor molecules prevents overlap between adjacent attachments. This effect, coupled with the random nature of receptor attachment, cause fragmentation of the available surface area for subsequent adsorption of receptors and leads to voids of varying sizes on the sensor surface [Fig. 1b]. Surface conjugation is allowed to proceed for a certain (often insufficient) incubation time, which results in a receptor surface density N₀ and an associated distribution of voids. These voids would eventually allow adsorption of parasitic molecules and dramatically reduce the Selectivity of label-free biosensing [Figs. 1b, 1c]. In sum, this first step determines both the density of receptors N₀, as well as the distribution of open voids of size r at time t, V(r,t), on the sensor surface.

In the second step, the “receptor functionalized sensor” is introduced to a solution containing target biomolecules as well as other parasitic molecules (at time t=0). The target molecules would diffuse through the solution and eventually reach the sensor surface. The sensor response is dictated by the net number of molecules (target or otherwise) captured on the surface. This response may be characterized by the widely used Langmuir model, i.e.,

$$\frac{d{N}_T}{dt}=k_F\left(N_0-N_T\right){\rho }_s-k_R{N}_T,$$ (1)

where N₀ represents the available binding sites (receptors) for the target (defined by processes in step (1), N_T represents the density of conjugated target-receptors, ρ_s is the target density at the surface, and k_F and k_R are the association and dissociation constants, respectively. Langmuir kinetics indicate that the steady state concentration (at t→∞, mass transport ensures that ρ_s=ρ_T, the bulk target density) of conjugated target molecules on the sensor surface is given by

$$N_T\left(t\to \infty \right)=\frac{k_T{N}_0{\rho }_T}{k_T{\rho }_T+1},$$ (2)

where k_T is the normalized reaction constant (≡k_F∕k_R). To account for the additional (uncorrelated) physisorption of parasitic (interfering) molecules on the sensor surface, one needs to generalize Eq. 2 in the following manner:

$$N\left(t\to \infty \right)=N_T+N_T^{\prime }+N_{\text{Geom}}=\frac{k_T{N}_0{\rho }_T}{k_T{\rho }_T+1}+\frac{k_T^{\prime }{N}_0{\rho }_T^{\prime }}{k_T^{\prime }{\rho }_T^{\prime }+1}+\frac{k_p{N}_p{\rho }_p}{k_p{\rho }_p+1}.$$ (3)

Here k_T, $k_T^{\prime }$, and k_p denote the normalized reaction constants for receptor-target, receptor-parasitic, and physisorption of parasitic molecules on sensor surface, respectively. The first term on the RHS denotes conjugated target molecules [denoted as A in Fig. 1c], the second term represents unselective binding of interfering species (at a density ${\rho }_T^{\prime }$) to the target molecules [denoted as B in Fig. 1c, e.g., the conjugation of DNA strands with base-pair mismatch], and the third term on the RHS of Eq. 3 denotes physisorption of parasitic molecules through the unpassivated regions on the sensor surface and this geometric component (N_Geom) arises from the spatially random layout of receptor molecules [denoted as C in Fig. 1c]. Here N_p denotes the density of available locations which can accommodate parasite molecules. For a parasitic molecule of size r_p the term N_p in Eq. 3 is determined by voids with effective radius r>r_p. Obviously, N_p decreases with increasing N₀. Note that the sensor technologies based on optical labeling (e.g., enzyme-linked immunosorbent assay) are not influenced by the third term of Eq. 3, but other technologies like electrical detection, surface plasmon resonance (SPR), etc. do depend on all terms of Eq. 3.

We define the signal, S, as the component due to the desired target-probe interaction and the noise, η, as the component due to the interfering species. From Eq. 3, we find that S∝N_T, while $\eta \propto N_T^{\prime }+N_{\text{Geom}}$. Note that a control device, introduced to the same density of interfering species, would produce an output signal equivalent to the noise component.

For maximum Selectivity, the first term in the RHS (signal) of Eq. 3 should dominate over other factors (noise). In other words, Selectivity can be quantified in terms of “signal noise ratio” (SNR) defined as

$$\text{SNR}\equiv \frac{S}{\eta }.$$ (4)

The SNR predicted by Eq. 4 is in addition to the noise that arises from statistical fluctuations in the density of captured molecules, ion concentration, etc.^{11, 12} To estimate SNR, we need to evaluate both signal and the noise components. Apart from the parameters like reaction constants and target molecule densities, the signal and noise components are entirely determined by two parameters [see Eqs. 3, 4]: N₀ and N_p. N₀ entirely determines the signal component, while N₀ and N_p are required to predict the noise component. In Sec. 3, we develop a model to predict N₀ and N_p for biosensors.

ANALYTICAL AND NUMERICAL MODELING OF SELECTIVITY

The above discussion indicates that the essence to Selectivity problem reduces to the calculation of N₀ and N_p [Eqs. 3, 4]. Here, we model the two step process of biomolecule detection (described in Sec. 2) to study this geometric component of Selectivity. The full solution of the two step problem requires three-dimensional simulation of diffusion limited aggregation of finite size particles with excluded volume interactions onto the sensor surface—a computationally challenging problem.¹³ A more intuitive and fruitful approach involves modifying the Langmuir model for diffusion limited capture to include the geometry of surface coverage through RSA of the receptor (or the target, and parasitic molecules), as discussed below. The quality of the approximation can be tested by comparing the theoretical prediction with experimental results.

Step 1: Diffusion limited RSA of receptor molecules: Calculation of N₀

Two key limitations preclude the straightforward use of the classical Langmuir model for surface adsorption of molecules to understand the Selectivity problem, i.e., the classical model (i) neglects the steric hindrance issues associated with random and irreversible attachment of receptors on sensor surface and (ii) it does not consider the effects of diffusion limited transport on the dynamics of molecule adsorption. For a given flux of molecules to the surface, however, the Langmuir model can be simply and suitably modified to account for the steric hindrance issues. This is done by replacing the term N₀−N_T in Eq. 1 by ϕ, the available area function. Moreover, instead of counting the number of particles N(t) as a function of time as in Eq. 1, we might instead focus on the integrated surface coverage, θ(t), by the molecules at given incubation time t. Obviously, θ(t) increases monotonically with time (just as N(t) would) and as such, the fractional area available for subsequent adsorption of additional particles, ϕ(t), decreases correspondingly, making it difficult for additional particles for surface adsorption. The key difference between classical Langmuir equation and the reformulation discussed above is that in general ϕ(t)≠1−θ(t) because of issues related to steric hindrance.^{8, 14}

The modified equation for irreversible (k_R=0, ρ₀ receptor density) receptor attachment is given as

$$\frac{d\theta }{dt}=k_F{\rho }_0\varphi \left(\theta \right).$$ (5)

To include the effects of mass transport to the sensor surface in Eq. 5, we may adopt the methodology provided in Refs. ^{15, 16} for diffusion limited Langmuir kinetics to define the generalized transport limited RSA equation appropriate for our purposes

$$\frac{d\theta }{dt}=\frac{k_F{\rho }_0\varphi \left(\theta \right)}{1+k_F{A}_D\varphi \left(\theta \right)N_{\text{ideal}}∕N_{\text{avo}}{C}_{D\left(t\right)}},$$ (6)

where N_avo is the Avogadro’s constant and $N_{\text{ideal}}=1∕\left(\pi r_0^2\right)$ the maximum density of adsorbed particles in ideal conditions. The other parameters A_D and C_D(t) and the calculation of ϕ(θ) by Monte Carlo method are discussed in Ref. 17 Note that this generalized RSA model [Eq. 6] predicts the dynamics of molecule adsorption over different surfaces like planar, cylindrical, or spherical and can be extended to complex surfaces like carbon nanotube nanocomposites¹⁸ (through appropriate C_D(t), see Ref. 17), a significant improvement over previous modeling efforts.^{19, 20}

To solve Eq. 6, one now needs a description of ϕ(θ). This function must reflect the remarkable fact that the surface coverage in two-dimensional RSA saturates at θ(t→∞)≡θ^∞=0.54. We find that the following phenomenological expression:

$$\varphi \left(\theta \right)=a\left(b-\theta \right)\left(c-\theta \right)$$ (7)

provides an excellent approximation to the numerical Monte Carlo results (see Ref. 17). The parameters a, b, and c are obtained by the requirements that: (i) as θ→0, ϕ=1, so that abc=1, (ii) θ→0.547, ϕ(θ)=0, so one of the roots of equation must be θ^∞=0.547, and (iii) ϕ(θ) is a monotonically increasing function of θ, so the other root should be greater than θ^∞. The parameters a=3, b=0.54, and c=0.6 not only satisfies the above requirements but also reproduces the numerical Monte Carlo results from RSA very well (see Sec. A, Ref. 17). RSA literature provides ϕ(θ) for higher order terms,^{14, 21} but for our purposes Eq. 7 provides sufficient accuracy to study the parametric dependence of incubation time and the geometric aspects of excluded interactions on SNR of biosensors.

Once we specify available area function ϕ(θ), Eqs. 6, 7 can be integrated numerically to solve the θ(t)—the evolution of surface coverage as a function of time. The receptor density after an incubation time t_incub is obtained by the relation $N_0=\theta ∕\pi r_0^2$, where r₀ is the receptor size. These results will be discussed in Sec. 4, but for now we continue with the formulation of the second step of the Selectivity problem.

Step 2: Size Selectivity of parasitic adsorption: Calculation of N_p

For a given the distribution of receptor molecules on sensor surface, as calculated in Step 1, the Selectivity of a sensor can be estimated by performing a second Langmuir-RSA for parasitic molecules onto the open voids of the first receptor RSA problem. Unfortunately, no analytical solutions [similar to Eq. 7] exist for the available surface area function for parasitic RSA and therefore numerical solutions cannot be avoided. However, instead of solely relying on the numerical solution of the second RSA problem (which provides little physical insight), we now look for an approximation to numerical problem that provides equivalent results, but with far greater transparency of physics, as discussed below.

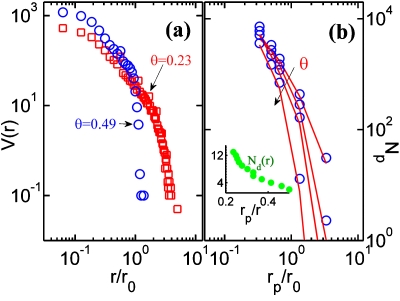
The second parasitic RSA problem is simplified if we begin by calculating the void size distribution, V(r,t) [Fig. 1a, open circles) on a sensor surface at a particular surface coverage θ(t_incub). Here we estimate the void distribution by a numerical scheme which overcomes the limitations of the methods based on traditional Voronoi–Dirichlet tessellation.²² Note that the void distribution shows a sharp cut-off at r₀ as the surface coverage approaches the asymptotic limits [Fig. 2a], as expected. For a parasitic species of size of r_p, only those voids with radius r>r_p can contribute toward nonselective adsorption. And in this case, one can partition the second parasitic RSA problem as the sum of disjointed RSA problems translated onto a series of disks, rather than the complete fragmented surface. Actually, if the parasitic binding is weak (as it is expected to be), even this simplified RSA problem need not be solved, rather the RSA problem onto a circular void of radius r reduces to the problem of maximum packing of disks in a circular void, generally known as the circle packing problem.⁹ The density of possible locations for parasitic adsorption, N_p, is determined by voids with r>r_p and the number of such possible locations in any given void can be obtained from circle packing literature. Hence N_p is given as

$$N_p\left(r_p,N_0\right)=\sum _{r>r_p}V\left(r,N_0\right)N_d\left(r_p∕r\right),$$ (8)

where V is the void distribution on the sensor surface [Fig. 2a] and N_d is the circle packing function⁹ [inset of Fig. 2b] which denotes the maximum number of circles of radius r_p which can be packed without overlap inside a circle of radius r. Figure 2b shows that N_p obtained using the approximate analysis compares well with the results from computationally expensive double RSA (DRSA) simulations (receptor RSA followed by parasitic RSA).

Figure 2.

(a) Void distribution for two different surface coverage by the receptor molecules. (b) The density of locations over which parasitic binding can take place, N_p, as a function of the size of parasitic molecules for different surface coverage. Symbols represent DRSA simulations while the solid lines represent the estimate using void distribution function [Eq. 8]. Inset shows the circle packing function⁹-number of disks of size r_p that can be packed inside a void of size r.

In this section, we provided estimates for N₀ [Eq. 6] and N_p [Eq. 8] through a modified RSA model and void distributions on the sensor surface. We will now use this two step model to study the Selectivity of label-free biosensors.

RESULTS AND DISCUSSIONS

Model validation

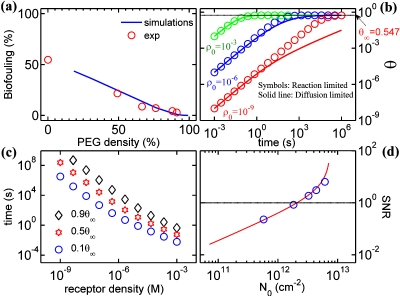
We begin by illustrating the validity of our model by comparing it with widely known passivation experiments in the literature that has so far not been interpreted by any other theoretical model. Nonspecific adsorption is one of the key challenges that affect the long term reliability of various devices. The obvious method to reduce such issues would be to passivate the surface using inert molecules like polyethylene glycol (PEG) that has long been used to prevent biofouling on surfaces.²³ Being a small molecule, PEG do cover the surface very effectively. To illustrate the efficiency of PEG in preventing biofouling, we use the formulation discussed in Sec. 3 with DRSA simulations: the first RSA covers the surface with PEG molecules (assumed as disks with Flory radius, 2.5 nm) while the second RSA represents biofouling due to fibrinogen on such a PEG coated surface. In Ref. 23, fibrinogen adsorption on PEG coupled surfaces of different grafting densities was experimentally studied. The surface density of the adsorbed molecular layer was determined using x-ray photoelectron spectroscopy. The results shown in Fig. 3a indicate that RSA simulations closely predict the experimental trends reported in Ref. 23. Satisfied that our model can explain the experimental observations correctly, we use it to further explore the Selectivity issues of biosensors.

Figure 3.

Numerical results. (a) Validation of modeling approach—double RSA simulations compare well with experiments for biofouling efficiency of PEG molecules (experimental data from Ref. 23, normalized to a surface coverage of θ^∞=0.547). (b) Diffusion limited RSA dynamics for various bulk receptor concentrations. (c) Incubation time required for a given surface coverage as a function of bulk receptor density, illustrating the influence of diffusion limited transport on achievable surface coverage. For low analyte densities, the surface is far from being fully saturated, which leads to increased probability of nonspecific adsorption. (d) Variation in SNR with receptor density. Reliable detection of target molecules require SNR>1. Solid line shows the results from an approximate analysis [Eq. 12].

Incubation time and mass transport effects

Since the Selectivity is directly proportional to N₀ [Eq. 4], optimal surface functionalization of receptors is very important (step 1 of Sec. 2). Here we illustrate the trade off between the concentration of receptors and the incubation time involved in surface functionalization procedure based on the model developed in Sec. 3A.

Equations 5, 6 predict the time dynamics of surface functionalization in diffusion limited regimes. Integration of Eq. 6 leads to an implicit expression for θ. However, for planar systems, a simplified explicit expression can be obtained by replacing ϕ(θ) in the denominator of Eq. 6 with unity. After integration (using the expressions for A_D and C_D(t) for planar sensors given Table I of Ref. 17), we obtain

$$\theta \left(t\right)=\frac{1-e^{F\left(t\right)}}{1∕b+e^{F\left(t\right)}∕c},$$ (9)

where $F\left(t\right)=\left(2a\left(b-c\right)k_F{\rho }_0∕K\right)\left(\sqrt{t}-ln\left(1-K\sqrt{t}\right)∕K\right)$, $K=k_F{N}_{\text{ideal}}{N}_{\text{avo}}\sqrt{2∕\text{D}}$, and D is the diffusion coefficient.

Figures 3b, 3c compares the incubation time required for various bulk receptor concentrations. The asymptotic surface coverage is only 54.7% which indicates that even at very high bulk receptor concentrations, significant area on the sensor surface is available for physisorption of parasite molecules. For a typical incubation time of 1 h, the bulk receptor concentration >1 μM is required to ensure maximum surface coverage. Cost considerations regarding the volume of receptor reagents to be used and the amount that can be recycled could be important factors in deciding the bulk receptor density for experiments and hence the incubation time needs to be tailored accordingly. Note that the results presented are valid for planar sensors with diffusion of molecules being one-dimensional toward the surface. Appropriate C_D(t) (Refs. ^{15, 16}) along with RSA dynamics on curved surfaces may shorten the settling time for cylindrical nanotube or nanowire based sensors.

Limits of SNR for label-free electrical detection

As discussed in Sec. 1, Selectivity can be described in terms of SNR as SNR=S∕η. Here we describe the SNR due to the of physisorbtion of parasitic molecules, i.e., η∝N_Geom. The SNR is now given as

$$\text{SNR}\equiv \frac{S}{\eta }=\frac{{\sigma }_T}{{\sigma }_p}\frac{N_T}{N_{\text{Geom}}},$$ (10)

the ratio of the first and third terms on the RHS of Eq. 3 scaled by a factor which denotes the signal transduction scheme (σ_T∕σ_p). For example, it could be the ratio of electrostatic charge of the target and the parasitic molecule for electrical detection, or the ratio of the thickness of the target molecular layer to the parasitic molecule for SPR, etc. Using Eqs. 3, 10, we obtain

$$\text{SNR}=\frac{{\sigma }_T}{{\sigma }_p}\frac{N_T}{N_{\text{geom}}}\approx \frac{{\sigma }_T{k}_T{\rho }_T}{{\sigma }_p{k}_p{\rho }_p}\frac{N_0}{N_p},$$ (11)

which can now be estimated quantitatively based on Eqs. 3, 4, 5, 6, 7, 8. The symbols in Fig. 3d show the numerical simulation results based on Eqs. 3, 4, 5, 6, 7, 8 with the parameters r_p∕r₀=0.5, k_p∕k_T=10⁻⁹, σ_p∕σ₀=0.1, and ρ_p∕ρ_T=10⁻⁹ (this ratio is equivalent to having a Selectivity of 1 ppb). The numerical results show that the SNR increases rapidly with increasing surface coverage (N₀) of receptor molecules, an intuitive result. In fact, the general shape of the SNR curve can be understood with the following simple argument:

For a given receptor density N₀ (or surface coverage $\theta =N_0\pi r_0^2$, r₀ the receptor density), the available area for physisorption of parasitic molecules is ${\theta }_{\text{avail}}={\theta }_{r,p}^{\infty }-\theta$, where ${\theta }_{r,p}^{\infty }$ is the asymptotic surface coverage for a DRSA consisting of receptor conjugation followed by parasitic conjugation. Note that ${\theta }_{r,p}^{\infty }$ can be different from θ^∞ for a single RSA process (as discussed in Sec. 3), especially if the parasitic molecules differ in size with the receptor molecules. Hence the density of parasitic molecules that can be placed on the sensor surface is $N_p=\left({\theta }_{r,p}^{\infty }-\theta \right)∕\pi r_p^2$. Now the SNR [Eq. 11] is given as

$$\text{SNR}\approx \frac{{\sigma }_T{k}_T{\rho }_T}{{\sigma }_p{k}_p{\rho }_p}\frac{r_0^2}{r_p^2}\frac{\theta }{{\theta }_{r,p}^{\infty }-\theta }.$$ (12)

Figure 3d shows that the analytic result [Eq. 12, shown as solid line] agrees well with RSA simulation results [symbols, Eq. 11] for the same parameter set used in the numerical simulation (see the paragraph above). For this comparison we assumed that ${\theta }_{r,p}^{\infty }={\theta }^{\infty }$, and this approximation serves well till ${\theta }_{r,p}^{\infty }<{\theta }^{\infty }$. The approximate result [Eq. 12] can be used to obtain SNR in the presence of any parasitic molecule with r_p<r₀. For r_p>r₀, DRSA simulations or void distributions are required for an accurate estimate. Note that the results shown in Fig. 3d were obtained by assuming a constant σ_T∕σ_p, which is not always valid. On the contrary, if we assume the charge to be proportional to the molecule size, the only change required is to replace σ_T∕σ_p in Eqs. 11, 12 by (r_T∕r_p)³ and all the qualitative features of the results will remain valid (r_T, the size of target molecules).

Figure 3d suggests several important conclusions. First, one finds that label-free Selectivity of 1 ppb with SNR>1 is possible with N₀>2×10¹² cm⁻², an achievable receptor density. This result provides an estimate for SNR of biosensors in the presence of physisorption of parasitic molecules and suggests that label-free sensors for electrical detection of biomolecules may be viable even in the presence of parasitic molecules at a much higher concentration (ρ_p∕ρ₀=10⁻⁹), provided sufficient incubation times are allowed for surface functionalization. Second, the plot highlights the importance of characterizing the properties of sensor surface to common biofouling agents so that accurate estimates of k_p∕k_T would lead to more quantitative SNR predictions. It turns out that incomplete surface functionalization with N₀<2×10¹² cm⁻² would rapidly erode SNR and make the technology irrelevant for parallel detection. Finally, additional intermediate surface passivation step by small inert molecules like PEG (after the receptor-incubation, but before the introduction of the target⁶) could reduce biofouling by parasitic molecules and helps in achieving better Selectivity.

Equations 11, 12 predicts that the asymptotic SNR (i.e., at t→∞) of label-free biosensors. However, at extremely low concentrations the signal due to target biomolecules could build up much at a much slower rate (diffusion limited transport¹⁵) while the component due to parasitic molecules might saturate faster (since they are at a higher density). This indicates that SNR is a time dependent variable, and the measurements should be performed after a critical waiting time to ensure SNR>1 for label-free biosensors. Alternative techniques like washing the sensor surface using appropriate buffer solutions to remove the adsorbed parasitic molecules, use of a control device to estimate the background signal due to the parasitic adsorption, etc. would be required to achieve parallel detection of multiple target molecules. The presence of a host of parasitic molecules in any real system can be accounted by our approach using appropriate size distribution of parasitic molecules and their surface reaction constants; however, competitive adsorption among parasitic molecules requires further analysis and is reserved for future studies.

Our simulation results provide many insights regarding the Selectivity of label-free schemes as compared to detection methods which use optical∕magnetic labels. (i) For an unpassivated sensor surface, label-free schemes are adversely affected by physisorbtion of parasitic (interfering) molecules on sensor surface. Indeed, at low receptor surface coverage, label-free schemes with SNR>1 is impossible without careful surface passivation. (ii) On the other hand, the presence of bulky labels (e.g., fluorophores∕magnetic nanoparticle) adversely affect the target-receptor conjugation efficiency of optical∕magnetic labeling schemes. Optimum receptor packing is crucial for such schemes to achieve better conjugation efficiency. (iii) For FET based sensors, there is an interesting trade off regarding molecules chosen for surface passivation: longer molecules reduces the electrostatic interference from interfering molecules by keeping them away from the sensor surface, but shorter molecules provide better surface coverage. This trade off establishes the limits of SNR for label-free schemes in the presence of surface passivation.

CONCLUSIONS

In the article, we have provided a geometro-physical perspective for Selectivity of nanobiosensors. From the elementary considerations of surface exclusion and diffusion limited transport, we estimate the incubation time required for surface functionalization. Based on our method of void distribution, we identify the dominant component of parasitic adsorption and illustrate that label-free schemes can indeed compete with other assay techniques, both in sensitivity as well as in Selectivity. The methodology we developed to address the Selectivity problem is quite generic and can be adapted easily to other scenarios in which molecules could be of different shapes (e.g., ellipsoids) or adsorption occurs over curvilinear surfaces such as cylindrical nanowire. Other significant effects like competitive adsorption of multiple target species needs to be taken into account for realistic protein assays, which is only a natural extension of the work presented in this paper.