Super-resolution biomolecular crystallography with low-resolution data

Abstract

X-ray diffraction plays a pivotal role in understanding of biological systems by revealing atomic structures of proteins, nucleic acids, and their complexes, with much recent interest in very large assemblies like the ribosome. Since crystals of such large assemblies often diffract weakly (resolution worse than 4 Å), we need methods that work at such low resolution. In macromolecular assemblies, some of the components may be known at high resolution, while others are unknown: current refinement methods fail as they require a high-resolution starting structure for the entire complex¹. Determining such complexes, which are often of key biological importance, should be possible in principle as the number of independent diffraction intensities at a resolution below 5 Å generally exceed the number of degrees of freedom. Here we introduce a new method that adds specific information from known homologous structures but allows global and local deformations of these homology models. Our approach uses the observation that local protein structure tends to be conserved as sequence and function evolve. Cross-validation with R_free determines the optimum deformation and influence of the homology model. For test cases at 3.5 – 5 Å resolution with known structures at high resolution, our method gives significant improvements over conventional refinement in the model coordinate accuracy, the definition of secondary structure, and the quality of electron density maps. For re-refinements of a representative set of 19 low-resolution crystal structures from the PDB, we find similar improvements. Thus, a structure derived from low-resolution diffraction data can have quality similar to a high-resolution structure. Our method is applicable to studying weakly diffracting crystals using X-ray micro-diffraction² as well as data from new X-ray light sources³. Use of homology information is not restricted to X-ray crystallography and cryo-electron microscopy: as optical imaging advances to sub-nanometer resolution^4,5, it can use similar tools.

A grand challenge in structural biology is to determine atomic structures of large macromolecular complexes. Unfortunately, growth of well-ordered crystals needed for high-resolution X-ray crystallography, is often precluded by inherent flexibility, disordered solvent, lipids, and other essential components; diffraction often is weak, anisotropic and has an effective resolution of worse than ~ 4 Å. Atomic interpretation of resulting electron density maps is limited to fitting rigid models. There is a need for accurate atomic structures from low-resolution diffraction data to reach mechanistic conclusions that critically depend on individually resolved residues.

X-ray crystal structures can achieve “super-resolution” where the estimated coordinate accuracy is better than the resolution limit of the diffraction data (typically, by 10x), by imposing constraints when interpreting observed diffraction data and electron density maps. Super-resolution arises from the excluded volumes of atoms: the scattering objects are always further apart than half of the wavelength of X-ray radiation typically used (1–2 Å). This atomicity leads to a solution of the phase problem for small molecule crystals⁶, and it allows estimation of coordinate errors⁷. Assuming polymers have standard chemical bond lengths and bond angles extends this concept to the resolution characteristic of macromolecular crystallography^8,9.

Low-resolution X-ray diffraction data at 5 Å contains, in principle, sufficient information to determine the true structure (the “target structure”) since the number of observable diffracted intensities exceeds the number of torsion-angle degrees of freedom of a macromolecule¹⁰. Although an exhaustive conformational search in torsion-angle space against the diffraction data should lead to an accurate structure at 5 Å resolution, such a search is computationally intractable. Our approach aids the search by adding known information to the observed data at low resolution. Instead of adding generic information about macromolecular stereochemistry (idealized chemical bond lengths, bond angles, and atom sizes that heralded the era of reciprocal-space restrained refinement^8,9), we add specific information for the particular macromolecule(s) or complex, deriving this information from known structures of homologous proteins or domains (the “reference model”).

The target structure often differs from the reference model by large-scale deformations, related to the approximate conservation of local polypeptide geometry as sequence and function evolve. How can such deformations be mathematically described? An early approach¹¹ used low-frequency normal modes, shown to reproduce large-scale collective changes in structures with very few degrees of freedom¹²; it has been used to refine protein structures with low-resolution X-ray or cryo-electron microscopy data^13,14. Here we take a very different approach. Instead of choosing special collective degrees of freedom, we use an extension of our Deformable Elastic Network (DEN) approach¹⁵. DEN fits of models into cryo-electron density maps allowing large deformations such as hinge bending. DEN defines springs between selected atom pairs using the reference model as the template. The equilibrium distance of each spring (distance at which its potential energy is minimum) is initially set to the distance between these atoms in the starting structure for refinement. As torsion angle molecular dynamics against a combined target function (comprising diffraction data, DEN, and energy, Eq. 1) proceeds, the equilibrium lengths of the DEN network are adjusted to incorporate the distance information from the reference model. The degree of this adjustment is controlled by a parameter, γ (Online Methods). Here we extend DEN to homology models, or more generally, any reference model, such as a predicted structure.

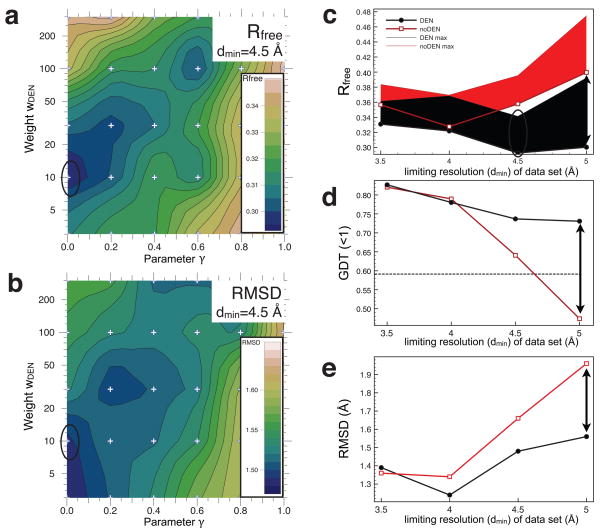
We first tested our method on a model system, the protein penicillopepsin whose structure had been determined to d_min=1.8 Å resolution (PDB ID 3app)¹⁶. Synthetic low resolution data sets were generated at 3.5, 4.0, 4.5, & 5.0 Å resolution (Online Methods). Optimum values for the γ and w_DEN parameters used for DEN refinement were obtained by a grid search against R_free (Fig. 1a for refinement at 4.5 Å resolution). With this standard protocol, referred to here as “DEN”, the R_free optimum is found at (γ, w_DEN) = (0,10) (marked by black ellipse). As a control, we performed a refinement using exactly the same protocol but with the DEN potential set to zero; this corresponds to a second standard protocol, referred to here as “noDEN”. We assess the quality of the resulting models by comparing the structures resulting from the DEN and noDEN refinements to the target structure (the 1.8 Å resolution crystal structure of penicillopepsin, 3app). Fig. 1b shows a contour plot of the all-atom root-mean-square difference (RMSD) between 3app and the corresponding DEN refined structures from Fig. 1a. The RMSD shows good agreement with the R_free values. Thus, the lowest R_free value should be a good predictor for the (γ, w_DEN) pair that gives the optimum structure in cases when a high resolution target structure is not known. The resulting electron density maps (Supplementary Fig. 1) are greatly improved showing better connectivity and sidechain definition compared to noDEN refinement.

Figure 1. Results for the penicillopepsin test calculations using the MLHL target function (experimental phase information).

In all panels, black lines refer to DEN refinements, whereas red lines refer to noDEN refinements. (a) Showing how the (γ, w_DEN) grid-search determines the values that give the best R_free value for the synthetic diffraction data set at d_min=4.5 Å. The R_free value is contoured using values calculated on a 6 × 5 grid (marked by small ‘+’ signs) where the parameter γ was [0.0, 0.2, 0.4, 0.06, 0.8, 1.0] and w_DEN was [3, 10, 30, 100, 300]. For each parameter pair we performed an extensive refinement protocol (Online Methods). The contour plot shows clear minima and maxima with the value of R_free varying from 0.295 to 0.35. (b) Showing the contour map of the all-atom RMSD between the target structure 3app and the DEN-refined structure (repeat with the lowest R_free value) at each grid point in (a). Again there are clear minima and maxima with the RMSD varying from 1.47 to 1.60 Å. (c) Showing the R_free value as a function of d_min of the four synthetic diffraction data sets. Thick lines mark the lowest R_free values obtained from the ten repeats using the optimum parameters; the corresponding thin lines mark the highest R_free values. For the synthetic data sets at d_min ≥ 4 Å, DEN refinement performs much better than noDEN reaching lower R_free values. (d) Showing how Zemla’s GDT (<1 Å) score¹⁷, which measures structural similarity to the target structure 3app, varies as a function of d_min; the dashed line indicates the GDT score of the initial model. At all resolutions, DEN out-performs noDEN and gives GDT values that are more favorable (higher) than those of the initial structure. (e) Showing how the RMSD of all atoms to the 3app target structure varies vs. d_min of the four synthetic diffraction data sets. Once again DEN gives lower RMSD values, especially at low-resolution. The DEN-refined models used in (d), and (e) correspond to the best models among ten repeats as assessed by R_free (black dots in panel (c)). Black ellipses indicate on the contour maps values corresponding to the structure with lowest R_free value obtained for d_min=4.5Å.

DEN refinement dramatically improves the structure compared to noDEN over a wide range of low resolution (Figs. 1c to 1e, Table 1), and with and without experimental phase information (compare Fig. 1 and Supplementary Fig. 2): The DEN R_free values (Fig. 1c) are nearly independent of the limiting resolution of the synthetic data sets (black), whereas they steadily increase for noDEN (red). For the data set at 5 Å resolution, DEN improves ₁₇ R_free by 0.1 (black double-arrow). The GDT(<1Å) score measures the fraction of atoms that fit the target structure well and thus focuses on the more accurate part of the structure (Fig. 1d). For data sets at d_min>4 Å, the GDT scores dramatically worsen for the structures refined without DEN: the resulting GDT score is worse than that of the initial model (dashed line). In contrast, the GDT score of the DEN refined models is consistently high. The RMSD to the target structure (3app) (Fig. 1e) is also significantly smaller with DEN. These improvements persist even when refinement cycles are added to the protocol without DEN (i.e., with w_DEN set to zero) (Supplementary Fig. 3).

Table 1.

DEN Refinement Improves Structures Refined against Four Synthetic Data Sets of Penicillopepsin^a

		Rfree			Rfree-Rwork		Ramachandran Score
Target Function	Resolution(Å)	DEN	noDEN	Improvement	DEN	noDEN	DEN	noDEN	Improvement
MLHL	3.50	0.331	0.357	0.0256	0.05	0.09	0.783	0.783	0.0000
MLHL	4.00	0.322	0.328	0.0058	0.07	0.09	0.754	0.772	−0.0184
MLHL	4.50	0.293	0.358	0.0651	0.02	0.11	0.702	0.632	0.0699
MLHL	5.00	0.300	0.400	0.0991	0.02	0.14	0.790	0.599	0.1912
MLF	3.50	0.378	0.390	0.0123	0.10	0.11	0.757	0.699	0.0588
MLF	4.00	0.347	0.391	0.0445	0.09	0.15	0.732	0.658	0.0735
MLF	4.50	0.348	0.413	0.0655	0.08	0.12	0.702	0.544	0.1581
MLF	5.00	0.341	0.425	0.0841	0.13	0.18	0.599	0.551	0.0478
Average	4.25	0.332	0.383	0.0503	0.07	0.12	0.727	0.655	0.0726
Minimum	3.50	0.293	0.328	0.0058	0.02	0.09	0.599	0.544	−0.0184
Maximum	5.00	0.378	0.425	0.0991	0.13	0.18	0.790	0.783	0.1912

^aStarting from a homology model of penicillopepsin (PDB 3app) that was built using the endothiapepsin structure (PDB 4ape) as a template with an initial RMSD of 1.7 Å, DEN refinements were performed (Online Methods). DEN refined structures are dramatically improved over noDEN structures, especially at low resolution (>4Å), with an average improvement of 0.078 in R_free for resolutions of 4.50 and 5.00 Å, with or without phases. At these same resolutions, the secondary structure definition also improved for DEN structures as shown by a higher Ramachandran Score (as determined by Molprobity³⁰). At the higher resolutions of 3.50 and 4.00 Å, the Ramachandran Score only improves without phase information, which shows that DEN provides little new information at higher resolution when experimental phase information is available. As expected, R_free values are lower when using phase information for both DEN and noDEN refinements with an average improvement of 0.042 for DEN and 0.045 for noDEN. In each column, green shading marks the most favorable maximum or minimum value (high Ramachandran Score or a low R-value);

pink shading marks the least favorable value.

In a broader test, we applied our method to 19 existing structures for which only low-resolution X-ray data are available (worse than 4 Å). To focus on DEN’s core strengths, we chose to re-refine the existing low-resolution structures with the help of a reference model that contains higher-resolution information. To minimize bias, we automated the re-refinement which is expected to limit structure improvement; as discussed below; much better results could be obtained by an investigator familiar with the structure and differences to the reference model.

For each selected PDB structure, a reference model was built by homology modeling on templates manually selected by simultaneously satisfying the three criteria of high sequence identity, high resolution, and large number of matched residues (Supplementary Tables 1 & 2). On average, 86% of the residues could be modeled. In some extreme cases (PDB 1av1, 2vkz, and 2bf1), the Main Chain RMSD of the template to the corresponding low-resolution PDB structure was around 10 Å, in which case structural similarity is likely to be limited and significant improvement is not expected. We included these cases to see if DEN can lead to improvements (2vkz and 2bf1, see below), and show that even in the worst case (1av1) DEN does not lead to a deterioration of the structure.

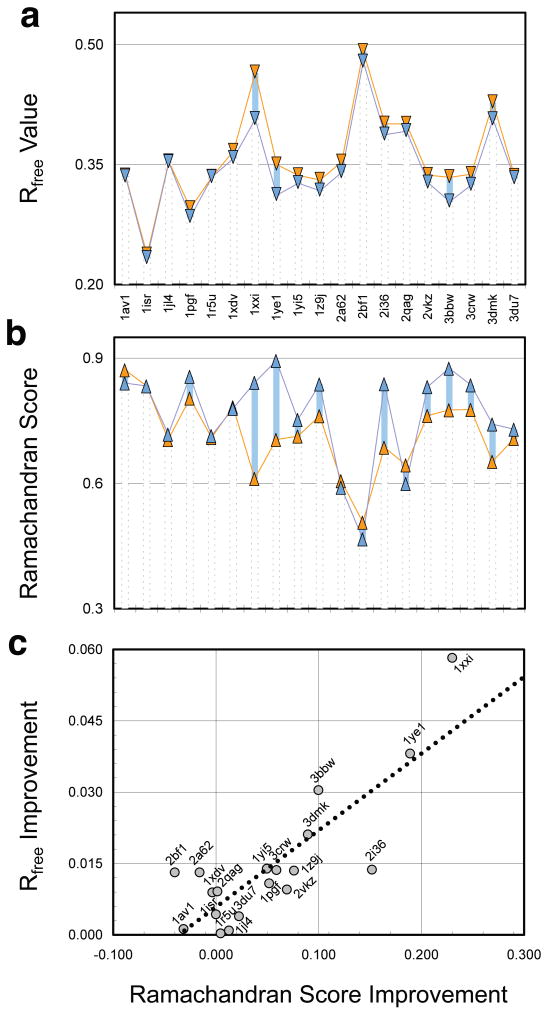
The R_free values of the DEN refined structures (Fig. 2a, Table 2, Supplementary Fig. 4) all improved relative to the noDEN structures. Eleven structures show an improvement of over 0.01, four an improvement of over 0.02, and the best an improvement of 0.058 (1xxi), a 12% improvement. The difference between R and R_free is on average 0.018 smaller for DEN vs. noDEN (Table 2); this indicates that overfitting is significantly reduced by DEN. Both the minimum and the maximum R_free values are generally lower for DEN than for noDEN (Supplementary Table 3), indicating that relevant, low-R_free regions of conformational space are better sampled.

Figure 2. Re-refinement of nineteen low-resolution PDB structures.

(a) R_free values of PDB structures refined with DEN (blue) and without DEN (noDEN, orange). In every case the DEN refined structure has the lower R_free value. For each protein, (γ, w_DEN) parameter optimization was performed (Online Methods, Supplementary Fig. 4), and the structure with the lowest R_free value used for analysis. (b) Fraction of residues in the favored region of the Ramachandran plot as determined by Molprobity³⁰ termed here Ramachandran Score. (c) Significant correlation (correlation coefficient 0.83) is seen between R_free Improvement and Ramachandran Score Improvement for DEN vs. noDEN.

Table 2.

DEN Refinement Improves Low Resolution Structures in the PDB^a

			Rfree			Rfree-Rwork		Ramachandran Score
PDB Identifier	Resolution(Å)	Number Residues	DEN	noDEN	Improvement	DEN	noDEN	DEN	noDEN	Improvement	Comments
1av1	4.00	804	0.335	0.336	0.0012	0.07	0.07	0.840	0.872	−0.0314
1isr	4.00	448	0.233	0.237	0.0043	0.07	0.07	0.833	0.833	0.0000
1jl4	4.30	557	0.353	0.354	0.0009	0.12	0.11	0.718	0.705	0.0127
1pgf	4.50	1102	0.284	0.295	0.0108	0.08	0.11	0.856	0.804	0.0519	Small differences throughout
1r5u	4.50	3517	0.334	0.335	0.0003	0.05	0.05	0.714	0.710	0.0046
1xdv	4.10	1517	0.358	0.367	0.0089	0.12	0.11	0.780	0.783	−0.0034
1xxi	4.10	3532	0.407	0.465	0.0582	0.05	0.12	0.842	0.612	0.2301	Large differences (~ 4 A domain motions)
1ye1	4.50	574	0.312	0.350	0.0381	0.08	0.15	0.894	0.705	0.1890	Small differences throughout
1yi5	4.20	1356	0.323	0.336	0.0139	0.07	0.09	0.758	0.709	0.0497	Local differences in several chains
1z9j	4.50	821	0.317	0.331	0.0135	0.07	0.09	0.838	0.762	0.0761	Large differences in chain A (domain motion)
2a62	4.50	319	0.340	0.353	0.0131	0.07	0.09	0.590	0.606	−0.0159
2bf1	4.00	304	0.479	0.492	0.0131	0.12	0.12	0.467	0.507	−0.0400
2i36	4.10	962	0.387	0.401	0.0137	0.02	0.03	0.839	0.687	0.1520	Local difference in chain B
2qag	4.00	702	0.392	0.401	0.0091	0.02	0.02	0.616	0.614	0.0016
2vkz	4.00	10941	0.327	0.337	0.0095	0.05	0.07	0.832	0.762	0.0692	Large differences in subdomain placements
3bbw	4.00	543	0.304	0.334	0.0304	0.01	0.04	0.876	0.776	0.0998	Significant local difference
3crw	4.00	485	0.324	0.338	0.0136	0.09	0.11	0.836	0.777	0.0589	Large difference in one domain (hinge motion)
3dmk	4.19	2127	0.407	0.428	0.0211	0.08	0.11	0.742	0.653	0.0896	Differences throughout, reference model only 50%
3du7	4.10	1839	0.332	0.336	0.0039	0.09	0.09	0.730	0.707	0.0225
Average	4.19	1708	0.345	0.359	0.0146	0.07	0.09	0.768	0.715	0.0535
Minimum	4.00	304	0.233	0.237	0.0003	0.01	0.02	0.467	0.507	−0.0400
Maximum	4.50	10941	0.479	0.492	0.0582	0.12	0.15	0.894	0.872	0.2301

^aNineteen PDB structures were re-refined with and without DEN (Online Methods). The tested proteins show a wide range of sizes extending from 304 residues for 2bf1 to 10941 residues for 1vkz. The final R_free, R_free − R_work values, as well as Ramachandran Scores are shown. In all cases, DEN refinement shows improvement of R_free as compared to noDEN; eleven out of nineteen cases show an R_free improvement that is larger than 0.01. In fifteen of the nineteen cases DEN refinement also improves the Ramachandran Score (four exceptions are 2bf1, 1av1, 2a62 and 1xdv). As would be expected R_free is larger than R_work (the R-factor that was optimized) with average differences of 0.07 and 0.09 for DEN and noDEN refinement, respectively. In each column, green shading marks the most favorable maximum or minimum value (high Ramachandran Score or low R-value);

pink shading marks the least favorable value. The comments refer to the differences between the reference models and the corresponding DEN-refined crystal structures for the cases with γ<1 (cf. Supplementary Table 4). Two particular examples of these differences are shown in Supplementary Fig. 5.

The Ramachandran Score shows that DEN refinement generally improves the secondary structure compared to noDEN (Fig. 2b and Table 2) with an average increase of 0.05. The largest improvement (0.23 or 37%) is again seen for 1xxi. There is high correlation between R_free and the Ramachandran Score Improvements (Fig. 2c). The four cases where the Ramachandran Score has slightly worsened (1av1, 1xdv, 2a62, 2bf1) are all cases with an optimal value of γ=1.0 (Supplementary Table 4). In these (and five additional cases with γ=1.0) the reference model is ignored, as it does not provide useful distances. As expected, the average R_free improvement in these nine cases is small (0.0061, Supplementary Table 4). In contrast, for the ten cases with γ<1, the average R_free improvement is significant (0.022, Supplementary Table 4). These ten successful cases cover a variety of differences between the reference model and the crystal structure, including large (sub-)domain motions, hinge motions, local structural differences, or differences throughout (Table 2 and Supplementary Fig. 5).

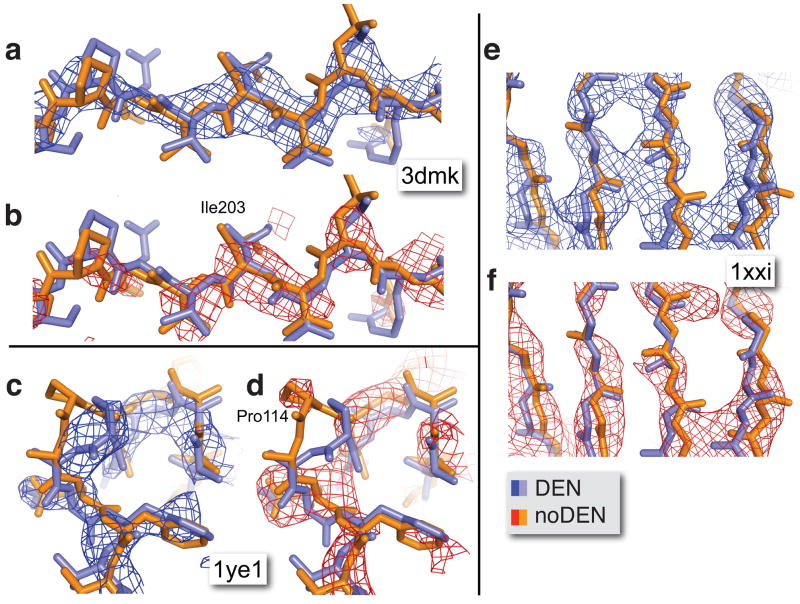
We calculated electron density maps from experimental intensities combined with model phases from the DEN and noDEN refined structures. In the three cases shown (Fig. 3) the noDEN backbone density is broken in several places (red), making it difficult to correctly trace the backbone. In contrast, the DEN maps show a continuous backbone density (blue). The DEN refined coordinates also show clear improvements, e.g. with DEN, Pro114 in the 1ye1 structure (Fig. 3c & 3d) is shifted by 3.2 Å into well-defined electron density (blue); very little density is visible for noDEN (red). Such improved interpretability of electron density maps indicates that the phases calculated from DEN refined structures are superior to those from noDEN refined structures.

Figure 3. Electron density map improvement upon DEN refinement for three structures 3dmk, 1ye1, and 1xxi.

The 1ye1 (c,d) and 1xxi (e,f) structures are among the cases that benefit most from DEN refinement, whereas the 3dmk (a,b) structure showed only moderate improvement of the R_free value (Table 2). Nevertheless, in all three cases DEN refinement dramatically improves the electron density maps. The structures refined with DEN (DEN, in blue) and without DEN (noDEN, in orange) are superimposed, and the corresponding phase combined σ_A-weighted 2F_o-F_c electron density maps are shown in blue and red, respectively. The density maps for 3dmk and 1xxi were B-factor sharpened (B_sharp = −50 Ų) and the contour level was set to 1.5 σ.

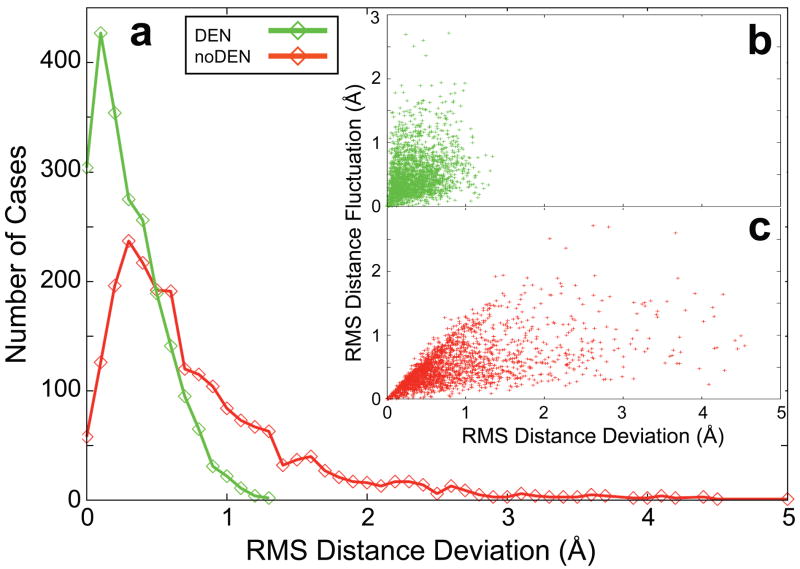
How does DEN increase the accuracy of the refined structure? For the penicillopepsin test case at 4.5 Å resolution we analyzed the distances between atom pairs not well defined by the diffraction data, specifically those with large root-mean-square fluctuations (RMSF) between the ten models of the noDEN refinement repeats (Fig. 4 Inset). These distances are much closer to the distances in the target structure (3app) for DEN compared to noDEN, showing that DEN provides information for distances that are not well defined by the diffraction data.

Figure 4. DEN provides information for degrees of freedom that are weakly defined by the experimental diffraction data.

(a) Showing DEN (green) and noDEN (red) histograms of, RMSDD, the root-mean-square deviation of DEN restraint distances in the target structure (3app) from those in the ten refinement repeats (starting from the 4ape initial model with d_min=4.5Å, the MLHL target function²⁴, and DEN optimum parameters (γ,w_DEN)=(0,10); see Fig. 1a). The largest RMSDD is much smaller for DEN compared to noDEN. Inset: the RMS Fluctuations of each distance over the ten repeats of noDEN refinement (RMSF) are plotted against RMSDD for DEN (b, green) and noDEN (c, red). Large RMSF values (>1.5 Å) represent the DEN distances that are not well defined by the diffraction data. For DEN, these distances have small RMSDD values (<1.0 Å) whereas for noDEN they have large RMSDD values. Restraint distances are much closer to the distances in the target structure for DEN, which effectively provides information missing from low-resolution experimental data.

Performance can be much improved by manually selecting cutoff criteria and structural elements used for DEN. For the unligated SIV gp120 structure¹⁸ (PDB 2bf1) we restricted the DEN network to the main chain and Cβ-atoms of the reference model (HIV gp120-antibody complex at 2.0 Å resolution¹⁹, PDB 2nxz) and to regions of the structure considered reliable predictors of SIV gp120 structure (at least 35.8 % local sequence identity, Supplementary Table 2). Refinement with optimum DEN parameters resulted in a 4% lower R_free value and 8% higher Ramachandran Score. With such judicious manual choice of the network, DEN used the reference model distances (γ=0.4, rather than γ=1 for automated DEN), and produced a more accurate structure as assessed by R_free.

Cross-validation with R_free allows determination of the optimum parameter values (particularly γ) yielding more accurate models at low resolution even when no high-resolution model is available. DEN can be applied to predicted structures, which have shown promise in molecular replacement ²⁰ and to RNA/DNA. DEN can be easily modified in future developments: for example, individual atomic weights could account for model error, variations in a family of homologous structures, or predicted loop conformations. Criteria for selection of distances can also be modified as done manually for 2bf1.

METHODS SUMMARY

The total energy function consists of a weighted sum of three terms

$$E_{\mathit{total}}=E_{\mathit{geometric}}+w_a{E}_{\text{ML}}+w_{\text{DEN}}{E}_{\text{DEN}}(\gamma )$$ (1)

where E_geometric is a “geometric” or stereochemical energy function commonly used for macromolecular crystal structure refinement²¹, E_ML is a maximum likelihood target function that incorporates experimental X-ray amplitude (and optionally phase information) ^22–24, E_DEN (γ) is the DEN potential (Online Methods), and w_a and w_DEN are relative weights. Such combination energy functions have been used for refinement of macromolecules since their first introduction for energy refinement ²⁵ and application to X-ray refinement⁹. The refinement protocol uses repeats of torsion angle dynamics²⁶ against E_total and B-factor refinement (Online Methods).

For DEN, the target sequence must be sufficiently close to an homologous sequence (sequence identity at least 30%), which means that the target and homolog will be structurally similar. It also requires that the homolog structure was determined at sufficiently high resolution (at least 3.5 Å resolution), so that it will contain useful specific high-resolution information about the target. Homology models for the target sequence were constructed using standard well-accepted methods such as SegMod²⁷ or MODELLER²⁸. Often, multiple homology models were combined to cover the entire target structure even when it consists of multiple domains and polypeptide chains.

Our approach is a major advance over conventional modeling of low resolution X-ray diffraction data by fitting rigid bodies²⁹ since it accounts for deformations of the models while at the same time using a minimal set of variables (the single-bond torsion angles) (for five cases, our re-refinement achieved a substantial improvement in R_free over rigid-body refined structures, Supplementary Table 1). Optionally, we turn off the DEN potential during the last refinement repeats to assess the robustness of the improvement achieved by DEN. The radius of convergence of DEN refinement is very large: in tests, automatic correction of polypeptide chain register in α-helices was observed, a notoriously difficult problem for macromolecular refinement.