Abstract
AIM
To assess the accuracy of skinfold equations in estimating percentage body fat in children with cerebral palsy (CP), compared with assessment of body fat from dual energy X-ray absorptiometry (DXA).
METHOD
Data were collected from 71 participants (30 females, 41 males) with CP (Gross Motor Function Classification System [GMFCS] levels I–V) between the ages of 8 and 18 years. Estimated percentage body fat was computed using established (Slaughter) equations based on the triceps and subscapular skinfolds. A linear model was fitted to assess the use of a simple correction to these equations for children with CP.
RESULTS
Slaughter’s equations consistently underestimated percentage body fat (mean difference compared with DXA percentage body fat −9.6/100 [SD 6.2]; 95% confidence interval [CI] −11.0 to −8.1). New equations were developed in which a correction factor was added to the existing equations based on sex, race, GMFCS level, size, and pubertal status. These corrected equations for children with CP agree better with DXA (mean difference 0.2/100 [SD=4.8]; 95% CI −1.0 to 1.3) than existing equations.
INTERPRETATION
A simple correction factor to commonly used equations substantially improves the ability to estimate percentage body fat from two skinfold measures in children with CP.
Although accurate assessment of nutritional status for children with cerebral palsy (CP) is important from clinical and research perspectives, physical impairments and growth differences hinder evaluation and interpretation in this population. Difficulties in measurement of stature arise from altered body posture and fixed contractures that interfere with reliable estimation of height or recumbent length. Equations that estimate height from segmental measures1 have been developed and are widely used. Additionally, it is possible to use specialized chair scales or weigh a child along with a caregiver.2 These modifications have allowed clinicians to obtain reliable measures of height and weight. Despite these improvements in measurement ability, clinicians continue to have challenges in interpreting growth and nutritional status in children with CP.
Because children with CP often have malnutrition associated with short stature, simple measurements of weight and height are not adequate to identify nutritional abnormalities. Known alterations in body composition in malnourished children with CP include increased total body water, depleted fat and muscle stores, short stature, and decreased bone density.3-5 Reliable measures of weight and height have allowed the use of weight-for-height centiles and body mass index (BMI), but the validity of these measures in assessing nutritional status in children with CP has been called into question.3
Reliable and valid methods that are also quick and readily available are needed to estimate fat mass (as an indicator of nutritional status) for research and to guide clinical care for children with CP because of the constraints described above. Dual-energy X-ray absorptiometry (DXA) is one method for accurately estimating fat mass (as well as fat-free mass and bone), but it requires specialized equipment, emits low levels of radiation, and is expensive.6 Bioelectrical impedance analysis is a less costly alternative that uses an electrical current to assess total body water. This estimate is used with standard equations to estimate fat and fat-free mass. However, bioelectrical impedance analysis is relatively expensive for use in an everyday clinical setting, and its accuracy for children with CP has been examined in limited situations.6 Doubly labeled water has been used to assess fat mass in children with CP, but it is time consuming and most often used in research settings.4
From a clinical perspective, the most attractive tool to estimate fat mass is anthropometry because it only requires a skinfold caliper and an individual who is properly trained to use it. The widely used ‘Slaughter equations’ utilize skinfold measurements to estimate percentage body fat in otherwise healthy children7 and have been shown to be accurate in subsequent studies using DXA as the criterion standard.8,9 However, others have found their predictive ability inadequate,10 particularly in specific populations such as African-American prepubertal children.11 Nevertheless, these equations are commonly used in clinical and research settings to estimate percentage body fat.
The predictive ability of these equations has been examined for children with CP, but the studies were small and limited in scope,4,6,12 with only one sample of children with CP>28 (53 participants)13 that examined solely children with quadriplegic CP. In all cases, the Slaughter equations underestimated percentage body fat compared with the criterion standard, DXA,6,13 or the deuterium dilution technique.4,12 None of the studies proposed alternative estimation techniques for this population.
The purpose of this study was twofold. First, to confirm that the Slaughter equations underestimate percentage body fat in children with CP. This study would distinguish itself by the use of a relatively large sample of children with varying degrees of severity of CP. Second, given corroboration of this previous finding, possible corrections to the existing Slaughter equations would be estimated, and their ability to predict percentage body fat more accurately would be assessed.
METHOD
This research was designed as a sub-study of the North American Growth in Cerebral Palsy Project, which has been described elsewhere.14 Anthropometry, pubertal staging, and DXA were performed at baseline for all participants at three different sites: the University of North Carolina, the University of Virginia, and the Hattie Larlham Center for Children with Disabilities.
Participants
One hundred and two individuals with CP who participated in the North American Growth in Cerebral Palsy Project (ages 2–30y; Gross Motor Function Classification System [GMFCS] levels I–V) were enrolled in the study. Participants at the University of North Carolina and the Hattie Larlham Center for Children with Disabilities were at GMFCS levels III–V, whereas those at the University of Virginia were at GMFCS levels I and II. The study was approved by the institutional review boards of each institution. Informed consent was obtained from each participant’s parent or legal guardian, and assent was obtained from the participant when possible.
Inclusion/exclusion criteria
Those individuals with a history of genetic, metabolic, or neurodegenerative disease, or children with medical conditions affecting growth, were excluded. Only those aged 8 to 18 years were included in these analyses, as this was the suggested age range for use of the Slaughter equations.
Clinical assessment and measurement of functional impairment
Participants were assessed for functional motor impairment using the GMFCS,15 a reliable and valid method of communicating motor function for research and clinical purposes. GMFCS levels range from I to V, with individuals at level V having the greatest motor impairment. For statistical and clinical considerations, the GMFCS was further categorized into two groups: ‘more severe’ (GMFCS levels III, IV, V) and ‘less severe’ (GMFC levels I, II).
Measures of maturation
Development of secondary sex characteristics (breasts in females; pubic hair in males) was assessed by a developmental pediatrician or the research coordinator using the methods of Tanner.16 Observers were trained in the assessment of sexual maturation by one of the principal investigators of the American Academy of Pediatrics, Pediatric Research in Office Settings network study of sexual maturation in females. Details of the training are published elsewhere.17,18
Anthropometry
Anthropometry was performed using techniques described in The Methods of Auxological Anthropometry.19 The mean of two measurements of subscapular and triceps skinfolds was calculated in all participants using Holtain skinfold calipers (Holtain Ltd, Crymych, UK). Anthropometric data were collected by one individual at each site using the same methods. As with the North American Growth in Cerebral Palsy Project protocol, measurements were obtained from the unaffected side (in hemiplegia) or less affected side, if there was significant asymmetry.
Dual energy X-ray absorptiometry
Whole-body DXA was performed using Hologic Delphi W machines (CMS, MI, USA) with Discovery software, version 12.3 (Bellingham WA, USA). Exchange of each site’s calibration spine phantom confirmed the reliability of pooling results from the three scanners. Percentage body fat excluding the head was estimated and considered the reference from which to compare Slaughter-estimated percentage body fat.
Body fat calculation
The original Slaughter equations7 based on the triceps and subscapular skinfolds were used to estimate percentage body fat for each individual. Given that the primary aim was to assess their accuracy, the recommendations for their use were strictly followed. That is, percentage body fat was estimated only for children aged 8 to 18 years. The definition of pubertal status used by Slaughter et al.7 was used here as well: prepubescent was defined as a Tanner stage of 1 or 2, pubescent was characterized as Tanner stage 3, and post-pubescent was defined as a Tanner stage of 4 or 5. It is unclear which criteria were used by Slaughter et al.;7 others11 have speculated they used pubic hair development.
Statistical analysis
All analyses used SAS version 9.1 (SAS Institute Inc, Cary, NC, USA). To assess agreement between DXA and the Slaughter estimates for percentage body fat, an initial graphical examination was performed, plotting the individual pairs of estimates and visually assessing the overall proximity to the identity line. Bland and Altman20 figures were created, in which differences between the two estimates were plotted against the values of the DXA estimates. To gauge the overall bias and precision of the equation-predicted percentage body fat, means and standard deviations of the difference values were computed, respectively, overall, and for various subgroups (sex, race, pubertal status, GMFCS category, and size). Finally, to get an overall statistic quantifying agreement (i.e. proximity to the identity line), the concordance correlation coefficient (CCC)21 was computed. A value of 1 indicates perfect agreement; CCC values of <0.5 were considered to indicate poor agreement, CCC values of between 0.5 and 0.7 moderate agreement, and values >0.7 good to excellent agreement.
We then explored possible corrections to the Slaughter equations. The results of the graphical examinations were used to determine whether a simple correction to the Slaughter-estimated percentage body fat may be sufficient, allowing this correction to vary by factors such as sex, race, etc. A linear model was fitted in which the difference between the two estimates was modeled initially as a function of sex, race (white or black), GMFCS category (less or more severe), pubertal status, and size (sum of triceps and subscapular skinfold not more than 35mm vs >35mm). This model also included all pairwise interactions between the factors listed. In a stepwise fashion, the least significant interaction term was dropped from the model until only factors and/or their interactions that were marginally statistically significant (p<0.10) remained. The resulting estimates from the model represented corrections to be made to the original Slaughter equations for levels of these significant factors. The validity of the model assumptions (i.e. normality and constant variance) was assessed by a graphical examination of the resulting residuals.22
The agreement analysis was then repeated on these corrected equations, including computation of the CCC. It was expected that the level of agreement estimated using these data would be overly optimistic given these equations were developed from the very same data.23 Thus, 200 bootstrap samples of the data were taken, in which 200 new datasets were compiled, each a random sample (with replacement) of the original data. The CCC was then computed on each of these bootstrap samples, and the mean difference between the original CCC and each bootstrap CCC represented an estimate of the bias induced by using the original data to assess the validity of these new equations. The CCC for the corrected equations was then adjusted by subtracting this bias estimate; this new value of the concordance represented the agreement one would expect if applying these corrected equations to an entirely separate dataset.
RESULTS
Anthropometric and DXA data were available from 71 participants aged 8 to 18 years from the three sites (Table I); an additional 31 participants outside this age range were excluded. The original Slaughter equations are listed in Table II; separate equations exist for those ‘smaller’ individuals (sum of triceps and subscapular skinfolds not more than 35mm) as well as for larger individuals (sum >35mm). Within both of these groups, separate equations are recommended for males and females; for males in the smaller group, further stratification of these equations was made based on race and pubertal status.
Table I.
Characteristics of participants
| Mean (SD) |
||||||
|---|---|---|---|---|---|---|
| Characteristic | Frequency (%) |
Age (y) | BMI | Percentage body fat, DXA |
Triceps skinfold, mm |
Subscapular skinfold, mm |
| Overall | 71 (100) | 12.8 (2.9) | 19.7 (4.6) | 29.9 (11.6) | 12.7 (7.4) | 11.7 (6.6) |
| Site | ||||||
| University of North Carolina | 45 (64) | 12.6 (2.8) | 19.1 (4.6) | 28.6 (10.8) | 11.0 (6.0) | 10.2 (5.2) |
| Cleveland | 8 (11) | 14.7 (3.3) | 19.6 (3.6) | 36.1 (6.3) | 14.9 (6.3) | 14.1 (3.6) |
| University of Virginia | 18 (25) | 12.6 (2.9) | 21.3 (5.0) | 30.3 (14.8) | 15.9 (9.7) | 14.7 (9.1) |
| Gender | ||||||
| Male | 41 (58) | 12.7 (2.9) | 19.5 (4.3) | 26.9 (12.6) | 11.7 (7.6) | 11.5 (7.3) |
| Female | 30 (43) | 13.1 (3.0) | 20.0 (5.1) | 33.9 (8.9) | 14.0 (7.0) | 12.0 (5.4) |
| Race | ||||||
| White | 52 (73) | 12.9 (3.1) | 20.0 (4.7) | 31.6 (11.3) | 13.5 (7.6) | 12.3 (6.9) |
| Black | 19 (27) | 12.7 (2.4) | 19.0 (4.5) | 25.0 (11.6) | 10.6 (6.3) | 10.2 (5.4) |
| GMFCS level | ||||||
| 1 | 14 (20) | 12.4 (3.0) | 20.6 (4.4) | 30.3 (13.8) | 15.2 (8.3) | 13.8 (7.9) |
| 2 | 4 (6) | 13.4 (3.1) | 23.7 (6.8) | 30.4 (20.5) | 18.1 (14.8) | 17.8 (13.7) |
| 3 | 5 (7) | 14.3 (3.5) | 25.1 (5.7) | 23.8 (11.9) | 11.2 (7.0) | 10.7 (4.6) |
| 4 | 14 (20) | 11.9 (2.5) | 18.4 (4.6) | 27.8 (11.2) | 10.1 (4.6) | 9.4 (5.7) |
| 5 | 34 (48) | 13.1 (3.0) | 18.7 (3.6) | 31.3 (9.9) | 12.3 (3.6) | 11.3 (5.1) |
| Tanner stage | ||||||
| 1 (Prepubescent) | 13 (20) | 9.4 (0.8) | 16.5 (3.9) | 28.8 (11.4) | 10.6 (6.1) | 9.1 (7.5) |
| 2 (Prepubescent) | 6 (9) | 11.2 (2.2) | 18.9 (4.9) | 27.5 (9.7) | 11.0 (5.3) | 9.2 (5.3) |
| 3 (Pubescent) | 12 (18) | 11.8 (2.7) | 21.3 (5.3) | 38.2 (12.2) | 17.1 (10.1) | 15.5 (8.9) |
| 4 (Postpubescent) | 17 (26) | 14.1 (2.4) | 19.0 (3.3) | 26.2 (10.4) | 10.8 (6.5) | 10.0 (4.1) |
| 5 (Postpubescent) | 17 (26) | 15.5 (1.7) | 20.9 (4.9) | 26.6 (11.5) | 12.5 (7.0) | 12.6 (5.5) |
| Triceps+subscapular skinfold | ||||||
| ≤35mm | 56 (79) | 12.7 (3.0) | 18.3 (3.7) | 26.2 (10.0) | 9.5 (3.8) | 9.3 (4.0) |
| >35mm | 15 (21) | 13.4 (2.9) | 25.0 (4.0) | 43.4 (6.0) | 24.4 (5.5) | 20.9 (6.2) |
Table II.
Original Slaughter equations and corrections for children with cerebral palsy
| Population | Original Slaughter equation for predicting percentage body fat7 |
|---|---|
| Sum (triceps, subscapular)≤35mm | |
| Males | |
| Prepubescenta white | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −1.7 |
| Prepubescent black | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −3.2 |
| Pubescent white | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −3.4 |
| Pubescent black | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −5.2 |
| Postpubescent white | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −5.5 |
| Postpubescent black | % Body fat=1.21(tri+sub)−0.008(tri+sub)2 −6.8 |
| Females (all) | % Body fat=1.33(tri+sub)−0.013(tri+sub)2 −2.5 |
| Sum (triceps, subscapular)>35mm | |
| Males (all) | % Body fat=0.783(tri+sub)+1.6 |
| Females (all) | % Body fat=0.546(tri+sub)+9.7 |
| Cerebral-palsy-specific corrections to Slaughter-estimated percentage body fatb | |
|
| |
| Overall correction | +12.2 |
| Additional correction for | |
| Males | −5.0 |
| More severe GMFCS | +5.1 |
| Black race | −3.1 |
| Pubescent | +2.0 |
| Postpubescent | −4.6 |
| Sum (triceps, subscapular) >35mm | −3.2 |
Prepubescent, Tanner stage 1, 2; pubescent, Tanner stage 3; postpubescent, Tanner stage 4, 5.
Instructions for using these corrections on a given child with CP: always add 12.2 to the Slaughter-estimated percentage body fat. Then, if the individual falls within each of the additional categories, add that respective correction as well. For example, for a black pubescent male at GMFCS level 1 whose sum (triceps, subscapular)<35mm, the predicted percentage body fat=Slaughter percentage body fat+12.2−5.0−3.1+2.0. Tri+sub, triceps skinfold+subscapular skinfold. GMFCS, Gross Motor Function Classification System.
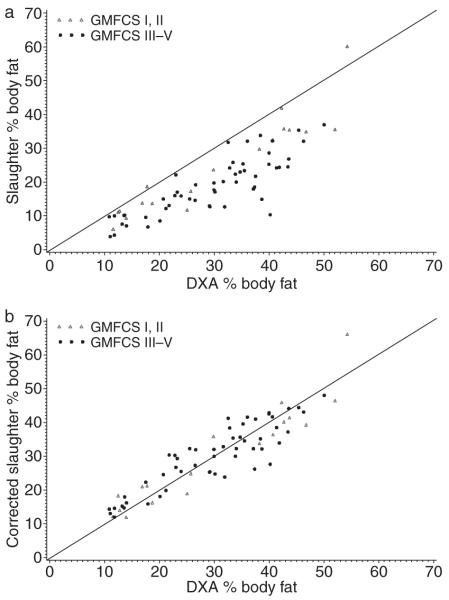
Overall, the Slaughter equations underestimated percentage body fat compared with the percentage body fat estimate from DXA (Table III, Figs 1a and S1a [supplementary material published online]). The mean overall difference between the two estimates was −9.6/100 (SD 6.2); the fact that the 95% confidence interval (CI) does not contain 0 (−11.0 to −8.1) indicates this underestimate is statistically significant at the 0.05 level. Analysis of the difference for various subgroups shows that the Slaughter equations are not particularly accurate for any group of children with CP (Table III). The CCC measuring the amount of agreement between these two estimates was 0.62, indicating only moderate agreement between the two methods and further confirming that the Slaughter equations are not appropriate for this population of individuals in predicting percentage body fat.
Table III.
Overall error of predicted percentage body fat: original and corrected Slaughter equations
| Difference (predicted percentage body fat-DXA percentage body fat)a |
||||
|---|---|---|---|---|
| Original Slaughter equations |
CP corrected Slaughter equations |
|||
| Mean (SD)b | 95% CI | Mean (SD)b | 95% CI | |
| Overall | −9.6 (6.2) | (−11.0 to −8.1) | 0.2 (4.8) | (−1.0 to 1.3) |
| Sex | ||||
| Male | −8.0 (5.9) | (−9.8 to −6.1) | −0.1 (4.4) | (−1.5 to 1.3) |
| Female | −11.8 (6.0) | (−14.0 to −9.5) | 0.5 (5.3) | (−1.5 to 2.5) |
| Race | ||||
| White | −10.1 (6.5) | (−11.9 to −8.2) | 0.1 (5.1) | (−1.3 to 1.5) |
| Black | −8.3 (5.2) | (−10.8 to −5.8) | 0.3 (3.9) | (−1.6 to 2.2) |
| GMFCS category | ||||
| Less severe | −5.7 (5.4) | (−8.4 to −3.0) | −0.1 (5.1) | (−2.6 to 2.5) |
| More severe | −10.9 (5.9) | (−12.5 to −9.3) | 0.2 (4.8) | (−1.1 to 1.6) |
| Tanner stage | ||||
| 1, 2 (Prepubescent) | −10.8 (7.3) | (−14.3 to −7.2) | −0.0 (5.4) | (−2.6 to 2.6) |
| 3 (Pubescent) | −11.6 (7.2) | (−16.2 to −7.0) | −0.0 (5.7) | (−3.6 to 3.6) |
| 4, 5 (Postpubescent) | −7.9 (5.3) | (−9.7 to −6.0) | −0.1 (4.4) | (−1.6 to 1.5) |
| Triceps+subscapular skinfold | ||||
| ≤35mm | −10.2 (6.2) | (−11.8 to −8.5) | 0.3 (4.6) | (−0.9 to 1.5) |
| >35mm | −7.3 (5.9) | (−10.5 to −4.1) | −0.3 (5.5) | (−3.4 to 2.7) |
Individual difference between equation-predicted percentage body fat and DXA percentage body fat.
The mean difference provides an estimate of the bias (systematic error) of the equation-predicted percentage body fat, whereas the SD of this difference provides a measure of the precision of the prediction. DXA, dual energy X-ray absorptiometry; GMFCS, Gross Motor Function Classification System.
Figure 1.
Slaughter equations (a) original and (b) corrected versus dual energy X-ray absorptiometry (DXA) for percentage body fat. GMFCS, Gross Motor Function Classification System.
The consistent underestimate of percentage body fat by the Slaughter equations (Figs 1a and S1a) suggested a simple correction might be suitable, allowing variation based on certain factors. After following the model selection procedure, the final model of the difference between the Slaughter and DXA percentage body fat included sex, GMFCS category, and pubertal status (p<0.01), as well as race and size (p<0.10). These main effects predicted differences between the two estimates, and their corresponding parameter estimates signified the corrections specific to each value of these factors (Table II). Hence, in estimating percentage body fat for an individual with CP, one must first use the appropriate original Slaughter equation in Table II, and then add the overall correction factor of 12.2/100 body fat. To this, one then adds or subtracts any additional correction(s) depending on the individual’s sex, race, pubertal status, CP severity, and size; the number of additional corrections will range from 0 to 5.
The agreement analysis for these corrected equations reveals the excellent predictive ability of the new equations (Table III, Figs 1b and S1b). Here, the mean overall difference between the corrected estimate for percentage body fat and the DXA value was 0.2/100 (95% CI −1.0 to 1.3). The precision of this CI, as well as being centered on 0, suggests clinical equivalence between the two estimates. Examination of these mean differences for each subgroup reveals the relative suitability of these corrected equations for any individual with CP. The SDs of these individual differences (overall SD 4.8) indicate that although the corrected equations account for the bias of the original Slaughter equations, there is still a moderate degree of individual variability with the new predicted measures. The Bland–Altman plot (Fig. S1b) shows that although these corrected equations present a substantial improvement in predicting percentage body fat, there is some deterioration of performance for individuals with a large percentage body fat.
The CCC between the corrected equations and DXA was 0.91, indicating excellent agreement. However, as mentioned previously, one would expect this estimate to be inflated, as one is measuring agreement on data from which the corrections were estimated. The mean difference between the CCC from the 200 bootstrap samples and 0.91 was 0.12, which is a measure of this optimism. In other words, if one were to evaluate the validity of these corrected equations externally, one would expect an agreement roughly equal to CCC=0.91−0.12=0.79. This value still suggests excellent agreement and hence predictive ability of these corrected equations applied to individuals in the future.
DISCUSSION
This study supports previous findings that the Slaughter equations used to estimate percentage body fat by skinfolds are not accurate in children with CP.4,6,12,13 This study is an important addition given its characteristics: a relatively large sample size including ambulatory and non-ambulatory children with CP and the use of DXA as the comparison measure of percentage body fat. More important, however, is this study’s proposal of simple corrections to these widely used equations to estimate body fat in children with CP more accurately.
The root cause(s) of the poor performance of the Slaughter equations in this population remains unclear. It is possible that these equations, developed two decades ago using underwater weighing as the criterion standard, are not accurate in most populations of children. However, previous research has shown the validity of these equations in otherwise healthy children,24 even when using DXA as the reference.8,9 Here, the fact that their performance was significantly worse for children with more severe motor impairment indicates that there may be some underlying factors unique to children with CP that render these equations inappropriate in this particular population. Others12 have hypothesized that using skinfolds may underestimate total body fat because children with CP have relatively large internal rather than peripheral fat deposits. Our data reveal that those individuals at GMFCS level V as a group have higher percentage body fat (Table I). This result could be due partly to decreased physical activity (and reduced lean mass), or the fact that most received gastrostomies. Here, 25 of the 34 (74%) individuals at GMFCS level V were fed by gastrostomy tube, and on average they had higher percentage body fat (33.8/100 vs 24.4/100), consistent with previous observations.25 Nevertheless, the relatively poor performance of less impaired individuals with higher percentage body fat (Fig. S1) indicates that the original equations do not perform well for those with larger percentage body fat, regardless of the cause. Even though this study was sufficiently large to identify factors associated with the underperformance of these equations and to make necessary corrections, the sample size was inadequate to examine possible underlying factors, such as reduced physical activity, gastrostomy use, etc. Further research is also needed to determine if children with CP are unique for regional fat distribution.
The proposed corrections that improve the performance of the Slaughter equations are important from both a clinical and research perspective. These corrections provide a simple modification to an existing set of equations that subsequently produces accurate estimates of percentage body fat in children with CP. Most children with CP have decreased percentage body fat, but others have noted that those fed by gastrostomy feeding tubes may accumulate excess body fat.25 In either case, reliable methods for estimating percentage body fat for children with CP would be extremely valuable. Statistical techniques applied to this dataset indicate the generalizability of these corrected equations in the future to individuals with CP. However, their accuracy should be verified in future studies. It is possible that further refinement of these equations is necessary. Given that children with CP have body compositions inherently different to other children, it may be beneficial to develop altogether new equations rather than estimate corrections to existing equations. Unfortunately, the sample size in this case did not allow the development of entirely new equations unique to children with CP. Even though these corrected equations provide more accurate measures of percentage body fat, there is evidence that this accuracy diminishes somewhat for larger individuals. This inaccuracy could be due to increased measurement error when using skinfold calipers on larger individuals in general, or some other cause(s) that could not be detected here.
This study has other limitations. It would have been beneficial to include a group of otherwise healthy children to examine further the general accuracy of the Slaughter equations. However, as already noted, previous research has validated these equations in healthy children and has applied them to children with CP. This study confirms in a larger and more general setting the inaccuracy of these popular equations for use in children with CP. Developing new predictive equations requires a large set of individuals. Although this study is large compared with others with similar aims, it is relatively small for developing entirely new equations. Nevertheless, this examination led to the conclusion that a simple modification to current equations would be sufficient, and the size of this study lends itself to estimating such corrections.
In undertaking such a study, the accuracy of the criterion standard must be discussed. Compared with established methods, such as the isotope-dilution technique or underwater weighing, DXA has been observed to be accurate for estimating percentage body fat,26 including adults with CP.27 In recent years DXA has undergone significant improvements as an assessment tool for body composition. Shypailo et al.28 found a shift to higher percentage body fat for children when they compared body fat measurements using the newer version (12.1:3) of Hologic software with the previous version (11.2). This newer version was enhanced to include dynamic detection thresholds for individuals weighing <40kg. This change in detection thresholds for lower weights may result in the detection of bone not measured in earlier versions, which would have biased the body composition measurements toward a higher lean value. It is important to note that all of our work was carried out using the newer software version (12.3).
CONCLUSION
Assessing the nutritional status of children with CP is extremely important. At the same time, this assessment has proved difficult and unreliable in this population. Regardless of the underlying causes, it is known that the body composition of children with CP is different from that of typically growing children. It is vital to develop and validate inexpensive and straightforward tools for estimating body composition of these children as a marker of nutritional adequacy. This study provides confirmation that the popular Slaughter equations underestimate body fat in children with CP. More importantly, simple corrections of these equations improve the ability to estimate percentage body fat in this population. This study can be seen as the first to suggest a clinically viable alternative that is relatively accurate, inexpensive, and accessible for estimating body fat in children with CP.
Supplementary Material
ACKNOWLEDGMENTS
Research conducted at the University of North Carolina was supported by the General Clinical Research Centers program of the Division of Research Resources, National Institutes of Health (RR00046), and a career award from the National Institute of Arthritis, Musculoskeletal, and Skin Diseases (K24 AR02132). Work done at the Hattie Larlham Center for Children with Disabilities was supported by the Louise H and David S Ingalls Foundation and the Reuter Foundation. DXA was provided by the Kent State Health Science Center and performed by Linnea Ray. Research carried out at the University of Virginia was supported by the Kluge Research Fund and the Children’s Hospital Committee of the University of Virginia, the Genentech Foundation for Growth and Development, the National Center for Medical Rehabilitation Research (grants 5 R01 HD35739-04, 1 F32 HD08615-01A1, 1 R24 HD39631-01, K24-HD041504-01), and the University of Virginia General Clinical Research Center (M01RR00847).
REFERENCES
- 1.Stevenson RD. Use of segmental measures to estimate stature in children with cerebral palsy. Arch Pediatr Adolesc Med. 1995;149:658–62. doi: 10.1001/archpedi.1995.02170190068012. [DOI] [PubMed] [Google Scholar]
- 2.Kuperminc MN, Stevenson RD. Growth and nutrition disorders in children with cerebral palsy. Dev Disabil Res Rev. 2008;14:137–46. doi: 10.1002/ddrr.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Samson-Fang LJ, Stevenson RD. Identification of malnutrition in children with cerebral palsy: poor performance of weight-for-height centiles. Dev Med Child Neurol. 2000;42:162–8. doi: 10.1017/s0012162200000293. [DOI] [PubMed] [Google Scholar]
- 4.Stallings VA, Cronk CE, Zemel BS, Charney EB. Body composition in children with spastic quadriplegic cerebral palsy. J Pediatr. 1995;126(5 Pt 1):833–9. doi: 10.1016/s0022-3476(95)70424-8. [DOI] [PubMed] [Google Scholar]
- 5.Henderson RC, Lark RK, Gurka MJ, et al. Bone density and metabolism in children and adolescents with moderate to severe cerebral palsy. Pediatrics. 2002;110(1 Pt 1):e5. doi: 10.1542/peds.110.1.e5. [DOI] [PubMed] [Google Scholar]
- 6.Liu LF, Roberts R, Moyer-Mileur L, Samson-Fang L. Determination of body composition in children with cerebral palsy: bioelectrical impedance analysis and anthropometry vs dual-energy x-ray absorptiometry. J Am Diet Assoc. 2005;105:794–7. doi: 10.1016/j.jada.2005.02.006. [DOI] [PubMed] [Google Scholar]
- 7.Slaughter MH, Lohman TG, Boileau RA, et al. Skinfold equations for estimation of body fatness in children and youth. Hum Biol. 1988;60:709–23. [PubMed] [Google Scholar]
- 8.Steinberger J, Jacobs DR, Raatz S, Moran A, Hong CP, Sinaiko AR. Comparison of body fatness measurements by BMI and skinfolds vs dual energy X-ray absorptiometry and their relation to cardiovascular risk factors in adolescents. Int J Obes. 2005;29:1346–52. doi: 10.1038/sj.ijo.0803026. [DOI] [PubMed] [Google Scholar]
- 9.Rodriguez G, Moreno LA, Blay MG, et al. Body fat measurement in adolescents: comparison of skinfold thickness equations with dual-energy X-ray absorptiometry. Eur J Clin Nutr. 2005;59:1158–66. doi: 10.1038/sj.ejcn.1602226. [DOI] [PubMed] [Google Scholar]
- 10.Loftin M, Nichols J, Going S, et al. Comparison of the validity of anthropometric and bioelectric impedance equations to assess body composition in adolescent females. Int J Body Compos Res. 2007;5:1–8. [PMC free article] [PubMed] [Google Scholar]
- 11.Cameron N, Griffiths PL, Wright MM, et al. Regression equations to estimate percentage body fat in African prepubertal children aged 9 y. Am J Clin Nutr. 2004;80:70–5. doi: 10.1093/ajcn/80.1.70. [DOI] [PubMed] [Google Scholar]
- 12.van den Berg-Emons RJ, van Baak MA, Westerterp KR. Are skinfold measurements suitable to compare body fat between children with spastic cerebral palsy and healthy controls? Dev Med Child Neurol. 1998;40:335–9. doi: 10.1111/j.1469-8749.1998.tb15385.x. [DOI] [PubMed] [Google Scholar]
- 13.Arrowsmith FE. Nutritional assessment and rehabilitation of children with quadriplegic cerebral palsy (Thesis) Department of Paediatrics, University of Sydney; 2006. [Google Scholar]
- 14.Liptak GS, O’Donnell M, Conaway M, et al. Health status of children with moderate to severe cerebral palsy. Dev Med Child Neurol. 2001;43:364–70. doi: 10.1017/s001216220100069x. [DOI] [PubMed] [Google Scholar]
- 15.Palisano R, Rosenbaum P, Walter S, Russell D, Wood E, Galuppi B. Development and reliability of a system to classify gross motor function in children with cerebral palsy. Dev Med Child Neurol. 1997;39:214–23. doi: 10.1111/j.1469-8749.1997.tb07414.x. [DOI] [PubMed] [Google Scholar]
- 16.Tanner JM. Growth at adolescence. 2nd revised edn. Blackwell Science; London: 1978. p. 348. [Google Scholar]
- 17.Herman-Giddens ME, Slora EJ, Wasserman RC, et al. Secondary sexual characteristics and menses in young girls seen in office practice: a study from the pediatric research in office settings network. Pediatrics. 1997;99:505–12. doi: 10.1542/peds.99.4.505. [DOI] [PubMed] [Google Scholar]
- 18.Worley G, Houlihan CM, Herman-Giddens ME, et al. Secondary sexual characteristics in children with cerebral palsy and moderate to severe motor impairment: a cross-sectional survey. Pediatrics. 2002;110:897–902. doi: 10.1542/peds.110.5.897. [DOI] [PubMed] [Google Scholar]
- 19.Cameron N. The methods of auxological anthropology. Vol. 3. Plenum Press; New York: 1986. [Google Scholar]
- 20.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;i:307–10. [PubMed] [Google Scholar]
- 21.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–68. [PubMed] [Google Scholar]
- 22.Muller KE, Fetterman BA. Regression and ANOVA: an integrated approach using SAS software. SAS Institute; Cary, NC: 2002. p. 565. [Google Scholar]
- 23.Harrell FE, Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15:361–87. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 24.Janz KF, Nielsen DH, Cassady SL, Cook JS, Wu YT, Hansen JR. Cross-validation of the Slaughter skinfold equations for children and adolescents. Med Sci Sports Exerc. 1993;25:1070–6. [PubMed] [Google Scholar]
- 25.Sullivan PB, Alder N, Bachlet AM, et al. Gastrostomy feeding in cerebral palsy: too much of a good thing? Dev Med Child Neurol. 2006;48:877–82. doi: 10.1017/S0012162206001927. [DOI] [PubMed] [Google Scholar]
- 26.Haarbo J, Gotfredsen A, Hassager C, Christiansen C. Validation of body composition by dual energy X-ray absorptiometry (DEXA) Clin Physiol. 1991;11:331–41. doi: 10.1111/j.1475-097x.1991.tb00662.x. [DOI] [PubMed] [Google Scholar]
- 27.Hildreth HG, Johnson RK, Goran MI, Contompasis SH. Body composition in adults with cerebral palsy by dual-energy X-ray absorptiometry, bioelectrical impedance analysis, and skinfold anthropometry compared with the 18O isotope-dilution technique. Am J Clin Nutr. 1997;66:1436–42. doi: 10.1093/ajcn/66.6.1436. [DOI] [PubMed] [Google Scholar]
- 28.Shypailo RJ, Butte NF, Ellis KJ. DXA: can it be used as a criterion reference for body fat measurements in children? Obesity. 2008;16:457–62. doi: 10.1038/oby.2007.81. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.