Genome-wide synteny through highly sensitive sequence alignment: Satsuma

Abstract

Motivation: Comparative genomics heavily relies on alignments of large and often complex DNA sequences. From an engineering perspective, the problem here is to provide maximum sensitivity (to find all there is to find), specificity (to only find real homology) and speed (to accommodate the billions of base pairs of vertebrate genomes).

Results: Satsuma addresses all three issues through novel strategies: (i) cross-correlation, implemented via fast Fourier transform; (ii) a match scoring scheme that eliminates almost all false hits; and (iii) an asynchronous ‘battleship’-like search that allows for aligning two entire fish genomes (470 and 217 Mb) in 120 CPU hours using 15 processors on a single machine.

Availability: Satsuma is part of the Spines software package, implemented in C++ on Linux. The latest version of Spines can be freely downloaded under the LGPL license from http://www.broadinstitute.org/science/programs/genome-biology/spines/

Contact: grabherr@broadinstitute.org

1 INTRODUCTION

The problem of identifying DNA sequences that share a common origin dates back to the beginning of modern genomics, and a number of sequence alignment programs have been developed over the past 30 years [an incomplete list includes FASTA (Lipman and Pearson, 1985); the BLAST family, including blastz and MegaBlast (Altschul et al., 1990; Huang et al., 1991; Zhang et al., 2000; Schwartz et al., 2003), http://blast.wustl.edu; SSEARCH (Pearson, 1991); MUMmer (Delcher et al., 1999); BLAT (Kent, 2002); PatternHunter (Li et al., 2003; Ma et al., 2002)]. Comparative genome biology aims to find genomic differences as well as similarities. From a computational perspective, this requires providing pairwise sequence alignments at maximum sensitivity, specificity and acceptable speed. While full dynamic programming approaches (such as in Smith, 1981) in theory yield maximal sensitivity, it is not practical to apply them to large datasets (e.g. entire vertebrate genomes), because of the high computational cost. Two other approaches have been used to address this issue: (i) suffix-tree-based methods (e.g. MUMmer, Delcher et al., 1999), which are very fast, but limited to highly similar sequences; and (ii) k-tuple, or seeded matches (Kent, 2002; Ma et al., 2002; Schwartz et al., 2003), where specific regions are considered for more thorough alignments if a minimum number of seeds (either consecutive runs of bases, ‘k-tuples’, ‘k-mers’, or windows that allow for mismatches in certain positions but not others) can be matched perfectly between both sequences, so that the size of the seed (i.e. the minimum number of bases that need to match) determines the runtime of the program versus its sensitivity. Seeded aligners generally require genomic sequences to be masked for repeats and/or these programs dynamically filter out seeds that occur too many times, to avoid runtimes that increase exponentially with seed frequency (Schwartz et al., 2003).

Satsuma is a new sequence alignment program, which, in contrast, finds sequence matches through cross-correlation, a widely used technique in audio signal processing. When we treat genomic sequences as if they were audio signals, applying cross-correlation is like finding decayed echoes of originally identical acoustic patterns—in this case homologous DNA that has diverged over time (for similar, yet conceptually different approaches applying cross-correlation to DNA sequence, see Brodzik, 2005; Katoh et al., 2002; Rockwood et al., 2005). Cross-correlation computes a measure of similarity between two analog signals in the time domain as a function of time-lag, or relative shift between them, resulting in a sliding dot product of both signals. This operation can be done in the frequency domain as a number of multiplications at computational cost that is linear with the signal length; given that the transformation back and forth between time and frequency domains is computed rapidly using the fast Fourier transform (FFT) algorithm (Cooley and Tukey, 1965), cross-correlation can be computed very efficiently (Oppenheim and Schafer, 1975; Rabiner and Gold, 1986). However, it is not computationally possible to Fourier-transform large sequences such as entire chromosomes at once (runtime = O(n * log(n))), so Satsuma divides genomic sequences (the query and the target) into windows (4096 bp by default) that overlap in the query sequence (overlap = one-fourth of the size). When a query window is compared to a target window, nucleotides from both sequence windows are translated into four numeric signals, one for each base (or letter, A, C, G and T), and cross-correlation is applied to each signal pair. After summing up the results for all letters, we are left with a function that indicates the letter similarity between query and target when shifted relative to each other: the higher the value, the more bases match across the entire overlap. While random base matches are expected and constitute background noise, a higher-than-average number of bases that match due to homology produce a signal that rises above the noise. After picking out all the good signals, it is still not known where in the overlap the significant alignment is located, so all valid shift positions are followed up by a filter that searches for blocks in which a minimum number of bases match (45% by default) over a minimum length (28 bases). A second filter, the alignment probability model, determines the ‘viability’ of each block: based on the length, identity, CG composition and target sequence size, Satsuma estimates the probability that a block is random noise and only keeps the ones that pass a threshold (P = 10⁻⁵ by default). Up to this point, all blocks are gap-free; thus, a subsequent dynamic programming step merges overlapping blocks into alignments with gaps.

Thus far, Satsuma can overcome two intrinsic problems inherent to seeded alignment approaches: (i) no implicit or explicit assumptions are made about the pattern in which sequences have to match (as seeds require); and (ii) the need for repeat-masking (either with a repeat library, which might not be available for all genomes, or based on k-mer counting, which will make the aligner blind to gene families) is eliminated, since the runtime does not increase with repeated regions. However, even though the comparison of two sequence windows is fast, applying this algorithm exhaustively (i.e. each target is compared to each query window) results in computational runtimes of O(n * m), with n and m being the sizes of the sequences to be compared. While this might be acceptable for certain tasks, such as aligning fungal genomes or cDNAs to larger genomes, it is impractical for whole-genome comparison. To make the runtime characteristic more linear with genome sizes, Satsuma implements a ‘synteny search’ algorithm, analogous to the paper-and-pencil game battleship, which takes advantage of the fact that the order and orientation of homologous sequences is highly conserved even for distant organisms [e.g. human and opossum (Mikkelsen et al., 2007) or human and chicken (International Chicken Genome Sequencing Consortium, 2004)]. First, query and target windows are mapped out on a grid as squares, and only a small fraction of the grid is searched for initial alignment hits. Then, only the squares in the neighborhood of hits are searched iteratively for more hits, thus following syntenic stretches (sinking the enemy's long ships), so that, in the end, only a small fraction of the entire grid has to be looked at. This strategy, implemented as a highly parallelized process, dramatically reduces CPU time and allows for comparing large sequences (for implementation details of all algorithms, see Section 2).

2 METHODS

2.1 Cross-correlation/FFT

To align query and target sequences, both are first cut into chunks (4096 bp), where the target chunks overlap by a quarter of the chunk size, and two chunks are compared pairwise sequentially. DNA sequence is transformed into floating point sequence ‘signals’, where, in the case of nucleotide alignments, there are four signals for each sequence, one for each letter (A, C, G and T): initially, each position for which an unambiguous base occurs is set to 1, the remaining positions are set to 0. Ambiguous base codes (IUPAC) are split among the letters so that they sum up to 1 (e.g. ‘K’ sets ‘T’ and ‘G’ to 0.5 each). By using information entropy as measure, we de-emphasize simple sequence repeats, such as homo-polymer runs, to lessen the effect of overshadowing and undershadowing other signals (a long run of A's in the target, for example, will add a non-random signal over the entire window size that reflects the base composition in the query sequence), which we found to not significantly alter the results, but increases the efficiency of signal selection. After subtracting the mean from each signal to normalize over sliding overlap lengths and adding zero-padding of another 4096 bases (otherwise signals would look periodic), the cross-correlation theorem is applied by first Fourier-transforming each signal using the FFT algorithm, multiplying signals (one with the complex conjugate of the other, and then transforming back into letter/signal space). As a result (and after adding up the signals for each letter), we obtain a function that shows positive spikes indicating the number of positions the signals have to be shifted across each other so that a higher-than-expected number of matches can be found.

2.2 Signal selection

To determine shift positions, Satsuma requires signals in the back-transformed function to be 1.8 times stronger than the SD of all values within windows of 256 (This is inefficient; improving this algorithm will dramatically speed up the process. In most cases, due to the chunking, non-homologous sequences are compared, resulting in noise only without signals. On average, ∼250 distinct shift positions are evaluated). A subsequent step now goes back into letter space, shifts sequences accordingly, and determines the regions in both query and target where more letters match than expected: this is implemented efficiently and is linear in time given the overlap size between sequences, by requiring a minimum of 13 matching bases in local, adjacent windows of at least 28 bp in size. Each match that is found is then tested by the match scoring algorithm (see below) and either rejected or accepted. The latter are collected and stored.

2.3 Match scoring

Here, the goal is to determine the probability that an alignment of length N represents a real biological signal and not random chance. Let R denote the number of random matches in the alignment; then R ∼Binomial(N, P) where P is the probability of a random match at a single site. The value of P depends on the GC content in both sequences; let n_gc and ν_gc denote the number of G's and C's in the query and target, let n_at and ν_at be the number of A's and T's. Then the expected number of random matches is

with the binomial SD

since N is typically large, R is distributed approximately Normal(μ, σ²). We can use the normal cdf to estimate the probability P_l of finding a local alignment of length N and identity at least x bases by chance

Finally, we compute P_real, the probability of finding exactly zero matches of equal or better quality by chance. If the target genome size is S, then the number of false matches can be approximated by Poisson(2P_lS) (the factor of 2 accounts for potential reverse complement matches). This gives the probability of zero random matches

[For comparison, BLAST (Karlin and Altschul 1990) similarly scores sequence pairs and computes an E-value, the expected number of random matches with equal or better score. A Poisson's distribution is used to approximate the P-value, the probability of finding at least one such random match, by P = 1 − exp(− E)].

2.4 Merging overlapping alignments

After initial gap-free alignments are done, Satsuma first collects all blocks from all chunks, sorts them, and finds blocks that overlap in both the query and the target sequences by at least 1 bp. A simple dynamic programming algorithm with empirical penalties is used to merge these blocks, allowing for insertions and deletions (mismatch penalty = 1, gap penalty = 1 per gap + 0.5 per gap base) in transitions between blocks.

2.5 Battleship search

The entire space spanning both genomes is mapped onto a grid with 1 ‘pixel’ spanning 24 by 24 elementary blocks of 4096 × 4096 bp² each, where blocks overlap in the query sequence by 1024 bp. All pixels are kept in an ordered priority queue, and their respective sequences are aligned according to the ranking. To initialize the process (nothing is known in the beginning), we first start with 24mer matches unique to the query and target, followed by a configurable number of full line searches, i.e. evenly spaced regions (8192 bp in length) in the target genome are aligned against all of the query sequence. Hits that survive a dynamic programming step (the synteny filter, which finds a path through alignments that preserve order and orientation, see next paragraph) serve as initiation points. From that point on, pixels containing hits and their eight bordering pixels are distributed to search processes, with a map of the grid constantly updated centrally when search processes finish. Hits, detected by the synteny filter, and pixels neighboring these hits, are ranked according to alignment identity in the priority queue and distributed for search (each pixel is only processed once at maximum). This strategy, just like in the paper-and-pencil game, attempts to follow along the length of battleships until the entire ship is sunk, and this algorithm, while not optimal, does not depend on the shape of the ship as long as it is contiguous. In case there are not enough high-ranking pixels in the queue (which happens when multiple ships come to an end, i.e. there are large-scale re-arrangements in the genome), more initiation points are searched, and the choice of regions in the target genome is based on the size of coverage gaps in the target. To further increase efficiency, regions in the query that are already well covered with syntenic hits are omitted. The process comes to an end when no more initiation points in coverage gaps of at least 3 pixels can be found (we note that this is not necessarily the optimal stop criterion).

2.6 Synteny filter

To filter out homologous alignments based on large-scale synteny, Satsuma applies a dynamic programming chaining algorithm to only keep matches that are, over certain lengths, syntenically consistent with each other in order and orientation. First, Satsuma assigns a value to the cost of a match to be removed: the initial penalty is −ln(1 - alignment probability), which, for repeat matches (i.e. there are multiple hits in the target and/or query sequence), is decreased exponentially with the copy number of matches. If two matches are chained together, the connection is penalized by the sum of all matches in between that would be skipped as a result. In addition, the cost to connect two matches is hierarchically computed based on: (i) whether the query and target chromosome identifiers match (0 if so, an empirically determined flat penalty if not); (ii) whether the two matches are the same orientation (0 if so, the flat penalty if not); and (iii) how well the differences between matches compare in the query and the target sequence, i.e. if the distances are the same, the penalty is 0, and the penalty goes up with increasing discrepancy, plus another empirically determined penalty proportional to the square root of the absolute difference in target coordinates to favor smaller connections over large ones. Iteratively removing syntenic matches from the original set and re-applying the synteny filter to the rest allows for recovering syntenic matches to large-scale duplications (> 1 Mb) in the query sequence. Since syntenic matches might be dropped by mistake, Satsuma applies another round of alignments as a post-processing step, augmenting the syntenic set by comparing sequence that falls in between the original syntenic matches.

2.7 Architecture and parallelization

The battleship search is implemented in a completely asynchronous fashion, such that one process is the master (i.e. it continuously runs dynamic programming and re-sorts the pixel priority queue as data comes in), which farms out lists of pixels to be searched to slaves that run on a compute farm or a multi-processor machine. As soon as a slave finishes the task, it reports back with the results and fetches a new set of pixels. Communication between master and slaves is implemented via TCP/IP. This asynchronous implementation has a number of implications: (i) at any given time, it is the best guess that decides how to prioritize pixels, without having the entire information that would be available in a linear implementation; (ii) computational load can vary throughout the process, i.e. one can take advantage of all free CPUs available at any time, provided the computational cost to process a single set of pixels is low (∼5 min with the default parameters); and (iii) the exact sequence in which pixels are searched is undefined, since the order in which pixels are processed depends on the timing, number of available CPUs, etc. and is thus not deterministic. We ran experiments under different conditions and found that, while the size of the search space might vary, the resulting alignments are very stable and only minimally depend on processing order.

2.8 Visualization

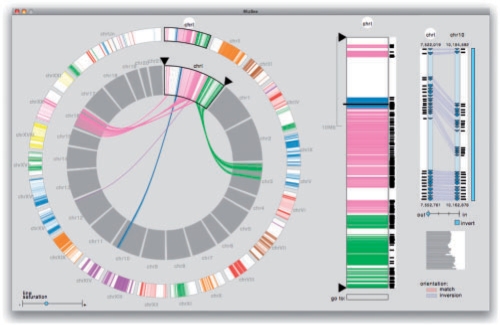
Satsuma interfaces with the synteny browser MizBee (Meyer et al. 2009), a visualization tool designed for exploring multiscale conservation relationships in comparative genomics data. MizBee augments Satsuma by enabling efficient browsing of syntenic data across a range of scales from the genome to individual orthologous matches, shown in Figure 1. The design of MizBee is grounded in perceptual principles, and includes numerous visual encoding techniques to enhance cues about conservation relationships such as proximity, size, similarity and orientation. The development of MizBee was guided in part by the data Satsuma generates, and the scientific questions the users of Satsuma ask. More information about MizBee, as well as freely available executables and example data from Satsuma (stickleback versus pufferfish genome), can be found at http://mizbee.org.

Fig. 1.

MizBee is a multiscale synteny browser that interfaces with Satsuma to enable efficient exploration of conserved syntenic data (Meyer et al., 2009). Shown here are results from Satsuma on the stickleback–pufferfish dataset. On the left is the genome view, where the stickleback genome is shown in the outer ring, and the pufferfish genome on the inner ring along with the user-selected chromosome 1 from the stickleback genome. The connecting edges indicate the location of conserved syntenic blocks between the two species, and the edge color is determined based on the linked pufferfish chromosome. In the middle of the window is the chromosome view that provides details about the size and location of the syntenic blocks for the selected stickleback chromosome, along with the average similarity score for each block shown in the histogram to the right of the bar. The rightmost view shows a user-selected syntenic block, where information about the similarity, orientation, location and size of conserved features within the block are shown. The three views are linked using variety of mechanisms, such as color, interaction and highlighting, and users interactively select chromosomes and blocks using either the mouse or keyboard. MizBee, and the shown Satsuma dataset, can be freely downloaded from http://mizbee.org.

3 RESULTS

3.1 Specificity, Sensitivity and Speed

3.1.1 Specificity

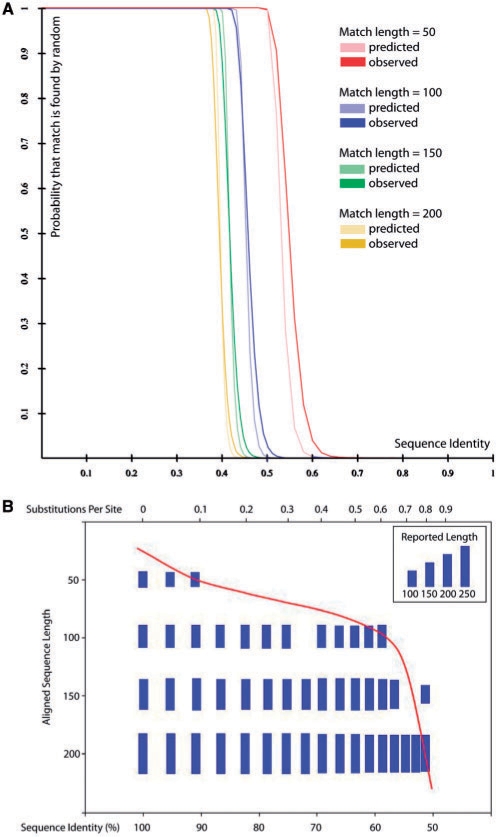
The alignment probability model decides which matches are regarded as homologous and which are not, and thus directly controls Satsuma's specificity. Consistent with expectations, the model predicts that the shorter the alignment, the higher an identity is required in order to be ‘real’ (Fig. 2A). Most notably, for all different lengths, there is a marked and steep drop so that at length 100, an identity of 0.45 indicates almost certainly that the alignment is noise, but increasing the identity to 0.52 predicts the alignment to be almost certainly real. To test the actual accuracy, we implemented a NULL model: sampling random alignments between non-homologous sequences from two organisms (lizard and chicken), where one sequence was, in addition, complemented but not reversed to ensure that no homology was to be found, while preserving the non-randomness of local base composition (analogous to Schwartz et al., 2003). Figure 2A shows that the model's prediction (for length 50, 100, 150 and 200 bp) resembles the observation from the NULL model very closely overall. We note that, for short alignments (∼50 bp), it is simple sequence repeats (preserved in structure when complementing sequence) that cause the observation to shift slightly to the right (data not shown).

Fig. 2.

Specificity and sensitivity. (A) Specificity: Satsuma's match probability model predicts that a single, gap-free alignment of given length, identity and GC/AT composition is found by random chance given the target genome size (lizard, 1.7 Gb) in light colors (y-axis), over the match identity (x-axis). This is compared to a Null model (see Section 2) shown in dark colors. (B) Sensitivity: identical sequences of different lengths (50, 100, 150 and 200 bp) were inserted into non-homologous DNA from the human genome and mutated by randomly changing bases over the entire region (base substitution rate, x-axis, top), resulting in a decrease in sequence identity (x-axis, bottom). Each bar indicates that the alignment was correctly identified by Satsuma given the length of the sequence to be found over increasing mutation rates.

3.1.2 Sensitivity

Satsuma finds matches by examining all bases from one genome within a window to all bases from another genome in the window in parallel, and then selects how far to shift sequences relative to each other to match them up. The signal-to-noise ratio (and thus how well Satsuma succeeds in picking out signals from the background noise) determines the limits of its sensitivity. To put this to the test, we randomly selected two non-homologous sequences from the human genome (∼8 kb each), and inserted identical sequence of different lengths. We then gradually introduced ‘mutations’ (random single nucleotide changes) to one sequence by randomly changing bases to emulate genomic divergence, and ran Satsuma on those sequences to determine the effective sensitivity (Fig. 2B). Signals from short matches (50 bp) tend to be overshadowed by noise rather quickly with increasing divergence (> 10%), as 50 bp constitute only 1.2% of a 4096 bp window. Matches of length 100 bp (2.4% of the window), however, can be detected down to base-pair-substitution rates of 0.6 (or sequence identity 59%), and matches of even longer sizes can be detected down to substitution rates of 0.8 or about 50% sequence identity. We do note that all of these matches are gap-free, and thus alignments containing gaps (insertions and deletions) will have to consist of consecutive gap-free blocks of certain identity and length in order to be detected (see Section 2).

3.1.3 Speed

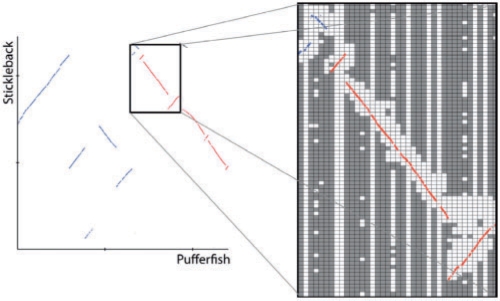
The teleost fishes stickleback (Gasterosterus aculeatus, gasAcu1) and pufferfish (Tetraodon nigroviridis, tetNig1) feature small genomes for vertebrates, at 470 and 217 Mb, respectively (excluding chrUnk). Those genomes are about as large as possible for an all-sequences-against-all comparison to still be computationally feasible, so this dataset was ideal for evaluating the battleship synteny search versus the straightforward exhaustive search. The exhaustive search took ∼150 h on 600 CPUs (90 000 CPU hours total) distributed in a server farm managed by Load Share Facility (LSF), while the battleship search ran from start to completion overnight on 15 processors on a single machine (120 CPU hours total), a factor of several hundred times faster, while recovering all syntenic hits found in the exhaustive search. Figure 3 shows a synteny plot of pufferfish chromosome 1 versus three stickleback chromosomes, with the actual grid pixels searched marked in white. We also note that there are very few false hits, indicating that the algorithm performs well in distinguishing syntenic from non-syntenic homology.

Fig. 3.

(A) Synteny between pufferfish chromosome 1 (x-axis) and stickleback chromosomes a (blue), b (red) and c (black), (B) Zoom-in into region depicting the search space (white) overlaid with the matches (red and blue).

We then tested the scalability of the algorithm to larger genome pairs: with a runtime of 230 CPU hours for 8.3% of the human genome (chromosome 1, 250 Mb, as the target sequence) against all of dog (2.4 Gb, query sequence), we estimate that aligning two entire mammalian genomes takes <3000 CPU hours in total when processing one target chromosome at a time.

3.2 Duplications, rearrangements and repeats

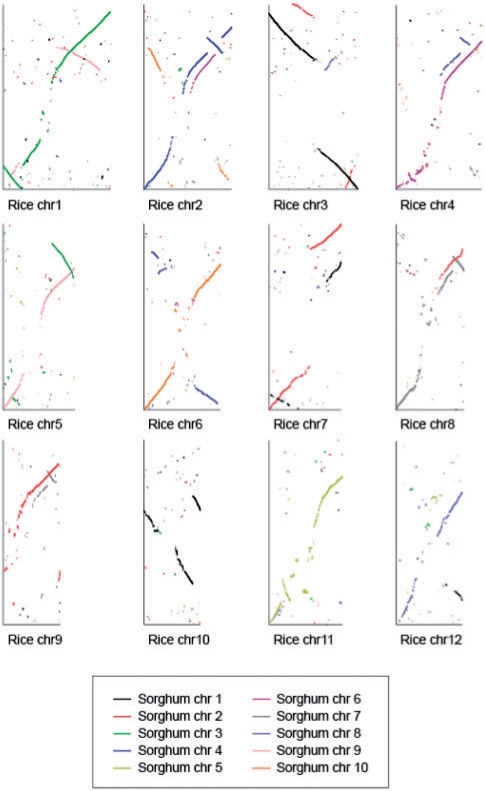
The genomes of flowering plants, such as the grasses rice (Oryza sativa) and sorghum (Sorghum bicolor), exhibit a number of large-scale duplications, rearrangements, as well as high levels of interspersed repeats, comprising 40% (rice) and 61% (sorghum) of the genomes (Paterson et al., 2009; Yu et al., 2005). Satsuma aligned the 390 and 750 Mb genomes in 480 CPU hours, the genome-wide synteny plots of the 12 rice chromosomes against the sorghum genome are shown in Figure 4. In addition to capturing rearrangements ranging from several kb up to tens of Mb, Satsuma finds both orthologous as well as paralogous syntenic matches. We note that the high repeat content somewhat elevates the noise levels compared to vertebrate genomes; however, the syntenic signal is still clearly visible [for protein-based synteny maps (Paterson et al., 2009)].

Fig. 4.

Alignment of two grass genomes: Oryza sativa (x-axis, target, one graph per chromosome), and Sorghum bicolor (y-axis, query, chromosomes are color-coded). The plots show re-arrangements and large-scale segmental duplications in both genomes.

3.3 Comparison with blastz

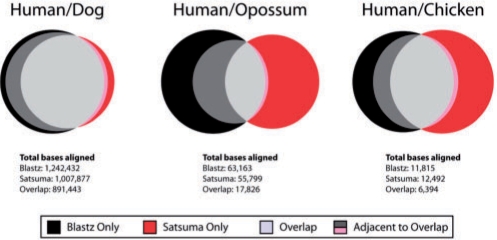
We compared Satsuma to the widely used alignment chains generated by the alignment program blastz and provided by the UCSC genome browser (http://genome.ucsc.edu, Chiaromonte et al., 2002; Schwartz et al., 2003) on datasets of different evolutionary distances. As a test set, we aligned ∼2.8 Mb from human chrX (hg18, 149,830,243-152,627,579) to the syntenic regions in three genomes, the closest being dog (CanFam2, chrX: 122,150,346-124,566,871), somewhat further out the marsupial opossum (monDom4, chrX: 32,807,449-34,657,981) and, quite distant, the homologous region in chicken (galGal3, chr4: 9,761,583-18,789,149). An overview of the comparison is shown in Figure 5. On the dog/human dataset, Satsuma aligned a somewhat smaller fraction of the human genome (36%) compared with the blastz chain (44%) overall, with the majority of aligned bases being found by both methods (72% of bases in blastz chain alignments are also contained in Satsuma alignments, 88.5% of Satsuma alignments are also contained in blastz chains). The most significant disagreements stem from differences in determining alignment boundaries: 23% of the blastz chains (10% of the sequence) resides in regions adjacent to alignments that were identified by both methods, i.e. blastz is more inclusive when determining how far alignments should extend. Of the remaining blastz- and Satsuma-only alignments (i.e. isolated regions in which only one method found an alignment, and this alignment is not located adjacent to an alignment that the other method found), Satsuma finds a slightly larger fraction than blastz (6.2% and 5.4% of all human bases, respectively).

Fig. 5.

Comparison of Satsuma and blastz chained alignments (http://genome.ucsc.edu). Datasets: (A) human/dog (∼60 Myr apart, Lindblad-Toh et al., 2005); (B) human/opossum (∼130 Myr apart, Mikkelsen et al., 2007); and (C) human/chicken (∼350 Myr apart, International Chicken Genome Sequencing Consortium, 2004). Shown are the blastz-only bases (black) and Satsuma-only bases (red), i.e. bases in alignments that were only found by either one alignment program and not adjacent or overlapping with matches found by the other program. Bases in overlaps (i.e. both aligners found the same bases) are shown in light gray, and bases in alignments adjacent to alignments found by both aligners are shown in dark gray and pink.

Notably, differences between the two methods are more pronounced on the opossum/human dataset, where again blastz aligns more bases (2.4% versus 2.0%), but the overlap is relatively small (28.2% of the total 63 163 of bases in blastz chain alignments are also contained in Satsuma alignments, 31.9% of the total 55 799 of bases in Satsuma alignments are also contained in blastz chains). The amount of blastz extensions, however, is a much larger fraction than when using the dog dataset, with 33.8% of all bases aligned by blastz residing in regions that extend off of alignments found by Satsuma as well [for a discussion on the issue of determining alignment boundaries, and possible over-extending versus under-extending alignments (Frith et al., 2008)]. The fraction of stand-alone Satsuma-only alignments (1.3% of all bases and 67% of Satsuma-aligned bases) and blastz-only (0.9% of all bases and 38% of blastz-aligned bases) alignments is comparable. Lastly, the genome of the chicken, being an avian reptile, is quite far diverged from human. Here, Satsuma aligns slightly more bases (12.5 versus 11.8 kb), with about half of the bases found by both methods and ∼2 kb being blastz extensions off of shared alignments, and Satsuma detecting 5.7 kb of sequence undetected by blastz and 3.2 kb of sequence alignments reported only in the blastz chain. Table 1 compares matches found by Satsuma and blastz that at least partially overlap annotated exons (RefSeq) in the chicken and opossum genomes. While there are more exons found by blastz-only than are found by Satsuma-only in the human/opossum alignments, Satsuma appears more sensitive in detecting orthologous exons on the chicken/human dataset.

Table 1.

Comparison of Satsuma and blastz alignments between chicken and human and opossum/human in regards to exons (RefSeq) in the chicken and opossum genomes, in a region on the human X chromosome

	Chicken	Opossum
Annotated exons	255	131
Exons found by both	31	39
Exons found by Satsuma only	19	3
Exons found by blastz only	3	8
Non-exons found by both	0	39
Non-exons Satsuma only	16	135
Non-exons blastz only	5	51

For a runtime comparison, we ran blastz with default parameters on 140 pairs of randomly chosen, non-repeat-masked sequence samples from human chr1 and dog, using the chunking strategy (1 Mb versus 30 Mb chunks) described for the original human–mouse blastz alignments (Schwartz et al., 2003). From the mean runtime of 34 min, and given that the chunking required by blastz scales up its runtime at O(n * m), we estimate that aligning 250 Mb of human chromosome 1 to the 2.4 Gb dog genome would take ∼11 500 CPU hours, compared to 230 CPU hours for Satsuma.

4 DISCUSSION AND FUTURE DIRECTIONS

Satsuma is a sequence aligner that implements very different strategies than other programs, most notably a search strategy on a global level and cross-correlation at the local level. While this eliminates the need for repeat masking, another key feature gained by a seed-less approach is Satsuma's innate ignorance of the exact nature of sequences: any two sequences of anything, as long as they can be translated into vectors or matrices of floating point numbers, can be aligned. As a practical implication, Satsuma is, as of now, fully capable of incorporating ambiguous base codes into alignments at all stages, which, for example, allows for protein–protein and protein–nucleotide searches. In the future, additional sequence information can easily be added to increase sensitivity beyond the nucleotide level: for example, only ∼40% of the genome sequences of mouse and human can be aligned to each other (Schwartz et al., 2003), and this is probably close to the limit of what can be done with nucleotide sequence alone. However, it has been shown that local DNA topography is conserved in some cases where the nucleotide sequence is not (Parker et al., 2009). Since topography can be represented as a single number per location, this information could increase the fraction of aligned genome overall if used throughout the entire alignment process in addition to nucleotide sequence, which might not only fill gaps in alignment coverage, but recover entire regions that were simply unalignable before.

We close by noting that Satsuma is still a work in progress, with improvements both in algorithms as well as engineering (e.g. eliminating the need to hold entire genome sequences in memory for random access) under way. In addition, we are adding entire new features, such as a novel context-sensitive, detailed alignment algorithm, SLAP (P. Russell et al., manuscript in preparation), as a post-processing step to recover sequence alignments with many and/or large gaps in between, or adjacent to matches that Satsuma finds now. Another aspect involves mining of large datasets at different levels of locality, from a genome-wide view down to the nucleotide level, where our approach is to interface with a multi-level, interactive graphical synteny browser, MizBee (see Section 2). Even as it stands now, a working version of Satsuma, fully capable of aligning two entire genomes at good sensitivity, specificity and within a reasonable time can be downloaded freely under the GNU Lesser General Public License agreement from http://www.broadinstitute.org/science/programs/genome-biology/spines/.