Skip to main content
PMC home page
Springer logoLink to Springer
. 2010 Feb 25;120(8):1673–1687. doi: 10.1007/s00122-010-1284-y

QTL detection by multi-parent linkage mapping in oil palm (Elaeis guineensis Jacq.)

N Billotte 1,✉, M F Jourjon 3, N Marseillac 1, A Berger 1, A Flori 1, H Asmady 8, B Adon 2, R Singh 6, B Nouy 1, F Potier 1, S C Cheah 6, W Rohde 5, E Ritter 7, B Courtois 1, A Charrier 4, B Mangin 3
PMCID: PMC2859221  PMID: 20182696

Abstract

A quantitative trait locus (QTL) analysis designed for a multi-parent population was carried out and tested in oil palm (Elaeis guineensis Jacq.), which is a diploid cross-fertilising perennial species. A new extension of the MCQTL package was especially designed for crosses between heterozygous parents. The algorithm, which is now available for any allogamous species, was used to perform and compare two types of QTL search for small size families, within-family analysis and across-family analysis, using data from a 2 × 2 complete factorial mating experiment involving four parents from three selected gene pools. A consensus genetic map of the factorial design was produced using 251 microsatellite loci, the locus of the Sh major gene controlling fruit shell presence, and an AFLP marker of that gene. A set of 76 QTLs involved in 24 quantitative phenotypic traits was identified. A comparison of the QTL detection results showed that the across-family analysis proved to be efficient due to the interconnected families, but the family size issue is just partially solved. The identification of QTL markers for small progeny numbers and for marker-assisted selection strategies is discussed.

Electronic supplementary material

The online version of this article (doi:10.1007/s00122-010-1284-y) contains supplementary material, which is available to authorized users.

Introduction

Oil palm (Elaeis guineensis Jacquin) is a cross-fertilising arborescent monocot of the genus Elaeis that originates from West Africa (Hartley 1988). Its diploid genome consists of 16 homologous chromosome pairs (Schwendiman et al. 1982). Its physical size estimated by flow cytometry is 3.9 pg/2C (Rival et al. 1997). Oil palm is the world’s leading source of vegetable oil and fat with an annual production of 40 million tons of palm oil along with 4.4 million tons of palm kernel oil (USDA). For the best varieties oil yields per hectare are ten times greater than soybean yields. The breeding scheme used by CIRAD (France) and its partners (Gascon and de Berchoux 1964) is a variant of the reciprocal breeding scheme of Comstock et al. (1949). It exploits the heterosis obtained by crossing parents from two groups of populations, DELI and AFRICA, as their production components are complementary (Meunier and Gascon 1972).

The fruit of oil palm is a drupe. It is made of pulp (mesocarp) from which palm oil is extracted, an endocarp called the shell, and a kernel that also contains oil. Three fruit varieties exist due to a major bi-allelic co-dominant gene called Sh, which controls the presence or absence of the shell and the degree of endocarp lignification (Beirnaert and Vanderweyen 1941). The dura type (genotype Sh+/Sh+) produces large fruits with a thick shell and relatively little mesocarp in weight terms. The pisifera type (genotype Sh−/Sh−) is usually female-sterile, and its rare fruits are relatively small, without any apparent shell and with a relatively large amount of mesocarp. The tenera type is the hybrid Sh+/Sh− genotype with fruits that have a shell of intermediate thickness and they contain abundant mesocarp. The tenera varieties, naturally more productive for palm oil, are the commercial varieties that are improved and distributed to planters.

The use of molecular markers has been discussed since the 1990s to genetically improve the oil palm (Jones 1989; Baudouin 1992; Jack and Mayes 1993; Mayes et al. 1996, 2000). Various genetic mapping strategies have been proposed by Ritter et al. (1990), Stam (1993), Grattapaglia and Sederoff (1994) and Schiex and Gaspin (1997) for a cross between heterozygous parents of cross-fertilising species from which lines cannot be obtained. Mayes et al. (1997) published the first genetic map in oil palm using restriction fragment length polymorphism (RFLP) markers. Moretzsohn et al. (2000) published a second linkage map in oil palm using amplified fragment length polymorphism (AFLP) markers. A reference genetic map with a high marker density has been produced for oil palm (Billotte et al. 2005). Singh et al. (2008) published the first map for oil palm containing gene specific cDNA-RFLP markers.

Few QTL analyses exploited these linkage maps, which were established on a single mapping population in each case. Rance et al. (2001) used the map of Mayes et al. (1997) to detect QTLs for traits including yield of fruit and its components and measures of vegetative growth. More recently, a framework map of a selected oil palm parent was used to detect QTLs controlling the oil palm quality measured in terms of iodine value and fatty acid composition (Singh et al. 2009).

Several quantitative traits mean numerous QTLs for which heterozygosity and allelic diversity cannot be well sampled by only one or two mapping parents for a cross-fertilising diploid species. Extrapolation of QTL results to other progenies or gene pools can be disappointing due to an absence of polymorphism at the QTL, different associations between the marker alleles and the QTL, new alleles at the QTL, and/or other unpredicted effects.

The number of individuals studied, the magnitude of the QTL effect, and the heritability of the trait have a very strong influence over the power of QTL detection tests (Melchinger et al. 1998). Given the substantial bulk of oil palm, the standard planting density is 143 palms per hectare. For cost reasons, current classical genetic trials involve a small number of palms, usually between 60 and 75 per family. This is sufficient to estimate the average characteristics of a given cross, but less appropriate for QTL detection. Small numbers of individuals per cross like in classical genetic trials raise the problem of bias-free sampling of segregating marker alleles and QTLs in the progeny. Likewise, only QTLs with a sufficient effect are detected, whilst the other QTLs remain undetectable (Paterson et al. 1990).

The use of several parents (or families) better samples the allelic richness at the targeted QTLs. Depending on the gene pool, such an approach provides more effective detection and evaluation of the effects of the QTLs and their stability (Muranty 1996). For instance, Knott et al. (1996) and Elsen et al. (1997) proposed methods for multi-marker mapping of QTLs in half-sib populations.

The main purpose of our study was to test a QTL search by multi-parent linkage mapping in full-sib families with a small number of individuals using the strategy of Muranty (1996) based on a 2 × 2 complete factorial genetic experiment. This article describes our work stage by stage: phenotypic characterisation of the genetic material studied, construction of a consensus genetic map of the multiple cross design using SSR (single sequence repeat) loci, and QTL searches by two approaches: (1) a within-family analysis for four separate families assuming a total of four QTL alleles per family, (2) an across-family analysis allowing unique QTL alleles for all parents with a total of eight alleles. For that purpose, a new extension of the software MCQTL (Jourjon et al. 2005) was especially designed for crosses between heterozygous parents. Twenty-six quantitative phenotypic traits for vegetative growth and yield were studied.

Materials and methods

Parameter estimation population

A phenotypic characterisation of crosses derived from AFRICA and DELI parents was performed based on a genetic trial planted in 1986 by the SOCFINDO estate (Medan, Indonesia). This location offers highly favourable agro-climatic conditions for oil palm growing. The trial is testing 15 full-sib families. Each family is a single cross between two heterozygous parents: one tenera parent from AFRICA and one dura parent of the DELI population introduced into Indonesia in the nineteenth century. The genome of each parent was a mosaic of fixed or heterozygous parts obtained from successive inter-crossing, back-crossing or selfing of ancestors. The experimental design is a randomized complete block design (RCBD) with 5 replications of 15 palms per replication (i.e. 75 different palms per family). A control cross LM2T × DA10D, a best hybrid from a first breeding cycle, was represented twice (150 palms).

Individual phenotypic trait recording

The fruit variety and 26 vegetative or yield traits were available for all crosses of the genetic trial. Fruit yield and its components bunch number and weight were individually recorded over two periods: an immature period from 3–5 years after planting and a mature period from 6–9 years after planting. The physical bunch components for mature palms were recorded on surviving palms over two successive years (2 bunch analyses/palm/climatic season, i.e. 8 bunch analyses/palm). The palm oil iodine value (proportion of unsaturated fatty acids) was estimated by two measurements for each genotype. The number of spikelets per bunch was measured on the analysed bunches of the control cross LM2T × DA10D. Vegetative growth measurements were made for the surviving 15-year-old palms.

Phenotypic characterisation

Statistical analyses of phenotypic data were carried out using SAS software (SAS Institute Inc., USA). The range and distribution of the values were checked to assess the quality of the records, and the distribution of the residual errors was checked by an analysis of variance (ANOVA). Some records were discarded in the case of Ganoderma disease symptoms, which could have affected phenotypic values in the past life of the palm. The value distributions followed normality according to the Kolmogorov–Smirnov test (Chakravarti et al. 1967).

Estimation of parent means and variances

Two ANOVA mixed linear models with (model I) or without (model II) interaction effects between parents were used to model the phenotypic value of the genotypes. The results showed that interaction effects between the DELI and AFRICA parents were negligible or non-existent (data not shown). A model II ANOVA was, therefore, adopted. The variances were estimated and the parent means of the trait phenotypic values corrected by the Sh gene effect were compared using the Tukey’s test (Siegel and Tukey 1960) for each variety (dura or tenera). The heritability of the phenotypic traits was not estimated, as the parents were not present in the experimental trial.

Relationships between phenotypic traits

The correlations between traits were calculated on the basis of the individual variables according to the classic Pearson model. The correlations were calculated between the residual errors of the model II ANOVA. These “intra” correlations were those estimated from the individual phenotypic values minus the additive effects of the fixed factors of the ANOVA (replication, DELI parent, AFRICA parent, off-springs dura or tenera variety, etc.). The correlation thresholds were considered at a risk α of 5 and 1%.

Multi-parent mapping population

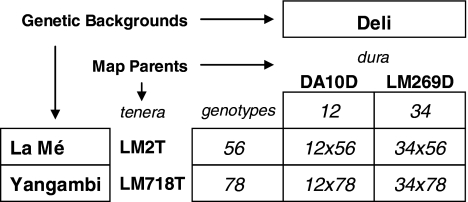
Within the genetic trial, a 2 × 2 complete factorial mating experiment of four unrelated parents was genotyped and used for QTL analyses (Fig. 1). These four parents belonged to the La Mé population from AFRICA (tenera LM2T), the Yangambi population from AFRICA (tenera LM718T) and the DELI population (dura DA10D, dura LM269D). The LM2T × DA10D cross was represented by 116 palms and each other cross by 61 palms after eliminating dead, illegitimate or abnormal trees. That LM2T × DA10D cross was previously used to establish a reference high-density linkage map of the oil palm (Billotte et al. 2005). The phenotypic data of the multi-parent mapping population were corrected to eliminate the effect of environmental factors. For each trait, the effect of the blocks was estimated and the effect of the experimental plots was predicted, under the assumption that these last effects where normally distributed inside the blocks. The phenotypic data were also standardised in mean and variance for both dura and tenera varieties to eliminate the Sh major gene effect, which could bias the QTL search results. Finally, the environmental-free and Sh-corrected values Y ck used for the QTL search were values where all genotypes had their means and variances brought back to those of tenera-like genotypes: Y ck = μ + αc + δcT + E ck where μ is the trait global mean, αc is the mean of cross c, δcT is the additive effect of the tenera variety within-cross c, and E ck is the standardised residual error.

Fig. 1.

Fig. 1

Open in a new tab

Multi-parent mating design of four connected full-sibs families, with eight potential alleles segregating from parent genotypes ij

SSR analyses

A total of 390 simple sequence repeat (SSR or microsatellite) marker loci developed in oil palm (Billotte et al. 2001, 2005) along with 21 transferable coconut (Cocos nucifera L.) SSRs were screened for polymorphism in the four parents of the multi-parent design. The SSRs were of the (GA)n, (GT)n and (CCG)n types. Microsatellite loci were named mEgCIR when amplified by oil palm SSR primers and mCnCIR when amplified by coconut SSR primers. A subset of 278 SSRs was selected for linkage mapping, including 255 SSRs mapped on the LM2T × DA10D reference high-density linkage map of oil palm (Billotte et al. 2005). The criteria for choosing these SSRs were (1) a good distribution along the genome, with an average density of 10–20 cM, which is appropriate for QTL analyses (Muranty 1996), (2) the highest proportion of polymorphism in the three genetic backgrounds. Total genomic DNA was extracted from freeze-dried leaf samples of each progeny and parent using the commercial DNeasy Plant Mini Kit extraction kit following the manufacturer’s protocol (Qiagen, USA). SSRs were genotyped as described by Billotte et al. (2005). The genotype configurations of the SSRs, as well as of the Sh locus, were coded according to the nomenclature of Ritter et al. (1990), which latter comprises nine cases of one to four alleles segregating in a cross between heterozygous parents. Molecular data regarding E-Agg/M-CAA132, an AFLP marker close to the Sh locus, were available for the LM2T × DA10D genotypes (Billotte et al. 2005) and added to the data set. χ2 tests for segregation distortion were carried out for all loci comparing the observed ratio with the expected ratio for each specific locus configuration (1:1, 3:1, 1:1:1:1 or 1:2:1). χ2 analyses were performed at thresholds of P = 0.05 and P = 0.01.

SSR linkage mapping

Each cross between heterozygous parents was considered to be a double pseudo-test cross (Grattapaglia and Sederoff 1994). Linkage phases between markers were determined using JoinMap v. 3.0 (Van Ooijen and Voorrips 2001). In a few cases, the estimated phase between marker alleles segregating from a parent was different from one cross to another involving that parent. The same phase in different crosses was necessary to map the alleles that were common to several parents and crosses and to attribute the same effect to the allele (value and sign). The allelic phases were, therefore, corrected when necessary based on the crosses LM2T × DA10D and LM718T × LM269D for which the number and density of markers were the highest. The CARTHAGÈNE software (Schiex and Gaspin 1997) lacks an algorithm to estimate the linkage phases between markers and it only analyses marker data with already estimated phases. CARTHAGÈNE has the significant advantage of simultaneously generating and estimating the reliability of several maximum likelihood multipoint maps with relative orders of markers more probable than those estimated by JoinMap (Schiex and Gaspin 1997). An integrated SSR linkage map was, therefore, established for each cross using CARTHAGÈNE, at LOD 3.0 with a maximum recombination threshold of 0.5. The Haldane mapping function was used to convert recombination frequencies into map distances (Haldane 1919). Finally, the individual Haldane linkage maps of the four crosses were integrated into a unique Haldane consensus linkage map of the multiple cross design, also using CARTHAGÈNE.

QTL search methodology

The 2 × 2 factorial mating design corresponded to an incomplete factorial allelic design of eight alleles in segregation (Fig. 1). The QTL search was performed using a new module of the MCQTL software (Jourjon et al. 2005). This module, MCQTL Outbred, was developed to analyse one or more related crosses between diploid heterozygous parents. Small differences exist between MCQTL Outbred and Elsen et al. (1999)’s approaches implemented in QTLMAP (INRA, France). Marker phases of parent design are assumed to be known and QTL genotypes are inferred with an exact multimarkers method in MCQTL Outbred, whereas marker phases of parent design are estimated and QTL genotype inferred with an approximate multimarkers method in QTLMAP.

However, the main difference is that MCQTL Outbred allows a connected model to take into account that parents can be shared between families whereas QTLMAP allows only a disconnected model, i.e. within-family QTL effects.

We used the two models implemented in MCQTL Outbred: (1) the within-family model for four separate families, which deals with each family separately and assumes a total of four QTL alleles per family, (2) the across-family model, which allows unique QTL alleles for all parents for a total of eight alleles. We considered a genome-wide risk α of 4% for the within-family analyses. This is equivalent to a chromosome significance of 0.25% and corresponds to a global risk of 16% for the across-family analysis assuming the independence of the four within-family analyses and using the Bonferroni correction. The Haldane’s consensus linkage map of the multiple cross design was used regardless of the QTL search model for a better comparison of the results. A code was added to the name of each QTL in the tables and figures to indicate which model(s) enabled its detection. We assumed that both models identified the same QTL when the confidence regions overlapped.

Within-family analyses

Initially, we used a previous version of MCQTL Outbred, limited to a within-family model with additive and dominance QTL effects (not published), using the Sh-corrected data of the cross LM2T × DA10D. No or negligible dominance effects were found at the QTLs (data not shown). Therefore, an additive model was adopted for the subsequent QTL analyses, using only the Sh-corrected data. The within-family model was a simple regression additive model (Haley and Knott 1992). The corrected phenotypic value Y ck of the kth individual of cross c was modelled by

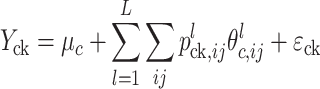graphic file with name M1.gif

where μ c is the global mean in cross c, L − 1 is the number of genetic cofactors, 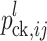Inline graphic is the probability of the individual having genotype ij at the QTL or cofactor locus l given the marker information, 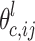Inline graphic is the genotype mean at locus l in cross c and 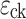Inline graphic is the residual error. The derivation of the parent allele origin probabilities was performed as per Jourjon et al. (2005). The genotype probabilities at the markers were computed every 5 cM. The iterative QTL mapping (iQTLm) technique of Charcosset et al. (2000) was the scan method used to deal with a multiple QTL model of the genome, with an exclusive window of 5 cM around the putative QTL and a forward stepwise method to select genetic cofactors from the whole genome. A genome-wide Fisher test significance threshold was estimated trait by trait for each cross by the re-sampling method and permutation of the trait data (1,000 iterations) according to Churchill and Doerge (1994). F threshold values were very similar whatever the cross or the trait (data not shown) and averaged 8.6 for the 4% risk α within-family analysis. The QTL search was performed based on this F threshold of 8.6 (or LOD threshold of 3.7). The confidence region of a significant QTL (of the type LOD − x) was defined as the chromosome segment corresponding to a 1 LOD unit decrease from the LOD max (Van Ooijen 1992). The contribution of a QTL to trait phenotypic variance was estimated by the R 2 coefficient (percentage of the explained phenotypic variance). At any given QTL, the sum of the two QTL allelic effects of each parent was null by constraint of the model.

Across-family model

This model was a generalised linear regression model. The approach is similar to half-sib analyses proposed by Knott et al. (1996) and later extended to full-sib analyses by Van Kaam et al. (1998). It assumed the same locations of QTLs and genetic cofactors for all crosses. The within-family residual variances were assumed to be equal. The 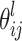Inline graphic allelic effects of a QTL at a locus l were assumed to be independent of the cross. This implied that additive allelic effects depended only on the parents. The model was made estimable for all the QTL allelic effects by generalising the constraints applied to the within-family model, i.e., the sum of the allelic effects at a given QTL were fixed to zero for each parent. The across-family model was applied using the genotype probabilities previously computed and the Sh-corrected data for each cross. Iterative QTL mapping (iQTLm) was the scan method, as it was for the within-family model. At each position l of a QTL, a Fisher test was performed under the null hypothesis of all parameters indexed to l. A genome-wide Fisher test significance threshold was estimated trait by trait by the re-sampling method and permutation of the trait data (1,000 iterations) according to Churchill and Doerge (1994), which was adapted to the multiple cross design by limiting permutations of the trait data to within-family permutations. The average significant F threshold value was 4.5 at the genome-wide global risk α of 16%. The QTL search was performed based on this F threshold of 4.5 (or LOD threshold of 3.9) with a forward cofactor selection threshold of 4.0. The model parameters were estimated for each significant QTL (position, confidence region, R 2, effects).

Results

Characterisation of individual phenotypic traits

No significant deviation was found from the 1:1 segregation ratio expected within each cross for the Sh major gene. No values deviated significantly from a normal distribution (P > 0.05): the distribution was mono-modal and symmetric with no out of norm values (data not shown). The ANOVA analysis of the phenotypic data showed that no or negligible interaction existed between replications and the other factors of the experimental design (data not shown). At the 1% limit, no vegetative trait depended on the dura or tenera variety of the palm. All in all, there was no significant correlation between the individual vegetative traits and the yield traits (data not shown). Only one strong correlation existed between the vegetative traits, between the mature frond petiole width (P_W) and thickness (P_T). Correlations between production traits are given in Table 1, including the strong classic negative correlation between bunch number (Bn) and average bunch weight (aBwt). The phenotypic means and variances for the Sh-corrected traits in the factorial mating experiment are given in Table 2. Between-cross variances were relatively higher for bunch number, average bunch weight, fruit number, average fruit weight, iodine value, petiole width, and leaflet dimensions. Apart from the stem height and the oil/mesocarp percentage, all the means revealed a significant contrast for the multiple cross design.

Table 1.

Significant intra-correlations between the individual phenotypic traits of the oil palm production

graphic file with name 122_2010_1284_Tab1_HTML.jpg

Open in a new tab

Intra-correlations are those estimated on the individual phenotypic values from which were cut off the effects of the fixed factors of the ANOVA model II (replication, parent DELI, parent AFRICA, variety dura or tenera, etc)

Significant α correlation thresholds are 5% (*) and 1% (**)

Correlations above 0.5 are in bold

Table 2.

Individual phenotypic traits, coefficients of variation of crude data and off-springs phenotypic means corrected by the Sh major gene effect, estimated for each parent of the 2 × 2 complete factorial mating design

N Trait Acronym Coefficients of variation (%) Phenotypic means corrected by the Sh effect
2 × 2 factorial Intra-cross Inter-cross DELI parent AFRICA parent
1 Fruit variety Type dura tenera dura tenera dura tenera DA10D LM269D LM2T LM718T
Production
2 Average bunch number/palm/year at 3–5 years Bn3_5 22.2 21.1 2.5 2.5 12.8 13.3 27.3a 26.2b 29.2a 23.6b
3 Average bunch weight at 3–5 years (kg) Bwt3_5 30.6 30.0 2.5 2.7 23.3 23.3 5.1a 6.2b 5.0a 7.1b
4 Fresh fruit bunch yield/palm/year at 3–5 years (kg/palm/year) FFB3_5 20.1 19.1 2.9 2.9 8.3 6.6 136.2a 145.7b 143.1a 152.3b
5 Palm oil yield/palm/year at 3–5 years (ton/ha/year) PO3_5 24.8 22.4 4.1 3.0 9.1 11.6 4.0a 4.5b 4.3a 4.7b
6 Average bunch number/palm/year at 6–9 years Bn6_9 38.6 35.5 3.8 3.5 34.1 31.6 18.0a 12.4b 17.5a 11.7b
7 Average bunch weight at 6–9 years (kg) Bwt6_9 34.6 34.3 2.2 2.6 29.4 31.4 13.3a 18.1b 13.2a 20.7b
8 Fresh fruit bunch yield/palm/year at 6–9 years (kg/palm/year) FFB6_9 16.2 17.9 2.6 2.5 6.6 6.2 219.9a 196.7b 216.5a 215.2a
9 Palm oil yield/palm/year at 6–9 years (ton/ha/year) PO6_9 21.5 19.0 3.6 2.5 7.1 4.4 6.6a 6.2b 6.5a 6.8a
Bunch components
10 Average weight of the analysed bunch (kg) aBwt 35.3 40.3 3.7 4.4 28.9 34.2 18.0a 24.2b 17.4a 28.9b
11 Average number of spikelets per bunch Spikelets – – 2.4 2.6 – –
12 Average number of fruits per bunch Fn 35.1 34.0 3.7 3.6 26.0 25.6 1,388.2a 1,959.4b 1,390.8a 1,949.3b
13 Average weight of the fruit (g) Fwt 18.9 19.5 2.3 3.1 10.6 13.4 8.9a 8.6a 8.9a 10.8b
14 Fruit to bunch ratio (%) %FB 4.5 5.2 0.7 0.8 1.8 3.3 66.4a 68.0b 66.9a 69.4b
15 Pulp to fruit ratio (%) %PF 9.1 4.7 1.0 0.8 2.3 2.4 68.5a 68.9a 68.5a 69.9b
16 Palm oil to pulp ratio (%) %POP 6.7 5.3 1.1 1.1 1.4 0.6 56.4a 56.1a 55.1a 54.4a
17 Palm oil industrial extraction rate (%) IER 13.5 11.0 1.9 1.4 2.5 6.2 21.9a 22.6b 21.8a 22.9b
18 Iodine value (proportion of unsaturated fatty acids) I 9.7 4.1 0.7 0.7 3.0 2.9 54.5a 54.0a 55.0a 52.3b
19 Kernel to fruit ratio (%) %KF 16.8 19.9 2.4 3.2 8.1 5.9 9.8a 9.5a 10.5a 9.9b
Vegetative growth
20 Stem height (m) Ht 9.6 9.8 1.7 1.7 1.7 3.2 685.6a 684.1a 644.8a 660.8a
21 Average number of leaves per crown Leaf_n 18.1 16.8 3.2 3.3 7.1 7.7 33.8a 35.9b 34.1a 38.0b
22 Average length of the leaf L17 (cm) L17_L 7.0 5.9 1.1 1.2 2.3 1.5 636.1a 657.3b 647.3a 652.9a
23 Petiole average width of the leaf L17 (cm) P_W 14.9 9.8 1.4 1.4 7.3 7.4 9.3a 9.2a 8.9a 10.1b
24 Petiole average thickness of the leaf L17 (cm) P_T 9.5 8.3 1.6 1.7 2.8 2.4 4.7a 4.5b 4.6a 4.6a
25 Average number of leaflets per leaf L17 Lt_n 4.8 4.9 0.8 0.9 1.6 1.0 169.1a 171.7b 174.1a 172.9a
26 Leaflet average length of the leaf L17 (cm) Lt_L 8.9 9.4 1.3 1.3 8.3 8.6 107.9a 96.4b 96.2a 104.8b
27 Leaflet average width of the leaf L17 (cm) Lt_W 11.0 10.8 1.4 1.5 10.8 8.6 6.1a 6.8b 6.8a 6.0b
Open in a new tab

IER = 0.855 × %FB × %PF × %POP/10,000

The means are compared according to the Tukey’s test at the risk threshold α of 5%

The letter a or b indicates the significant identical or different means within each of the two genetic backgrounds DELI or AFRICA

SSR linkage maps of the multiple cross design

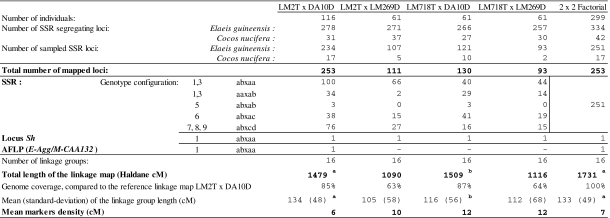
The integrated SSR map for LM2T × DA10D had 16 linkage groups (LG) and 253 loci, including 251 SSRs, the Sh locus and its marker E-Agg/M-CAA132 (Table 3). It measured 1,479 cM with an average marker density of 6 cM. The linkage groups spanned 134 cM on average with a range of 61–250 cM (LG 4). The marker locus E-Agg/M-CAA132 was mapped at 7.4 cM from the Sh locus at the end of LG 4. The most informative SSR loci, with three or four alleles, represented 47% of the mapped loci and had an average density of 32 cM on the genome. The regions with low marker density in LM2T × DA10D were also generally regions with low marker density on the other maps. These latter were elaborated with 111, 130 or 93 marker loci, including the Sh locus. Their average density was between 10 and 12 cM. The two maps involving the parent LM269D were shorter because some distal chromosomal portions were not represented. On an average, the four maps shared three common SSR loci on each LG (48 in all). Distances between common loci were found to be heterogeneous on some groups (nos. 7, 12, 15, 16). The unified consensus map of the 2 × 2 factorial design consisted of 253 loci (251 SSR, the Sh locus and its marker E-Agg/M-CAA132) like the SSR map of LM2T × DA10D (Fig. 2). In relation to the reference map of LM2T × DA10D (Billotte et al. 2005), the SSR consensus map measuring 1,731 cM revealed good genome coverage. The average marker density was 7 cM.

Table 3.

Segregating loci and establishment of the single and multiple cross SSR linkage maps of the 2 × 2 factorial mating design

graphic file with name 122_2010_1284_Tab3_HTML.jpg

Open in a new tab

aLocus mEgCIR3739 being excluded

bLocus mEgCIR3260 being excluded

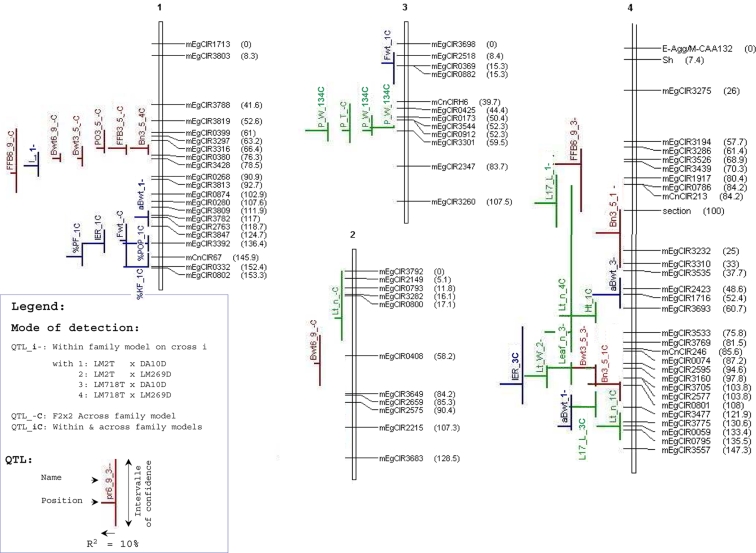
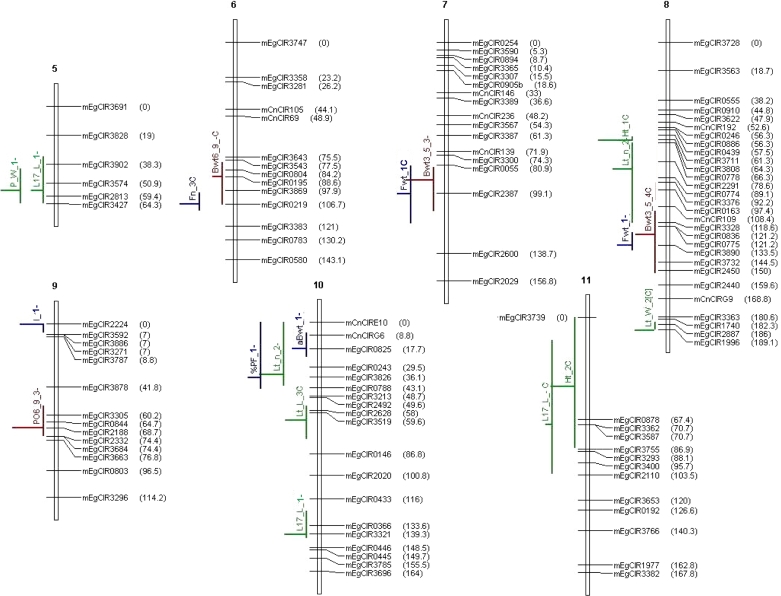
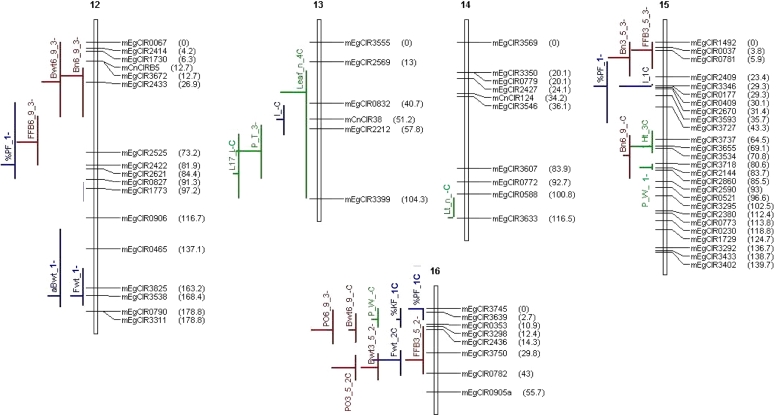
Fig. 2.

Fig. 2

Fig. 2

Fig. 2

Open in a new tab

Seventy-six QTLs of vegetative and production traits identified in four connected crosses on a 2 × 2 factorial mating design, at an α genome-wide risk of 4% per population by the iQTLm scan method using a within-family or an across-family model, under MCQTL Outbred (INRA, Toulouse, France). The QTLs are located on the Haldane’s consensus SSR linkage map of the 2 × 2 complete factorial design, constructed at LOD 3.0 and Recmax = 0.5. The linkage map encompasses 253 markers (251 SSRs, the Sh locus and its AFLP marker E-Agg/M-CAA132). The names and the positions (cM) of the markers are given on the right side of the linkage groups. mEgCIR: E. guineensis SSR marker, mCnCIR: Cocos nucifera SSR marker. The names, positions and confidence regions of the QTLs are given on the left side of the linkage groups. In red: are figured the QTLs of production traits; in blue: the QTLs of bunch quality traits, in green: the QTLs of vegetative traits

Effect of the Sh locus on quantitative phenotypic traits

The QTL analysis performed on the initial phenotypic data of the LM2T × DA10D cross showed that, except for the totally determined variety, eight yield traits were strongly influenced by the region of the Sh locus (Table 4). The Sh effect amounted to around 20% of the phenotypic variability in bunch number and total bunch weight for mature palms (Bn6_9, Bwt6_9). The Sh effect was very strong for four bunch components (Fwt, FB%, PF%, KF%) and for the resulting palm oil industrial extraction rate. The Sh effect reached 90% of the variation in the mesocarp/fruit percentage (PF%). The Sh locus did not have any significant effect on the yield traits of immature palms, on the average number of spikelets per bunch (spikelets), on the average number of fruits per bunch (F n), or on the palm oil/mesocarp percentage (POP%).

Table 4.

Effects of the Sh region on the LM2T × DA10D traits, estimated on the crude phenotypic traits

Trait Code Linkage group Positiona (cM) Closest marker locus F b value R 2 (%) Estimated effects
Genetic background QTLc
LM2T × DA10D LM2T DA10D
Production
 Average bunch number/palm/year at 3–5 years Bn3_5 – – – – – – – –
 Average bunch weight at 3–5 years (kg) Bwt3_5 – – – – – – – –
 Fresh fruit bunch yield/palm/year at 3–5 years (kg/palm/year) FFB3_5 – – – – – – – –
 Average bunch number/palm/year at 6–9 years Bn6_9 4 5.0 Sh 16.9 24.0 19.5 1.6 0.5
 Average bunch weight at 6-9 years (kg) Bwt6_9 – – – – – – – –
 Fresh fruit bunch yield/palm/year at 6–9 years (kg/palm/year) FFB6_9 4 5.0 Sh 12.0 18.0 219.8 15.7 2.0
Bunch components
 Average weight of the analysed bunch (kg) aBwt 4 5.0 Sh 9.1 15.4 15.5 1.2 0.0
 Average weight of the fruit (g) Fwt 4 7.4 Sh 72.0 59.5 8.9 1.3 0.1
 Fruit to bunch ratio (%) %FB 4 7.4 Sh 25.3 33.6 65.7 1.9 0.0
 Pulp to fruit ratio (%) %PF 4 7.4 Sh 439.5 89.8 67.0 10.8 0.8
 Palm oil industrial extraction rate (%) IER 4 12.4 Sh 56.2 52.9 20.7 2.5 0.7
 Kernel to fruit ratio (%) %KF 4 5.0 Sh 39.6 45.2 10.8 1.2 0.3
Open in a new tab

aFrom the first marker of the linkage group

b4% genome-wide F threshold = 8.6

cParent allelic effect (absolute value of the effect of one or the other QTL allele)

QTLs identified using within-family analyses

At a risk α of 4% at the genome level (8.6 ≤ F), 60 QTLs of 24 traits were identified in the four crosses (Table 5). The smallest number of QTLs per cross concerned the crosses with the parent LM269D. No QTL was detected for the fruits/bunch ratio or the average number of spikelets per bunch. Only one QTL was significantly present in three out of the four crosses (that for petiole width P_W), and all the other significant QTLs were specific to one or another of the crosses. In fact, in many cases, other crosses also showed a peak in the region of the QTL but this peak did not reach significance (data not shown). The QTLs had an average confidence region of 19 cM (±12 cM) when five particular regions exceeding 50 cM were excluded from the calculation. The minimum, average and maximum R 2 effects were 23, 31 and 45%, respectively. The gene pool effects estimated in each cross by the within-family model were coherent with the means per cross that were previously estimated (Supplementary material).

Table 5.

Synopsis of the QTL detected using the within-family or across-family models of MCQTL Outbred, at the α genome-wide risk of 4% per family

Identified QTL by the model(s) Code Single cross F2 × 2 Design Total
1 2 3 4 C
LM2T × DA10D LM2T × LM269D LM718T × DA10D LM718T × LM269D
Within-family model only i- 15 4 13 0 – 32
Within-family and across models iC 13 5 5(1) 5(1) (28) 28
Across model only -C – – – – 16 16
Total 28 9 18 (1) 5 (1) 44 76
Percentage 37% 12% 24% (+1%) 7% (+1%)
79% 21% (+37%) 100%
Open in a new tab

The 4% genome-wide F threshold is 8.6 for the within-family model, 4.5 for the across-family model

Within brackets (): QTL already detected on another single cross

QTLs identified using the across-family model

At a global risk of 16% at the genome level (4.5 ≤ F), i.e., 4% per cross, 44 QTLs were detected by the across-family model, of which 16 QTLs had not yet been identified by the within-family analyses (Table 5). The QTLs had an average confidence region of 22 cM (±14 cM) when four particular regions exceeding 50 cM were excluded from the calculation. The minimum, average and maximum R 2 effects were 6, 10 and 24%, respectively. Although their estimation was arbitrary by definition of the model with two opposite allelic effects for a given parent, the parent substitution allelic effects at the QTL were coherent with the amplitude of the within-cross phenotypic standard deviations, which were calculated per DELI or AFRICA parent (Supplementary material).

Comparison of the within-family and across-family models

At a risk α of 4% per cross at the genome level, a total of 76 QTLs were identified, of which 42% (32) were identified by the within-family analyses only and 21% (16) were identified by the across-family analysis only (Fig. 2; Table 5). The positions and confidence regions of the QTLs estimated by the two types of analyses were generally the same. When a QTL was detected by both analyses, its R 2 value as estimated by the across-family analysis was on an average 60% lower than that estimated by the within-family analyses (Supplementary material). Two types of QTLs were observed with respect to their F and R 2 values as estimated by the within-family model (data not shown): (1) QTLs whose F values at given R 2 effects were relatively high, and which were mostly detected by the across-family model; (2) QTLs whose F values were relatively low at given R 2 effects in a smaller number in a given cross, and which were often not identified by the across-family model. We shall not give details of the QTL effects as those estimations by MCQTL Outbred are currently being validated.

Discussion

Phenotypic characterisation of the genetic material

An additive genetic determinism model was evidenced from our data set irrespective of the quantitative phenotypic trait studied. This point aligns with similar conclusions from previous genetic studies of DELI × AFRICA material and of the species in general (Gascon and de Berchoux 1964; Noiret et al. 1966; Baudouin et al. 1989). QTL search algorithms based on a purely additive analysis model can be used. This point is important because to our knowledge there is no linear QTL search model to date that makes it possible to test and estimate dominance or epistasis effects in the simultaneous analysis of several crosses between heterozygous parents. However, epistasis may be important in some of the studied complex traits. If so, neglecting it may produce a bias in the effects and position estimations of the QTLs. Regrettably, epistatic interactions cannot be assessed with few individuals. The DELI or AFRICA parents had significant effects in general on the value of the off-springs individual traits. Therefore, it was reasonable to expect numerous QTLs specific to each of those gene pools (and each of the parents). However, the low within-cross variances may not have been enough for efficient QTL detection within a cross if the traits were not accurately observed or in cases with relatively large environmental effects (such as for the fruits/bunch ratio). The variance between full-sib families probably accounted for a fair share of the variance associated with the markers. The close or co-localised QTLs are in coherence with associated or pleiotropic genes affecting strongly correlated traits, such as the bunch number in immature and mature palms and the average bunch weight in immature and mature palms. Different genes would be involved in the three relatively independent bunch components, namely the palm oil/pulp percentage, the pulp/fruit percentage and the fruits/bunch percentage.

Efficacy of the multi-parent mapping design and QTL search models

Our search for QTLs by multi-parent linkage mapping proved to be efficient in oil palm given the relatively large number of QTLs identified when compared with those from a single bi-parental cross. The larger population size of the multi-parent system provides greater detection power for the QTLs of a given parent shared by several crosses. On the other hand, the multi-parent method does not alleviate (or only slightly alleviates) the strong consequences of the small number of individuals per cross in our system, which explains why QTLs could be identified by one model but not the other. Many QTLs that were identified by the within-family model were not detected by the across-family model. Chances are for those to be artifacts due to the small sample size and less dense linkage map. This is even clearer because the environmental effect has been eliminated. If not artifacts, they could be explained according to the theoretical simulations by Muranty (1996): the power of detection of a given QTL decreases with the rising number of parents for QTLs whose effects are small, especially when the family size is small. In addition, it is surprising that very few QTL were identified in more than one cross. More number of QTLs should be shared among crosses having common parents. Despite not significant, the maximum F values often observed in other crosses, at the same position than the QTL evidenced in a given cross, are a strong indication that QTLs are effectively shared but not significantly evidenced due to the small sample size again. Muranty (1996) and Melchinger et al. (1998) demonstrated also through simulation studies that, even with large numbers of individuals, the statistical power of QTL detection remains modest for QTLs with limited effects. If a QTL was detected in a given family, it in fact had little chance of also being detected in one or more other families. In our study, we started by estimating the parent marker phases separately in each of the crosses. This practical approach may have generated a few errors. False QTLs might undoubtedly have occurred but no more than a few. This point needs to be checked by using new statistical methods for phase estimation in multiple-cross data (such as that carried out by Wu et al. (2002) using a maximum likelihood method) and by repeating the detection experiment on an independent dataset.

We will not compare our QTL results with those obtained on a single cross by Rance et al. (2001) or Singh et al. (2009). Indeed, there is about no common markers between our respective genetic maps allowing to align linkage groups and to compare QTLs. A good strategy for our teams to do so would be to re-analyse our respective mapping populations using a common set of co-dominant markers, such like SSR markers, quite dense and well-distributed along the genome.

Validation and integrated use of QTL markers in oil palm

The critical question is whether the QTLs are real or artifacts. The QTLs identified by the two types of analyses were located coherently with respect to correlations between phenotypic traits. The QTLs of complex traits (oil yield, average bunch weight, oil extraction rate) were often associated with one of their components. The QTLs for strongly correlated traits were often logically co-localised (e.g., bunch number and average bunch weight). The QTLs of parameters measured at different ages were often found in the same zones. Some doubt remains about the validity of some QTLs detected by the within-family model only and those that displayed large confidence intervals. It will be essential to validate and estimate the existence and positions of the QTLs by our multi-parent linkage method on another larger sample of individuals. That work could be also undertaken as by Utz et al. (2000) using re-sampling and cross-checking methods, and by validating with independent samples. It is clear that large families should be used to better detect QTLs or quite simply to guarantee their reality (Xu 1998). Given the bulk of oil palm, planting 100 individuals per cross is already a restrictive maximum in the field. However, this could be considered in conventional genetic trials if efforts are made to integrate QTL detection and the use of QTL markers into classical breeding schemes. Specifically, genetic field testing could be easily adapted so as to systematically generate, validate and exploit QTL information. Based on our study, a way is by across-family analysis using genetic blocks of small factorial or diallele designs connected to each other by common parents. Melchinger et al. (2004) also recommended exploring other biometric and QTL mapping methods, including Bayesian (Bink et al. 2002) and identity-by-descent-based methods (Yi and Xu 2000). Lastly, the question remains how to estimate the true effect of a given QTL allele to be selected, since MCQTL Outbred only gives arbitrary values of substitution allelic effects. Here, a pragmatic approach could be to perform a variance analysis for the different genotypic classes of the QTL marker alleles either on the progeny themselves used for the QTL detection or better on independent sets of individuals issued from the selfing of the parents being selected. These genetic materials are currently available in commercial oil palm seed gardens. It will also be advisable to specify which research approach is the most promising for marker-assisted selection and has a high probability of being implemented and/or successful: What support will it provide for conventional selection schemes and improved seed production? What role should early selection play? What new neutral or gene markers need to be developed to ensure marker-assisted selection that is as efficient as possible?

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material (PDF 79 kb) (79KB, pdf)

Acknowledgments

Our sincere thanks are extended to the Commission of the European Communities for its financial backing of this research (EC project no. ICA4-CT-2001-10066-Directorate General of Research-INCO-Dev.). We are grateful to the SOCFINDO estate (Medan, Indonesia) and to the CNRA La Mé Station (Ivory Coast) for providing plant samples and phenotypic observations for this study. We are grateful to Dr H. Muranty and Pr. A. Gallais (INRA, France) for their theoretical advice on the concept of this study. We thank Dr. T. Schiex (INRA, France) for his help in using the CARTHAGENE software, as well as Dr. J. F. Rami (CIRAD, France). Finally, we thank the reviewers of this journal for their corrections and kind help to improve this article.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  1. Baudouin L. Utilisation des marqueurs moléculaires pour l’amélioration du palmier à huile. I. Marqueurs protéiques. Oléagineux. 1992;47:681–691. [Google Scholar]
  2. Baudouin L, Fondjo Kamga, Le Guen V. Etude génétique de la transmission et de l’expression des composantes de la production de régimes chez le palmier à huile. Oléagineux. 1989;44:77–86. [Google Scholar]
  3. Beirnaert A, Vanderweyen R (1941) Contribution à l’étude génétique et biométrique des variétés d’Elaeis guineensis Jacq. Publications de l’Institut National pour l’Etude Agronomique du Congo Belge. Série scientifique n° 27
  4. Billotte N, Risterucci AM, Barcelos E, Noyer JL, Amblard P, Baurens FC. Development, characterisation, and across-taxa utility of oil palm (Elaeis guineensis Jacq.) microsatellite markers. Genome. 2001;44:413–425. doi: 10.1139/gen-44-3-413. [DOI] [PubMed] [Google Scholar]
  5. Billotte N, Marseillac N, Risterucci AM, Adon B, Brottier P, Baurens FC, Singh R, Herrán A, Asmady BillotC, Amblard P, Durand-Gasselin T, Courtois B, Asmono D, Cheah SC, Rohde W, Ritter E, Charrier A. Microsatellite-based high density linkage map in oil palm (Elaeis guineensis Jacq.) Theor Appl Genet. 2005;110:754–765. doi: 10.1007/s00122-004-1901-8. [DOI] [PubMed] [Google Scholar]
  6. Bink MCAM, Uimari P, Sillanpaa MJ, Janss LLG, Jansen RC. Multiple QTL mapping in related plant populations via a pedigree-analysis approach. Theor Appl Genet. 2002;104:751–762. doi: 10.1007/s00122-001-0796-x. [DOI] [PubMed] [Google Scholar]
  7. Chakravarti IM, Laha RG, Roy J. Handbook of methods of applied statistics. New York: Wiley; 1967. pp. 392–394. [Google Scholar]
  8. Charcosset A, Mangin B, Moreau L, Combes L, Jourjon MF, Gallais A (2000) Heterosis in maize investigated using connected RIL populations. In: Quantitative genetics and breeding methods: the way ahead. Les colloques no. 96, INRA Editions, Paris, pp 89–98
  9. Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Comstock RE, Robinson HF, Harvey PH. A breeding procedure designed to make maximum use of both general and specific combining ability. Agron J. 1949;41:360–367. [Google Scholar]
  11. Elsen JM, Knott SA, Le Roy P, Haley CS. Comparison between some approximate maximum-likelihood methods for quantitative trait locus detection in progeny test designs. Theor Appl Genet. 1997;95:236–245. doi: 10.1007/s001220050554. [DOI] [Google Scholar]
  12. Elsen JM, Mangin B, Goffinet B, Boichard D, Le Roy P. Alternative models for QTL detection in livestock. I. General introduction. Genet Sel Evol. 1999;31:224–231. doi: 10.1186/1297-9686-31-3-213. [DOI] [Google Scholar]
  13. Gascon JP, de Berchoux C. Caractéristiques de la production d’Elaeis guineensis (Jacq.) de diverses origines et de leurs croisements. Application à la sélection du palmier à huile. Oléagineux. 1964;19:75–84. [Google Scholar]
  14. Grattapaglia D, Sederoff R. Genetic linkage maps of Eucalyptus grandis and Eucalyptus urophylla using a pseudo-test cross mapping strategy and RAPD markers. Genetics. 1994;137:1121–1137. doi: 10.1093/genetics/137.4.1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Haldane JBS. The combination of linkage values and the calculation of distance between the loci of linked factors. J Genet. 1919;8:299–309. doi: 10.1007/BF02983270. [DOI] [Google Scholar]
  16. Haley CS, Knott SA. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity. 1992;69:315–324. doi: 10.1038/hdy.1992.131. [DOI] [PubMed] [Google Scholar]
  17. Hartley CWS. The oil palm. 2. London: Longman; 1988. [Google Scholar]
  18. Jack PL, Mayes S. Use of molecular markers for oil palm breeding. II. Use of DNA markers (RFLPs) Oléagineux. 1993;48:1–8. [Google Scholar]
  19. Jones LH. Prospects for biotechnology in oil palm (Elaeis guineensis Jacq.) and coconut (Cocos nucifera) improvement. Biotechnol Genet Eng. 1989;7:281–296. [Google Scholar]
  20. Jourjon MJ, Jasson S, Marcel J, Ngom B, Mangin B. MCQTL: multi-allelic QTL mapping in multi-cross design. Bioinformatics. 2005;21:128–130. doi: 10.1093/bioinformatics/bth481. [DOI] [PubMed] [Google Scholar]
  21. Knott SA, Elsen JM, Haley CS. Methods for multiple marker mapping of quantitative trait loci in half-sib populations. Theor Appl Genet. 1996;93:71–80. doi: 10.1007/BF00225729. [DOI] [PubMed] [Google Scholar]
  22. Mayes S, James C, Horner SF, Jack PL, Corley RHV. The application of restriction fragment length polymorphism for the genetic fingerprinting of oil palm (E. guineensis Jacq.) Mol Breeding. 1996;2:175–180. doi: 10.1007/BF00441432. [DOI] [Google Scholar]
  23. Mayes S, Jack PL, Marshall DF, Corley RHV. Construction of a RFLP genetic linkage map for oil palm (Elaeis guineensis Jacq.) Genome. 1997;40:116–122. doi: 10.1139/g97-016. [DOI] [PubMed] [Google Scholar]
  24. Mayes S, Jack PL, Corley RHV. The use of molecular markers to investigate the genetic structure of an oil palm breeding programme. Heredity. 2000;85:288–293. doi: 10.1046/j.1365-2540.2000.00758.x. [DOI] [PubMed] [Google Scholar]
  25. Melchinger AE, Utz HF, Schön CC. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maizes reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics. 1998;149:383–403. doi: 10.1093/genetics/149.1.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Melchinger AE, Utz HF, Schön CC. QTL analyses of complex traits with cross validation, bootstrapping and other biometric methods. Euphytica. 2004;137:1–11. doi: 10.1023/B:EUPH.0000040498.48379.68. [DOI] [Google Scholar]
  27. Meunier J, Gascon JP. Le schéma général d’amélioration du palmier à huile à l’I.R.H.O. Oléagineux. 1972;27:1–12. [Google Scholar]
  28. Moretzsohn MC, Nunes CDM, Ferreira ME, Grattapaglia D. RAPD linkage mapping of the shell thickness locus in oil palm (Elaeis guineensis Jacq.) Theor Appl Genet. 2000;100:63–70. doi: 10.1007/s001220050009. [DOI] [Google Scholar]
  29. Muranty H. Power of tests for quantitative trait loci detection using full-sib families in different schemes. Heredity. 1996;76:156–165. doi: 10.1038/hdy.1996.23. [DOI] [Google Scholar]
  30. Noiret JM, Gascon JP, Bénard G. Contribution à l’étude de l’hérédité des caractéristiques de la qualité du régime et du fruit d’Elaeis guineensis Jacq. Oléagineux. 1966;21:343–349. [Google Scholar]
  31. Paterson AH, Deverna JW, Lanini B, Tanksley SD. Fine mapping of quantitative trait loci using selected overlapping recombinant chromosomes, in an interspecific cross of tomato. Genetics. 1990;124:735–742. doi: 10.1093/genetics/124.3.735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rance KA, Mayes S, Price Z, Jack PL, Corley RHV. Quantitative trait loci for yield components in oil palm (Elaeis guineensis Jacq.) Theor Appl Genet. 2001;103:1302–1310. doi: 10.1007/s122-001-8204-z. [DOI] [Google Scholar]
  33. Ritter E, Gebhardt C, Salamini F. Estimation of recombination frequencies and construction of RFLP linkage maps in plants from crosses between heterozygous parents. Genetics. 1990;224:645–654. doi: 10.1093/genetics/125.3.645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Rival A, Beule T, Barre P, Hamon S, Duval Y, Noirot M. Comparative flow cytometric estimation of nuclear DNA content in oil palm (Elaeis guineensis) tissue-culture and seedling derived plants. Plant Cell Rep. 1997;16:884–887. doi: 10.1007/s002990050339. [DOI] [PubMed] [Google Scholar]
  35. Schiex T, Gaspin C. Carthagene: Constructing and joining maximum likelihood genetic maps. Proc Int Conf Intell Syst Mol Biol. 1997;5:258–267. [PubMed] [Google Scholar]
  36. Schwendiman J, Pallares P, Amblard P. Premiers examens des accidents de fertilité chez l’hybride interspécifique de palmier à huile Elaeis melanococca × E. guineensis. Oléagineux. 1982;37:331–341. [Google Scholar]
  37. Siegel S, Tukey JW. A non parametric sum of rank procedure for relative spread in unpaired samples. J Am Stat Assoc. 1960;55:429–444. doi: 10.2307/2281906. [DOI] [Google Scholar]
  38. Singh R, Tan SG, Panandam JM, Rahman RA, Cheah SC. Identification of cDNA-RFLP markers and their use for molecular mapping in oil palm (Elaeis guineensis) AsPac J Mol Biol Biotechnol. 2008;16(3):53–63. [Google Scholar]
  39. Singh R, Tan SG, Panandam JM, Rahman RA, Ooi LCL, Low ETL, Sharma M, Jansen J, Cheah SC. Mapping quantitative trait loci (QTLs) for fatty acid composition in an interspecific cross of oil palm. BMC Plant Biol. 2009;9:114. doi: 10.1186/1471-2229-9-114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stam P. Construction of integrated genetic linkage maps by means of a new computer package: JOINMAP. Plant J. 1993;3:739–744. doi: 10.1111/j.1365-313X.1993.00739.x. [DOI] [Google Scholar]
  41. Utz HF, Melchinger AE, Schön CC. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics. 2000;154:1839–1849. [PMC free article] [PubMed] [Google Scholar]
  42. Van Kaam JBCHM, van Arendonk JAM, Groenen MAM, Bovenhuis H, Vereijken ALJ, Crooijmans RPMA, van der Poel JJ, Veenendaal A. Whole genome scan for quantitative trait loci affecting body weight in chickens using a three generation design. Livest Prod Sci. 1998;54:133–150. doi: 10.1016/S0301-6226(97)00171-1. [DOI] [Google Scholar]
  43. Van Ooijen JW. Accuracy of mapping quantitative trait loci in autogamous species. Theor Appl Genet. 1992;84:803–811. doi: 10.1007/BF00227388. [DOI] [PubMed] [Google Scholar]
  44. Van Ooijen JW, Voorrips RE. JoinMap® 3.0, Software for the calculation of genetic linkage maps. Wageningen, The Netherlands: Plant Research International; 2001. [Google Scholar]
  45. Wu R, Ma XC, Painter I, Zeng ZB. Simultaneous maximum likelihood estimation of linkage and linkage phases in outcrossing species. Theor Popul Biol. 2002;61:349–363. doi: 10.1006/tpbi.2002.1577. [DOI] [PubMed] [Google Scholar]
  46. Xu S. Mapping quantitative trait loci using multiple families of line crosses. Genetics. 1998;148(1):517–524. doi: 10.1093/genetics/148.1.517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yi N, Xu S. Bayesian mapping of quantitative trait loci under the identity-by-descent-based variance component model. Genetics. 2000;156:411–422. doi: 10.1093/genetics/156.1.411. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material (PDF 79 kb) (79KB, pdf)

Articles from TAG. Theoretical and Applied Genetics. Theoretische Und Angewandte Genetik are provided here courtesy of Springer

RESOURCES